Abstract
This research paper presents the Buckley-James Q-learning (BJ-Q) algorithm, a cutting-edge method designed to optimize personalized treatment strategies, especially in the presence of right censoring. We critically assess the algorithm’s effectiveness in improving patient outcomes and its resilience across various scenarios. Central to our approach is the innovative use of the survival time to impute the reward in Q-learning, employing the Buckley-James method for enhanced accuracy and reliability. Our findings highlight the significant potential of personalized treatment regimens and introduce the BJ-Q learning algorithm as a viable and promising approach. This work marks a substantial advancement in our comprehension of treatment dynamics and offers valuable insights for augmenting patient care in the ever-evolving clinical landscape.
Keywords:
Q-learning; reinforcement learning; precision medicine; Buckley-James Method; survival analysis MSC:
62N01
1. Introduction
In the dynamic landscape of modern healthcare, personalized treatment strategies [1,2] have emerged as a transformative paradigm, offering patients tailored interventions that maximize therapeutic outcomes. This becomes especially crucial when dealing with right-censored medical data, where the actual event times are not fully observed due to various factors, such as patients being lost to follow-up. This challenge has prompted the exploration of innovative solutions.
Survival analysis, a critical field in statistics and healthcare, focuses on understanding and modeling time-to-event data. In this context, data frequently involves the time it takes for a patient to experience a particular outcome or failure. However, real-world survival data often include censoring [3], indicating that the exact event time remains unknown for some observations. This complexity poses significant challenges for informed decision-making based on such data.
The Buckley-James (BJ) method, a well-established statistical technique [4,5,6], has played a pivotal role in the imputation of censored survival times using covariate information. This method offers a robust solution for dealing with incomplete or censored data, enabling researchers to derive meaningful inferences and predictions. Recognizing its favorable attributes, several researchers have explored extensions of the penalized BJ method for high-dimensional right-censored data and investigated their properties in large samples [7,8,9,10,11]. However, while the BJ method effectively handles data imputation, optimizing treatment decisions under severe right censoring remains a considerable challenge.
Reinforcement learning, specifically Q-Learning [12,13,14], has emerged as a powerful framework for decision-making within sequential and uncertain environments. Q-Learning finds extensive application in fields like robotics, gaming, and autonomous systems. It aims to learn optimal policies by maximizing cumulative rewards over time; while it shows promise in personalized treatment optimization, applying Q-Learning directly to censored survival data remains challenging due to the domain’s inherent complexities.
Numerous strategies have been proposed in the literature for Q-Learning in the context of survival outcomes. Goldberg and Kosorok [15] introduced a dynamic treatment regime estimator based on the Q-learning framework. To address issues related to varying treatment options and censoring, they suggested a modification of survival data to ensure uniform treatment stages without missing values, accompanied by the use of a standard Q-learning framework and inverse probability weighting to handle censoring. Similarly, Huang et al. [16] tackled a related problem using backward recursion, particularly in the context of recurrent disease clinical trials. In their setting, patients receive an initial treatment and may transition to salvage treatment in the case of treatment resistance or relapse. Simoneau et al. [17] extended the dynamic treatment regime estimator to non-censored outcomes, incorporating weighted least squares in censored time-to-event data scenarios. Additionally, Wahed and Thall [18] proposed a dynamic treatment regime estimator that uses a full likelihood specification. In a different approach, Xu et al. [19] developed a Bayesian alternative, incorporating a dependent Dirichlet process prior with a Gaussian process measure to model disease progression dynamics.
Building upon the foundational work of Goldberg and Kosorok [15], this study introduces an innovative approach to Q-Learning. Instead of relying on inverse probability weighting to address censoring, we propose a novel fusion of the Buckley-James method with Q-Learning. This integration has the transformative potential to reshape decision-making across diverse domains, with a particular focus on healthcare. By harnessing the imputed data generated by the Buckley-James method, we empower a Q-Learning agent to optimize treatment strategies.
In this exploration of BJ-Q Learning, we delve into the harmonious integration of these two methodologies and the collaborative approach to address the distinctive challenges posed by censored survival data. This integration empowers decision-makers to optimize treatments, promising improved outcomes for both individuals and populations and providing valuable insights into the future of personalized, data-driven decision-making within the realm of survival analysis. The article is structured as follows: In Section 2, we delve into reinforcement learning and Q-Learning. Section 3 is dedicated to discussing the Buckley-James method and introducing the BJ-Q Learning algorithm. Section 4 covers the generation of synthetic patient datasets and the construction of a comprehensive simulation study. Finally, Section 5 offers a discussion of the findings and implications.
2. Reinforcement Learning and Q-Learning
Reinforcement learning (RL) is a machine learning paradigm that focuses on learning to make sequential decisions in order to maximize cumulative rewards. Q-learning [12,13,14] is a widely used RL algorithm that aims to find an optimal policy for an agent interacting with an environment.
Within the realm of long-term patient care, the application of reinforcement learning can be described as follows. Each patient’s journey involves distinct clinical decision points throughout their treatment. At these pivotal moments, a range of actions, such as treatments, is taken, and the patient’s current state is documented. In return, the patient receives a random numerical reward.
In a more formal context, consider a complex multistage decision problem with T decision points. Here, represents the patient’s random state at stage t, where t spans from 1 to . Furthermore, we create to capture the vector encompassing all states up to and including stage t. Similarly, signifies the action chosen at stage t, and is the vector comprising all actions taken up to and including stage t. We employ lowercase letters to denote specific instances of these random variables and vectors. The random reward, denoted as , hinges on an elusive, time-dependent deterministic function that depends on all states up to stage and all prior actions up to stage t. A trajectory, in this context, can be conceived as an instantiation of the tuple . It is paramount to highlight that we refrain from making any assumptions regarding the problem’s Markovian nature. In the medical context, a trajectory represents a comprehensive record of patient attributes at different decision points, the treatments administered, and the corresponding medical outcomes, all expressed in numerical terms.
Moving forward, a policy, or dynamic treatment regime, is framed as a collection of decision rules. Formally, a policy is delineated as a sequence of deterministic decision rules, represented as . For any given pair , the outcome of the t-th decision rule, , denotes the action to be undertaken. Our overarching aim is to identify a policy that maximizes the expected cumulative reward. The crux of this quest is captured by the Bellman Equation [20], characterizing the optimal policy as one adhering to the following recursive relationship:
In this equation, the value function is coined as the expected cumulative reward from stage to the final stage T. This takes into account the history up to stage , denoted as , and the utilization of the optimal policy from that point onward.
The pursuit of a policy that leads to a high expected cumulative reward is the central objective in reinforcement learning. One straightforward approach involves learning transition distribution functions and the reward function using observed trajectories, followed by the recursive solution of the Bellman equation. However, this approach proves to be inefficient, both in terms of computational and memory requirements. In the subsequent section, we introduce the Q-learning algorithm, which offers a more memory-efficient and computationally streamlined alternative.
Q-learning, as introduced by Watkins and Dayan [12], stands as a pivotal algorithm for tackling reinforcement learning problems. Q-learning leverages a backward recursion strategy to compute the Bellman equation without the necessity of complete knowledge about the process’s dynamics. To provide a more formal perspective, we express the time-dependent optimal Q-function, as defined by Goldberg and Kosorok [15], in the following manner:
It is noteworthy that , which implies that
In order to estimate the optimal policy, a backward estimation of Q-functions is conducted across time steps . This yields a sequence of estimators, denoted as The estimated policy is given by
3. Q-Learning with Buckley-James Method
In medical decision-making and treatment optimization, the ultimate objective is to design a reward system that encourages the selection of optimal treatment policies. This typically involves quantifying the effectiveness of a treatment policy by maximizing the cumulative survival time of patients under that policy. Ideally, the reward should directly reflect the sum of survival times, providing an intuitive measure of treatment success. However, a significant obstacle often arises in real-world medical studies—censoring. Censoring occurs when complete information about patient outcomes, especially survival times, is unavailable. It can result from patients being lost to follow-up, withdrawing from the study, or events not occurring within the observation period. This issue presents a major challenge for Q-learning, a popular reinforcement learning approach, as it traditionally relies on complete outcome information to assign rewards.
In the domain of medical decision-making and reinforcement learning, one of the key challenges is the presence of censoring, which obscures the true survival times of patients. Censoring occurs when the exact event times are not fully observed, making it difficult to evaluate the effectiveness of different treatment policies. To address this challenge, we turn to the Buckley-James (BJ) method [4,5,6], a statistical technique commonly used in medical decision-making under censored data.
The core concept behind the BJ method is to impute or estimate missing or censored survival times based on the available data and the statistical characteristics of the patient population. Specifically, for patients with partially censored survival times, the BJ method provides imputed survival times. These imputed survival times are a blend of the known information from the data and statistical estimation methods. In the context of reinforcement learning, these imputed survival times serve as if they were actual observed survival times.
Now, how does this concept tie into the formulation of a reward for reinforcement learning? To evaluate different treatment policies, we need a metric to measure their performance. The reward is defined as the cumulative sum of imputed survival times over a patient’s trajectory under a particular treatment policy. Mathematically, the reward is calculated as
Here, represents the imputed survival time for stage t. This cumulative sum of imputed survival times serves as the reward, allowing us to assess the performance of different treatment policies while considering both observed and imputed survival times.
3.1. Buckley-James Method for Stage T
Moving on to the Buckley-James method specific to stage t [4,5,6], let us outline the methodology. We begin with a random sample of n subjects, each with their respective (possibly transformed) failure time and censoring time for stage t. Additionally, represents the p-dimensional vector of bounded covariates for stage t. It is assumed that and are conditionally independent given . Under right censoring, observed data for stage t consist of , where represents the observed event time, and is an indicator function.
To model the relationship between covariates and event times for stage t, a semiparametric accelerated failure time (AFT) model is used. It takes the form
Here, is an unknown p-dimensional vector of regression parameters for stage t, and is an independent and identically distributed random error variable following an unknown common distribution function .
Traditional least-squares methods are inadequate in the presence of right censoring due to incomplete time-to-event observations for stage t. To overcome this, the Buckley-James method for stage t replaces the incomplete with its conditional expectation given the available data, which can be expressed as
Approximating this formulation leads to the following expression for stage t:
Here, represents the Kaplan–Meier estimator of , based on the samples of residuals for stage t. It is calculated as
Obtaining paves the way for the resulting BJ estimator for stage t, which is found as the solution to the following equation:
However, solving this equation for stage t can be challenging due to its discontinuity and non-monotonicity in and the involvement of estimating . To overcome these complexities for stage t, a Nelder–Mead simplex algorithm is often employed to iteratively solve a modified estimating equation. This modified least-squares estimating equation for stage t is defined as
Solving Equation for with b fixed yields the following closed-form solution:
It has been demonstrated that if the initial estimator is consistent and asymptotically normal, the kth stage estimator also possesses similar asymptotic properties for any . Therefore, the final BJ estimator for stage t is defined as
The imputed survival response outcome for stage t is also defined as
3.2. BJ-Q Learning
We provide a more detailed description of the BJ-Q Learning algorithm with a specific focus on the Q-learning process and how it is integrated with the Buckley-James (BJ) method to handle censored survival data. The objective is to learn an optimal treatment policy by maximizing the expected total imputed survival reward over a patient’s trajectory. Algorithm 1 is outlined as follows:
| Algorithm 1 BJ-Q Learning Algorithm. |
|
This comprehensive algorithm combines Q-learning with the Buckley-James method, allowing it to effectively handle censored survival data and provide optimal treatment policies.
4. Simulation
In our comprehensive simulation study, we meticulously engineered synthetic patient datasets that faithfully replicate the intricate dynamics of medical treatment and the subsequent analysis of survival times. Our approach thoughtfully incorporates the notion of evolving treatment strategies across different stages, akin to the complex clinical scenarios examined in the pioneering work of Goldberg and Kosorok [15]. Specifically, we implement two-stage treatment strategies to capture the multifaceted nature of real-world medical interventions, where patients may undergo changes in their treatment plans as their conditions evolve.
4.1. Data Generation with Survival Time
In the first stage of our simulation, we created patient data with the following attributes:
- Survival Time (1st Stage): The primary focus was on modeling survival time. We employed a formula to simulate patient survival times based on various patient-specific factors. The survival time was calculated using the following formula:where represents a random variable sampled from a normal distribution. The use of , , and instead of specific positive numerical values adds flexibility to the model, reflecting the real-world variability in medical outcomes.
- Treatment Assignment: To create diversity within the dataset, we assigned patients to one of three distinct treatment groups with specific characteristics:
- -
- Treatment A (Aggressive Treatment): Patients in this group typically exhibit a large tumor size, high severity, and are assigned to simulate an aggressive treatment approach.
- -
- Treatment B (Mild Treatment): Patients in this group are characterized by a moderate tumor size, medium severity, and receive a milder treatment option.
- -
- Placebo (Treatment P): Patients in this group have a small tumor size, low severity, and are assigned to a placebo treatment group.
These assignments were made in accordance with predefined proportions: 16% of patients received Treatment A, 68% received Treatment B, and the remaining 16% received the placebo. - Tumor Size and Severity: We assigned unique values to tumor size and disease severity for each treatment group to mimic real-world scenarios:
- -
- “A” (Aggressive Treatment): Large tumor size, high severity.
- -
- “B” (Mild Treatment): Moderate tumor size, medium severity.
- -
- “P” (Placebo): Small tumor size, low severity.
- Survival Months Reward (ignoring censoring): We calculate baseline survival months based on patient characteristics and introduce treatment-specific adjustments according to the following equations:
- If a patient has a large tumor size () and high severity (), treatment A leads to prolonged survival compared to treatment B and the placebo:where is set to a positive integer.
- If a patient has a moderate tumor size () and medium severity (), treatment B results in an extended survival period compared to treatment A and the placebo:where is set to a positive integer.
- If a patient has a small tumor size () and low severity (), the placebo treatment yields a longer survival duration than treatment A and B:
The second stage of our data generation process aimed to create a baseline dataset without introducing any censoring, as well as datasets with varying levels of censoring. This stage was crucial for comparison with scenarios involving censoring and accounted for treatment transitions.
- Treatment Assignment in Stage 2: We introduced transitions between treatments for patients moving from the first stage to the second stage:
- -
- Half of the patients who received Treatment A in the first stage retained Treatment A in the second stage, while the other half received Treatment B.
- -
- Similarly, half of the patients who received Treatment B in the first stage retained Treatment B in the second stage, while the other half received the placebo (Treatment P).
- -
- All patients who initially received the placebo (Treatment P) continued to receive the placebo in the second stage.
- Tumor Size and Severity: We maintained the distinct distributions for tumor size and disease severity across the three treatment groups to retain the realism of the data.
- Survival Time Calculation (2nd Stage): Survival times in this stage were generated following the same formula as in stage 1 but without the introduction of censoring, serving as a baseline. We also considered two scenarios with censoring according to the following equations:
- Thirty Percent Censoring: In this scenario, we introduced censoring by generating censoring times from a uniform distribution , where and are chosen values that result in 30 percent of the data being censored.
- Fifty Percent Censoring: Similarly, in this scenario, we introduced censoring with 50 percent of the data being censored, again generating censoring times from .
4.2. BJ-Q Learning and Optimal Policy Estimation
In the third stage of our study, we applied the BJ-Q learning algorithm, a reinforcement learning technique, to learn the optimal treatment policy for each patient and subsequently calculated the expected survival times under these optimal policies.
- BJ-Q Learning: In contrast to the conventional Q-learning method, we adopted the Buckley-James Q (BJ-Q) learning algorithm, as described in Algorithm 1. Given the presence of censoring in the second stage, with both 30 percent and 50 percent censoring, we adopted a two-step approach. First, we implemented the Buckley-James method, as outlined in Section 3.1, to address the censoring issue. Subsequently, we applied the Q-learning algorithm.
- Optimal Policy Estimation: Following the application of BJ-Q learning, we derived the optimal treatment policy for each patient. This policy specified the most suitable treatment choices, with a unique combination denoted as “AA,” “AB,” “BB,” “BP,” or “PP,” signifying the treatment selections for both the first and second stages. The policy recommendations were tailored to each patient’s specific attributes, ensuring that patients with more severe conditions, for example, were directed towards appropriate treatments. This dual-letter notation delineated the treatment for the first stage (first letter) and the treatment for the second stage (second letter), offering a comprehensive and personalized approach to patient care.
- Survival Time with Combined Treatment: With the BJ-Q learning-based optimal policy in place for each patient, we calculated the survival time for each individual. This involved simulating survival times under their respective optimal treatments. The survival time estimation was performed considering the same formula as in the first and second stages, taking into account factors like tumor size, severity, and random noise. The resulting expected survival times provided valuable insights into the potential outcomes under personalized treatment decisions.
Our study aimed to assess the effectiveness of personalized treatment policies in improving patient outcomes. The estimated expected survival times under these optimized policies allowed us to evaluate the potential benefits of tailoring treatments to individual patient characteristics using the BJ-Q learning algorithm. Furthermore, we conducted a comprehensive analysis by employing boxplots across various sample sizes n and under different levels of censoring rates. This allowed us to gain insights into the robustness and generalizability of the personalized treatment approach, providing a more holistic understanding of its impact on patient survival.
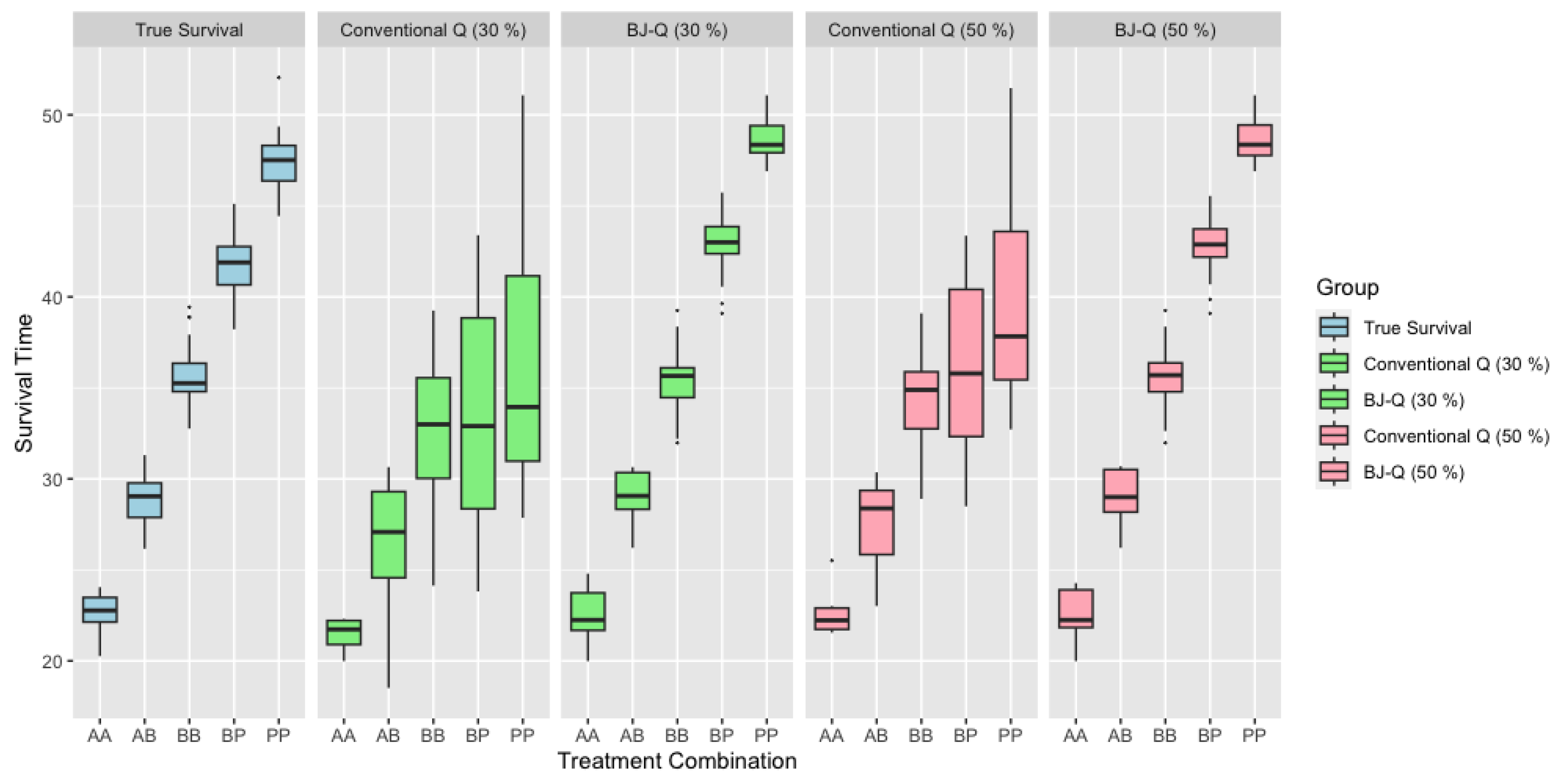
In Figure 1, we provide a detailed comparison of survival times for each treatment combination in scenarios where the sample size n is relatively small. The first boxplot in the figure showcases the actual, uncensored survival times. In the second and fourth boxplots, we depict scenarios with 30% and 50% censoring, respectively, in the survival data, without any adjustment for censoring. Conversely, the third and fifth boxplots show the results when we have applied the Buckley-James method to adjust for censoring. Notably, the third boxplot corresponds to BJ-Q (30%) and the fifth to BJ-Q (50%). Upon close examination, we can discern that the distributions of the boxplots for each treatment combination in the adjusted scenarios, particularly under BJ-Q (30%) and BJ-Q (50%), exhibit remarkable similarity. This consistency suggests the robustness of the personalized treatment approach implemented with the BJ-Q learning algorithm in the face of varying levels of censoring.
Figure 1.
Survival Time across different treatments with under 30% and 50% right censoring when .
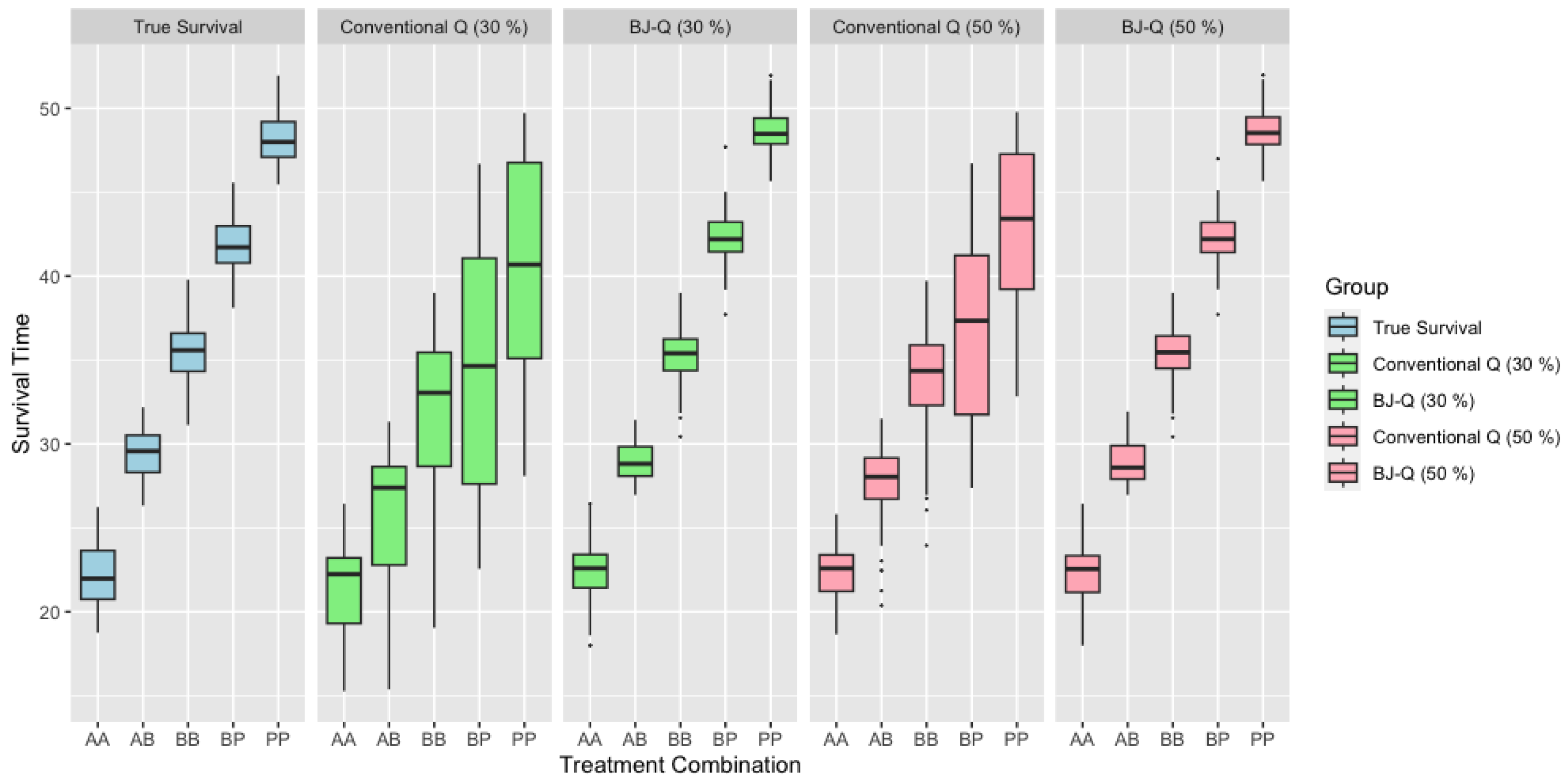
When considering scenarios with medium sample sizes, as illustrated in Figure 2, we can observe similar patterns and trends in the survival time comparisons. These figures provide a comprehensive view of survival times for various treatment combinations under different sample size conditions. The patterns seen in these larger sample sizes mirror the findings from the smaller sample size scenario, suggesting consistent outcomes across a range of sample sizes. Such uniformity reinforces the robustness of the personalized treatment approach as implemented with the BJ-Q learning algorithm, further substantiating its potential to optimize patient survival in real-world medical settings.
Figure 2.
Survival time across different treatments with under 30% and 50% right censoring when .
Table 1 and Table 2 offer an extensive comparative analysis of survival times across a spectrum of treatment groups, each delineated by distinct censoring scenarios, under and , respectively. The data for each group are organized systematically, with summary statistics calculated for various treatment codes: ‘AA’, ‘AB’, ‘BB’, ‘BP’, and ‘PP’. The summary statistics encompass several measures: The mean represents the arithmetic average of survival times, which sets a central point for the distribution within each treatment group. The standard deviation (SD) assesses the spread of survival times around the mean, reflecting the variability across the treatment groups. The median is the value separating the higher half from the lower half of the survival time data, serving as a resistant measure of central tendency that is less influenced by extreme values. The interquartile range (IQR) captures the spread of the central 50% of the data, providing insight into the data distribution’s variability. Finally, the first quartile (Q1) and third quartile (Q3) mark the 25th and 75th percentiles, respectively, offering further detail on the data distribution by identifying the range of the lower and upper quarters of the dataset.

Table 1.
Summary statistics for different groups under different methods under .

Table 2.
Summary statistics for different groups under different methods under .
Upon a detailed review of Table 1 and Table 2, it becomes evident that the adaptive Buckley-James Q-learning approach (BJ-Q learning) aligns more closely with the actual survival group in terms of critical statistical metrics like the mean, median, Q1 (first quartile), and Q3 (third quartile) compared to the traditional Q-learning method. Moreover, the adaptive BJ-Q learning method exhibits a lower standard deviation (SD), suggesting greater consistency in its survival time predictions. This reduced variability and dispersion in the survival estimates provided by the adaptive BJ-Q learning algorithm indicate its superior reliability, especially in conditions marked by right censoring. Consequently, the adaptive BJ-Q learning algorithm is recommended for application in such settings, owing to its enhanced robustness.
5. Discussion
The development of the BJ-Q learning algorithm signifies a pivotal advancement in the application of predictive analytics in healthcare. This algorithm is not limited to enhancing survival predictions and optimizing treatment protocols; it also holds potential for improving resource distribution, clinical trial design, and the evaluation of healthcare cost efficiency. The ability of the BJ-Q learning algorithm to optimize patient care while efficiently utilizing healthcare resources illustrates its critical role in advancing personalized medicine.
Nonetheless, a significant limitation of this study is its exclusive reliance on simulated data for algorithm validation. These simulations were carefully designed to emulate real-world scenarios of right censoring, providing evidence of the algorithm’s utility. However, the absence of empirical validation with actual clinical datasets introduces a degree of uncertainty regarding its real-world effectiveness and operational performance in healthcare settings.
To summarize, the BJ-Q learning algorithm marks a substantial leap forward in personalized healthcare. It adeptly addresses the challenges of censoring and furnishes customized treatment recommendations, heralding a new era in patient care. Its adaptability to different data scales and robustness across varied conditions highlight its potential as a valuable asset for healthcare practitioners and researchers. Future endeavors to apply and refine BJ-Q learning within real clinical contexts are essential for harnessing its full potential to revolutionize healthcare decision-making and improve patient outcomes.
Author Contributions
Conceptualization, J.L. and J.-M.K.; methodology, J.L. and J.-M.K.; software, J.L.; validation, J.L. and J.-M.K.; writing—original draft preparation, J.L.; writing—review and editing, J.L.; visualization, J.L.; supervision, J.-M.K.; project administration, J.-M.K.; funding acquisition, J.-M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Date are generated within the article.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Carini, C.; Menon, S.M.; Chang, M. Clinical and Statistical Considerations in Personalized Medicine; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Kosorok, M.R.; Moodie, E.E. Adaptive Treatment Strategies in Practice: Planning Trials and Analyzing Data for Personalized Medicine; SIAM: Philadelphia, PA, USA, 2015. [Google Scholar]
- Leung, K.M.; Elashoff, R.M.; Afifi, A.A. Censoring issues in survival analysis. Annu. Rev. Public Health 1997, 18, 83–104. [Google Scholar] [CrossRef] [PubMed]
- Buckley, J.; James, I. Linear regression with censored data. Biometrika 1979, 66, 429–436. [Google Scholar] [CrossRef]
- Lai, T.L.; Ying, Z. Large sample theory of a modified Buckley-James estimator for regression analysis with censored data. Ann. Stat. 1991, 19, 1370–1402. [Google Scholar] [CrossRef]
- Jin, Z.; Lin, D.; Ying, Z. On least-squares regression with censored data. Biometrika 2006, 93, 147–161. [Google Scholar] [CrossRef]
- Johnson, B.A.; Lin, D.Y.; Zeng, D. Penalized Estimating Functions and Variable Selection in Semiparametric Regression Models. J. Am. Stat. Assoc. 2008, 103, 672–680. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Nan, B.; Zhu, J.; Beer, D.G. Doubly Penalized Buckley-James Method for Survival Data with High-Dimensional Covariates. Biometrics 2008, 64, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Johnson, B.A. On lasso for censored data. Electron. J. Stat. 2009, 3, 485–506. [Google Scholar] [CrossRef]
- Li, Y.; Dicker, L.; Zhao, S. The Dantzig Selector for Censored Linear Regression Models. Stat. Sin. 2014, 24, 251–268. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Choi, T.; Choi, S. Censored broken adaptive ridge regression in high-dimension. Comput. Stat. 2024; in press. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Hasselt, H. Double Q-learning. In Proceedings of the Advances in Neural Information Processing Systems 23 (NIPS 2010), Vancouver, BC, Canada, 6–9 December 2010; Volume 23. [Google Scholar]
- Lyu, L.; Cheng, Y.; Wahed, A.S. Imputation-based Q-learning for optimizing dynamic treatment regimes with right-censored survival outcome. Biometrics 2023, 79, 3676–3689. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, Y.; Kosorok, M.R. Q-learning with censored data. Ann. Stat. 2012, 40, 529. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Ning, J.; Wahed, A.S. Optimization of individualized dynamic treatment regimes for recurrent diseases. Stat. Med. 2014, 33, 2363–2378. [Google Scholar] [CrossRef] [PubMed]
- Simoneau, G.; Moodie, E.E.; Nijjar, J.S.; Platt, R.W.; the Scottish Early Rheumatoid Arthritis Inception Cohort Investigators. Estimating optimal dynamic treatment regimes with survival outcomes. J. Am. Stat. Assoc. 2020, 115, 1531–1539. [Google Scholar] [CrossRef]
- Wahed, A.S.; Thall, P.F. Evaluating joint effects of induction–salvage treatment regimes on overall survival in acute leukaemia. J. R. Stat. Soc. Ser. C Appl. Stat. 2013, 62, 67–83. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Müller, P.; Wahed, A.S.; Thall, P.F. Bayesian nonparametric estimation for dynamic treatment regimes with sequential transition times. J. Am. Stat. Assoc. 2016, 111, 921–950. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957; pp. 24–73. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).