Abstract
To test the relationships of stochastic dominance, this paper firstly proposes two new consistent K-S-type statistics based on a quantile rule. Then, we consider their asymptotic properties. We introduce the bootstrap method to calculate the p-values of our proposed tests and use the Monte Carlo method to compare the power of our proposed test with the DD test and the BD test. The simulations showed that our test performed better than these two tests. Finally, we applied our proposed tests to compare the visibility of four provinces in China and compared the effects with the DD test and BD test. The empirical results showed that the conclusions of our proposed method are more-consistent with the dominance relationships of the four provinces. For a given significance level, the results of our proposed test demonstrate that the visibility of Jiangxi province is the best. The next one is the visibility of Hubei province, which outperforms the visibility of Anhui province. The visibility of Hunan province is the poorest.
MSC:
62P20; 62E20; 62F40
1. Introduction
Lehmann [1] first introduced the stochastic dominance theory, which is a well-established theory and has been widely applied in economics and the finance area. It takes into account different types of preferences of decision-makers and mainly concentrates on the comparison of two populations or portfolios [2]. Based on the stochastic predominance theory, scholars have constructed many different types of statistics to test stochastic dominance. Referring to the literature of Zhu [3], the statistics for testing stochastic dominance can be divided into three categories. The first type is the Kolmogorov–Smirnov (K-S)-type statistics. McFadden [4] first adopted this type of statistic to test the first-order stochastic dominance. Barrett and Donald [5] extended the conclusions of McFadden [4] to higher-order scenarios and developed a consistency test based on the K-S-type statistic. Barrett et al. [6] applied the K-S-type test in Barrett and Donald [5] to test Lorenz dominance and derive some asymptotic properties and simulation results. Donald and Hsu [7] introduced the re-centering function into the calculation of critical values and, finally, established the K-S-type statistic, which improves the efficacy of the test. The second type is the t-type statistics, which was first proposed by Kaur et al. [8] to test the second-order stochastic dominance. Then, Anderson [9] constructed an improved t-statistic inspired by Pearson’s goodness-of-fit test and completed tests for the first-order, the second-order, and the third-order stochastic dominance. Furthermore, Davidson and Duclos [10] improved the t-statistic proposed by Kaur et al. [8] and extended it to the situation of dependent samples. Based on the tests proposed by Anderson [9] and Davidson and Duclos [10], Ledwina and Wyłupek [11] presented two new tests for stochastic ordering in a standard two-sample scheme. The third type is integral-type statistics, which were proposed and promoted by several scholars; see, for example, Deshpande and Singh [12], Eubank et al. [13], Schmid and Trede [14], Hall and Yatchew [15], and Lee et al. [16].
Since the calculation of integral-type statistics is too complicated, researchers often choose two other types of statistics to test the dominance relationships. Compared with the t-type statistics, the K-S-type statistics are applicable to all distributions and are highly robust. So, they are the most-widely used in stochastic dominance testing issues. Motivated by the work in Barrett and Donald [5], this paper proposes another consistent K-S-type test based on a quantile rule. To this end, the empirical quantile functions are utilized to construct the K-S-type statistics for the first-order stochastic dominance and the second-order stochastic dominance. Then, we investigate the asymptotic properties of the two proposed statistics. To calculate the p-values of the proposed tests, the bootstrap method is introduced. Besides, we apply the Monte Carlo method to obtain the rejection rates and compare the power performance of our K-S test with the Davidson and Duclos (DD) test and the Barrett and Donald (BD) test. These two tests were proposed by Davidson and Duclos [10] and Barrett and Donald [5], respectively. Finally, we apply our proposed tests to analyze the visibility data of four central provinces, namely Hunan, Hubei, Anhui, and Jiangxi provinces.
The rest of the present paper is organized as follows. Section 2 introduces the definitions of the first-order stochastic dominance and the second-order stochastic dominance. Then, the equivalent definitions based on quantile rules are given for these two stochastic dominance relationships. These two equivalent definitions are used to construct our test statistics. After expressing the null/alternative hypotheses for the first-order stochastic dominance and the second-order stochastic dominance, the test statistics are given in Section 3. We show the asymptotic properties of the proposed statistics in this section as well. To end Section 3, we exhibit how to calculate the p-values of the proposed tests employing the bootstrap method. Section 4 compares the power of our proposed test with the DD test and the BD test. The simulations show that our test performs better and is more robust than the DD test and the BD test. In Section 5, we applied our two tests to analyze the visibility data of four provinces in China. We found that the visibility of the four provinces can be correctly compared by our proposed test. But, the DD test and the BD test fail to do this work. For a given significance level , we see from our tests that the visibility of Jiangxi province is the best, while the visibility of Hunan province is the poorest. Finally, we conclude this paper in Section 6.
2. Definitions and Equivalent Properties
Stochastic dominance theory is based on the expected utility theory [17], which has a wide range of applications in measuring social welfare, poverty measurement, portfolio selection, and evaluation. In contrast to the expected utility theory, stochastic dominance theory does not require commanding the specific expression of the utility function; some relevant assumptions about the utility function are enough for researchers to compare two populations. This paper is concerned with the relationships of the first-order stochastic dominance and the second-order stochastic dominance. The first-order stochastic dominance is targeted at decision-makers with increasing utility functions. The second-order stochastic dominance is applicable to risk-averse decision-makers with increasing and concave utility functions. Formally, if u is a utility function and we let , , then we can give the definitions of these two stochastic dominance relationships as follows.
Definition 1
([18]). For two random variables X and Y, Y is said to stochastic dominate X with the first order, denoted by , if .
Definition 2
([19]). For two random variables X and Y, Y is said to stochastic dominate X with the second order, denoted by , if .
By Definitions 1 and 2, it is obvious that if . That is to say, the relationship of the first-degree stochastic dominance is stronger than the relationship of the second-degree stochastic dominance. For more details about the above two stochastic dominance relationships, readers can refer to Levy [20].
The main purpose of this paper is to test whether there is the first-order or the second-order stochastic dominance relationship between two populations. However, it is complicated to complete our purpose using the above two definitions since u is arbitrary in and . So, we introduce the following Theorem 1, which gives the equivalent definitions for the first-order and the second-order stochastic dominance relationships based on quantile functions.
Theorem 1
([21]). Let and be the quantile functions of X and Y, respectively:
- (i)
- if and only if .
- (ii)
- if and only if .
Here, , , and F and G are the cumulative distribution functions of X and Y, respectively.
Theorem 1 tells us that we can determine whether or not there is a stochastic dominance relationship between two populations by using the images of the quantile functions and their associated function curves, for example if X has the normal distribution and Y has the normal distribution . We draw the plots of the quantile functions of X and Y in Figure 1 for all . It can be seen from Figure 1 that the plot of the quantile function of Y always lies above that of X. This implies that by Theorem 1 (i). On the other hand, if X has the normal distribution with the quantile function , Y has the normal distribution with the quantile function . We draw the plots of and for all in Figure 2. It is obvious from Figure 2 that the plot of lies above that of for all , which implies by Theorem 1 (ii).
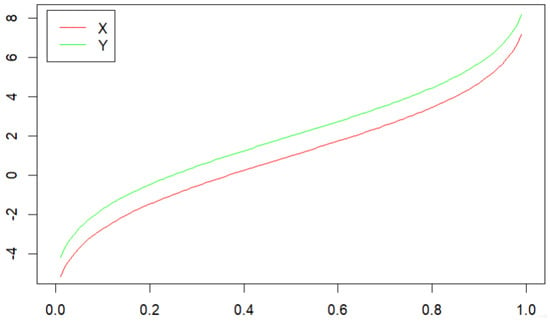
Figure 1.
The plots of and , where X has the normal distribution and Y has the normal distribution .
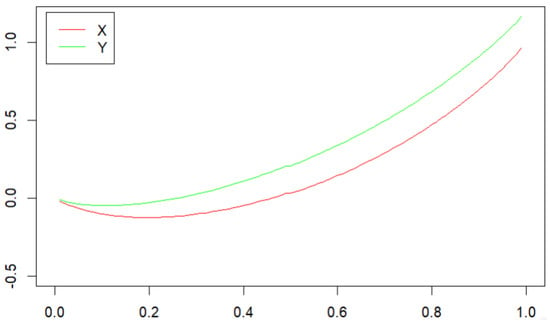
Figure 2.
The plots of and , where X has the normal distribution and Y has the normal distribution .
3. Test Statistics
To test whether there is a stochastic dominance relationship between X and Y, this section constructs two K-S-type test statistics based on the samples, and then, the asymptotic properties of the proposed statistics are investigated. According to Theorem 1, we first present the null hypothesis, the alternative hypothesis, and the corresponding test statistic for the first-order stochastic dominance relationship in Section 3.1.
3.1. Test Statistic for the First-Order Stochastic Dominance
Using Theorem 1 (i), whether Y stochastic dominates X with the first-order can be expressed by the following hypotheses:
If we accept the null hypothesis , then it means that we cannot reject Y stochastic dominating X with the first order, and if we reject the null hypothesis , it shows that we have a high degree of certainty that Y does not stochastic dominate X with the first order.
Based on the above hypotheses, we construct a K-S-type statistic as follows:
where
and are the estimators of the corresponding quantile functions. M and N are the sizes of two samples from X and Y, respectively. We will accept if and only if is big enough. Otherwise, we will reject the null hypothesis .
3.2. Test Statistic for the Second-Order Stochastic Dominance
Using Theorem 1 (ii), whether Y stochastic dominates X with the second order can be expressed by the following hypotheses:
If we accept the null hypothesis , then it means that we cannot reject Y stochastic dominating X with the second order, and if we reject the null hypothesis , it shows that we have a high degree of certainty that Y does not stochastic dominate X with the second order.
Based on the above hypotheses, we construct a K-S-type statistic as follows:
where
Similarly, we will accept the null hypothesis if and only if is big enough. Otherwise, we will reject the null hypothesis .
In this paper, we chose to utilize the empirical distribution to estimate . Denote the cumulative distribution functions of two mutually independent populations X and Y by and , respectively. The simple random samples from X and Y are and with sample sizes M and N, respectively. Then, for , the concrete forms of and are given, respectively, as follows:
where
and is the indicator function for the set A.
3.3. Asymptotic Properties
In this section, we will investigate the asymptotic properties of our proposed statistics. Firstly, we introduce some basic assumptions.
Assumption 1.
- (i)
- and have a common support , where is the bounded closed interval on R and .
- (ii)
- and are continuously differentiable on the interior of their supports with strictly positive derivatives and .
- (iii)
- and are simple random samples from X and Y, respectively. M and N satisfy
Assumption 1 (i) defines the cumulative distribution functions in a bounded closed interval that guarantees the values of the quantile functions are finite. Assumption 1 (ii) guarantees the existence of quantile functions and density functions of two populations. Assumption 1 (iii) makes assumptions about sampling independence and sample size to prevent the degeneration of the limiting distribution when the sample size is too large.
Under Assumption 1, the next step is to deduce the asymptotic distributions of our proposed K-S-type statistics. Since our proposed statistics are constructed based on the empirical distribution functions, we need a lemma for the quantile process, which can be found in Section 21 of Van der Vaart [22]. This lemma is shown as follows.
Lemma 1
([22]). Under the conditions of Assumption 1, when ,
where represents weak convergence and represents the Brownian Bridge process composed of F. Meanwhile, represents the Brownian Bridge process composed of G. They are two independent Brownian Bridge processes.
The first result in this lemma is related to the convergence of the quantile process. Its proof can be found in Corollary 21.5 in Van der Vaart [22]. The second result can be obtained based on the first result and the continuity of quantile functions by using the continuous mapping theorem.
From Lemma 1 and Slutsky’s theorem, it is not difficult to derive the following theorem.
Theorem 2.
Under the conditions of Assumption 1, when ,
where
Next, we investigate the asymptotic distributions of our proposed K-S-type statistics. Whether or not our proposed K-S-type statistics are degenerate depends on the null hypothesis. In the following Theorem 3, we will discuss the asymptotic distributions of our proposed K-S-type statistics under different situations.
Theorem 3.
Let
Under the conditions of Assumption 1, for , when :
- (i)
- If is true and , then
- (ii)
- If is true and , then
- (iii)
- If is not true, then
Proof.
Recall that is continuous on C if is a continuous function and C is a compact set. Based on this conclusion and noting that the support of is , we can easily conclude that both and are continuous functions. By Theorem 2 and the continuous mapping theorem, the following results are easily derived:
If , then there exists and , such that and . Thus, it is easily concluded that
and
if is true. This completes the proof of Theorem 3 (i).
If is true and , then there exists , such that and for all . According to Assumption 1 (iii), we can easily conclude that
and
Therefore, the proof of Theorem 3 (ii) is complete.
Referring to the proof of Theorem 3 (ii), we can easily obtain the opposite results of (ii) if is not true. Thus, the proof of Theorem 3 (iii) is complete. □
3.4. Bootstrap Method for Approximating p-Value
In Section 3.3, we discussed the asymptotic properties of our K-S-type statistics and proved that our proposed statistics have excellent properties such as asymptotic normality. In this section, we introduce the process of the bootstrap method to approximate the p-values of our tests. Shao and Tu [23] found that this method can improve the efficiency and robustness of the test. So, it is extensively applied to many statistical tests, especially in the situations where the distribution of the sample is unknown or the original sample needs to be enlarged.
Denote the sample sets from X and Y by , , respectively. We draw independent and identically distributed samples of sizes m and n from these two sets, then we can obtain the bootstrap samples and . Based on these two samples, we obtain the bootstrap estimators of and ( and ) as follows.
According to the above estimators, we derive the bootstrap statistic:
for testing , and
for testing . By Theorem 11 in Sergio and Salim [24], we can conclude the following theorem under Assumption 1.
Theorem 4.
Under Assumption 1, for , as ,
where
and represents the conditional probability under the bootstrap samples.
Theorem 4 indicates that the statistics constructed by the bootstrap method are also consistent if the sample size is large enough, which provides the theoretical foundation for the subsequent empirical analysis. Based on Theorems 3 and 4, we can calculate the p-values for our two tests as follows.
However, directly calculating the p-values by the above equations is impossible since we do not know the exact distributions of and under the null hypothesis, and therefore, we approximate the p-values utilizing the Monte Carlo method. We set the times of resampling as B, and the estimated statistic for each bootstrap sample is denoted as , then the p-values for our two tests can be approximated as follows.
For a given level of significance , if , then we reject the null hypothesis . Otherwise, there is no apparent evidence to reject it.
4. Monte Carlo Simulations
In this section, we conduct a Monte Carlo simulation to compare the performance of our proposed statistics (denoted by K-S) with the two statistics introduced by Davidson and Duclos [10] (denoted by DD) and Barrett and Donald [5] (denoted by BD), respectively. Let and be the observations drawn from the independent populations X and Y, respectively. In Section 4.1, we give a brief introduction of these two statistics.
4.1. DD Statistic and BD Statistic
4.1.1. DD Statistic
The DD test statistic is a modified version of the statistic in Kaur et al. [8]. It is exactly analogous to the t test statistics. The main superiority of the DD statistic is that it can make high-order dominance testing feasible. The concrete forms of the DD statistics for testing the first-order and second-order stochastic dominance are given as follows.
where
and
4.1.2. BD Statistic
The BD statistic is a typical K-S-type statistic. The concrete forms of the BD statistics for testing the first-order and second-order stochastic dominance are given as follows.
The definitions of and are the same as above. The main difference between our proposed statistics and the BD statistics is that the BD statistics are constructed based on the empirical distribution function, while our statistics are constructed based on the empirical quantile function. The simulations show that this change can have a good effect.
As suggested by Hansen [25], the grid point method is used to approximate the supremum of the statistics both in the BD test and our proposed test. The core of the grid point method is to divide the interval into small grids, then calculate the maximum values in each small grid and take the maximum value of these values as an approximation of the supremum. For example, if the interval is and the length of small grids is 0.01, then the set of grid points is . Compared with the BD statistics, we can control the length of the interval to 1 regardless of any distribution. This will promote the accuracy and efficiency of our simulations. In this paper, we set the length of each grid as 0.01.
4.2. Simulations
Next, we make a comparison of the powers of the DD test and BD test with our test by using the R language. To this end, we used the bootstrap method in Section 3.4 to obtain p-values of our tests. The method of obtaining the p-values of BD test is similar to ours. Besides, to approximate the supremum of the statistics, we applied the function gridSearch() in the Package NMOF to achieve it. For the approximated p-values of the DD test, we borrowed them from Bai et al. [26] and Bai et al. [27].
Based on the approximated p-values, we performed R-times Monte Carlo simulations to obtain the rejection rates. For each simulation, we assumed that X and Y are two normally distributed populations, i.e., and , and the following four different cases were considered in the process of the simulations.
Case 1: and . In this case, X and Y have the same distribution. The rejection rates ought to have a relative frequency that is close to the nominal significance level .
Case 2: and . In this case, it is easy to verify that and .
Case 3: and . In this case, we have , but we cannot say that .
Case 4: and . Both and should be rejected. The rejection rates of this case should converge to 1 as the sample size increases.
In each case, to balance the time and accuracy of the simulation results, the experimental replication, bootstrap replication, and sample size were selected as . To improve the speed and efficiency of the simulation, we exerted several functions in the Package Parallel to conduct parallel computing. The simulation results are listed in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6.

Table 1.
Rejection rates for testing FSD ().

Table 2.
Rejection rates for testing FSD ().

Table 3.
Rejection rates for testing FSD ().

Table 4.
Rejection rates for testing SSD ().

Table 5.
Rejection rates for testing SSD ().

Table 6.
Rejection rates for testing SSD ().
For Case 1, we can easily find from Table 1, Table 2 and Table 3 that the rejection rates of our K-S test are more robust than the DD test when and . As for , the rejection rates of our K-S test are a little higher than the nominal level when is smaller than 200. But, they decrease to 0.1 when the sample size increases. However, the fluctuations of the rejection rates of the DD test are still large when the sample size increases to 400. For the BD test, the fluctuations of their rejection rates are greater than our K-S test at any significance level.
For Case 2, we see from Table 1, Table 2 and Table 3 that the rejection rates of all tests equal approximately zero, as they are supposed to be. Moreover, the rejection rate of our K-S test and BD test of each sample size is closer to zero than the DD test. This means that our K-S test and the BD test outperform the DD test. Meanwhile, the performance of our proposed K-S test is not inferior to the BD test.
The rejection rates of Cases 3 and 4 are supposed to increase to 1 as increases. This can be easily seen from Table 1, Table 2 and Table 3. As the sample size gradually increased, all three tests demonstrated great power performance and were consistent with our expectations.
Then, we analyzed the simulation results of SSD experiments. From Table 4, Table 5 and Table 6, it is easily found that the rejection rates of our K-S test in Case 1 are more robust than the DD test and the BD test for all three nominal levels. In Case 2, when and , the rejection rates of our K-S test and the BD test decrease to zero rapidly and are lower than the DD test in almost every sample size. When , even the rejection rates of the DD test and the BD test decline to a lower level than our K-S test as reaches 200. As the sample size continues to expand, the rejection rates of the DD test demonstrate a remarkable rebound phenomenon. But, for our K-S test, the rejection rates drop to zero steadily. Meanwhile, the convergence rate is also faster than the BD test. Unlike the FSD experiment, the rejection rates in Case 3 converge to zero eventually. The rejection rates of three tests show a great performance in both Cases 3 and 4.
According to the above simulation results, we can conclude that three tests have different performances in Cases 1 and 2. Our K-S test performs better than the DD test and the BD test when the two distributions are identical. In Case 2, when the dominance relationship is , the performance of our K-S test and the BD test is better than the DD test. Moreover, when , we find that the speed of the rejection rate converging to zero in our K-S test is faster than that in the BD test when we test the SSD relationship in Case 2. In Cases 3 and 4, all three tests demonstrate great effects. Therefore, on the whole, our proposed K-S tests are better than the other two tests.
5. Empirical Analysis
In this section, we apply our K-S test to analyze the environmental monitoring data of four central provinces in China. The data were obtained from Douglas and Zhang [28]. This data set consists of 1.63 million observations and 11 variables. These observations were collected from numerous meteorological stations in 34 Chinese provinces. Several important environmental monitoring indicators such as temperature, visibility, wind speed, and precipitation are included in this data set. Douglas and Zhang [28] utilized a linear double-difference approach to investigate some environmental monitoring data and found that the air quality in the pilot areas has improved significantly after implementing the local emissions trading pilot policy in China. We selected the visibility data of Hunan, Hubei, Anhui, and Jiangxi provinces as our research objects. Visibility is an important indicator in environmental monitoring, which is defined as the maximum distance from which a person with normal vision can see the outline of a target under the prevailing weather. This indicator plays a very important role in monitoring transportation, border security, and air transport. Moreover, it can be used as an important indicator of air quality since it can reflect the degree of atmospheric pollution. As the four central provinces in China, Hunan, Hubei, Anhui, and Jiangxi are geographically adjacent and have little difference in regional development level. So, it is significant to compare the relevant data of these four provinces.
Firstly, to obtain a preliminary understanding of the first-order stochastic dominance relationship between the four provinces, we drew the plots of the estimated quantile functions based on the visibility data of the four provinces. The estimated quantile functions were calculated by Equation (1), and their plots are drawn in Figure 3. We easily see from Figure 3 that the plot of the estimated quantile function for the data from Jiangxi province is located above that of Anhui, Hubei, and Hunan provinces. This reveals that the visibility of Jiangxi province stochastic dominates the other three provinces with the first order. The plot of the estimated quantile function for the data from Hubei province crosses that of Anhui province many times. But, it is always above that of Hunan province. This means that the visibility of Hubei province stochastic dominates that of Hunan province with the first order.
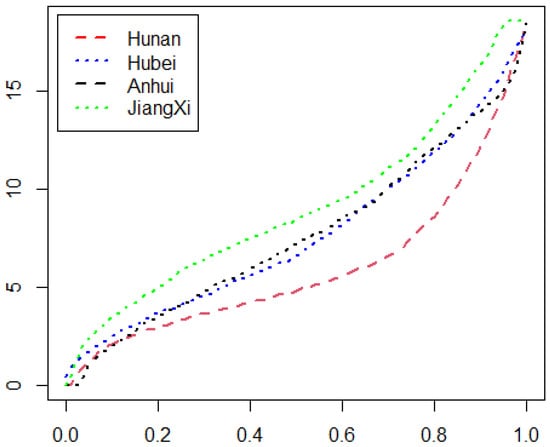
Figure 3.
The plots of the estimated quantile functions.
Then, we applied our proposed tests to analyze whether there is a stochastic dominance relationship or not between the visibility of the four provinces and compared the effects with the DD test and the BD test. To complete the bootstrap method, the size of the original sample was set as of the number of visibility data, and the times of resampling were set as . Table 7, Table 8 and Table 9 give the p-values for the tests of the first-order stochastic dominance relationship between the visibility of the four provinces.

Table 7.
The p-values of the K-S tests for the first-order stochastic dominance.

Table 8.
The p-values of the DD tests for the first-order stochastic dominance.

Table 9.
The p-values of the BD tests for the first-order stochastic dominance.
We discuss the results of our K-S tests first. For the given significance level , it can be seen from the last line of Table 7 that the visibility of Jiangxi province stochastic dominates that of the other three provinces with the first order. Meanwhile, the first number in the third line of Table 7 is . This means that the visibility of Hubei province stochastic dominates that of Hunan province with the first order. For other cases, the p-values are zero, which indicates we cannot accept that there are first-order stochastic dominance relationships between each other.
In Table 8, the first and the second numbers in the third line are 0.073 and 0.052, respectively. This means that, when the given significance level , the DD test gives a result that we should accept Anhui Hunan and Anhui Hubei. In fact, these two results are wrong since the estimated quantile functions of Anhui and Hubei have several intersections. Similar to the estimated quantile function of Anhui and Hunan, we see from Table 9 that the BD test gives a result of accepting Anhui Hunan, but it is wrong. By contrast, our K-S test always gives the right judgment.
Based on the visibility data of Jiangxi, Anhui, Hubei, and Hunan provinces, if we repeatedly calculate the values of by Equation (1) and draw the plots of for these four provinces in Figure 4, as can be seen, the second-order stochastic dominance relationships between provinces are more significant than the first-order ones. The plot related to Jiangxi province always lies above that of the other three provinces. This indicates the visibility data of Jiangxi province stochastic dominate those of other provinces with the second order. The related curves of Hubei and Anhui are also above Hunan.
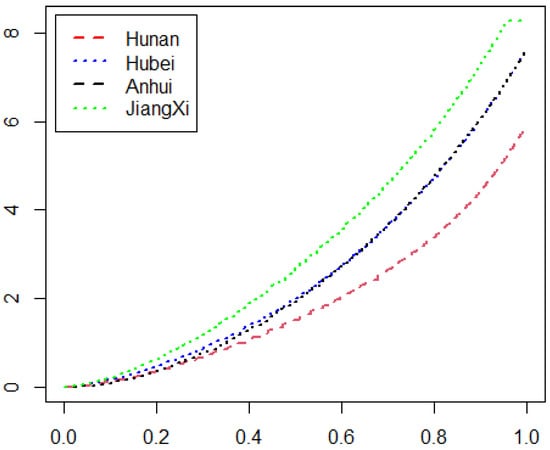
Figure 4.
The plots of for different provinces.
Table 10, Table 11 and Table 12 show the p-values of the tests for the second-order stochastic dominance relationship between the visibility of the four provinces. If the significance level , all three tests indicate that the visibility of Jiangxi province stochastic dominates that of the other three provinces with the second order. The visibility of Hubei province stochastic dominates that of Hunan province with the second order as well. These two conclusions can also be derived from the results obtained from Table 7, Table 8 and Table 9 since the relationship of the first-order stochastic dominance is stronger than the second-order stochastic dominance. Besides, the results of all three tests also reveal that Anhui Hunan. The divergence between these three tests is in judging the second-order stochastic dominance relationship between the visibility of Hubei and Anhui province.

Table 10.
The p-values of the K-S tests for the second-order stochastic dominance.

Table 11.
The p-values of the DD tests for the second-order stochastic dominance.

Table 12.
The p-values of the BD tests for the second-order stochastic dominance.
For the given significance level , the DD test and the BD test show that we should accept both Hubei Anhui and Anhui Hubei, while our proposed test indicates that we should accept Hubei Anhui, but reject Anhui Hubei. When we accept the null and alternative hypotheses at the same time, it often indicates that the two populations have the same distributions. But, if we carefully observe the curves in Figure 4, we can find that the curve of Hubei province is still a little higher than Anhui province, which means that our test results are more accurate.
Based on the above discussion, we can say that our K-S test has a better performance than the DD test and the BD test if we use them to test the first and the second stochastic dominance relationships for the visibility data of the four central provinces in China. To end this section, we summarize the results of our proposed test obtained from Table 7 and Table 10 for significance level . The conclusions are shown in Table 13, where “✓✓” means that there are first-order and the second-order stochastic dominance relationships between the column labels and the row labels, and “✓” means that the column labels stochastic dominate the row labels with the second order, but not with the first order. According to the results stated in Table 13, for the given significance level , we can conclude that the visibility of Jiangxi province is the best. The next one is the visibility of Hubei province, which outperforms the visibility of Anhui province. The visibility of Hunan province is the poorest.

Table 13.
Summary of the comparisons on the visibility of four provinces.
6. Conclusions and Extensions
This paper is devoted to proposing a consistent K-S-type test based on a quantile rule. To this end, we constructed the K-S-type statistics for our tests and explored their asymptotic properties under some assumptions. To obtain the p-values of our proposed tests, we introduced the bootstrap method. Then, we applied the Monte Carlo method to obtain the rejection rates and compared the power performance of our proposed test with the DD test and the BD test. The simulations showed that our test performed better and was more robust than the other two tests. Finally, for the given significance level , we applied our proposed test to compare the visibility of the four central provinces in China and compared the effects with the DD tests and the BD tests.
In the future, at least three topics can be further considered. Firstly, due to the strict assumptions of integer stochastic dominance, sometimes, there may not be an integer stochastic dominance relationship between two populations. Therefore, we can try to apply our K-S test to test whether there is a fractional degree stochastic dominance relationship or an almost stochastic dominance relationship between two populations. Secondly, we assumed that the samples of the two populations in this paper are independent and identically distributed. However, most samples are dependent on our real lives. We can improve our proposed statistics or bootstrap method to handle dependent samples such as paired or time series samples. Thirdly, in the empirical analysis of our paper, we applied our proposed test to compare the visibility conditions of the four central provinces. However, measuring the environmental level of a region through a single indicator is often not enough. In the future, maybe, we can improve our proposed test to apply it to multidimensional situations to obtain a more-comprehensive result.
Author Contributions
H.H. methodology, writing and original draft preparation. G.Q. methodology, writing and original draft preparation. W.Z. supervision and project administration. G.Q. editing and methodology. All authors conceived of the study, participated in its design and coordination, drafted the manuscript, participated in the sequence alignment. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Nature Science Foundation of China under Grant Nos. 71971204, 71871208, and 11701518, the Excellent Youth Foundation under Grant No. 2208085J43, and the foundation of Anhui Xinhua University under Grant Nos. 2017kyqd01, 2021xbxm006, and DSJF001.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lehmann, E.L. Testing Statistical Hypotheses, 2nd ed.; J. Wiley and Sons: New York, NY, USA, 1986. [Google Scholar]
- Post, T.W. Empirical tests for stochastic dominance efficiency. J. Financ. 2003, 58, 1905–1931. [Google Scholar] [CrossRef]
- Zhu, Z. Nth Order Stochastic Dominance Test with Applications. Ph.D. Thesis, Northeast Normal University, Changchun, China, 2017. [Google Scholar]
- McFadden, D. Studies in the Economics of Uncertainty; Springer: New York, NY, USA, 1989. [Google Scholar]
- Barrett, G.F.; Donald, S.G. Consistent tests for stochastic dominance. Econometrica 2003, 71, 71–104. [Google Scholar] [CrossRef]
- Barrett, G.F.; Donald, S.G.; Bhattacharya, D. Consistent nonparametric tests for Lorenz dominance. J. Bus. Econ. Stat. 2014, 32, 1–13. [Google Scholar] [CrossRef]
- Donald, S.G.; Hsu, Y.C. Improving the power of tests of stochastic dominance. Econom. Rev. 2016, 35, 553–585. [Google Scholar] [CrossRef]
- Kaur, A.; Rao, B.L.S.P.; Singh, H. Testing for second-order stochastic dominance of two distributions. Econom. Theory 1994, 10, 849–866. [Google Scholar] [CrossRef]
- Anderson, G. Nonparametric tests of stochastic dominance in income distributions. Econometrica 1996, 64, 1183–1193. [Google Scholar] [CrossRef]
- Davidson, R.; Duclos, J.Y. Statistical inference for stochastic dominance and for the measurement of poverty and inequality. Econometrica 2000, 68, 1435–1464. [Google Scholar] [CrossRef]
- Ledwina, T.; Wyłupek, G. Nonparametric tests for stochastic ordering. Test 2012, 21, 730–756. [Google Scholar] [CrossRef]
- Deshpande, J.V.; Singh, H. Testing for second order stochastic dominance. Commun. Stat.-Theory Methods 1985, 14, 887–893. [Google Scholar] [CrossRef]
- Eubank, R.; Schechtman, E.; Yitzhaki, S. A test for second order stochastic dominance. Commun. Stat.-Theory Methods 1993, 22, 1893–1905. [Google Scholar] [CrossRef]
- Schmid, F.; Trede, M. Testing for first-order stochastic dominance: A new distribution-free test. J. R. Stat. Soc. Ser. D Stat. 1996, 45, 371–380. [Google Scholar] [CrossRef]
- Hall, P.; Yatchew, A. Unified approach to testing functional hypotheses in semiparametric contexts. J. Econom. 2005, 127, 225–252. [Google Scholar] [CrossRef]
- Lee, K.; Linton, O.; Whang, Y.J. Testing for time stochastic dominance. J. Econom. 2023, 235, 352–371. [Google Scholar] [CrossRef]
- Morgenstern, O.; Von Neumann, J. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Hadar, J.; Russell, W. Rules for ordering uncertain prospects. Am. Econ. Rev. 1969, 59, 25–34. [Google Scholar]
- Hanoch, G.; Levy, H. The efficiency analysis of choices involving risk. Rev. Econ. Stud. 1975, 36, 335–346. [Google Scholar] [CrossRef]
- Levy, H. Stochastic Dominance, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Levy, H.; Kroll, Y. Ordering uncertain options with borrowing and lending. J. Financ. 1978, 33, 553–574. [Google Scholar] [CrossRef]
- Van der Vaart, A.W. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Shao, J.; Tu, D. The Jackknife and Bootstrap; Springer Science and Business Media: Berlin, Germany, 2012. [Google Scholar]
- Sergio, A.; Salim, B. Strong approximations for weighted bootstrap of empirical and quantile processes with applications. Stat. Methodol. 2013, 35, 553–585. [Google Scholar]
- Hansen, B.E. Inference when a nuisance parameter is not identified under the null hypothesis. Econom. J. Econom. Soc. 1996, 64, 413–430. [Google Scholar] [CrossRef]
- Bai, Z.; Li, H.; Liu, H.; Wong, W.K. Test statistics for prospect and Markowitz stochastic dominances with applications. Econom. J. 2011, 14, 278–303. [Google Scholar] [CrossRef]
- Bai, Z.; Li, H.; McAleer, M.; Wong, W.K. Stochastic dominance statistics for risk averters and risk seekers: An analysis of stock preferences for USA and China. Quant. Financ. 2015, 15, 889–900. [Google Scholar] [CrossRef]
- Douglas, A.; Zhang, S. Carbon-trading pilot programs in China and local air quality. AEA Pap. Proc. 2021, 111, 391–395. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).