A Hyperstructural Approach to Semisimplicity

Abstract

In this paper, we provide the basic properties of (semi)simple hypermodules. We show that if a hypermodule M is simple, then $\left(End\right(M),·)$ is a group, where $End\left(M\right)$ is the set of all normal endomorphisms of M. We prove that every simple hypermodule is normal projective with a zero singular subhypermodule. We also show that the class of semisimple hypermodules is closed under internal direct sums, factor hypermodules, and subhypermodules. In particular, we give a characterization of internal direct sums of subhypermodules of a hypermodule.

1. Introduction

Let H be a non-empty set and $P^{*}\left(H\right)$ be the set of all non-empty subsets of H. The function $\circ :H\times H⟶P^{*}\left(H\right)$ is called a hyperoperation on H. The image of the element $(a,b)\in H\times H$ under this operation is not a single element, but a non-empty subset of the set H. Thanks to this idea, the theory of hyperstructures was introduced by Marty in [1] as a natural and interesting generalization of the theory of algebraic structures. Following [1], Marty defines hypergroups using the hyperoperation on a set. Let H be a non-empty set and a function $+:H\times H⟶{\mathcal{P}}^{*}\left(H\right)$ be a hyperoperation on H. Then, $(H,+)$ is called a hypergroupoid. Moreover, for any non-empty subsets X and Y of H, define

$$X+Y=\bigcup \{x+y|x\in Xandy\in Y\}.$$

We simply write $a+X$ and $X+a$ instead of $\left\{a\right\}+X$ and $X+\left\{a\right\}$, respectively, for any $a\in H$ and any non-empty subset X of H. A hypergroupoid $(H,+)$ is called a

(1)

Semihypergroup if for every $a,b,c\in H$, we have $a+(b+c)=(a+b)+c$;

(2)

Quasihypergroup if for every $x\in H$, $x+H=H=H+x$.

If the hypergroupoid $(H,+)$ is a semihypergroup and quasihypergroup, then it is called a hypergroup. A non-empty subset S of a hypergroup $(H,+)$ is called a subhypergroup of H if for every $a\in S$, $a+S=S=S+a$.

Another generalization of algebraic structures was made by V. M. Buchstaber as follows: Let H be a non-empty set and $n\in {\mathbb{Z}}^{+}$. By ${\left(H\right)}^n$ we denote the symmetric nth power of the set H. An n-valued multiplication on H is a map

$$\begin{gathered} \mu :H\times H⟶{\left(H\right)}^n, \\ \mu (a,b)=[c_1,c_2,...,c_n],c_k={\left(\mu (a,b)\right)}_k. \end{gathered}$$

The map $\mu$ defines an n-valued group structure on H if it is associative, and has a unit and an inverse [2]. The properties of this n-valued group structure and its applications to other branches of mathematics were studied in the same paper. Also, the algebraic 2-valued group structure on Kummer varieties and its relationship with integrable billiard systems within pencils of quadrics was studied in [3]. Studies on n-valued algebraic structures continue. Now, let us show two generalizations of the group structure in the diagram below: When generalizations of the group structure are obtained, it is not difficult to think of concepts of other algebraic structures according to this concept. Motivated by this, Krasner introduced hyperfields, hyperrings, and hypermodules in his papers [4,5]. In the literature, hyperring structures (respectively, hyperfield) are known as Krasner hyperrings (respectively, Krasner hyperfields). Krasner [5] solves a problem in the approximation of a complete valued field by a sequence of such fields by using hyperfields. Recently, as more general structures of Krasner hyperrings and Krasner hyperfields, these notions of general hyperrings and general hypermodules have been introduced and studied by many authors in a series of papers [6,7,8,9].

Let $p\in \mathbb{P}$, where $\mathbb{P}$ is the set of all positive prime integers. Consider the group ${\mathbb{Z}}_p=\{\overline{0},\overline{1},...,\overline{p-1}\}$. It is well known that ${\mathbb{Z}}_p$ is cyclic and has only trivial subgroups. The group ${\mathbb{Z}}_p$ has a very special place in the category of Abelian groups and has applications in all branches of mathematics. In particular, very important studies have been carried out on groups that can be written as direct sums of ${\mathbb{Z}}_p^{\prime }$s. When module theory is considered as an abstract generalization of Abelian groups, the definition of a simple module is given with the help of the structure of the group ${\mathbb{Z}}_p$. A module M is called simple if it has only trivial submodules. Since every Abelian group is a $\mathbb{Z}$-module, simple $\mathbb{Z}$-modules are completely the groups ${\mathbb{Z}}_p$ for all $p\in \mathbb{P}$. The direct sum of simple modules is semisimple modules. For detailed information about (semi)simple modules, refer to [10,11]. The place and importance of “simple modules” in module theory, and especially in the theory of Abelian groups, is undisputed, as can be seen in the studies carried out so far. Therefore, it is a natural result to study the concept of simplicity in hypermodules.

The main purpose of this paper is to develop similar results in (semi)simple hypermodules motivated by the works on (semi)simple modules, which are one of the most important concepts of module theory, and thus, concepts of ring theory. We give examples of (semi)simple hypermodules and focus on the basic properties of (semi)simple hypermodules. We show that if a hypermodule M is simple, then $\left(End\right(M),·)$ is a group, where $End\left(M\right)$ is the set of all normal endomorphisms of M. We define the annihilator concept, which is the starting point of the notion of singularity in module theory, for hypermodules and prove that every simple hypermodule is normal projective with the help of this. We also show that the class of semisimple hypermodules is closed under internal direct sums, factor hypermodules, and subhypermodules. In particular, we characterize internal direct sums of subhypermodules of a hypermodule.

2. Preliminaries

This section briefly recalls the main concepts and results related to types of hyperrings and hypermodules. To better understand the topic, we start with some fundamental definitions of hypercompositional algebra presented in the books [12,13] and overview articles [8,14,15,16,17].

A hypergroup $(H,+)$ is called a canonical hypergroup if

(1)

For every $a,b\in H$, $a+b=b+a$, that is, it is commutative;

(2)

There exists a unique $0\in H$ such that for each $a\in H$ there exists a unique element $a^{\prime }$ in H, denoted by $-a$, such that $0\in a+(-a)$;

(3)

For every $a,b,c\in H$, if $c\in a+b$, then $a\in c+(-b):=c-b$.

As is proved in [18], if $(H,+)$ is a canonical hypergroup, then $a+0=a$ for all $a\in H$.

Let $(R,+,.)$ be a hyperstructure. $(R,+,.)$ called a (Krasner) hyperring if

(1)

$(R,+)$ is a canonical hypergroup.

(2)

$(R,.)$ is a monoid with a bilaterally absorbing element 0, i.e.,

(a)

$a.b\in R$ for all $a,b\in R$;

(b)

$a.(b.c)=(a.b).c$ for all $a,b,c\in R$;

(c)

$a.0=0.a=0$ for all $a\in R$;

(d)

There exists an identity element $1_R\in R$ such that $a=a.1_R=1_R.a$ for every $a\in R$.

(3)

The multiplication distributes over the addition on both sides.

A hyperring $(R,+,.)$ is called commutative if it is commutative concerning the multiplication.

Let $(R,+,·)$ be a hyperring and I be a non-empty subset of R. I is called a left hyperideal (respectively, right hyperideal) of R provided $(I,+)$ is a subhypergroup and $r.a\in I$ (respectively, $a.r\in I)$ for all $a\in I$, and $r\in R$. I is said to be hyperideal of R if it is both a right and a left hyperideal of R.

A left Krasner hypermodule over a hyperring R (or left Krasner R-hypermodule) is a canonical hypergroup $(M,+)$ together with a map $R\times M⟶M$ such that to every $(r,m)$, where $r\in R$ and $m\in M$, there corresponds a uniquely determined element $rm\in M$ and the following conditions are satisfied:

(1)

$r(m_1+m_2)=r{m}_1+r{m}_2$;

(2)

$(r+s)m=rm+sm$;

(3)

$(r.s)m=r\left(sm\right)$;

(4)

$1_{R}m=m$ and $r{0}_M=0_{R}m=0_M$.

for any $m,m_1,m_2\in M$ and $r,s\in R$.

Throughout this paper, for a simple explanation, when we say hypermodule, we mean the left Krasner hypermodule. A non-empty subset N of an R-hypermodule M is called a subhypermodule of M, denoted by $N\le M$ if N is an R-hypermodule under the same hyperoperations of M. It is clear that M and $\left\{0_M\right\}$ are trivial subhypermodules of M. It is known that a non-empty subset N of an R-hypermodule M is a subhypermodule of M if and only if $a-b\subseteq M$ and $ra\in M$ for all $a,b\in M$ and $r\in R$.

Let R be a hyperring. It follows from Lemma 3.1 in [19] that R is an R-hypermodule. We will denote this hypermodule with ${}_{R}R$ in this study. Then, a non-empty subset I of R is a left hyperideal of R if and only if it is a subhypermodule of the hypermodule ${}_{R}R$.

Let M be a hypermodule over a hyperring R and K be a subhypermodule of M. Consider the set $\frac{M}{K}=\{a+K|a\in M\}$. Then, $\frac{M}{K}$ is a hypermodule over the hyperring R under the hyperoperation defined as $+:\frac{M}{K}\times \frac{M}{K}⟶{\mathcal{P}}^{*}\left(\frac{M}{K}\right)$ and the external operation $\odot :R\times \frac{M}{K}⟶\frac{M}{K}$ defined as $(a+K)+(a^{\prime }+K)=\{b+K|b\in a+a^{\prime }\}$ and $r\odot (a+K)=ra+K$ for every $a,a^{\prime },b\in M$ and $r\in R$. The hypermodule $\frac{M}{K}$ is called the quotient hypermodule of the hypermodule M.

Let M and N be R-hypermodules. A function $f:M⟶P^{*}\left(N\right)$ is called an Rhomomorphism if

(1)

$f\left(m_1{+}_M{m}_2\right)\subseteq f\left(m_1\right){+}_{N}f\left(m_2\right)$ for all $m_1,m_2\in M$;

(2)

$f\left(rm\right)=rf\left(m\right)$ for all $r\in R$ and $m\in M$.

f is called a strong homomorphism whenever $f\left(m_1{+}_M{m}_2\right)=f\left(m_1\right){+}_{N}f\left(m_2\right)$ for all $m_1,m_2\in M$. A single-valued function $f:M⟶N$ is called a normal homomorphism if

(1)

$f\left(m_1{+}_M{m}_2\right)=f\left(m_1\right){+}_{N}f\left(m_2\right)$ for all $m_1,m_2\in M$;

(2)

$f\left(rm\right)=rf\left(m\right)$ for all $r\in R$ and $m\in M$.

3. Direct Sums of Hypermodules

Let R be a hyperring and M be an R-hypermodule. For a family of subhypermodules ${\left\{M_i\right\}}_{i\in I}$ of M, the sum of this family is denoted by ${\sum }_{i\in I}{M}_i$ and it is the set of these elements $x\in M$ where x is an element of the set ${\sum }_{i\in I_0}{m}_i$ with finite subset $I_0\subseteq I$ for every $i\in I_0$, $m_i\in M_i$. That is,

$${\sum }_{i\in I}{M}_i=\{x\in M|x\in {\sum }_{i\in I_0}{m}_i,m_i\in M_{i}and{I}_{0}isafinitesubsetofI\}.$$

It is well known that ${\sum }_{i\in I}{M}_i$ is a subhypermodule of M.

In [20], the direct sum of the family of subhypermodules of a hypermodule is defined. Here, for this direct sum definition, similar to the direct sum of modules, we will define it as the internal direct sum as follows.

Definition 1.

Let M be a hypermodule and ${\left\{M_i\right\}}_{i\in I}$ be a non-empty collection of subhypermodules of M. The hypermodule M is said to be an internal direct sum of the subhypermodules ${\left\{M_i\right\}}_{i\in I}$ and denoted by ${⨁}_{i\in I}{M}_i$ if the following conditions are satisfied:

(1) 

$M={\sum }_{i\in I}{M}_i$;

(2) 

$M_i\bigcap \left({\sum }_{i\ne k}{M}_k\right)=\left\{0_M\right\}$.

Condition $\left(2\right)$ means that a nonzero element in $M_i$ is not a member of the sets which are a sum of elements in the other $M_k$’s. According to [21], ${\left\{M_i\right\}}_{i\in I}$ is called independent if it satisfies condition $\left(2\right)$. We now give the following theorem as the main conclusion of this section.

Theorem 1.

Let M be a hypermodule and ${\left\{M_i\right\}}_{i\in I}$ be a non-empty collection of subhypermodules of M. Then, M is an internal direct sum of the subhypermodules ${\left\{M_i\right\}}_{i\in I}$ if and only if every element $m\in M$ belongs to the set $m_{i_1}+m_{i_2}+...+m_{i_n}$, which is uniquely determined by distinct elements $m_{i_j}\in M_{i_j}$ for every $j\in \{1,2,...,n\}$.

Proof. 

$(\Rightarrow )$ Assume that $m\in m_{i_1}+m_{i_2}+...+m_{i_n}$ and $m\in m_{i_1^{*}}+m_{i_2^{*}}+...+m_{i_t^{*}}$, where $m_{i_u}\in M_{i_u}$ and $m_{i_v^{*}}\in M_{i_v^{*}}$ for every $1\le u\le n$ and $1\le v\le t$. If $n\le t$, then we obtain $m_{i_{n+1}}=m_{i_{n+2}}=...=m_{i_t}=0_M$ and so we can assume that $n=t$. Now, let us show the number of hypermodules with $M_{i_u}=M_{i_v^{*}}$ by p. We can take it as being

$$M_{i_1}=M_{i_1^{*}},M_{i_2}=M_{i_2^{*}},\dots ,M_{i_p}=M_{i_p^{*}}$$

without the restriction of generality. Therefore,

$$\begin{array}{c}\hfill \begin{array}{ccc}{0}_M\hfill & \in \hfill & m-m\hfill \\ & \subseteq \hfill & (m_{i_1}+m_{i_2}+...+m_{i_n})-(m_{i_1^{*}}+m_{i_2^{*}}+...+m_{i_n^{*}})\hfill \\ & =\hfill & (m_{i_1}-m_{i_1^{*}})+(m_{i_2}-m_{i_2^{*}})+...+(m_{i_p}-m_{i_p^{*}})+m_{i_{p+1}}+m_{i_{p+2}}...+m_{i_n}\hfill \\ & & (-m_{i_{p+1}^{*}})+(-m_{i_{p+2}^{*}})+...+(-m_{i_n^{*}})\hfill \end{array}\end{array}$$

and so there exist elements $(1\le u\le p)$$x_u\in m_{i_u}-m_{i_u^{*}}$ such that

$$0_M\in x_1+x_2+...+x_p+m_{i_{p+1}}+m_{i_{p+2}}+...+m_{i_n}+(-m_{i_{p+1}^{*}})+(-m_{i_{p+2}^{*}})...+(-m_{i_n^{*}}).$$

Put $x_1^{*}=x_2+...+x_p+m_{i_{p+1}}+m_{i_{p+2}}+...+m_{i_n}+(-m_{i_{p+1}^{*}})+(-m_{i_{p+2}^{*}})...+(-m_{i_n^{*}})$. It follows that $x_1^{*}\in M_{i_2}+M_{i_3}+...+M_{i_n}+...+M_{i_n^{*}}$. Thus, $0\in x_1+x_1^{*}$ and then

$$x_1=-x_1^{*}\in M_{i_1}\bigcap (M_{i_2}+M_{i_3}+...+M_{i_n}+...+M_{i_n^{*}})=0_M.$$

We have $0_M=x_1\in m_{i_1}-m_{i_1^{*}}$ and then $0_M\in m_{i_1}-m_{i_1^{*}}$. So we can write $m_{i_1}=m_{i_1^{*}}$. By continuing with the same method, these equations $m_{i_u}=m_{i_u^{*}}$$(2\le u\le n)$ are obtained, and therefore, $m\in M$ belongs to the set $m_{i_1}+m_{i_2}+...+m_{i_n}$, which is uniquely determined by distinct elements $m_{i_u}\in M_{i_u}$ for every $u\in \{1,2,...,n\}$.

$(\Leftarrow )$ The equality $M={\sum }_{i\in I}{M}_i$ is clear. Let $m\in M_j\bigcap \left({\sum }_{i\ne j}{M}_i\right)$. Then, there exists a set $m_{i_1}+m_{i_2}+...+m_{i_n}\subseteq M_{i_1}+M_{i_2}+...+M_{i_n}$ such that m is an element of the set $m_{i_1}+m_{i_2}+...+m_{i_n}$. On the other hand, $m\in \left\{m\right\}\subseteq M_j$ and so $m=0_M$ by assumption. This means that the sum $M={\sum }_{i\in I}{M}_i$ is an internal direct sum. □

More specifically, a hypermodule M is an internal direct sum of subhypermodules $M_1$ and $M_2$, that is, $M=M_1\oplus M_2$ if and only if, for every element $m\in M$, there exists a unique element $m_1\in M_1$ and a unique element $m_2\in M_2$ such that m is an element of the set $m_1+m_2$.

Remark 1.

Krasner gave a method for the construction of hyperrings (see [4]). Let $(S,+,.)$ be a commutative ring with unity and $(H,.)$ be a subgroup of the monoid $(S,.)$. Then, ${\left\{aH\right\}}_{a\in S}$ is a partition of S and so this partition defines an equivalence relation on S as follows:

$$“a\sim b⟺aH=bH”.$$

Let $R:=\frac{S}{H}$ be the set of all equivalence classes $aH$. Define

$$aH+bH=\left\{cH\right|cH\subseteq \{x+y|x\in aHandy\in bH\}\}\subseteq P^{*}\left(R\right)$$

and

$$aH·bH=abH.$$

Then, $(R,+,.)$ is a commutative hyperring. In particular, if $(S,+,.)$ is a field, then $(R,+,.)$ is a hyperfield.

Example 1.

Let $G=\{-1,1\}$ be the multiplicative group of the ring $(\mathbb{Z},+,.)$. By Remark 1, $(\frac{\mathbb{Z}}{G},+,.)$ is a commutative and unity hyperring. Since $G=\{-1,1\}$, we can write

$$aG+bG=\left\{\right(a+b)G,(a-b\left)G\right\}.$$

It follows that $\frac{\mathbb{Z}}{G}$ is a $\frac{\mathbb{Z}}{G}$-hypermodule. It is easy to see that the subhypermodules (hyperideals) of $\frac{\mathbb{Z}}{G}$ are of the form $<aG>$. In particular, $\frac{\mathbb{Z}}{G}=<1G>$ and so $\frac{\mathbb{Z}}{G}=<0G>\oplus <1G>$.

Now, let us show that the hypermodule $\frac{\mathbb{Z}}{G}$ has no direct summands other than $<0G>$ and $<1G>$. Assume that $\frac{\mathbb{Z}}{G}=<aG>\oplus <bG>$, where $a,b\ne 0,1$. Let d be the greatest common divisor of integers a and b. Then, there exist integers $u,v\in \mathbb{Z}$ such that $d=ua+vb$. It follows that $dG\in u\left(aG\right)+v\left(bG\right)$ and $dG\in (-u)\left(aG\right)+(-v)\left(bG\right)$. Thus, the element $dG$ belongs to these sets $u\left(aG\right)+v\left(bG\right)$ and $(-u)\left(aG\right)+(-v)\left(bG\right)$, a contradiction by Theorem 1.

Example 2.

Given the hyperring $\frac{\mathbb{Z}}{G}$ in Example 1, let us denote by M the factor hypermodule of the $\frac{\mathbb{Z}}{G}$-hypermodule $\frac{\mathbb{Z}}{G}$ according to subhypermodule $<6G>$. Put $\overline{a}=aG+<6G>$, where $aG\in \frac{\mathbb{Z}}{G}$. Then, we have the following table:

$$\begin{array}{ccccccc}{+}_{6G}\hfill & \overline{0}& \overline{1}& \overline{2}& \overline{3}& \overline{4}& \overline{5}\\ \overline{0}\hfill & \left\{\overline{0}\right\}& \left\{\overline{1}\right\}& \left\{\overline{2}\right\}& \left\{\overline{3}\right\}& \left\{\overline{4}\right\}& \left\{\overline{5}\right\}\\ \overline{1}\hfill & \left\{\overline{1}\right\}& \{\overline{0},\overline{2}\}& \{\overline{1},\overline{3}\}& \{\overline{2},\overline{4}\}& \{\overline{3},\overline{5}\}& \{\overline{0},\overline{4}\}\\ \overline{2}\hfill & \left\{\overline{2}\right\}& \{\overline{1},\overline{3}\}& \{\overline{0},\overline{4}\}& \{\overline{1},\overline{5}\}& \{\overline{0},\overline{2}\}& \{\overline{1},\overline{3}\}\\ \overline{3}\hfill & \left\{\overline{3}\right\}& \{\overline{2},\overline{4}\}& \{\overline{1},\overline{5}\}& \left\{\overline{0}\right\}& \left\{\overline{1}\right\}& \left\{\overline{2}\right\}\\ \overline{4}\hfill & \left\{\overline{4}\right\}& \{\overline{3},\overline{5}\}& \left\{\overline{2}\right\}& \left\{\overline{1}\right\}& \{\overline{0},\overline{2}\}& \{\overline{1},\overline{3}\}\\ \overline{5}\hfill & \left\{\overline{5}\right\}& \{\overline{0},\overline{4}\}& \{\overline{1},\overline{3}\}& \left\{\overline{2}\right\}& \{\overline{1},\overline{3}\}& \{\overline{0},\overline{4}\}\end{array}$$

It follows that M is the direct sum of these subhypermodules $\{\overline{0},\overline{3}\}$ and $\{\overline{0},\overline{2},\overline{4}\}$.

Let M be an R-hypermodule. In [22], M is called normal projective if for every surjective $g\in Ho{m}_R(K,N)$ and every $f\in Ho{m}_R(M,N)$ there exists $\overline{f}\in Ho{m}_R(M,K)$ such that $g\overline{f}=f$.

Theorem 2.

Let R be a hyperring. Then, R is a normal projective R-hypermodule.

Proof. 

Let A and B be R-hypermodules and $f:R⟶B$ be a normal homomorphism. In addition, suppose that $g:A⟶B$ be a surjective normal homomorphism of hypermodules A and B.

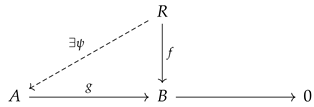
Since g is surjective, there exists an element $a\in A$ such that $f\left(1_R\right)=g\left(a\right)$. Consider the function $\psi :R⟶A$ such that $\psi \left(r\right)=\psi \left(r{1}_R\right)=r·a$ for all $r\in R$. Then, $\psi$ is a normal homomorphism. Let s be an element of R. Then, $\left(g\psi \right)\left(s\right)=g\left(\psi \left(s\right)\right)=g(s·a)=s·g\left(a\right)=s·f\left(1_R\right)=f\left(s{1}_R\right)=f\left(s\right)$ and so $g\psi =f$, which means that R is a normal projective R-hypermodule. □

4. Simple Hypermodules

In module theory and homological algebra, simple modules are one of the basic concepts of these theories and are studied by many researchers. By using the concept of simple modules some notions of module theory are defined and characterizations of the classes of rings are given. For example, a module M is semisimple if and only if it is a sum of simple submodules. A module M is Artinian if and only if it is linear compact and its factor modules have a simple submodule. A module M is semi-Artinian if and only if its factor modules have a simple submodule. A module M is a V-module if and only every simple module is M-injective. A ring R is semisimple if and only if its modules are injective (projective). A ring R is a left $SSI$-ring if and only if every semisimple module is injective. Many more of these examples could be given by a researcher working in modules and rings theory. Moreover, in recent years, types of injectivity and projectivity have been studied with the help of (semi)simple modules. Refer to the books [10,11,23,24,25] and the papers [26,27,28,29,30,31,32,33,34] for detailed information.

In this section, we obtain the basic properties of simple hypermodules and give some examples of these hypermodules. In particular, we prove that every simple hypermodule is normal projective with a zero singular subhypermodule.

Definition 2

([35]). Let R be a hyperring and M be a nonzero R-hypermodule. M is called simple if M has only the subhypermodules $\left\{0_M\right\}$ and M.

Example 3.

Given the set $M=\{0,1,2\}$, define the hyperoperation “+” and the multiplication “·” by the following tables:

$$\begin{array}{cccc}\hfill +& 0& 1& 2\\ 0& \left\{0\right\}& \left\{1\right\}& \left\{2\right\}\\ 1& \left\{1\right\}& \{0,2\}& \{0,1\}\\ 2& \left\{2\right\}& \{0,1\}& \{0,1\}\end{array}$$

and

$$\begin{array}{cccc}.& 0& 1& 2\\ 0& 0& 0& 0\\ 1& 0& 1& 2\\ 2& 0& 2& 1\end{array}$$

Then, M is a hypermodule over the hyperring M. Therefore, <1> = <2> = M and so M is a simple hypermodule.

Lemma 1.

A nonzero hypermodule M is simple if and only if the zero subhypermodule $\left\{0_M\right\}$ is a maximal subhypermodule of M.

Proof. 

$(\Rightarrow )$ By definition.

$(\Leftarrow )$ Let N be a subhypermodule of M. Therefore, $\left\{0_M\right\}\le N\le M$. Since $0_M$ is a maximal subhypermodule of M, $N=\left\{0_M\right\}$ or $N=M$, it means that M is a simple hypermodule. □

Let M and N be hypermodules and $f:M⟶N$ be a normal homomorphism. The set $\{m\in M|f\left(m\right)=0_N\}$ is called the kernel of f and denoted by $Ker\left(f\right)$. Then, it is easy to see that $Ker\left(f\right)$ is a subhypermodule of M and the normal homomorphism f is injective if and only if $Ker\left(f\right)=\left\{0_M\right\}$.

Lemma 2.

Let $f:M⟶N$ be a nonzero normal homomorphism of hypermodules and M be a simple hypermodule. Then,

(1) 

f is injective;

(2) 

$f\left(M\right)$ is a simple subhypermodule of N.

Proof. 

$\left(1\right)$ Since M is simple and $ker\left(f\right)$ is a subhypermodule of M, we conclude that $Ker\left(f\right)=M$ or $Ker\left(f\right)=\left\{0_M\right\}$. From the hypothesis that f is a nonzero normal homomorphism, it is clear that $Ker\left(f\right)=\left\{0_M\right\}$. Thus, f is injective.

$\left(2\right)$ Let A be a subhypermodule of $f\left(M\right)$. Therefore, $f^{-1}\left(A\right)$ is a subhypermodule of M. Since M is a simple hypermodule, we can write $f^{-1}\left(A\right)=\left\{0_M\right\}$ or $f^{-1}\left(A\right)=M$.

If $f^{-1}\left(A\right)=\left\{0_M\right\}$, then $f^{-1}\left(A\right)\subseteq Ker\left(f\right)=\left\{0_M\right\}$ by $\left(1\right)$. It follows that $f\left(f^{-1}\left(A\right)\right)=A=\left\{0_N\right\}$. In addition, if $f^{-1}\left(A\right)=M$, then $A=f\left(f^{-1}\left(A\right)\right)=f\left(M\right)$, which means that $f\left(M\right)$ is a simple hypermodule. □

The next result is a direct consequence of Lemma 2.

Corollary 1.

Let $f:M⟶N$ be a nonzero surjective normal homomorphism of hypermodules. If M is simple, then N is too.

Now, we give a characterization of a simple hypermodule in the following theorem. This theorem completely determines the structure of a simple hypermodule.

Theorem 3.

Let R be a hyperring and M be an R-hypermodule. Then, the following statements are equivalent:

(1) 

M is simple.

(2) 

If there exist hypermodules $B\le A$ such that M is isomorphic to $\frac{A}{B}$, then B is a maximal subhypermodule of A.

(3) 

There exists an R-hypermodule A and a maximal subhypermodule B of A such that M is isomorphic to $\frac{A}{B}$.

(4) 

There exists a maximal left hyperideal I of R such that M is isomorphic to $\frac{R}{I}$.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$ Let $\mathsf{\Psi }:\frac{A}{B}⟶M$ be a normal isomorphism of hypermodules. Since M is simple, $0_M$ is a maximal subhypermodule of M and so $B={\mathsf{\Psi }}^{-1}\left(0_M\right)$ is a maximal subhypermodule of A.

$\left(2\right)\Rightarrow \left(3\right)$ Consider the isomorphism $M\cong \frac{M}{\left\{0_M\right\}}$. It follows from $\left(2\right)$ that $0_M$ is a maximal subhypermodule M.

$\left(3\right)\Rightarrow \left(1\right)$ By Corollary 1, it is enough to show that $\frac{A}{B}$ is simple, where B is a maximal subhypermodule of A. Since B is a maximal subhypermodule of A, $\frac{A}{B}$ has the only subhypermodules $\left\{0_M\right\}$ and $\frac{A}{B}$. Thus, $\frac{A}{B}$ is simple.

$\left(1\right)\Rightarrow \left(4\right)$ Let $0\ne m\in M$. Therefore, $Rm=\{r·m|r\in R\}$ is a subhypermodule of M. Consider the normal epimorphism $\lambda :R⟶Rm$ via $\lambda \left(r\right)=rm$ for all $r\in R$. It follows that $Ker\left(\lambda \right)$ is a left hyperideal of R and $M=Rm\cong \frac{R}{Ker\left(\lambda \right)}$. Since M is simple, by Corollary 1, we obtain that $\frac{R}{Ker\left(\lambda \right)}$ is simple. This means that $Ker\left(\lambda \right)$ is a maximal left ideal of R.

$\left(4\right)\Rightarrow \left(3\right)$ It is clear. □

Now, we give other examples of simple hypermodules.

Example 4.

Let $R=\{0,1,2\}$ and $A=\{0,2\}$. Define the hyperaddition “+” and multiplication “·” by the following:

$$\begin{array}{cccc}+& \mathsf{0}& \mathsf{1}& \mathsf{2}\\ \mathsf{0}& \mathsf{\left\{}\mathsf{0}\mathsf{\right\}}& \left\{\mathsf{1}\right\}& \left\{\mathsf{2}\right\}\\ \mathsf{1}& \left\{\mathsf{1}\right\}& R& \left\{\mathsf{1}\right\}\\ \mathsf{2}& \left\{\mathsf{2}\right\}& \mathsf{\left\{}\mathsf{1}\mathsf{\right\}}& A\end{array}$$

and

$$\begin{array}{cccc}.& \mathsf{0}& \mathsf{1}& \mathsf{2}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{1}& \mathsf{0}& \mathsf{1}& \mathsf{2}\\ \mathsf{2}& \mathsf{0}& \mathsf{2}& \mathsf{0}\end{array}$$

Then, R is a hyperring and A is the only left maximal hyperideal of R. So, Theorem 3, $\frac{R}{A}=\{A,1+A,2+A\}$ is a simple R-hypermodule with the following hyperaddition “⊎”

$$\begin{array}{cccc}\mathsf{\uplus }& A& \mathsf{1}+A& \mathsf{2}+A\\ A& A& \mathsf{1}+A& \mathsf{2}+A\\ \mathsf{1}+A& \mathsf{1}+A& \mathsf{1}+A& \mathsf{1}+A\\ \mathsf{2}+A& \mathsf{2}+A& \mathsf{1}+A& \{A,\mathsf{2}+A\}\end{array}$$

and the external operation $\odot :R\times \frac{R}{A}⟶\frac{R}{A}$ via $r\odot (a+A)=ra+A$ for all $r\in R$ and $a+A\in \frac{R}{A}$. Also, if M is any simple hypermodule over the hyperring, it is seen that the M is isomorphic to $\frac{R}{A}$ by using Theorem 3 again.

Example 5.

Given the ring ${\mathbb{Z}}_4=\{\overline{0},\overline{1},\overline{2},\overline{3}\}$ and ${\mathbb{Z}}_4^{*}=\{\overline{1},\overline{3}\}$. Using Remark 1, we obtain that $\frac{{\mathbb{Z}}_4}{{\mathbb{Z}}_4^{*}}=\{\left\{\overline{0}\right\},\left\{\overline{2}\right\},{\mathbb{Z}}_4^{*}\}$. As in Remark 1, we consider the following tables:

$$\begin{array}{cccc}+\hfill & \left\{\overline{0}\right\}& \left\{\overline{2}\right\}& {\mathbb{Z}}_4^{*}\\ \left\{\overline{0}\right\}& \left\{\overline{0}\right\}& \left\{\overline{2}\right\}& {\mathbb{Z}}_4^{*}\\ \left\{\overline{2}\right\}& \left\{\overline{2}\right\}& \left\{\overline{0}\right\}& {\mathbb{Z}}_4^{*}\\ {\mathbb{Z}}_4^{*}& {\mathbb{Z}}_4^{*}& {\mathbb{Z}}_4^{*}& \{\left\{\overline{0}\right\},\left\{\overline{2}\right\}\}\end{array}$$

and

$$\begin{array}{cccc}.\hfill & \left\{\overline{0}\right\}& \left\{\overline{2}\right\}& {\mathbb{Z}}_4^{*}\\ \left\{\overline{0}\right\}& \left\{\overline{0}\right\}& \left\{\overline{0}\right\}& \left\{\overline{0}\right\}\\ \left\{\overline{2}\right\}& \left\{\overline{0}\right\}& \left\{\overline{0}\right\}& \left\{\overline{2}\right\}\\ {\mathbb{Z}}_4^{*}& \left\{\overline{0}\right\}& \left\{\overline{2}\right\}& {\mathbb{Z}}_4^{*}\end{array}$$

Then, $(\frac{{\mathbb{Z}}_4}{{\mathbb{Z}}_4^{*}},+,.)$ is a commutative hyperring with unity. Let $R=\frac{{\mathbb{Z}}_4}{{\mathbb{Z}}_4^{*}}$ and $M=\{\left\{\overline{0}\right\},\left\{\overline{2}\right\}\}$. Therefore, M is a maximal hyperideal of R and then $\frac{R}{M}=\{M,{\mathbb{Z}}_4^{*}+M\}$. It follows that M and $\frac{R}{M}$ are simple R-hypermodules.

Example 6.

Let F be a field with zero characteristic and G be the set of all nth roots of unity in F, where n is a positive integer. It is well known that G is a cyclic subgroup of $(F\setminus \{0\},·)$. Following Remark 1 and Lemma 1, the $\frac{F}{G}$-hypermodule $\frac{F}{G}$ is simple.

Recall from [6,36] that a subhypermodule N of a hypermodule M is small and denoted by $N\ll M$ if whenever $K\le M$, $N+K=M$ or $K+N=M$ implies that $K=M$, or equivalently $N+K\ne M$ and $K+N\ne M$ for every proper subhypermodule K of M.

Proposition 1.

Let R be a hyperring. Then, every simple R-hypermodule has only one small subhypermodule.

Proof. 

The proof is straightforward. □

Let M be an R-hypermodule. In [7], a subhypermodule N of M is called essential in M and denoted by $N⊵M$ if $N\cap L=\left\{0_M\right\}$ implies $L=\left\{0_M\right\}$ for every proper subhypermodule L of M.

Proposition 2.

Let M be a simple hypermodule. Then,

(1) 

$M⊵M$.

(2) 

M and $\left\{0_M\right\}$ are the only direct summands of M.

Proof. 

It is clear by definition. □

Let M and N be two hypermodules over a hyperring R. The set of all normal homomorphisms from M to N is denoted by $Ho{m}_R(M,N)$. For $f,g\in Ho{m}_R(M,N)$ and $m\in M$, as in [37], define

$$f\oplus g=\{h\in Hom(M,N\left)\right|h\left(m\right)\in f\left(m\right)+g\left(m\right)\}.$$

Then, $(Ho{m}_R(M,N),\oplus )$ is a canonical hypergroup. Let $M=N$ and so $Ho{m}_R(M,M)=En{d}_R\left(M\right)$. For any element $m\in M$ and $f,g\in En{d}_R\left(M\right)$, we consider the operation on $En{d}_R\left(M\right)$ by $(f·g)\left(m\right)=f\left(g\right(m\left)\right)$. It follows from lemma 2 in [37] that $En{d}_R\left(M\right)$ is a hyperring.

Theorem 4.

Let M be a simple R-hypermodule. Then, $(En{d}_R\left(M\right),·)$ is a group.

Proof. 

Clearly, the identity map $I_M:M⟶M$ is a normal homomorphism and so $I_M$ is the identity element of $(En{d}_R\left(M\right),·)$. Therefore, by lemma 2 in [37], it will suffice to show every nonzero element of $En{d}_R\left(M\right)$ has an inverse. Let $0\ne f\in En{d}_R\left(M\right)$. It follows from Lemma 2 that f is injective and $f\left(M\right)=M$. So f is invertible. This means that $(En{d}_R\left(M\right),·)$ is a group. □

Now, we will investigate when simple hypermodules are normal projective. Let M be an R-hypermodule, $K\le M$, and L be a non-empty subset of M. Consider the set

$$(K:L)=\{r\in R|rL\subseteq K,thatis,r·a\in Kforalla\in L\}.$$

Lemma 3.

Let R be a hyperring, M be an R-hypermodule, $K\le M$, and L be a non-empty subset of M. Then, $(K:L)$ is a left hyperideal of R. In particular, $(K:L)$ is a hyperideal of R in the case that L is a subhypermodule of M.

Proof. 

Since L is a non-empty subset of M, we obtain $m\in L$, and so, $0_R·m=0_M\in K$. Therefore, $0_R\in (K:L)\ne \varnothing$. Let $u,v\in (K:L)$ and $r\in R$. Now, for all $a\in L$, $(u-v)·a=u·a-v·a\in K$ and $\left(ru\right)·a=r(u·a)\in K$. It follows that $u-v,ru\in (K:L)$. Thus, $(K:L)$ is a left hyperideal of R.

Next, we suppose that L is a subhypermodule of M. Let $r\in R$, $u\in (K:L)$ and $a\in L$ be any elements. Then, $\left(ur\right)a=u\left(ra\right)\in K$ and so $(K:L)$ is a hyperideal of R. □

Now, set $K=\left\{0_M\right\}$ and let L be a subhypermodule of an R-hypermodule M. Then, by Lemma 3, $(0_M:L)$ is a hyperideal of R. We say $(0_M:L)$ is the annihilator of L in R and is written by $(0_M:L)=Ann\left(L\right)$.

Let R be a hyperring, M be an R-hypermodule, S be a non-empty set of R, and K be a subhypermodule of M. Consider the set

$$\left(K{:}_{M}S\right)=\{m\in M|Sm\subseteq K,thatis,s·m\in Kforalls\in S\}.$$

Lemma 4.

Let R be a hyperring, M be an R-hypermodule, $K\le M$, and S be a right hyperideal of R. Then, $\left(K{:}_{M}S\right)$ is a subhypermodule of M containing K.

Proof. 

For every $s\in S$, $s·0_M=0_M\in K$, and so, $0_M\in \left(K{:}_{M}S\right)\ne \varnothing$. Let $m_1,m_2\in \left(K{:}_{M}S\right)$ and $r\in R$. For all $s\in S$, $s·(m_1-m_2)=s·m_1-s·m_2\in K$ because K is a subhypermodule of K. Moreover, $s·\left(r{m}_1\right)=\left(sr\right)·m_1\in K$. This means that $\left(K{:}_{M}S\right)$ is a subhypermodule of M.

Let $k\in K$. Then, $sk\in K$ for all $s\in S$. It follows that $k\in \left(K{:}_{M}S\right)S$, and so, $K\subseteq \left(K{:}_{M}S\right)$. This completes the proof. □

Let M be an R-hypermodule and $m\in M$. Then, by Lemma 3, $(0_M:m)=ann\left(m\right)$ is a left hyperideal of R. The left hyperideal $(0_M:m)$ is called the annihilator of m in R.

Theorem 5.

Let $M_1$ and $M_2$ be two R-hypermodules. If $M_1\cong M_2$, then $Ann\left(M_1\right)=Ann\left(M_2\right)$. In particular, if the elements $m_1\in M_1$ and $m_2\in M_2$ are connected under this isomorphism, then $Ann\left(m_1\right)=Ann\left(m_2\right)$.

Proof. 

Let $f:M_1⟶M_2$ be a normal isomorphism, $r\in Ann\left(M_1\right)$ and $m_2\in M_2$. Since f is surjective, there exists an element $m_1$ of $M_1$ such that $m_2=f\left(m_1\right)$. Now,

$$r·m_2=r·f\left(m_1\right)=f(r·m_1)=f\left(0_{M_1}\right)=0_{M_2}$$

that is, $r\in Ann\left(M_2\right)$. So, $Ann\left(M_1\right)\subseteq Ann\left(M_2\right)$. If a similar method is applied, $Ann\left(M_2\right)\subseteq Ann\left(M_1\right)$. This means that $Ann\left(M_2\right)=Ann\left(M_1\right)$, as required. □

It is well known that a ring $(R,+,.)$ with identity is a division ring, that is, $(R\setminus \left\{0_R\right\},.)$ is a group if and only if ${}_{R}R$ is a simple module. We give an analogous characterization of this fact for hyperrings.

Theorem 6.

Let R be a hyperring. Then, the R-hypermodule R is simple if and only if $(R\setminus \left\{0_R\right\},·)$ is a group.

Proof. 

The proof is straightforward. □

Let M be an R-hypermodule. Consider the set

$$Z\left(M\right)=\{m\in M|I·m=0_{M}forsomeessentiallefthyperidealIofR\}.$$

Now, we prove the following theorem.

Theorem 7.

Let M be an R-hypermodule. Then, $Z\left(M\right)$ is a subhypermodule of M.

Proof. 

Obviously, $0_M\in Z\left(M\right)$. Let $m_1,m_2\in Z\left(M\right)$ and $m\in m_1+m_2$. Firstly, we will show that $m\in Z\left(M\right)$. Since $m_1,m_2\in Z\left(M\right)$, we have $Ann\left(m_1\right)⊵R$ and $Ann\left(m_2\right)⊵R$, and so, $Ann\left(m_1\right)\cap Ann\left(m_2\right)⊵R$. Now, we consider the annihilator of the set $m_1+m_2$, that is,

$$Ann(m_1+m_2)=(0_M:(m_1+m_2))=\{r\in R|r·x=0_{M}forallx\in m_1+m_2\}.$$

If $r\in Ann\left(m_1\right)\cap Ann\left(m_2\right)$, then we can write $r·(m_1+m_2)=r·m_1+r·m_2=0_M+0_M=0_M$. Because of this, we obtain $r·m\in r·(m_1+m_2)=\{r·a\in M|a\in m_1+m_2\}=\left\{0_M\right\}$, and so, $r·m=0_M$. It follows that $Ann\left(m_1\right)\cap Ann\left(m_2\right)\subseteq Ann\left(m\right)⊵R$. Hence, $m_1+m_2\subseteq Z\left(M\right)$.

Let $r\in R$ and $m\in Z\left(M\right)$. Suppose that $s\in R\setminus Ann\left(m\right)$. Therefore, $s·(r·m)=\left(sr\right)·m\ne 0_M$, and then, $sr\notin Ann\left(m\right)$. Since $Ann\left(m\right)⊵R$, we can write $0_M\ne t\left(sr\right)\in Ann\left(m\right)$ for some element $t\in R$. Note that $ts\ne 0_R$. Now, $\left(ts\right)·(r·m)=0_M$, and so, $ts\in Ann\left(m\right)$. This means that $Ann\left(rm\right)$ is an essential left hyperideal of R. Hence, $Z\left(M\right)$ is a subhypermodule of M. □

Let M be a hypermodule. We say the subhypermodule $Z\left(M\right)$ is a singular subhypermodule of M.

Lemma 5.

Let M be an R-hypermodule and $N⊵M$. Then, $\frac{M}{N}=Z\left(\frac{M}{N}\right)$.

Proof. 

Let $m+N\in \frac{M}{N}\setminus Z\left(\frac{M}{N}\right)$. Therefore, there exists an element $r\in R$ such that $r·(m+N)=r·m+N\ne N$, and so, $r·m\notin N$. This is a contradiction by assumption. □

By Theorem 2, a hyperring R is normal projective. It can be seen that every direct summand of R is normal projective. Using this fact we give the next result:

Theorem 8.

Let M be a simple R-hypermodule with zero singular subhypermodule. Then, M is normal projective.

Proof. 

By Theorem 3, there exists a left maximal hypermodule I of R such that M is isomorphic to $\frac{R}{I}$. If I is essential in R, it follows from Lemma 5 that $Z\left(\frac{R}{I}\right)=\frac{R}{I}$. By Theorem 5, we can write $\frac{R}{I}=Z\left(\frac{R}{I}\right)\cong Z\left(M\right)=0$, a contradiction. Therefore, there exists a left hyperideal J of R with $I\cap J=\left\{0_R\right\}$. Since I is a maximal left hyperideal of R, we obtain that $R=I\oplus J$, and so, J is normal projective. Hence, $J\cong M$ is normal projective. □

Corollary 2.

Let M be a simple hypermodule. Then, $M=Z\left(M\right)$ or M is normal projective.

Proof. 

By Theorem 8. □

Example 7.

Consider the hyperring $R=\{0,1,2,3\}$ with the following tables:

$$\begin{array}{ccccc}\hfill +& 0& 1& 2& 3\\ 0& \left\{0\right\}& \left\{1\right\}& \left\{2\right\}& \left\{3\right\}\\ 1& \left\{1\right\}& \{0,2\}& \{1,3\}& \{0,2\}\\ 2& \left\{2\right\}& \{1,3\}& \left\{0\right\}& \left\{1\right\}\\ 3& \left\{3\right\}& \{0,2\}& \left\{1\right\}& \{0,2\}\end{array}$$

and

$$\begin{array}{ccccc}.& 0& 1& 2& 3\\ 0& 0& 0& 0& 0\\ 1& 0& 1& 2& 3\\ 2& 0& 2& 0& 2\\ 3& 0& 3& 2& 1\end{array}$$

It follows that $N=\{0,2\}$ is a simple R-hypermodule and $Z\left(N\right)=N$. Thus, N is singular.

Example 8.

Let $\mathbb{R}$ be the set of real numbers and H be a subgroup of the multiplicative group of $\mathbb{R}$. Since $\mathbb{R}$ is a field, by Remark 1, $\frac{\mathbb{R}}{H}$ is a hyperfield, and so, $0_{\frac{\mathbb{R}}{H}}$ is a maximal hyperideal of $\frac{\mathbb{R}}{H}$. Therefore, the $\frac{\mathbb{R}}{H}$-hypermodule $\frac{\mathbb{R}}{H}$ is simple by Lemma 1. Hence, $\frac{\mathbb{R}}{H}$ is normal projective according to Theorem 2.

5. Semisimple Hypermodules

Let R be a hyperring and M be an R-hypermodule. By $Soc\left(M\right)$ we denote the sum of all simple subhypermodules of M.

Example 9.

Let us take the hyperring R as the hyperring in Example 4. Assume that M is the R-hypermodule R. Then, $Soc\left(M\right)=\{0,2\}\ne M$.

In this section, we introduce the concept of semisimple hypermodules. We show that the class of semisimple hypermodules is closed under internal direct sums, factor hypermodules, and subhypermodules.

Definition 3.

Let R be a hyperring and M be an R-hypermodule. M is called semisimple if $M=Soc\left(M\right)$, that is, it is the sum of simple R-subhypermodules of M.

Example 10.

Let $R=\{0,1,2,3\}$ with hyperoperation “+” and operation “.”:

$$\begin{array}{ccccc}+& \mathsf{0}& \mathsf{1}& \mathsf{2}& \mathsf{3}\\ \mathsf{0}& \mathsf{\left\{}\mathsf{0}\mathsf{\right\}}& \left\{\mathsf{1}\right\}& \left\{\mathsf{2}\right\}& \left\{\mathsf{3}\right\}\\ \mathsf{1}& \left\{\mathsf{1}\right\}& \{\mathsf{0},\mathsf{1}\}& \left\{\mathsf{3}\right\}& \{\mathsf{2},\mathsf{3}\}\\ \mathsf{2}& \left\{\mathsf{2}\right\}& \mathsf{\left\{}\mathsf{3}\mathsf{\right\}}& \mathsf{\left\{}\mathsf{0}\mathsf{\right\}}& \mathsf{\left\{}\mathsf{1}\mathsf{\right\}}\\ \mathsf{3}& \left\{\mathsf{3}\right\}& \{\mathsf{2},\mathsf{3}\}& \left\{\mathsf{1}\right\}& \{\mathsf{0},\mathsf{1}\}\end{array}$$

and

$$\begin{array}{ccccc}.& \mathsf{0}& \mathsf{1}& \mathsf{2}& \mathsf{3}\\ \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{1}& \mathsf{0}& \mathsf{0}& \mathsf{0}& \mathsf{0}\\ \mathsf{2}& \mathsf{0}& \mathsf{0}& \mathsf{2}& \mathsf{2}\\ \mathsf{3}& \mathsf{0}& \mathsf{0}& \mathsf{2}& \mathsf{2}\end{array}$$

Then, R is an R-hypermodule. It is easy to see that the only proper subhypermodules of R are $M_0=\left\{0\right\}$, $M_1=\{0,1\}$, and $M_2=\{0,2\}$. Therefore, $M_1$ and $M_2$ are simple subhypermodules of M, and so we can write $R=M_1+M_2$. This means that the R-hypermodule R is semisimple.

Now, we will prove the main theorem that gives the characterization of semisimple hypermodules. Firstly we need the following key lemmas.

Lemma 6.

Assume that $M={\sum }_{k\in K}{M}_k$ is a semisimple hypermodule, where each $M_k$ is a simple subhypermodule of M for every $k\in K$. Let A be any subhypermodule of M. Then, there exists an index set $J\subseteq K$ such that $M=A\oplus \left({⨁}_{j\in J}{M}_j\right)$.

Proof. 

Let A be any subhypermodule of M. Now, we consider the following set:

$$\mathsf{\Gamma }=\{L\subseteq K|A+\left({\sum }_{l\in L}{M}_l\right)=A\oplus \left({⨁}_{l\in L}\right)M_l\}.$$

Then, $\varnothing \in \mathsf{\Gamma }$, and so, $\mathsf{\Gamma }\ne \varnothing$. Therefore, $\mathsf{\Gamma }$ is an ordered set by “⊆”. For any chain $\mathsf{\Lambda }\subseteq \mathsf{\Gamma }$, let $L_0={\bigcup }_{L\in \mathsf{\Lambda }}L$. Now, we show that $L_0\in \mathsf{\Gamma }$. Suppose that $0\in a+m_{i_1}+m_{i_2}+...+m_{i_n}$, where $a\in A$, $i_1,i_2,...,i_n\in L$, and $m_{i_1}\in M_{i_1},m_{i_2}\in M_{i_1},...,M_{i_n}$. Since $\mathsf{\Lambda }$ is chain, there exists $L^{\prime }$ in $\mathsf{\Gamma }$ with $i_1,i_2,...,i_n\in L_{\prime }$. It follows that the sum $a+m_{i_1}+m_{i_2}+...+m_{i_n}$ belongs to the direct sum $A\oplus \left({⨁}_{l\in L}{M}_l\right)$, and so, $a=m_{i_1}=m_{i_2}=...=m_{i_n}=0$. Let $B=A\oplus \left({⨁}_{j\in J}{M}_j\right)$. If $k\in K$, then $A+M_k\ne A\oplus M_k$ since J is maximal. So, $M_k\subseteq B$. This implies that $M={\sum }_{k\in K}{M}_k=B$. Hence, $M=A\oplus \left({⨁}_{j\in J}{M}_j\right)$, as required. □

Lemma 7.

Let M be an R-hypermodule and m be a nonzero element of M. Then, $Rm$ contains a maximal subhypermodule.

Proof. 

Let A be a proper subhypermodule of $Rm$. Now, we consider the set:

$$\mathsf{\Omega }=\{B\subset Rm|A\subseteq B\}.$$

Then, $\mathsf{\Omega }$ is an ordered set by “⊆”. If a similar method to that used in the proof of Lemma 6 is applied, the set $\mathsf{\Omega }$ has a maximal element, say U. It is obvious that U is a maximal subhypermodule of $Rm$. □

Theorem 9.

The following conditions are equivalent for a hypermodule M.

(1) 

M is semisimple.

(2) 

M is a direct sum of simple subhypermodules.

(3) 

Every subhypermodule of M is a direct summand of M.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$ If $M={\sum }_{k\in K}{M}_k$, where $M_k$ is a simple subhypermodule of M for every $k\in K$, there exists an index set $J\subseteq K$ such that $M=\left\{0_M\right\}\oplus \left({⨁}_{j\in J}{M}_j\right)={⨁}_{j\in J}{M}_j$ by Lemma 6.

$\left(2\right)\Rightarrow \left(3\right)$ Suppose that $M={⨁}_{k\in K}{M}_k$, where each $M_k$ is a simple subhypermodule of M for every $k\in K$. Let A be any submodule of M. It follows from Lemma 6 that $M=A\oplus \left({⨁}_{j\in J}{M}_j\right)$ for some subset $J\subseteq K$. This completes the proof of $\left(2\right)\Rightarrow \left(3\right)$.

$\left(3\right)\Rightarrow \left(1\right)$ By the hypothesis, there exists a submodule A of M with $M=Soc\left(M\right)\oplus A$. Let m be a nonzero element of A. It follows from Lemma 7 that $Rm$ has a maximal submodule, say U. Again applying the hypothesis, U is a direct summand of M, and so, we can write $M=U\oplus V$ for some submodule V of M. Clearly, V is simple, and then, $V\subseteq Soc\left(M\right)\cap A=\left\{0_M\right\}$, a contradiction. Hence, $M=Soc\left(M\right)$, that is, it is semisimple. □

Corollary 3.

Every subhypermodule of a semisimple hypermodule is semisimple.

Proof. 

Let M be a semisimple hypermodule and A be any subhypermodule of M. If B is a subhypermodule of A, then it follows from Theorem 9 that M has the decomposition $M=B\oplus B^{\prime }$ for some subhypermodule $B^{\prime }$ of M. By modularity, we can write $A=A\cap M=A\cap (B\oplus B^{\prime })=B\oplus (A\cap B^{\prime })$. Again applying Theorem 9, we obtain that A is semisimple. □

Proposition 3.

Let M be a hypermodule. Then, $Soc\left(M\right)=\bigcap \left\{N\right|N⊵M\}$ and $Soc\left(M\right)$ is the largest semisimple subhypermodule of M.

Proof. 

Let N be an essential subhypermodule of M. If S is a simple subhypermodule of M, then $0\ne S\cap N=S\subseteq N$. It follows that $Soc\left(M\right)\subseteq N$, and so, we can write $Soc\left(M\right)\subseteq \bigcap \left\{N\right|N⊵M\}$.

Set $N_0=\bigcap \left\{N\right|N⊵M\}$ and let A be any submodule of $N_0$. By Zorn’s lemma, we choose a subhypermodule B of M such that it is maximal in the set of all subhypermodules $E\subseteq M$ with $A\cap E=0$. By Proposition 3.11-(1) in [21], we can write $A\oplus B⊵M$. It follows from the definition of $N_0$ that $A\subseteq N_0\subseteq A\oplus B$. Now, let us apply the modular law

$$\begin{array}{c}\hfill \begin{array}{ccc}{N}_0\hfill & =\hfill & N_0\cap (A\oplus B)\hfill \\ & =\hfill & A\oplus (N_0\cap B).\hfill \end{array}\end{array}$$

This means that A is a direct summand of $N_0$, and so, $N_0$ is a semisimple subhypermodule of M according to Theorem 9. Hence, we obtain $Soc\left(M\right)=N_0=\bigcap \left\{N\right|N⊵M\}$. □

The next result is crucial.

Corollary 4.

Let M be an R-hypermodule. Then, M is semisimple if and only if $N⊵M$ implies that $N=M$.

Proof. 

By Proposition 3. □

Lemma 8.

Let $f:M⟶N$ be a normal homomorphism of hypermodules. Then, $f\left(Soc\right(M\left)\right)\subseteq Soc\left(N\right)$.

Proof. 

It follows from Corollary 1. □

Observe from Lemma 8 that for every $f\in End\left(M\right)$$f\left(Soc\right(M\left)\right)\subseteq Soc\left(M\right)$.

Corollary 5.

Every factor hypermodule of a semisimple hypermodule is semisimple.

Proof. 

Let M be a semisimple hypermodule and U be any subhypermodule of M. Consider the normal epimorphism $\varphi :M⟶\frac{M}{U}$ via $\psi \left(m\right)=m+U$ for all $m\in M$. Therefore, $\frac{M}{U}=\psi \left(M\right)=\psi \left(Soc\left(M\right)\right)\subseteq Soc\left(\frac{M}{U}\right)$ according to Lemma 8. This implies that $\frac{M}{U}$ is a semisimple hypermodule. □

Now, we shall prove the next result.

Theorem 10.

Let R be a hyperring. Then, $Soc{(}_{R}R)$ is a hyperideal of R.

Proof. 

Since any intersection of left hyperideals of R is a left hyperideal of R, it follows from Proposition 3 that $Soc{(}_{R}R)$ is a left hyperideal of R. Let $r\in R$ and let $f{:}_{R}R{⟶}_{R}R$ by $f\left(s\right)=sr$ for all $s\in R$. Then, for any elements $u,v,s\in R$,

$$f(u+v)=(u+v)s=us+vs=f\left(u\right)+f\left(v\right)$$

and

$$f\left(us\right)=\left(us\right)r=u\left(sr\right)=uf\left(s\right).$$

This means that f is a normal homomorphism of hypermodules. By Lemma 8, we have $f\left(Soc{(}_{R}R)\right)=Soc{(}_{R}R)r\subseteq Soc{(}_{R}R)$, and so, $Soc{(}_{R}R)R\subseteq Soc{(}_{R}R)$, that is, $Soc{(}_{R}R)$ is a right hyperideal of R. Hence, $Soc{(}_{R}R)$ is a hyperideal of R. □

Proposition 4.

Let M be a hypermodule and K be a subhypermodule of M. Then, $Soc\left(K\right)=K\cap Soc\left(M\right)$.

Proof. 

The inclusion $Soc\left(K\right)\subseteq K\cap Soc\left(M\right)$ is clear by definition. Let $m\in K\cap Soc\left(M\right)$. By Corollary 3, $Rm$ is semisimple, and so, $m=1_R·m\in Rm\subseteq Soc\left(K\right)$. Therefore, $K\cap Soc\left(M\right)\subseteq Soc\left(K\right)$. So, we deduce that $Soc\left(K\right)=K\cap Soc\left(M\right)$. □

Theorem 11.

Let ${\left\{M_i\right\}}_{i\in I}$ be a family of subhypermodules of an R-hypermodule M. If the sum ${\sum }_{i\in I}{M}_i$ is an internal direct sum, then $Soc\left({⨁}_{i\in I}{M}_i\right)={⨁}_{i\in I}Soc\left(M_i\right)$.

Proof. 

Let ${\sum }_{i\in I}{M}_i={⨁}_{i\in I}{M}_i$. For every $i\in I$, it is clear that $Soc\left(M_i\right)\subseteq Soc\left({⨁}_{i\in I}{M}_i\right)$, and so, ${⨁}_{i\in I}Soc\left(M_i\right)\subseteq Soc\left({⨁}_{i\in I}{M}_i\right)$. Let $m={\left(m_i\right)}_{i\in I}\in Soc\left({⨁}_{i\in I}{M}_i\right)$. Consider the normal homomorphism ${\pi }_k:{⨁}_{i\in I}{M}_i⟶M_k$ via ${\pi }_k\left({\left(m_i\right)}_{i\in I}\right)=m_k$ for all ${\left(m_i\right)}_{i\in I}\in {⨁}_{i\in I}{M}_i$. By Lemma 8, we obtain ${\pi }_k\left(m\right)={\pi }_k\left({\left(m_i\right)}_{i\in I}\right)=m_k\in Soc\left(M_k\right)$. It follows that $m={\left(m_i\right)}_{i\in I}\in {⨁}_{i\in I}Soc\left(M_i\right)$. This completes the proof. □

The following is a direct consequence of Theorem 11.

Corollary 6.

Every direct sum of semisimple subhypermodules of a hypermodule is semisimple.

Lemma 9.

If an R-hypermodule M is semisimple, then $Rad\left(M\right)=\left\{0_M\right\}$.

Proof. 

Let M be a semisimple Krasner R-hypermodule and m be a nonzero element of M. By Theorem 9, $Rm$ is a direct summand of M, and so, there exists a proper subhypermodule K of M such that $M=Rm+K$. This means that $Rm$ is not small in M. Hence, $Rad\left(M\right)=\left\{0_M\right\}$. □

Proposition 5.

Let M be an R-hypermodule and N be a semisimple subhypermodule of M. If $N\subseteq Rad\left(M\right)$, then N is small in M.

Proof. 

Given a subhypermodule K with $M=N+K$, since N is semisimple, by Theorem 9 N has a decomposition $N=(N\cap K)\oplus V$ for some subhypermodule V of N. Now, we can write

$$M=N+K=\left[\right(N\cap K)\oplus V]+K=V+K.$$

Note that $\left\{0_M\right\}=(N\cap K)\cap V=K\cap V$, and thus, $M=V\oplus K$. Using Lemma 9, $Rad\left(M\right)=Rad\left(V\right)\oplus Rad\left(K\right)=Rad\left(K\right)$, and then, $V\subseteq N\subseteq Rad\left(M\right)=Rad\left(K\right)\subseteq K$. Since $\left\{0_M\right\}=V\cap K=V$, it follows that N is a small subhypermodule of M. □

6. Discussion

The basic properties of (semi)simple hypermodules have been provided. We have shown that if a hypermodule M is simple, then $\left(End\right(M),·)$ is a group, where $End\left(M\right)$ is the set of all normal endomorphisms of M. We have proved that every simple hypermodule is normal projective with a zero singular subhypermodule. We have shown that the class of semisimple hypermodules is closed under internal direct sums, factor hypermodules, and subhypermodules. In particular, we have given a characterization of internal direct sums of subhypermodules of a hypermodule.

7. Conclusions

In this study, the properties of the (semi)simple module concept, which is among the most fundamental topics of module theory, in the hypermodule structure were investigated. The connection of (semi)simple hypermodules with other subjects could be studied and their results in multivalued groups could be studied. In addition, the properties of the (semi)simple concept in weak hypermodules could be examined, and the results it provides that are different from (semi)simple hypermodules could be obtained.