1. Introduction
Graph domination can model problems such as resource allocation, vehicle routing, dominating queens, etc. Furthermore, graph dominations have significant applications in chemistry because chemical structures are often represented as graphs. For example, domination theory is utilized to encrypt binary strings into DNA sequences. Methods like the basic method and the insertion method employ graph domination to encrypt any chemical formula. Each chemical formula is converted into a binary string through graph domination and subsequently encrypted using DNA steganography [
1].
The total and double total domination numbers have been widely studied on many chemical graphs such as the hexagonal grid, nanotubes, pyrene network, pyrene torus network, and hexabenzocoronene [
2,
3,
4,
5,
6,
7].
In this paper, we study total and double total domination on chains of octagons and octagonal grids. These systems are geometric objects obtained by arranging mutually congruent regular octagons in a plane. The octagonal chain and octagonal grid are special cases of octagonal graphs. An octagonal graph is a finite two-connected geometric graph where each interior face is bounded by a regular octagon or quadrangle with a side length of 1. Octagonal graphs have garnered significant interest from mathematicians due to their intriguing combinatorial properties. In [
8], the number of isomers of tree-like octagonal graphs is determined by the generating functions. Further, in [
9], it is demonstrated that every convex octagon has a side with a relative length of at most 1, a bound which is asymptotically tight. Combinatorial properties of fixed-boundary octagonal random tilings are explored in [
10]. In [
11], the connection between the number of perfect matchings in octagonal chain graphs and the Hosoya index of caterpillar trees is identified. More recently, in [
12], the authors examined the Wiener indices in certain types of random octagonal chains, and in [
13], the authors studied perfect matchings in random octagonal chain graphs.
We determine the exact values for the total domination number on a linear and on a double octagonal chain and an upper bound for the total domination number on a triple octagonal chain. Furthermore, we determine the exact values for the double total domination number on a linear and on a double octagonal chain and an upper bound for the double total domination number on a triple octagonal chain and on an octagonal grid .
Apart from this Introduction, the rest of this paper is organized as follows.
Section 2 presents the necessary preliminaries regarding total and double total domination. This section also serves to provide the foundational concepts and definitions that are essential for understanding graph theory.
Section 3 gives the exact values for the total domination number
on a linear and on a double octagonal chain and an upper bound for the total domination number on a triple octagonal chain.
Section 4 deals with double total domination and gives the double total dominating number
for a linear and a double octagonal chain and an upper bound for the double total domination number on a triple octagonal chain and for an arbitrary octagonal grid
.
2. Preliminaries
Total domination in graphs, initially introduced in [
14], has garnered significant attention and has evolved into a thoroughly explored area within graph theory. This concept has become foundational in the study of various graph theoretical properties and applications. Some more recent work about total domination can be found in [
15,
16,
17,
18,
19,
20].
Let G be a graph with the vertex set and edge set . The degree of a vertex , denoted by , is the number of edges that are incident to the vertex v. The maximum degree of a graph G, denoted by , is the highest degree among the vertices of G. Similarly, the minimum degree of a graph G, denoted by , is the lowest degree among the vertices of G.
The open neighborhood of v is , and the closed neighborhood of v is . For a set , its open neighborhood is the set , and its closed neighborhood is the set . A set is an open packing of G if the open neighborhoods of the vertices of S are pairwise disjoint in G. The open packing number of G, denoted by , is the maximum cardinality among all open packings of G.
A set
is a dominating set of a graph
G if every vertex
y in
is adjacent to some vertex in
D. The domination number
is the cardinality of the smallest dominating set. Open packings are the natural dual object of total dominating sets [
21]. Moreover, for every graph
G, it holds that
, and if
is both a dominating set and an open packing, then
[
22].
Total domination is the stronger version of domination. A set is a total dominating set of a graph G with no isolated vertex if every vertex y in is adjacent to some vertex in D. The total domination number is the cardinality of the smallest total dominating set. A set is a k-total dominating set of a graph G with no isolated vertex if each vertex in has at least k neighbors in D. The k-total domination number is the cardinality of the smallest k-total dominating set. For , the 2-total dominating set is called the double total dominating set.
Each vertex in the octagonal system is either of degree two or of degree three. It follows that on the octagonal system, there is no k-total domination for .
The domination polynomial of
G is the polynomial
, where
is the number of dominating sets of size
i. A root of
is called a domination root of
G. We denote the set of distinct domination roots by
. The characterization of graphs using domination polynomials is studied in [
23].
For more foundational concepts and definitions that are crucial for understanding graph theory, see [
24].
3. Total Domination Number of Octagonal Grid ,
We define an octagonal grid
as a grid with
m octagons in a row and
n octagons in a column. The octagonal row is also called an octagonal chain because it is constructed by consecutively connected octagons. There are
n octagonal chains on
. When
, it forms a linear octagonal chain; for
, it becomes a double octagonal chain; and for
, it is a triple octagonal chain. To label vertices in
, we use
subrows and
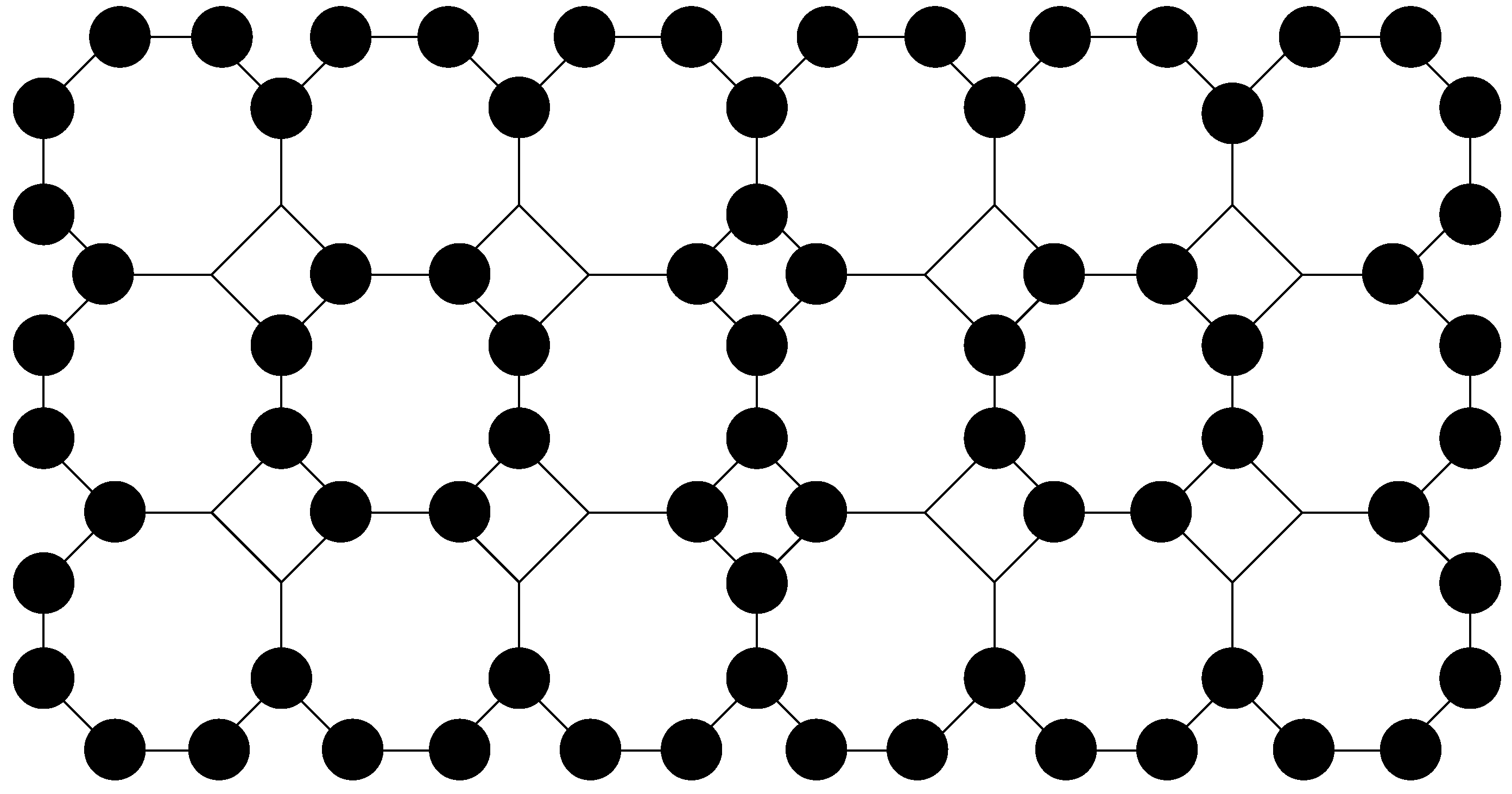
subcolumns. The vertex set
is defined as
where
,
. See
Figure 1.
Specifically, the border vertices on are vertices which are located on the top and on the bottom, on the left and on the right border of the graph.
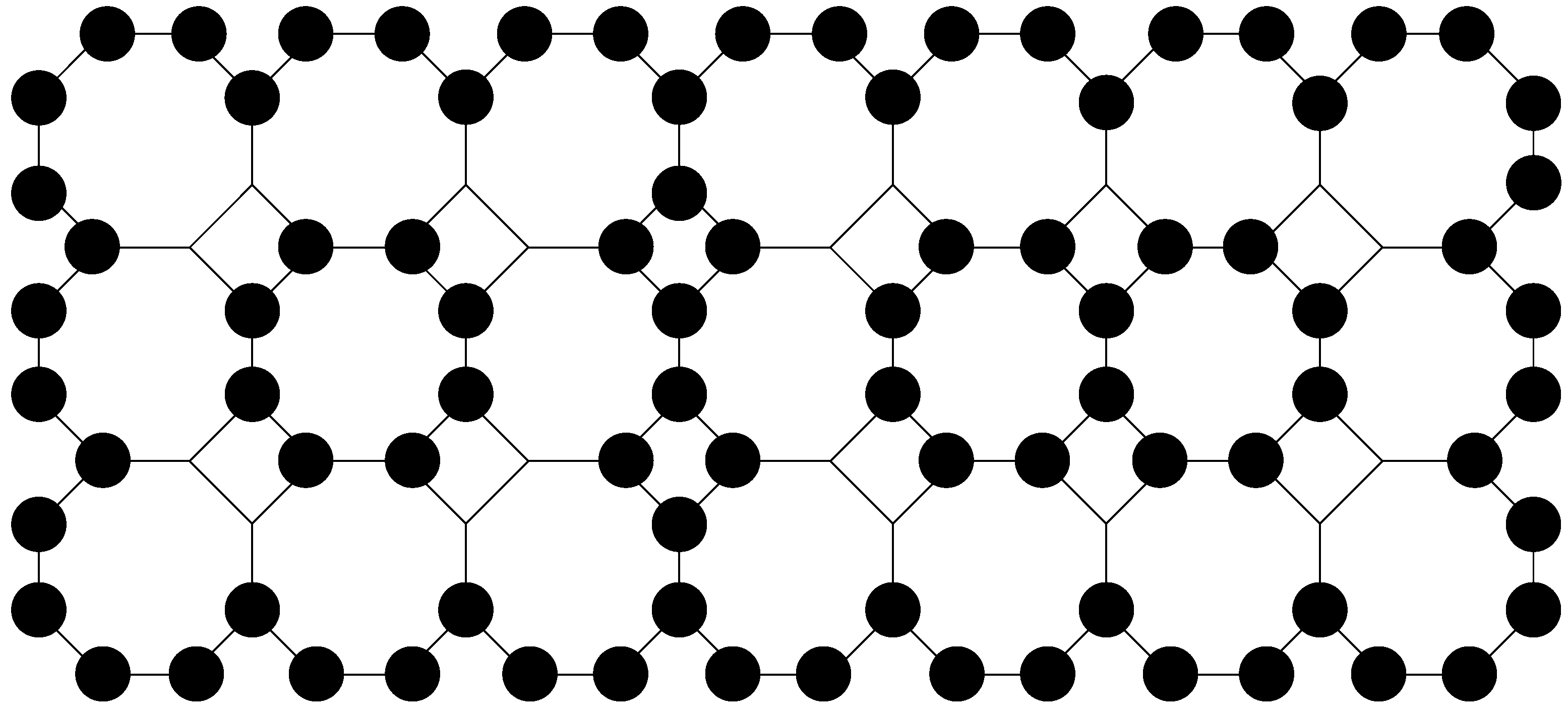
Theorem 1. For a linear octagonal chain with m octagons, it holds that Proof of Theorem 1. We define , where
D is the total dominating set on
, with each vertex being total dominated by exactly one vertex. See
Figure 2. Any total dominating set where each vertex in the graph is total dominated by exactly one vertex is minimal. If you remove just one arbitrary vertex from the total dominating set, at least one vertex on the graph will not be total dominated. It follows that
□
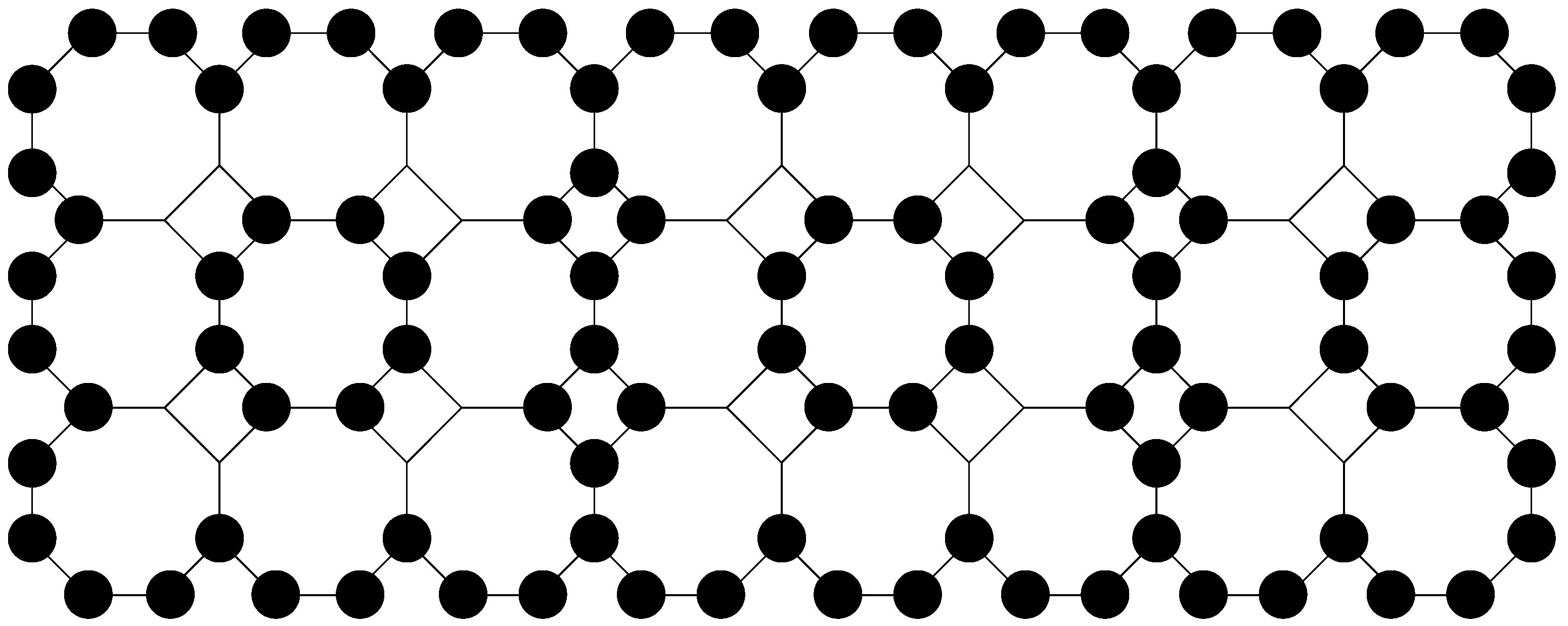
Theorem 2. For a double octagonal chain with m octagons, it holds that Proof of Theorem 2. We define
∪
∪
∪
∪
, where
It is easy to see that all vertices are total dominated by set
D, so
See
Figure 3. Vertices
∪
total dominate all vertices on the first four subrows on
. This structure is optimal as follows. Firstly, each vertex is total dominated by exactly one vertex. Secondly, because of the grid structure, vertices from some subrow can only total dominate vertices from the subrow below or subrow above.
Further, vertices from the fifth, sixth and seventh subrows must be total dominated. Vertices from the fifth row must not be in the total dominating set because vertices from the fourth row would then be total dominated by two vertices. To total dominate vertices from the fifth subrow, we need at least all vertices from the sixth subrow. This ensures that every vertex in the first five subrows is also total dominated by exactly one vertex.
Finally, to total dominate vertices from the sixth subrow, we need at least
vertices from the seventh subrow which are adjacent to the vertices from the sixth subrow. In such a case, all vertices from the sixth subrow are total dominated by exactly one vertex. Furthermore, all vertices from the seventh subrow are total dominated by exactly one vertex except for vertices
and
, which are total dominated by two vertices. However, both vertices
and
must be in the total dominating set to total dominate
and
, respectively. See
Figure 3. It follows that
□
Theorem 3. From Ref. [25], for , it holds that The statement proved in Theorem 3 will be used in our following Theorem 4.
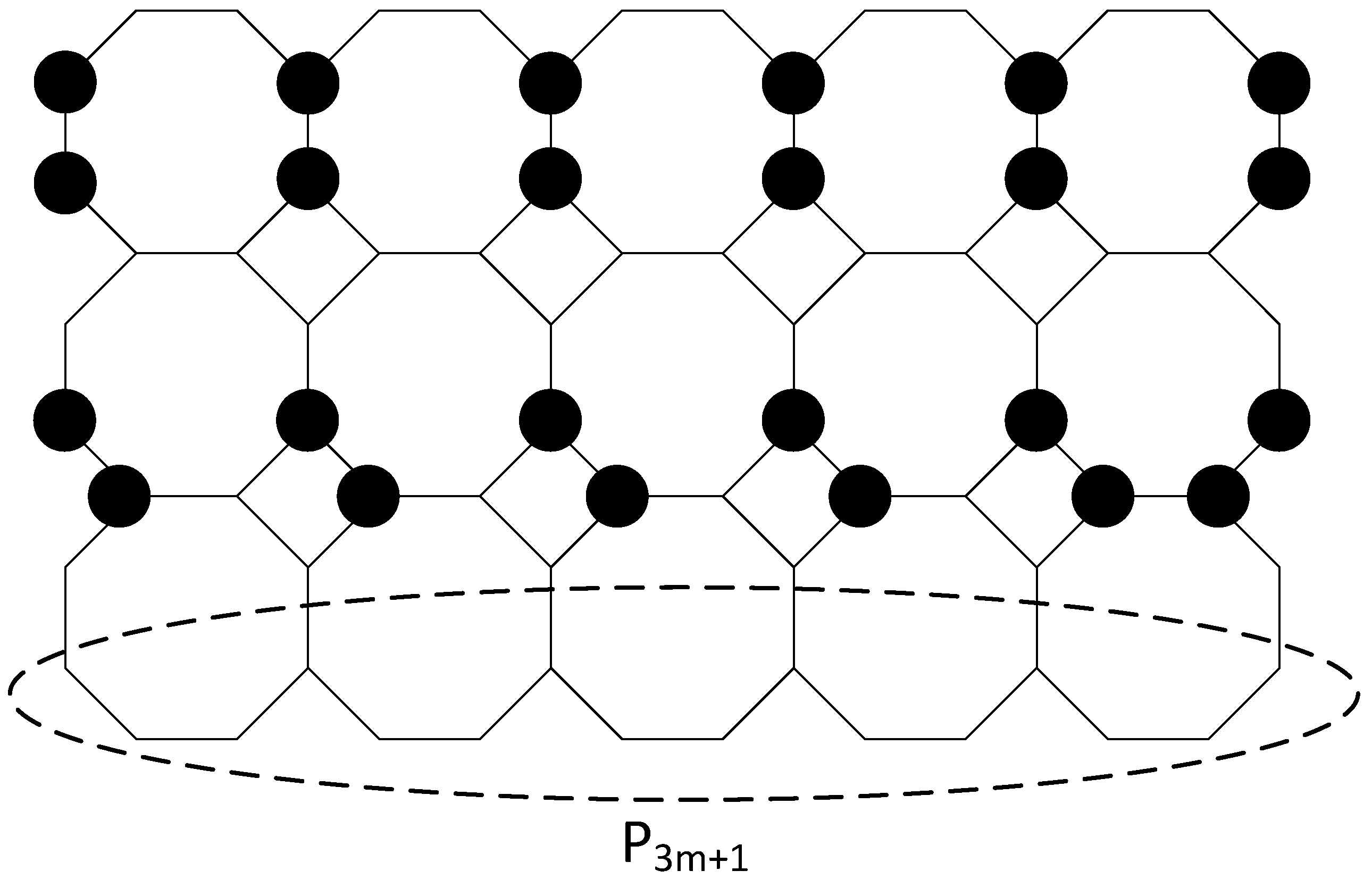
Theorem 4. For a triple octagonal chain with m octagons, it holds that Proof of Theorem 4. We define ∪∪ ∪∪. According to Theorem 2, this is a minimal total dominating set on and .
It is easy to see that if we have on , all vertices from the first eight subrows on are total dominated. This is optimal because a maximum of eight subrows can be total dominated by vertices from two octagonal rows. In more detail, the last subrow on the second octagonal row is the seventh subrow. Therefore, only vertices from the third octagonal row which can be total dominated from vertices belonging to the second octagonal row are vertices on the eighth subrow.
Further, we notice that vertices on the 9th and 10th subrows make a path
. See
Figure 4.
From Theorem 3, it follows that
Furthermore, if
, then
. Then,
together with the minimal total dominating set on
is the total dominating set on
, and
□
4. Double Total Domination on Octagonal Grid
Theorem 5. For a linear octagonal chain with m octagons, it holds that Proof of Theorem 5. In the linear octagonal chain, every vertex is adjacent to at least one vertex of degree two. To achieve double total domination, all vertices on the graph must be in the double total domination set. There are
vertices on the linear octagonal chain; hence,
□
Lemma 1. There are exactly border vertices on , and each of them must be in any double total dominating set.
Proof of Lemma 1. First, we see that there are exactly vertices on the border of . There are on the top and on the bottom borders, respectively. Furthermore, there are on each side border. Hence, there are border vertices. Further, all of them are adjacent to at least one vertex of degree two. So, they all must be in any double total dominating set. □
Proof of Lemma 2. From Lemma 1, it follows that the border on has 20 vertices, and each of them must be in any double total dominating set. The remaining four internal vertices which form are only total dominated once. To double total dominate , we need at least two more vertices. Therefore, □
Theorem 6. For a double octagonal chain with octagons, it holds that Proof of Theorem 6. From Lemma 1, it follows that the border on
has
vertices, and each of them must be in any double total dominating set. We note the border vertices with
B. Next, we define
∪
∪
∪
,
. See
Figure 5.
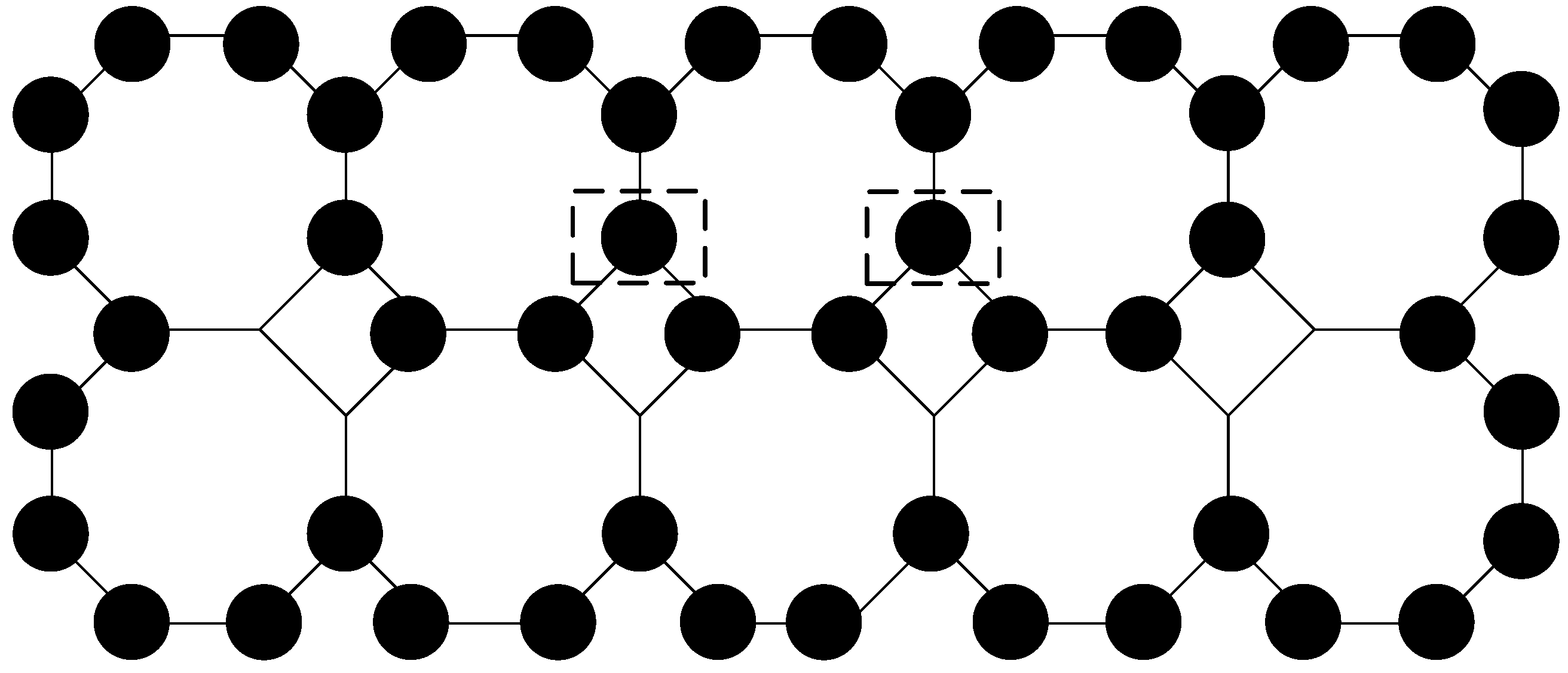
D is the double total domination set on
, and
Therefore,
Now we will prove that
D is the minimal double total dominating set. First, according to Lemma 1, all border vertices must be in
D. Second, most of internal vertices on
are double total dominated by exactly two vertices. Only vertices
are double total dominated by three vertices. See
Figure 5. They are highlighted with dashed rectangles. If we were to remove vertices
from
D, then vertices
∪
would be just total, not double total dominated. Furthermore, vertices
are the best choice to double total dominate vertices which are only total dominated. This is because each vertex total dominates two different vertices, which is the best possible in this scenario. Hence,
D is minimal. □
Proof of Lemma 3. If we rotate and , we obtain and , respectively. Hence, the equalities hold. □
Theorem 7. For a triple octagonal chain with octagons, it holds that Proof of Theorem 7. Let be an octagonal chain with and B its border vertices. Because of Lemma 1, .
.
Let
D =
B∪
∪
,
. See
Figure 6.
D is the double total dominating set, and
For
, we construct the double total dominating set with all border vertices and vertices
Then
.
Let
B∪
∪
. See
Figure 7.
D is the double total dominating set, and
For
, we construct the double total dominating set with all border vertices and vertices
Then
.
Let B
. See
Figure 8.
D is the double total dominating set, and
For , we construct the double total dominating set with all border vertices and vertices
Then
□
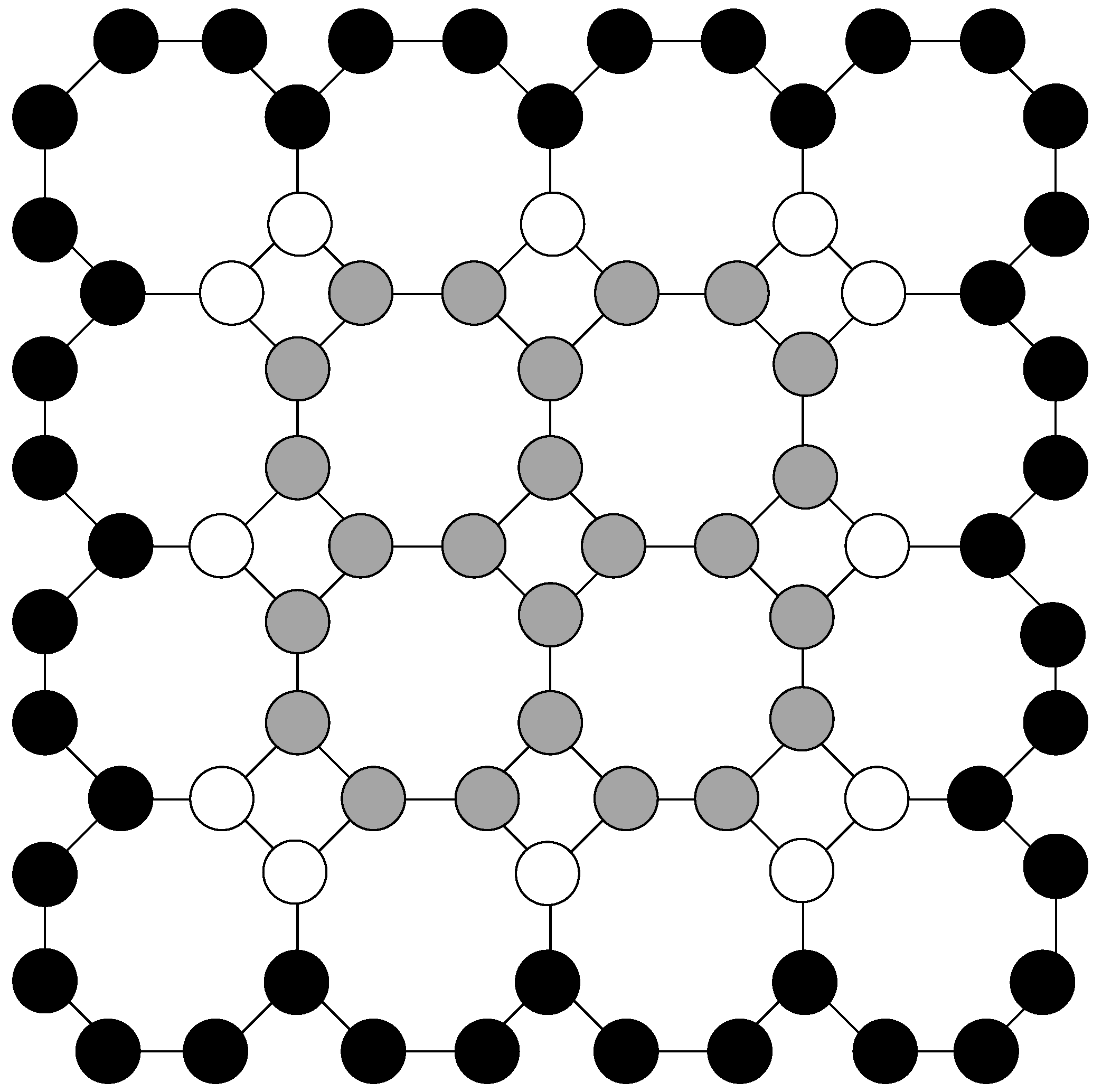
Proof of Theorem 8. From Lemma 1, it follows that the border on
has
vertices, and each of them must be in any double total dominating set. The border vertices double total dominate border vertices and total dominate only a few internal vertices, but most of the internal vertices are not dominated at all. See
Figure 9. The border vertices are colored black. White internal vertices are total dominated, and gray internal vertices are not dominated at all. The gray vertices make an octagonal grid
. Again, any double total dominating set on
will contain its border vertices. Therefore,
□
5. Conclusions
In this paper, we conducted a study to determine the exact values of the total domination number for linear and double octagonal chains. Additionally, we established an upper bound for the total domination number on a triple octagonal chain. Furthermore, our investigation extended to the exact values of the double total domination number for both linear and double octagonal chains. We also derived an upper bound for the double total domination number in the context of a triple octagonal chain and an octagonal grid, , where .
Our findings suggest that some of these established bounds may indeed be minimal. This opens up intriguing possibilities for further research to verify these minimality claims and potentially identify tighter bounds for various configurations.
In future work, we plan to expand our exploration to other chemical graph structures such as more general octagon graphs and tiling graphs.
Author Contributions
Conceptualization, A.K.; methodology, A.K. and A.K.B.; validation, A.K. and A.K.B.; formal analysis, A.K. and A.K.B.; investigation, A.K.B.; data curation, A.K.B.; writing—original draft preparation, A.K.; writing—review and editing, A.K.B.; visualization, A.K. and A.K.B.; supervision, A.K.; project administration, A.K.B.; All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Faculty of Economics, Josip Juraj Strossmayer University of Osijek, 31000 Osijek.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Quadras, J.; Sajiya Merlin Mahizl, A.; Rajasingh, I.; Sundara Rajan, R. Domination in certain chemical graphs. J. Math. Chem. 2015, 53, 207–219. [Google Scholar] [CrossRef]
- Bermudo, S.; Higuita, R.A.; Rada, J.P. K-domination and total k-domination numbers in catacondensed hexagonal system. Math. Biosci. Eng. 2022, 19, 7138–7155. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Zhu, E.; Shao, Z.; Gutman, I.; Klobučar, A. Total domination and open packing in some chemical graphs. J. Math. Chem. 2018, 56, 1481–1493. [Google Scholar] [CrossRef]
- Klobučar, A.; Klobučar, A. Total and Double total Domination Number on Hexagonal Grid. Mathematics 2019, 11, 1110. [Google Scholar] [CrossRef]
- Klobučar, A.; Klobučar, A. Double total domination number in certain chemical graphs. AIMS Math. 2022, 7, 19629–19640. [Google Scholar]
- Klobučar Barišić, A.; Klobučar, A. Double total Domination Number on Some Chemical Nanotubes. Kragujevac J. Math. 2026, 50, 415–423. [Google Scholar] [CrossRef]
- Mojdeh, D.A.; Habibi, M.; Badakhshian, L. Total and connected domination in chemical graphs. Ital. J. Pure Appl. Math. 2018, 39, 393–401. [Google Scholar]
- Brunvoll, J.; Cyvin, S.J.; Cyvin, B.N. Enumeration of tree-like octagonal systems. J. Math. Chem. 1997, 21, 193–196. [Google Scholar] [CrossRef]
- Su, Z.; Ding, R. The relative lengths of sides of convex hexagons and octagons. J. Appl. Math. Comput. 2008, 28, 265–270. [Google Scholar] [CrossRef]
- Destainville, N.; Mosseri, R.; Bailly, F. Fixed-boundary octagonal random tilings: A combinatorial approach. J. Stat. Phys. 2001, 102, 147–190. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, B. Kekulé Structures of octagonal chains and the Hosoya index of caterpillar trees. J. Zhejiang Univ. Sci. 2013, 30, 274–277. [Google Scholar]
- Wei, S.; Ke, X.; Wang, Y. Wiener indices in random cyclooctane chains. Wuhan Univ. J. Nat. Sci. 2018, 23, 498–502. [Google Scholar] [CrossRef]
- Wei, S.; Chen, N.; Ke, X.; Hao, G.; Huang, J. Perfect Matchings in Random Octagonal Chain Graphs. J. Math. 2021, 3, 1–5. [Google Scholar] [CrossRef]
- Cockayne, E.J.; Dawes, R.M.; Hedetniemi, S.T. Total domination in graphs. Networks 1980, 10, 211–219. [Google Scholar] [CrossRef]
- Henning, M.A.; Yeo, A. Total Domination in Graphs. In Springer Monographs in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Sigarreta, J.M. Total domination on some graph operators. Mathematics 2021, 9, 241. [Google Scholar] [CrossRef]
- Li, L.; Yue, J.; Zhang, X. Double total domination number of Cartesian product of paths. AIMA Math. 2023, 8, 9506–9519. [Google Scholar] [CrossRef]
- Bermudo, S. Total Domination on Tree Operators. Mediterr. J. Math. 2023, 20, 42. [Google Scholar] [CrossRef]
- Cabrera-Martínez, A.; Villamar, I.R.; Rueda-Vázquez, J.M.; Sigarreta Almira, J.M. Double total domination in the generalized lexicographic product of graphs. Quaest. Math. 2023, 47, 689–703. [Google Scholar] [CrossRef]
- Antony, D.; Chandran, L.S.; Gayen, A.; Gosavi, S.; Jacob, D. Total Domination, Separated-Cluster, CD-Coloring: Algorithms and Hardness. In Lecture Notes in Computer Science, Proceedings of the LATIN 2024: Theoretical Informatics, Puerto Varas, Chile, 18–22 March 2024; Soto, J.A., Wiese, A., Eds.; Springer Nature Switzerland: Cham, Switzerland; pp. 97–113.
- Henning, M.A. Packing in trees. Discrete Math. 1998, 186, 145–155. [Google Scholar] [CrossRef]
- Henning, M.A.; Rautenbach, D.; Schäfer, P.M. Open packing, total domination and P3-Radon number. Discrete Math. 2009, 313, 992–998. [Google Scholar] [CrossRef]
- Akbari, S.; Alikhani, S.; Peng, Y. Characterization of graphs using domination polynomials. Eur. J. Comb. 2010, 31, 1714–1724. [Google Scholar] [CrossRef]
- Saoub, K.R. Graph Theory: An Introduction to Proofs, Algorithms, and Applications, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2021. [Google Scholar]
- Klobučar, A. Total domination numbers of Cartesian products. Math. Commun. 2004, 9, 35–44. [Google Scholar]
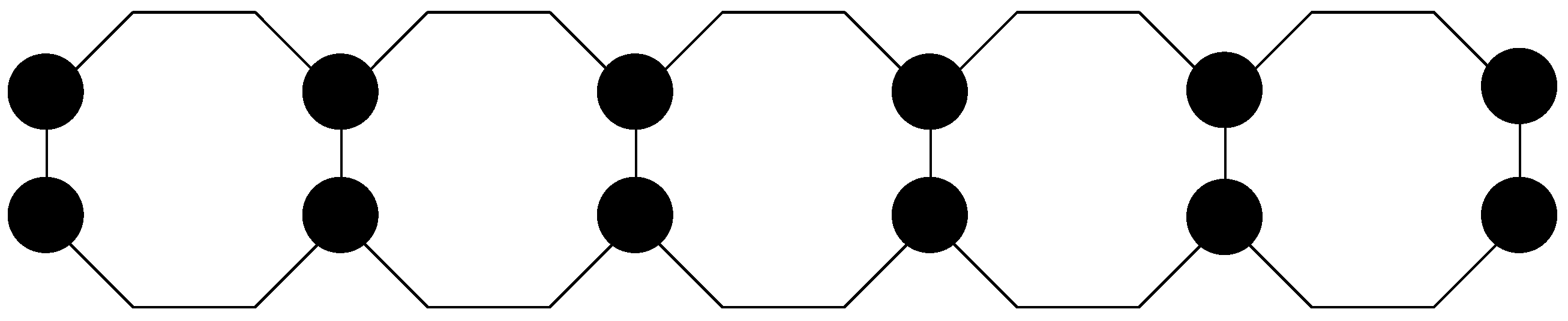
Figure 1.
with 7 subrows and 10 subcolumns. Labeled vertices are presented in gray color, while others are presented in black.
Figure 1.
with 7 subrows and 10 subcolumns. Labeled vertices are presented in gray color, while others are presented in black.
Figure 2.
Black vertices are in the total dominating set on , while other vertices are omitted for simplicity, i.e., there are no black circles for omitted vertices.
Figure 2.
Black vertices are in the total dominating set on , while other vertices are omitted for simplicity, i.e., there are no black circles for omitted vertices.
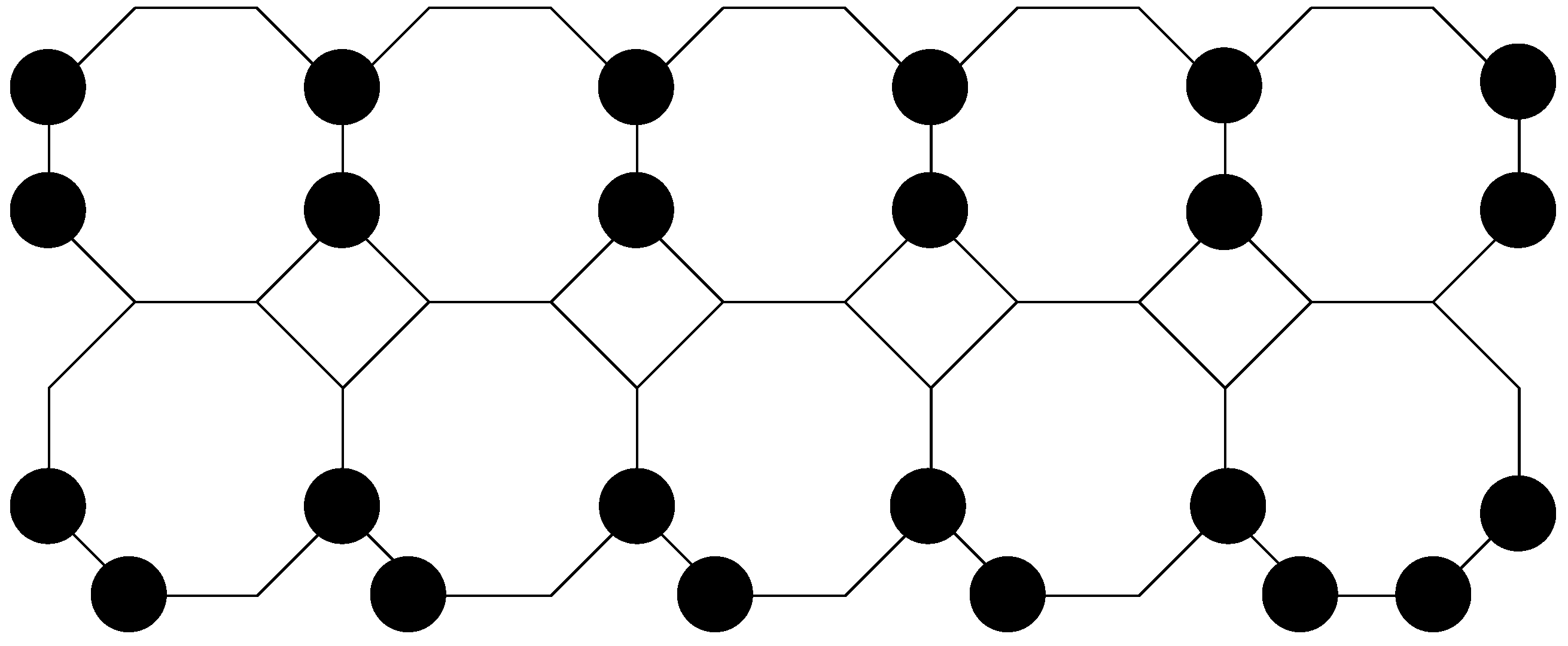
Figure 3.
Black vertices are in the total dominating set on , while other vertices are omitted for simplicity.
Figure 3.
Black vertices are in the total dominating set on , while other vertices are omitted for simplicity.
Figure 4.
and on . Black vertices are in , while other vertices are omitted for simplicity. Vertices making a path are circled with a dashed line.
Figure 4.
and on . Black vertices are in , while other vertices are omitted for simplicity. Vertices making a path are circled with a dashed line.
Figure 5.
Black vertices are in the double total dominating set on , while other vertices are omitted for simplicity. Vertices which are double total dominated by 3 vertices are highlighted with dashed rectangles.
Figure 5.
Black vertices are in the double total dominating set on , while other vertices are omitted for simplicity. Vertices which are double total dominated by 3 vertices are highlighted with dashed rectangles.
Figure 6.
Black vertices are in the double total dominating set on , while other vertices are omitted for simplicity.
Figure 6.
Black vertices are in the double total dominating set on , while other vertices are omitted for simplicity.
Figure 7.
Black vertices are in the double total dominating set on , while other vertices are omitted for simplicity.
Figure 7.
Black vertices are in the double total dominating set on , while other vertices are omitted for simplicity.
Figure 8.
Black vertices are in the double total dominating set on , while other vertices are omitted for simplicity.
Figure 8.
Black vertices are in the double total dominating set on , while other vertices are omitted for simplicity.
Figure 9.
inside of .
Figure 9.
inside of .
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).