Figure 1.
Different plots of the joint pdf of the MOBEL distribution: (1.a) , (1.b) , (1.c) , and (1.d) .
Figure 1.
Different plots of the joint pdf of the MOBEL distribution: (1.a) , (1.b) , (1.c) , and (1.d) .
Figure 2.
Different plots of the joint reliability function of the MOBEL distribution: (2.a) , (2.b) , (2.c) and (2.d) .
Figure 2.
Different plots of the joint reliability function of the MOBEL distribution: (2.a) , (2.b) , (2.c) and (2.d) .
Figure 3.
Different plots of the joint hazard of the MOBEL distribution: (3.a) , (3.b) , (3.c) and (3.d) .
Figure 3.
Different plots of the joint hazard of the MOBEL distribution: (3.a) , (3.b) , (3.c) and (3.d) .
Figure 4.
Estimated PDF and the PP plots of different distributions for the first data set.
Figure 4.
Estimated PDF and the PP plots of different distributions for the first data set.
Figure 5.
The pdf for the marginal distributions of and .
Figure 5.
The pdf for the marginal distributions of and .
Figure 6.
P-P plot estimated for the MOBEL distribution and other distributions for the real data set.
Figure 6.
P-P plot estimated for the MOBEL distribution and other distributions for the real data set.
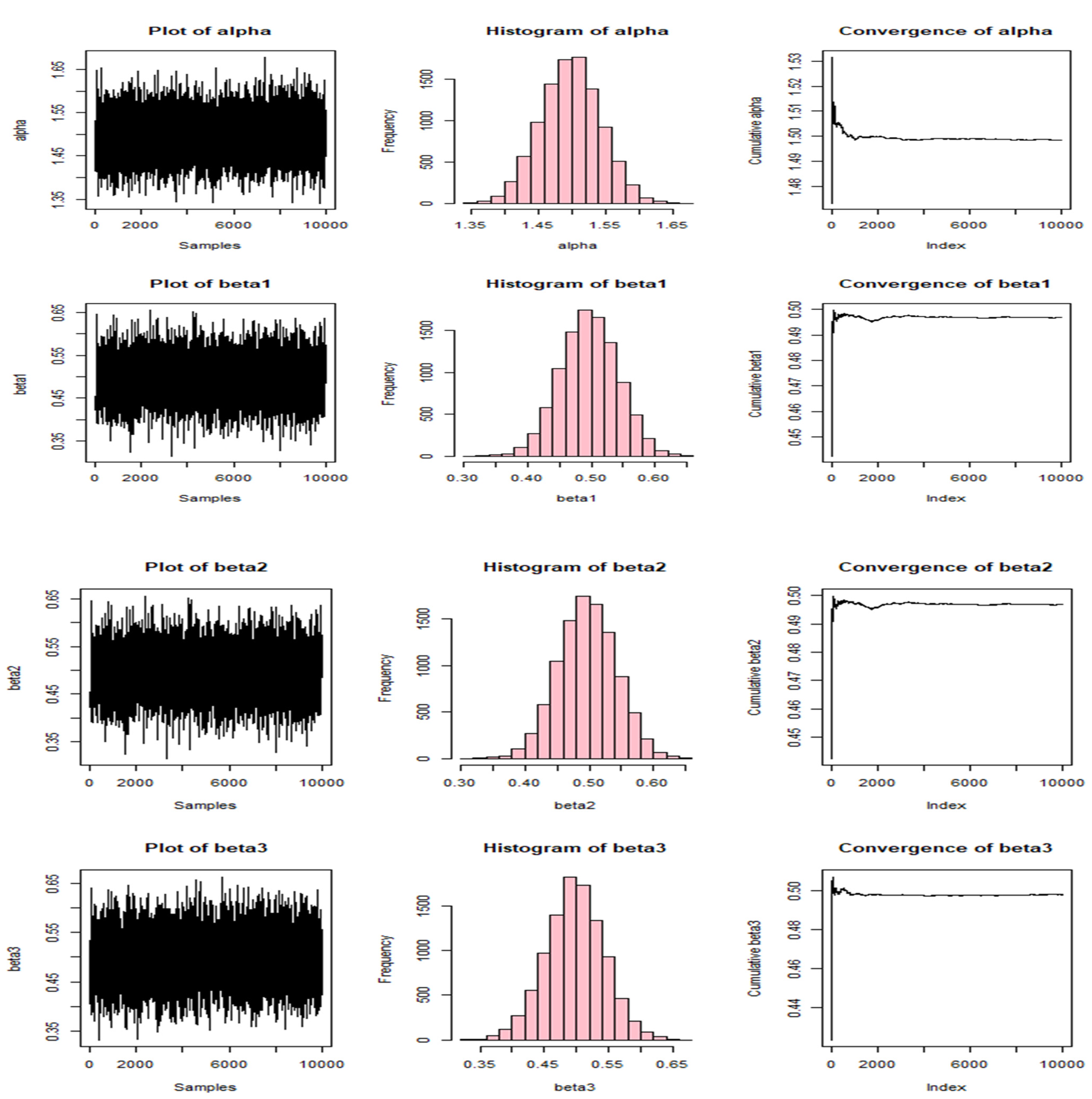
Figure 7.
MCMC plots for the parameters of the MOBEL distribution.
Figure 7.
MCMC plots for the parameters of the MOBEL distribution.
Table 1.
Scoring times from 42 American Football (NFL) matches.
Table 1.
Scoring times from 42 American Football (NFL) matches.
| | | | | |
|---|
| 02.05 | 03.98 | 05.78 | 25.98 | 10.40 | 14.25 |
| 09.05 | 09.05 | 13.80 | 49.75 | 02.98 | 02.98 |
| 00.85 | 00.85 | 07.25 | 07.25 | 03.88 | 06.43 |
| 03.43 | 03.43 | 04.25 | 04.25 | 00.75 | 00.75 |
| 07.78 | 07.78 | 01.65 | 01.65 | 11.63 | 17.37 |
| 10.57 | 14.28 | 06.42 | 15.08 | 01.38 | 01.38 |
| 07.05 | 07.05 | 04.22 | 09.48 | 10.35 | 10.35 |
| 02.58 | 02.58 | 15.53 | 15.53 | 12.13 | 12.13 |
| 07.23 | 09.68 | 02.90 | 02.90 | 14.58 | 14.58 |
| 06.85 | 34.58 | 07.02 | 07.02 | 11.82 | 11.82 |
| 32.45 | 42.35 | 06.42 | 06.42 | 05.52 | 11.27 |
| 08.53 | 14.57 | 08.98 | 08.98 | 19.65 | 10.70 |
| 31.13 | 49.88 | 10.15 | 10.15 | 17.83 | 17.83 |
| 14.58 | 20.57 | 08.87 | 08.87 | 10.85 | 38.07 |
Table 2.
Kolmogorov–Smirnov distances and the associated p values.
Table 2.
Kolmogorov–Smirnov distances and the associated p values.
| Distribution | KS Distance | p Value |
|---|
| 0.2619 | 0.1860 |
| 0.2381 | 0.1859 |
| max {} | 0.2659 | 0.1121 |
Table 3.
ML estimates, standard errors, and information criteria for the first data set.
Table 3.
ML estimates, standard errors, and information criteria for the first data set.
| Models | Parameter | ML Estimates | SE | AIC | BIC | HQIC | CAIC |
|---|
| BELO | | |
0.0007
| 288.431 | 293.644 | 290.342 | 289.063 |
|
1.1013
|
0.0003
|
| |
0.0009
|
| |
0.0006
|
| BBurr III | | |
0.0004
| 635.197 | 642.147 | 637.745 | 636.278 |
| | 0.0005 |
| | 0.0004 |
| | 0.0009 |
| BCESF-Lomax | | 1.1727 | 0.0011 | 598.389 | 608.815 | 602.211 | 600.789 |
| 2.1179 | 0.0010 |
| 1.5014 | 0.0004 |
| 2.2098 | 0.0010 |
| 1.9132 | 0.0005 |
| 3.1330 | 0.0007 |
| BLomax | | | 0.0006 | 1102.35 | 1107.56 | 1104.26 | 1102.98 |
| |
0.0005
|
| |
0.0006
|
Table 4.
ML estimates with measures of the goodness-of-fit test of the marginal distribution based on the second data.
Table 4.
ML estimates with measures of the goodness-of-fit test of the marginal distribution based on the second data.
| Measures of Goodness of Fit | | |
|---|
| | | |
|---|
| 0.12 | 0.8638 | 0.16 | 0.5447 |
Table 5.
ML estimates, standard errors, and information criteria for the second data set.
Table 5.
ML estimates, standard errors, and information criteria for the second data set.
| Models | Parameter | ML Estimates | SE | AIC | BIC | HQIC | CAIC |
|---|
| MOBEL | | 0.9943 | | 172.972 | 178.709 | 175.157 | 173.494 |
| | |
| 1.5662 | |
| 1.6951 | |
| BCESF-beta | | 0.2046 | 1.0957 | 234.203 | 242.611 | 238.893 | 237.856 |
| 0.6867 | 23.6962 |
| 1.0879 | 3.4571 |
| 0.3995 | 0.3978 |
| 1.9584 | 1.1201 |
| 0.1997 | 0.9945 |
| BBurr III | | 2.7392 | 5.7227 | 278.388 | 283.992 | 280.181 | 279.988 |
| 0.7712 | 1.0234 |
| 0.5846 | 0.0028 |
| 0.6739 | 0.5796 |
| BCESF-Lomax | | 0.9809 | 1.4173 | 487.127 | 495.534 | 491.816 | 490.779 |
| 1.7997 | 4.0088 |
| 1.5167 | 0.0278 |
| 2.2331 | 0.1100 |
| 1.9212 | 0.0447 |
| 3.1467 | 0.2184 |
| BLomax | | 1.1621 | 0.0038 | 792.186 | 795.661 | 793.46 | 792.494 |
| 1.2659 | 0.0547 |
| 1.4091 | 0.6255 |
Table 6.
Averages of the ML estimates, variances, estimated risks, and 95% confidence intervals of the parameter .
Table 6.
Averages of the ML estimates, variances, estimated risks, and 95% confidence intervals of the parameter .
| n | Parameter | Average | Var | ER | UL | LL | Length |
|---|
| 30 | | 0.3864 | 0.0024 | 0.0099 | 0.4819 | 0.2911 | 0.1908 |
| 0.6400 | 0.0082 | 0.0098 | 0.8171 | 0.4629 | 0.3542 |
| 0.5669 | 0.0094 | 0.0094 | 0.7041 | 0.4297 | 0.2744 |
| 0.1340 | 0.0014 | 0.0057 | 0.2070 | 0.0610 | 0.1459 |
| 50 | | 0.3706 | 0.0018 | 0.0068 | 0.4541 | 0.2871 | 0.1669 |
| 0.6342 | 0.0052 | 0.0064 | 0.7756 | 0.4927 | 0.2829 |
| 0.5829 | 0.0060 | 0.0128 | 0.7349 | 0.4309 | 0.3040 |
| 0.1464 | 0.0009 | 0.0038 | 0.2071 | 0.0858 | 0.1213 |
| 100 | | 0.2892 | 0.00004 | 0.0002 | 0.3018 | 0.2764 | 0.0254 |
| 0.5914 | 0.0004 | 0.0005 | 0.6329 | 0.5501 | 0.0829 |
| 0.4787 | 0.0003 | 0.0007 | 0.5106 | 0.4469 | 0.0638 |
| 0.1212 | 0.0002 | 0.0064 | 0.1474 | 0.0950 | 0.0524 |
Table 7.
Averages of the ML estimates, variances, estimated risks, and 95% confidence intervals of the parameters .
Table 7.
Averages of the ML estimates, variances, estimated risks, and 95% confidence intervals of the parameters .
| n | Parameter | Average | Var | ER | UL | LL | Length |
|---|
| 30 | | 0.6294 | 0.0210 | 0.0378 | 0.9139 | 0.3451 | 0.5689 |
| 0.8245 | 0.0234 | 0.0290 | 1.1247 | 0.5242 | 0.6006 |
| 2.0707 | 0.1734 | 0.1784 | 2.8870 | 1.2543 | 1.6327 |
| 0.6396 | 0.0192 | 0.1490 | 0.9109 | 0.3684 | 0.5426 |
| 50 | | 0.5148 | 0.0069 | 0.0072 | 0.6784 | 0.3511 | 0.3273 |
| 0.7784 | 0.0181 | 0.0189 | 1.0422 | 0.5144 | 0.5277 |
| 2.0164 | 0.1587 | 0.1590 | 2.7973 | 1.2356 | 1.5618 |
| 0.6402 | 0.0119 | 0.3252 | 0.8544 | 0.4261 | 0.4283 |
| 100 | | 0.5146 | 0.0054 | 0.0056 | 0.6583 | 0.3708 | 0.2875 |
| 0.7441 | 0.0138 | 0.0139 | 0.9746 | 0.5134 | 0.4611 |
| 1.8939 | 0.1067 | 0.1180 | 2.5344 | 1.2534 | 1.2809 |
| 0.6442 | 0.0103 | 0.1369 | 0.8429 | 0.4455 | 0.3973 |
Table 8.
Averages of the ML estimates, relative absolute biases, variances, estimated risks and 95% confidence intervals of the reliability and hazard rate functions .
Table 8.
Averages of the ML estimates, relative absolute biases, variances, estimated risks and 95% confidence intervals of the reliability and hazard rate functions .
| n | rf and hrf | Average | RAB | Var | ER | UL | LL | Length |
|---|
| 30 | | 0.8603 | 0.0611 | 0.0007 | 0.0005 | 0.9131 | 0.8075 | 0.1056 |
| 0.3325 | 0.4124 | 0.0029 | 0.0781 | 0.4393 | 0.2257 | 0.2136 |
| 50 | | 0.8270 | 0.0201 | 0.0003 | 0.0001 | 0.8593 | 0.7948 | 0.0645 |
| 0.2729 | 0.1595 | 0.0011 | 0.0700 | 0.3393 | 0.2066 | 0.1326 |
| 100 | | 0.8707 | 0.0739 | 0.0001 | 0.0007 | 0.8879 | 0.8536 | 0.0344 |
| 0.3549 | 0.5078 | 0.0001 | 0.0807 | 0.3818 | 0.3279 | 0.0538 |
Table 9.
Averages of the ML estimates, relative absolute biases, variances, estimated risks and 95% confidence intervals of the reliability and hazard rate functions .
Table 9.
Averages of the ML estimates, relative absolute biases, variances, estimated risks and 95% confidence intervals of the reliability and hazard rate functions .
| n | rf and hrf | Average | RAB | Var | ER | UL | LL | Length |
|---|
| 30 | | 0.8195 | 0.0589 | 0.0007 | 0.0004 | 0.8711 | 0.7679 | 0.1032 |
| 0.2148 | 1.2208 | 0.0052 | 0.1045 | 0.3559 | 0.0737 | 0.2822 |
| 50 | | 0.8207 | 0.0604 | 0.0004 | 0.0004 | 0.8581 | 0.7832 | 0.0749 |
| 0.2204 | 1.3734 | 0.0024 | 0.1048 | 0.3158 | 0.1249 | 0.1908 |
| 100 | | 0.8189 | 0.0582 | 0.0003 | 0.0004 | 0.8553 | 0.7824 | 0.0728 |
| 0.2160 | 1.2334 | 0.0022 | 0.1043 | 0.3089 | 0.1231 | 0.1858 |
Table 10.
ML estimates and standard errors for the parameters for the first real data set.
Table 10.
ML estimates and standard errors for the parameters for the first real data set.
| Parameter | Estimate | SE |
|---|
| 0.4876 | 0.0002 |
| 0.7822 | 0.0010 |
| 1.9049 | 0.0090 |
| 0.8999 | 0.0100 |
Table 11.
ML estimates and standard errors of the reliability and hazard rate functions for the first real data set.
Table 11.
ML estimates and standard errors of the reliability and hazard rate functions for the first real data set.
| rf and hrf | Estimate | SE |
|---|
| 0.8249 | 0.0002 |
| 0.2713 | 0.3476 |
Table 12.
Averages of the ML predictors and bounds of the future observation under two-sample prediction .
Table 12.
Averages of the ML predictors and bounds of the future observation under two-sample prediction .
| s | | Average | UL | LL | Length |
|---|
| 1 | | 0.0758 | 0.2670 | 0.0129 | 0.2542 |
| 0.0496 | 0.1751 | 0.0088 | 0.1664 |
| 12 | | 1.6103 | 4.9987 | 0.4895 | 4.5092 |
| 0.7386 | 2.3923 | 0.2634 | 2.1289 |
| 18 | | 3.9922 | 12.6913 | 0.7063 | 11.985 |
| 1.3738 | 4.9545 | 0.43951 | 4.5150 |
Table 13.
ML predictors and bounds of the future observation for the first real data set under two-sample prediction.
Table 13.
ML predictors and bounds of the future observation for the first real data set under two-sample prediction.
| s | | ML Predictor | UL | LL | Length |
|---|
| 1 | | 0.1679 | 0.4819 | 0.0462 | 0.4356 |
| 0.1067 | 0.3076 | 0.0165 | 0.2911 |
| 12 | | 0.5647 | 1.4856 | 0.1856 | 1.2970 |
| 0.3215 | 0.1231 | 0.1231 | 0.7358 |
| 18 | | 1.2861 | 3.7801 | 0.3380 | 3.4420 |
| 0.6105 | 1.9066 | 0.2196 | 1.6869 |
Table 14.
Averages of the Bayes estimates, relative absolute biases, estimated risks and 95% credible intervals for the parameters of the MOBEL distribution using informative prior .
Table 14.
Averages of the Bayes estimates, relative absolute biases, estimated risks and 95% credible intervals for the parameters of the MOBEL distribution using informative prior .
| n | Parameter | Average | RAB | ER | UL | LL | Length |
|---|
| 30 | | 0.2974 | 0.0086 | 9.8501 × 10−6 | 0.2998 | 0.2945 | 0.0052 |
| 0.5976 | 0.0039 | 6.5955 × 10−6 | 0.5996 | 0.5961 | 0.0035 |
| 0.5009 | 0.0019 | 2.0227 × 10−6 | 0.5028 | 0.4991 | 0.0036 |
| 0.1990 | 0.0049 | 1.6111 × 10−6 | 0.1999 | 0.19705 | 0.0029 |
| 50 | | 0.2978 | 0.0072 | 6.7380 × 10−6 | 0.3006 | 0.2960 | 0.0040 |
| 0.5992 | 0.0012 | 1.0058 × 10−6 | 0.6000 | 0.5973 | 0.0027 |
| 0.5009 | 0.0019 | 1.9952 × 10−6 | 0.5026 | 0.4992 | 0.0034 |
| 0.2006 | 0.0032 | 7.8541 × 10−7 | 0.2017 | 0.1995 | 0.0022 |
| 100 | | 0.3006 | 0.0021 | 1.1069 × 10−6 | 0.3018 | 0.2989 | 0.0029 |
| 0.5992 | 1.2643 × 10−3 | 6.1737 × 10−7 | 0.5012 | 0.4983 | 0.0028 |
| 0.4992 | 0.0015 | 1.9803 × 10−6 | 0.5013 | 0.4968 | 0.0044 |
| 0.1996 | 1.6118 × 10−3 | 3.4928 × 10−7 | 0.2003 | 0.1984 | 0.0019 |
Table 15.
Averages of the Bayes estimates, relative absolute biases, estimated risks and 95% credible intervals for the parameters of the MOBEL distribution using informative prior .
Table 15.
Averages of the Bayes estimates, relative absolute biases, estimated risks and 95% credible intervals for the parameters of the MOBEL distribution using informative prior .
| n | Parameter | Average | RAB | ER | UL | LL | Length |
|---|
| 30 | | 0.5004 | 0.0009 | 1.1133 × 10−6 | 0.5016 | 0.4987 | 0.0028 |
| 0.7518 | 0.0024 | 3.6609 × 10−6 | 0.7531 | 0.7500 | 0.0030 |
| 1.9981 | 0.0009 | 4.2708 × 10−6 | 1.9993 | 1.9963 | 0.0017 |
| 0.9976 | 0.0024 | 6.4350 × 10−6 | 0.9996 | 0.9959 | 0.0036 |
| 50 | | 0.5005 | 1.1060 × 10−3 | 7.4852 × 10−7 | 0.5014 | 0.4987 | 0.0027 |
| 0.7489 | 1.3481 × 10−3 | 1.9269 × 10−6 | 0.7508 | 0.7473 | 0.0030 |
| 1.9999 | 4.4200 × 10−5 | 2.2045 × 10−7 | 2.0006 | 1.9989 | 0.0016 |
| 1.0001 | 6.5875 × 10−5 | 5.8951 × 10−7 | 1.0016 | 0.9982 | 0.0033 |
| 100 | | 0.5005 | 1.04103 × 10−3 | 7.4172 × 10−7 | 0.5013 | 0.4989 | 0.0023 |
| 0.74989 | 1.3363 × 10−4 | 4.1987 × 10−7 | 0.7509 | 0.7485 | 0.0024 |
| 2.0002 | 1.34274 × 10−4 | 1.7647 × 10−7 | 2.0007 | 1.9992 | 0.0015 |
| 1.0002 | 0.0002 | 1.6193 × 10−7 | 1.0007 | 0.9991 | 0.0015 |
Table 16.
Averages of the Bayes estimates, relative absolute biases, estimated risks and 95% credible intervals of the reliability and hazard rate functions, using informative prior .
Table 16.
Averages of the Bayes estimates, relative absolute biases, estimated risks and 95% credible intervals of the reliability and hazard rate functions, using informative prior .
| n | Parameter | Estimate | SE |
|---|
| 42 | | 0.2996 | 0.0005 |
| 0.6001 | 0.0006 |
| 0.4994 | 0.0005 |
| 0.1998 | 0.0004 |
Table 17.
Averages of the Bayes estimates, relative absolute biases, estimated risks and 95% credible intervals of the reliability and hazard rate functions, using informative prior .
Table 17.
Averages of the Bayes estimates, relative absolute biases, estimated risks and 95% credible intervals of the reliability and hazard rate functions, using informative prior .
| n | rf and hrf | Average | RAB | ER | UL | LL | Length |
|---|
| 30 | | 0.0040 | 0.2414 | 2.9936 × 10−6 | 0.0056 | 0.0017 | 0.0039 |
| 0.2868 | 0.0054 | 2.9411 × 10−5 | 0.2884 | 0.2844 | 0.0039 |
| 50 | | 0.0046 | 0.1275 | 7.2942 × 10−7 | 0.0056 | 0.0037 | 0.0019 |
| 0.2874 | 0.0034 | 2.9260 × 10−5 | 0.2890 | 0.2857 | 0.0033 |
| 100 | | 0.0051 | 0.0322 | 2.4805 × 10−7 | 0.0058 | 0.0036 | 0.0021 |
| 0.2891 | 0.0025 | 2.8764 × 10−5 | 0.2899 | 0.2879 | 0.0019 |
Table 18.
Bayes estimates and standard errors for the parameters of the MOBEL distribution for the first real data set.
Table 18.
Bayes estimates and standard errors for the parameters of the MOBEL distribution for the first real data set.
| n | rf and hrf | Average | RAB | ER | UL | LL | Length |
|---|
| 30 | | 0.0049 | 0.0665 | 6.3879 × 10−7 | 0.0059 | 0.0031 | 0.0029 |
| 0.28926 | 0.0029 | 2.9184 × 10−5 | 0.2904 | 0.2876 | 0.0028 |
| 50 | | 0.0051 | 0.0432 | 2.1493 × 10−7 | 0.0057 | 0.0042 | 0.0015 |
| 0.2879 | 0.0015 | 2.8941 × 10−5 | 0.2888 | 0.2862 | 0.0026 |
| 100 | | 0.0054 | 0.0179 | 1.1937 × 10−7 | 0.0059 | 0.0046 | 0.0013 |
| 0.2884 | 0.0001 | 2.8918 × 10−5 | 0.2894 | 0.2868 | 0.0025 |
Table 19.
Bayes estimates and standard errors of the reliability and hazard rate functions for the first real data set.
Table 19.
Bayes estimates and standard errors of the reliability and hazard rate functions for the first real data set.
| rf and hrf | Estimate | SE |
|---|
| 0.0043 | 0.0004 |
| 0.2897 | 0.0003 |
Table 20.
Bayes predictors and bounds, of the future observation .
Table 20.
Bayes predictors and bounds, of the future observation .
| n | s | | Average | UL | LL | Length |
|---|
| 30 | 1 | | 3.9994 | 4.0009 | 3.9973 | 0.0036 |
| 6.9998 | 7.0009 | 6.9977 | 0.0033 |
| 12 | | 3.9985 | 4.0001 | 3.9962 | 0.0039 |
| 6.9977 | 6.9998 | 6.9963 | 0.0035 |
| 18 | | 3.9979 | 3.9995 | 3.9954 | 0.0041 |
| 6.9992 | 7.0001 | 6.9959 | 0.0042 |
| 50 | 1 | | 3.9999 | 4.0008 | 3.9983 | 0.0025 |
| 6.9993 | 7.0003 | 6.9976 | 0.0027 |
| 12 | | 4.0022 | 4.0036 | 3.9999 | 0.0036 |
| 6.9995 | 7.0003 | 6.9974 | 0.0029 |
| 18 | | 4.0025 | 4.0045 | 3.9999 | 0.0046 |
| 7.0008 | 7.0019 | 6.9986 | 0.0033 |
| 100 | 1 | | 3.9993 | 4.0000 | 3.9975 | 0.0025 |
| 6.9999 | 7.0016 | 6.9994 | 0.0022 |
| 12 | | 4.0005 | 4.0015 | 3.9988 | 0.0027 |
| 7.0001 | 7.0010 | 6.9986 | 0.0024 |
| 18 | | 4.0025 | 4.0041 | 3.9999 | 0.0042 |
| 6.9994 | 7.0012 | 6.9982 | 0.0030 |
Table 21.
Bayes predictors for the first real data set.
Table 21.
Bayes predictors for the first real data set.
| s | | Predictor |
|---|
| 1 | | 4.0006 |
| 6.9995 |
| 12 | | 4.0020 |
| 6.9995 |
| 18 | | 4.0021 |
| 6.9998 |
Table 22.
ML estimates and standard errors for the parameters for the second real data set.
Table 22.
ML estimates and standard errors for the parameters for the second real data set.
| Parameters | Estimates | SE |
|---|
| | |
| | |
| | |
| | |
Table 23.
ML estimates and standard errors of the reliability and hazard rate functions for the second real data set.
Table 23.
ML estimates and standard errors of the reliability and hazard rate functions for the second real data set.
| rf and hrf | Estimates | Se |
|---|
| | |
| | |
Table 24.
ML predictors and bounds of the future observation for the second real data set under two-sample prediction.
Table 24.
ML predictors and bounds of the future observation for the second real data set under two-sample prediction.
| s | | Predictors | UL | LL | Length |
|---|
| 10 | | | | 0.1445 | 0.1053 |
| | | | |
| 12 | | | | | |
| | | | |
| 18 | | | | | |
| | | | |
Table 25.
Bayes estimates and standard errors for the parameters of the MOBEL distribution for the second real data set.
Table 25.
Bayes estimates and standard errors for the parameters of the MOBEL distribution for the second real data set.
| n | Parameters | Estimates | SE |
|---|
| 50 | | 0.2988 | 0.0004 |
| 0.5992 | 0.0006 |
| 0.4988 | 0.0006 |
| 0.2004 | 0.0004 |
Table 26.
Bayes estimates and standard errors of the reliability and hazard rate functions for the second real data set.
Table 26.
Bayes estimates and standard errors of the reliability and hazard rate functions for the second real data set.
| rf and hrf | Estimate | SE |
|---|
| 0.03412 | 0.0006 |
| 0.38929 | 0.0007 |
Table 27.
Bayes predictors for the second real data set.
Table 27.
Bayes predictors for the second real data set.
| s | | Predictors | UL | LL | Length |
|---|
| 10 | | 3.9997 | 4.0019 | 3.9988 | 0.0031 |
| 6.9981 | 6.9985 | 6.9952 | 0.0032 |
| 12 | | 3.9995 | 4.00008 | 3.9970 | 0.0031 |
| 7.0001 | 7.0005 | 6.9982 | 0.0022 |
| 18 | | 3.9993 | 4.0009 | 3.9984 | 0.0025 |
| 6.9983 | 6.9999 | 6.9969 | 0.0030 |