On the Lanczos Method for Computing Some Matrix Functions
Abstract
1. Introduction
2. Lanczos Approximation of , , , and
3. Main Achievements
- (i)
- A is symmetric positive definite ⇒ is also symmetric positive definite;
- (ii)
- .
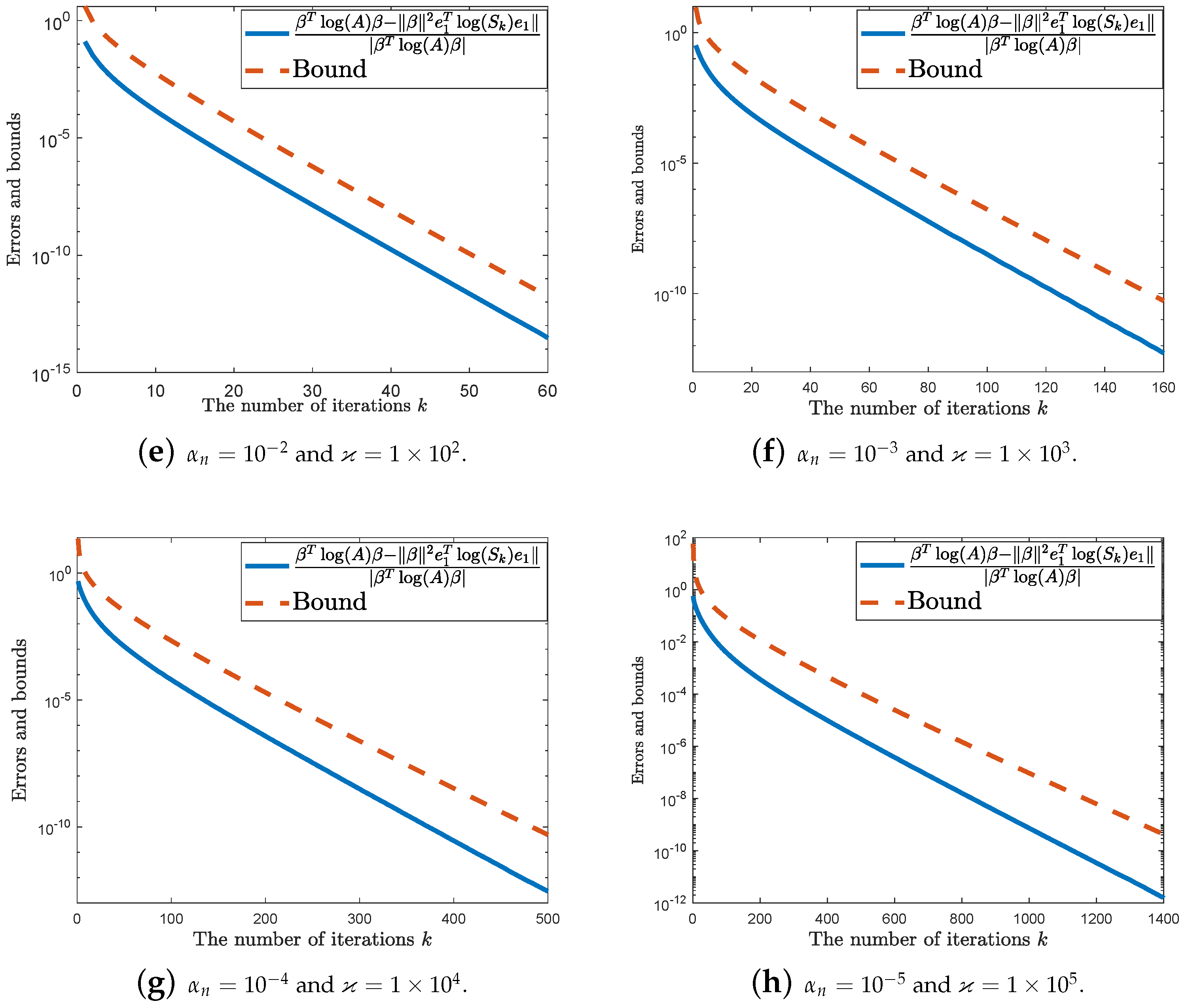
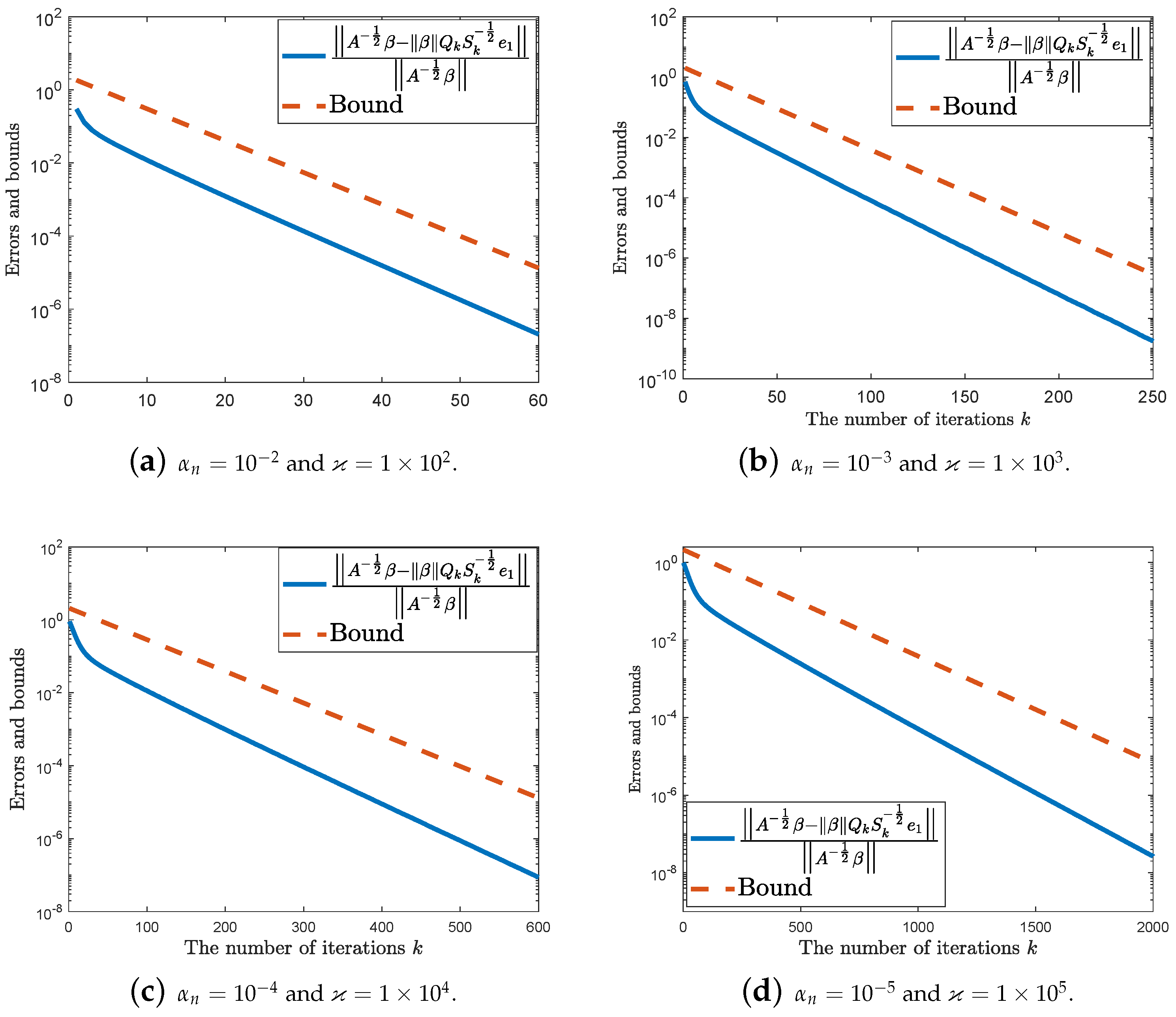
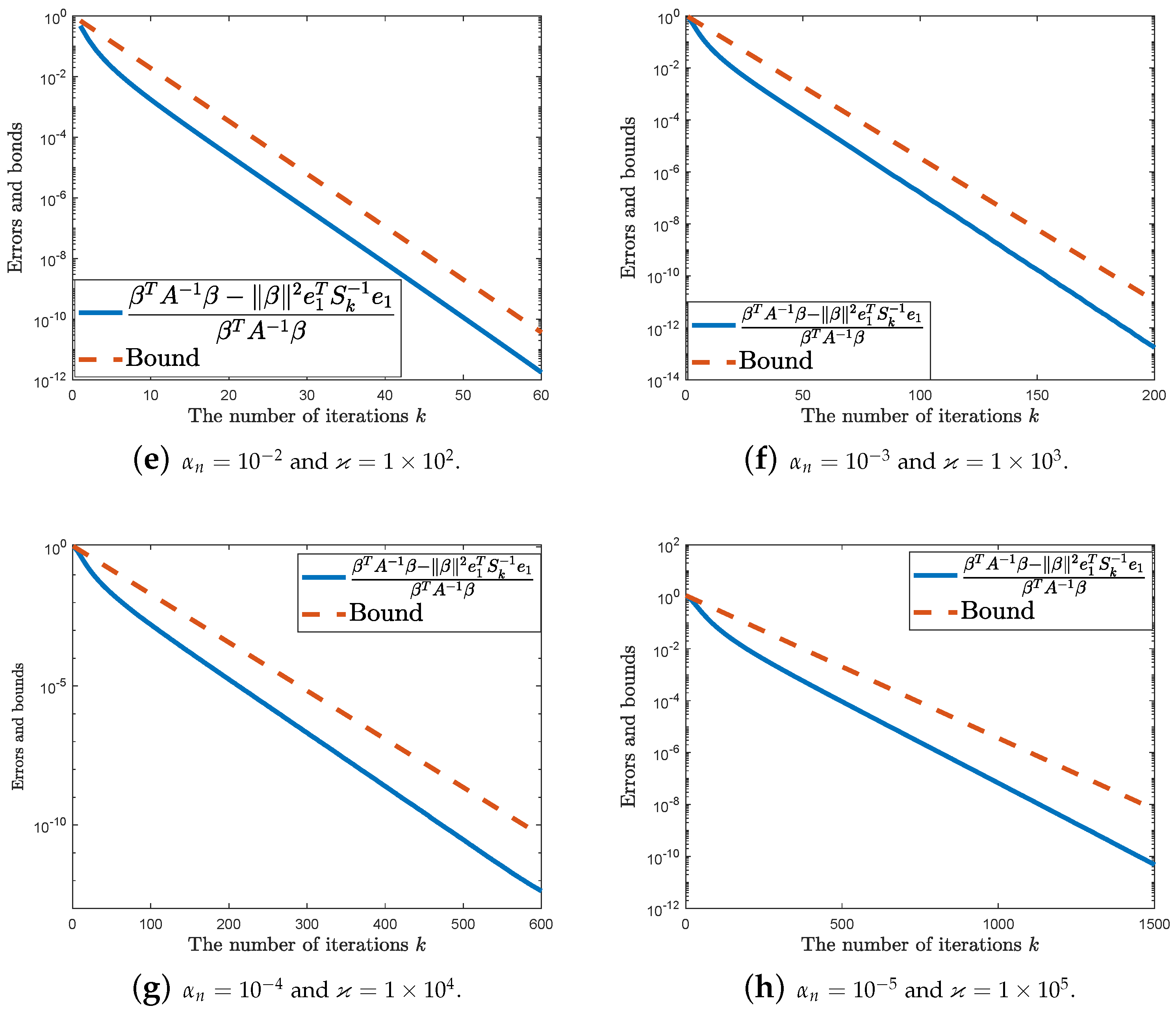
4. Numerical Experiments
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cuchta, T.; Grow, D.; Wintz, N. Discrete matrix hypergeometric functions. J. Math. Anal. Appl. 2023, 518, 126716. [Google Scholar] [CrossRef]
- Cuchta, T.; Luketic, R. Discrete hypergeometric Legendre polynomials. Mathematics 2021, 9, 2546. [Google Scholar] [CrossRef]
- Güttel, S. Rational Krylov approximation of matrix functions: Numerical methods and optimal pole selection. GAMM-Mitteilungen 2013, 36, 8–31. [Google Scholar] [CrossRef]
- Ilic, M.D.; Turner, I.W.; Simpson, D.P. A restarted Lanczos approximation to functions of a symmetric matrix. IMA J. Numer. Anal. 2009, 30, 1044–1061. [Google Scholar] [CrossRef]
- Ubaru, S.; Chen, J.; Saad, Y. Fast estimation of tr(f(A)) via stochastic Lanczos quadrature. SIAM J. Matrix Anal. Appl. 2017, 38, 1075–1099. [Google Scholar] [CrossRef]
- Golub, G.H.; Meurant, G. Matrices, Moments and Quadrature with Applications; Princeton University Press: Princeton, NJ, USA, 2009; Volume 30. [Google Scholar]
- Frommer, A.; Schweitzer, M. Error bounds and estimates for Krylov subspace approximations of Stieltjes matrix functions. BIT Numer. Math. 2015, 56, 865–892. [Google Scholar] [CrossRef]
- Chen, T.; Hallman, E. Krylov-aware stochastic trace estimation. SIAM J. Matrix Anal. Appl. 2023, 44, 1218–1244. [Google Scholar] [CrossRef]
- Druskin, V.L.; Knizhnerman, L.A. Error bounds in the simple Lanczos procedure for computing functions of symmetric matrices and eigenvalues. Comput. Math. Math. Phys. 1991, 31, 20–30. [Google Scholar]
- Frommer, A.; Kahl, K.; Lippert, T.; Rittich, H. 2-norm error bounds and estimates for Lanczos approximations to linear systems and rational matrix functions. SIAM J. Matrix Anal. Appl. 2013, 34, 1046–1065. [Google Scholar] [CrossRef]
- Higham, N.J. Functions of Matrices: Theory and Computation; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Cuchta, T.; Grow, D.; Wintz, N. A dynamic matrix exponential via a matrix cylinder transformation. J. Math. Anal. Appl. 2019, 479, 733–751. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; Johns Hopkins University Press: Baltimore, MD, USA, 2012. [Google Scholar]
- Saad, Y. Analysis of Some Krylov Subspace Approximations to the Matrix Exponential Operator. SIAM J. Numer. Anal. 1992, 29, 209–228. [Google Scholar] [CrossRef]
- Wainwright, M.J.; Jordan, M.I. Log-determinant relaxation for approximate inference in discrete Markov random fields. IEEE Trans. Signal Process. 2006, 54, 2099–2109. [Google Scholar] [CrossRef]
- Thron, C.; Dong, S.J.; Liu, K.F.; Ying, H.P. Padé-Z2 estimator of determinants. Phys. D-Rev. Part. Fields Gravit. Cosmol. 1998, 57, 1642–1653. [Google Scholar] [CrossRef]
- Affandi, H.; Fox, E.; Adams, R.; Taskar, B. Learning the parameters of determinantal point process kernels. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1224–1232. [Google Scholar]
- Arioli, M.; Loghin, D. Matrix Square-Root Preconditioners for the Steklov-Poincaré Operator; Technical Report RAL-TR-2008-003; Rutherford Appleton Laboratory: Didcot, UK, 2008. [Google Scholar]
- Tang, J.; Saad, Y. A Probing Method for Computing the Diagonal of the Inverse of a Matrix; Report UMSI–2010–42; Minnesota Supercomputer Institute, University of Minnesota: Minneapolis, MN, USA, 2010. [Google Scholar]
- Meurant, G. Estimates of the trace of the inverse of a symmetric matrix using the modified Chebyshev algorithms. Numer. Algorithms 2009, 51, 309–318. [Google Scholar] [CrossRef]
- Bai, Z.; Fahey, M.; Golub, G.H. Some large Scale computation problems. J. Comput. Appl. Math. 1996, 74, 71–89. [Google Scholar] [CrossRef]
- Bai, Z.; Golub, G.H. Bounds for the trace of the inverse and the determinant of symmetric positive definite matrices. Ann. Numer. Math. 1997, 4, 29–38. [Google Scholar]
- Dong, S.J.; Liu, K.F. Stochastic estimation with Z2 noise. Phys. Lett. B 1994, 328, 130–136. [Google Scholar] [CrossRef]
- Ortner, B.; Krauter, A.R. Lower bounds for the determinant and the trace of a class of Hermitian matrices. Linear Algebra Its Appl. 1996, 236, 147–180. [Google Scholar] [CrossRef]
- Brezinski, C.; Fika, P.; Mitrouli, M. Moments of a linear operator, with applications to the trace of the inverse of matrices and the solution of equations. Numer. Linear Algebra Appl. 2012, 19, 937–953. [Google Scholar] [CrossRef]
- Wu, L.; Laeuchli, J.; Kalantzis, V.; Stathopoulos, A.; Gallopoulos, E. Estimating the trace of the matrix inverse by interpolating from the diagonal of an approximate inverse. J. Comput. Phys. 2016, 326, 828–844. [Google Scholar] [CrossRef]
- Beals, R.; Wong, R. Special Functions and Orthogonal Polynomials; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Olver, F.; Lozier, D.; Boisvert, R.; Clark, C. The NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Bernstein, S.N. Sur l, ordre de la meilleure approximation des fonctions continues par les polynômes de degré donné. R. Acad. Med. Belg. 1912, 4, 1–104. [Google Scholar]
- Zhan, X. Matrix Inequalities; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Zhang, L.; Shen, C.; Li, R. On the generalized Lanczos trust-region method. SIAM J. Optim. 2017, 27, 2110–2142. [Google Scholar] [CrossRef]


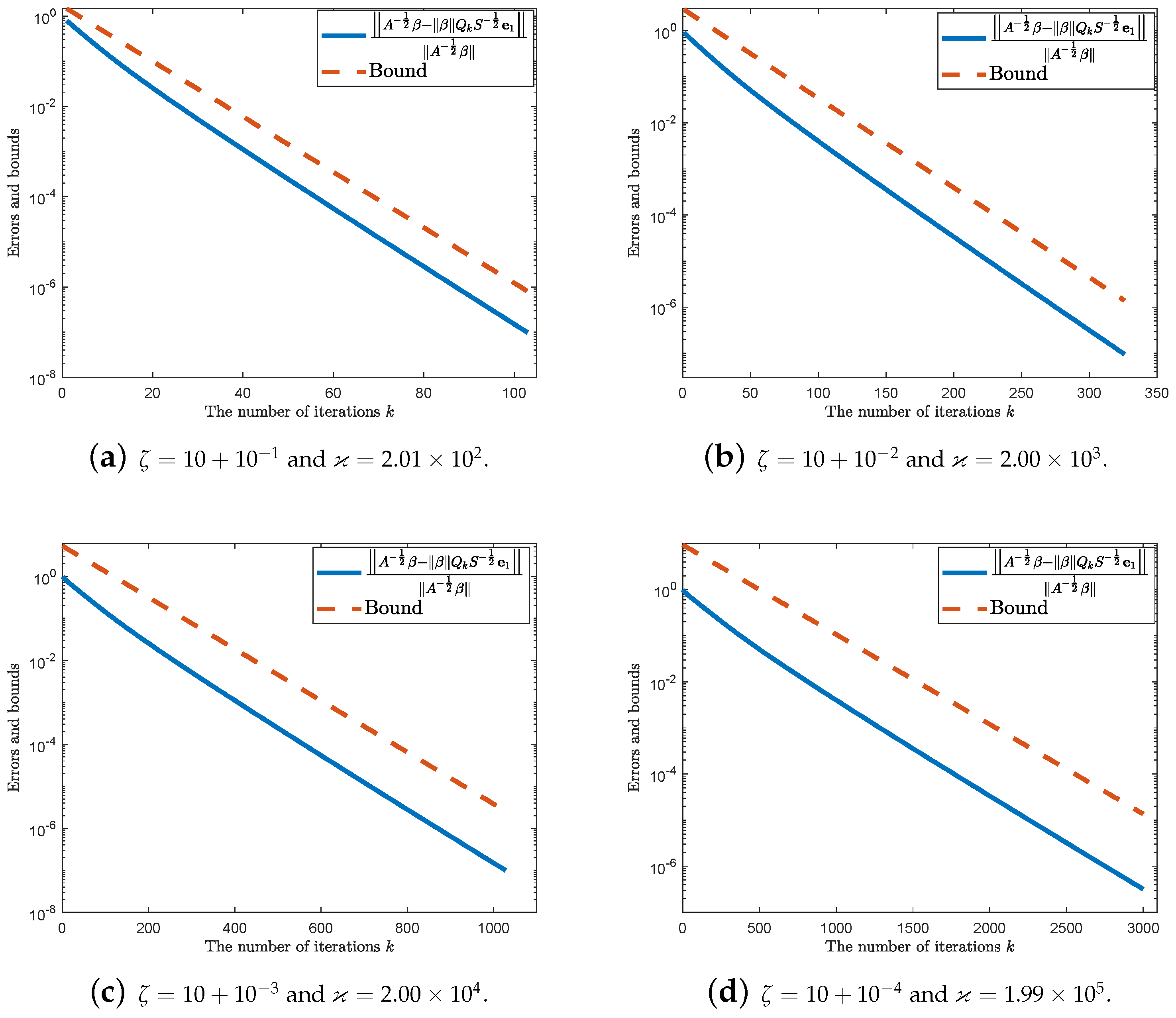
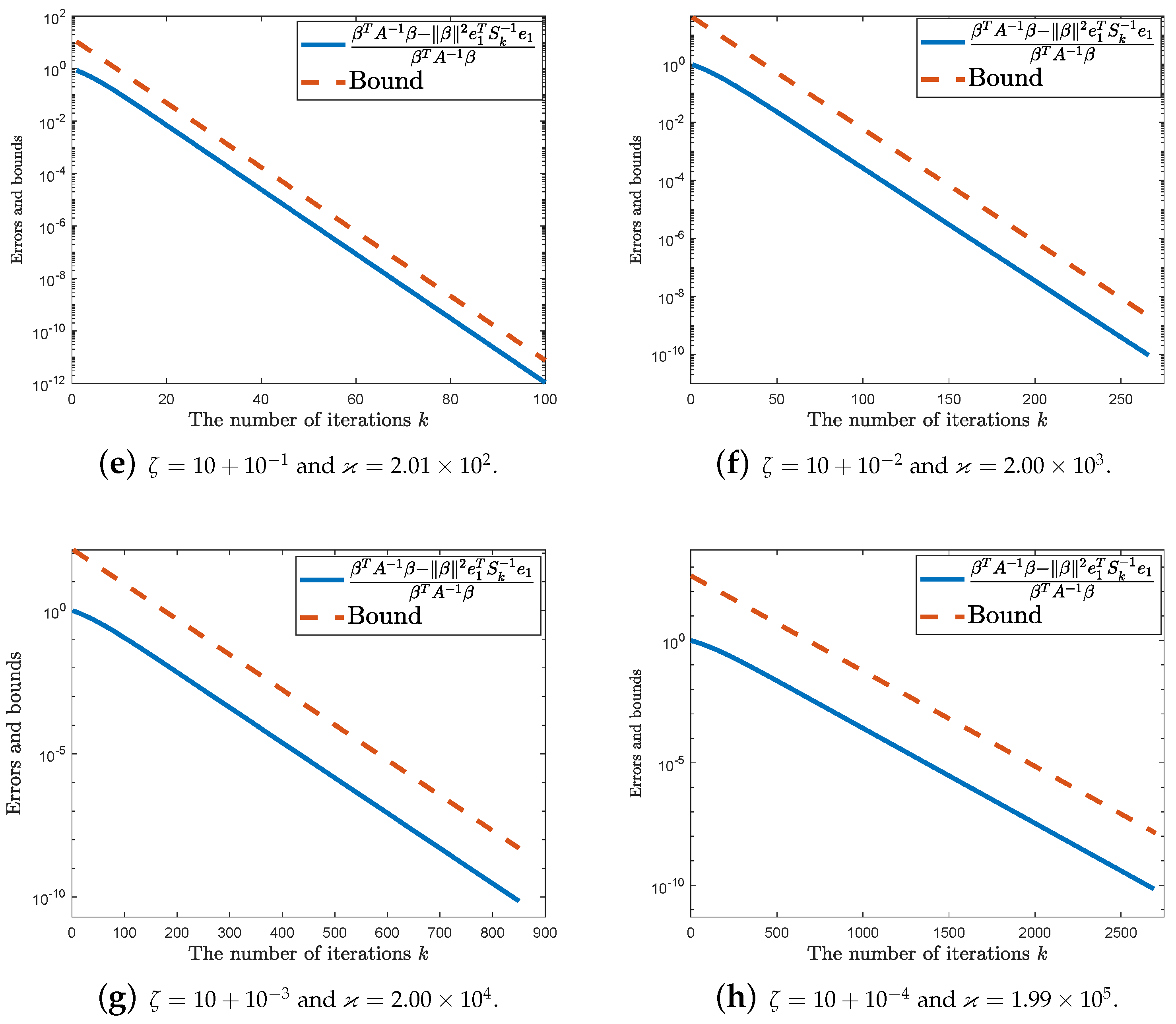

| 2.01 × | 2.00 × | 2.00 × | 1.99 × |
| 1 × | 1 × | 1 × | 1 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Y.; Srivastava, H.M.; Liu, X. On the Lanczos Method for Computing Some Matrix Functions. Axioms 2024, 13, 764. https://doi.org/10.3390/axioms13110764
Gu Y, Srivastava HM, Liu X. On the Lanczos Method for Computing Some Matrix Functions. Axioms. 2024; 13(11):764. https://doi.org/10.3390/axioms13110764
Chicago/Turabian StyleGu, Ying, Hari Mohan Srivastava, and Xiaolan Liu. 2024. "On the Lanczos Method for Computing Some Matrix Functions" Axioms 13, no. 11: 764. https://doi.org/10.3390/axioms13110764
APA StyleGu, Y., Srivastava, H. M., & Liu, X. (2024). On the Lanczos Method for Computing Some Matrix Functions. Axioms, 13(11), 764. https://doi.org/10.3390/axioms13110764







