Using Artificial Neural Networks to Solve the Gross–Pitaevskii Equation

Abstract

The current work proposes the incorporation of an artificial neural network to solve the Gross–Pitaevskii equation (GPE) efficiently, using a few realistic external potentials. With the assistance of neural networks, a model is formed that is capable of solving this equation. The adaptation of the parameters for the constructed model is performed using some evolutionary techniques, such as genetic algorithms and particle swarm optimization. The proposed model is used to solve the GPE for the linear case ($\gamma =0$) and the nonlinear case ($\gamma \ne 0$), where $\gamma$ is the nonlinearity parameter in GPE. The results are close to the reported results regarding the behavior and the amplitudes of the wavefunctions.

1. Introduction

Bose–Einstein condensates (BECs) have become a subject of research in many areas of physics, quantum optics, condensed matter physics, and atomic physics, among others. The Gross–Pitaevskii equation has been successfully used to study a wide range of Bosonic systems. Various analytical and numerical solutions have been employed to estimate the energy eigenstates and the eigenvalues of the GPE for several applicable physical potentials. The BECs in a box, the gravitational surface trap, the harmonic trap, the double-Well Potential and the Jacobian elliptic potentials are a few potentials [1,2,3,4,5] that have been used in the above-mentioned research areas. Also, recently, artificial neural networks (ANNs) and physics-informed neural networks (PINNs) have been used to estimate the condensate wavefunctions described by the Gross–Pitaevskii equation in one-dimensional (1D) physical structures [6,7]. ANNs and PINNs give competitive advantages against other numerical techniques due to their fast solvability and the reliability of the results in the case of nonlinear differential equations (like the Gross–Pitaevskii equation). Furthermore, in recent decades, several experiments have been performed and compared to theoretical predictions. For instance, the experimental measurements on BECs of trapped alkali–metal vapors [8,9] are in good agreement with the estimated results created by the Gross–Pitaevskii theory.

This article considers hybrid models that utilize neural networks [10,11] to solve the previously mentioned Gross—Pitaevskii equation for various potentials. Neural networks have been employed in many real-world problems in a variety of scientific areas, such as problems from physics [12,13,14], solving differential Equations [15,16], agriculture problems [17,18], problems derived from chemistry [19,20,21], problems found in economics [22,23,24], problems in medicine [25,26], etc. A common way to express neural networks is as functions $N(\overrightarrow{x},\overrightarrow{w})$, where the vector $\overrightarrow{x}$ stands for the input pattern and the vector $\overrightarrow{w}$ defines the vector of parameters under estimation, which is usually called a weight vector. According to the authors of [27], a neural network can be defined as the following summation:

$$N\left(\overrightarrow{x},\overrightarrow{w}\right)=\sum _{i=1}^K{w}_{(d+2)i-(d+1)}\sigma \left(\sum _{j=1}^d{x}_j{w}_{(d+2)i-(d+1)+j}+w_{(d+2)i}\right).$$

(1)

Neural networks have also been incorporated in the past to solve differential equations. For example, consider the work of Lagaris et al. [28], where different models based on neural networks were incorporated for a series of differential equation cases. Aarts and de Ver [29] proposed a method that utilizes neural networks to model and solve partial differential equations. Also, Parisi et al. have proposed [30] a method that trains neural networks with genetic algorithms in order to solve differential equations. Tsoulos et al. [31] suggested a method that constructs neural networks with the assistance of grammatical evolution [32] to solve differential equations. A review of methods that involve neural networks for the solutions of differential equations can be found in the work of Kumar et al. [33]. Recently, Zhang and Li [34] proposed a scheme that incorporates artificial neural networks to solve Caputo fractional-order differential equations.

Furthermore, artificial neural networks have also been used in a variety of problems derived from physics, such as quantum mechanics problems [35], problems that appear in particle physics [36], solutions for the quantum many-body problem [37], heat transfer problems [38], etc.

The parameter K represents the number of processing nodes and the parameter d stands for the dimension of vector $\overrightarrow{x}$. The function $\sigma (x)$ is commonly known as the sigmoid function, and it is defined as follows:

$$\sigma (x)={\displaystyle \frac{1}{1+exp(-x)}}.$$

(2)

The estimation of the optimal set of parameters for a neural network is also called training of the neural network, and a variety of methods have been proposed in the recent literature for training neural networks. These methods include the Back Propagation method [39,40], the RPROP method [41,42], the ADAM optimizer [43], etc. Also, evolutionary techniques that are considered a group of global optimization methods [44,45] have been used to train neural networks. A characteristic that distinguishes evolutionary techniques is that they try to imitate natural processes through vector operations. Furthermore, as optimization methods are global, they can avoid local minima of the objective function by aiming for the global minimum of the function. As far as artificial neural networks are concerned, this behavior results in finding lower values of the neural network error. In the relevant literature, there are several research publications that focus on the application of evolutionary techniques in the training of artificial neural networks, such as the application of genetic algorithms [46], the incorporation of the particle swarm optimization method [47,48], the use of the differential evolution method [49,50], ant colony optimization [51], the gray wolf optimizer [52], the whale optimization method [53], etc. In this article, modified versions of two evolutionary techniques were incorporated to solve the Gross–Pitaevskii equation with a model that utilizes an artificial neural network. The above two techniques were chosen for the optimization of the proposed model as they have proven their value in a number of difficult optimization problems. Also, since artificial neural networks have an extended set of local minima using their ability to produce candidate solutions that are modified with natural processes, these local minima can be avoided by aiming for an optimal configuration of the artificial neural network parameters.

The proposed technique utilizes two global optimization techniques for numerical solutions to the equation. Both techniques create populations of candidate solutions that are combined with each other in a series of steps, with the ultimate goal of solving the equation numerically. These candidate solutions include the parameters of an artificial neural network-based model. Given the ability of artificial neural networks to adapt to each function, but also with the use of well-tested global optimization techniques, greater certainty is provided for the numerical solution of the equation.

The rest of this paper is organized in the following sections: in Section 2, the proposed models utilized here and the associated optimization methods are presented; in Section 3, the experimental results are shown and discussed; and finally, in Section 4, some conclusions are presented.

2. The Proposed Method

This section begins with the description of the used model and continues with the definition of the optimization methods utilized to train this model. The method of artificial neural networks can solve problems faster, whereas analytical techniques do not have significant success. It is worth mentioning that the linear and nonlinear solutions of GPE can describe different limits of physical systems, e.g., Bose–Einstein condensates or any other physical system. Furthermore, the eigenfunctions can have zero values at specific boundary points due to the physical properties of the system under investigation. Lastly, the external potential influences the GPE solution by introducing different terms in the GPE equation and, as a result, they describe different physical systems.

2.1. The GPE Equation

We solve the eigenvalue problem in the case of a nonlinear Schrödinger equation (GPE equation). For the case of a one-dimensional problem, the ground states and higher modes of a Bose–Einstein condensate (BEC) in a time-independent external potential are described by

$$\left(-{\displaystyle \frac{h^2}{2m}}\Delta +V_{ext}(x)+g_s{\left|\Psi (x)\right|}^2\right)\Psi (x)=\mu \Psi (x)$$

(3)

where m, $\mu$, $g_s$, and $V_{ext}$ are the mass of the atom, the chemical potential, the non-linearity parameter and an external potential, respectively. The above-mentioned equation is time-independent GPE which describes the dynamics of a BEC with the nonlinear term $g_s$.

Considering that the wavefunction $\Psi (x)$ is normalized to one, the GPE equation can be written as:

$$\left(-{\displaystyle \frac{d^2}{d{x}^2}}+{\tilde{V}}_{ext}(x)+\gamma {\Psi }^2(x)\right)\Psi (x)=\epsilon \Psi (x)$$

(4)

where $x\in \left[a,b\right]$ and we use the rescaled values (L natural length scale, $x\to xL$ and $\Psi \to \sqrt{N}\Psi /L^{3/2}$). The length scale is arbitrary and may depend on various physical parameters. Furthermore, the dimensional quantities are described by the following relations:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\tilde{V}}_{ext}(x)={\displaystyle \frac{2m{L}^2{V}_{ext}}{\hslash }},\\ \hfill \gamma ={\displaystyle \frac{2Nm{g}_s}{L{\hslash }^2}},\\ \hfill ϵ={\displaystyle \frac{2m\mu L^2}{{\hslash }^2}}\end{array}\end{array}$$

(5)

In the current investigation, we assume that the potential can be described by three distinct models: Bose–Einstein condensates, gravitational trap and harmonic trap.

2.1.1. Bose–Einstein Condensates (BEC) in a Box

Here, the potential is provided from the following equation:

$${\tilde{V}}_{ext}(x)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}x\in [0,1]\hfill \\ \infty \hfill & otherwise\hfill \end{array}\right.$$

(6)

with standard boundary conditions (${\psi }_n(0)=0$ and ${\psi }_n(1)=0)$ and natural length scale $L=\hslash /\sqrt{2m\mu }$ and “n” is the mode of the solution of the wavefunction.

2.1.2. Gravitational Trap

The used external potential (gravitational) has the following form:

$${\tilde{V}}_{ext}(x)=\left\{\begin{array}{cc}\mathrm{mgx}\hfill & \mathrm{if}x>0\hfill \\ \infty \hfill & otherwise\hfill \end{array}\right.$$

(7)

where m is the mass of the atom and g is the gravitational acceleration. The boundary conditions are ${\Psi }_n(0)=0$ and ${\Psi }_n(\infty )=0$ and Equation (4) yields

$$\left(-{\displaystyle \frac{d^2}{d{x}^2}}+x+\gamma {\Psi }_n^2(x)\right){\Psi }_n(x)={\epsilon }_n{\Psi }_n(x)$$

(8)

with natural length scale $L={({\hslash }^2/2m^{2}g)}^{1/3}$.

2.1.3. Harmonic Trap

In this case, the potential is defined as:

$${\tilde{V}}_{ext}(x)={\displaystyle \frac{1}{2}}{\omega }^2{x}^2$$

(9)

The wavefunctions vanish as x reaches ∞ and Equation (4) yields

$$\left(-{\displaystyle \frac{d^2}{d{x}^2}}+x^2+\gamma {\Psi }_n^2(x)\right){\Psi }_n(x)={\epsilon }_n{\Psi }_n(x)$$

(10)

with natural length scale $L=\sqrt{\hslash /m\omega }$.

2.2. The Used Model

The used model is defined as:

$${\Psi }_n(x)=x(1-x)N(\overrightarrow{w},x)$$

(11)

where $N(\overrightarrow{w},x)$ stands for an artificial neural network. This model is used for the case of BEC potential since it vanishes at $x=0$ and $x=1$. Models with similar properties incorporating a neural network have also been utilized in the other two potentials. The differential equation presented in Equation (4) is solved in current work by dividing the space $\left[a,b\right]$ into m equidistant points. These points form the set $T=\left[x_0=a,x_1,x_2,\dots ,x_m=b\right]$. Hence, by applying the model of Equation (11) to every point of the set, the following function should be minimized in order to numerically solve the differential equation of (4):

$$\underset{\overrightarrow{w}}{min}\sum _{i=1}^m{\left(\left(-{\displaystyle \frac{d^2}{d{x}^2}}+\mathrm{Vext}\left(x_i\right)+\gamma {\Psi }_n^2\left(x_i\right)\right){\Psi }_n\left(x_i\right)-{\epsilon }_n{\Psi }_n\left(x_i\right)\right)}^2$$

(12)

In order to minimize the previously defined equation, two distinct evolutionary techniques will be used: a modified version of the genetic algorithm and a variant of the particle swarm optimization method.

2.3. The Used Genetic Algorithm

A modified version of a genetic algorithm is proposed to solve the differential Equation (11). Initially, genetic algorithms were proposed by John Holland [54] and they are inspired by biology. The main genetic algorithm starts by creating an initial population of potential solutions for the current optimization problem. The potential solutions are called chromosomes, and they change repeatedly through a series of iterations, also called generations. In every generation, biologically inspired operations are applied on the chromosomes, such as selection, crossover, and mutation [55]. Genetic algorithms have been applied to a wide series of optimization and practical problems from the relevant literature, such as electromagnetics [56], placement of wind turbines [57], feature selection [58], power flow [59], transportation scheduling [60], etc. Furthermore, genetic algorithms have been incorporated to train neural networks in a series of recent works, such as the paper of Leung et al. [61], where they have been utilized to construct the structure of neural networks. Moreover, they have been applied to the problem of rainfall-runoff forecasting [62] by training neural networks, and they have also been utilized to evolve neural networks for the deformation modulus of rock masses [63], etc.

The main steps of the used modified genetic algorithm are listed below.

• Initialization Step

  (a)

  Define $N_C$ as the number of chromosomes and $N_G$ as the number of allowed generations.

  (b)

  Set K as the number of processing nodes (weights) for the artificial neural network.

  (c)

  Randomly produce $N_C$ chromosomes. Every chromosome is considered a potential set of parameters for the artificial neural network.

  (d)

  Set $p_s$ as the selection rate and $p_m$ as the mutation rate with the assumption that $p_s\le 1$ and $p_m\le 1$.

  (e)

  Set iter = 0 as the generation number.

• Fitness calculation

  (a)

  For $i=1,\dots ,N_C$, do

  • Create the neural network $N(x,{\overrightarrow{g}}_i)$ for chromosome $g_i$.
  • Create the model ${\Psi }_n(x,g_i)$ for chromosome $g_i$ as

    $${\Psi }_n(x,g_i)=x(x-1)N(x,{\overrightarrow{g}}_i)$$

    using Equation (11).
  • Calculate the fitness $f_i$ as

    $$f_i=\sum _{j=1}^m{\left(\left(-{\displaystyle \frac{d^2}{d{x}^2}}+\mathrm{Vext}\left(x_j\right)+\gamma {\Psi }_n^2\left(x_j,g_i\right)\right){\Psi }_n\left(x_j,g_i\right)-{\epsilon }_n{\Psi }_n\left(x_j,g_i\right)\right)}^2$$

    (13)

  (b)

  EndFor

• Genetic operations

  (a)

  Selection procedure. Initially, the chromosomes are sorted according to their fitness, the first $\left(1-p_s\right)\times N_C$ are copied without changes to the next generation and the remaining are substituted by chromosomes that will produced in the crossover procedure.

  (b)

  Crossover procedure. During this step, for every couple $\tilde{z},\tilde{w}$ of produced offsprings, two chromosomes denoted as z and w are selected from the current population using tournament selection. The new chromosomes are constructed using the following equations:

  $$\begin{array}{ccc}\hfill \widetilde{z_i}& =& a_i{z}_i+\left(1-a_i\right)w_i\hfill \\ \hfill \widetilde{w_i}& =& a_i{w}_i+\left(1-a_i\right)z_i\hfill \end{array}$$

  (14)

  where $a_i$ is a random number with the property $a_i\in [-0.5,1.5]$ [64].

  (c)

  Mutation procedure. In this procedure, a random number r is selected for each element j of every chromosome $g_i$. If $r\le p_m$, then the corresponding element $g_{i,j}$ is changed randomly using the following scheme [64]:

  $$g_{i,j}=\left\{\begin{array}{cc}{g}_{i,j}+\Delta \left(\mathrm{iter},r_j-g_{i,j}\right)\hfill & t=0\hfill \\ g_{i,j}-\Delta \left(\mathrm{iter},g_{i,j}-l_j\right)\hfill & t=1\hfill \end{array}\right.$$

  (15)

  where t is a random number that accepts the values 0 or 1. The function $\Delta (\mathrm{iter},y)$ is defined as:

  $$\Delta (\mathrm{iter},y)=y\left(1-r^{{\left(1-{\displaystyle \frac{\mathrm{iter}}{N_G}}\right)}^b}\right)$$

  (16)

  The number r is a random number in $[0,1]$ and the parameter b controls the magnitude of change in the chromosome.

• Termination Check

  (a)

  Set $iter=iter+1$

  (b)

  A termination rule that was initially introduced in the work of Tsoulos [65] is used here.

  At each iteration iter, the algorithm calculates the variance, denoted as ${\sigma }^{(\mathrm{iter})}$, of the best fitness value up to that iteration. This variance will continually drop as the algorithm will discover lower values or these values will remain constant. In this case, the variance for the last iteration where a lower value was discovered is recorded, and if the variance falls below half of this record, then there is probably no new minimum for the algorithm to find and therefore it should terminate. The suggested termination rule is defined as:

  $$\mathrm{iter}\ge N_G\mathrm{OR}{\sigma }^{(\mathrm{iter})}\le {\displaystyle \frac{{\sigma }^{(\mathrm{klast})}}{2}}$$

  (17)

  where $\mathrm{klast}$ is the last generation where a new lower value for the best fitness was located.

  (c)

  If the termination rule does not hold, then go to step 2.

• Application of local optimization

  (a)

  Obtain the chromosome with the lowest fitness value in the population and denote it as $g_{\mathrm{best}}$.

  (b)

  Apply a local search procedure to chromosome $g_{\mathrm{best}}$. In the current work, a Broyden–Fletcher–Goldfarb–Shannon (BFGS) variant of Powell [66] was used. The use of local minimization techniques is important in order to reliably find a true local minimum from the global optimization method. In the optimization theory, the region of attraction $A\left(x^{*}\right)$ of some local minimum $x^{*}$ is defined as:

  $$A\left(x^{*}\right)=\left\{x:x\in S,L(x)=x^{*}\right\}$$

  (18)

  where $L(x)$ stands for the used local optimization method. Global optimization methods, in most cases, identify points that are inside the region of attraction $A\left(x^{*}\right)$ of a local minimum $x^{*}$ but not necessarily the actual local minimum. For this reason, it is considered necessary to have a combination of the global optimization method with local optimization techniques. Moreover, according to the relevant literature, the error function of artificial neural networks may contain a very large number of local minimums, making the aforementioned combination important in the process of finding an optimal set of parameters for the artificial neural network.

2.4. The Used PSO Variant

Particle swarm optimization (PSO) [67] is another evolutionary technique used to tackle global optimization problems. The PSO method forms a population of candidate solutions, called particles. These particles are evolved through a series of steps until some stopping criteria are met. Two vectors are used in the PSO method: the current position of the particle and the velocity of each particle, denoted as $\overrightarrow{p}$ and $\overrightarrow{u}$, respectively. The PSO method was tested on a wide series of problems from various areas, such as physics [68,69], chemistry [70,71], medicine [72,73], economics [74], etc. Additionally, the PSO technique was applied successfully on neural network training [75]. The proposed work utilizes an implementation of PSO, as suggested by Charilogis and Tsoulos [76] and this implementation is used to minimize the function of Equation (12). The method has the following steps:

• Initialization

  (a)

  Set $\mathrm{iter}=0$ as the iteration counter.

  (b)

  Define $N_C$ as the number of particles and $N_G$ as the number of allowed generations.

  (c)

  Set $p_l\in [0,1]$ as the local search rate.

  (d)

  Set the parameters $c_1,c_2$ in the range $[1,2]$.

  (e)

  Initialize the m particles $p_1,p_2,\dots ,p_{N_C}$. Each particle represents a set of parameters for the artificial neural network.

  (f)

  Randomly initialize the corresponding velocities $u_1,u_2,\dots ,u_{N_C}$.

  (g)

  For $i=1,\dots ,N_C$, carry out ${\mathrm{pb}}_i=p_i$. The vector ${\mathrm{pb}}_i$ denotes the best-located position for the particle $p_i$.

  (h)

  Set $p_{\mathrm{best}}=arg{min}_{i\in 1\dots N_C}f\left(p_i\right)$, where the function $f(p)$ denotes the fitness value of particle p.

• Check for termination. The same termination scheme as in the genetic algorithm is used here.
• For $i=1,\dots ,N_C$, Do

  (a)

  Compute the velocity $u_i$ as:

  $$u_i=\omega u_i+r_1{c}_1\left({\mathrm{pb}}_i-p_i\right)+r_2{c}_2\left(p_{\mathrm{best}}-p_i\right)$$

  (19)

  with

  • The parameters $r_1,r_2$ are randomly selected numbers in [0,1].
  • The variable $\omega$ stands for the inertia value and is computed as:

    $${\omega }_{\mathrm{iter}}=0.5+{\displaystyle \frac{r}{2}}$$

    (20)

    where r denotes a random number with the property $r\in [0,1]$ [77]. The above inertia calculation mechanism gives the particle optimization method the ability to more efficiently explore the search space of the objective function and consequently identify regions where the artificial neural network parameters will more effectively solve the equation.

  (b)

  Compute the new position of the particle as $p_i=p_i+u_i$

  (c)

  Draw a random number $r\in [0,1]$. If $r\le p_l$, then $p_i=\mathrm{LS}\left(x_i\right)$, where $\mathrm{LS}(x)$ is the same local search optimization procedure used in the genetic algorithm.

  (d)

  Create the neural network $N(x,{\overrightarrow{p}}_i)$ for particle $p_i$.

  (e)

  Create the associated model ${\Psi }_n(x,p_i)$ for particle $p_i$ as

  $${\Psi }_n(x,p_i)=x(x-1)N(x,{\overrightarrow{p}}_i)$$

  using Equation (11).

  (f)

  Calculate the corresponding fitness value $f_i$ of $p_i$ using Equation (13).

  (g)

  If $f\left(p_i\right)\le f\left({\mathrm{pb}}_i\right)$, then ${\mathrm{pb}}_i=p_i$

• End For
• Set $p_{\mathrm{best}}=arg{min}_{i\in 1\dots N_C}f\left(x_i\right)$
• Set $\mathrm{iter}=\mathrm{iter}+1$.
• Go to Step 2 to check for termination.

3. Results

All the used algorithms as well as the provided machine learning models were coded in ANSI C++ with the assistance of the freely available Optimus optimization environment, which can be downloaded from https://github.com/itsoulos/GlobalOptimus/ (accessed on 9 August 2024). The experiments were conducted on an AMD Ryzen 5950X with 128 GB of RAM, running Debian Linux. The values used for the simulation parameters are shown in

Table 1. The experimental values used in the conducted experiments.

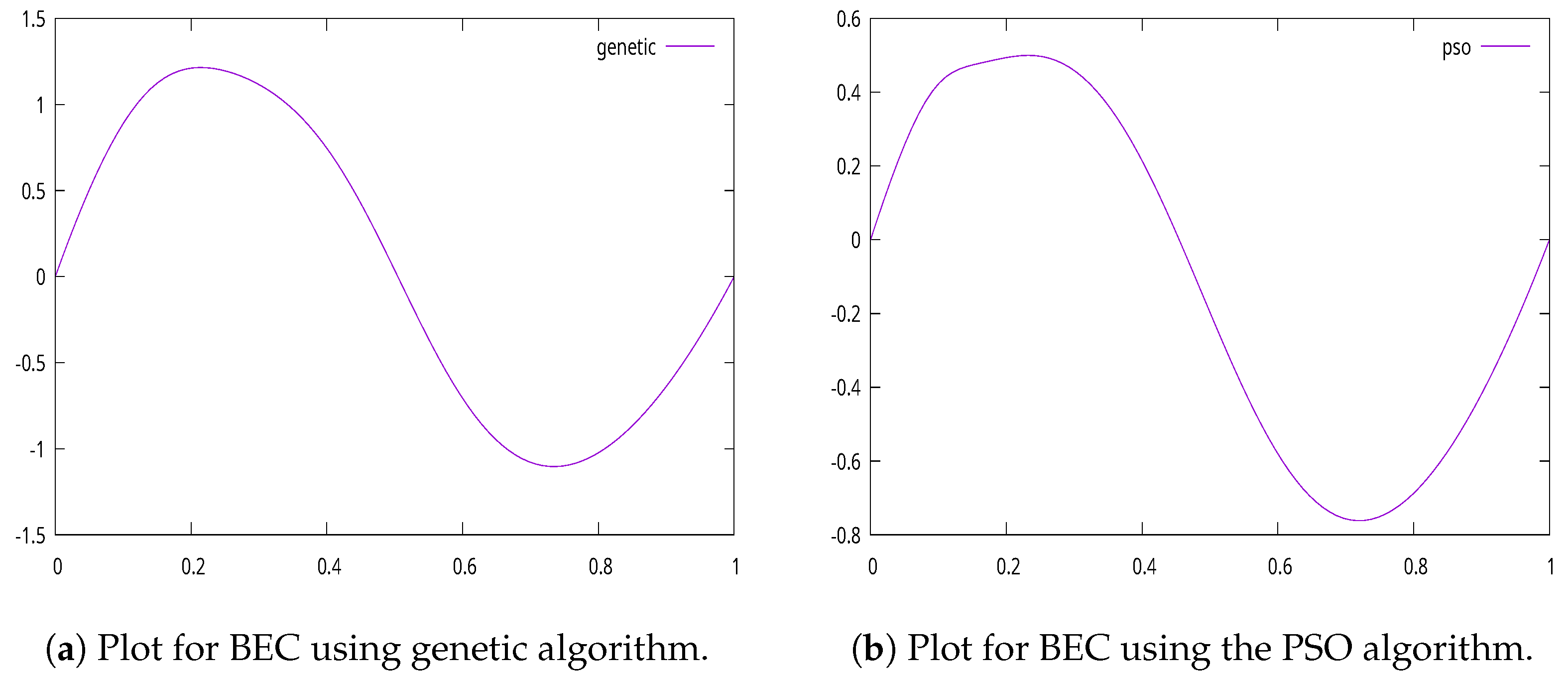
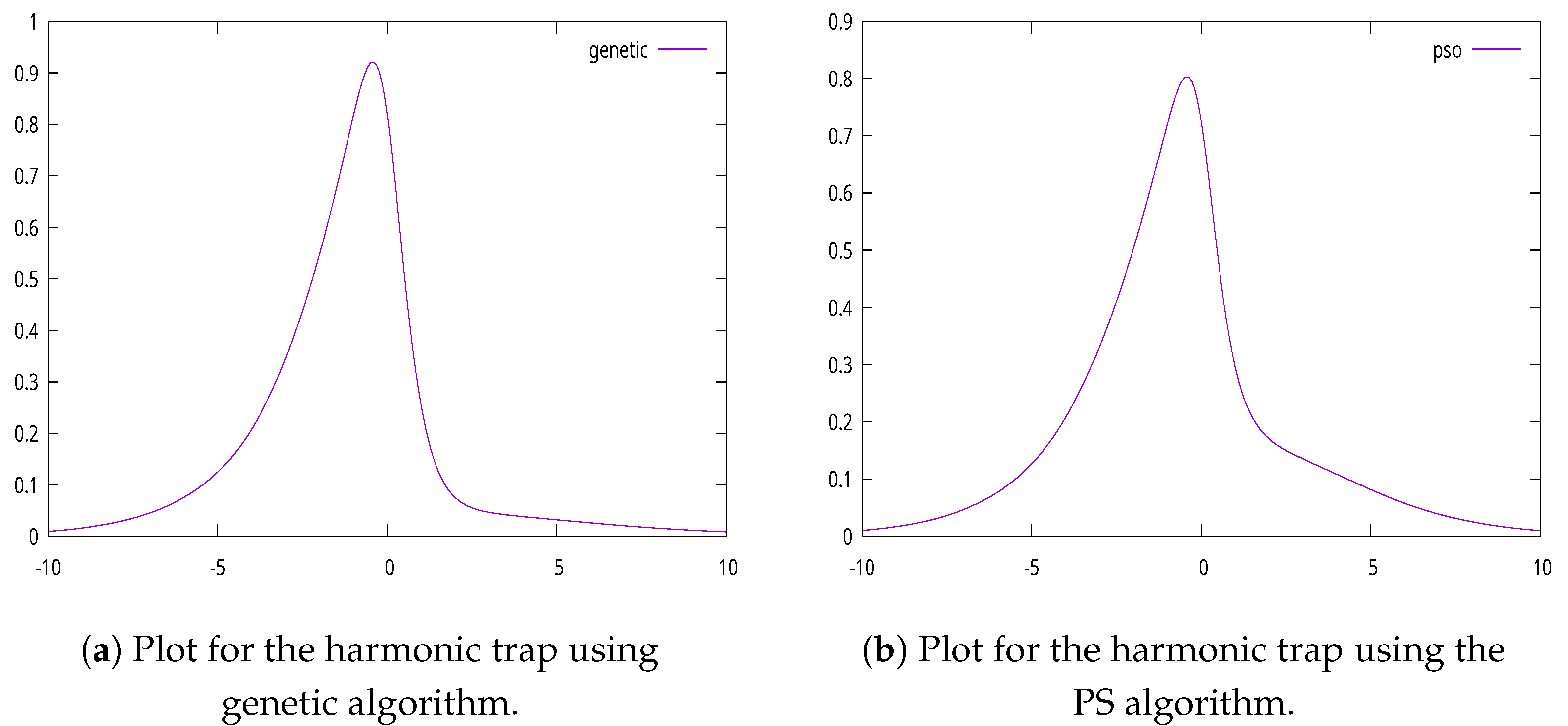
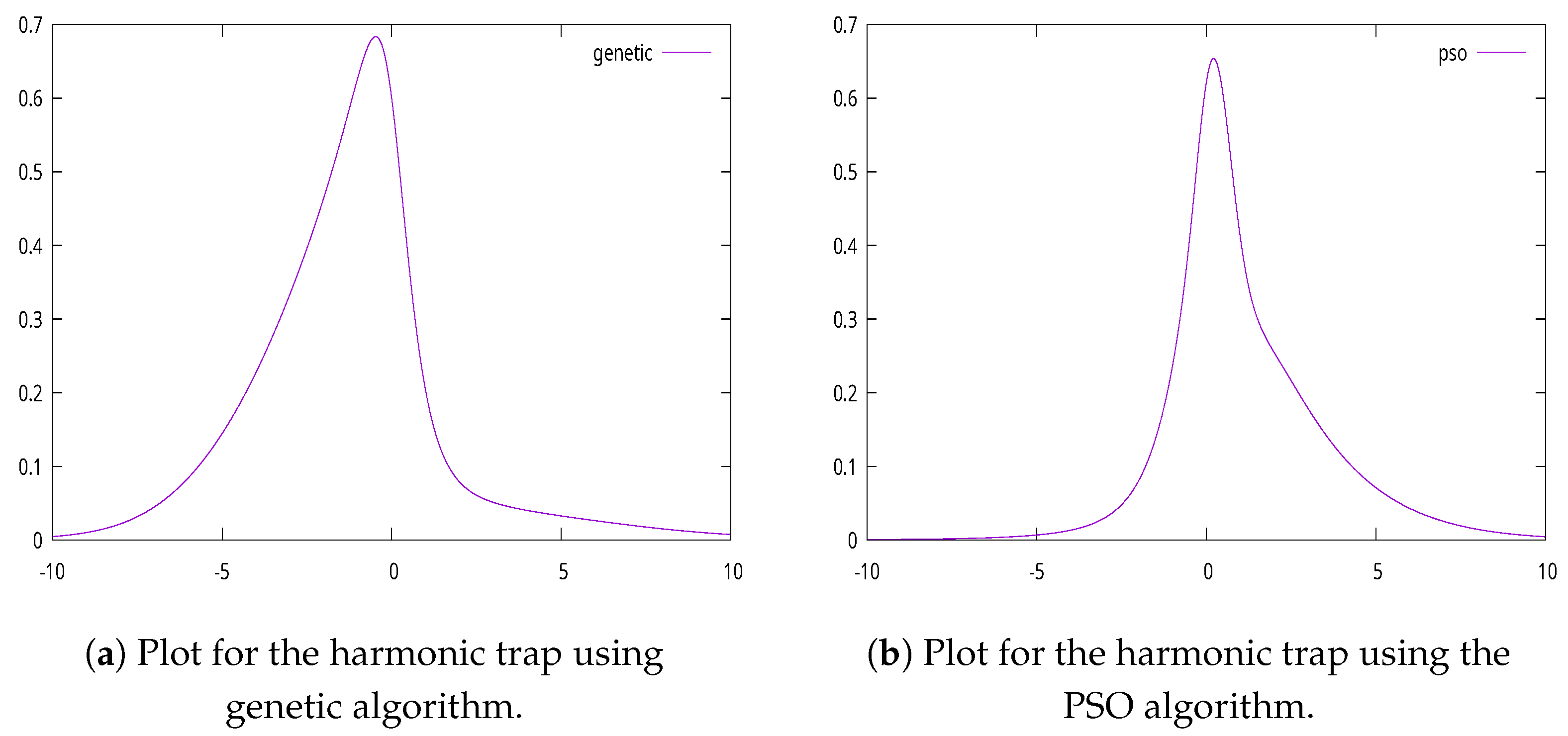
Parameter	Meaning	Value
m	Number of points used to divide the interval $[a,b]$	100
$N_C$	Number of chromosomes/particles	500
$N_G$	Maximum number of allowed generations	200
$p_S$	Selection rate	0.90
$p_M$	Mutation rate	0.05
$p_l$	Local search rate	0.01

.

Figure 1 and Figure 2 depict the plots for the used model and for the BEC potential. The values $\gamma =9.1865$ and ${\epsilon }_n=23$ were used in the first case and the values $\gamma =9.8271$ and ${\epsilon }_n=54$ were used in the second case.

As it is induced from the figures, the wavefunctions vanish at the $x=0$ and $x=1$. Also, the genetic algorithm and the PSO variant achieved similar simulation results.

Figure 3 and Figure 4 demonstrate the application of the proposed model to the gravitational trap potential. The first figure represents the results for both optimization methods using the values $gamma=45.4993$ and ${\epsilon }_n=10$ and the second stands for the simulation results for $gamma=193.6644$ and ${\epsilon }_n=20$. The above results have the proper, expected behavior, making the proposed numerical algorithms particularly significant for GPE.

These wavefunctions obey the boundary conditions (${\Psi }_n(0)=0$ and ${\Psi }_n(\infty )=0$) for both optimization algorithms (genetic algorithm and the PSO variant).

Furthermore, Figure 5 and Figure 6 demonstrate the application of the proposed method to the harmonic trap potential using the genetic algorithm and the PSO method. For the first case, the values $\gamma =218.6985$ and ${\epsilon }_n=30$ were used and the values $\gamma =203.1434$ and ${\epsilon }_n=30$ were used for the second case. Once again, the approximation of the proposed model is close to the experimental values.

The results fulfill the condition as x goes to ∞ the wavefunctions vanish. From the physical point of view, the above-illustrated results have the expected behavior and magnitudes as reported in earlier works [5]. The proposed model, based on an artificial neural network, was able to numerically solve the equation for a number of different potentials. Moreover, genetic algorithms and the modified version of particle swarm optimization show similar behavior in terms of training the proposed model.

Moreover, an experimental comparison between various optimization methods for training the proposed model for the first potential is shown in

Table 2. Experimental results for the BEC potential for two distinct cases, using a series of optimization methods. Numbers in cells denote average value for the minimum value obtained for Equation (12).

Method	BEC1	BEC2
Adam	77.93	12.24
Bfgs	3.35	8.97
Differential Evolution	3.17	8.87
Genetic	$2.22\times {10}^{-4}$	$5.11\times {10}^{-5}$
PSO	$5.35\times {10}^{-5}$	$3.8\times {10}^{-3}$

. The column BEC1 denotes the results for the case $\gamma =9.1865$ and ${\epsilon }_n=23$ and the column BEC2 represents the results for the values $\gamma =9.8271$ and ${\epsilon }_n=54$.

The proposed techniques, genetic and PSO in the table, had significantly lower values than the rest without it being clear which of the two is superior in effectiveness.

Furthermore, in order to measure the effectiveness of the proposed methodology, a series of additional experiments were conducted where some parameters were altered. In

Table 3. Experimental results for the experiment with different values for the number of chromosomes. The values $\gamma =9.1865$ and ${\epsilon }_n=23$ were used and the BEC potential was used.

Chromosomes	Execution Time	Minimum Fitness
100	102.64	0.113
200	187.40	0.0065
400	416.65	0.0057
500	830.81	$2.2\times {10}^{-4}$
600	967.19	$2.1\times {10}^{-5}$

, the results from the application of the modified genetic algorithm to train the proposed model are listed. In this table, the number of chromosomes varies from 100 to 600. The execution time is measured in seconds.

The column Execution time outlines the average execution time and the column Minimum fitness the average value for the best fitness obtained. As expected, increasing the number of chromosomes also leads to lower values of the minimum fitness, but at the same time, can significantly increase the execution time required. A satisfactory compromise between the execution time and the accuracy of the generated solution appears to be found at values of 400–600 of the genetic algorithm chromosomes.

Furthermore, for the same potential and for the genetic algorithm, the effect of changing the value of the application rate $p_l$ of the local optimization method on the final result was studied. These results are outlined in

Table 4. Experimental results for the experiment with different values for the local search rate parameter $p_l$. The values $\gamma =9.1865$ and ${\epsilon }_n=23$ were used and the BEC potential was used.

pl	Execution Time	Minimum Fitness
0.001	61.54	0.0095
0.002	72.38	0.0073
0.005	255.342	0.0069
0.01	830.81	$2.2\times {10}^{-4}$
0.02	1091.374	$2.93\times {10}^{-6}$

.

This parameter appears to have a more drastic effect on the effectiveness of the genetic algorithm, since even for its lower values the genetic algorithm shows significant effectiveness. Naturally, as this parameter increases, so too does the use of the local search method, and consequently, the required computing time increases significantly.

4. Conclusions

In this work, we have applied the genetic algorithm and the PSO algorithm to estimate the eigenfunctions of the 1D Gross–Pitaevskii equation, which has been used to describe the ground state of several quantum systems of identical bosons. We have used a few models to describe the external potential, e.g., the BEC in a box, the gravitational trap and the harmonic trap. The standard boundary conditions have been applied in our research system. In our investigation, we have researched the behavior of eigenfunctions of the Gross–Pitaevskii equation on nonlinearity parameters. The numerical results show that the eigenfunctions have the proper dependence on the position x (1-dimensional problem). More specifically, for the case of the BEC in the box, the numerically found eigenfunctions completely agree with previously reported results [5]. In the case of a gravitational trap, the eigenfunction vanishes for $x=0$ and $x=\infty$. Moreover, in the case of the harmonic trap, the wavefunction vanishes as x reaches ∞. The two different numerical algorithms have similar predictions for every used potential.

In the future, it would be interesting to study other techniques that make use of machine learning models to solve the equation in question. For example, constructing artificial neural networks could also be applied to this problem. Another method that could be applied is radial basis networks [78], which was presented relatively recently for solving differential Equations [79].

Although the result looks very promising, the techniques used to solve the specific equation nevertheless require significant computing time for the effective training of the artificial neural networks found in the proposed models. For this reason, the use of innovative parallel processing techniques, which take advantage of modern parallel computing structures such as the MPI method [80] and the OpenMP [81] method, is deemed necessary.