Abstract
A reduced-dimension (RD) method based on the proper orthogonal decomposition (POD) technology and the linearized Crank–Nicolson mixed finite element (CNMFE) scheme for solving the 2D nonlinear extended Fisher–Kolmogorov (EFK) equation is proposed. The method reduces CPU runtime and error accumulation by reducing the dimension of the unknown CNMFE solution coefficient vectors. For this purpose, the CNMFE scheme of the above EFK equation is established, and the uniqueness, stability and convergence of the CNMFE solutions are discussed. Subsequently, the matrix-based RDCNMFE scheme is derived by applying the POD method. Furthermore, the uniqueness, stability and error estimates of the linearized RDCNMFE solution are proved. Finally, numerical experiments are carried out to validate the theoretical findings. In addition, we contrast the RDCNMFE method with the CNMFE method, highlighting the advantages of the dimensionality reduction method.
Keywords:
extended Fisher–Kolmogorov equation; proper orthogonal decomposition; mixed finite element; uniqueness and stability; error estimates; numerical experiment MSC:
65M60
1. Introduction
The primary goal of this research study is to apply the POD-based reduced-dimension method to solve the following nonlinear extended Fisher–Kolmogorov (EFK) equation:
where is a bounded convex polygonal domain with boundary . is the time interval, where . Coefficient is a positive constant. is the known initial function. is the Lipschitz continuous function of u, that is, there exists a positive constant C such that
For simplicity, we assume that in the following theoretical analysis.
When in (1), the second-order diffusion equation is obtained, which is called the standard Fisher–Kolmogorov equation. Coullet et al. [1] added a stabilizing fourth-order derivative term to obtain Equation (1) and called it the extended Fisher–Kolmogorov equation. The EFK equation has a very important physical background. It has been applied to various kinds of physics and engineering problems. Because of the complexity of the equation, it is difficult to obtain its analytical solution. Therefore, it is very important to solve the equation numerically.
There are many numerical methods for solving PEDs, for instance, the direct local boundary integral equation method [2], the Fourier pseudo-spectral method [3], the modified cubic B-spline and polynomial-based differential quadrature method [4,5], the explicit finite difference method (EFDM) [6,7], the radial basis function (RBF) method [8], physics-informed neural networks (PINNs) [6,9,10] and so on. These numerical methods are also used to solve EFK equations. He [11] used a three-level linearly implicit finite difference method to solve 1D and 2D EFK equations, and the method is second-order convergent in both the time and space directions. Kumar et al. [12] proposed two RBF-based mesh-free schemes for the numerical simulation of nonlinear EFK models. Tarbiyati and Nemati [13] presented a method for initializing weights in PINNs by using FD to study the one-dimensional diffusion (heat) equation, the FK equation and the nonlinear Burgers equation. Sultan and Zhang [14] used the moving mesh finite difference method (MMFDM) in conjunction with PINNs to solve the FK equation.
In addition, various fourth-order finite difference schemes [15,16,17,18], which have fourth-order and second-order accuracy in space and time variables, respectively, have been developed to solve EFK equations. Sweilam et al. [19] studied the stochastic EFK equation by combining the compact finite difference scheme and the semi-implicit Euler–Maruyama approach. Danumjaya and Pani [20] applied mixed finite element methods to solve EFK equations with different types of boundary conditions. Doss and Nandini [21] employed a splitting technique to derive an -Galerkin mixed finite element scheme for EFK equations. Wang et al. [22] used a new linearized CNMFE method to study EFK equations, in which belongs to the weaker space instead of the classical space. In this paper, we establish a CNMFE scheme for the 2D EFK equation and analyze the uniqueness, stability and convergence of the CNMFE solutions.
However, in practical problems, using the CNMFE method to solve EFK equations is a problem with a large number of unknowns, which makes running extremely slow, leads to an increase in rounding errors, and makes it difficult to obtain accurate numerical solutions. Therefore, it is crucial to lessen the number of unknowns in the CNMFE method for EFK equations to reduce the computational load, save CPU running time, and minimize the accumulation of rounding errors in the calculation process. The proper orthogonal decomposition (POD) technology, reducing the amount of unknowns in numerical schemes, is an efficient dimensionality reduction method for solving partial differential equations (PDEs). It reduces CPU running time and reduces the accumulation of round-off errors. The POD technology can be applied to the numerical methods for various PDEs, such as the finite difference method [23,24,25], the Schwarz domain decomposition method [26], the finite spectral element method [27,28], etc. For reduced-dimension FE and MFE models based on POD techniques, there are two dimensionality reduction methods. One method is that the optimized models are established by reducing the dimension of the FE or MFE subspace. The parabolic equation [29], the Sobolev equation [30], the Burgers equation [31] and some other PDEs [32,33,34,35] are solved by the reduced-dimension method of constructing the POD subspace. The other is a new reduced-dimension method for the CNFE [36,37] and CNMFE [38,39,40,41] solution coefficient vectors proposed by Luo et al. in 2020. In [42], Luo and Yang combined the unknown solution coefficient vector dimensionality reduction method and the continuous space–time finite element method to study 2D non-stationary incompressible Navier–Stokes equations.
There are existing order reduction methods for EFK equations, such as that in the [24], which combines the high-order compact finite difference scheme with the POD method to obtain the spatial sixth-order accuracy while greatly shortening the calculation time. The article in [40] uses the POD technique to reduce the dimensionality of two-grid CNMFE solution coefficient vectors, in which the matrix theory is used to deeply explore the stability and convergence of TGRDECNMFE solutions. However, the reduced-dimension method proposed in this paper is theoretically significantly different from the above research methods. This paper integrates POD technology with the linearized CNMFE method, and proposes a new reduced-dimension method for 2D nonlinear EFK equations. In this study, we adopt the CN fully discrete format in the temporal direction to achieve second-order time accuracy. Additionally, we linearize the nonlinear term to significantly enhance computational speed and efficiency while preserving model accuracy. Unlike [40], our work utilizes traditional finite element techniques to analyze uniqueness, stability, and convergence of the RDCNMFE solutions. Our proposed method combines the advantages of POD and linearized CNMFE methods for effective dimensionality reduction of the nonlinear EFK equation. This approach not only maintains accuracy but also greatly improves computational speed and efficiency, providing a novel insight and solution for solving the EFK equation.
The structure of this paper is as follows. In Section 2, we propose the CNMFE scheme and discuss the uniqueness, stability and convergence of the CNMFE solutions. In Section 3, we generate the POD basis to derive the reduced-dimension matrix model of the CNMFE solution coefficient vectors and analyze the uniqueness, stability and error estimate of the RDCNMFE solutions. In Section 4, we employ the numerical experiments of the 1D and 2D EFK equations to verify the effectiveness of the RDCNMFE method and correctness of theoretical analysis. In Section 5, we summarize the major conclusions and findings.
2. The Crank–Nicolson Mixed Finite Element Method of the EFK Equation
2.1. The CNMFE Schemes
The Sobolev spaces and their corresponding norms mentioned in this paper adhere to standard definitions (see [43]). In order to develop the CNMFE scheme of the EFK Equation (1), we initially introduce a diffusion term , resulting in the following two lower-order equations:
Let . With Green’s formula, the mixed functional form of (3) is as follows.
Problem 1.
Find : satisfying
Let be the quasi-uniform triangulation subdivision on . The FE subspace , spanned by the orthonormal basis under the inner product in , is defined as follows:
in which is generated by th degree polynomials on .
For given integer , let , , and . Therefore, we can rewrite Problem 1 at time in the following form.
Let represent the CNMFE approximations of solutions for Problem 1 at . Thus, the CNMFE model of Problem 1 can be constructed as follows.
Problem 2.
Find satisfying
Remark 1.
2.2. The Uniqueness, Stability and Convergence of the CNMFE Solutions
By employing the base functions of the FE space , the solutions of Problem 2 can be formulated in the form of
where is the orthonormal base, satisfying
and are the unknown coefficient vectors of CNMFE solutions. From the expression of the solutions of (13), Problem 2 can be represented equivalently in the following matrix model.
Problem 3.
Find and satisfying
where
and
Theorem 1.
Problem 3 has the unique solutions .
Proof of Theorem 1.
Problem 3 can be written as
where stands for the unit matrix, and denotes zero column vector of .
From the definitions of matrices and , we know that they are positive definite and thus invertible. From (15), we can conclude that the coefficient matrix is invertible as well. Hence, there exists a unique set of solutions for Problem 3. □
In order to prove the stability of the CNMFE solutions, we need to introduce the properties of in Problem 3.
Lemma 1
([44] (Lemma 1.19)). Matrix satisfies the following inequality:
Theorem 2.
The CNMFE solutions are unconditionally stable.
Proof of Theorem 2.
We represent (14) as
Substituting the second formula of (17) into the first formula, we obtain
Taking the inner product of (18) and , we have
Combining Lemma 1 with the global Lipschitz-continuity of , the first term of (21) can be estimated as
where and are bounded. Combining (20), (21) and (22), we have
Multiplying both sides of the inequality of (23) by and summing from 2 to , we have
noting that , then
Applying the Gronwall Lemma to (25), we obtain
And because
Due to , we can easily obtain
In order to analyze the convergence of the linearized CNMFE scheme, we first need to establish the projection operator .
Lemma 2.
Let satisfy the following relation:
and
In order to facilitate theoretical analysis, the errors can be decomposed into
In order to obtain the error estimates, we introduce the following lemma, which is easily obtained by Taylor expansion.
Lemma 3.
and satisfy the following estimates
Based on Lemmas 2 and 3, the following theorems for Crank–Nicolson fully discrete error estimates is obtained.
Theorem 3.
With , assume that the solution’s regular properties for (4) satisfy , , . Then, there exists a positive constant C independent of h and such that
where .
Proof of Theorem 3.
Multiplying (41) by and adding it to (40) and using Cauchy–Schwarz inequality and Young inequality, we obtain
For the nonlinear term , using the Young inequality, we have
Noting that
Summing from , the resulting inequality becomes
Choosing , when , , and using the discrete Gronwall Lemma and Lemma 3, we obtain
Theorem 4.
With and , assume that the solution’s regular properties for (4) satisfy , , . Then, there exists a positive constant C independent of h and such that
where .
3. The Reduced-Dimension Method of the Crank–Nicolson Mixed Finite Element Solution Coefficient Vectors of the EFK Equation
3.1. Construction of POD Basis Vectors
Firstly, we need to compute the initial K-step solution coefficient vectors of Problem 3, which will yield two snapshot matrices and . Secondly, we need to compute the positive eigenvalues and arrange them in descending order of , and the associated eigenvectors to form the matrix . Finally, choosing the first d column vectors of as a set of POD bases , they satisfy the following equalities:
where and of vector . When , it follows that
Here, denotes the unit vectors whose nth component is 1. Therefore, is a set of optimal POD bases.
Remark 2.
Since the order of matrix is much larger than the order of matrix , and the eigenvalues of and are equal, we first calculate the initial d eigenvalues of matrix and their corresponding eigenvectors . Then, we use the relation to obtain the eigenvectors of , and generate a set of POD basis vectors .
3.2. Formulation of the RDCNMFE Scheme
Firstly, letting , , and and represent the RDCNMFE solution coefficient vectors. Secondly, we can instantly obtain the first K RDCNMFE solution vectors and from Section 3.1. Finally, by using instead of in Problem 3, the following matrix-based RDCNMFE scheme can be established.
Problem 4.
Find and satisfying
in which are the first K solution coefficient vectors for Problem 3. The definitions of matrix , vector , as well as FE basis function vectors are given in Section 2.2.
3.3. The Uniqueness, Stability and Error Estimate of the RDCNMFE Solutions
For the RDCNMFE solutions of Problem 4, the unique, stable and convergent properties are as follows.
Theorem 5.
Under the same assumptions as Theorems 3 and 4, if are the weak solutions to Problem 1 and are the solutions to Problem 4, then for any , the RDCNMFE solutions have uniqueness and unconditional stability, and the following error estimate is obtained.
Proof of Theorem 5.
(1) Discuss the uniqueness of the RDCNMFE solutions.
For , Theorem 1 guarantees the uniqueness of solutions to Problem 3. Therefore, the solutions generated from first and fourth formulas in Problem 4 must also be unique.
For , using , , the last three formulas of Problem 4 can be converted to
For , the set of solutions for Problem 3 is unique. Since (62)–(64) follow the same formats as Problem 3, the set of solutions for (62)–(64) is also unique.
- (2)
- Demonstrate the stability of the RDCNMFE solutions.
When , since the vectors in and are orthonormal, using Theorem 2, we have
When , since is a positive definite symmetric matrix, we can rewrite (62) as
Taking the inner product of (67) and ,
Using the same technique as (22), we have
Using the Gronwall Lemma for (75),
And
So we have
Thus, noting that , we obtain
- (3)
- Analyze the error estimate of the RDCNMFE solutions.
Taking the inner product of (83) and ,
Combining Lemma 1 with the global Lipschitz-continuity of , the first term of (86) can be estimated as
Multiplying both sides of (88) by , and summing from to , we obtain
Noting that
Applying the Gronwall Lemma for (91),
And
Thus, we obtain
Further, from , we obtain
□
4. The Numerical Examples for the EFK Equations
In order to verify the effectiveness of the RDCNMFE method, we can compare the errors and orders between the genuine, CNMFE and RDCNMFE solutions and CPU runtime on different time nodes. In order to calculate the error, we use the norm
as the errors, where and are the exact and approximate solutions respectively; 0 can be omitted here.
We here adopt the numerical experiment that the following nonlinear EFK equation has a genuine solution. Generally speaking, it has no genuine solution.
Example 1.
The 1D EFK model (97) problem is considered with a genuine solution given in the following form:
The genuine solution of the auxiliary variable is
and the time-dependent source term is
Firstly, the initial 20 CNMFE solution vectors are obtained by calculating Problem 3 to establish the snapshot matrixes and . Secondly, we calculate the eigenvalues (arranged decreasingly) and the associated eigenvectors of the matrixes . Then, we find that , so that we just need to extract the first 6 eigenvectors of the matrix to construct a set of POD basis vectors , where . Finally, we compute the RDCNMFE solutions of (97) by Problem 4 and the CNMFE solutions of (97) by Problem 3 when and at . And they are compared with the genuine solution, respectively, exhibited in Figure 1 and Figure 2. As evident from Figure 1 and Figure 2, the RDCNMFE and CNMFE solutions closely mirror the genuine solution.
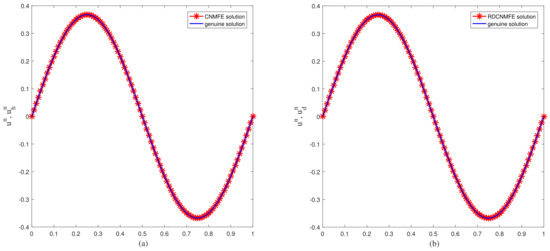
Figure 1.
(a) The comparison of and at T = 1. (b) The comparison of and at T = 1.
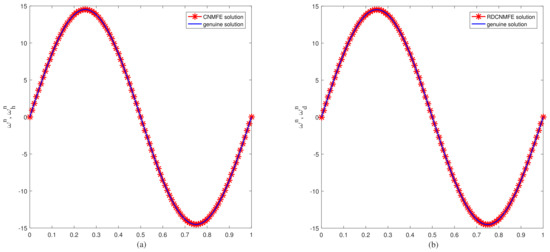
Figure 2.
(a) The comparison of and at T = 1. (b) The comparison of and at T = 1.
To facilitate comparison, we present in Table 1 and Table 2 the errors and convergence orders of the CNMFE and RDCNMFE solutions for u and , respectively, under the conditions of = 1/10,000 and at . Notably, the analysis of these tables reveals that the errors and convergence rates achieved by the RDCNMFE method closely mirror those of the CNMFE method, so this is consistent with the previous theoretical analysis.

Table 1.
errors and order between the genuine, CNMFE and RDCNMFE solutions of u when = 1/10,000 at T = 1.

Table 2.
errors and order between the genuine, CNMFE and RDCNMFE solutions of when = 1/10,000 at T = 1.
To further substantiate the efficiency of the RDCNMFE method, we have documented the errors and the CPU runtime required to compute the solutions using CNMFE and RDCNMFE methods, with and = 1/10,000, at various time points . These findings, derived from solving Problems 3 and 4, are summarized in Table 3.

Table 3.
Comparison of errors and CPU runtime of CNMFE and RDCNMFE solutions when .
As demonstrated in Table 3, the RDCNMFE method consumes much less CPU run time than the CNMFE method. This numerical example demonstrates that the RDCNMFE method significantly reduces CPU running time.
Example 2.
The 2D EFK model (97) problem is considered with genuine solution given in the following form:
The genuine solution of the auxiliary variable is
and the time-dependent source term is
We compute the RDCNMFE solutions of (97) by Problem 4 and the CNMFE solutions of (97) by Problem 3 when and at . And they are compared with the genuine solution, respectively, exhibited in Figure 3 and Figure 4. As evident from Figure 3 and Figure 4, the RDCNMFE and CNMFE solutions closely mirror the genuine solution.
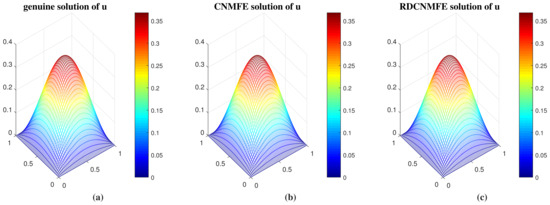
Figure 3.
(a) The genuine solution at T = 1. (b) The CNMFE solution at T = 1. (c) The RDCNMFE solution at T = 1.
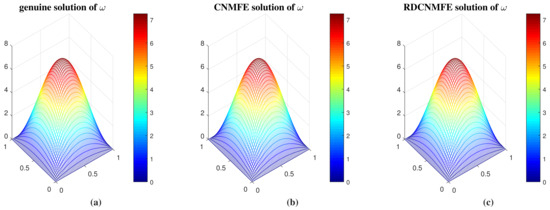
Figure 4.
(a) The genuine solution at T = 1. (b) The CNMFE solution at T = 1. (c) The RDCNMFE solution at T = 1.
For comparison, we give the errors and convergence orders of the CNMFE and RDCNMFE solutions for u and when and at in Table 4, Table 5, Table 6 and Table 7, respectively. As can be observed from Table 4, Table 5, Table 6 and Table 7, the errors and convergence rates of the RDCNMFE method are nearly identical to the CNMFE method, which aligns with the previous theoretical analysis. Figure 5 offers a more visual representation of the comparative results of the error convergence orders between and and between and when and .

Table 4.
errors and order between the genuine, CNMFE and RDCNMFE solutions of u when at T = 1.

Table 5.
errors and order between the genuine, CNMFE and RDCNMFE solutions of when at T = 1.

Table 6.
errors and order between the genuine, CNMFE and RDCNMFE solutions of u when at T = 1.

Table 7.
errors and order between the genuine, CNMFE and RDCNMFE solutions of when at T = 1.
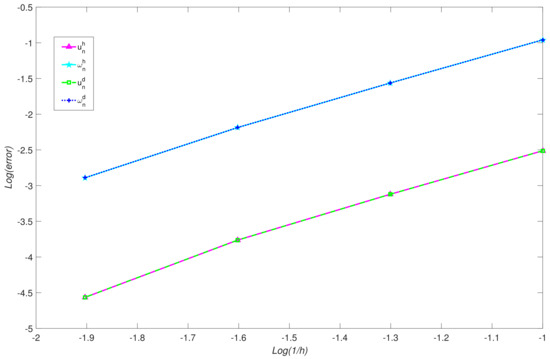
Figure 5.
Comparison of error results of u and when .
Additionally, we offer maximum absolute error when and for u and in Table 8. As can be seen from Table 8, the error obtained by the RDCNMFE method is not only quite close to that obtained by the CNMFE method, but even shows a slightly lower error level. This shows that the RDCNMFE method has some advantages over the CNMFE method in maintaining error control.

Table 8.
errors between the genuine, CNMFE and RDCNMFE solutions of u and when at T = 1.
To provide additional evidence for the effectiveness of the RDCNMFE method, we recorded the errors and the CPU running time for computing the CNMFE and RDCNMFE solutions when and at , respectively. These results are obtained by solving Problems 3 and 4 and shown in Table 9 and Table 10.

Table 9.
Comparison of errors and CPU runtime of CNMFE and RDCNMFE solutions when .

Table 10.
Comparison of errors and CPU runtime of CNMFE and RDCNMFE solutions when .
By comparing the linear equation systems in Problems 3 and 4, it can be seen that the CNMFE scheme maintains the solution coefficient vectors and as M-dimensional column vectors at each time node, which directly leads to higher computational complexity. On the contrary, the RDCNMFE scheme greatly reduces the dimension of the solution coefficient vectors from M to through POD technology. This method greatly reduces the amount of data processing, thereby significantly reducing the computational cost. As demonstrated in Table 9 and Table 10, with the increase in time, the CNMFE method with degrees of freedom requires considerable CPU runtime at each time node. When , the running time increases by approximately 30 s for every additional s, and when , the running time increases by approximately 300 s for every additional s. While performing at the same time node, the RDCNMFE method, with only degrees of freedom, requires very minimal CPU runtime. When , there is an increase in running time of only about s for every additional s, and when , there is an increase in running time of only about 1 s for every additional s. The calculation time of the CNMFE method is approximately 70 times greater than that of the RDCNMFE method when . This experiment demonstrates that the RDCNMFE method significantly reduces CPU running time. Furthermore, the results from Table 9 and Table 10 indicate that the RDCNMFE method produces slightly less errors compared to the CNMFE method.
According to the simulation results of the above two numerical examples, it is clear that the RDCNMFE method surpasses the CNMFE method, proving it as an effective numerical method for solving the nonlinear EFK equation.
5. Conclusions
In this study, we have focused on the reduced-dimension method of Crank–Nicolson mixed finite element solution coefficient vectors for 2D nonlinear EFK equations In order to give a full demonstration of the effectiveness of the reduced-dimension method, we have established the CNMFE scheme of the 2D nonlinear EFK equation and discussed the uniqueness, stability, and convergence of the CNMFE solution. Then, we have generated the POD basis based on the initial K CNMFE solutions, constructed the RDCNMFE matrix model, and employed the traditional finite element techniques to analyze the uniqueness, stability and error estimation of the RDCNMFE solution. Additionally, numerical experiments have been conducted to comparatively evaluate the performance of the two methods. Compared with the CNMFE method, the RDCNMFE method has fewer degrees of freedom at each time node. This characteristic enables the RDCNMFE method to greatly reduce computational load, running time, and error accumulation. In particular, this paper has simplified the actual calculation by linearizing the nonlinear term without iterative numerical calculation. Therefore, the RDCNMFE method constitutes a novel numerical technique for tackling nonlinear PDEs.
However, the methods presented in this paper exhibit certain limitations when applied to solving the EFK equation. The fourth-order derivative coefficient significantly impacts the convergence and accuracy of the numerical solutions. Notably, the current methods are not suitable for situations where the fourth-order coefficient takes on smaller values . In future research, we will endeavor to address this issue. And we intend to extend the scope of application of this method to PDEs with variable coefficients (in this paper, the coefficient is a constant).
Practical problems usually have no exact solutions. In order to assess the viability of the proposed method, we initially discuss its convergence using problems that possess exact solutions. This step verifies the feasibility of the method. Once feasibility is confirmed, we can confidently apply the method to practical problems without exact solutions.
Author Contributions
Conceptualization, X.C. and H.L.; methodology, X.C.; numerical simulation, X.C.; formal analysis, X.C.; writing—original draft preparation, X.C.; validation, X.C. and H.L.; writing—review, H.L.; supervision, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (12161063) and the Program for Innovative Research Team in Universities of Inner Mongolia Autonomous Region (NMGIRT2207).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the reviewers and editors for their invaluable comments, which greatly refined the content of this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| POD | proper orthogonal decomposition |
| CNMFE | Crank–Nicolson mixed finite element |
| RDCNMFE | reduced-dimension Crank–Nicolson mixed finite element |
| EFK | extended Fisher–Kolmogorov |
References
- Coullet, P.; Elphick, C.; Repaux, D. Nature of spatial chaos. Phys. Rev. Lett. 1987, 58, 431–434. [Google Scholar] [CrossRef] [PubMed]
- Ilati, M.; Dehghan, M. Direct local boundary integral equation method for numerical solution of extended Fisher-Kolmogorov equation. Eng. Comput.-Ger. 2018, 34, 203–213. [Google Scholar] [CrossRef]
- Liu, F.N.; Zhao, X.P.; Liu, B. Fourier pseudo-spectral method for the extended Fisher-Kolmogorov equation in two dimensions. Adv. Differ. Equ.-Ny. 2017, 2017, 94. [Google Scholar] [CrossRef]
- Bashan, A.; Ucar, Y.; Yagmurlu, N.M.; Esen, A. Numerical solutions for the fourth order extended Fisher-Kolmogorov equation with high accuracy by differential quadrature method. Sigma J. Eng. Nat. Sci. 2018, 9, 273–284. [Google Scholar]
- Awasthi, A. Polynomial based differential quadrature methods for the numerical solution of fisher and extended Fisher-Kolmogorov equations. Int. J. Appl. Comput. Math. 2017, 3, 665–677. [Google Scholar]
- Savović, S.; Ivanović, M.; Min, R. A Comparative Study of the Explicit Finite Difference Method and Physics-Informed Neural Networks for Solving the Burgers’ Equation. Axioms 2023, 12, 982. [Google Scholar] [CrossRef]
- Savović, S.; Djordjevich, A.; Tse, P.W.; Nikezić, D. Explicit finite difference solution of the diffusion equation describing the flow of radon through soil. Appl. Radiat. Isot. 2011, 69, 237–240. [Google Scholar] [CrossRef]
- Dehghan, M.; Shafieeabyaneh, N. Local radial basis function-finite-difference method to simulate some models in the nonlinear wave phenomena: Regularized long-wave and extended Fisher–Kolmogorov equations. Eng. Comput.-Ger. 2021, 37, 1159–1179. [Google Scholar] [CrossRef]
- Noorizadegan, A.; Cavoretto, R.; Young, D.L.; Chen, C.S. Stable weight updating: A key to reliable PDE solutions using deep learning. Eng. Anal. Bound. Elem. 2024, 168, 105933. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, Y. Learning finite difference methods for reaction-diffusion type equations with FCNNImage. Comput. Math. Appl. 2022, 123, 115–122. [Google Scholar] [CrossRef]
- He, D.D. On the L∞-norm convergence of a three-level linearly implicit finite difference method for the extended Fisher-Kolmogorov equation in both 1D and 2D. Comput. Math. Appl. 2016, 71, 2594–2607. [Google Scholar] [CrossRef]
- Kumar, S.; Jiwari, R.; Mittal, R.C. Radial basis functions based meshfree schemes for the simulation of non-linear extended Fisher–Kolmogorov model. Wave Motion 2022, 109, 102863. [Google Scholar] [CrossRef]
- Tarbiyati, H.; Nemati, S.B. Weight initialization algorithm for physics-informed neural networks using finite differences. Eng. Comput.-Ger. 2024, 40, 1603–1619. [Google Scholar] [CrossRef]
- Sultan, S.; Zhang, Z. A comparative investigation of a time-dependent mesh method and physics-informed neural networks to analyze the generalized Kolmogorov–Petrovsky–Piskunov equation. Inter. J. Numer. Methods Fluids 2024, 96, 651–669. [Google Scholar] [CrossRef]
- Li, S.G.; Xu, D.; Zhang, J.; Sun, C.J. A new three-level fourth-order compact finite difference scheme for the extended Fisher-Kolmogorov equation. Appl. Numer. Math. 2022, 178, 41–51. [Google Scholar] [CrossRef]
- Qiao, L.; Nikan, O.; Avazzadeh, Z. Some efficient numerical schemes for approximating the nonlinear two-space dimensional extended Fisher-Kolmogorov equation. Appl. Numer. Math. 2023, 185, 466–482. [Google Scholar] [CrossRef]
- Kadri, T.; Omrani, K. A fourth-order accurate finite difference scheme for the extended-Fisher-Kolmogorov equation. Bull. Korean Math. Soc. 2018, 55, 297–310. [Google Scholar]
- Ismail, K.; Atouani, N.; Omrani, K. A three-level linearized high-order accuracy difference scheme for the extended Fisher-Kolmogorov equation. Eng. Comput.-Ger. 2021, 2, 1215–1225. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Elsakout, D.M.; Muttardi, M.M. Numerical solution for stochastic extended Fisher-Kolmogorov equation. Chaos Solitons Fractals 2021, 151, 111213. [Google Scholar]
- Danumjaya, P.; Pani, A.K. Mixed finite element methods for a fourth order reaction diffusion equation. Numer. Methods Partial. Differ. Equ. 2012, 28, 1227–1251. [Google Scholar] [CrossRef]
- Doss, L.J.T.; Nandini, A.P. An H1-Galerkin mixed finite element method for the extended Fisher-Kolmogorov equation. Int. J. Numer. Anal. Model. Ser. B 2012, 3, 460–485. [Google Scholar]
- Wang, J.F.; Li, H.; He, S.; Gao, W.; Liu, Y. A new linearized Crank-Nicolson mixed element scheme for the extended Fisher-Kolmogorov equation. Sci. World J. 2013, 2013, 756281. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.Z.; Zhang, X.H. A reduced fourth-order compact difference scheme based on a proper orthogonal decomposition technique for parabolic equations. Bound. Value Probl. 2019, 130, 130. [Google Scholar] [CrossRef]
- Xu, B.Z.; Zhang, X.H.; Ji, D.B. A reduced high-order compact finite difference scheme based on POD technique for the two dimensional extended Fisher-Kolmogorov equation. IAENG Int. J. Appl. Math. 2020, 50, 474–483. [Google Scholar]
- Luo, Z.D.; Teng, F. A reduced-order extrapolated finite difference iterative scheme based on POD method for 2D Sobolev equation. Appl. Math. Comput. 2018, 329, 374–383. [Google Scholar] [CrossRef]
- Song, J.P.; Rui, H.X. A reduced-order Schwarz domain decomposition method based on POD for the convection-diffusion equation. Comput. Math. Appl. 2024, 160, 60–69. [Google Scholar] [CrossRef]
- Luo, Z.D.; Teng, F.; Xia, H. A reduced-order extrapolated Crank-Nicolson finite spectral element method based on POD for the 2D non-stationary Boussinesq equations. J. Math. Anal. Appl. 2019, 471, 564–583. [Google Scholar] [CrossRef]
- Luo, Z.D.; Jiang, W.R. A reduced-order extrapolated Crank-Nicolson finite spectral element method for the 2D non-stationary Navier-Stokes equations about vorticity-stream functions. Appl. Numer. Math. 2020, 147, 161–173. [Google Scholar] [CrossRef]
- Luo, Z.D.; Li, L.; Sun, P. A reduced-order MFE formulation based on POD method for parabolic equations. Acta. Math. Sci. 2013, 33, 1471–1484. [Google Scholar]
- Liu, Q.; Teng, F.; Luo, Z. A reduced-order extrapolation algorithm based on CNLSMFE formulation and POD technique for two-dimensional Sobolev equations. Appl. Math. J. Chinese Univ. 2014, 29, 171–182. [Google Scholar] [CrossRef]
- Luo, Z.D.; Zhou, Y.J.; Yang, X.Z. A reduced finite element formulation based on proper orthogonal decomposition for Burgers equation. Appl. Numer. Math. 2009, 59, 1933–1946. [Google Scholar] [CrossRef]
- Song, J.P.; Rui, H.X. A reduced-order characteristic finite element method based on POD for optimal control problem governed by convection-diffusion equation. Comput. Methods Appl. Mech. Eng. 2022, 391, 114538. [Google Scholar] [CrossRef]
- Song, J.P.; Rui, H.X. Reduced-order finite element approximation based on POD for the parabolic optimal control problem. Numer. Algorithms 2024, 95, 1189–1211. [Google Scholar] [CrossRef]
- Luo, Z.D. A POD-based reduced-order stabilized Crank-Nicolson MFE formulation for the Non-Stationary parabolized Navier-Stokes equations. Math. Model. Anal. 2015, 20, 346–368. [Google Scholar] [CrossRef]
- Luo, Z.D. A POD-based reduced-order TSCFE extrapolation iterative format for two-dimensional heat equations. Bound. Value Probl. 2015, 2015, 59. [Google Scholar] [CrossRef]
- Luo, Z.D. The reduced-order extrapolating method about the Crank-Nicolson finite element solution coefficient vectors for parabolic type equation. Mathematics 2020, 8, 1261. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Luo, Z.D. The reduced-dimension technique for the unknown solution coefficient vectors in the Crank-Nicolson finite element method for the Sobolev equation. J. Math. Anal. Appl. 2022, 513, 126207. [Google Scholar] [CrossRef]
- Teng, F.; Luo, Z.D. A reduced-order extrapolation technique for solution coefficient vectors in the mixed finite element method for the 2D nonlinear Rosenau equation. J. Math. Anal. Appl. 2020, 485, 123761. [Google Scholar] [CrossRef]
- Luo, Z.D. The dimensionality reduction of Crank-Nicolson mixed finite element solution coefficient vectors for the unsteady Stokes equation. Mathematics 2022, 10, 2273. [Google Scholar] [CrossRef]
- Li, Y.J.; Teng, F.; Zeng, Y.H.; Luo, Z.D. Two-grid dimension reduction method of Crank-Nicolson mixed finite element solution coefficient vectors for the fourth-order extended Fisher-Kolmogorov equation. J. Math. Anal. Appl. 2024, 536, 128168. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Li, Y.J.; Zeng, Y.T.; Cai, Y.H.; Luo, Z.D. The dimension reduction method of two-grid Crank-Nicolson mixed finite element solution coefficient vectors for nonlinear fourth-order reaction diffusion equation with temporal fractional derivative. Commun. Nonlinear Sci. 2024, 133, 107962. [Google Scholar] [CrossRef]
- Luo, Z.D.; Yang, J. The reduced-order method of continuous space-time finite element scheme for the non-stationary incompressible flows. J. Comput. Phys. 2022, 456, 111044. [Google Scholar] [CrossRef]
- Adams, R.A. Sobolev Spaces; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Luo, Z.D. The Founfations and Applications of Mixed Finite Element Methods; Chinese Science Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).