A Modified Fractional Newton’s Solver

Abstract

Fractional calculus extends the conventional concepts of derivatives and integrals to non-integer orders, providing a robust mathematical framework for modeling complex systems characterized by memory and hereditary properties. This study enhances the convergence rate of the Caputo-based Newton’s solver for solving one-dimensional nonlinear equations. By modifying the order to $1+\eta$, we provide a thorough analysis of the convergence order and present numerical simulations that demonstrate the improved efficiency of the proposed modified fractional Newton’s solver. The numerical simulations indicate significant advancements over traditional and existing fractional Newton-type approaches.

1. Introduction

Nonlinear mathematical models play a critical role in various scientific and engineering fields, providing essential insights into complex phenomena that cannot be adequately described by linear equations [1,2,3]. Many of these models are derived from polynomial equations with a single variable. Typically, these equations are expressed in the following manner:

$$f\left(x\right)=0,$$

(1)

where $x\in \mathbb{C}$.

A classic example from electrical engineering is the diode equation [4], which describes the relationship between current and voltage in a semiconductor diode. This nonlinear equation captures the exponential connection between voltage and current in a diode, as shown below:

$$I\left(V\right)=I_s\left(exp\left({\displaystyle \frac{V}{n{V}_t}}\right)-1\right),$$

(2)

where I represents the diode current, $I_s$ is the reverse saturation current, V is the voltage across the diode, n is the ideality factor, and $V_t$ is the thermal voltage ($kT/q$ where k is Boltzmann’s constant, T is temperature, and q is the charge of an electron). This equation is pivotal in understanding the nonlinear behavior of diodes, which are fundamental components in modern electronics.

Nonlinear behavior is also frequently observed in mechanical systems [5]. For instance, the equation

$$F\left(x\right)=kx+c{x}^3,$$

(3)

mathematically represents a nonlinear spring model, where F stands for the applied force, x for the displacement, k for the stiffness, and c for the nonlinear coefficient. This model is essential in understanding the behavior of materials and structures under varying loads.

In chemical kinetics, nonlinear reaction models are essential for describing the rates of reactions. The Michaelis–Menten equation [6] is a prominent example, given by:

$$v={\displaystyle \frac{V_{max}\left[S\right]}{K_m+\left[S\right]}},$$

(4)

where v is the reaction rate, $V_{max}$ is the maximum reaction rate, $\left[S\right]$ is the substrate concentration, and $K_m$ is the Michaelis constant. This nonlinear equation describes how the reaction rate depends on the concentration of the substrate, crucial for understanding enzyme kinetics.

Another example is the van der Waals equation in thermodynamics [7], which corrects the ideal gas law to account for the finite size of molecules and the attraction between them. The van der Waals equation is given by:

$$\left(P+{\displaystyle \frac{a}{V^2}}\right)(V-b)=RT,$$

(5)

where P is the pressure, V is the volume, T is the temperature, R is the gas constant, and a and b are substance-specific constants. This nonlinear equation is fundamental in describing the behavior of real gases, especially under high pressure and low temperature.

In economics, nonlinear equations are used to model complex market behaviors. The Cobb–Douglas production function is a well-known nonlinear model [8] that describes the relationship between inputs (capital and labor) and the amount of output produced:

$$Q=A{L}^{\alpha }{K}^{\beta },$$

(6)

where Q is the total production (output), L is the labor input, K is the capital input, A is a constant representing total factor productivity, and $\alpha$ and $\beta$ are the output elasticities of labor and capital, respectively. This model is fundamental in the study of production and economic growth.

Among several existing methods for solving nonlinear equations, the Newton–Raphson solver [7], also known as Newton’s solver, is renowned for its rapid convergence (quadratic) and its effectiveness in approximating the root of a real-valued function $f\left(x\right)=0$. Newton’s solver is described as follows:

$$x_{j+1}=x_j-{\displaystyle \frac{f\left(x_j\right)}{f^{\prime }\left(x_j\right)}},j=0,1,2,\dots ,$$

(7)

where $f^{\prime }\left(x\right)$ must not be zero at any step of the iteration. This solver is widely used due to its simplicity and efficiency in finding solutions to nonlinear equations.

Fractional calculus, which has historical origins dating back to the 17th century, is not a recent area of research. However, in recent times, it has emerged as a powerful tool for solving real-world problems [9,10,11,12]. One fundamental concept in fractional calculus is the Caputo fractional derivative. The Caputo fractional derivative [13] of $f\left(x\right)$ of order $\eta >0$ is defined as

$${}_0{}^{C}D_a^{\eta }f(x)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma (m-\eta )}}{\int }_a^x{\displaystyle \frac{d{f}^{\left(m\right)}\left(t\right)}{d{t}^m}}{\displaystyle \frac{dt}{{(x-t)}^{\eta +1-m}}},\hfill & m-1<\eta \le mm\in \mathbb{N},\hfill \\ {\displaystyle \frac{d{f}^{\left(m\right)}\left(x\right)}{d{x}^m}},\hfill & \eta =m\in \mathbb{N},\hfill \end{array}\right.$$

(8)

where $\Gamma (·)$ represents the gamma function. The Caputo fractional derivative provides a means of extending traditional calculus to non-integer orders, offering new perspectives and techniques for solving differential equations.

It is essential to acknowledge that employing the Caputo fractional derivative for solving nonlinear algebraic equations is unconventional and less prevalent compared to traditional root-finding techniques such as the Newton–Raphson solver (simply Newton’s solver) or the bisection method. Conventional approaches may often be more effective and straightforward, depending on the specific problem at hand. Utilizing the Caputo fractional derivative to identify roots represents a sophisticated technique requiring a meticulous examination of the problem’s characteristics and numerical methodologies. The fractional Newton’s solver, using the Caputo differential operator instead of an integer-order derivative, provides several compelling benefits when solving one-dimensional nonlinear equations of the form $f\left(x\right)=0$. One key advantage is the flexibility and enhanced convergence properties offered by fractional calculus. The Caputo derivative generalizes the concept of differentiation to non-integer orders, which allows for a smoother and more adaptive approximation of the function’s behavior around its roots. This flexibility can lead to improved accuracy, particularly in cases where the standard Newton’s solver may struggle due to sharp changes or irregularities in the function’s behavior. Additionally, the fractional derivative introduces a memory effect, taking into account the function’s history over an interval, which can help in capturing more complex dynamics of nonlinear equations, leading to faster convergence in certain scenarios. This characteristic makes the solver especially useful when dealing with highly nonlinear equations where traditional integer-order methods might fail to converge or do so more slowly. Furthermore, using the Caputo derivative often results in a more stable solution process, reducing sensitivity to initial guesses and mitigating issues like overshooting or divergence near singularities. These advantages can be particularly appealing to reviewers looking for innovative, robust methods for nonlinear equation solving.

The objective of this research study is to enhance Newton’s solver by incorporating the Caputo fractional derivative. To the best of the authors’ knowledge, previous attempts in this area are documented in the literature (e.g., [14,15,16,17]). This study aims to build on these efforts, providing a more comprehensive and effective approach to solving nonlinear equations.

The remainder of this article is structured as follows: In Section 2, the research methodology based on the generalized Taylor’s formula is presented. Section 3 modifies an existing fractional-order Caputo-based Newton’s solver and discusses its convergence order in depth. The next section, Section 4, provides numerical simulations that demonstrate the effectiveness of the proposed modified fractional Newton’s solver in solving one-dimensional nonlinear equations from various scientific and engineering fields. The article concludes with an emphasis on the main findings and suggestions for future research directions.

2. Research Methodology for Modified Method

After reading the extensive literature available on fractional methods for solving nonlinear equations, this research study is focused on a recently proposed fractional Newton’s solver based on the Caputo differential operator. The method (the authors called their method CFN) is originally given in [17] and written as follows:

$$x_{j+1}=x_j-\Gamma (1+\eta ){\displaystyle \frac{f\left(x_j\right)}{{}_0{}^{C}D_a^{\eta }f(x_j)}},j=0,1,2,\dots .$$

(9)

It may further be noted that the method (9) is also discussed in [18,19] wherein authors of the papers have identified the issues with the order of convergence in the CFN method. It is also worth mentioning that a second-order fractional Newton–Raphson method is proposed in [20]. The authors in [17] proved that the order of convergence of the method (9) is $2\eta$ with $\eta \in (0,1]$. However, reproducing the error equation for the method (9) reveals that the method could have a different order of convergence if it is modified in some way. Therefore, the fractional Newton’s solver of Caputo-type given above is modified in the following form:

$$x_{j+1}=x_j-{\left[\Gamma (1+\eta ){\displaystyle \frac{f\left(x_j\right)}{{}_0{}^{C}D_a^{\eta }f(x_j)}}\right]}^{{\displaystyle \frac{1}{\eta }}},j=0,1,2,\dots ,$$

(10)

where $\eta \in (0,1]$ is the fractional order of the Caputo differential operator. We call the above solver the modified version of the fractional Newton’s solver of Caputo-type given in (9). This section is further devoted to the study of a major theorem, which is the building block of the modified fractional Newton’s solver based on the Caputo differential operator. The generalized Taylor’s formula for the Caputo derivative of a function is an extension of the classical Taylor series, incorporating fractional calculus. The Caputo derivative is a commonly used definition for fractional derivatives, particularly because it allows for initial conditions expressed in the same way as for integer-order differential equations.

Theorem 1 

(Generalized Taylor’s formula [21]). Let us suppose that ${}_0{}^{C}D_a^{\gamma \eta }f(x)$ for $\gamma =0,1,2,\dots ,n+1,$ where $0<\eta \le 1,$ then we have the generalized Taylor’s expansion for $f\left(x\right)$ as follows:

$$f\left(x\right)=\sum _{i=0}^n{\displaystyle \frac{{(x-a)}^{i\eta }}{\Gamma (i\eta +1)}}{{}_0{}^{C}D_a}^{i\eta }f\left(a\right)+{\displaystyle \frac{{}_0{}^{C}D_a^{(n+1)\eta }f(\beta )}{\Gamma \left(\right(n+1)\eta +1)}}{(x-a)}^{(n+1)\eta },$$

(11)

where $a\le \beta \le x,\forall x\in (a,b]$ and $f\left(\zeta \right)=0$ as ζ is the exact root for $f\left(x\right)$.

Taylor’s expansion of $f\left(x\right)$ (satisfying the conditions of Theorem 1) centered at $\zeta$ in terms of the Caputo fractional derivative is given as follows:

$$f\left(x\right)={\displaystyle \frac{{}_0{}^{C}D_{\zeta }^{\eta }f(\zeta )}{\Gamma (\eta +1)}}{(x-\zeta )}^{\eta }+{\displaystyle \frac{{}_0{}^{C}D_{\zeta }^{2\eta }f(\zeta )}{\Gamma (2\eta +1)}}{(x-\zeta )}^{2\eta }+{\displaystyle \frac{{}_0{}^{C}D_{\zeta }^{3\eta }f(\zeta )}{\Gamma (3\eta +1)}}{(x-\zeta )}^{3\eta }+\mathcal{O}{(x-\zeta )}^{4\eta }.$$

(12)

The above expression can be expressed in a more compact form as follows:

$$f\left(x\right)={\displaystyle \frac{{}_0{}^{C}D_{\zeta }^{\eta }f(\zeta )}{\Gamma (\eta +1)}}[{(x-\zeta )}^{\eta }+C_2{(x-\zeta )}^{2\eta }+C_3{(x-\zeta )}^{3\eta }]+\mathcal{O}{(x-\zeta )}^{4\eta },$$

(13)

where $C_{\gamma }={\displaystyle \frac{\Gamma {(\eta +1)}_0^{\mathrm{C}}{D}_{\zeta }^{\gamma \eta }f\left(\zeta \right)}{\Gamma {(\gamma \eta +1)}_0^{\mathrm{C}}{D}_{\zeta }^{\eta }f\left(\zeta \right)}},$ for $\gamma \ge 2.$

Likewise, Taylor’s expansion for the corresponding Caputo fractional derivative of $f\left(x\right)$ can be expressed as,

$${}_0{}^{C}D_a^{\eta }f(x)=\sum _{i=0}^n{\displaystyle \frac{{(x-a)}^{i\eta }}{\Gamma (i\eta +1)}}{}_0{}^{C}D_a^{(i+1)\eta }f(a)+{\displaystyle \frac{{}_0{}^{C}D_a^{(n+2)\eta }f(\beta )}{\Gamma \left(\right(n+1)\eta +1)}}{(x-a)}^{(n+1)\eta }.$$

(14)

The above equation can also be written in the following form:

$${}_0{}^{C}D_a^{\eta }f(x)={\displaystyle \frac{{}_0{}^{C}D_{\zeta }^{\eta }f(\zeta )}{\Gamma (\eta +1)}}\left[\Gamma (\eta +1)+{\displaystyle \frac{\Gamma (2\eta +1)}{\Gamma (\eta +1)}}{C}_2{(x-\zeta )}^{\eta }+{\displaystyle \frac{\Gamma (3\eta +1)}{\Gamma (2\eta +1)}}{C}_3{(x-\zeta )}^{2\eta }\right]+\mathcal{O}{(x-\zeta )}^{3\eta }.$$

(15)

The results given above are utilized in the convergence analysis of the modified fractional Newton’s solver based on the Caputo differential operator.

3. Modified Fractional Method with Convergence Analysis

In this important section, we present the modified order of convergence for the fractional Newton’s method based on the Caputo differential operator.

Theorem 2. 

Consider a continuous function $f:D\subseteq \mathbb{R}\to \mathbb{R}$ is having the Caputo fractional derivative of order $j\eta$, where j is a positive integer and η can have any value in the domain $0<\eta \le 1$ within the interval D containing ζ (zero of the given function $f\left(x\right)$). Moreover, assume that ${}_0{}^{C}D_{\zeta }^{\eta }f(x)$ be continuous and non-zero at ζ. If an initial approximation $x_0$ is closer to ζ then the local convergence order of the modified fractional order iterative method proposed as follows:

$$x_{j+1}=x_j-{\left[\Gamma (1+\eta ){\displaystyle \frac{f\left(x_j\right)}{{}_0{}^{C}D_a^{\eta }f(x_j)}}\right]}^{{\displaystyle \frac{1}{\eta }}}j=0,1,2,\dots ,$$

(16)

is at least of convergence order $1+\eta$ where $\eta \in (0,1]$, bearing the following error equation:

$$e_{j+1}={\displaystyle \frac{1}{\eta }}{\displaystyle \frac{\left[{(\eta +1)}^2-\Gamma (2\eta +1)\right]}{\Gamma {(\eta +1)}^2}}{C}_2{e}_j^{\eta +1}+\mathcal{O}{\left(e_j\right)}^{2\eta },$$

(17)

where, $C_{\gamma }={\displaystyle \frac{\Gamma (\eta +1){}_0{}^{C}D_{\zeta }^{\gamma \eta }f(\zeta )}{\Gamma (\gamma \eta +1){}_0{}^{C}D_{\zeta }^{\eta }f(\zeta )}},$ for $\gamma \ge 2.$

Proof. 

Let $x_j,j=0,1,\dots$ be the sequence of iterates resulted from (16), aiming to approximate the zero $\zeta$ of the nonlinear function $f\left(x\right)$. Now using Taylor’s expansion of nonlinear function $f\left(x\right)$ as given in (1) and its corresponding Caputo fractional derivative ${}_0{}^{C}D_{\zeta }^{\eta }f(x)$ at $x_j$ around $\zeta$ and using the fact that $e_j=x_j-\zeta$. A Newton-like quotient can be expressed in terms of error as follows:

$${\displaystyle \frac{f\left(x_j\right)}{{}_0{}^{C}D_{\zeta }^{\eta }f(x_j)}}={\displaystyle \frac{e_j^{\eta }+C_2{e}_j^{2\eta }+C_3{e}_j^{3\eta }+\mathcal{O}{\left(e_j\right)}^{4\eta }}{\Gamma (\eta +1)+\frac{\Gamma (2\eta +1)}{\Gamma (\eta +1)}{C}_2{e}_j^{\eta }+\frac{\Gamma (3\eta +1)}{\Gamma (2\eta +1)}{C}_3{e}_j^{2\eta }+\mathcal{O}{\left(e_j\right)}^{3\eta }}}.$$

(18)

By extracting $\Gamma (\eta +1)$ common from the denominator, the above equation can be re-written as

$${\displaystyle \frac{f\left(x_j\right)}{{}_0{}^{C}D_{\zeta }^{\eta }f(x_j)}}={\displaystyle \frac{e_j^{\eta }+C_2{e}_j^{2\eta }+\mathcal{O}{\left(e_j\right)}^{3\eta }}{\left[\Gamma (\eta +1)\right]\left[1+\frac{\Gamma (2\eta +1)}{{\left(\Gamma (\eta +1)\right)}^2}{C}_2{e}_j^{\eta }+\frac{\Gamma (3\eta +1)}{\Gamma (\eta +1)\Gamma (2\eta +1)}{C}_3{e}_j^{2\eta }\right]+\mathcal{O}{\left(e_j\right)}^{3\eta }}},$$

(19)

or

$${\displaystyle \frac{f\left(x_j\right)}{{}_0{}^{C}D_{\zeta }^{\eta }f(x_j)}}={\displaystyle \frac{e_j^{\eta }+C_2{e}_j^{2\eta }+\mathcal{O}{\left(e_j\right)}^{3\eta }}{\Gamma (\eta +1)}}{\left[1+\left({\displaystyle \frac{\Gamma (2\eta +1)}{{\left(\Gamma (\eta +1)\right)}^2}}{C}_2{e}_j^{\eta }+{\displaystyle \frac{\Gamma (3\eta +1)}{\Gamma (\eta +1)\Gamma (2\eta +1)}}{C}_3{e}_j^{2\eta }\right)\right]}^{-1}.$$

(20)

Now using the binomial formula given as: ${(1+x)}^{-1}=1-x+x^2-x^3+,\dots ,$ where $\left|x\right|<1$ and ignoring the third- and higher-order powers of $e_j$, one obtains the following:

$${\displaystyle \frac{f\left(x_j\right)}{{}_0{}^{C}D_{\zeta }^{\eta }f(x_j)}}={\displaystyle \frac{e_j^{\eta }}{\Gamma (\eta +1)}}+\left({\displaystyle \frac{\Gamma {(\eta +1)}^2-\Gamma (2\eta +1)}{\Gamma {(\eta +1)}^3}}\right)C_2{e}_j^{2\eta }+\mathcal{O}{\left(e_j\right)}^{3\eta }.$$

(21)

Putting the above result into (16) leads to the following:

$$e_{j+1}=e_j-{\left[e_j^{\eta }+{\displaystyle \frac{\left(\Gamma {(\eta +1)}^2-\Gamma (2\eta +1)\right)}{\Gamma {(\eta +1)}^2}}{C}_2{e}_j^{2\eta }\right]}^{{\displaystyle \frac{1}{\eta }}}+\mathcal{O}{\left(e_j\right)}^{3\eta }.$$

(22)

Extracting $e_j^{\eta }$ common and using the binomial formula ${(1+x)}^n=1+nx+{\displaystyle \frac{n(n-1)}{2!}}{x}^2+\dots$ where n is negative or fractional and $\left|x\right|<1$, we can simplify the above expression as follows:

$$e_{j+1}=-{\displaystyle \frac{1}{\eta }}{\displaystyle \frac{\left[\Gamma {(\eta +1)}^2-\Gamma (2\eta +1)\right]}{\Gamma {(\eta +1)}^2}}{C}_2{e}_j^{1+\eta }+\mathcal{O}{\left(e_j\right)}^{2\eta +1},$$

(23)

where $C_{\gamma }={\displaystyle \frac{\Gamma (\eta +1){}_0{}^{C}D_{\zeta }^{\gamma \eta }f(\zeta )}{\Gamma (\gamma \eta +1){}_0{}^{C}D_{\zeta }^{\eta }f(\zeta )}},$ for $\gamma \ge 2.$ □

The above error Equation (23) for the modified fractional Newton’s solver reveals that the solver (16) possesses the convergence order of $1+\eta$. When $\eta \to 1$, one retains the classical Newton’s solver with quadratic convergence. It is also worth mentioning here that not every continuous function has a Caputo derivative. The function must be at least absolutely continuous, meaning it should have a well-defined, integrable first derivative for the Caputo derivative to exist.

It is important to note that in the classical Newton’s solver (7), we construct the tangent to the $f-$curve at a point near r (where r is a zero of f) and find where the tangent line intersects the x-axis. Consequently, in successive iterations, we approach the exact root (under certain assumptions). However, regarding the modified fractional version of Newton’s solver proposed in the present research study, the graphical interpretation cannot guarantee that subsequent iterations approach a zero of f. This uncertainty arises because there is currently no geometrical interpretation of the Caputo fractional derivative.

In addition, we refer the interested reader to the works of Anastassiou and Argyros in [22,23] to find further applications of Newton, Newton-like, and other solvers to solve nonlinear equations involving various types of fractional derivatives, including Caputo’s. The focus of the works is on Banach space-valued operators of a real domain.

4. Numerical Simulations

In this section, we apply the proposed modified fractional Newton’s solver, detailed in (16), to simulate nonlinear equations where the classical Newton–Raphson (NR) method ($\eta =1$) either fails or requires an excessive number of iterations to approximate all the simple roots of nonlinear equations of the type (1). These simulations were executed using MAPLE software 2022 on a laptop with Windows 11, powered by an Intel(R) Core(TM) i7–1065G7 CPU at 1.30 GHz (1.50 GHz) and equipped with 24 GB of RAM. Each table includes the fractional-order ($\eta$), the approximate root at the final iteration, the absolute error at the final iteration, the absolute functional value at the final iteration, and the CPU time measured in seconds during the numerical simulations. In addition to tabular results, we have also shown numerical simulations via graphs of the absolute errors versus number of iterations for each numerical experiment under consideration.

Problem 1. 

We begin by considering the first nonlinear equation taken from [17], a sixth degree polynomial, as shown below:

$$f_1(x)=-12.84x^6-25.6x^5+16.55x^4-2.21x^3+26.71x^2-4.29x-15.21.$$

(24)

The six exact roots for the above nonlinear polynomial are given as follows: ${\zeta }_1=0.82366+0.24769i$, ${\zeta }_2=0.82366-0.24769i$, ${\zeta }_3=-2.62297$, ${\zeta }_4=-0.584$, ${\zeta }_5=-0.21705+0.99911i$, and ${\zeta }_6=-0.21705-0.99911i$.

The numerical simulations for the nonlinear equation $f_1(x)$ in Problem 1 are given in

Table 1. Numerical simulations for the proposed modified fractional Newton’s solver (16) of the nonlinear function $f_1\left(x\right)$ with 500 iterations in Problem 1.

$\mathit{\eta }$	Approximate Root	$\left|{\mathit{x}}_{\mathit{j}+1}-{\mathit{x}}_{\mathit{j}}\right|$	$\mathit{f}\left({\mathit{x}}_{\mathit{j}+1}\right)$	CPU Time (s)
0.65	$-2.1706\times {10}^{-1}-9.9912\times {10}^{0}i$	$2.5264\times {10}^{-8}$	$9.4272\times {10}^{-4}$	$9.27$
$0.75$	$-2.6230-1.0381\times {10}^{-15}i$	$9.9684\times {10}^{-18}$	$1.5152\times {10}^{-4}$	$6.64$
$0.85$	$-5.84\times {10}^{-1}-2.6598\times {10}^{-16}i$	$1.5078\times {10}^{-17}$	$9.0\times {10}^{-8}$	$6.5$
$0.95$	$-2.6230-6.5024\times {10}^{-21}i$	$7.7536\times {10}^{-20}$	$1.73\times {10}^{-6}$	$8.48$
$1.0$ (classical)	$-2.6230$	$1.2783\times {10}^{-20}$	$3.4106\times {10}^{-13}$	$9.41$

. It can be observed from this Table that the modified Newton fractional method with convergence order $1+\eta$ is working well enough when different fractional orders are chosen at random. It is also noted the approximate roots are obtained as the complex numbers when the initial guess $x_0=-2.2$ is taken. Taking different values of $\eta$ we obtain several roots of the nonlinear Equation (24) with a very small absolute error obtained at the final iteration and so is the absolute functional value with reasonably small CPU time consumed in seconds. The performance of the solver (16) shows that it can be used to find approximate solutions of different kinds of nonlinear equations where the classical Newton ($\eta =1$) does not have several degrees of freedom when it comes to order of the derivative.

When comparing the numerical simulations of the proposed modified fractional Newton’s solver (9) with those from the fractional Newton’s solver presented in previous studies, several key differences emerge as shown in

Table 2. Numerical simulations for the fractional Newton’s solver (9) given in [17,18,19] of the nonlinear function $f_1\left(x\right)$ with 500 iterations in Problem 1.

$\mathit{\eta }$	Approximate Root	$\left|{\mathit{x}}_{\mathit{j}+1}-{\mathit{x}}_{\mathit{j}}\right|$	$\mathit{f}\left({\mathit{x}}_{\mathit{j}+1}\right)$	CPU Time (s)
$0.65$	$7.1053\times {10}^{-1}-8.7444\times {10}^{-2}i$	$1.7489\times {10}^{-1}$	$1.1329\times {10}^1$	$11.01$
$0.75$	$8.2366\times {10}^{-1}-2.4769\times {10}^{-1}i$	$4.1231\times {10}^{-10}$	$1.3\times {10}^{-8}$	$7.21$
$0.85$	$8.2366\times {10}^{-1}+2.4769\times {10}^{-1}i$	0	$1\times {10}^{-9}$	$6.87$
$0.95$	$-2.6230\times {10}^0+2.4448\times {10}^{-17}i$	$1.0015\times {10}^{-9}$	$1.7824\times {10}^{-6}$	$9.57$

for $f_1\left(x\right)$. The proposed solver exhibits a more consistent approach towards the approximate roots, particularly with decreasing values of $\eta$, as evident from the smaller changes in $\left|x_{j+1}-x_j\right|$ and the lower values of $f\left(x_{j+1}\right)$. For instance, at $\eta =0.65$, the proposed solver yields a more accurate result in terms of the functional $f\left(x_{j+1}\right)$ and takes less CPU time (9.27 s vs. 11.01 s). Moreover, the modified solver converges faster for $\eta =0.75$ and $\eta =0.85$ as indicated by smaller values of $\left|x_{j+1}-x_j\right|$ and $f\left(x_{j+1}\right)$, with reduced computational time compared to the classical method. These improvements highlight the efficiency of the proposed approach, especially in terms of accuracy and computational cost across different values of $\eta$.

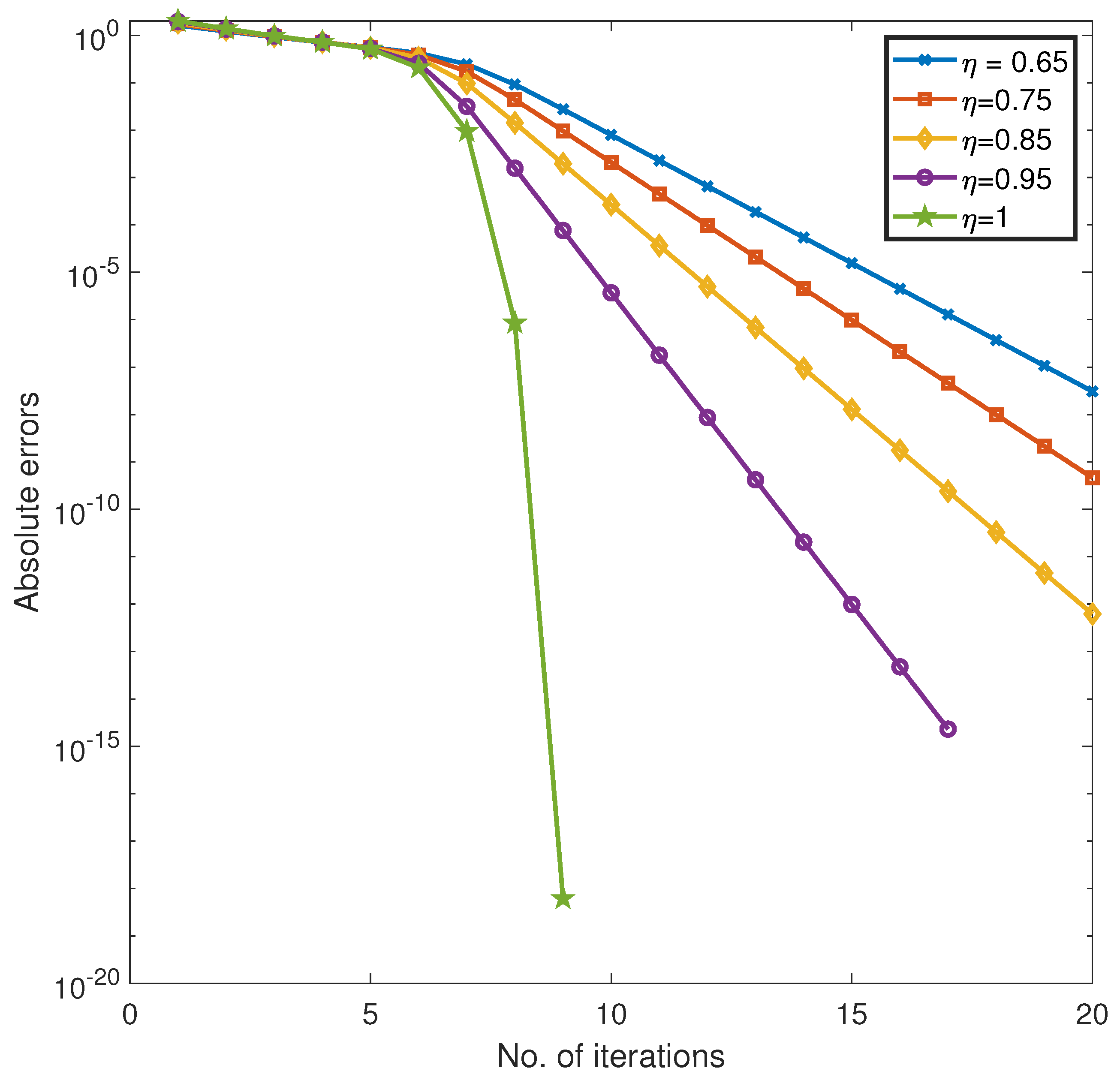
The graph in Figure 1 demonstrates the superiority of the fractional Newton’s solver in solving the nonlinear equation presented in Problem 1. It showcases the behavior of absolute errors versus the number of iterations, comparing various fractional orders of $\eta$, including $\eta =0.65$, $\eta =0.75$, $\eta =0.85$, $\eta =0.95$, and the classical Newton’s solver ($\eta =1$). In this case, the classical Newton solver exhibits rapid convergence but is limited to finding only one real root. In contrast, the fractional Newton’s solver, with its flexibility in adjusting the order $\eta$, achieves remarkable convergence properties while providing the ability to approximate multiple complex roots of the nonlinear equation. The graph reveals that fractional values of $\eta$ result in consistent reduction of absolute errors over iterations, with lower values of $\eta$ demonstrating more gradual convergence. However, this gradual nature allows the fractional method to explore multiple potential solutions, a capability that the classical method lacks due to its limited degrees of freedom. This comparison illustrates the powerful and versatile nature of the fractional Newton’s solver given in (16). Not only does it converge efficiently for a wide range of $\eta$ values, but it also uncovers multiple roots that the classical method fails to find. The ability to control the fractional order adds significant flexibility, making the fractional Newton’s solver an invaluable tool for addressing nonlinear equations with multiple roots and complex behaviors, as observed in Problem 1.

Problem 2. 

As a second numerical problem, we have chosen a well-known mathematical model [5] used in the mechanical systems as a nonlinear spring model given in (3) where the applied force F is replaced by $f_2$, the stiffness constant k is chosen to 1 whereas the nonlinear coefficient c is taken to be 2. The nonlinear model takes the following shape:

$$f_2\left(x\right)=x^3+2x.$$

(25)

The three exact roots for the above nonlinear polynomial $f_2\left(x\right)$ are given as follows:

$${\zeta }_1=0,{\zeta }_2=\sqrt{2}i,{\zeta }_3=-\sqrt{2}i.$$

(26)

The numerical simulations for the nonlinear equation $f_2\left(x\right)$ in Problem 2 using only 10 iterations are given in

Table 3. Numerical simulations for the modified fractional Newton’s solver (16) of the nonlinear function $f_2\left(x\right)$ with 10 iterations in Problem 2.

$\mathit{\eta }$	Approximate Root	$\left|{\mathit{x}}_{\mathit{j}+1}-{\mathit{x}}_{\mathit{j}}\right|$	$\mathit{f}\left({\mathit{x}}_{\mathit{j}+1}\right)$	CPU Time (s)
$0.65$	$3.1975\times {10}^{-3}$	$7.9161\times {10}^{-3}$	$6.3950\times {10}^{-3}$	$1.53$
$0.75$	$5.7332\times {10}^{-4}$	$2.0788\times {10}^{-3}$	$1.1466\times {10}^{-3}$	$1.80$
$0.85$	$4.2327\times {10}^{-5}$	$2.6665\times {10}^{-4}$	$8.4653\times {10}^{-5}$	$1.45$
$0.95$	$1.8778\times {10}^{-7}$	$3.6881\times {10}^{-6}$	$3.7555\times {10}^{-7}$	$1.50$
$1.0$ (classical)	0	$6.1685\times {10}^{-19}$	0	$1.95$

. It can be observed from this Table that the modified Newton fractional method with convergence order $1+\eta$ is working well enough when different fractional orders are chosen at random. It is also noted that the approximate roots are obtained near zero when the initial guess $x_0=5.8$ is assumed. This initial guess is far away from the exact one even though the proposed method (16) does not fail to converge. Taking different values of $\eta$, we obtained the real solution (0) of the nonlinear Equation (25) with a very small absolute error obtained at the final iteration and so is the absolute functional value with reasonably small CPU time consumption measured in seconds. The performance of the solver (16) shows that it can be used to find approximate solutions of different kinds of nonlinear equations.

When comparing the numerical simulations of the proposed modified fractional Newton’s solver (9) with those of the fractional Newton’s solver given in previous studies for the nonlinear function $f_2\left(x\right)$, we observe in

Table 4. Numerical simulations for the fractional Newton’s solver (9) given in [17,18,19] of the nonlinear function $f_2\left(x\right)$ with 10 iterations in Problem 2.

$\mathit{\eta }$	Approximate Root	$\left|{\mathit{x}}_{\mathit{j}+1}-{\mathit{x}}_{\mathit{j}}\right|$	$\mathit{f}\left({\mathit{x}}_{\mathit{j}+1}\right)$	CPU Time (s)
$0.65$	$-7.8883\times {10}^{-2}-1.5085\times {10}^{-1}i$	$2.1191\times {10}^{-1}$	$3.3768\times {10}^{-1}$	$2.11$
$0.75$	$-1.1981\times {10}^{-2}-5.4832\times {10}^{-2}i$	$8.7828\times {10}^{-2}$	$1.1209\times {10}^{-1}$	$2.04$
$0.85$	$-1.1489\times {10}^{-2}-5.6827\times {10}^{-2}i$	$9.0049\times {10}^{-2}$	$1.1577\times {10}^{-1}$	$1.75$
$0.95$	$8.4891\times {10}^{-5}-1.1730\times {10}^{-4}i$	$4.5455\times {10}^{-4}$	$2.8959\times {10}^{-4}$	$1.72$

that the proposed solver provides significantly better convergence. For instance, at $\eta =0.65$, the proposed solver shows a much smaller value of $\left|x_{j+1}-x_j\right|$ ($7.9161\times {10}^{-3}$ vs. $2.1191\times {10}^{-1}$) and a lower value of $f\left(x_{j+1}\right)$ ($6.3950\times {10}^{-3}$ vs. $3.3768\times {10}^{-1}$) with reduced CPU time (1.53 s vs. 2.11 s). The trend continues across other values of $\eta$, where the modified solver achieves smaller values of both $\left|x_{j+1}-x_j\right|$ and $f\left(x_{j+1}\right)$, suggesting improved convergence behavior. Overall, the modified solver demonstrates enhanced efficiency in terms of accuracy and computational time.

Additionally, the graph in Figure 2 illustrates the behavior of absolute errors versus the number of iterations for Problem 2, using different values of the fractional order $\eta$ in the fractional Newton solver. The absolute errors are plotted on a logarithmic scale along the vertical axis, while the number of iterations is represented on the horizontal axis. The simulation results show the convergence behavior for various values of $\eta$, including $\eta =0.65$, $\eta =0.75$, $\eta =0.85$, $\eta =0.95$, and $\eta =1$, which corresponds to the classical Newton’s method. The graph clearly shows that the classical method, represented by $\eta =1$, achieves the smallest absolute errors within a few iterations, reducing the error to approximately zero before the tenth iteration. As the value of $\eta$ decreases, the convergence rate becomes slower, with larger values of $\eta$ exhibiting faster convergence. Nevertheless, even with the smallest value of $\eta =0.65$, the method still converges effectively, although more iterations are required. This behavior highlights the efficiency of the fractional Newton solver across a range of fractional orders, allowing for flexible control over convergence speed depending on the choice of $\eta$. Moreover, as shown in Figure 2, the classical Newton’s solver achieves the smallest absolute errors but converges to only one real root. In contrast, the other curves for different $\eta$ values can find multiple roots of the nonlinear equation in Problem 2.

Problem 3. 

As a third numerical problem, we have chosen a nonlinear equation containing a trigonometric function from [24]:

$$f_3\left(x\right)=8x-cos\left(x\right)-2x^2.$$

(27)

The nonlinear Equation (27) has been simulated with the proposed modified fractional Newton’s solver given in (16) taking an initial guess $x_0=1.0$. It may be further noted that the fractional-order derivatives of (27) are not always possible to obtain in closed form, so we have attempted to solve it only for $\eta =1/2$ for which the Caputo half-order derivative of (27) is as follows:

$$\begin{array}{cc}\hfill {}_0{}^{C}D_{\zeta }^{1/2}{f}_3\left(x\right)& =-3.009x^{{\displaystyle \frac{3}{2}}}+9.027\sqrt{x}-1.414cosxFresnelS\left(0.798\sqrt{x}\right)\hfill \\ \hfill & +1.414sinxFresnelC\left(0.798\sqrt{x}\right).\hfill \end{array}$$

(28)

The equation above (computed by MAPLE software 2022) contains special functions $FresnelS(·)$ and $FresnelC(·)$ known as the Fresnel sine integral and Fresnel cosine integral, respectively.

The numerical simulations presented in

Table 5. Numerical simulations by the modified fractional Newton’s solver (16) of the nonlinear function $f_3\left(x\right)$ with different number of iterations (N) in Problem 3 for $\eta =1/2$.

N	Approximate Root	$\left|{\mathit{x}}_{\mathit{j}+1}-{\mathit{x}}_{\mathit{j}}\right|$	$\mathit{f}\left({\mathit{x}}_{\mathit{j}+1}\right)$	CPU Time (s)
10	$1.5583\times {10}^{-1}$	$3.7165\times {10}^{-3}$	$2.1016\times {10}^{-1}$	$3.35$
50	$1.3269\times {10}^{-1}$	$9.9800\times {10}^{-5}$	$3.5095\times {10}^{-2}$	$4.20$
100	$1.3031\times {10}^{-1}$	$2.3300\times {10}^{-5}$	$1.7012\times {10}^{-2}$	$6.23$
200	$1.2917\times {10}^{-1}$	$5.6000\times {10}^{-6}$	$8.3573\times {10}^{-3}$	$7.54$
400	$1.2862\times {10}^{-1}$	$1.4000\times {10}^{-6}$	$4.1377\times {10}^{-3}$	$8.95$

demonstrate the performance of the modified fractional Newton’s solver for the nonlinear equation $f_3\left(x\right)$ in Problem 3, with a fractional order of $\eta =1/2$. As the number of iterations N increases, the approximate root converges towards 0.12862, with the absolute difference $\left|x_{j+1}-x_j\right|$ decreasing progressively from $3.7165\times {10}^{-3}$ after 10 iterations to $1.4000\times {10}^{-6}$ after 400 iterations. The functional value $f\left(x_{j+1}\right)$ also decreases, indicating that the solver is successfully reducing the error in each iteration. The CPU time required for the simulations increases gradually, from 3.35 s for 10 iterations to 8.95 s for 400 iterations, reflecting the computational cost associated with a higher number of iterations. Overall, the results show steady convergence towards the approximate root, with both the error and functional values reducing consistently as the number of iterations increases, confirming the effectiveness of the fractional-order solver for this trigonometric nonlinear problem.

When comparing the numerical simulations of the modified fractional Newton’s solver (16) and the fractional Newton’s solver (9) for the nonlinear function $f_3\left(x\right)$, the modified solver in

Table 6. Numerical simulations for the fractional Newton’s solver (9) given in [17,18,19] of the nonlinear function $f_3\left(x\right)$ with different number of iterations (N) in Problem 3 for $\eta =1/2$.

N	Approximate Root	$\left|{\mathit{x}}_{\mathit{j}+1}-{\mathit{x}}_{\mathit{j}}\right|$	$\mathit{f}\left({\mathit{x}}_{\mathit{j}+1}\right)$	CPU Time (s)
10	$5.5119\times {10}^{-2}$	$2.3892\times {10}^{-1}$	$5.6360\times {10}^{-1}$	$3.84$
50	$5.5116\times {10}^{-2}$	$2.3899\times {10}^{-1}$	$5.6363\times {10}^{-1}$	$4.47$
100	$5.5116\times {10}^{-2}$	$2.3899\times {10}^{-1}$	$5.6363\times {10}^{-1}$	$7.98$
200	$5.5116\times {10}^{-2}$	$2.3899\times {10}^{-1}$	$5.6363\times {10}^{-1}$	$8.01$
400	$5.5116\times {10}^{-2}$	$2.3899\times {10}^{-1}$	$5.6363\times {10}^{-1}$	$10.13$

shows clear improvements in convergence and accuracy. After 10 iterations, the modified solver gives an approximate root of $1.5583\times {10}^{-1}$, with $\left|x_{j+1}-x_j\right|=3.7165\times {10}^{-3}$ and $f\left(x_{j+1}\right)=2.1016\times {10}^{-1}$, which is considerably better than (9)’s result of $5.5119\times {10}^{-2}$, with a larger error $\left|x_{j+1}-x_j\right|=2.3892\times {10}^{-1}$ and $f\left(x_{j+1}\right)=5.6360\times {10}^{-1}$. As the number of iterations increases, the modified solver continues to refine the root, reaching $\left|x_{j+1}-x_j\right|=1.4000\times {10}^{-6}$ and $f\left(x_{j+1}\right)=4.1377\times {10}^{-3}$ after 400 iterations, whereas the solver (9) stagnates with no improvement in the error ($\left|x_{j+1}-x_j\right|=2.3899\times {10}^{-1}$ and $f\left(x_{j+1}\right)=5.6363\times {10}^{-1}$) even at 400 iterations. Furthermore, the CPU time for the modified solver remains competitive, increasing linearly with iterations. This demonstrates that the proposed solver not only provides more accurate results but also maintains computational efficiency.

Problem 4. 

As a final numerical problem, we have chosen a nonlinear equation containing an exponential function from [24]:

$$f_4\left(x\right)=x-exp(-x)-x^3.$$

(29)

The nonlinear Equation (29) has been simulated with the proposed modified fractional Newton’s solver given in (16) taking an initial guess $x_0=-3.3$. Once again, we have attempted to solve it only for $\eta =1/2$ for which the Caputo half-order derivative of (27) is as follows:

$${}_0{}^{C}D_{\zeta }^{1/2}{f}_4(x)=1.128\sqrt{x}-1.805x^{5/2}+exp\left(-x\right)erfi\left(\sqrt{x}\right).$$

(30)

The equation above (computed by MAPLE software 2022) contains a special function $erfi(·)$ known as the imaginary error function.

The numerical simulations in

Table 7. Numerical simulations by the modified fractional Newton’s solver (16) of the nonlinear function $f_4\left(x\right)$ with different number of iterations (N) in Problem 4 for $\eta =1/2$.

N	Approximate Root	$\left|{\mathit{x}}_{\mathit{j}+1}-{\mathit{x}}_{\mathit{j}}\right|$	$\mathit{f}\left({\mathit{x}}_{\mathit{j}+1}\right)$	CPU Time (s)
10	$-2.3812$	$7.0010\times {10}^{-3}$	$3.0247\times {10}^{-1}$	$2.01$
50	$-2.3328$	$2.3300\times {10}^{-4}$	$5.5520\times {10}^{-2}$	$3.21$
100	$-2.3272$	$5.6000\times {10}^{-5}$	$2.7330\times {10}^{-2}$	$5.36$
200	$-2.3244$	$1.4000\times {10}^{-5}$	$1.3540\times {10}^{-2}$	$6.84$
400	$-2.3231$	$3.0000\times {10}^{-6}$	$6.7400\times {10}^{-3}$	$7.85$

illustrate the behavior of the modified fractional Newton’s solver for the nonlinear equation $f_4\left(x\right)$ in Problem 4, where an exponential term is included, with a fractional order of $\eta =1/2$. Starting with an initial guess of $x_0=-3.3$, the solver steadily converges towards an approximate root of −2.3231 as the number of iterations increases. The absolute error $\left|x_{j+1}-x_j\right|$ decreases consistently from $7.0010\times {10}^{-3}$ after 10 iterations to $3.0000\times {10}^{-6}$ after 400 iterations. The functional value $f\left(x_{j+1}\right)$ also shows continuous improvement, reducing from $3.0247\times {10}^{-1}$ at 10 iterations to $6.7400\times {10}^{-3}$ after 400 iterations, indicating the solver’s effectiveness in minimizing the residual error. The CPU time required for each simulation grows incrementally from 2.01 s at 10 iterations to 7.852 s at 400 iterations, demonstrating that higher precision and lower error come at the cost of increased computational effort. These results suggest that the solver efficiently handles the nonlinear equation involving exponential functions, providing steady convergence as the number of iterations increases.

When comparing the numerical simulations for the modified fractional Newton’s solver (16) and the fractional Newton’s solver (9) for the nonlinear function $f_4\left(x\right)$, it becomes clear that the modified fractional Newton’s solver (16) converges faster and provides more accurate results as shown in

Table 8. Numerical simulations for the fractional Newton’s solver (9) given in [17,18,19] of the nonlinear function $f_4\left(x\right)$ with different number of iterations (N) in Problem 4 for $\eta =1/2$.

N	Approximate Root	$\left|{\mathit{x}}_{\mathit{j}+1}-{\mathit{x}}_{\mathit{j}}\right|$	$\mathit{f}\left({\mathit{x}}_{\mathit{j}+1}\right)$	CPU Time (s)
10	$-5.3583+1.9518\times {10}^{-1}i$	$6.0531\times {10}^{-1}$	$6.5265\times {10}^1$	$3.14$
50	$-6.84+3.4057\times {10}^{-1}i$	$7.7088\times {10}^{-1}$	$6.2853\times {10}^2$	$5.24$
100	$-7.8406+3.8351\times {10}^{-1}i$	$8.2178\times {10}^{-1}$	$2.0819\times {10}^3$	$6.03$
200	$-8.9963+4.1217\times {10}^{-1}i$	$8.5426\times {10}^{-1}$	$7.3813\times {10}^3$	$8.31$
400	$-10.202+4.2826\times {10}^{-1}i$	$8.715\times {10}^{-1}$	$2.5950\times {10}^4$	$9.59$

. After just 10 iterations, the modified solver achieves an approximate root of −2.3812 with $\left|x_{j+1}-x_j\right|=7.0010\times {10}^{-3}$ and $f\left(x_{j+1}\right)=3.0247\times {10}^{-1}$, while the solver (9) results in a complex root of $-5.3583+1.9518\times {10}^{-3}i$ with a much larger error $\left|x_{j+1}-x_j\right|=6.0531\times {10}^{-1}$ and $f\left(x_{j+1}\right)=6.5265\times {10}^1$. As the number of iterations increases, the modified solver consistently refines the root, achieving $\left|x_{j+1}-x_j\right|=3.0000\times {10}^{-6}$ and $f\left(x_{j+1}\right)=6.7400\times {10}^{-3}$ after 400 iterations. In contrast, the solver (9) exhibits significantly higher errors throughout, with $\left|x_{j+1}-x_j\right|=8.715\times {10}^{-1}$ and $f\left(x_{j+1}\right)=2.5950\times {10}^4$ at 400 iterations. Furthermore, the CPU time for the modified solver remains much lower, ranging from 2.01 s to 7.85 s, compared to the other solver’s times, which increase drastically from 3.14 s to 9.59 s. These results highlight the improved convergence and computational efficiency of the modified fractional Newton’s solver.

5. Conclusions with Future Remarks

This study explores fractional calculus, which extends the concepts of derivatives and integrals beyond traditional integer orders. This advanced mathematical framework is particularly effective in modeling complex systems that exhibit memory and inheritance properties. Fractional calculus is notably significant in fields such as control theory, signal processing, and biology, as it enables the development of more detailed and accurate models than those based on integer-order calculus. Primary objective of the present research study is to accelerate the convergence of the Caputo-based Newton’s solver when applied to solving one-dimensional nonlinear equations. We conduct numerical simulations using a modified order in the fractional Newton’s solver and provide a comprehensive analysis of the convergence rate. This approach offers new insights into this intricate mathematical solver.

The fractional order $\eta$ of the Caputo derivative is chosen arbitrarily. Ensuring that a randomly selected order $\eta$ will effectively approach the zero of the function under consideration is an issue that warrants future research. This problem could potentially be addressed using optimization techniques.