Abstract
In this paper, we consider the fractional Schrödinger–Hirota (FSH) equation in the sense of a conformable fractional derivative. Through a traveling wave transformation, we change the FSH equation to an ordinary differential equation. We obtain several exact solutions through the auxiliary equation method, including soliton, exponential and periodic solutions, which are useful to analyze the behaviors of the FSH equation. We show that the auxiliary equation method improves the speed of the discovery of exact solutions.
MSC:
35C07; 35C08
1. Introduction
The Schrödinger equation, also known as the Schrödinger wave equation, is a fundamental partial differential equation (PDE) in quantum mechanics. It describes the motion of microscopic particles by combining the concept of matter waves with the wave equation [1]. The Hirota equation is a nonlinear partial differential equation (NLPDE). It describes nonlinear wave behavior in certain physical systems [2]. There are also some papers about the Schrödinger equation and Hirota equation from the perspective of differential geometry [3,4]. The Gaussian curvature, mean curvature and other geometric properties of the soliton surfaces and hypersurfaces of the equations in Euclidean and Minkowski spaces are studied in [5,6,7,8].
The Schrödinger–Hirota (SH) equation combines the Schrödinger equation with the Hirota equation. It is an NLPDE with a dispersion term, which can capture the nonlinear coupling effects in some complex nonlinear wave phenomena. However, with the advancement of technology, especially in the fields of high-precision measurement and ultrafast optics, traditional models have shown their limitations. Therefore, the demand for the exploration of more complex systems has prompted us to seek more precise mathematical tools to describe the behavior of light waves. As a generalization of the integer-order SH equation, the fractional Schrödinger–Hirota (FSH) equation has been proven to be a powerful tool in describing the propagation behavior of light waves in optical fibers. The fractional derivatives enable us to describe the effects of non-local and non-Markov processes on light wave propagation more accurately [9], therefore providing new possibilities for the understanding and design of novel fiber optic devices. In this paper, we focus on the FSH equation; it is given as follows [1]:
where x is the spatial variable, t is the time variable and is the complex short wave envelope. and d are constants, where a is the spatio-temporal dispersion, b is the Landau coefficient, c is the third-order dispersion and d is the nonlinear dispersion. , are the modified fractional derivatives; are constants satisfying .
The exact solutions of the FSH equation are crucial in understanding the dynamic behavior of complex systems. There are many methods used to find the exact solutions of the FSH equation, such as the Hirota bilinear method [10], Jacobi elliptic function expansion method [11], Darboux transform method [12] and so on [13].
In this paper, we obtain some exact solutions of (1) through the traveling wave transformation [14] and auxiliary equation method [15]. We also give the figures and contour plots of the amplitudes of these solutions. When studying the solutions and properties of these equations, differential geometry tools such as manifolds, connections and curvatures can be used [16,17,18,19]. The geometric structures of the manifolds [20] can be used in analyzing the behaviors of the solutions. We hope to reveal the influence of fractional derivatives on the propagation behaviors of light waves through these exact solutions.
The auxiliary equation method used in this paper is highly efficient in solving certain NLPDEs. It converts an NLPDE into a lower-dimensional ODE, which reduces the difficulty in solving equations. Appropriate auxiliary equations can systematically generate multiple solutions and verify the structures of the solutions, therefore providing a powerful exploration tool for the analysis of the properties of the solution space.
2. Preliminaries
2.1. Conformable Fractional Derivatives
Firstly, we review the definition and properties of conformable fractional derivatives.
Definition 1
([21]). For a function , its conformable fractional derivative of order at t is defined by
where and . If the limit above exists, f is said to be differentiable of order at t. If f is differentiable of order α in the interval for some , and exists, we define the conformable fractional derivative of order of f at 0 to be .
By definition, is simply the normal derivative of f when and the normal right-hand derivative of f when .
Lemma 1
([21]). Let , , and be differentiable of order α at . Then,
- 1.
- for any constant λ;
- 2.
- for any ;
- 3.
- for any ;
- 4.
- ;
- 5.
- ;
- 6.
- When is differentiable in the normal sense, .
2.2. Auxiliary Equation Method
Here, we introduce the basic idea of the auxiliary equation method briefly [22]. We consider an NLPDE as
F is the polynomial of the shown variables. It contains the nonlinear term of the unknown function and the linear highest derivative term.
Step 1. Then, we consider the following transformation:
where is the phase of the traveling wave, and the wave number k and wave speed v are constants. With the derivative substitution
substituting (4) into (3) yields
where G is the polynomial of the shown variables.
Step 2. Assume that the solution of (5) is given as follows:
where are unknown constants to be determined. N is called the equilibrium constant, which can be determined by the homogeneous equilibrium principle. In detail, the linear derivative term of the highest order and the nonlinear term of the highest power in Equation (5) cancel each other out. A new auxiliary equation satisfying the following conditions is defined in [15].
where and are real parameters. Some solutions of (7) have been given in Table 1 of [23].
3. Application of Auxiliary Equation Method to FSH Equation
The traveling wave transformation for the FSH Equation (1) is performed as follows.
where is the wave number of the soliton, and k, r, and are constants that need to be determined. Substituting (8) into (1) yields the following.
Re:
Im:
Integrating (10) and taking the constant as zero, we have the following result.
By balancing (9) and (11) with homogeneous power, the following formula can be obtained.
From Equation (12), we have
Then, we consider (9) under the constraints of Equation (13). By using the homogeneous balance principle in (9), we have , i.e., . Considering all of the above conditions, the scheme is presented in the representative form as follows.
where satisfies the auxiliary Equation (7). Substituting (14) into (9), we can obtain the following algebraic equation system.
A group of solutions of (15) are obtained as follows.
Therefore, we obtain exact solutions of (14) as
4. Exact Solutions of FSH Equation
4.1. Method for Derivation of Exact Solutions
For Equation (7), let ; then, . Substituting
into (7), we have
i.e.,
The problem of solving Equation (7) becomes the problem of solving the following Equation (19).
where .
Devising the following transformation
and substituting it into Equation (19), we have
Therefore, is a solution of Equation (19) if and only if is a solution of the following Riccati equation:
This indicates that the Bäcklund transformation of Equation (19) and the nonlinear superposition formula of the solution can be indirectly derived from that of the Riccati Equation (21) through the transformation (20).
For example, integrating Equation (21), we obtain a solution
and substitute it into Equation (20), and we have
For , we have
so
For and , we have
This is the first solution that we give in Section 4.2. The exact solutions of the Riccati Equation (21) are well known; similarly, we can obtain other exact solutions of (1), which we give in Section 4.2.
4.2. Six Exact Solutions of FSH Equation
In this section, we give six exact solutions of (1) using the method introduced in Section 4.1. The solutions of (7) have also been provided in [23,24]. Here, we take
We divide the coefficients of (7) into three cases.
Case 1. When and , Equation (7) has the following solutions:
Hence, Equation (1) has the following solutions, respectively:
4.3. Physical and Geometry Interpretation
In this section, by selecting appropriate parameter values, we render amplitude images of the soliton, exponential and periodic solutions in the form of 3D, 2D and contour plots. Figure 1 represents the bright soliton with parameters . Figure 2 represents the hyperbolic function solution with parameters . Figure 3 represents the exponential solution with parameters . Figure 4 represents the soliton solution with parameters . Figure 5 and Figure 6 represent the periodic solutions and with parameters .
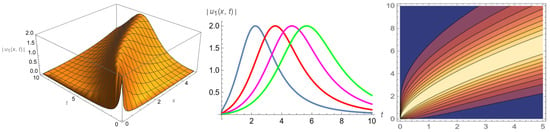
Figure 1.
The 3D, 2D and contour plots of .
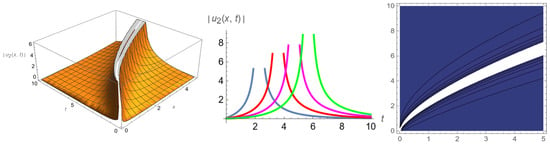
Figure 2.
The 3D, 2D and contour plots of .
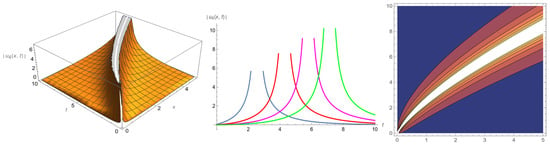
Figure 3.
The 3D, 2D and contour plots of .
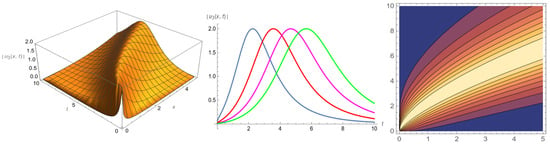
Figure 4.
The 3D, 2D and contour plots of .
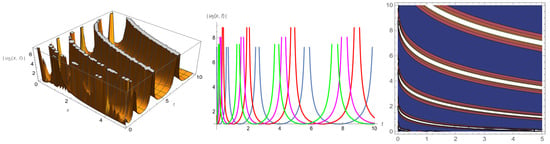
Figure 5.
The 3D, 2D and contour plots of .
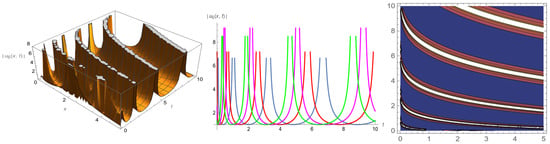
Figure 6.
The 3D, 2D and contour plots of .
In quantum mechanics, the amplitude (modulus) of a solution is usually related to the probability density or strength of the system. It can be used to describe specific quantum states or dynamic behaviors. For example, in quantum computing, quantum simulation or quantum field theory, the information of the amplitude distribution is crucial in understanding the behavior of quantum systems, predicting experimental results and conducting theoretical analysis.
Figure 1 and Figure 4 show that the amplitude of the soliton waves does not change with time. They only move forward along the space axis with the specific wave velocities and propagation directions. Figure 2 and Figure 3 show that the amplitude of the wave gradually increases with the change in the spatial position. Figure 5 and Figure 6 show that the periodic wave moves left or right along the space axis with a constant amplitude.
5. Conclusions
From the above discussion, we see that the auxiliary equation method is an effective way to obtain exact traveling wave solutions of fractional NLPDEs. The results given in our paper show that the method can generate multiple solutions for the given equation, thus enriching the diversity of the solutions.
The auxiliary equation method not only plays a significant role in obtaining exact solutions of NLPDEs, but can also be widely applied in other fields. For example, it can be used to optimize the loss functions in machine learning models by improving the convergence speed and accuracy of the algorithm. When dealing with nonlinear and multivariable systems, it can help to design more accurate and efficient controllers. When simulating complex fluid flows and turbulent phenomena, it can be used to simplify the calculations and improve the simulation accuracy. When studying the mechanical properties of new materials, it can be used to analyze the stress–strain relationships and other key performance indicators.
Although the auxiliary equation method is highly effective in two-dimensional problems, in higher-dimensional problems, the complexity of the auxiliary equation and the solution structures increases greatly, which means that it may no longer be directly applicable or may require more complex techniques to be implemented. For some PDEs, the solution found by the auxiliary equation method may not be unique or may not satisfy all conditions. This requires further mathematical analysis to verify the existence and uniqueness of the solution. The auxiliary equation method is mainly used to find general solutions; when applying boundary and initial conditions to the solution, it may require further processing in combination with other methods.
Author Contributions
The authors contributed equally to this article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ekici, M.; Mirzazadeh, M.; Sonmezoglu, A.; Ullah, M.Z.; Asma, M.; Zhou, Q.; Moshokoa, S.P.; Biswas, A.; Belic, M. Dispersive optical solitons with Schrödinger–Hirota equation by extended trial equation method. Optik 2017, 136, 451–461. [Google Scholar] [CrossRef]
- Ahmad, A.; Seadawy, A.R.; Ahmed, S.; Rizvi, S.T. Dynamical forms of breathers, rogue waves, lump and their interactions for Schrödinger–Hirota equation. Opt. Quantum Electron. 2023, 55, 730. [Google Scholar] [CrossRef]
- Radha, B.; Rossen, D. The Schrödinger equation as a moving curve. Phys. Lett. A 1999, 260, 62–67. [Google Scholar]
- Li, Y.; Abdel-Aziz, H.; Serry, H.; El-Adawy, F.; Saad, M. Geometric visualization of evolved ruled surfaces via alternative frame in Lorentz-Minkowski 3-space. AIMS Math. 2024, 9, 25619–25635. [Google Scholar] [CrossRef]
- Erdoğdu, M.; Yavuz, A. Differential geometric aspects of nonlinear Schrödinger equation. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2021, 70, 510–521. [Google Scholar] [CrossRef]
- Li, Y.; Erdoğdu, M.; Yavuz, A. Differential Geometric Approach of Betchow-Da Rios Soliton Equation. Hacet. J. Math. Stat. 2023, 52, 114–125. [Google Scholar] [CrossRef]
- Li, Y.; Güler, E.; Toda, M. Family of right conoid hypersurfaces with light-like axis in Minkowski four-space. AIMS Math. 2024, 9, 18732–18745. [Google Scholar] [CrossRef]
- Li, Y.; Güler, E. Right Conoids Demonstrating a Time-like Axis within Minkowski Four-Dimensional Space. Mathematics 2024, 12, 2421. [Google Scholar] [CrossRef]
- O’regan, D.; Aderyani, S.R.; Saadati, R.; Inc, M. Soliton Solution of the Nonlinear Time Fractional Equations: Comprehensive Methods to Solve Physical Models. Axioms 2024, 13, 92. [Google Scholar] [CrossRef]
- Biswas, S.; Ghosh, U.; Raut, S. Construction of fractional granular model and bright, dark, lump, breather types soliton solutions using Hirota bilinear method. Chaos Solitons Fractals 2023, 172, 113520. [Google Scholar] [CrossRef]
- Feng, Q. Jacobi Elliptic Function Solutions For Fractional Partial Differential Equations. IAENG Int. J. Appl. Math. 2016, 46, 121–129. [Google Scholar]
- Xu, B.; Shi, P.-C.; Zhang, S.-J. Non-Differentiable fractional odd-soliton solutions of local fractional generalized Broer-Kaup system by extending Darboux transformation. Therm. Sci. 2023, 27, 77–86. [Google Scholar] [CrossRef]
- Sulaiman, T.-A.; Bulut, H.; Atas, S.-S. Optical solitons to the fractional Schrödinger-Hirota equation. Appl. Math. Nonlinear Sci. 2019, 4, 535–542. [Google Scholar] [CrossRef]
- Ma, H.-C.; Yu, Y.-D.; Ge, D.-J. New exact travelling wave solutions for Zakharov–Kuznetsov equation. Commun. Theor. Phys. 2009, 51, 609. [Google Scholar]
- Sirendaoreji, N. Traveling Wave Solutions of Nonlinear Wave Equations—Theory and Applications of Auxiliary Equation Method; Science Press: Beijing, China, 2019. [Google Scholar]
- Bobenko, A.; Pinkall, U. Discrete surfaces with constant negative Gaussian curvature and the Hirota equation. J. Differ. Geom. 1996, 43, 527–611. [Google Scholar] [CrossRef]
- Li, Y.; Aquib, M.; Khan, M.A.; Al-Dayel, I.; Masood, K. Analyzing the Ricci Tensor for Slant Submanifolds in Locally Metallic Product Space Forms with a Semi-Symmetric Metric Connection. Axioms 2024, 13, 454. [Google Scholar] [CrossRef]
- Li, Y.; Aquib, M.; Khan, M.-A.; Al-Dayel, I.; Youssef, M.Z. Geometric Inequalities of Slant Submanifolds in Locally Metallic Product Space Forms. Axioms 2024, 13, 486. [Google Scholar] [CrossRef]
- Li, Y.; Gezer, A.; Karakas, E. Exploring Conformal Soliton Structures in Tangent Bundles with Ricci-Quarter Symmetric Metric Connections. Mathematics 2024, 12, 2101. [Google Scholar] [CrossRef]
- Schlag, W. Stable Manifolds for an Orbitally Unstable Nonlinear Schrödinger Equation. Ann. Math. 2009, 169, 139–227. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Du, Y.-J.; Yin, T.-L.; Pang, J. The exact solutions of Schrdinger-Hirota equation based on the auxiliary equation method. Opt. Quantum Electron. 2024, 56, 712. [Google Scholar] [CrossRef]
- Sirendaoreji, N. Exact travelling wave solutions for four forms of nonlinear Klein–Gordon equations. Phys. Lett. A 2007, 363, 440–447. [Google Scholar] [CrossRef]
- Liu, S.-S.; Liu, S.-D. Nonlinear Equations in Physics; Peking University Press: Beijing, China, 2000; Volume 7, pp. 32–35. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).