1. Introduction
When the bootstrap sample size B is small or moderate, bootstrap confidence regions, including bootstrap confidence intervals, tend to have undercoverage: the probability that the confidence region contains the parameter vector is less than the nominal large-sample coverage probability . Then, coverage can be increased by increasing the nominal coverage of the large-sample bootstrap confidence region. For example, if the undercoverage of the nominal large-sample 95% bootstrap confidence region with is 2%, the coverage is increased to 97%. This procedure is known as calibrating the confidence region. Calibration tends to be difficult since the amount of undercoverage is usually unknown. This paper provides a simple method for improving the coverage and provides a method for visualizing some bootstrap confidence regions.
Using correction factors for large-sample confidence intervals, tests, prediction intervals, prediction regions, and confidence regions improves the coverage performance for a moderate sample size n. If confidence regions are used for hypothesis testing, then this calibration reduces the type I error. For a random variable X, let Note that correction factors as are used in large-sample confidence intervals and large-sample tests if the limiting distribution is or , but a or cutoff is used: with and with if as . For moderate n, the test or confidence interval with the correction factor has better level or coverage than the test or confidence interval that does not use the correction factor, in that the simulated level or coverage is closer to the nominal level or coverage.
Sometimes, the test statistic has a
or
distribution under normality, but the test statistic (possibly scaled by multiplying by
k) is asymptotically normal or asymptotically
for a large class of distributions. The
t test and
t confidence interval for the sample mean are examples where the asymptotic normality holds by the central limit theorem. Many
F tests for linear models, experimental design models, and multivariate analyses also satisfy
as
, where
is the test statistic. See, for example, Olive (2017) [
1].
Section 1.1 reviews prediction intervals, prediction regions, confidence intervals, and confidence regions. Several of these methods use correction factors to improve the coverage, and several bootstrap confidence intervals and regions are obtained by applying prediction intervals and regions to the bootstrap sample.
Section 1.2 reviews a bootstrap theorem and shows that some bootstrap confidence regions are asymptotically equivalent.
Section 2.1 gives a new bootstrap confidence region with a simple correction factor, while
Section 2.2 shows how to visualize some bootstrap confidence regions.
Section 3 presents some simulation results.
1.1. Prediction
Regions and Confidence Regions
Consider predicting a future test value given past training data , where are independent and identically distributed (iid). A large-sample prediction interval (PI) for is , where the coverage is eventually bounded below by as . We often want as . A large-sample PI is asymptotically optimal if it has the shortest asymptotic length: the length of converges to as , where is the population shorth, the shortest interval covering at least of the mass.
Let the data
have joint probability density function or probability mass function
with parameter space
and support
. Let
and
be statistics such that
Then, the interval
is a large-sample
confidence interval (CI) for
if
is eventually bounded below by
for all
as the sample size
Consider predicting a future test value , given past training data , where are iid. A large-sample prediction region is a set such that is eventually bounded below by as . A prediction region is asymptotically optimal if its volume converges in probability to the volume of the minimum volume covering region or the highest density region of the distribution of
A large-sample confidence region for a vector of parameters is a set such that is eventually bounded below by as For testing versus , we fail to reject if is in the confidence region and reject if is not in the confidence region.
For prediction intervals, let
be the order statistics of the training data. Open intervals need more regularity conditions than closed intervals. For the following prediction interval, if the open interval
was used, we would need to add the regularity condition that the population percentiles
and
are continuity points of the cumulative distribution function
See Frey (2013) [
2] for references.
Let
and
, where
. A large-sample
percentile prediction interval for
is
The bootstrap percentile confidence interval given by Equation (
2) is obtained by applying the percentile prediction interval (1) to the bootstrap sample
, where
is a test statistic. See Efron (1982) [
3].
A large-sample
bootstrap percentile confidence interval for
is an interval
containing
of the
. Let
and
. A common choice is
The shorth (
c) estimator of the population shorth is useful for making asymptotically optimal prediction intervals. For a large-sample
PI, the nominal coverage is
. Undercoverage occurs if the actual coverage is below the nominal coverage. For example, if the actual coverage is 0.93 for a large-sample 95% PI, then the undercoverage is 0.02. Consider intervals that contain
c cases
. Compute
. Then, the estimator shorth (
c)
is the interval with the shortest length. The shorth (
c) interval is a large-sample
PI if
as
that often has the asymptotically shortest length. Let
. Frey (2013) [
2] showed that for large
and iid data, the large-sample
shorth (
) prediction interval has maximum undercoverage ≈
, and then used the large-sample
PI shorth (
c) =
The shorth confidence interval is a practical implementation of Hall’s (1988) [
4] shortest bootstrap percentile interval based on all possible bootstrap samples, and is obtained by applying shorth PI (3) to the bootstrap sample
See Pelawa Watagoda and Olive (2021) [
5]. The large-sample
shorth (
c) CI =
To describe Olive’s (2013) [
6] nonparametric prediction region, Mahalanobis distances will be useful. Let the
column vector
be a multivariate location estimator, and let the
symmetric positive definite matrix
be a dispersion estimator. Then, the
ith squared sample Mahalanobis distance is the scalar
for each observation
where
. Notice that the Euclidean distance of
from the estimate of center
T is
, where
is the
identity matrix. The classical Mahalanobis distance
uses
, the sample mean, and sample covariance matrix, where
Let the
location vector be
, which is often the population mean, and let the
dispersion matrix be
, which is often the population covariance matrix. If
x is a random vector, then the population squared Mahalanobis distance is
Like prediction intervals, prediction regions often need correction factors. For iid data from a distribution with a
nonsingular covariance matrix, it was found that the simulated maximum undercoverage of prediction region (9) without the correction factor was about 0.05 when
. Hence, correction factor (8) is used to obtain better coverage for small
n. Let
for
and
If
and
, set
. Let
be the
th sample quantile of the
, where
. Olive (2013) [
6] suggests that
may be needed for the following prediction region to have a good volume, and
for good coverage. Of course, for any
n, there are distributions that will have severe undercoverage.
The large-sample
nonparametric prediction region for a future value
given iid data
is
Olive’s (2017, 2018) [
1,
7] prediction region method confidence region applies prediction region (9) to the bootstrap sample. Let the bootstrap sample be
. Let
and
be the sample mean and sample covariance matrix of the bootstrap sample.
The large-sample
prediction region method confidence region for
is
where the cutoff
is the
th sample quantile of the
for
. Note that the corresponding test for
rejects
if
.
Olive’s (2017, 2018) [
1,
7] large-sample
modification of Bickel and Ren’s (2001) [
8] confidence region is
where the cutoff
is the
th sample quantile of the
Note that the corresponding test for
rejects
if
.
Shift region (9) to have center
, or equivalently, to change the cutoff of region (11) to
to obtain Pelawa Watagoda and Olive’s (2021) [
5] large-sample
hybrid confidence region,
Note that the corresponding test for rejects if .
Rajapaksha and Olive (2024) [
9] gave the following two confidence regions. The names of these confidence regions were chosen since they are similar to Bickel and Ren’s and the prediction region method’s confidence regions.
The large-sample
BR confidence region is
where the cutoff
is the
th sample quantile of the
. Note that the corresponding test for
rejects
if
.
The large-sample
PR confidence region for
is
where
is the
th sample quantile of the
for
. Note that the corresponding test for
rejects
if
.
Assume that
are iid
. Then, Chew’s (1966) [
10] large-sample
classical prediction region for multivariate normal data is
The next bootstrap confidence region is similar to what would be obtained if the classical prediction region (15) for multivariate normal data was applied to the bootstrap sample. The large-sample
standard bootstrap confidence region for
is
where
or
, where
as
.
If
, then a hyperellipsoid is an interval, and confidence intervals are special cases of confidence regions. Suppose the parameter of interest is
, and there is a bootstrap sample
where the statistic
is an estimator of
based on a sample of size
n. Let
and let
Let
and
be the sample mean and variance of
. Then, the squared Mahalanobis distance
is equivalent to
, which is an interval centered at
just long enough to cover
of the
. Efron (2014) [
11] used a similar large-sample
confidence interval assuming that
is asymptotically normal. Then, the large-sample
PR CI is
The large-sample
BR CI is
, which is an interval centered at
just long enough to cover
of the
. The large-sample
hybrid CI is
.
The following prediction region will be used to develop a new correction factor for bootstrap confidence regions. See
Section 2.1. Data splitting divides the training data
into two sets:
H and the validation set
V, where
H has
of the cases and
V has the remaining
cases
.
The estimator
is computed using data set
H. Then, the squared validation distances
are computed for the
cases in the validation set
V. Let
be the
th order statistic of the
, where
Haile, Zhang, and Olive’s (2024) [
12] large-sample
data splitting prediction region for
is
1.2. Some Confidence Region Theories
Some large-sample theories for bootstrap confidence regions are given in the references in
Section 1.1. The following theorem of Pelawa Watagoda and Olive (2021) [
5] and its proof are useful.
Theorem 1. (a) Suppose as , (i) , and (ii) with and . Then, (iii) , (iv) , and (v) .
(b) Then, the prediction region method gives a large-sample confidence region for provided that and the sample percentile of the is a consistent estimator of the percentile of the random variable in that
Proof. With respect to the bootstrap sample,
is a constant, and the
are iid for
. Fix
B. Then,
where the
are iid with the same distribution as
u. For fixed
B, the average of the
is
by the Continuous Mapping Theorem, where
is an asymptotic multivariate normal approximation. Note that if
, then
Hence, as , and (iii), (iv), and (v) hold. Hence, (b) follows. □
Under regularity conditions, Bickel and Ren (2001), Olive (2017, 2018), and Pelawa Watagoda and Olive (2021) [
1,
5,
7,
8] proved that (10), (11), and (12) are large-sample confidence regions. For Theorem 1, usually (i) and (ii) are proven using large-sample theory. Then,
are well behaved. If
then
, and (13) and (14) are large-sample confidence regions. If
is “not too ill conditioned," then
for large
n, and confidence regions (13) and (14) will have coverage near
. See Rajapaksha and Olive (2024) [
9].
If
and
, where
U has a unimodal probability density function symmetric about zero, then the confidence intervals from
Section 1.1, including (2) and (3), are asymptotically equivalent (use the central proportion of the bootstrap sample, asymptotically). See Pelawa Watagoda and Olive (2021) [
5].
3. Results
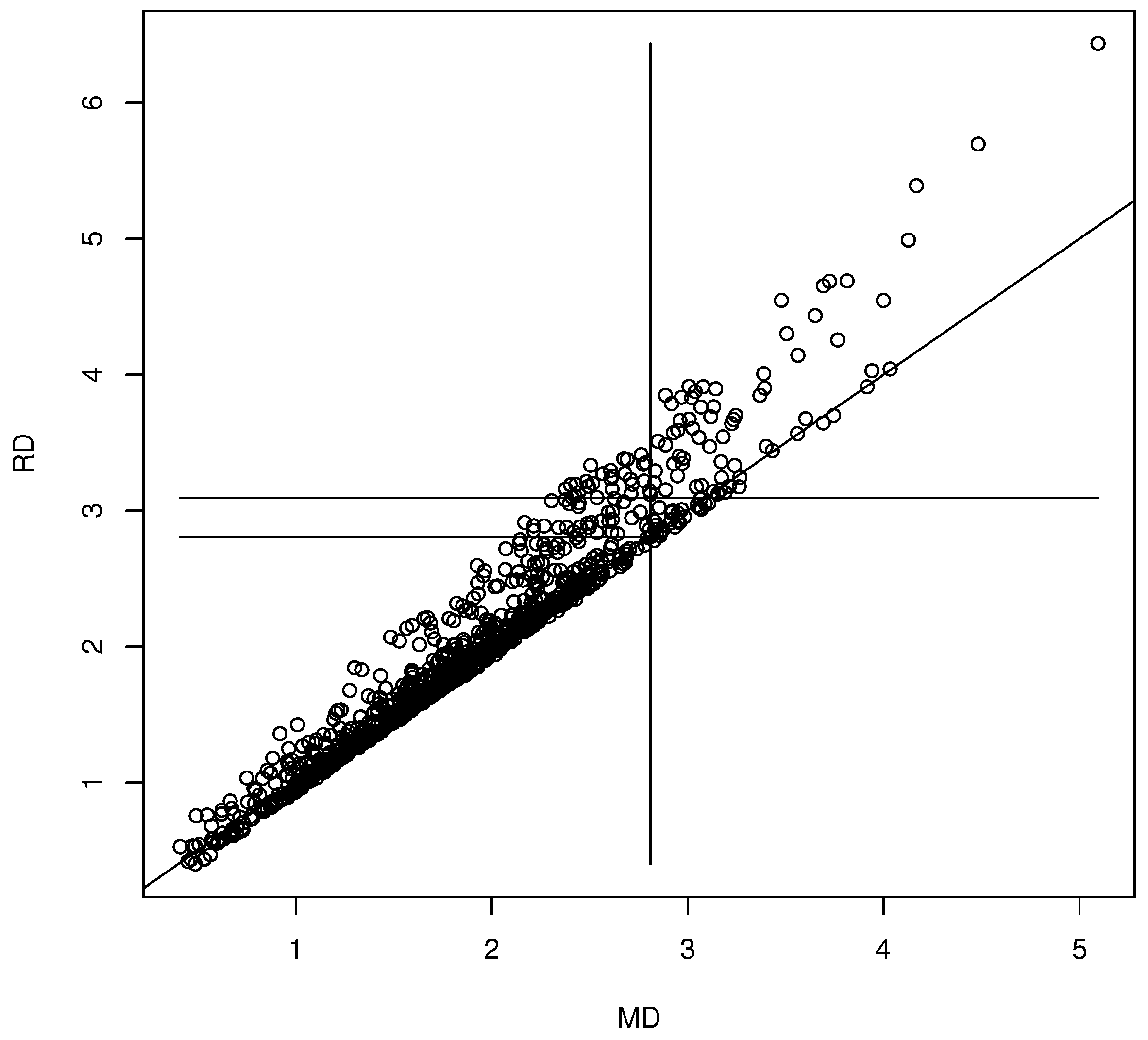
Example 1. We generated for . The coordinate-wise median was the statistic . The nonparametric bootstrap was used with for the 90% confidence region (10). Then, the th sample quantile of the is the 90.4% quantile. The DD plot of the bootstrap sample is shown in Figure 1. This bootstrap sample was a rather poor sample: the plotted points cluster about the identity line, but for most bootstrap samples, the clustering is tighter (as in Figure 2). The vertical line MD = 2.9098 is the cutoff for the prediction region method 90% confidence region (10). Hence, the points to the left of the vertical line correspond to , which are inside confidence region (10), while the points to the right of the vertical line correspond to , which are outside of confidence region (10). The long horizontal line RD = 3.0995 is the cutoff using the robust estimator. When , under mild regularity conditions, The short horizontal line is RD = 2.8074, and MD = 2.8074 = is approximately the cutoff that would be used by the standard bootstrap confidence region (mentally drop a vertical line from where the short horizontal line ends at the identity line). Variability in DD plots increases as MD increases. Inference after variable selection is an example where the undercoverage of confidence regions can be quite high. See, for example, Kabaila (2009) [
23]. Variable selection methods often use the Schwarz (1978) [
24] BIC criterion, the Mallows (1973) [
25]
criterion, or lasso due to Tibshirani (1996) [
26]. To describe a variable selection model, we will follow Rathnayake and Olive (2023) [
27] closely. Consider regression models where the response variable
Y depends on the
vector of predictor
x only through
. Multiple linear regression models, generalized linear models, and proportional hazards regression models are examples of such regression models. Then, a model for variable selection can be described by
where
is a
vector of predictors,
is an
vector, and
is a
vector. Given that
is in the model,
, and
E denotes the subset of terms that can be eliminated given that the subset
S is in the model. Since
S is unknown, candidate subsets will be examined. Let
be the vector of
a terms from a candidate subset indexed by
I, and let
be the vector of the remaining predictors (out of the candidate submodel). Then,
Suppose that
S is a subset of
I and that model (20) holds. Then,
where
denotes the predictors in
I that are not in
Underfitting occurs if submodel
I does not contain
S.
To clarify the notation, suppose that , a constant corresponding to , is always in the model, and . Then, there are possible subsets of that contain 1, including and . There are subsets such that . Let and The full model uses
Let correspond to the set of predictors selected by a variable selection method such as forward selection or lasso variable selection. If is , use zero padding to form the vector from by adding 0s corresponding to the omitted variables. For example, if and , then the observed variable selection estimator As a statistic, with probabilities for , where there are J subsets, e.g., . Then, the variable selection estimator , and with probabilities for , where there are J subsets.
Assume
p is fixed. Suppose model (20) holds, and that if
, where the dimension of
is
, then
, where
is the covariance matrix of the asymptotic multivariate normal distribution. Then,
where
adds columns and rows of zeros corresponding to the
not in
, and
is singular unless
corresponds to the full model. This large-sample theory holds for many models.
If
are pairwise disjoint and if
then the collection of sets
is a
partition of
Then, the Law of Total Probability states that if
form a partition of
S such that
for
, then
Let sets
satisfy
for
Define
if
. Then, a Generalized Law of Total Probability is
Pötscher (1991) [
28] used the conditional distribution of
to find the distribution of
Let
be a random vector from the conditional distribution
. Let
Denote
by
Then, Pötscher (1991) [
28] used the Generalized Law of Total Probability to prove that the cumulative distribution function (cdf) of
is
Hence, has a mixture distribution of the with probabilities , and has a mixture distribution of the with probabilities
For the following Rathnayake and Olive (2023) [
27] theorem, the first assumption is
as
. Then, the variable selection estimator corresponding to
underfits with probability going to zero, and the assumption holds under regularity conditions, if BIC and AIC is used for many parametric regression models such as GLMs. See Charkhi and Claeskens (2018) [
29] and Claeskens and Hjort (2008, pp. 70, 101, 102, 114, 232) [
30]. This assumption is a necessary condition for a variable selection estimator to be a consistent estimator. See Zhao and Yu (2006) [
31]. Thus, if a sparse estimator that performs variable selection is a consistent estimator of
, then
as
. Hence, Theorem 2 proves that the lasso variable selection estimator is a
consistent estimator of
if lasso is consistent. Charkhi and Claeskens (2018) [
29] showed that
if
for the maximum likelihood estimator with AIC, and gave a forward selection example. For a multiple linear regression model where
S is the model with exactly one predictor that can be deleted, then only
and
are positive. If the
criterion is used, then it can be shown that
, and
. Theorem 2 proves that
w is a mixture distribution of the
with probabilities
.
Theorem 2. Assume as , and let with probabilities , where as . Denote the positive by . Assume
. Then,where the cdf of w is . Rathnayake and Olive (2023) [
27] suggested the following bootstrap procedure. Use a bootstrap method for the full model, such as the nonparametric bootstrap or the residual bootstrap, and then compute the full model and the variable selection estimator from the bootstrap data set. Repeat this
B times to obtain the bootstrap sample for the full model and for the variable selection model. They could only prove that the bootstrap procedure works under very strong regularity conditions such as a
in Theorem 2, where
is known as the oracle property. See Claeskens and Hjort (2008, pp. 101–114) [
30] for references for the oracle property. For many statistics, a bootstrap data cloud
and a data cloud from
B iid statistics
tend to have similar variability. Rathnayake and Olive (2023) [
27] suggested that when
T is the variable selection estimator
, the bootstrap data cloud often has more variability than the iid data cloud, and that this result tends to increase the bootstrap confidence region coverage.
For variable selection with the vector , consider testing versus with , where oftentimes, . Then, let and let for . The shorth estimator can be applied to a bootstrap sample to obtain a confidence interval for . Here, and . The simulations used , , and . Let the multiple linear regression model for . Hence, with ones and zeros.
The regression models used the residual bootstrap with the forward selection estimator
.
Table 1 gives results for when the iid errors
with
,
, and
.
Table 1 shows two rows for each model giving the observed confidence interval coverages and average lengths of the confidence intervals. The nominal coverage was 95%. The term “reg" is for the full model regression, and the term “vs" is for forward selection. The last six columns give results for the tests. The terms pr, hyb, and br are for prediction region method (10), hybrid region (12), and Bickel and Ren region (11). The 0 indicates that the test was
versus
, while the 1 indicates that the test was
versus
. The length and coverage = P (fail to reject
) for the interval
or
, where
or
is the cutoff for the confidence region. The cutoff will often be near
if the statistic
T is asymptotically normal. Note that
is close to 2.45 for the full model regression bootstrap tests. For the full model,
len
as
for the simulated data, and the shorth 95% confidence intervals have simulated length
The variable selection estimator and the full model estimator were similar for
, and
. The two estimators differed for
and
because
often occurred for
and 4. In particular, the confidence interval coverages for the variable selection estimator were very high, but the average lengths were shorter than those for the full model. If
was never selected, then
for all runs, and the confidence interval would be [0, 0] with 100% coverage and zero length.
Note that for the variable selection estimator with , the average cutoff values were near 2.7 and 3.0, which are larger than the cutoff 2.448. Hence, using the standard bootstrap confidence region (16) would result in undercoverage. For , the bootstrap estimator often appeared to be approximately multivariate normal. Example 2 illustrates this result with a DD plot.
Example 2. We generated and for with the iid and . Then, we examined several bootstrap methods for multiple linear regression variable selection. The nonparametric bootstrap draws n cases with replacement from the n original cases, and then selects variables on the resulting data set, resulting in . If is , use zero padding to form the vector from by adding 0s corresponding to the omitted variables. Repeat times to obtain the bootstrap sample . Typically, the full model or the submodel that omitted was selected. The residual bootstrap using the full model residuals was also used, where for where the are sampled with replacement from the full model residuals . Forward selection and backward elimination could be used with the or BIC criterion, or lasso could be used to perform the variable selection. Let be obtained from by leaving out the fifth value. Hence, if then . Figure 2 shows the DD plot for the confidence region corresponding to the using forward selection with the criterion. This confidence region corresponds to the test , e.g., . Plots created with backward elimination and lasso were similar. Rathnayake and Olive (2023) [27] obtained the large-sample theory for the variable selection estimators for multiple linear regression and many other regression methods. The limiting distribution is a complicated non-normal mixture distribution by Theorem 2, but in simulations, where S is known, the often appeared to have an approximate multivariate normal distribution. A small simulation study was conducted on large-sample 95% confidence regions. The coordinate-wise median was used since this statistic is moderately difficult to bootstrap. We used 5000 runs. Then, the coverage within [0.94, 0.96] suggests that the true coverage is near the nominal coverage 0.95. The simulation used 10 distributions, where xtype = 1 for
xtype = 2, 3, 4, and 5 for
; xtype = 6, 7, 8, and 9 for a multivariate
with
d = 3, 5, 19, or
d, given by the user; and xtype=10 for a log-normal distribution shifted to have the coordinate-wise median =
0. If
w corresponds to one of the above distributions, then
with
. Then, the population coordinate-wise median is
0 for each distribution.
Table 2 shows the coverages and average cutoff for four large-sample confidence regions: (10), (19), with
, (19) with
, and (19) with
. The coverage is the proportion of times that the confidence region contained
, where
is a
vector. Each confidence region has a cutoff,
, that depends on the bootstrap sample, and the average of the 5000 cutoffs is given. Here,
for confidence region (10), while
for confidence region (19), where the cutoff also depends on
. The coverages were usually between 0.94 and 0.96. The average cutoffs for the prediction region method’s large-sample 95% confidence region tended to be very close to the average cutoffs for confidence region (19) with
. Note that
and
are the cutoffs for the standard bootstrap confidence region (15). The ratio of volumes of the two confidence regions is volume (10)/volume (19)
.
4. Discussion
The bootstrap was due to Efron (1979) [
32]. Also, see Efron (1982) [
3] and Bickel and Freedman (1981) [
33]. Ghosh and Polansky (2014) and Politis and Romano (1994) [
34,
35] are useful references for bootstrap confidence regions. For a small dimension
p, nonparametric density estimation can be used to construct confidence regions and prediction regions. See, for example, Hall (1987) and Hyndman (1986) [
36,
37] Visualizing a bootstrap confidence region is useful for checking whether the asymptotic normal approximation for the statistic is good since the plotted points will then tend to cluster tightly about the identity line. Making five plots corresponding to five bootstrap samples can be used to check the variability of the plots and the probability of obtaining a bad sample. For Example 1, most of the bootstrap samples produced plots that had tighter clustering about the identity line than the clustering in
Figure 1.
The new bootstrap confidence region (19) used the fact that bootstrap confidence region (10) is simultaneously a prediction region for a future bootstrap statistic and a confidence region for with the same asymptotic coverage . Hence, increasing the coverage as a prediction region also increases the coverage as a confidence region. The data splitting technique used to increase the coverage only depends on the being iid with respect to the bootstrap distribution. Correction factor (8) increases the coverage, but this calibration technique needed intensive simulation.
Calibrating a bootstrap confidence region is useful for several reasons. For simulations, computation time can be reduced if
B can be reduced. Using correction factor (8) is faster than using the two-sample bootstrap of
Section 2.1, but the two-sample bootstrap can be used to check the accuracy of (8), as in
Table 2 with
. For a nominal 95% prediction region, correction factor (8) increases the coverage to at most 97.5% of the training data. Coverage for test data
tends to be worse than coverage for training data. Using the cutoff
of (8) gives better coverage than using cutoff
with
. The two calibration methods in this paper were first applied to prediction regions, and work for bootstrap confidence regions (10) and (11) since those two regions are also prediction regions for
.
Plots and simulations were conducted in
R. See R Core Team (2020) [
38]. Welagedara (2023) [
39] lists some
R functions for bootstrapping several statistics. The programs used are in the collection of functions
slpack.txt. See
http://parker.ad.siu.edu/Olive/slpack.txt, accessed on 1 August 2024. The function
ddplot4 applied to the bootstrap sample can be used to visualize the bootstrap prediction region method’s confidence region. The function
medbootsim was used for
Table 2. Some functions for bootstrapping multiple linear regression variable selection with the residual bootstrap are
belimboot for backward elimination using
,
bicboot for forward selection using BIC,
fselboot for forward selection using
,
lassoboot for lasso variable selection, and
vselboot for all of the subsets’ variable selection with
.