Remarks on the Mathematical Modeling of Gene and Neuronal Networks by Ordinary Differential Equations

Abstract

In the theory of gene networks, the mathematical apparatus that uses dynamical systems is fruitfully used. The same is true for the theory of neural networks. In both cases, the purpose of the simulation is to study the properties of phase space, as well as the types and the properties of attractors. The paper compares both models, notes their similarities and considers a number of illustrative examples. A local analysis is carried out in the vicinity of critical points and the necessary formulas are derived.

1. Introduction

In this article, we study Neural Networks, called also Artificial Neural Networks (ANN), and their mathematical models, using ordinary differential equations. The motivation for the study of ANNs came from attempts to understand the principles and organization of the human brain. Understanding came that human brains work differently from digital computers. Their effectiveness comes from high complexity, nonlinear modes of regulation, and parallelism of actions. The elements of the human brain were called neurons.

These elements still perform calculations faster than the fastest digital computers. The human brain is able to perceive information about the environment in the form of images and, moreover, it can process the received information needed for interaction with the environment.

At birth, the human brain has a ready structure for learning which, in familiar terms, is understood as experience. So, the neural network is designed to model the way in which the human brain solves usual problems and performs a particular task. A particular interest in ANN stems from the fact that an important group of neural networks is needed to solve a problem computations through the process of learning. So, following [1], an ANN can generally be imagined as a parallel distributed processor, consisting of separate units, which is able to analyze experimental data and prepare them for use.

Many natural processes involve networks of elements that affect each other following a general pattern of conditions and the updating rules for any elements. Both genomic networks and neuronal networks are of this kind. In mathematical models of networks of both types, the regulatory effect of one element to the outputs of other elements is defined by a weight matrix. Therefore, the models describing the evolution of these networks have a lot in common. But, there are also differences. This paper compares models using systems of ordinary differential equations. To distinguish between these systems, we use the designations GRN system and ANN system. At the same time, we realize that the term ANN system has too general a meaning. An ANN system in the established sense is understood as a network that operates according to certain rules and is focused on performing certain tasks. At the same time, the networks undergo training and thus improve their qualities. This article looks at neural networks from a different point of view. We are interested in the behavior of systems of both types for different forms of interaction of elements. The structure of both systems assumes the presence of attractors that determine future states. The description and comparison of possible attractors for the systems of both types is our result.

ANNs are made up of many interconnected elements. Weighted signals from different elements are received by a separate element and processed. A positive signal is understood as an excitatory connection, while negative one means an inhibitory connection. The received signals are linearly summed and modified by a nonlinear sigmoidal function which is called an activation one. The activation function controls the amplitude of an output. “Each neuron has a sigmoid transfer function, and a continuous positive and bounded output activity that evolves according to weighted sums of the activities in the networks. Neural networks with arbitrary connections are often called recurrent networks” [2]. The dynamics of the continuous time recurrent neural network with n units, can be described by the system of ordinary differential equations (ODE) ([3])

$$x_i^{\prime }=-b_i{x}_i+f_i\left(\mathsf{\Sigma }{a}_{ij}{x}_j\right)+I_i\left(t\right),$$

(1)

where $x_i$ is the internal state of the i-th unit, $b_i$ is the time constant for the i-th unit, $a_{ij}$ are connection weights, $I_i\left(t\right)$ is the input to the i-th unit, and $f_i\left(\mathsf{\Sigma }{a}_{ij}{x}_j\right)$ is the response function of the i-th unit. Usually, f is taken as a sigmoidal function. There are particular response functions that are non-negative. For instance, functions $f_i\left(z\right)=(1+exp{\left({\mu }_i(z-{\theta }_i)\right)}^{-1}$ were used in [4]. More general cases can be modeled by the system using the function $f_i\left(z\right)=tanh(a_{i}z-{\theta }_i),$ which takes values in the open interval $(-1,1).$ If the recurrent neural networks without input are considered, the system

$$x_i^{\prime }=f_i\left(\mathsf{\Sigma }(a_{ij}{x}_j-{\theta }_i)\right)-b_i{x}_i$$

(2)

can be considered.

Applications of Artificial Neural Networks are multiple. They can be used in different fields. These fields can be categorized as function approximations, including time series prediction and modeling; pattern and sequence recognition, novelty detection and sequential decision making; and data processing, including filtering and clustering. For applications in Machine Learning (ML), Deep Learning and related problems, consult the review article [5]. For neuroscience applications and their relation to ML, and machine learning using biologically realistic models of neurons to carry out the computation, consider the review [6]. The problems of pattern recognition by ANNs, including applications in manufacturing industries, were studied and analyzed in the review paper [7]. In the paper [8], the ANN approach is applied for the study of a genetic system.

In this article, we mainly study properties of the mathematical model of a three-dimensional ANN, but part of our results will refer to two-dimensional or, more generally, to n-dimensional networks. In particular, we provide information on the types of possible attractors, and their birth and evolution under changes in multiple parameters. The asymptotic properties of the system are important for prediction of future states. This, in turn, can provide instruments for control and management of the modeling network. We use analytical tools for the study of the phase space and its elements. A set of formulas is obtained for the local analysis near equilibria. The necessary data for the analysis were collected by conducting computational experiments and constructing several examples. A broader study involves examining the model and interpreting the findings for the actual process being modeled. Examples of this approach are the works [9,10].

Let us describe the structure of the paper. The Problem formulation section provides the necessary material for the study. The Preliminary results section describes some basic properties of the main systems of ordinary differential equations. It deals also with technical details concerning nullclines, critical points, local analysis by linearization, and some special cases. The next two sections concern some particular but important cases. The systems possessing critical points of the type focus, and systems exhibiting the inhibition-activation behavior, are treated. Both types of systems can have periodic solutions, and that means that cyclic processes can occur in the modeled network. The system of the special triangular structure is analyzed in Section 6. It is convenient for analysis and the main conclusions can be transferred to systems of arbitrary dimensions. The process of birth of stable periodic trajectories from stable critical points of the type focus is considered in Section 7. The mechanism of the Andronov–Hopf bifurcation is illustrated for two-dimensional and three-dimensional neuronal systems. As a by-product, an example of a 3D system that has three limit cycles is constructed. Some suggestions on the management of neuronal systems are provided in Section 7. The possibility of effectively changing the properties of the system, and therefore to partially controlling the network in question, is emphasized. The last section summarizes the results obtained so far, and outlines further studies in this direction.

2. Problem Formulation

The mathematical model using ordinary differential equations, is

$$\left\{\begin{array}{c}{\displaystyle \frac{d{x}_1}{dt}=2\frac{1}{1+e^{-2(a_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3-{\theta }_1)}}-1-b_1{x}_1,}\hfill \\ \\ {\displaystyle \frac{d{x}_2}{dt}=2\frac{1}{1+e^{-2(a_{21}{x}_1+a_{22}{x}_2+a{w}_{23}{x}_3-{\theta }_2)}}-1-b_2{x}_2,}\hfill \\ \\ {\displaystyle \frac{d{x}_3}{dt}=2\frac{1}{1+e^{-2(a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3-{\theta }_3)}}-1-b_3{x}_3.}\hfill \end{array}\right.$$

(3)

The same system can be written as ([11])

$$\left\{\begin{array}{c}{\displaystyle \frac{d{x}_1}{dt}=tanh(a_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3-{\theta }_1)-b_1{x}_1,}\hfill \\ \\ {\displaystyle \frac{d{x}_2}{dt}=tanh(a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3-{\theta }_2)-b_2{x}_2,}\hfill \\ \\ {\displaystyle \frac{d{x}_3}{dt}=tanh(a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3-{\theta }_3)-b_3{x}_3,}\hfill \end{array}\right.$$

(4)

since

$$2\frac{1}{1+e^{-2z}}-1=\frac{1-e^{-2z}}{1+e^{-2z}}=-\frac{e^{-2z}-1}{e^{-2z}+1}=-tanh(-z)=tanh\left(z\right).$$

The elements of this 3D network are called neurons. The connections between them are synapses (or nerves). There is an algorithm that describes how the impulses are propagated through the network. In the above model, this algorithm is encoded by the matrix

$$W=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right).$$

(5)

Each neuron accepts signals from others and produces a single output. The extent to which the input of neuron i is driven by the output of neuron j is characterized by its output and synaptic weight $a_{ij}.$ The dynamic evolution leads to attractors of the system (4), and it was experimentally observed in neural systems. In theoretical modeling, the emphasis is put on the attractors of a system. We wish to study them for System (4).

Similar systems arise in the theory of genetic regulatory networks. The difference is that the nonlinearity is represented by a positive valued sigmoidal functions. One of such systems is

$$\left\{\begin{array}{c}{\displaystyle \frac{d{x}_1}{dt}=\frac{1}{1+e^{-{\mu }_1(a_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3-{\theta }_1)}}-b_1{x}_1,}\hfill \\ \\ {\displaystyle \frac{d{x}_2}{dt}=\frac{1}{1+e^{-{\mu }_2(a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3-{\theta }_2)}}-b_2{x}_2,}\hfill \\ \\ {\displaystyle \frac{d{x}_3}{dt}=\frac{1}{1+e^{-{\mu }_3(a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3-{\theta }_3)}}-b_3{x}_3.}\hfill \end{array}\right.$$

(6)

Notice that System (3), and therefore also System (4), can be obtained from System (6), where ${\mu }_i=2,$ $i=1,2,3,$ by two arithmetic operations, namely multiplication of the nonlinearity in (6) by 2 and subtracting 1. This changes the range of values in (3) to $(-1,1).$

Systems of the form (6) were studied before by many authors. The interested reader may consult the works ([12,13,14,15,16,17,18,19,20]). Similar systems appear in the theory of telecommunication networks ([21]).

In this article, we study the different dynamic regimes for System (4) which can be observed under various conditions. In particular, we first speak about critical points in System (4) and evaluate the number of them. Then, we focus on periodic regimes, study their attractiveness for other trajectories. This can be performed, under some restrictions, for systems of relatively high dimensionality. Also, the evidences of chaotic behavior are presented.

3. Preliminary Results

This section contains the description of basic properties of systems under consideration, and provides information about nullclines, critical points, and their role in the study.

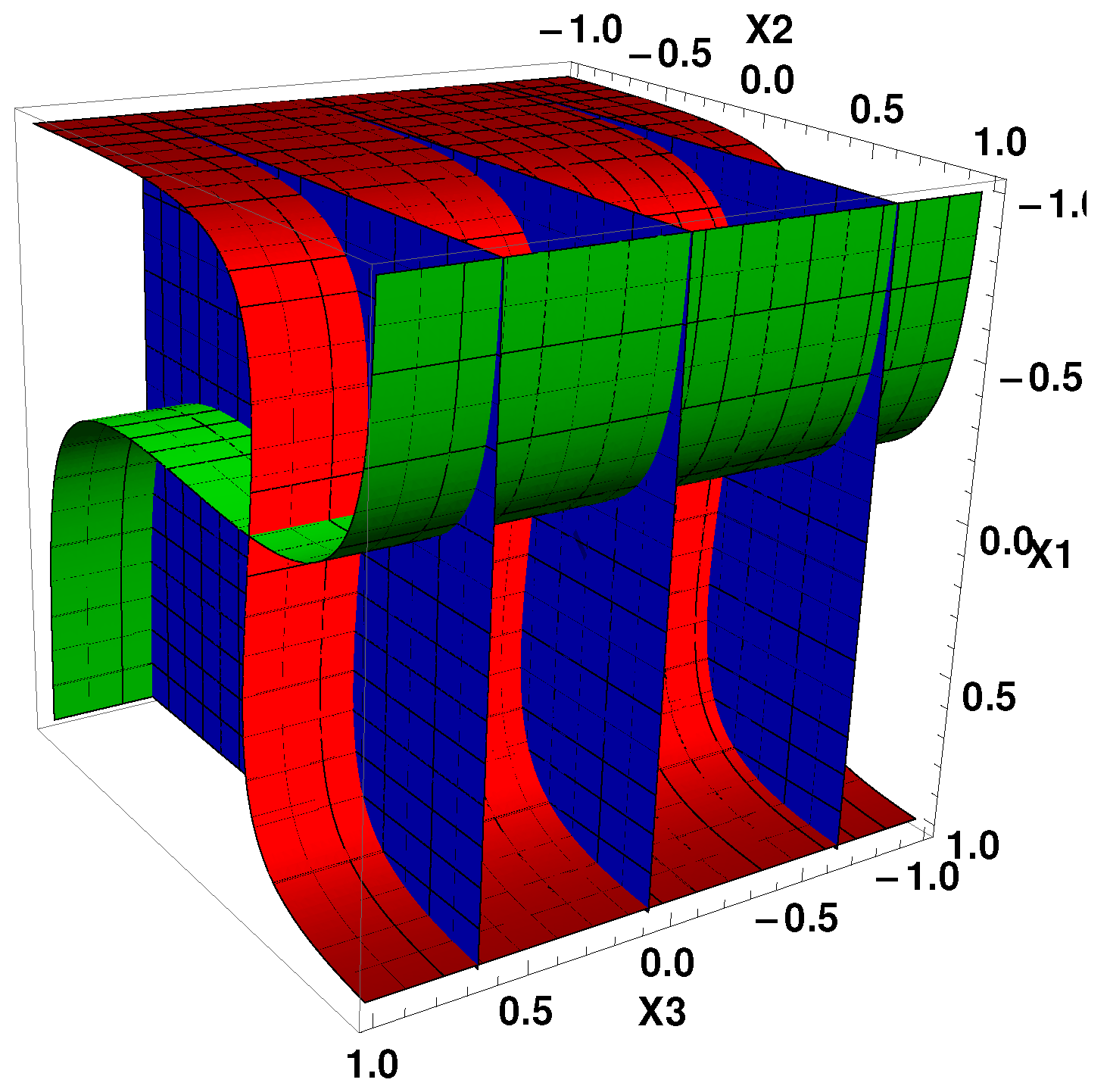
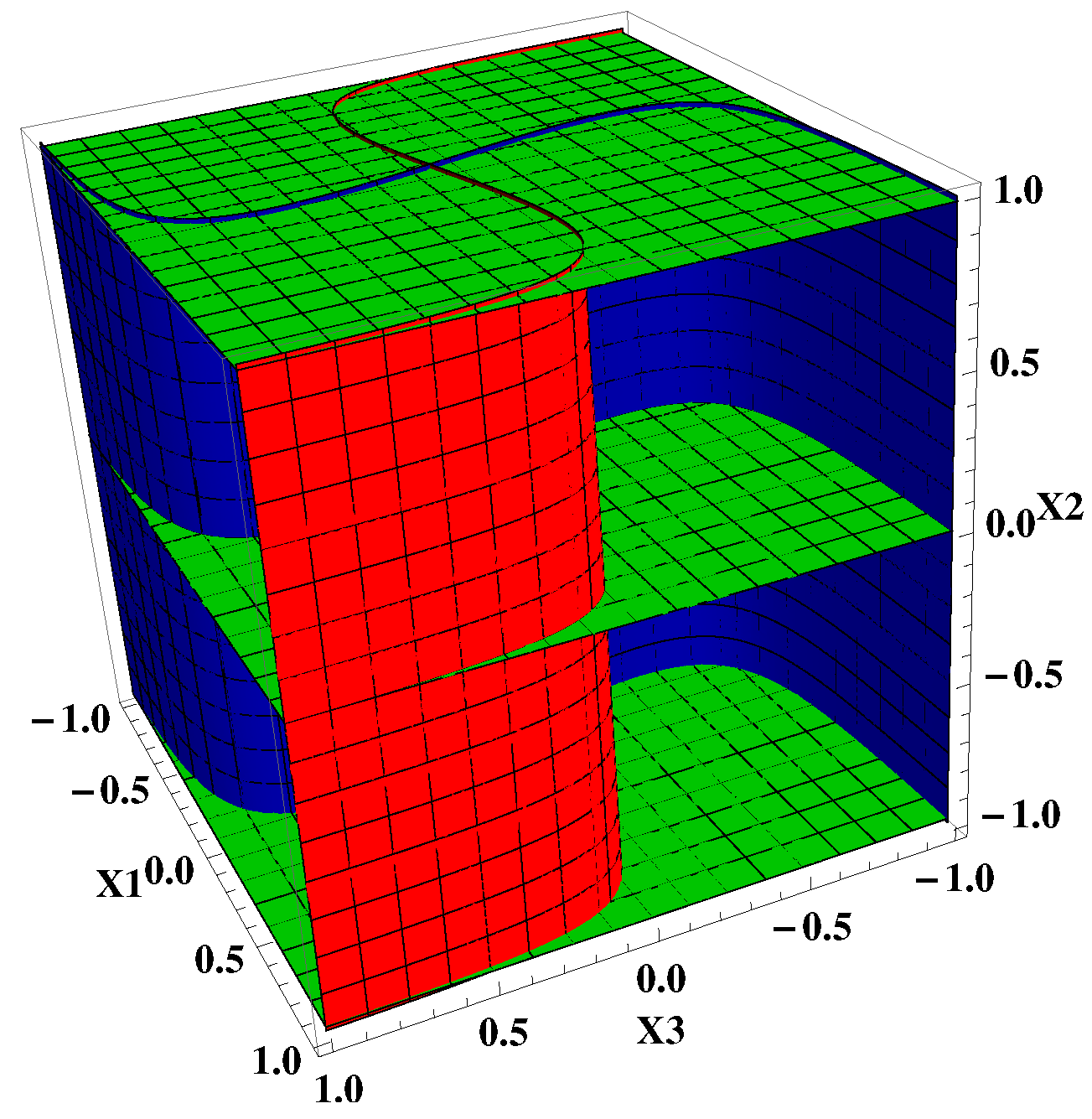
3.1. Invariant Set

Consider the 3D system (4).

Proposition 1. 

System (4) has an invariant set $Q_3=\{-1/b_1<x_1<1/b_1,$$-1/b_2<x_2<1/b_2,$$-1/b_3<x_3<1/b_3\}.$

Proof. 

By inspection of the vector field generated by System (4) on the opposite faces of the three-dimensional cube $Q_3.$ Notice, that the value range for the function tanh z is $(-1,1).$□

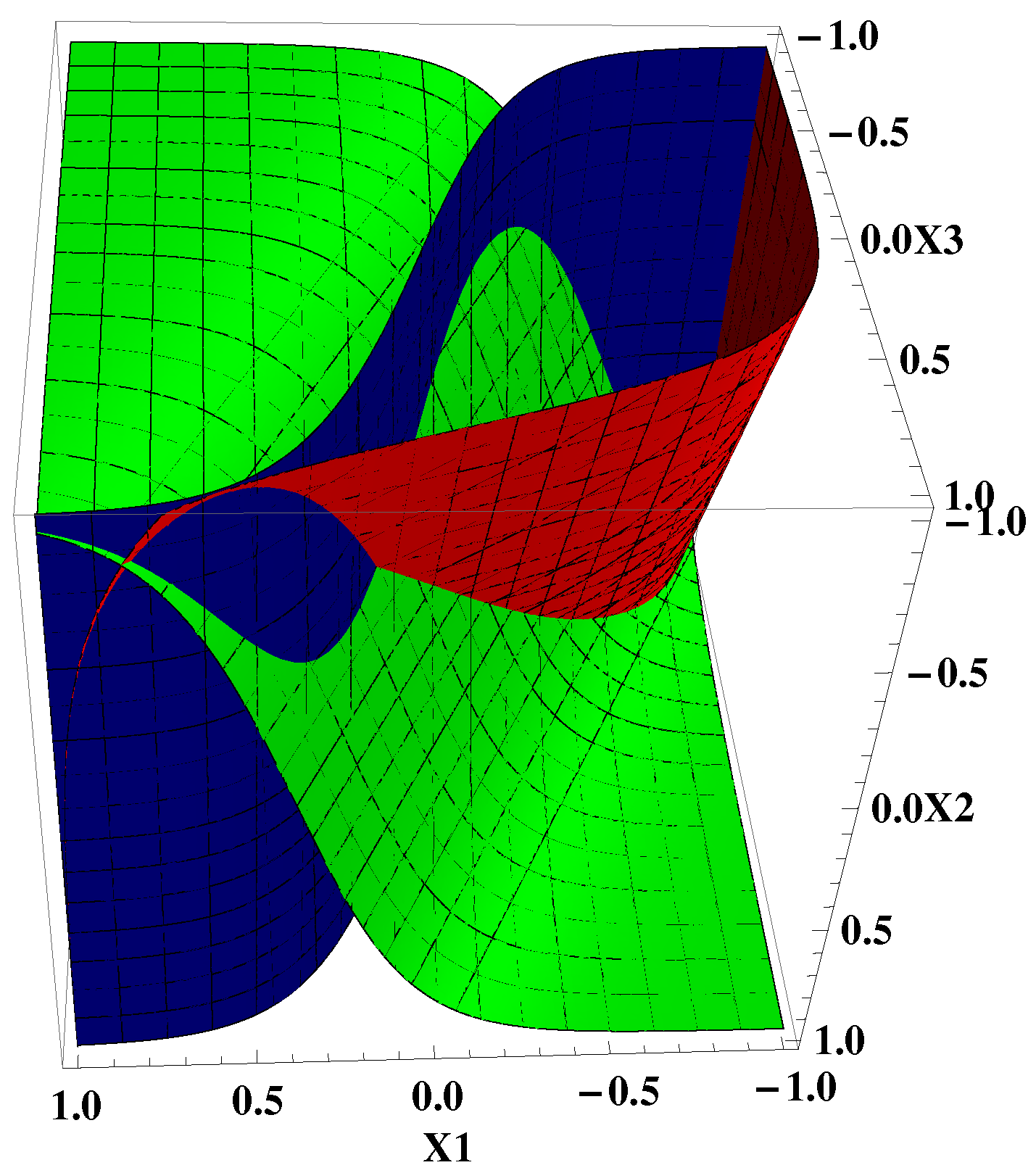
3.2. Nullclines

The nullclines for the system are defined by the relations

$$\left\{\begin{array}{c}{\displaystyle x_1=\frac{1}{b_1}tanh(a_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3-{\theta }_1),}\hfill \\ \\ {\displaystyle x_2=\frac{1}{b_2}tanh(a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3-{\theta }_2),}\hfill \\ \\ {\displaystyle x_3=\frac{1}{b_3}tanh(a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3-{\theta }_3).}\hfill \end{array}\right.$$

(7)

Example 1. 

Consider the system with the matrix

$$W=\left(\begin{array}{ccc}1.2& 1.5& 0\\ -1.5& 1.2& 0\\ 0& 0& 1.2\end{array}\right)$$

(8)

and $b_1=b_2=b_3=1,{\theta }_1={\theta }_2=0.5,{\theta }_3=1$.

The three nullclines for system (4) with matrix (8) are depicted in Figure 1.

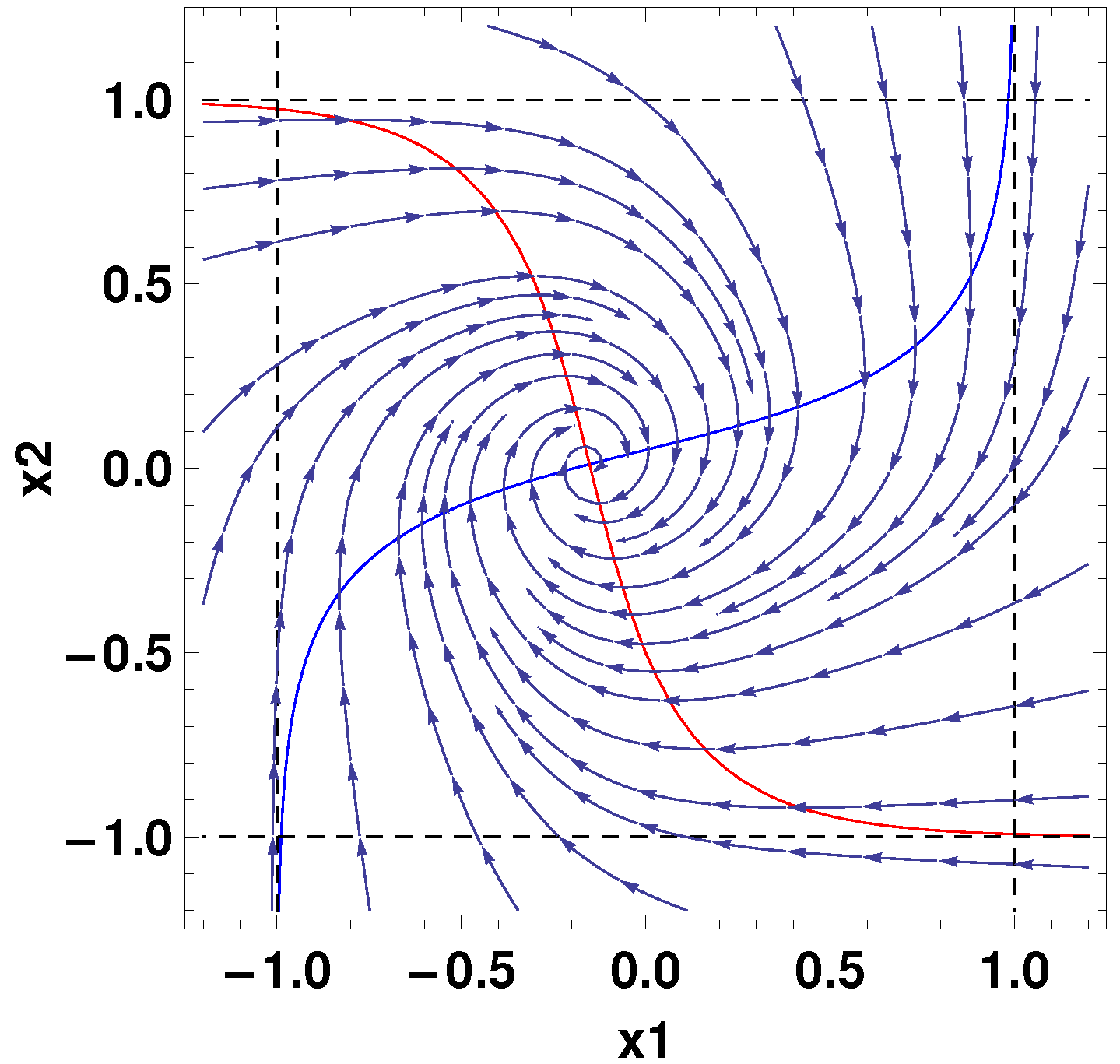
3.3. Critical Points

The critical points, which are also called the equilibria, can be obtained from System (4). Geometrically, they are the cross points of the nullclines. The nullclines are defined by the relations

$$\left\{\begin{array}{c}{\displaystyle x_1-\frac{1}{b_1}tanh(a_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3-{\theta }_1)=0,}\hfill \\ \\ {\displaystyle x_2-\frac{1}{b_2}tanh(a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3-{\theta }_2)=0,}\hfill \\ \\ {\displaystyle x_3-\frac{1}{b_3}tanh(a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3-{\theta }_3)=0.}\hfill \\ \end{array}\right.$$

(9)

Proposition 2. 

All critical points are in the invariant set.

The nullclines are located in the sets $\{-1/b_1<x_1<1/b_1,$ $-1/b_2<x_2<1/b_2,$$-1/b_3<x_3<1/b_3\}$, respectively, and these sets intersect by the invariant set $Q_3$ only.

Proposition 3. 

At least one critical point exists.

The invariant set $Q_3$ may be considered as a topological ball. Since the vector field on the border is directed inward, $Q_3$ is mapped into itself continuously. The continuous contraction mapping $Q_3$ to $Q_3$ has a fixed point. Any fixed point is a solution of the system (7).

Remark 1. 

The number of critical points may be greater, up to 27, but finite.

Remark 2. 

Both assertions 2 and 3 are valid for the n-dimensional case also.

Example 2. 

Consider System (4) with the matrix

$$W=\left(\begin{array}{ccc}1.2& 2& 0\\ -2& 1.2& 0\\ 0& 0& 1.2\end{array}\right)$$

(10)

and $b_1=b_2=b_3=1,{\theta }_1=0.7,{\theta }_2=0.3,{\theta }_3=0.25$. There is one critical point $(-0.122;0.362;$$0.640)$.

The three nullclines for system (4) with matrix (10) are depicted in Figure 2.

Example 3. 

Consider example of multiple critical points and the system (4) with the matrix

$$W=\left(\begin{array}{ccc}1.2& 2& 0\\ -2& 1.2& 0\\ 0& 0& 1.2\end{array}\right)$$

(11)

and $b_1=b_2=b_3=1,{\theta }_1=0.7,{\theta }_2=0.3,{\theta }_3=0.01$.

The three nullclines for system (4) with matrix (11) are depicted in Figure 3.

There are three critical points $(-0.122;0.362;0.640)$, $(-0.122;0.362;0.050)$ and $(-0.122;$$0.362;-0.675)$.

3.4. Linearization at a Critical Point

Let $(x_1^{*},x_2^{*},x_3^{*})$ be a critical point. The linearization around it is given by the system

$$\left\{\begin{array}{c}{\displaystyle u_1^{\prime }=-b_1{u}_1+a_{11}{g}_1{u}_1+a_{12}{g}_1{u}_2+a_{13}{g}_1{u}_3,}\hfill \\ {\displaystyle u_2^{\prime }=-b_2{u}_2+a_{21}{g}_2{u}_1+a_{22}{g}_2{u}_2+a_{23}{g}_2{u}_3,}\hfill \\ {\displaystyle u_3^{\prime }=-b_3{u}_3+a_{31}{g}_3{u}_1+a_{32}{g}_3{u}_2+a_{33}{g}_3{u}_3,}\hfill \end{array}\right.$$

(12)

where

$$g_1=\frac{4e^{-2(a_{11}{x}_1^{*}+a_{12}{x}_2^{*}+a_{13}{x}_3^{*}-{\theta }_1)}}{{[1+e^{-2(a_{11}{x}_1^{*}+a_{12}{x}_2^{*}+a_{13}{x}_3^{*}-{\theta }_1)}]}^2},$$

(13)

$$g_2=\frac{4e^{-2(a_{21}{x}_1^{*}+a_{22}{x}_2^{*}+a_{23}{x}_3^{*}-{\theta }_2)}}{{[1+e^{-2(a_{21}{x}_1^{*}+a_{22}{x}_2^{*}+a_{23}{x}_3^{*}-{\theta }_2)}]}^2},$$

(14)

$$g_3=\frac{4e^{-2(a_{31}{x}_1^{*}+a_{32}{x}_2^{*}+a_{33}{x}_3^{*}-{\theta }_3)}}{{[1+e^{-2(a_{31}{x}_1^{*}+a_{32}{x}_2^{*}+a_{33}{x}_3^{*}-{\theta }_3)}]}^2}.$$

(15)

One has

$$A-\lambda I=\left|\begin{array}{ccc}{a}_{11}{g}_1-b_1-\lambda & a_{12}{g}_1& a_{13}{g}_1\\ a_{21}{g}_2& a_{22}{g}_2-b_2-\lambda & a_{23}{g}_2\\ a_{31}{g}_3& a_{32}{g}_3& a_{33}{g}_3-b_3-\lambda \end{array}\right|$$

(16)

and the characteristic equation for $b_1=b_2=b_3=1$ is

$$\begin{array}{c}\det |A-\lambda I|=-{\mathsf{\Lambda }}^3+(a_{11}{g}_1+a_{22}{g}_2+a_{33}{g}_3){\mathsf{\Lambda }}^2\hfill \\ +[g_1{g}_2(a_{12}{a}_{21}-a_{11}{a}_{22})+g_1{g}_3(a_{13}{a}_{31}-a_{11}{a}_{33})\hfill \\ +g_2{g}_3(a_{23}{a}_{32}-a_{22}{a}_{33})]\mathsf{\Lambda }\hfill \\ +g_1{g}_2{g}_3(a_{11}{a}_{22}{a}_{33}+a_{12}{a}_{23}{a}_{31}+a_{13}{a}_{21}{a}_{32}\hfill \\ -a_{11}{a}_{23}{a}_{32}-a_{12}{a}_{21}{a}_{33}-a_{13}{a}_{22}{a}_{31})=0,\hfill \end{array}$$

(17)

where $\mathsf{\Lambda }=\lambda +1.$

3.5. Regulatory Matrices With Zero Diagonal Elements

Set $a_{11}=a_{22}=a_{33}=0.$ The regulatory matrix is

$$W=\left(\begin{array}{ccc}0& a_{12}& a_{13}\\ a_{21}& 0& a_{23}\\ a_{31}& a_{32}& 0\end{array}\right)$$

(18)

and the system of differential equations takes the form

$$\left\{\begin{array}{c}{\displaystyle x_1^{\prime }=tanh(a_{12}{x}_2+a_{13}{x}_3-{\theta }_1)-x_1,}\hfill \\ {\displaystyle x_2^{\prime }=tanh(a_{21}{x}_1+a_{23}{x}_3-{\theta }_2)-x_2,}\hfill \\ {\displaystyle x_3^{\prime }=tanh(a_{31}{x}_1+a_{32}{x}_2-{\theta }_3)-x_3.}\hfill \end{array}\right.$$

(19)

Let $(x_1^{*},x_2^{*},x_3^{*})$ be a critical point. The respective linearized system around it is

$$\left\{\begin{array}{c}{\displaystyle u_1^{\prime }=-u_1+a_{12}{g}_1{u}_2+a_{13}{g}_1{u}_3,}\hfill \\ {\displaystyle u_2^{\prime }=-u_2+a_{21}{g}_2{u}_1+a_{23}{g}_2{u}_3,}\hfill \\ {\displaystyle u_3^{\prime }=-u_3+a_{31}{g}_3{u}_1+a_{32}{g}_3{u}_2,}\hfill \end{array}\right.$$

(20)

where $g_1,$$g_2,$$g_3,$ given in (13) to (15), are computed assuming that the regulatory matrix is (18). The characteristic equation for $\mathsf{\Lambda }=\lambda +1$ takes the form

$$\begin{array}{c}-{\mathsf{\Lambda }}^3+B\mathsf{\Lambda }+C=0,\hfill \end{array}$$

(21)

where

$$B=g_1{g}_2\left(a_{12}{a}_{21}\right)+g_1{g}_3\left(a_{13}{a}_{31}\right)+g_2{g}_3\left(a_{23}{a}_{32}\right),$$

(22)

$$C=g_1{g}_2{g}_3(a_{12}{a}_{23}{a}_{31}+a_{13}{a}_{21}{a}_{32}).$$

(23)

Equation (21) has the form

$$y^3+py+q=0.$$

(24)

Recall the Cardano formulas for Equation (24). This equation has complex roots if

$$Q:={\left(\frac{p}{3}\right)}^3+{\left(\frac{q}{2}\right)}^2$$

(25)

is positive. The complex roots can be obtained as

$$y_{2,3}=-\frac{a+b}{2}\pm i(a-b)\frac{\sqrt{3}}{2},$$

(26)

where

$$a={(-\frac{q}{2}+\sqrt{Q})}^{\frac{1}{3}},b={(-\frac{q}{2}-\sqrt{Q})}^{\frac{1}{3}}$$

are real cubic roots satisfying $a·b=-\frac{p}{3}.$ The real root of Equation (24) is $y_1=a+b.$

Example 4. 

Consider System (19) with the matrix

$$W=\left(\begin{array}{ccc}0& 1.2& 2\\ -2& 0& 1.2\\ 0.1& 0.1& 0\end{array}\right)$$

(27)

and $b_1=b_2=b_3=1,{\theta }_1=0.3,{\theta }_2=0.3,{\theta }_3=0.01$.

The three nullclines for system (19) with matrix (53) are depicted in Figure 4.

There is a single critical point $(-0.496;0.311;-0.308).$ The characteristic numbers obtained by the linearization process are ${\lambda }_1=-1.125,{\lambda }_{2,3}=-0.937\pm 1.178i$.

4. Focus Type Critical Points

Consider again Equation (21). In our notation,

$$Q:=-{\left(\frac{B}{3}\right)}^3+{\left(\frac{C}{2}\right)}^2.$$

(28)

Suppose that $Q>0.$ Let $(x_1^{*},x_2^{*},x_3^{*})$ be a critical point in question. The associated characteristic numbers $\lambda$ are

$$\begin{array}{c}{\displaystyle {\lambda }_1=-1+(a+b),}\hfill \\ {\displaystyle {\lambda }_{2,3}=-1-\frac{a+b}{2}\pm i(a-b)\frac{\sqrt{3}}{2},}\hfill \end{array}$$

(29)

where

$$a={\left(\frac{C}{2}+\sqrt{Q}\right)}^{\frac{1}{3}},b={\left(\frac{C}{2}-\sqrt{Q}\right)}^{\frac{1}{3}}$$

(30)

are the real values of cubic roots, and Q is given by (28). We will call such a critical point 3D-focus. It is unstable if the real part $-1-\frac{a+b}{2}$ is positive. We arrive at the following assertion.

Proposition 4. 

Let $(x_1^{*},x_2^{*},x_3^{*})$ be a critical point of the system (19). Suppose that

$${\left(\frac{C}{2}\right)}^2>{\left(\frac{B}{3}\right)}^3.$$

(31)

Then, $Q>0$ and this critical point is a 3D-focus.

Proof. 

Follows from (28) to (30). □

Corollary 1. 

Suppose the condition $B<0$ holds for a critical point. Then, this point is a 3D-focus.

Proof. 

The relation (31) is fulfilled if $B<0.$ □

Proposition 5. 

Suppose $(x_1^{*},x_2^{*},x_3^{*})$ is a critical point of type focus of the system (19). This point is an unstable focus if the condition $-1-\frac{a+b}{2}>0$ holds.

Proof. 

Follows from (29), since then the real part of ${\lambda }_{2,3}$ in (29) is positive. □

Example 5. 

Consider System (19) with the matrix

$$W=\left(\begin{array}{ccc}0& 1.5& 3\\ -3& 0& 1.5\\ 3& 0.1& 0\end{array}\right)$$

(32)

and $b_1=b_2=b_3=1,{\theta }_1=0.6,{\theta }_2=0.3,{\theta }_3=0.1$.

The three nullclines for system (19) with matrix (32) are depicted in Figure 5.

The system has three critical points: $p_1$, $p_2$ and $p_3$ at $(0.790;-0.836;0.975)$, $(0.176;-0.248;$$0.384)$ and $(-0.982;0.819;-0.995)$. The characteristic numbers $\lambda$ are given in

Table 1. The characteristic numbers $\lambda$.

-	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$
$p_1$	−0.9268	−1.0366 − 0.6101 i	−1.0366 + 0.6101 i
$p_2$	1.1972	−2.0986 − 0.8406 i	−2.0986 + 0.8406 i
$p_3$	−0.9821	−1.0090 − 0.2189 i	−1.0090 + 0.2189 i

.

5. Inhibition-Activation

Consider the system

$$\left\{\begin{array}{c}{\displaystyle x_1^{\prime }=tanh(a_{12}{x}_2+a_{13}{x}_3-{\theta }_1)-x_1,}\hfill \\ {\displaystyle x_2^{\prime }=tanh(a_{21}{x}_1+a_{23}{x}_3-{\theta }_2)-x_2,}\hfill \\ {\displaystyle x_3^{\prime }=tanh(a_{31}{x}_1+a_{32}{x}_2-{\theta }_3)-x_3,}\hfill \end{array}\right.$$

(33)

where $a_{12},$$a_{13},$$a_{23}$ are negative, $a_{21},$ $a_{31},$$a_{32}$ are positive.

Let the regulatory matrix be

$$W=\left(\begin{array}{ccc}0& -1& -1\\ 1& 0& -1\\ 1& 1& 0\end{array}\right),$$

(34)

and ${\theta }_1={\theta }_2={\theta }_3=\theta .$ There is a single critical point. Introduce

$$g_1=\frac{4e^{-2(-x_2-x_3-\theta )}}{{[1+e^{-2(-x_2-x_3-\theta )}]}^2},$$

(35)

$$g_2=\frac{4e^{-2(x_1-x_3-\theta )}}{{[1+e^{-2(x_1-x_3-\theta )}]}^2},$$

(36)

$$g_3=\frac{4e^{-2(x_1+x_2-\theta )}}{{[1+e^{-2(x_1+x_2-\theta )}]}^2}.$$

(37)

The range of values of $g_i$ is the interval $(0,1).$ The linearized system is

$$\left\{\begin{array}{c}{\displaystyle u_1^{\prime }=-u_1-g_1{u}_2-g_1{u}_3,}\hfill \\ {\displaystyle u_2^{\prime }=-u_2+g_2{u}_1-g_2{u}_3,}\hfill \\ {\displaystyle u_3^{\prime }=-u_3+g_3{u}_1+g_3{u}_2.}\hfill \end{array}\right.$$

(38)

One can obtain the matrix

$$A-\lambda I=\left|\begin{array}{ccc}-1-\lambda & -g_1& -g_1\\ g_2& -1-\lambda & -g_2\\ g_3& g_3& -1-\lambda \end{array}\right|$$

(39)

and the characteristic equation

$$\begin{array}{c}\det |A-\lambda I|=-{\lambda }^3-3{\lambda }^2+(g_1{g}_2+g_1{g}_3+g_2{g}_3-3)\lambda \hfill \\ +(g_1{g}_2+g_1{g}_3+g_2{g}_3-1)=0.\hfill \end{array}$$

(40)

The roots of the characteristic equation are

$$\left\{\begin{array}{c}{\displaystyle {\lambda }_1=-1,}\hfill \\ {\displaystyle {\lambda }_2=-1-\sqrt{g_1{g}_2+g_1{g}_3+g_2{g}_3}i,}\hfill \\ {\displaystyle {\lambda }_3=-1+\sqrt{g_1{g}_2+g_1{g}_3+g_2{g}_3}i.}\hfill \end{array}\right.$$

(41)

Summing up, we arrive at the following assertion.

Proposition 6. 

A critical point of System (33) under the above conditions is 3D-focus; that is, the following is true: there is 2D-subspace with a stable focus and attraction in the remaining dimension.

6. The Case of Triangular Regulatory Matrix

We consider the special case of the regulatory matrix being in triangular form,

$$W=\left(\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ 0& a_{22}& ...& a_{2n}\\ ...\\ 0& 0& ...& a_{nn}\end{array}\right).$$

(42)

Since the presentation for the general case differs little from the three-dimensional case, let us consider the n-dimensional variant. The system of differential equations takes the form

$$\left\{\begin{array}{c}{\displaystyle x_1^{\prime }=tanh(a_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n-{\theta }_1)-x_1,}\hfill \\ {\displaystyle x_2^{\prime }=tanh(\phantom{a_{21}{x}_1+}{a}_{22}{x}_2+...+a_{2n}{x}_n-{\theta }_2)-x_2,}\hfill \\ ...\hfill \\ {\displaystyle x_n^{\prime }=tanh(\phantom{a_{31}{x}_1+a_{32}{x}_2+}{a}_{nn}{x}_n-{\theta }_n)-x_n,}\hfill \end{array}\right.$$

(43)

where $n>1.$ Suppose that the coefficients $a_{ij}$ take values in the interval $(0;1].$

6.1. Critical Points

The critical points of System (43) can be determined from

$$\left\{\begin{array}{c}{\displaystyle x_1=tanh(a_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n-{\theta }_1),}\hfill \\ {\displaystyle x_2=tanh(\phantom{a_{21}{x}_1+}{a}_{22}{x}_2+...+a_{2n}{x}_n-{\theta }_2),}\hfill \\ ...\hfill \\ {\displaystyle x_n=tanh(\phantom{a_{31}{x}_1+a_{32}{x}_2+}{a}_{nn}{x}_n-{\theta }_n).}\hfill \end{array}\right.$$

(44)

Since the right sides in (44) are less than unity in modulus, all critical points locate in $(-1;1)\times (-1;1)\times ...\times (-1;1).$ Due to sigmoidal character of the function $tanhz,$ the last equation in (44) may have one , two or three roots.

Proposition 7. 

There are, at most, three values for $x_n$ in System (44).

Proposition 8. 

At most, $3^n$ critical points are possible in System (43).

Proof. 

The last equation in (44) may have, at most, three roots, due to the S-shape of the graph to a sigmoidal function on the right side. Consequently, the penultimate equation in (44) may have, at most, $3\times 3$ roots $x_{n-1}$. In total, there are nine roots. Proceeding in this way, we obtain, at most, $3^n$ roots for the very first equation in (44), and therefore, at most $3^n$ critical points for System (43). Hence, the proof. □

6.2. Linearized System

The linearized system is

$$\left\{\begin{array}{c}{\displaystyle u_1^{\prime }=-u_1+a_{11}{g}_1{u}_1+a_{12}{g}_1{u}_2+...+a_{1n}{g}_1{u}_n,}\hfill \\ {\displaystyle u_2^{\prime }=-u_2+a_{22}{g}_2{u}_2+...+a_{2n}{g}_2{u}_n,}\hfill \\ ...\hfill \\ {\displaystyle u_n^{\prime }=-u_n+a_{nn}{g}_n{u}_n,}\hfill \end{array}\right.$$

(45)

where

$$g_1=\frac{4e^{-2(a_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n-{\theta }_1)}}{{[1+e^{-2(a_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n-{\theta }_1)}]}^2},$$

(46)

$$g_2=\frac{4e^{-2(a_{22}{x}_2+...+a_{2n}{x}_n-{\theta }_2)}}{{[1+e^{-2(a_{22}{x}_2+...+a_{2n}{x}_n-{\theta }_2)}]}^2},$$

(47)

$$\dots$$

$$g_n=\frac{4e^{-2(a_{nn}{x}_n-{\theta }_n)}}{{[1+e^{-2(a_{nn}{x}_n-{\theta }_n)}]}^2}.$$

(48)

The values of $g_i$ are positive and not greater than unity. The characteristic values for a critical point are to be obtained from

$$A-\lambda I=\left|\begin{array}{cccc}{a}_{11}{g}_1-1-\lambda & a_{12}{g}_1& ...& a_{1n}{g}_1\\ 0& a_{22}{g}_2-1-\lambda & ...& a_{2n}{g}_2\\ ...& ...& ...& ...\\ 0& 0& ...& a_{nn}{g}_n-1-\lambda \end{array}\right|$$

(49)

and

$$\begin{array}{c}\det |A-\lambda I|=(a_{11}{g}_1-1-\lambda )(a_{22}{g}_2-1-\lambda )...\hfill \\ ...(a_{nn}{g}_n-1-\lambda )=0.\hfill \end{array}.$$

(50)

Evidently,

$$\left\{\begin{array}{c}{\displaystyle {\lambda }_1=-1+a_{11}{g}_1,}\hfill \\ {\displaystyle {\lambda }_2=-1+a_{22}{g}_2,}\hfill \\ ...\hfill \\ {\displaystyle {\lambda }_n=-1+a_{nn}{g}_n.}\hfill \end{array}\right.$$

(51)

Therefore, the characteristic values for any critical point are real, and the following assertion follows.

Proposition 9. 

The triangular system (43) cannot have critical points of type focus.

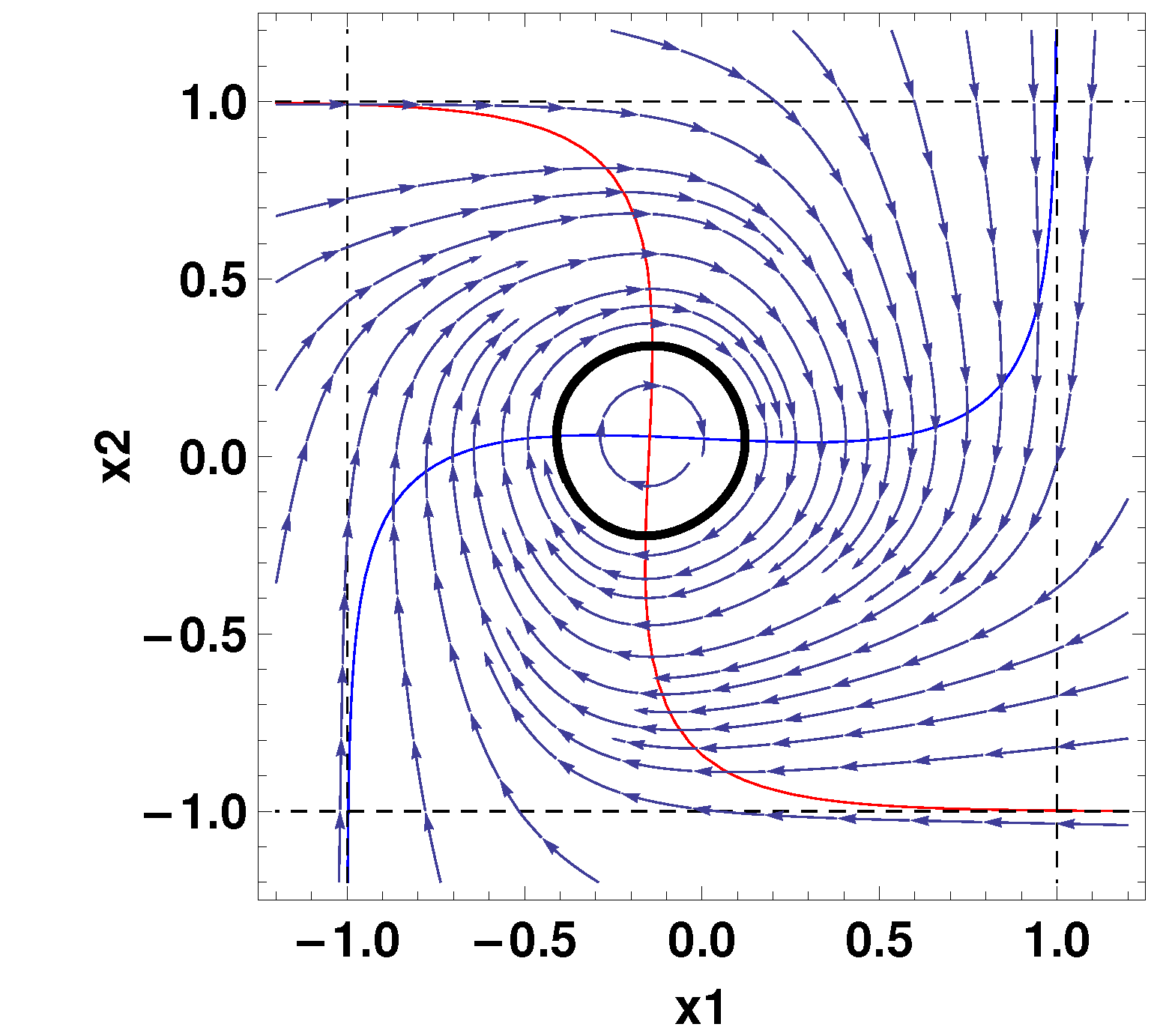
7. Systems with Stable Periodic Solutions: Andronov–Hopf Type Bifurcations

7.1. 2D Case

We first study the second-order system

$$\left\{\begin{array}{c}{\displaystyle \frac{d{x}_1}{dt}=tanh(k{x}_1+b{x}_2-{\theta }_1)-b_1{x}_1,}\hfill \\ \\ {\displaystyle \frac{d{x}_2}{dt}=tanh(a{x}_1+k{x}_2-{\theta }_2)-v_2{x}_2,}\hfill \end{array}\right.$$

(52)

where $b=-a=2,$ and $k>0$ is the parameter. Choose a k small enough that a unique critical point is a stable focus. Then, increase k until the stable focus turns to unstable one. Then, the limit cycle emerges, surrounding the critical point. This is called Andronov–Hopf bifurcation for 2D systems.

Example 6. 

Consider System (52) with the matrix

$$W=\left(\begin{array}{cc}k& 2\\ -2& k\end{array}\right)$$

(53)

and $k=0.5,$$b_1=b_2=1,$${\theta }_1=0.1,$${\theta }_2=0.3$.

The two nullclines and vector field for system (52) with matrix (53) are depicted in Figure 6.

There is one critical point: the stable focus. If the parameter k increases, the stable focus turns to an unstable one. Then, the limit cycle emerges, surrounding the critical point.

Example 7. 

Consider System (52) with the matrix

$$W=\left(\begin{array}{cc}k& 2\\ -2& k\end{array}\right)$$

(54)

and $k=1.1,b_1=b_2=1,{\theta }_1=0.1,{\theta }_2=0.3$.

The two nullclines, vector field and limit cycle for system (52) with matrix (54) are depicted in Figure 7.

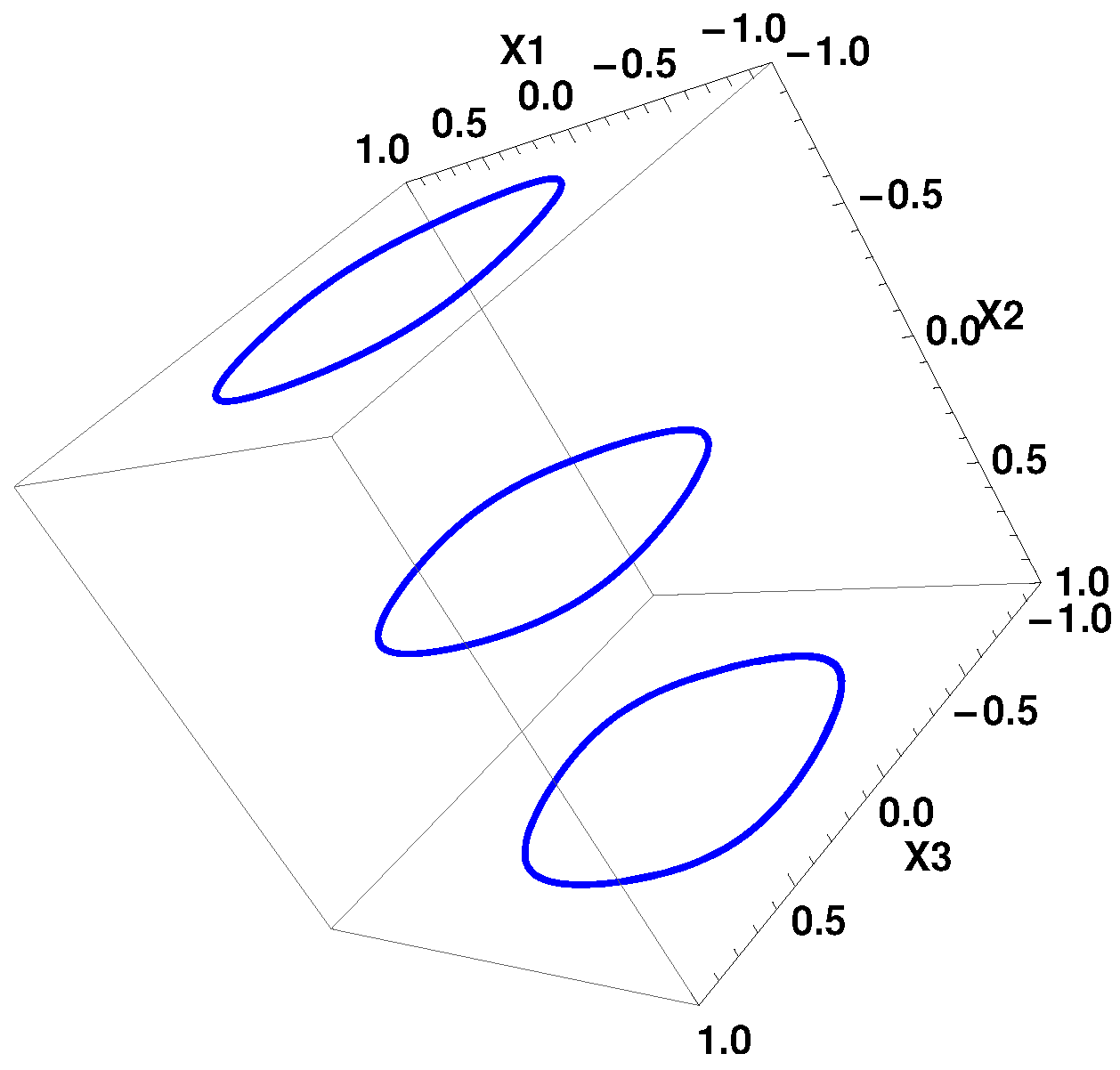
7.2. 3D Case

Consider now the 3D system with the matrix

$$W=\left(\begin{array}{ccc}k& 0& b\\ 0& a_{22}& 0\\ a& 0& k\end{array}\right),$$

(55)

where $a,b,k$ are as in 2D system (52). The second nullcline is defined by the relation

$$x_2=\frac{1}{b_2}tanh(a_{22}{x}_2-{\theta }_2).$$

(56)

Choose the parameters so that Equation (56) has three roots. Then, the second nullcline is a union of three parallel planes.

Example 8. 

Consider picture of nullclines in Figure 8. There are three periodic solutions in System (56) with the matrix (57) are depicted in Figure 9.

$$W=\left(\begin{array}{ccc}1.5& 0& 2\\ 0& 2.5& 0\\ -2& 0& 1.5\end{array}\right)$$

(57)

and $b_1=b_2=b_3=1,{\theta }_1=0.1,{\theta }_2=0,{\theta }_3=0.2$.

8. Control and Management of ANN

First, a citation from [22]: “Models of ANN are specified by three basic entities: models of the neurons themselves–that is, the node characteristics; models of synaptic interconnections and structures–that is, net topology and weights; and training or learning rules—that is, the method of adjusting the weights or the way the network interprets the information it receives”.

In this section, we discuss the problem of changing the behavior of the trajectories of System (4). This may be interpreted as partial control over the system. The system has as parameters the coefficients $a_{ij},$ the values ${\theta }_i$ and $b_i$ in the linear part. Properties of the system may be changed by varying any of mentioned.

We would like demonstrate how a system of the form (4) can be modified so that trajectories start to tend to some of indicated attractor. For this, consider the system (4), which has as attractors three limit cycles. This can be performed via three operations: (1) put the entries of the 2D regulatory matrix, which corresponds to 2D system with the limit cycle L, to the four corners of a 3D matrix A; (2) choose the middle element of the 3D matrix A so, that the equation $x_2=tanh(a_{22}{x}_2-{\theta }_2)$ with respect to $x_2$ has exactly three roots $r_1<r_2<r_3;$ (3) set the four remaining values of $a_{ij}$ to zero. Set also $b_i$ to unity. After finishing these preparations, the second nullcline will be three parallel planes $P_i$, going through $x_2=r_i,$ $i=1,2,3.$ Each of these planes will contain the limit cycle. Two side limit cycles will attract trajectories from their neighborhoods. The middle limit cycle will attract only trajectories, lying in the plane $P_2.$

Now, let us solve the problem of control. Let the limit cycle at $P_3$ be conditionally “bad”. The problem is to change the system so that all trajectories in $Q_3$ are attracted to the limit cycle which, at the beginning of the process, was in the plane $P_1.$ Problems of this kind may arise often. In the paper [20], a similar problem was treated mathematically for genetic networks.

Solution: Change ${\theta }_2$ so that the equation $x_2=tanh(a_{22}{x}_2-{\theta }_2)$ has now the unique root near $P_1.$ The second nullcline is now the plane, passing near $r_1.$ This operation is possible, since the graph of $tanh(a_{22}{x}_2-{\theta }_2)$ is sigmoidal, and changing ${\theta }_2$ means shifting the original plane $P_1$ in both directions. After that, only one attractor (limit cycle) remains. The problem is solved.

In neuronal systems, the $\theta$ parameters express the threshold of a response function f ([4]). In genetic networks, ${\theta }_i$ stands for the influence of external input on gene $i,$ which modulates the gene’s sensitivity of response ([23]). The technique of changing the $\theta$ parameters and thus shifting the nullclines was applied in the work [24] for building the partial control over model of genetic network.

9. Conclusions

Modeling of genetic and neural networks, using dynamical systems, is effective in both cases. The advantage of this approach, compared with other models, is the possibility of following the evolution of modeled networks. Both systems have invariant sets trapping the trajectories. As a consequence, the attracting sets exist. The structure and properties of attractors are important for the prediction of future states of networks. Both systems must have critical points. These points may be attractive (stable) or repelling. The limit cycles are possible in both cases. The attractors, exhibiting sensitivity to the initial data, are possible for three-dimensional GRN and ANN systems. Systems with specific structures can have predictable properties. For instance, the triangular systems cannot have critical points of the focus type. In contrast, the inhibition-activation systems typically have critical points of this type, and can suffer bifurcations of Andronov–Hopf type. Partial control and management are possible for GRN and ANN systems. In particular, some realistically large-sized GRN systems allow for control and management by changing the adjustable parameters. This problem is relevant to modern medicine.