Abstract
This paper considers polynomial characteristics useful for a better understanding of the behaviour of these functions. Taylor series for the polynomials are described by the items with even and odd derivatives and powered changes in the argument, which leads to more specific studying of their properties. Connections between the derivative and antiderivative of the polynomial functions are defined. The structure of polynomial functions reveals their specific characteristic that the mean value of their roots equals the mean value of the locations of the critical points such as the extrema and inflection points. Derivatives of the quadratic exponent in relation to an interesting connection of two transcendental numbers are also described. The discussed properties of the polynomials can be helpful for practical implementations and educational purposes.
Keywords:
polynomials; calculus; Taylor series; roots; derivative; antiderivative; extrema; inflection points; bell curve; transcendental numbers MSC:
26A06; 97I40; 97I50
1. Introduction
Polynomials present the main functions used in algebra, geometry, calculus, matrix analysis, numerical analysis, and many other areas of the mathematical and statistical description of objects and processes [1,2,3,4,5]. Various properties of polynomials have been studied in numerous works [6,7,8,9,10]. Starting with rational polynomial functions, multiple techniques have been developed for solving equations and inequalities, interpolation and approximation, building orthogonal systems of polynomials, complex analysis, dynamical systems, optimization, algorithms, and computational methods [10,11,12,13,14,15]. Polynomials have been widely applied in physics and other natural and technical sciences [16,17,18,19,20]. Although polynomials are studied in high school [21,22] and in spite of their popularity in college courses, there are hardly any known features of polynomial functions. For example, many specific and complicated relations between the roots of a polynomial and its derivative can be found in conjecture theorems by Gauss-Lukas, Bôcher, Sendov, Marden, and others [23,24,25,26,27,28].
This paper considers polynomial characteristics useful for a better understanding of these functions’ behaviour for practical implementations and educational purposes. A calculus student should be able to reproduce such derivations, but he/she should know in advance which problems to work on and what the aim of the research is. This paper shows that the standard calculus approaches can be extended and applied for the investigation of polynomial function features and other problems from different points of view, specifically via the Taylor series, so the work has also didactical aims.
Besides regular polynomials and their orthogonalized versions, there are multiple special polynomials of mathematical physics, which are usually orthogonal with some weight function [29,30,31]. Those are, just as a few examples, polynomials of Chebyshev, Laguerre, Jacoby, Legendre, Hermite, Gegenbauer, and others, with their various modifications and generalizations. An additional example of the derivatives of the quadratic exponent (Gaussian bell curve well known as the probability density function), corresponding to the first three Hermite polynomials, is considered in this paper. Completed with some analysis and geometrical construction, it yields a very unusual Pythagorean relation that combines pi and e transcendental numbers, useful for educational purposes.
The paper is structured as follows. After the introduction, Section 2 presents the Taylor series for polynomial functions described by the items with even and odd derivatives and powered changes in the argument, which leads to a more specific study of their properties. Section 3 discusses connections between the derivative and antiderivative of the polynomial functions. Section 4 describes the structure of polynomial functions and their specific characteristic that the mean value of their roots equals the mean value of the locations of their critical points such as the extrema and inflection points. Numerical examples are given in each section. Section 5 is devoted to the derivation of the connection of two transcendental numbers using the first three Hermite polynomials. Section 6 is a summary.
2. Taylor Series by Even and by Odd Powers
The Taylor series [32] for a differentiable function f(x) existing with all its derivatives in a point x = a can be expressed via these derivatives and powered deviations x − a as follows:
For convenience of further consideration, let us denote the deviation x − a = b, so x = a + b, then (1) can be rewritten as a function of the argument a + b decomposed into the series of the function and its derivatives in the point a multiplied by the powered deviations b:
For our purposes, let us also write a similar expression for the opposite deviation −b:
The mean value of the functions (2)–(3) and the half-difference of them can be introduced as follows:
Thus, the functions (2) and (3) can be presented as the mean value plus or minus the deviation from the mean, respectively:
For an illustration, if a = 0, x = b, and f(x) = exp(x), then the expression (4) corresponds to the hyperbolic sine and cosine functions cosh(x) and sinh(x).
Substituting (2) and (3) into the relation (4) yields expressions for the mean value
and for the deviation:
Therefore, we can split the Taylor series (2) into two parts related to the mean and deviation in (4): the mean in explicit form (6) is defined by the items with even derivatives and even-powered change b in the argument, and the deviation in explicit form (7) is defined by the items with odd derivatives and odd-powered change b in the argument.
Consider a polynomial of a degree n with real coefficients an, an−1, …, a1, a0 and with :
Its real and complex roots can be found from the equation f(x) = 0. The first derivative of the polynomial (8) is
The equation has n − 1 roots defining locations of the extrema/critical points: the real roots identify locations of the maxima/minima of the polynomial (8), where the second derivative is negative/positive in these locations, respectively. The inflection points can be found by the second derivative of the polynomial (8):
The equation has n − 2 roots defining the locations of the inflection points. The higher derivatives can be found as well; for example, the (n − 2)th order derivative is
The next derivative of the (n − 1)th order is
the n-th derivative equals the constant , and the next ones equal zero. All these derivatives can be used in the finite Taylor series (1)–(3) and in the decompositions (6) and (7) for polynomial functions.
The quadratic equation from (11) can be rewritten as
so its roots are
In the case n = 2, Formula (14) reduces to the roots of the regular quadratic equation. The only root of the linear equation from the derivative (12) equals
The notation m in (15) emphasizes the fact that it is the arithmetic mean value of the roots (14). As shown below, the mean value of all roots of the polynomial of the nth order (8) is a constant coinciding with the mean value of all n − 1 roots of its derivative (9) (the mean of extrema locations) and with the mean value of all n − 2 roots of the second derivative (10) (the mean of the inflection points’ locations), etc., and they equal the mean values of all roots of each next derivative, including (11) and (12). Although the roots of a polynomial depend on the intercept parameter a0, the whole structure of the curve can only move in a vertical direction in the plane with a change of the intercept, and the locations of extrema and inflection points remain the same.
Let us consider several examples of the applications of Formulas (6) and (7) to find some features of polynomials. For the quadratic polynomial
the condition for its first derivative defines the point of extremum’s location which also corresponds to the relation (15). The function value in the extremum point equals the expression (6), which with definition (4) can be presented as
because all higher derivatives equal zero. The second derivative is , so its sign is defined by the sign of the coefficient . For any values of a and b, if , then the left-hand side of (17)’s mean value of the function in the points x = a + b and x = a − b is bigger than its value f(a) at the point a (which is the mean value of a + b and a − b) at the right-hand side by the value a2b2. In other words, the function is convex, which corresponds to a positive second derivative. If , then the mean of the function values in the points x = a + b and x = a − b at the left-hand side of (17) is lesser than its value f(a) at the mean argument a at the right-hand side; in other words, the function is concave, which corresponds to a negative second derivative.
Formula (7) for the quadratic function (16) contains only the first derivative. Using the definition (4) and dividing the equation by b yields the expression:
At the left-hand side of (18), there is a tangent of the chord going between any two points x = a + b and x = a − b on the parabola (16), divided by the distance between these points (a + b) − (a − b) = 2b. At the right-hand side of (18), the derivative is in the middle point a. Thus, we see that for a quadratic parabola, such a chord and derivative are parallel lines with the same tangent. This equation corresponds to the Lagrange mean value theorem [33].
For the next example, consider a polynomial of the third order, or cubic parabola:
The relation (6), or (17) with , becomes
Repeating the consideration of the relation (17) on the expression (20) for a cubic parabola, we see that for the function behaves as a convex function, and for it behaves as a concave function. The equation corresponds to the criterion , which defines the point of inflection which is the same as relation (15) in the case n = 3. The Formula (7) for the cubic function (19) is similar to the expression (18) but with an additional constant from the third derivative, so it can be presented as follows:
The first derivative of (19) is , and the roots of the equation define the points of two extrema of a cubic parabola:
The general expression (14) in the case n = 3 reduces to the result (22).
In Formula (22), we also denote the first quotient item as a and the square root item as b, so the coefficient a defines the inflection point and the coefficient b equals the distance from a to the locations of the two extrema of this function. It is easy to show that the substitution of into the first derivative, needed in (21), yields ; thus, the expression (21) reduces to
For a positive a3, the tangent of the chord connecting two extrema points of a cubic parabola is negative; therefore, the first extremum is the maximum and the second one is the minimum, which corresponds to the known graph of this curve. It is easy to see that the tangent of the chords between each extremum and the inflection point equals the same constant proportional to the squared deviation b (up to the sign defining the direction). The distance in the vertical direction between the extrema and inflection points equals
and the cubic parabola is antisymmetric relative to the inflection point. It is interesting to note that for a quadratic parabola, its extremum value can be expressed similarly, as , where a is the location of the extremum and b defines deviations from it to the points of the roots.
A polynomial of the fourth order, or quartic parabola, can be written as
Its features can also be considered via its derivatives, so let us find them. The first one is
and the equation defines the three possible extrema of this curve. The second derivative is
and the equation yields solutions for the two inflection points:
This solution can be obtained from the general Formula (14) in the case n = 4. Let us denote the first and second items in (24) as a and b, respectively. The third and fourth derivatives are
and all these derivatives can be used in finding the finite Taylor decomposition (6) and (7) for this polynomial. For example, Formula (7) in this case is
The value a, as the location of the middle between inflection points (28), corresponds to the equation with the same solution when there is only the first derivative at the right-hand side (30). Thus, the tangent of the chord between two inflection points at the left-hand side (30) equals the tangent f′(a) at the point a in the middle of them.
For illustration, consider a numerical example with the quartic polynomial
with its several derivatives:
From the equation f’(x) = 0, we find the roots
which define the locations of the extrema of the curve (31). The second derivative in the points (33) equals
where the positive values indicate two minima and the negative value indicates one maximum in the behaviour of the curve (31). The distance between the points of minima is x3 − x1 = 4 − 1 = 3, and the middle point between them is (x3 + x1)/2 = 5/2 = 2.5. Taking the middle point for the parameter a = 2.5, and half of the distance between these two points as the parameter b = 3/2 = 1.5, we can use Formula (30) to identify which of the minima presents the global minimum. For this aim, we find and , then using them in (30) yields
The tangent of the chord connecting the points of minima is negative; therefore, the global minimum is located at the biggest root (33) value x3 = 4. It is in agreement with the values of the function at the extrema points: f(1) = −3.083, f(2) = −2.667, and f(4) = −5.333.
3. Relation of Polynomial Derivative and Antiderivative
Let us consider the relationships between the derivative and indefinite integral of a function. Suppose there is a real-valued differentiable and integrable function of one real variable, f(x), with its indefinite integral or antiderivative F(x) and derivative g(x),
The derivative of the antiderivative yields the original function, and the second derivative of the antiderivative coincides with the derivative of the original function:
Recalling that not any critical point is an extremum point and not any root of the second derivative is an inflection point, although the converse assertions are true, we can consider such a question: Which meaningful connections between the features of all three of these functions can be formulated? As it is well known [34], the critical/stationary points or positions of the extrema (maxima and minima) and inflection points of the function f(x) are defined by the location of the roots x* of the derivative g(x*) that can be expressed as follows:
The original function is related to its derivative by the operation of differentiation, and similarly, the antiderivative is related to the original function by the same operation. Thus, the stationary points, or the positions of the maxima, minima, and inflection points of the function F(x), are defined by the locations of the roots of the original function f() that can be written similarly to (56):
Both relations (38) and (39) can be combined in one statement: the extrema (and possible inflection points) of the original function are located at the roots of its derivative, and the roots of the original function define the locations of the extrema (and possible inflection points) of the antiderivative. Such connections can be continued. For example, it is easy to see that if the roots of the second derivative define the points of inflection for the original function, then the roots of the first derivative of the original function define the points of inflection for its antiderivative.
For numerical illustration, consider a polynomial cubic algebraic function (it corresponds to the first derivative in (32)) and its three roots:
Differentiation of it yields the derivative as a quadratic polynomial (which corresponds to the second derivative in (31)) with its two roots:
Integrating the function (40) yields the antiderivative (it corresponds to the function in (31)) as a quadric polynomial:
where the additional constant is taken as zero.
Due to (38), the roots of the derivative (41) define the positioning of the local maximum and minimum of the original function with its values at these points, respectively:
Similarly, due to (39), using the roots of the original function (40), we can find the positioning of the local extrema of the antiderivative function with its values at these points equal to
Other features of the polynomial relations can be also noted. For example, as mentioned above, the roots of the derivative in (41) and the roots of the original function (40) defining locations of the extrema of the antiderivative in (44) go in the interchanging order as follows:
4. Roots’ Mean Equals Critical Points’ Mean
Consider a polynomial of a degree n with real coefficients an, an−1, …, a1, a0, where which was presented as the function (8). Its real and complex roots r1, r2, …, rn can be found from the equation f(x) = 0, and with them, the function (8) can be represented as follows:
Opening the parentheses in (46) yields the relation
Comparison of the coefficients for the same power of x in expressions (8) and (47) yields the well-known Vieta’s formulas. Particularly for xn−1, the total of the roots equals, with the opposite sign, the quotient of the coefficients:
This relation can be re-written using the arithmetic mean mr value of these n roots:
It is possible to formulate the following property of polynomials.
Theorem 1.
The mean of the polynomial roots equals the mean of the locations of its critical points.
Proof of Theorem 1.
Consider the first derivative of the polynomial (8) given in the expression (9). The equation has n − 1 roots u1, u2, …, un−1, defining locations of the extrema and/or inflection points. Similar to (48), their total equals, with the opposite sign, the quotient of the second and first coefficients in (9):
It can be represented using the mean mu value of these n − 1 roots:
The result (51) coincides with the mean of the roots in (49); therefore,
which proves the theorem. □
Several remarks can be added. If the equation has real roots, they identify the locations of the extrema, so the maxima and minima of the polynomial (8) and the complex roots of the derivative could correspond to inflection points. The inflection points can be identified by the second derivative of the polynomial (8), given in the expression (10).
From the equation with its n − 2 roots v1, v2, …, vn−2, which identifies locations of the inflection points, similar to (50), the total of the roots equals, with the opposite sign, the quotient of the second and first coefficients in (10):
In turn, it can also be presented via the mean mv value of these n − 2 roots:
The result of (54) coincides with the mean of (51), so the equality (52) can be extended to the relations
We can see that it is possible to continue these equalities till the (n − 1)th derivative, with all of them equalling the same ratio as at the right-hand side of the relation (15), (51), or (54). The same property holds true for the antiderivatives of polynomials. Integrating (8) yields
From the equation , with its n + 1 roots w1, w2, …, wn+1, the sum of them equals, again, to the opposite by sign quotient of the second and first coefficients in (56):
Thus, it can be represented via the mean mw value of the n + 1 roots:
The result for the antiderivative (58) can be added to the series of equalities (55), and it can be continued for the next antiderivatives for the polynomial (56). In cases of root multiplicity in any of the polynomials, all the repeated values should be used in the means.
The roots of a polynomial (8) depend on the intercept parameter a0, but the possible extrema locations and inflection point locations do not depend on it; that is easy to see using a vertical shift of the graph of the polynomial on the xy-plane, when the extrema and inflection points hold the same locations on the x-axis, while the roots change their positions. Particularly, intersections with the x-axis can disappear entirely. Although the roots vary with the intercept change, their total remains constant, as shown in (48) and (49).
For a numerical illustration, consider the cubic polynomial with three roots (40) and their mean value of 7/3. Its derivative is a quadratic polynomial with two roots (41), and their mean value is also 7/3. Its roots define the locations of the minimum and the maximum of the cubic curve. The second derivative yields a linear function with one root (it corresponds to the third derivative in (32)), which indicates the position of the inflection point, which equals 7/3 too. Integrating the function (40) produces the antiderivative (42) as a quadric polynomial, with the mean value of roots equalling 7/3 as well. Thus, the means of all these functions are kept constant and equal. These four polynomials are presented together for comparison in Figure 1.
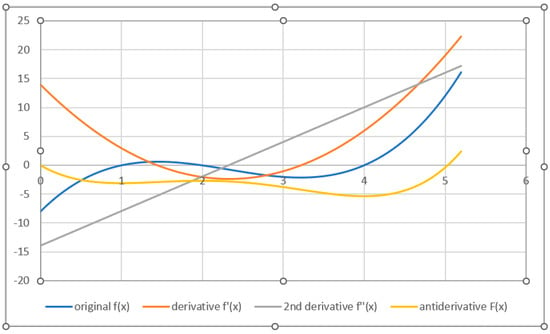
Figure 1.
Cubic polynomial f(x), its quadratic derivative f’(x), linear 2nd derivative f″(x), and quartic antiderivative F(x).
5. The First Hermite Polynomials and Connection of Two Transcendental Numbers
Let us consider the well-known probability density function (pdf), or p(x) of the standard normal distribution, also called the Gaussian curve, which has a bell-type shape defined by the following expression:
The constants pi and e in (59) are the famous infinite transcendental numbers—the first one presents the ratio of a circle’s circumference to its diameter, and the second one is the base of the natural logarithm:
The curve (59) reaches its extremum when its first derivative equals zero,
so, its maximum is located at the centre point x = 0:
The inflection points of the curve (59) are defined by the second derivative equal zero:
The polynomials 1, x, and x2 −1 with the exponents in (59), (61) and (63) coincide with the first three probabilists’ Hermite polynomials [35]. Due to (63), the inflection points are located at , where the pdf (59) has the value
defined via the product of and e numbers. The quotient of the maximum value (62) to the value at the inflection points (64) is
Figure 2 presents the bell curve (59), with its centre at the point O of the beginning of coordinates, the maximum value (62) at the point A, and the inflection point D (64) at x = 1. Let us describe an interesting geometric property on this curve.
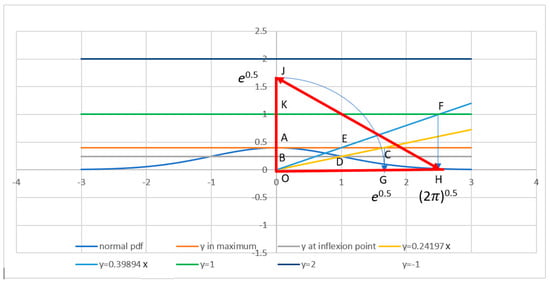
Figure 2.
Normal pdf, with the right triangle with legs and and hypotenuse 3.000245.
Besides the curve (59), Figure 2 also shows three horizontal lines: one line, BD, goes through the inflection point D, another line, AC, goes via the maximum point A and the point E located at x = 1, and the third line, KF, goes at the level y = 1. The ray OD starting from the point O and going through the inflection point D (due to (64), its equation is y = 0.24197x) crosses the line AE at the point C. Consider two similar triangles, OAC and OBD, with the following proportions of their sides:
The right-hand side ratio in (66) coincides with the quotient (65), and BD = 1 due to (63), so this proportion yields the length of the segment . We project the point C onto the x-axis at the point G. The point G from the x-axis can also be transferred to the y-axis at the point J, so the length of these segments is .
Another ray OE from the beginning of the coordinate O goes through the point E, intersecting the line AE at the line x = 1 (its equation is y = 0.39894x, due to (62)) and continues further, traversing the line y = 1 at the point F. Consider two other similar triangles, OAE and OKF, with their sides’ proportions:
With the segments AE = 1 and KO = 1, the proportion (67) leads to the equality KF = 1/AO. Then, taking (62) into account, we obtain the length of the segment , which we can project onto the x-axis to the point H, with the length of this segment . Connecting the points J and H, we obtain the right triangle OJH, with the legs (catheti) and . The Pythagorean theorem yields the length of its hypothenuse:
Numerically, this relation is
This is a fascinating outcome—after all, despite the complicated constructions of the right triangle with the legs and , the length of its hypothenuse happens to be amazingly close to the integer number 3. Indeed, the absolute deviation is only 0.000245, and the relative error is 0.000245/3, which is just 0.008%.
Squaring the relation (10) yields the following equality:
Thus, the two infinite transcendental numbers in such a simple linear combination yield the integer number 9 with an absolute error less than 0.0015 and the relative error 0.0015/9 = 0.00016, or 0.016%. Rounding up to the integer yields a very simple formula
by which we can estimate e by pi, or vice versa. For example, with a simple ratio approximation for pi with two correct decimals , we can find a similar complementary ratio for the number e = 9 − 2 × 22/7 = 19/7 = 2.71. Another known ratio approximation for pi is 223/71 = 3.1408, so it is easy to find, by (71), an approximation for the number e as 193/71 = 2.7183, then 2pi plus e yields the value (2 × 223 + 193)/71 = 639/71 = 9, which reproduces the relation (71).
Archimedes proved the sharp inequality 223/71 < pi < 22/7 [36]; therefore, the complementary inequality for the e number can be obtained: 193/71 > e > 19/7. The relations (68)–(71) present a new approximation for the connection of pi and e numbers, and searching by the net does not reveal it. There exist more complicated approximate relations of the power kind or of a lesser precision [36,37,38,39,40], but none of them is linear or as simple as (70) and (71).
6. Summary
This paper presents polynomial characteristics useful for a better understanding of these functions’ behaviour. The Taylor series for polynomial functions are considered by the items with even and odd derivatives and powered changes in the argument, which permits a more specific study of their properties. Connections between the derivative and antiderivative of the polynomial functions are discussed. The structure of polynomial functions reveals their specific property that the mean value of their roots equals the mean value of the locations of its critical points such as the extrema and inflection points, and the same is true for derivatives and antiderivatives of a higher order.
Numerical examples illustrated these properties. A fascinating feature of the quadratic exponent and its derivatives related to Hermite polynomials is found: a right triangle based on them has legs equal to the square roots of the transcendental numbers 2pi and e, with the hypothenuse equalling the value 3 with a precision of 0.008%. This unusual relation is described algebraically and graphically.
The discussed general relations for polynomials and their derivatives are useful in the analysis, and the obtained results present interesting and unexpected mathematical observations, demonstrating the power and beauty of mathematics. The innovative features of polynomials give students a better understanding of these functions and help instructors explain various abilities of calculus evaluations. Additional sources for the considered problems can be also found in [41,42,43,44,45,46,47,48,49,50].
Funding
This research received no external funding.
Data Availability Statement
No data is used in the paper.
Acknowledgments
The author thanks three anonymous reviewers whose comments and suggestions helped in improving the paper.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Barbeau, E.J. Polynomials; Springer: New York, NY, USA, 2003. [Google Scholar]
- Gautschi, W. Orthogonal Polynomials: Computation and Approximation; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Prasolov, V. Polynomials; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- McNamee, J.M. Numerical Methods for Roots of Polynomials, Part I; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- McNamee, J.M.; Pan, V.Y. Numerical Methods for Roots of Polynomials, Part II; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Govil, N.K. On the derivative of a polynomial. Proc. Am. Math. Soc. 1973, 41, 543–546. [Google Scholar] [CrossRef]
- Craven, T.; Csordas, G. On the number of real roots of polynomials. Pac. J. Math. 1982, 102, 15–28. [Google Scholar] [CrossRef][Green Version]
- Gulzar, M.H. On the zeros of a polynomial. Int. J. Sci. Res. Publ. 2012, 2, 1–7. [Google Scholar]
- Kostov, V.P.; Shapiro, B.Z. Something You Always Wanted to Know about Real Polynomials (But Were Afraid to Ask). arXiv 2008, arXiv:1703.04436v1. [Google Scholar]
- Nguen, H.; Nguen, O.; Vu, V. On the Number of Real Roots of Random Polynomials. arXiv 2014, arXiv:1402.4628v1. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo-Zaglia, M. Extrapolation Methods. Theory and Practice; North-Holland: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Borwein, P.; Erdélyi, T. Polynomials and Polynomial Inequalities; Springer: New York, NY, USA, 1995. [Google Scholar]
- Gautschi, W.; Golub, G.H.; Opfer, G. (Eds.) Applications and Computation of Orthogonal Polynomials; Birkhäuser: Basel, Switzerland, 1999. [Google Scholar]
- Mignotte, M.; Stefănescu, D. Polynomials: An Algorithmic Approach; Springer: Singapore, 1999. [Google Scholar]
- Duran, A.; Defez, E. Orthogonal matrix polynomials and quadrature formulas. Linear Algebra Its Appl. 2002, 345, 71–84. [Google Scholar] [CrossRef]
- Tratnik, N. The multivariable Zhang–Zhang polynomial of phenylenes. Axioms 2023, 12, 1053. [Google Scholar] [CrossRef]
- Grycan-Gerard, F.; Marco, J.-P. Polynomial entropy and polynomial torsion for fibered systems. Regul. Chaotic Dyn. 2023, 28, 613–627. [Google Scholar] [CrossRef]
- Parlak, A. The taut polynomial and the Alexander polynomial. J. Topol. 2023, 16, 720–756. [Google Scholar] [CrossRef]
- Zubova, S. Algorithm for constructing a polynomial solution of a program control problem for a dynamic system in partial derivatives. Model. Syst. Process. 2023, 16, 94–104. [Google Scholar] [CrossRef]
- Cuevas, E.; Luque, A.; Escobar, H. Interpolation and Polynomials. In Computational Methods with MATLAB; Cuevas, E., Ed.; Springer: Cham, Switzerland, 2024; pp. 77–101. [Google Scholar]
- Dede, Y.; Soybas, D. Preservice mathematics teachers’ concept images of polynomials. Qual. Quant. 2011, 45, 391–402. [Google Scholar] [CrossRef]
- Bolondi, G.; Ferretti, F.; Maffia, A. Monomials and polynomials: The long march towards a definition. Oxf. Acad. Teach. Math. Its Appl. 2020, 39, 1–12. [Google Scholar] [CrossRef]
- Marden, M. Geometry of Polynomials, 2nd ed.; American Mathematical Society: Providence, RI, USA, 1966. [Google Scholar]
- Marden, M. Conjectures on the Critical Points of a Polynomial. Am. Math. Mon. 1983, 90, 267–276. [Google Scholar] [CrossRef]
- Kalman, D. An elementary proof of Marden’s theorem. Am. Math. Mon. 2018, 115, 330–338. [Google Scholar] [CrossRef]
- Baron, G.; Drmota, M. Polynomial relations between polynomial roots. J. Algebra 1995, 177, 827–845. [Google Scholar] [CrossRef]
- Brown, J.E.; Xiang, G. Proof of the Sendov conjecture for polynomials of degree at most eight. J. Math. Anal. Appl. 1999, 232, 272–292. [Google Scholar] [CrossRef][Green Version]
- Schmeisser, G. The Conjectures of Sendov and Smale. In Approximation Theory: A Volume Dedicated to Blagovest Sendov; Bojoanov, B., Ed.; DARBA: Sofia, Bulgaria, 2002; pp. 353–369. [Google Scholar]
- Govil, N.K.; Rahman, Q.I. Functions of exponential type not vanishing in a half-plane and related polynomials. Trans. Am. Math. Soc. 1969, 137, 501–507. [Google Scholar] [CrossRef]
- Szego, G. Orthogonal Polynomials, 4th ed.; Volume 23 of American Mathematical Society, Colloquium Publications; American Mathematical Society: Providence, RI, USA, 1975. [Google Scholar]
- Chihara, T. An Introduction to Orthogonal Polynomials; Dover: Benton Harbor, MI, USA, 2011. [Google Scholar]
- Taylor’s Theorem. Available online: https://en.wikipedia.org/wiki/Taylor%27s_theorem (accessed on 12 December 2023).
- Lipovetsky, S. Equation of Finite Change and Structural Analysis of Mean Value. Axioms 2023, 12, 962. [Google Scholar] [CrossRef]
- Derivative Test. Available online: https://en.wikipedia.org/wiki/Derivative_test (accessed on 12 December 2023).
- Hermite Polynomials. Available online: https://en.wikipedia.org/wiki/Hermite_polynomials (accessed on 12 December 2023).
- Approximations of π. Available online: https://en.wikipedia.org/wiki/Approximations_of_%CF%80 (accessed on 12 December 2023).
- Mathematical Coincidence. Available online: https://en.wikipedia.org/wiki/Mathematical_coincidence (accessed on 12 December 2023).
- Relations between e and pi. Soft Question—What Are Your Favorite Relations between e and pi?—Mathematics Stack Exchange. Available online: https://math.stackexchange.com/questions/1541939/what-are-your-favorite-relations-between-e-and-pi (accessed on 12 December 2023).
- E to the pi. 217: E to the pi Minus pi—Explain xkcd. Available online: https://www.explainxkcd.com/wiki/index.php/217:_e_to_the_pi_Minus_pi (accessed on 12 December 2023).
- Felicetti, P. The Pythagorean Relationship between Pi, Phi and e. Available online: https://www.academia.edu/7489568/The_pythagorean_relationship_between_Pi_Phi_and_e (accessed on 12 December 2023).
- Glaeser, G. Math Tools: 500+ Applications in Science and Arts; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Lipovetsky, S. Book review: “Math Tools: 500+ Applications in Science and Arts, by G. Glaeser”. Technometrics 2018, 60, 263. [Google Scholar]
- Ochkov, V. 2^5 Problems for STEM Education; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Lipovetsky, S. Book review: “2^5 Problems for STEM Education, by V. Ochkov”. Technometrics 2020, 62, 557–558. [Google Scholar] [CrossRef]
- Stroud, K.A.; Booth, D.J. Advanced Engineering Mathematics; Macmillan International/Red Globe Press: London, UK, 2020. [Google Scholar]
- Lipovetsky, S. Book review: “Advanced Engineering Mathematics, by K.A. Stroud and D.J. Booth”. Technometrics 2021, 63, 566–570. [Google Scholar]
- Kalajdzievski, S. Math and Art: An Introduction to Visual Mathematics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022. [Google Scholar]
- Lipovetsky, S. Book review: “Math and Art: An Introduction to Visual Mathematics, by S. Kalajdzievski”. Technometrics 2022, 64, 425–426. [Google Scholar] [CrossRef]
- Lipovetsky, S. Several Mathematical Problems Useful for Teaching. SSRN. 2020. Available online: http://dx.doi.org/10.2139/ssrn.3687673 (accessed on 12 December 2023).
- Lipovetsky, S. Readability indices structure and optimal features. Axioms 2023, 12, 421. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).