Robust Variable Selection with Exponential Squared Loss for the Spatial Error Model
Abstract
:1. Introduction
- (1)
- We established a robust variable selection method for SEM, which employs the exponential squared loss and demonstrates good robustness in the presence of outliers in the observations and inaccurate estimation of the spatial weight matrix.
- (2)
- We designed a BCD algorithm to solve the optimization problem in SEM. We decomposed the exponential square loss component into the difference of convex functions and built a CCCP program for solving the BCD algorithm subproblems. We utilized an accelerated FISTA algorithm to solve the optimization problem with the adaptive lasso penalty term. We also provide the computational complexity of the BCD algorithm.
- (3)
- We verified the robustness and effectiveness of this method through numerical simulation experiments. The simulation results indicate that neglecting the spatial effects of error terms leads to a decrease in variable selection accuracy. When there is noise in the observations and inaccuracies in the spatial weight matrix, the method proposed in this paper outperforms the comparison methods in correctly identifying zero coefficients, non-zero coefficients, and median squared error (MedSE).
2. Model Estimation and Variable Selection
2.1. Spatial Error Model
2.2. Variable Selection Methods
2.3. The Selection of
2.4. The Selection of and
2.5. Estimation of Noise Variance
3. Model Solving Algorithm
3.1. Block Coordinate Descent Algorithm
| Algorithm 1 BCD algorithm framework. |
| 1. Set the initial iteration point , , ; 2. Repeat ; 3. Solve the subproblem about with initial point ; 4. Solve the subproblem about with initial point ; 5. Solve the subproblem with initial value , to obtain a solution , ensuring that , and that is a stationary point of . 6. Iterate until convergence. |
3.2. Solving Subproblem (16)
| Algorithm 2 Convex–concave procedure algorithm. |
| 1. Set an initial point and initialize . 2. Repeat 3. 4. Update the iteration counter: 5. Until convergence of |
| Algorithm 3 FISTA algorithm with backtracking step for solving (22). |
|
Require: Ensure: solution 1: Step 0. Select . Let 2: Step . 3: Determine the smallest non-negative integer which makes satisfy 4: 5: Let and calculate: 6: 7: 8: 9: Output . |
4. Numerical Simulations
4.1. Generation of Simulated Data
4.2. Unregularized Estimation on Gaussian Noise Data
4.3. Unregularized Estimation When the Observed Values of Y Have Outliers
4.4. Unregularized Estimation with Noisy Spatial Weight Matrix
4.5. Variable Selection with Regularizer on Gaussian Noise Data
4.6. Variable Selection with Regularizer on Outlier Data
5. Empirical Data Verification
6. Conclusions and Discussions
- The penalized exponential squared loss effectively selects non-zero coefficients of covariates. When there is noise in the observations and an inaccurate spatial weight matrix, the proposed method shows significant resistance to their impact, demonstrating good robustness.
- The block coordinate descent (BCD) algorithm proposed in this work is effective in optimizing the penalized exponential squared loss function.
- In numerical simulation experiments and empirical applications, variable selection results with lasso and adaptive lasso penalties were compared, and adaptive lasso consistently outperformed in various scenarios.
- It is noteworthy that ignoring the spatial effects of error terms (i.e., ) severely reduces the accuracy of this variable selection method. However, for general error models (when , ), the proposed method remains applicable.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| n = 30, q = 5 | n = 150, q = 5 | n = 300, q = 5 | |||||||
| Exp | Square | LAD | Exp | Square | LAD | Exp | Square | LAD | |
| , | |||||||||
| 4.171 | 3.072 | 3.098 | 3.254 | 3.123 | 3.084 | 3.078 | 3.146 | 3.074 | |
| 2.259 | 2.012 | 2.312 | 1.974 | 2.109 | 2.171 | 2.138 | 2.086 | 2.061 | |
| 1.118 | 1.659 | 1.834 | 1.672 | 1.678 | 1.702 | 1.579 | 1.617 | 1.708 | |
| 0.742 | 0.786 | 0.734 | 0.797 | 0.796 | 0.788 | 0.792 | 0.798 | 0.795 | |
| 1.300 | 0.804 | 1.808 | 1.164 | 1.040 | 1.105 | 1.121 | 1.081 | 1.094 | |
| MedSE | 1.703 | 0.764 | 1.695 | 0.224 | 0.371 | 0.458 | 0.236 | 0.245 | 0.297 |
| , | |||||||||
| 3.114 | 2.939 | 2.898 | 3.094 | 2.987 | 2.911 | 2.935 | 3.042 | 3.024 | |
| 2.011 | 2.157 | 1.964 | 1.891 | 2.020 | 2.059 | 2.052 | 2.003 | 2.022 | |
| 1.646 | 1.622 | 1.739 | 1.607 | 1.578 | 1.580 | 1.542 | 1.565 | 1.629 | |
| 0.507 | 0.502 | 0.500 | 0.510 | 0.510 | 0.500 | 0.509 | 0.509 | 0.506 | |
| 0.557 | 0.735 | 0.947 | 1.098 | 0.981 | 0.966 | 1.066 | 1.030 | 1.045 | |
| MedSE | 0.398 | 0.703 | 0.964 | 0.176 | 0.290 | 0.357 | 0.140 | 0.188 | 0.244 |
| , | |||||||||
| 2.910 | 2.957 | 2.922 | 3.082 | 3.000 | 2.912 | 2.942 | 3.029 | 3.027 | |
| 2.004 | 2.156 | 1.931 | 1.891 | 2.050 | 2.063 | 2.056 | 2.012 | 2.047 | |
| 1.885 | 1.632 | 1.711 | 1.609 | 1.594 | 1.620 | 1.544 | 1.572 | 1.612 | |
| 0.058 | 0.016 | 0.054 | 0.006 | 0.002 | 0.007 | 0.000 | 0.000 | 0.007 | |
| 0.581 | 0.740 | 0.938 | 1.107 | 0.979 | 0.974 | 1.070 | 1.031 | 1.047 | |
| MedSE | 0.517 | 0.648 | 0.962 | 0.185 | 0.293 | 0.372 | 0.139 | 0.185 | 0.242 |
| , | |||||||||
| 4.294 | 2.237 | 2.721 | 2.528 | 2.567 | 1.751 | 1.212 | 1.820 | 1.942 | |
| 0.096 | 2.414 | 1.975 | 1.233 | 1.381 | 1.673 | −0.259 | 1.257 | 1.873 | |
| 2.146 | 1.226 | 1.898 | 0.244 | 1.457 | 1.447 | 1.089 | 1.216 | 0.794 | |
| 0.911 | 0.964 | 0.929 | 0.987 | 0.991 | 0.999 | 1.000 | 0.995 | 1.000 | |
| 13.450 | 7.520 | 5.206 | 55.573 | 15.911 | 31.349 | 32.997 | 67.428 | 15.859 | |
| MedSE | 3.484 | 4.041 | 8.717 | 2.598 | 3.896 | 5.733 | 4.231 | 5.101 | 6.523 |
| , | |||||||||
| 3.314 | 2.475 | 2.978 | 2.623 | 2.747 | 2.168 | 1.433 | 2.119 | 1.942 | |
| 0.282 | 2.319 | 1.865 | 1.418 | 1.429 | 1.963 | −0.407 | 1.558 | 1.298 | |
| 2.693 | 1.259 | 1.840 | 0.275 | 1.595 | 1.636 | 1.209 | 1.394 | 1.018 | |
| 0.860 | 0.921 | 0.832 | 0.955 | 0.953 | 0.996 | 0.984 | 0.964 | 1.000 | |
| 12.508 | 7.199 | 4.851 | 6.237 | 20.207 | 3.899 | 18.063 | 40.884 | 25.945 | |
| MedSE | 3.163 | 3.674 | 7.766 | 2.449 | 4.086 | 5.785 | 4.624 | 5.503 | 6.422 |
| , | |||||||||
| 3.943 | 2.692 | 3.217 | 3.176 | 3.330 | 2.444 | 1.827 | 2.874 | 1.896 | |
| 0.362 | 2.673 | 1.921 | 1.623 | 1.718 | 2.273 | −0.573 | 1.892 | 1.911 | |
| 2.994 | 1.392 | 1.646 | 0.314 | 1.997 | 1.623 | 1.401 | 1.618 | 1.010 | |
| 0.595 | 0.695 | 0.500 | 0.785 | 0.795 | 0.883 | 0.866 | 0.812 | 0.931 | |
| 17.035 | 37.543 | 42.054 | 28.235 | 29.141 | 58.824 | 13.277 | 12.483 | 13.397 | |
| MedSE | 3.593 | 4.421 | 7.071 | 2.809 | 4.954 | 6.589 | 5.417 | 6.489 | 9.667 |
| n = 30, q = 20 | n = 150, q = 100 | n = 300, q = 200 | |||||||
| Exp | Square | LAD | Exp | Square | LAD | Exp | Square | LAD | |
| , | |||||||||
| 1.099 | 3.608 | 4.362 | 3.558 | 3.666 | 4.079 | 4.763 | 3.673 | 4.484 | |
| 1.237 | 2.772 | 2.246 | 4.340 | 2.275 | 2.726 | 1.996 | 2.440 | 2.662 | |
| −0.108 | 1.765 | 2.791 | 1.618 | 1.829 | 2.114 | 1.889 | 1.959 | 2.162 | |
| 0.510 | 0.598 | 0.500 | 0.532 | 0.679 | 0.500 | 0.545 | 0.674 | 0.500 | |
| 45.621 | 1.288 | 6.188 | 8.776 | 1.492 | 11.372 | 7.246 | 1.937 | 10.486 | |
| MedSE | 11.084 | 7.086 | 12.913 | 9.651 | 4.764 | 9.521 | 9.006 | 4.919 | 9.523 |
| , | |||||||||
| 1.088 | 2.958 | 3.044 | 3.127 | 3.033 | 3.005 | 3.086 | 2.962 | 3.037 | |
| 1.500 | 1.958 | 1.849 | 2.023 | 1.999 | 1.959 | 2.173 | 1.984 | 1.976 | |
| 1.112 | 1.753 | 1.695 | 1.312 | 1.618 | 1.658 | 1.225 | 1.615 | 1.596 | |
| 0.505 | 0.502 | 0.500 | 0.502 | 0.505 | 0.500 | 0.509 | 0.504 | 0.500 | |
| 19.757 | 0.183 | 0.557 | 0.587 | 0.335 | 0.723 | 0.410 | 0.353 | 0.704 | |
| MedSE | 6.721 | 2.618 | 2.710 | 2.043 | 1.985 | 2.540 | 2.176 | 1.930 | 2.357 |
| , | |||||||||
| 2.530 | 2.940 | 3.104 | 3.187 | 2.946 | 2.956 | 2.851 | 2.925 | 2.858 | |
| 1.599 | 1.928 | 1.729 | 1.665 | 2.029 | 1.839 | 2.298 | 1.928 | 1.960 | |
| 1.964 | 1.804 | 1.844 | 1.250 | 1.546 | 1.485 | 1.246 | 1.568 | 1.517 | |
| 0.492 | 0.401 | 0.500 | 0.430 | 0.321 | 0.500 | 0.408 | 0.321 | 0.500 | |
| 0.229 | 0.239 | 1.066 | 0.986 | 0.383 | 1.295 | 0.507 | 0.404 | 1.469 | |
| MedSE | 5.446 | 3.522 | 4.221 | 2.856 | 2.264 | 3.505 | 2.477 | 2.228 | 3.432 |
| , | |||||||||
| 0.731 | 2.994 | 2.911 | 3.556 | 3.025 | 3.083 | 2.995 | 2.977 | 2.896 | |
| 1.535 | 1.908 | 1.939 | 1.641 | 2.073 | 1.861 | 2.320 | 1.990 | 2.067 | |
| 2.216 | 1.834 | 2.009 | 1.102 | 1.575 | 1.596 | 1.257 | 1.607 | 1.486 | |
| 0.476 | 0.164 | 0.500 | 0.336 | 0.109 | 0.500 | 0.148 | 0.083 | 0.500 | |
| 3.716 | 0.259 | 1.777 | 2.420 | 0.371 | 2.517 | 0.471 | 0.389 | 2.854 | |
| MedSE | 9.766 | 3.359 | 5.954 | 4.412 | 2.107 | 4.720 | 2.360 | 2.082 | 4.605 |
| , | |||||||||
| −4.722 | 2.551 | 6.874 | −2.831 | 3.651 | 7.391 | −0.018 | 2.533 | 4.660 | |
| 8.293 | 2.333 | 4.512 | −2.847 | 2.325 | 2.775 | 0.048 | 2.883 | 0.733 | |
| 3.117 | 1.760 | 2.022 | 4.418 | 0.425 | 6.648 | −0.110 | 1.959 | 5.006 | |
| 0.508 | 0.821 | 0.500 | 0.717 | 0.898 | 0.500 | 0.833 | 0.903 | 0.500 | |
| 27.293 | 20.282 | 24.512 | 17.575 | 19.964 | 22.157 | 9.306 | 13.666 | 16.381 | |
| MedSE | 39.686 | 27.898 | 67.610 | 35.056 | 35.448 | 31.470 | 14.067 | 13.665 | 25.497 |
| , | |||||||||
| −0.634 | 2.694 | 3.102 | −2.223 | 3.472 | 4.273 | −0.018 | 2.608 | 2.457 | |
| 3.128 | 1.900 | 3.563 | −3.418 | 1.873 | 0.452 | 0.048 | 2.129 | 1.651 | |
| 1.783 | 2.053 | 2.287 | 7.501 | 0.888 | 4.250 | −0.110 | 1.498 | 3.339 | |
| 0.506 | 0.767 | 0.500 | 0.674 | 0.858 | 0.500 | 0.604 | 0.868 | 0.500 | |
| 32.226 | 29.173 | 27.807 | 12.572 | 14.280 | 15.795 | 9.519 | 14.606 | 13.914 | |
| MedSE | 15.091 | 19.440 | 28.257 | 23.328 | 24.803 | 57.961 | 4.067 | 19.192 | 10.382 |
| , | |||||||||
| 0.333 | 2.403 | 3.076 | −1.754 | 3.674 | 3.566 | −0.018 | 2.733 | 3.423 | |
| 2.118 | 1.904 | 3.280 | −3.263 | 2.101 | 0.280 | 0.048 | 2.335 | 1.651 | |
| 1.454 | 2.556 | 2.786 | 8.025 | 1.190 | 3.249 | −0.110 | 1.360 | 3.278 | |
| 0.499 | 0.655 | 0.500 | 0.603 | 0.801 | 0.500 | 0.390 | 0.805 | 0.500 | |
| 20.537 | 17.192 | 33.633 | 21.775 | 23.257 | 26.938 | 25.876 | 15.694 | 84.560 | |
| MedSE | 10.570 | 18.943 | 18.371 | 24.953 | 26.615 | 14.682 | 14.067 | 14.201 | 18.278 |
| , | |||||||||
| 0.271 | 2.498 | 3.162 | −1.888 | 3.922 | 3.214 | −0.018 | 2.932 | 4.047 | |
| 1.934 | 1.877 | 1.642 | −2.505 | 2.193 | 0.938 | 0.048 | 2.427 | 1.655 | |
| 1.054 | 2.561 | 1.787 | 3.895 | 1.224 | 3.179 | −0.110 | 1.403 | 1.953 | |
| 0.497 | 0.546 | 0.500 | 0.545 | 0.690 | 0.500 | 0.382 | 0.714 | 0.500 | |
| 25.288 | 21.138 | 30.855 | 25.724 | 62.474 | 21.793 | 52.331 | 16.704 | 7.310 | |
| MedSE | 10.854 | 19.911 | 17.329 | 14.779 | 18.196 | 22.821 | 14.067 | 11.641 | 18.816 |
| n = 30, q = 5 | n = 150, q = 5 | n = 300, q = 5 | |||||||
| Exp | Square | LAD | Exp | Square | LAD | Exp | Square | LAD | |
| , | |||||||||
| 4.053 | 3.151 | 3.030 | 3.321 | 3.111 | 3.131 | 3.048 | 3.145 | 3.161 | |
| 2.184 | 2.032 | 2.203 | 1.929 | 2.105 | 2.104 | 2.111 | 2.083 | 2.102 | |
| 1.146 | 1.726 | 1.790 | 1.661 | 1.701 | 1.642 | 1.592 | 1.700 | 1.710 | |
| 0.730 | 0.768 | 0.736 | 0.781 | 0.784 | 0.779 | 0.779 | 0.786 | 0.775 | |
| 1.228 | 0.953 | 1.509 | 1.362 | 1.126 | 1.265 | 1.214 | 1.174 | 1.225 | |
| MedSE | 1.605 | 0.945 | 1.272 | 0.280 | 0.394 | 0.537 | 0.228 | 0.270 | 0.329 |
| , | |||||||||
| 3.261 | 2.997 | 3.053 | 3.126 | 2.942 | 3.029 | 2.926 | 2.960 | 2.978 | |
| 2.001 | 1.957 | 2.074 | 1.877 | 2.023 | 2.010 | 2.042 | 1.997 | 1.997 | |
| 1.531 | 1.569 | 1.641 | 1.601 | 1.627 | 1.504 | 1.557 | 1.632 | 1.596 | |
| 0.513 | 0.520 | 0.500 | 0.525 | 0.512 | 0.510 | 0.529 | 0.524 | 0.531 | |
| 0.751 | 0.837 | 0.975 | 1.328 | 1.072 | 1.170 | 1.184 | 1.119 | 1.185 | |
| MedSE | 4.456 | 4.861 | 4.920 | 3.173 | 3.293 | 4.445 | 1.163 | 2.204 | 3.278 |
| , | |||||||||
| 3.103 | 2.376 | 3.016 | 2.991 | 2.348 | 2.567 | 1.889 | 2.577 | 1.983 | |
| 2.795 | 1.830 | 1.158 | 1.848 | 1.209 | 2.053 | 1.386 | 1.406 | 2.538 | |
| 0.701 | 1.062 | 0.921 | 0.067 | 1.317 | 0.839 | 1.237 | 1.594 | 1.130 | |
| 0.821 | 0.983 | 0.922 | 0.988 | 0.991 | 0.993 | 0.999 | 0.993 | 1.000 | |
| 22.181 | 24.467 | 26.215 | 12.463 | 20.053 | 24.074 | 4.611 | 3.030 | 4.237 | |
| MedSE | 5.652 | 3.988 | 8.597 | 3.345 | 3.917 | 6.431 | 1.427 | 3.925 | 6.045 |
| n = 30, q = 5 | n = 150, q = 5 | n = 300, q = 5 | |||||||
| Exp | Square | LAD | Exp | Square | LAD | Exp | Square | LAD | |
| Remove 30% | |||||||||
| , | |||||||||
| 2.354 | 2.881 | 3.018 | 3.018 | 3.122 | 3.127 | 3.037 | 3.090 | 3.127 | |
| 2.987 | 2.073 | 1.746 | 1.912 | 2.077 | 1.971 | 2.202 | 2.009 | 2.021 | |
| 1.239 | 1.620 | 1.547 | 1.791 | 1.698 | 1.552 | 1.529 | 1.693 | 1.656 | |
| 0.461 | 0.436 | 0.499 | 0.417 | 0.387 | 0.410 | 0.385 | 0.399 | 0.396 | |
| 1.457 | 1.266 | 1.811 | 1.340 | 1.313 | 1.362 | 1.367 | 1.377 | 1.332 | |
| MedSE | 1.473 | 0.984 | 1.323 | 0.417 | 0.447 | 0.575 | 0.272 | 0.353 | 0.386 |
| Remove 30% | |||||||||
| , | |||||||||
| 2.950 | 2.223 | 2.784 | 2.058 | 2.485 | 2.845 | 1.364 | 2.763 | 2.652 | |
| 1.032 | 2.676 | 2.846 | 2.162 | 1.694 | 1.471 | 0.513 | 1.640 | 1.773 | |
| 1.381 | 1.138 | 0.034 | −0.095 | 1.204 | 2.104 | 1.350 | 1.173 | 1.009 | |
| 0.880 | 0.860 | 0.744 | 0.893 | 0.927 | 0.907 | 0.938 | 0.933 | 0.933 | |
| 16.184 | 21.415 | 28.473 | 19.800 | 33.276 | 36.677 | 15.618 | 23.684 | 29.837 | |
| MedSE | 3.155 | 4.693 | 9.478 | 2.925 | 5.896 | 8.407 | 3.934 | 7.624 | 9.886 |
| Add 50% | |||||||||
| , | |||||||||
| 4.936 | 3.286 | 3.396 | 3.649 | 3.266 | 3.365 | 3.334 | 3.379 | 3.279 | |
| 1.816 | 2.287 | 2.220 | 2.120 | 2.220 | 2.092 | 2.103 | 2.167 | 2.210 | |
| 0.613 | 1.907 | 1.653 | 1.990 | 1.756 | 1.779 | 1.729 | 1.772 | 1.896 | |
| 0.381 | 0.425 | 0.500 | 0.364 | 0.415 | 0.443 | 0.408 | 0.419 | 0.430 | |
| 2.532 | 1.972 | 2.801 | 1.963 | 1.540 | 1.640 | 1.436 | 1.511 | 1.589 | |
| MedSE | 2.799 | 1.662 | 2.170 | 0.824 | 0.852 | 0.927 | 0.535 | 0.637 | 0.673 |
| n = 30, q = 5 | n = 300, q = 5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp + l1 | Exp + | S + l1 | S + | Lad + l1 | Lad + | Exp + l1 | Exp + | S + l1 | S + | Lad + l1 | Lad + | |
| Correct | 1.80 | 2.17 | 2.20 | 2.10 | 1.57 | 1.77 | 5.00 | 5.00 | 4.90 | 4.87 | 4.87 | 4.57 |
| Incorrect | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MedSE | 1.50 | 1.48 | 1.01 | 0.85 | 1.41 | 1.43 | 0.23 | 0.22 | 0.27 | 0.25 | 0.30 | 0.33 |
| Correct | 4.17 | 4.87 | 2.90 | 2.40 | 2.57 | 2.70 | 5.00 | 5.00 | 5.00 | 4.90 | 4.80 | 4.83 |
| Incorrect | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MedSE | 0.38 | 0.25 | 0.60 | 0.71 | 0.82 | 0.74 | 0.13 | 0.11 | 0.24 | 0.22 | 0.24 | 0.28 |
| Correct | 4.03 | 5.00 | 3.10 | 2.37 | 1.83 | 2.17 | 5.00 | 5.00 | 5.00 | 4.90 | 4.80 | 4.83 |
| Incorrect | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MedSE | 0.44 | 0.16 | 0.60 | 0.77 | 1.00 | 0.98 | 0.13 | 0.11 | 0.23 | 0.20 | 0.28 | 0.26 |
| Correct | 1.57 | 3.03 | 0.60 | 0.40 | 0.40 | 0.67 | 3.07 | 3.00 | 0.47 | 0.33 | 0.47 | 0.47 |
| Incorrect | 0.67 | 1.00 | 0.10 | 0.13 | 0.07 | 0.27 | 1.73 | 1.67 | 0.07 | 0.13 | 0.27 | 0.27 |
| MedSE | 3.39 | 3.72 | 3.65 | 3.92 | 6.13 | 5.26 | 3.89 | 3.90 | 5.36 | 5.92 | 5.54 | 6.81 |
| Correct | 0.90 | 3.00 | 0.50 | 0.20 | 0.37 | 0.77 | 2.10 | 2.00 | 0.43 | 0.20 | 0.57 | 0.67 |
| Incorrect | 0.00 | 0.00 | 0.10 | 0.10 | 0.10 | 0.17 | 1.07 | 1.00 | 0.03 | 0.00 | 0.17 | 0.27 |
| MedSE | 2.44 | 2.71 | 3.87 | 4.13 | 4.31 | 4.51 | 4.19 | 4.34 | 5.77 | 6.32 | 5.44 | 6.21 |
| Correct | 1.00 | 2.97 | 0.50 | 0.33 | 0.63 | 0.87 | 1.97 | 2.00 | 0.40 | 0.33 | 0.30 | 0.40 |
| Incorrect | 0.00 | 0.00 | 0.13 | 0.17 | 0.10 | 0.17 | 0.97 | 1.00 | 0.10 | 0.03 | 0.13 | 0.17 |
| MedSE | 2.63 | 3.21 | 4.36 | 4.50 | 4.36 | 4.67 | 4.65 | 4.94 | 6.77 | 7.52 | 7.04 | 7.67 |
| n = 30, q = 20 | n = 300, q = 200 | |||||||||||
| Exp + l1 | Exp + | S + l1 | S + | Lad + l1 | Lad + | Exp + l1 | Exp + | S + l1 | S + | Lad + l1 | Lad + | |
| Correct | 3.4 | 4.9 | 1.2 | 2.7 | 4.5 | 5.8 | 94.5 | 135.0 | 89.1 | 89.2 | 96.6 | 103.0 |
| Incorrect | 0.2 | 0.5 | 0.0 | 0.1 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MedSE | 7.4 | 7.2 | 9.0 | 7.0 | 3.4 | 3.8 | 4.3 | 2.8 | 4.9 | 5.1 | 4.2 | 4.3 |
| Correct | 5.2 | 8.3 | 4.8 | 5.3 | 10.3 | 11.6 | 178.0 | 198.0 | 170.0 | 166.0 | 188.0 | 191.0 |
| Incorrect | 0.2 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MedSE | 4.8 | 2.2 | 3.1 | 2.5 | 1.5 | 1.4 | 1.7 | 0.9 | 2.0 | 2.1 | 1.5 | 1.4 |
| Correct | 4.8 | 6.1 | 4.2 | 4.3 | 6.9 | 8.2 | 180.2 | 200.0 | 165.3 | 158.4 | 153.8 | 156.6 |
| Incorrect | 0.1 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MedSE | 5.6 | 4.3 | 3.6 | 3.5 | 2.1 | 2.1 | 1.8 | 0.9 | 2.1 | 2.2 | 2.4 | 2.3 |
| Correct | 5.5 | 8.0 | 0.7 | 0.6 | 1.1 | 2.4 | 20.0 | 20.0 | 7.7 | 6.6 | 4.1 | 10.1 |
| Incorrect | 1.1 | 1.6 | 0.0 | 0.0 | 0.1 | 0.2 | 3.0 | 3.0 | 0.1 | 0.0 | 0.1 | 0.0 |
| MedSE | 18.9 | 20.4 | 23.7 | 25.9 | 18.4 | 13.7 | 4.1 | 4.1 | 94.6 | 80.2 | 145.0 | 155.2 |
| Correct | 3.6 | 4.7 | 0.8 | 0.9 | 2.1 | 3.4 | 19.6 | 20.0 | 9.8 | 10.5 | 9.6 | 13.7 |
| Incorrect | 0.2 | 0.8 | 0.1 | 0.0 | 0.1 | 0.2 | 2.9 | 3.0 | 0.1 | 0.1 | 0.0 | 0.1 |
| MedSE | 11.3 | 12.3 | 14.8 | 18.9 | 8.3 | 7.8 | 4.1 | 4.1 | 6.3 | 5.3 | 6.2 | 5.6 |
| Correct | 3.8 | 4.8 | 0.9 | 1.5 | 2.6 | 3.8 | 19.6 | 20.0 | 9.2 | 8.7 | 12.6 | 14.8 |
| Incorrect | 0.1 | 0.5 | 0.3 | 0.1 | 0.1 | 0.2 | 2.9 | 3.0 | 0.1 | 0.0 | 0.1 | 0.1 |
| MedSE | 8.6 | 8.9 | 14.8 | 18.9 | 6.4 | 6.8 | 4.1 | 4.1 | 6.4 | 5.9 | 4.3 | 3.6 |
Appendix B
References
- Anselin, L. Spatial Econometrics: Methods and Models; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; John Wiley Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Wang, X.; Jiang, Y.; Huang, M.; Zhang, H. Robust variable selection with exponential squared loss. J. Am. Stat. Assoc. 2013, 108, 632–643. [Google Scholar] [CrossRef] [PubMed]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Zou, H.; Yuan, M. Composite quantile regression and the oracle model selection theory. Ann. Statist. 2008, 36, 1108–1126. [Google Scholar] [CrossRef]
- Liu, X.; Ma, H.; Deng, S. Variable Selection for Spatial Error Models. J. Yanbian Univ. Nat. Sci. Ed. 2020, 46, 15–19. [Google Scholar]
- Doğan, O. Modified harmonic mean method for spatial autoregressive models. Econ. Lett. 2023, 223, 110978. [Google Scholar] [CrossRef]
- Song, Y.; Liang, X.; Zhu, Y.; Lin, L. Robust variable selection with exponential squared loss for the spatial autoregressive model. Comput. Stat. Data Anal. 2021, 155, 107094. [Google Scholar] [CrossRef]
- Banerjee, S.; Carlin, B.P.; Gelfand, A.E. Hierarchical Modeling and Analysis for Spatial Data; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ma, Y.; Pan, R.; Zou, T.; Wang, H. A naive least squares method for spatial autoregression with covariates. Stat. Sin. 2020, 30, 653–672. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; Jiang, G. Robust regression shrinkage and consistent variable selection through the LAD-Lasso. J. Bus. Econ. Stat. 2007, 25, 347–355. [Google Scholar] [CrossRef]
- Forsythe, G.E. Computer Methods for Mathematical Computations; Prentice-Hall: Hoboken, NJ, USA, 1977. [Google Scholar]
- Yuille, A.L.; Rangarajan, A. The concave-convex procedure. Neural Comput. 2003, 15, 915–936. [Google Scholar] [CrossRef] [PubMed]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Liang, H.; Li, R. Variable selection for partially linear models with measurement errors. J. Am. Stat. Assoc. 2009, 104, 234–248. [Google Scholar] [CrossRef] [PubMed]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference. A Practical Information-Theoretic Approach; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2. [Google Scholar]
- Harrison, D., Jr.; Rubinfeld, D.L. Hedonic housing prices and the demand for clean air. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]

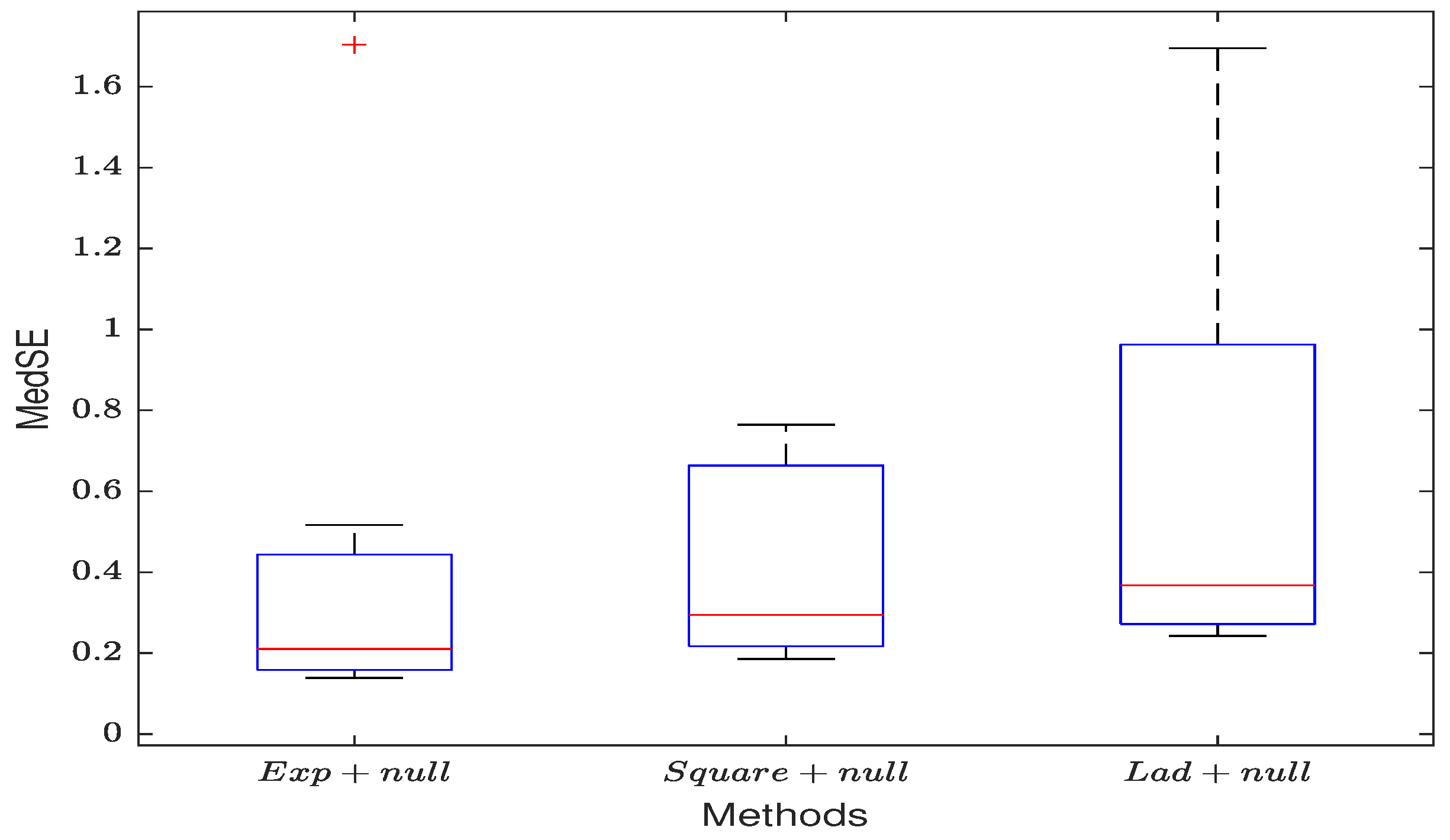

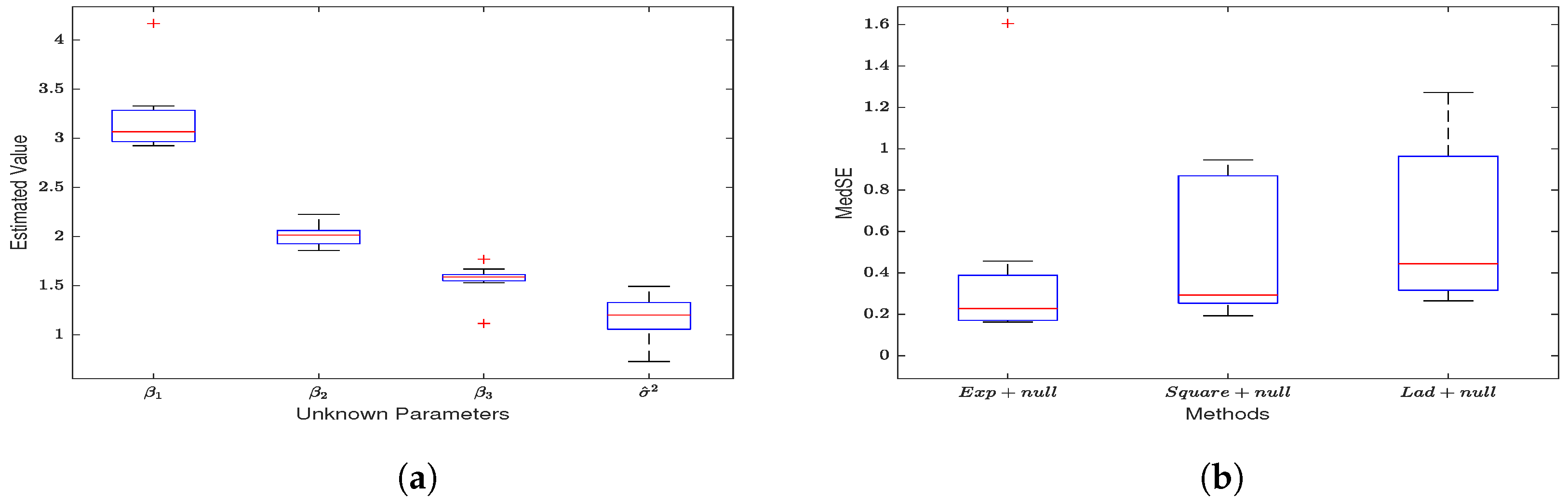
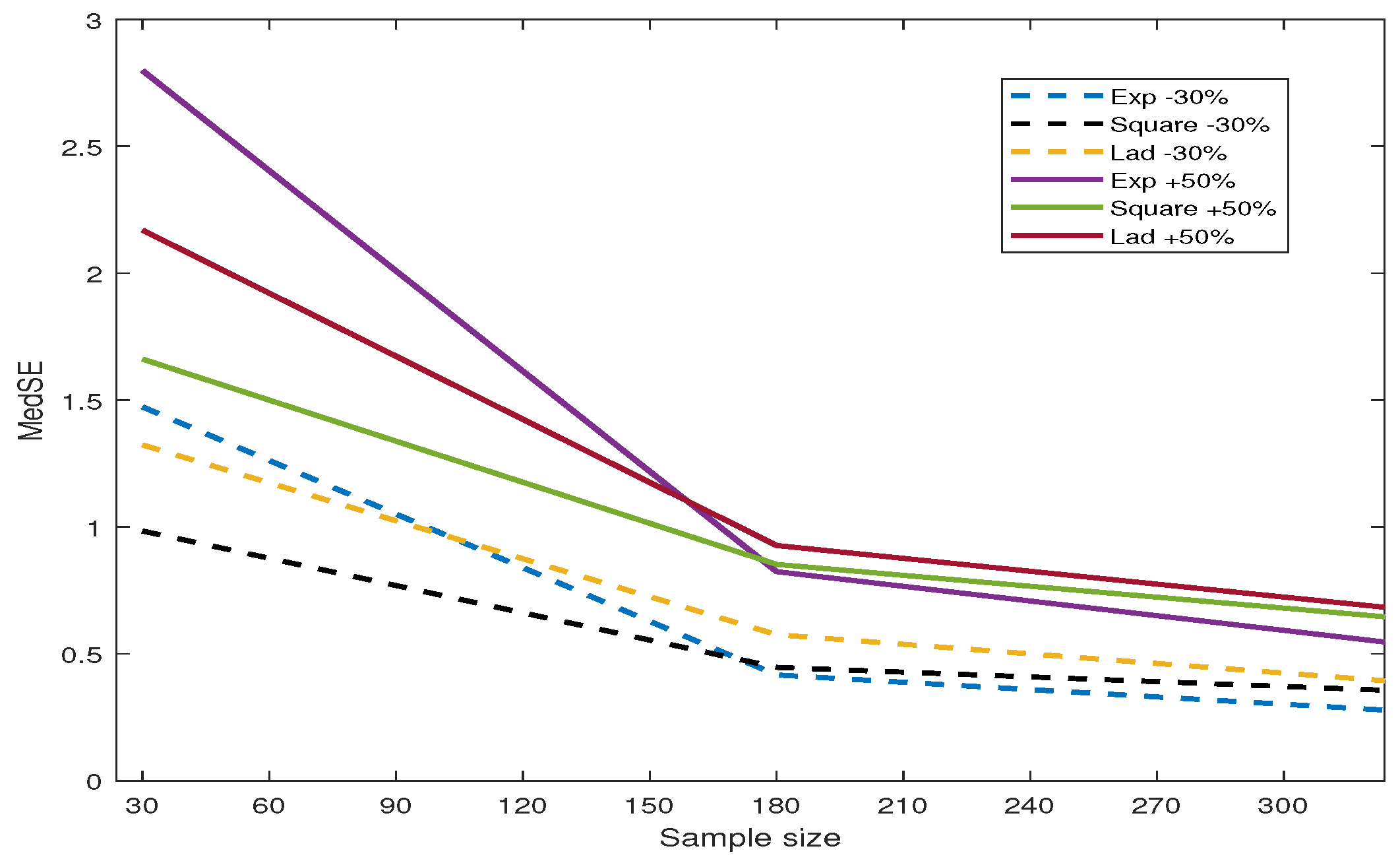

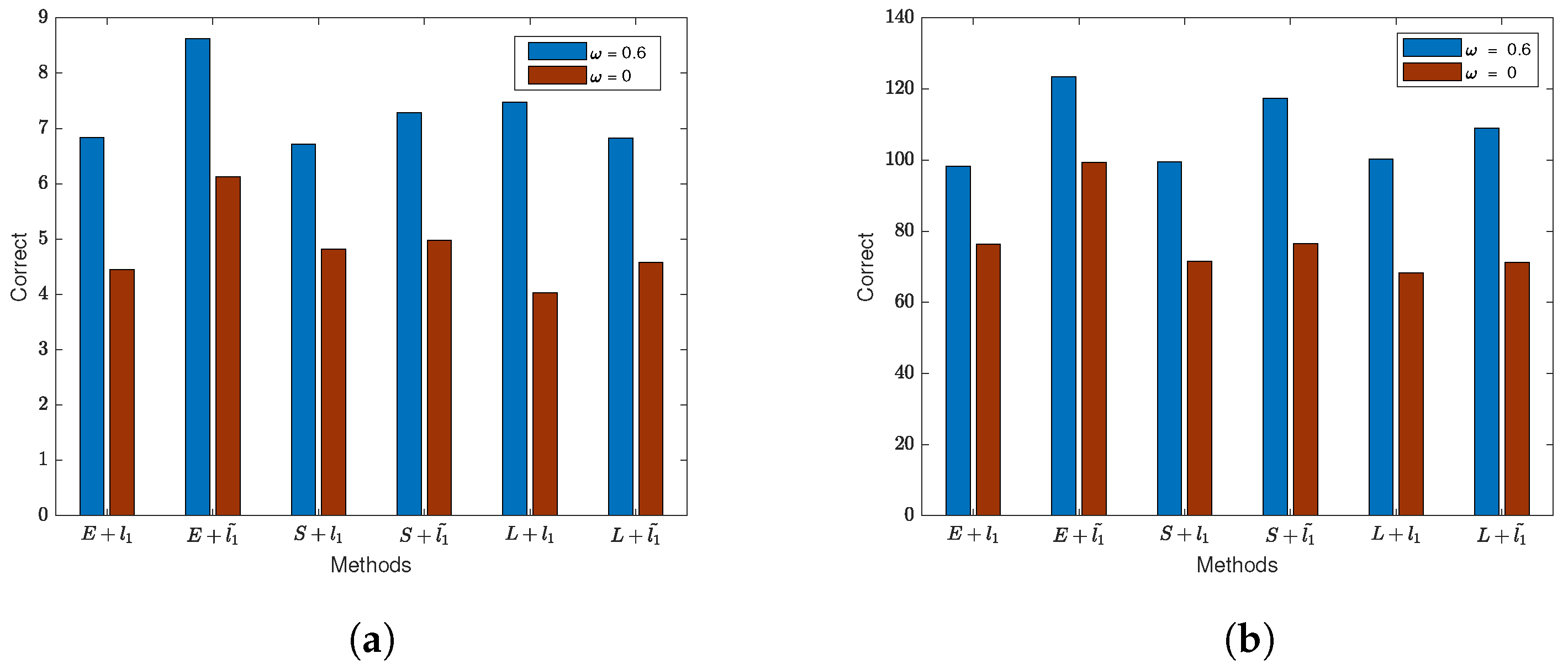
| n = 30, q = 5 | n = 300, q = 5 | |||||||||||
| Exp + l1 | Exp + | S + l1 | S + | Lad + l1 | Lad + | Exp + l1 | Exp + | S + l1 | S + | Lad + l1 | Lad + | |
| Correct | 1.80 | 2.03 | 1.70 | 2.37 | 1.43 | 2.13 | 5.00 | 5.00 | 4.90 | 4.93 | 4.53 | 4.67 |
| Incorrect | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MedSE | 1.39 | 1.47 | 0.91 | 0.93 | 1.59 | 1.08 | 0.22 | 0.21 | 0.27 | 0.31 | 0.35 | 0.34 |
| Correct | 0.33 | 0.23 | 0.50 | 0.53 | 0.43 | 0.57 | 3.27 | 4.07 | 0.67 | 0.47 | 0.37 | 0.83 |
| Incorrect | 0.00 | 0.20 | 0.13 | 0.07 | 0.07 | 0.23 | 0.10 | 0.10 | 0.17 | 0.13 | 0.03 | 0.13 |
| MedSE | 4.85 | 5.50 | 4.56 | 4.51 | 7.06 | 5.11 | 1.40 | 1.32 | 6.35 | 6.80 | 9.09 | 5.16 |
| Correct | 3.67 | 4.03 | 2.40 | 2.53 | 2.77 | 2.93 | 4.97 | 5.00 | 4.97 | 4.93 | 4.63 | 4.60 |
| Incorrect | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MedSE | 0.44 | 0.33 | 0.76 | 0.73 | 0.83 | 0.82 | 0.16 | 0.14 | 0.20 | 0.23 | 0.30 | 0.28 |
| n = 30, q = 5 | n = 300, q = 5 | |||||||||||
| Exp + l1 | Exp + | S + l1 | S + | Lad + l1 | Lad + | Exp + l1 | Exp + | S + l1 | S + | Lad + l1 | Lad + | |
| Remove 30% | ||||||||||||
| Correct | 1.50 | 2.77 | 1.63 | 1.63 | 1.77 | 1.87 | 4.93 | 5.00 | 4.60 | 4.20 | 3.87 | 4.20 |
| Incorrect | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MedSE | 1.39 | 1.27 | 1.20 | 1.07 | 1.17 | 1.19 | 0.27 | 0.24 | 0.29 | 0.37 | 0.43 | 0.40 |
| Correct | 0.40 | 2.20 | 0.77 | 0.53 | 0.47 | 0.67 | 1.13 | 3.00 | 0.43 | 0.53 | 0.30 | 0.40 |
| Incorrect | 0.00 | 0.00 | 0.03 | 0.17 | 0.07 | 0.17 | 0.10 | 0.77 | 0.07 | 0.07 | 0.27 | 0.13 |
| MedSE | 2.48 | 2.62 | 6.32 | 5.06 | 5.23 | 4.81 | 3.40 | 3.53 | 6.89 | 4.11 | 8.48 | 6.47 |
| Add 50% | ||||||||||||
| Correct | 0.40 | 0.73 | 1.37 | 1.20 | 1.03 | 1.87 | 4.63 | 5.00 | 3.47 | 3.17 | 3.20 | 3.53 |
| Incorrect | 0.00 | 0.03 | 0.00 | 0.03 | 0.00 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MedSE | 2.72 | 2.59 | 1.76 | 1.61 | 1.58 | 1.39 | 0.52 | 0.49 | 0.68 | 0.64 | 0.71 | 0.66 |
| Variable | Description |
|---|---|
| DIS | Weighted distance to five job centers in Boston |
| RAD | Highway convenience index |
| LSTAT | Proportion of lower income groups |
| RM | Average number of rooms |
| NOX | Nitric oxide concentration |
| CRIM | Per capita crime rate |
| ZN | The proportion of residential land |
| INDUS | The proportion of non-commercial land |
| CHAS | 1 if it is a river Otherwise 0 |
| AGE | Proportion of owner-occupied units built before 1940 |
| GAR | number of car spaces in garage (0 = no garage) |
| AGE | age of dwelling in years |
| TAX | Full property tax rate per 10,000 dollars |
| PTRATIO | Ratio of teachers to students in town |
| B-1000 | Percentage of blacks in the town |
| MEDV | Median owner-occupied home price |
| EXP | Square | LAD | |||||||
| E + l1 | E + | E + null | S + l1 | S + | S + null | L + l1 | L + | L + null | |
| CRIM | −0.0066 | −7.8600 × | −0.0066 | −0.0059 | −0.0059 | −0.0070 | −0.0035 | −0.0034 | −0.0063 |
| ZN | 3.1200 × | 0 | 3.3400 × | −4.3300 × | −4.0800 × | 3.8900 × | −8.0800 × | −8.7400 × | 1.5200 × |
| INDUS | 0.0015 | 0 | 0.0015 | 0.0017 | 0.0017 | 0.0013 | 0.0010 | 0.0010 | 0.0018 |
| CHAS | 0 | 0 | −0.0017 | 0.0025 | 0.0025 | 0.0048 | 1.0700 × | 1.1700 × | −0.0182 |
| NOX | −0.1908 | 0 | −0.1745 | −2.5800 × | −2.9800 × | −0.2578 | 4.5000 × | 5.2000 × | −0.1514 |
| RM | 0.0079 | 0.0076 | 0.0079 | 0.0146 | 0.0145 | 0.0067 | 0.0200 | 0.0199 | 0.0123 |
| AGE | −4.5400 × | 0 | −4.3100 × | −0.0012 | −0.0012 | −2.8700 × | −0.0014 | −0.0014 | −0.0012 |
| DIS | −0.1411 | −0.0105 | −0.1396 | −0.0107 | −0.0107 | −0.1571 | −5.8600 × | −6.3800 × | −0.1419 |
| RAD | 0.0635 | 0 | 0.0639 | 0.0103 | 0.0103 | 0.0701 | 3.6200 × | 3.9800 × | 0.0484 |
| TAX | −3.5600 × | −1.1700 × | −3.6200 × | −3.8000 × | −4.1000 × | −3.6400 × | −1.0600 × | −1.3500 × | −2.8700 × |
| PTRATIO | −0.0108 | 0 | −0.0106 | −0.0171 | −0.0166 | −0.0115 | −0.0032 | −0.0032 | −0.0081 |
| B-1000 | 3.2800 × | 2.1900 × | 3.2900 × | 3.9800 × | 4.0200 × | 2.8200 × | 6.0200 × | 5.6500 × | 4.3600 × |
| LSTAT | −0.2090 | −0.1818 | −0.2110 | −0.0249 | −0.0249 | −0.2279 | −0.0014 | −0.0014 | −0.1503 |
| 0.5173 | 0.6172 | 0.5174 | 0.6177 | 0.6190 | 0.5190 | 0.5164 | 0.5139 | 0.5000 | |
| 0.0192 | 0.0223 | 0.0192 | 0.0247 | 0.0247 | 0.0192 | 0.0294 | 0.0294 | 0.0206 | |
| BIC | −567.8321 | −491.5053 | −567.6874 | −446.1253 | −446.9024 | −564.2289 | −355.5156 | −356.8915 | −540.9918 |
| EXP | Square | LAD | |||||||
| E + l1 | E + | E + null | S + l1 | S + | S + null | L + l1 | L + | L + null | |
| CRIM | − | − | − | − | − | − | − | − | − |
| ZN | − | − | |||||||
| INDUS | + | + | + | + | + | + | + | + | |
| CHAS | − | + | + | + | − | ||||
| NOX | − | − | − | − | |||||
| RM | + | + | + | + | + | + | + | + | + |
| AGE | − | − | − | − | − | ||||
| DIS | − | − | − | − | − | − | − | − | |
| RAD | + | + | + | + | + | + | |||
| TAX | |||||||||
| PTRATIO | − | − | − | − | − | − | − | − | |
| B-1000 | + | ||||||||
| LSTAT | − | − | − | − | − | − | − | − | − |
| count + | 3 | 1 | 3 | 4 | 4 | 4 | 3 | 2 | 3 |
| count− | 5 | 3 | 6 | 5 | 5 | 5 | 5 | 6 | 7 |
| count | 8 | 4 | 9 | 9 | 9 | 9 | 8 | 8 | 10 |
| BIC | −567.83205 | −491.50529 | −567.68740 | −446.12530 | −446.90237 | −564.22889 | −355.5156 | −356.89146 | −540.99178 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Hou, Y.; Song, Y.; Zhou, F. Robust Variable Selection with Exponential Squared Loss for the Spatial Error Model. Axioms 2024, 13, 4. https://doi.org/10.3390/axioms13010004
Ma S, Hou Y, Song Y, Zhou F. Robust Variable Selection with Exponential Squared Loss for the Spatial Error Model. Axioms. 2024; 13(1):4. https://doi.org/10.3390/axioms13010004
Chicago/Turabian StyleMa, Shida, Yiming Hou, Yunquan Song, and Feng Zhou. 2024. "Robust Variable Selection with Exponential Squared Loss for the Spatial Error Model" Axioms 13, no. 1: 4. https://doi.org/10.3390/axioms13010004
APA StyleMa, S., Hou, Y., Song, Y., & Zhou, F. (2024). Robust Variable Selection with Exponential Squared Loss for the Spatial Error Model. Axioms, 13(1), 4. https://doi.org/10.3390/axioms13010004






