Finite-Time Passivity and Synchronization for a Class of Fuzzy Inertial Complex-Valued Neural Networks with Time-Varying Delays
Abstract
1. Introduction
2. Preliminaries
Model, Assumption, Definitions, and Lemmas
3. Main Results
3.1. Finite-Time Passivity
3.2. Finite-Time Synchronization
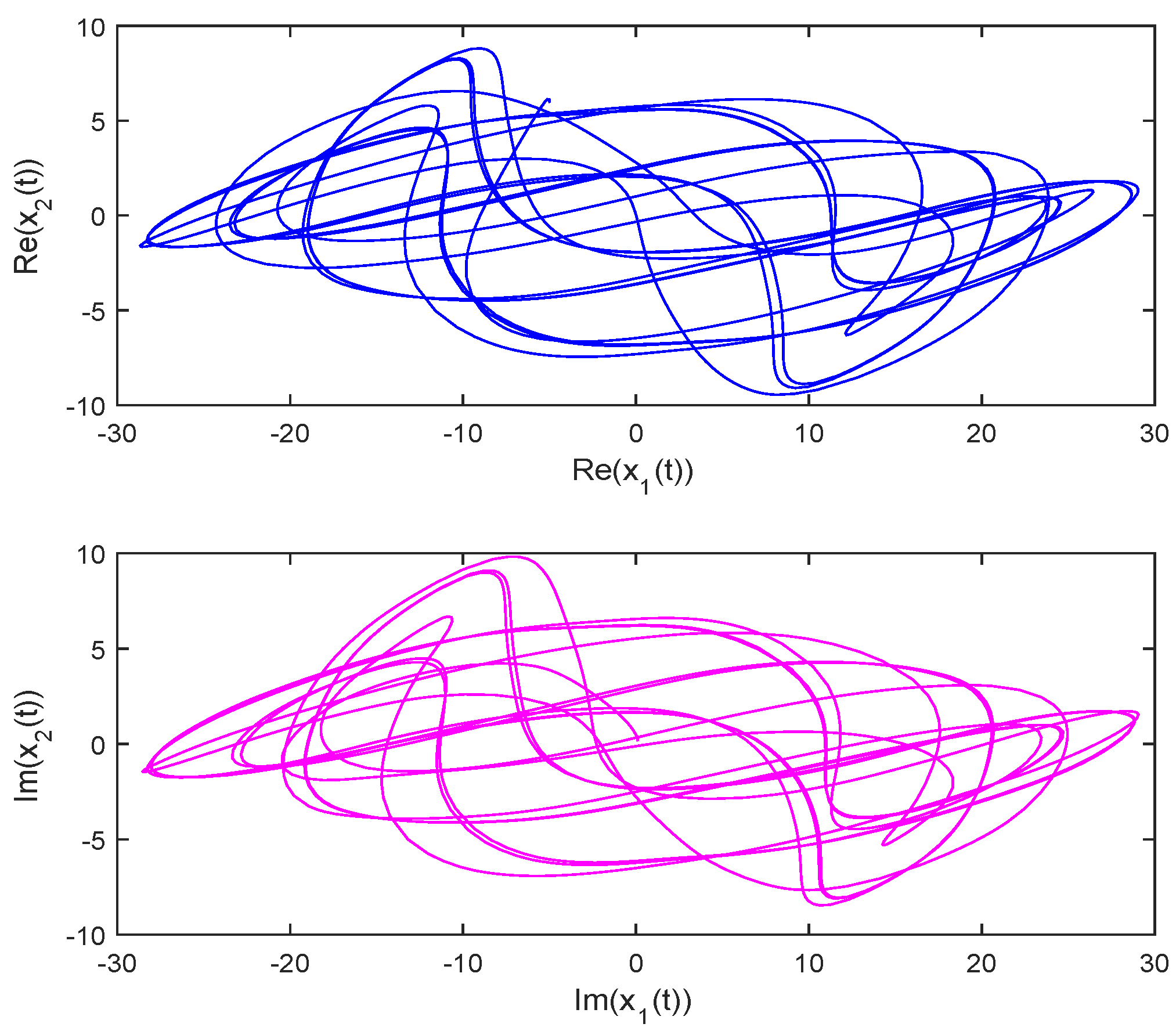
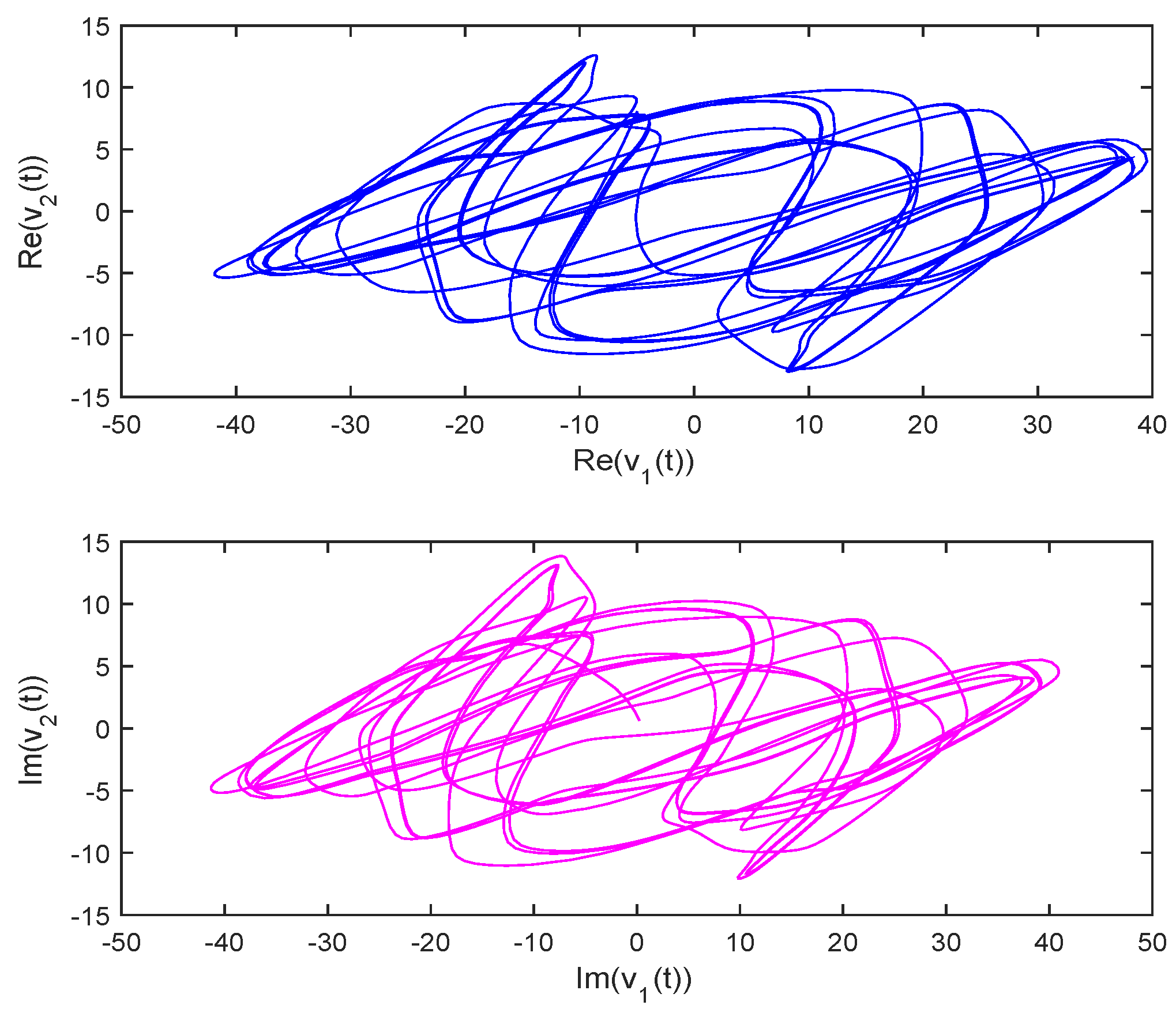
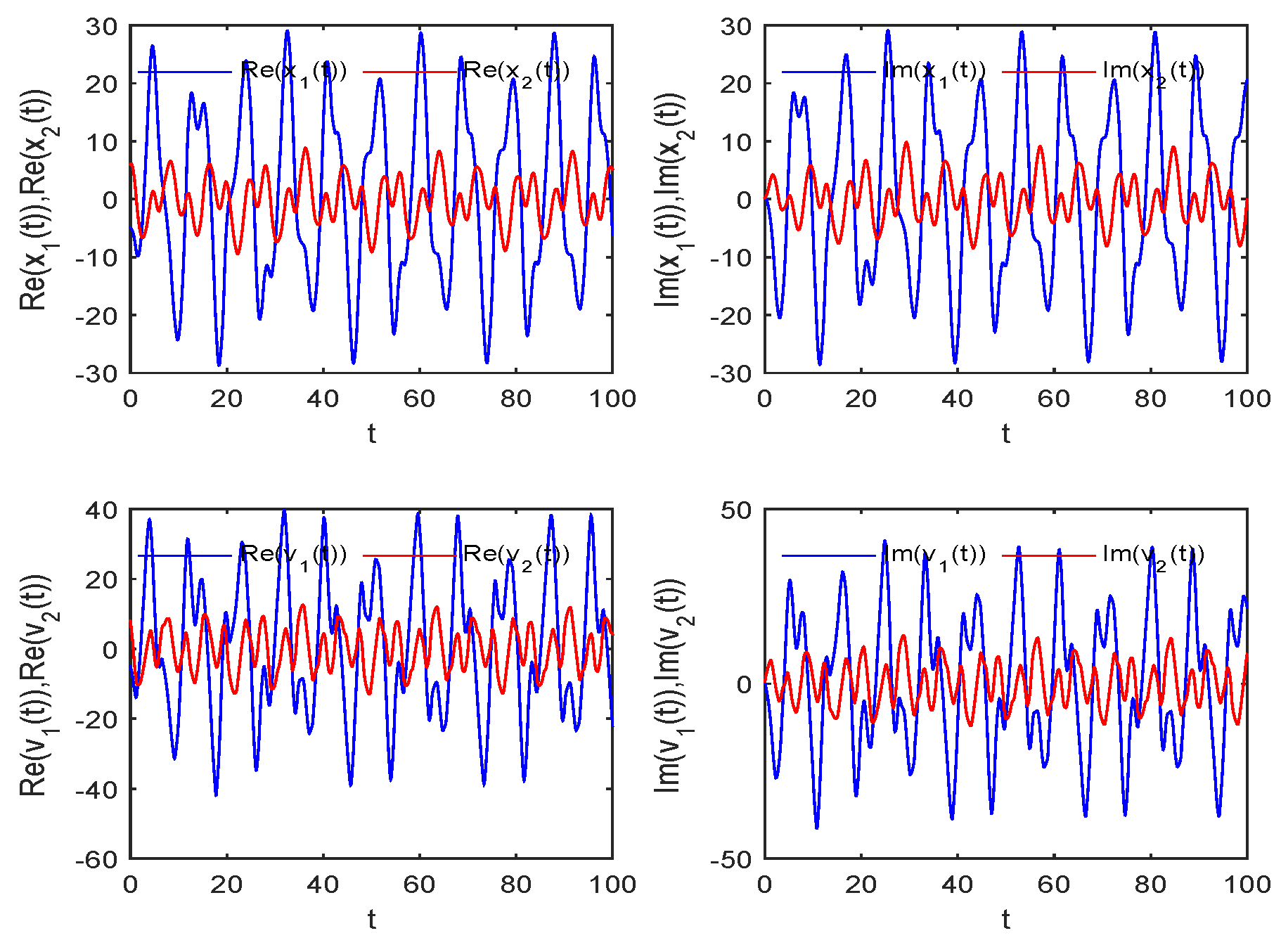
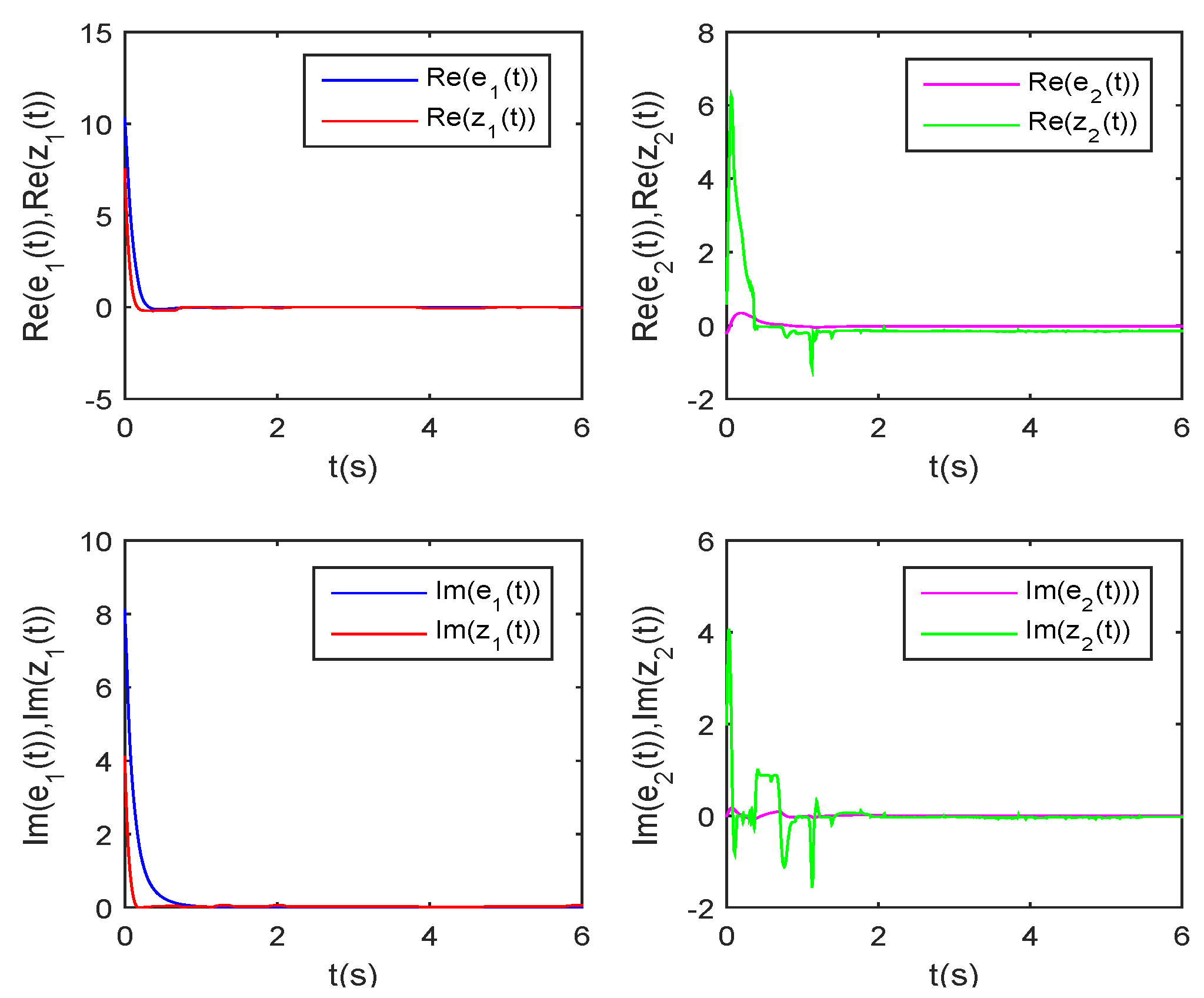
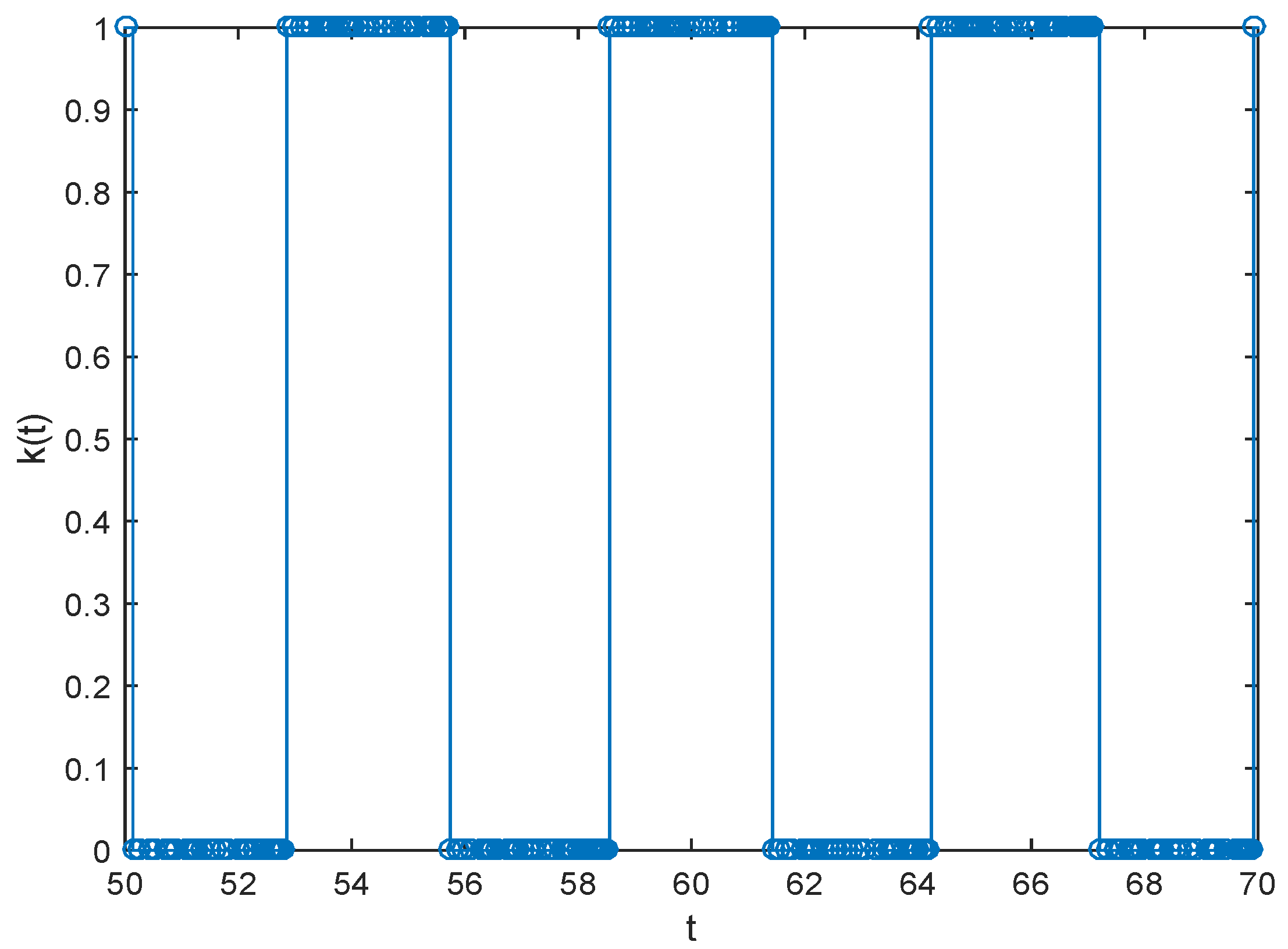
3.3. Example
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, J.Y.; Li, Y.T.; Wen, S.P. Mittag-Leffler synchronization and stability analysis for neural networks in the fractional-order multi-dimension field. Knowl.-Based Syst. 2021, 231, 107404. [Google Scholar] [CrossRef]
- Soltani, A.; Abadi, S. A novel control system for synchronizing chaotic systems in the presence of communication channel time delay; case study of Genesio-Tesi and Coullet systems. Nonlinear Anal. Hybrid Syst. 2023, 50, 101408. [Google Scholar]
- Huang, X.Q.; Lin, W.; Yang, B. Global finite-time stabilization of a class of uncertain nonlinear systems. Automatica 2005, 41, 881–888. [Google Scholar] [CrossRef]
- Wheeler, D.W.; Schieve, W.C. Stability and chaos in an inertial two-neuron system. Physica D 1997, 105, 267–284. [Google Scholar] [CrossRef]
- Jian, J.G.; Duan, L. Finte-time synchronization for fuzzy neutral-type inertial neural networks with time-varyiing coefficients and proportional delyas. Fuzzy Set Syst. 2020, 381, 51–67. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Premalatha, S.; Chandrasekar, A.; Cao, J.D. Stability and synchronization analysis of inertial memrisitve nerual networks with time delays. Cogn. Neurodyn. 2016, 10, 437–451. [Google Scholar] [CrossRef]
- Prakash, M.; Balasubramaniam, P.; Lakshmanan, S. Synchroinization of Markovian jumping inertial neural networks and its applications in image encryption. Neural Netw. 2016, 83, 86–93. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, T.; He, X.; Li, C. Global exponential stability of inertial memristor-based neural networks with time-varying delayed and impulses. Neural Netw. 2017, 95, 102–109. [Google Scholar] [CrossRef]
- Han, J.; Chen, G.C.; Hu, J.H. New results on anti-synchronization in predefined-time for a class of fuzzy inertial neural networks with mixed time delays. Neurocomputing 2022, 495, 26–36. [Google Scholar] [CrossRef]
- Tu, Z.W.; Cao, J.; Alsaedi, A.; Alsaadi, F. Global dissipativity of memristor-based neutral type inertial neural networks. Neural Netw. 2017, 88, 125–133. [Google Scholar] [CrossRef]
- Shanmugasundaram, S.; Udhayakumar, K.; Gunasekaran, D.; Rakkiyappan, R. Event-triggered impulsive control design for synchronization of inertial neural networks with time delyas. Neurocomputing 2022, 483, 322–332. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Cao, J.D. Novel finite-time synchronization criteria for inertial neural networks with time delays via integral inequality method. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1476–1485. [Google Scholar] [CrossRef] [PubMed]
- Han, S.Y.; Hu, C.; Yu, J.; Jiang, H.J.; Wen, S.P. Stabilization of inertial Cohen-Grossberg neural netwroks with generalized delays: A direct analysis approah. Chaos Solitons Fractals 2021, 142, 110432. [Google Scholar] [CrossRef]
- Wan, P.; Jian, J. Global convergence analysis of impulsive inertial neural networks with time-varying delays. Neurocomputing 2017, 245, 68–76. [Google Scholar] [CrossRef]
- Alimi, A.M.; Aouiti, C.; Assali, E.A. Finte-time and fixed-time synchronization of a class of inertial nerual networks with multi-proportional delays and its application to secure communication. Neurocomputing 2019, 332, 29–43. [Google Scholar] [CrossRef]
- Duan, L.Y.; Li, J.M. Fixed-time synchronization of fuzzy neutral-type BAM meeristive inertial neural networks with proportional delays. Inf. Sci. 2021, 576, 522–541. [Google Scholar] [CrossRef]
- Kong, F.C.; Ren, Y.; Sakthivel, R. Delay-dependent crteria for periodicity and exponential stability of inertial neural networks with time-varying delays. Neurocomputing 2021, 419, 261–272. [Google Scholar] [CrossRef]
- Zheng, C.C.; Yu, J.; Jiang, H.J. Fixed-time synchronization of discontinuous competitive neural networks with time-varying delays. Neural Netw. 2022, 153, 192–203. [Google Scholar] [CrossRef]
- Cao, Y.T.; Wang, S.Q.; Guo, Z.Y.; Huang, T.W.; Wen, S.P. Stabilization of memristive neural networks with mixed time-varying delays via continuous/periodic event-based control. J. Frankl. Inst. 2020, 357, 7122–7138. [Google Scholar] [CrossRef]
- Kumar, R.; Das, S. Exponential stability of inertial BAM neural network with time-varying impulses and mixed time-varying delays via matrix measure approach. Commun. Nonlinear Sci. Number. Simul. 2020, 81, 105016. [Google Scholar] [CrossRef]
- Zhang, G.D.; Zeng, Z.G. Stabilization of second-order memristive neural networks with mixed time delays via non-reduced order. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 700–706. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Chen, G.C.; Zhang, G.D. Exponential stabilization of fuzzy inertial neural networks with mixed delays. In Proceedings of the 3rd International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 8–11 November 2021; pp. 1–6. [Google Scholar]
- Xiao, J.; Zeng, Z.G. Finite-time passivity of nerual networks with time varying delay. J. Frankl. Inst. 2020, 357, 2437–2456. [Google Scholar] [CrossRef]
- Zhang, G.D.; Shen, Y.; Yin, Q.; Sun, J.W. Passivity analysis for memristor-based recurrent neural networks with discrete and distributed delays. Neural Netw. 2015, 61, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.M.; Zeng, K.; Hu, C.; Zhou, Y.J. Multiple finite-time synchronizaiton of delayed inertial neural networks via a unified control scheme. Konwl.-Based Syst. 2022, 236, 107785. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Ge, Q.B.; Li, Y.; Hu, J.H. Finite-time synchronization of memristor-based recurrent neural networks with inertial items and mixed delays. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2701–2711. [Google Scholar] [CrossRef]
- Wu, K.; Jian, J.G. Non-reduced order strategies for global dissipativity of memristive neural-type inertial neural networks with mixed time-varying delays. Neurocomputing 2021, 436, 174–183. [Google Scholar] [CrossRef]
- Tu, Z.W.; Cao, J.D.; Hayat, T. Matrix measure based dissipativity analysis for inertial delayed uncertain neural networks. Neural Netw. 2016, 75, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhao, Z.; Song, Q.; Hu, J. Multistability of complex-valued neural networks with time-varying delays. Appl. Math. Comput. 2017, 294, 18–35. [Google Scholar] [CrossRef]
- Ding, X.; Cao, J.; Alsaedi, A.; Alsaadi, F.; Hayat, T. Robust fixed-time synchronization for uncertain complex-valued neural networks with discontinuous activation functions. Neural Netw. 2017, 90, 42–55. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, D.; Yang, C.Y.; Fu, J. Synchronization of memristive complex-valued neural networks wtih time delays via pinning control method. IEEE Trans. Cybern. 2020, 50, 3806–3815. [Google Scholar] [CrossRef]
- Udhayakumar, K.; Rakkiyappan, R.; Rihan, F.A.; Banerjee, S. Projective Multi-Synchronization of Fractional-order Complex-valued Coupled Multi-stable Neural Networks with Impulsive Control. Neurocomputing 2022, 467, 392–405. [Google Scholar] [CrossRef]
- Huang, Y.L.; Wu, F. Finite-time passivity and synchronization of coupled complex-valued memristive neural networks. Inf. Sci. 2021, 580, 775–800. [Google Scholar] [CrossRef]
- Li, H.L.; Hu, C.; Cao, J.D.; Jiang, H.J.; Alsaedi, A. Quasi-projectived and complete synchronization of fractional-order complex-valued neural networks with time delays. Neural Netw. 2019, 118, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.L.; Wu, H.N.; Huang, T.W. Passivity-based synchronization of a class of complex dynamical networks with time-varying delays. Automatica 2015, 56, 105–112. [Google Scholar] [CrossRef]
- Nitta, T. Solving the XOR problem and the detection of symmetry using a single complex-valued neuron. Neural Netw. 2003, 16, 1101–1105. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.F.; Zhang, Z.Y.; Lin, C.; Chen, J. Synchronization and anti-synchronization for complex-valued inertial neural networks with time-varying delays. Appl. Math. Comput. 2021, 403, 126194. [Google Scholar] [CrossRef]
- Tang, Q.; Jian, J.G. Global exponential convergence for impulsive inertial complex-valued neural networks with time-varying delays. Math. Comput. Simul. 2019, 159, 39–56. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H.J.; Wang, L.M. Exponential and adaptive synchronziation of inertial complex-valued neural networks: A non-reduced order and non-separation approach. Neural Netw. 2020, 124, 55–59. [Google Scholar] [CrossRef]
- Long, C.Q.; Zhang, G.D.; Hu, J.H. Fixed-time synchronization for delayed inertial complex-valued neural networks. Appl. Math. Comput. 2021, 405, 126272. [Google Scholar] [CrossRef]
- Long, C.Q.; Zhang, G.D.; Zeng, Z.G.; Hu, J.H. Finite-time stabilization of complex-valued neural networks with proportional delays and inertial terms: A non-separation approch. Neural Netw. 2022, 148, 86–95. [Google Scholar] [CrossRef]
- Yang, T.; Yang, L.; Wu, C.; Chua, L. Fuzzy cellular neura networks: Theroy. In Proceedings of the IEEE International Workshop on Cellular Neural Networks and Applications, Seville, Spain, 24–26 June 1996; pp. 181–186. [Google Scholar]
- Han, J.; Chen, G.C.; Zhang, G.D. Anti-Synchronization Control of Fuzzy Inertial Neural Networks with Distributed Time Delays. In Proceedings of the International Conference on Neuromorphic Computing (ICNC), Wuhan, China, 11–14 October 2021; pp. 99–103. [Google Scholar]
- Aouiti, C.; Hui, Q.; Jallouli, H.; Moulay, E. Fixed-time stabilization of fuzzy neural-type inertial neural networks with time-varying delay. Fuzzy Sets Syst. 2021, 411, 48–76. [Google Scholar] [CrossRef]
- Xiao, Q.; Huang, T.W.; Zeng, Z.G. Pssivity and passification of fuzzy memristive inertial neural networks on time scales. IEEE Trans. Fuzzy Syst. 2018, 26, 3342–3353. [Google Scholar] [CrossRef]
- Li, X.F.; Huang, T.W. Adaptive synchronization for fuzzy inertial complex-valued neural networks with state-dependent coefficients and mixed delays. Fuzzy Sets Syst. 2021, 411, 174–189. [Google Scholar] [CrossRef]
- Wang, J.L.; Xu, M.; Wu, H.N.; Huang, T.W. Fintie-time Passivity of coupled neural networks with multiple weights. IEEE Trans. Netw. Sci. Eng. 2018, 5, 184–196. [Google Scholar] [CrossRef]
- Wang, J.L.; Wu, H.N.; Huang, T.W.; Ren, S.Y. Passivity and synchronization of linearly coupled rection-diffusion neural networks with adaptive coupling. IEEE Trans. Cybern. 2015, 45, 1942–1952. [Google Scholar] [CrossRef]
- Wu, A.; Zeng, Z. Passivity analysis of memristive nerual networks with different memductance functions. Commun. Nonlinear Sci. Number. Simul. 2014, 19, 274–285. [Google Scholar] [CrossRef]
- Tang, Y. Terminal sliding mode control for rigid robots. Automatica 1998, 34, 51–56. [Google Scholar] [CrossRef]
- Han, J.; Chen, G.; Wang, L.; Zhang, G.; Hu, J. Direct approach on fixed-time stabilization and projective synchronization of inertial neural networks with mixed time delays. Neurocomputing 2023, 535, 97–106. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J. Finite-Time Passivity and Synchronization for a Class of Fuzzy Inertial Complex-Valued Neural Networks with Time-Varying Delays. Axioms 2024, 13, 39. https://doi.org/10.3390/axioms13010039
Han J. Finite-Time Passivity and Synchronization for a Class of Fuzzy Inertial Complex-Valued Neural Networks with Time-Varying Delays. Axioms. 2024; 13(1):39. https://doi.org/10.3390/axioms13010039
Chicago/Turabian StyleHan, Jing. 2024. "Finite-Time Passivity and Synchronization for a Class of Fuzzy Inertial Complex-Valued Neural Networks with Time-Varying Delays" Axioms 13, no. 1: 39. https://doi.org/10.3390/axioms13010039
APA StyleHan, J. (2024). Finite-Time Passivity and Synchronization for a Class of Fuzzy Inertial Complex-Valued Neural Networks with Time-Varying Delays. Axioms, 13(1), 39. https://doi.org/10.3390/axioms13010039




