1. Introduction
Decompositions into “irreducible parts” play a central role in many structure theories and often the background is a purely order-theoretical one. The concepts of prime, coprime, join-irreducible, meet-irreducible, atom, and co-atom work well, and these types of elements can be used for the characterization of lattices of certain types. For example, a lattice is distributive if and only if every join-irreducible element is coprime. Similarly, a lattice is meet-pseudocomplemented if and only if each atom is coprime. Furthermore, lattices are decomposed into sublattices by these elements in order that properties of the sublattice generally help to derive properties of the original lattice.
Triangular norms (briefly t-norms) are a special class of aggregation operators that are used in a wide range of fields of application: applied mathematics (e.g., probability, statistics, decision theory) and computer sciences (e.g., artificial intelligence, operations research), as well as many applied fields (economics and finance, pattern recognition and image processing, data fusion, multicriteria decision aid, automated reasoning, etc.) [
1]. T-norms have become especially popular as models for fuzzy sets intersection. They act as an extended operator of meet that is used as a conjunction in fuzzy logic [
2]. They are also applied in probabilistic metric spaces, many-valued logic, non-additive measures and integrals, etc. [
3]. Many authors have studied with t-norms on bounded lattices [
4,
5,
6,
7,
8,
9]. Yılmaz and Kazancı have presented a method for generating t-norms on a finite distributive lattice by means of ∨-irreducible elements [
10]. Karaçal and Sağıroğlu have introduced the concepts of the
T-prime element and
T-prime radical element and have studied their properties on complete lattices [
11].
This paper is organized as follows. In
Section 2, we recall some preliminaries regarding the lattice theory and triangular norms. In
Section 3, we define the concept of the
T-irreducible element and investigate some algebraic properties of the sets of
T-irreducible elements and
T-prime elements. We also give some illustrative examples and characterizations of the sets of
T-irreducible elements and
T-prime elements on direct product of lattices. In
Section 4, we point out that Theorem 2 in [
11] is not true in general. We give some appropriate counterexamples. We suggest a necessary and sufficient condition that makes Theorem 2 [
11] correct.
3. Irreducibles and Primes Based on a T-Norm
In this section, our goal is to present a proper definition for the concepts of the T-irreducible element and T-prime elements in bounded lattices and study their algebraic properties. We investigate some features of the sets of T-irreducible elements and T-prime elements. We show that lattice isomorphism, which is generated by a t-norm T, preserves T-irreducible elements and T-prime elements. We investigate the relationship between the sets of T-prime elements and co-atoms under some conditions. We give some characterizations for the sets of T-irreducible elements and T-prime elements on product lattices. We present some related properties of these sets. Throughout the section, we illustrate our points with some examples.
Definition 8. Let T be a t-norm on L and .
- (i)
The element p is called if and only if it satisfies ⇒ or for all .
- (ii)
The element p is called if and only if it satisfies ⇒ or for all .
The sets of all T-prime elements and all T-irreducible elements of L are denoted by and , respectively.
Proposition 2. Let T be a t-norm on L. Then, .
Proof. Let and , for . Then, . Since x is T-prime, we have or . We also know that . So, and . Therefore, or . Thus, . □
Example 2. Let and . Then, the function T on defined byis a t-norm on [15]. Then, we obtain that Proposition 3. Let be t-norms on L and . Then, .
Proof. Let and for . Then, . Since x is -prime, or . Hence, . □
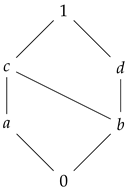
Example 3. Let be the lattice given with the following diagram:
Consider the t-norms on L defined by It is easy to see that . We have that , . So, we obtain that .
Remark 1. Since for any t-norm T on L, then . One can wonder whether or not holds, where and are two t-norms on L and . We give a negative answer to this question using a counterexample as follows:
Example 4. Let . Consider the t-norms , and , where is given by for all in L. We know that . We obtain that and . We see that it satisfies but it holds neither nor .
Let and be bounded lattices, be a lattice isomorphism, and T be a t-norm on . Then, it is straightforward that defined by is a t-norm on .
Theorem 1. Let and be bounded lattices, be a lattice isomorphism, and T be a t-norm on . Then, the following statements hold:
- (i)
If , then .
- (ii)
If , then .
Proof. - (i)
Let and . Then, we have . Since is a lattice isomorphism, we obtain that . Because , we have or . Thus, or and, hence, .
- (ii)
Let and . Therefore, . Since is one-to-one, then . Because , or . Hence, or . As a consequence, .
□
Proposition 4. Consider the t-norm on L. If , then it follows that .
Proof. Suppose that . Then, there exists an element x in . Since , then and hence there exists y in L such that . We obtain that but . Therefore, we obtain that , which is a contradiction. So, . □
Lemma 1. Let L be of finite length and . If we denote c as the single co-atom, then for any .
Proof. Let and in L. Since c is a co-atom, then and thus or . Let us denote . Assume that X is nonempty. Since L is of finite length, every chain in L is finite and so it has an upper bound. Thus, by Zorn ’s lemma, X has a maximal element. Let m be a maximal element of X. Then, for each and , we obtain that . If , then , which contradicts that m is a maximal element of X. Then, and hence m is a co-atom in L. Since , we obtain that . So, , which contradicts that . So, we obtain that . Then, it is required that , and it is equivalent to . □
Theorem 2. Let L be of finite length. Consider the t-norm on L. If , then .
Proof. - (i)
If , then we have that and . It is easily seen that . Therefore, .
- (ii)
If , then the set is nonempty, and let x be its element. If we denote c as the only element of , from Lemma 1 we have that . Since but , then . To show that , it follows from the fact that for the case or and, in such case, the second element is less than or equal to c, and it trivially satisfies the T-prime condition. The case and or is similar. Finally, if and , then , which also satisfies the T-prime condition.
□
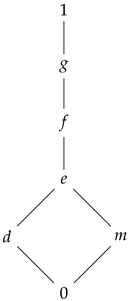
Example 5. Let be the lattice with the following diagram.
Consider the t-norm on L. It is easily seen that and . Consequently, we have that .
Proposition 5. Consider the t-norm on L. If , then .
Proof. Let .
- (i)
Let . Then, for , we obtain that , but . Hence, .
- (ii)
Let . Since , then there exist . Then, , but because . Thus, .
Consequently, . □
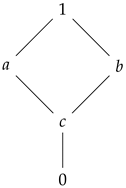
Example 6. Let be the lattice given by the following diagram:
It is easily seen that . Consider the t-norm on L. Then, but and . So, . Similarly, we get that . As a result, we obtain that .
The following example shows that the fact that does not imply that .
Example 7. Consider the lattice and the t-norm on L. Note that and hence .
- (i)
Let . Then, and hence . but .
Hence, .
- (ii)
Let . Then, .
- –
or .
- –
. Since but , we have that .
- (iii)
Let .
- –
. Since but , then .
- –
. We obtain that but . If , then we obtain that , which is a contradiction. Therefore, .
- (iv)
Let (.
- –
or .
- –
.
. But, . So, .
Therefore, .
So, . By the following, we characterize the sets of T-irreducible elements and T-prime elements on product lattices.
Theorem 3. Let and be two bounded lattices and be two t-norms on , respectively. Then, .
Proof. Suppose that . Hence, or . Therefore, and or and ).
Let . In this case, we have that
- (i)
and
or
- (ii)
and .
If
and
, then
. Hence
and
. Since
, we obtain that (
or
) and (
). Then,
or
. Hence,
. Similarly, if
and
, then we obtain that
. Therefore,
Assume that
and
. Then,
or
and
. Similarly, we have
or
and
. Let
and
.
That is a contradiction. Therefore, .
If , then and hence . So, we have and . Thus, and also or . Therefore, .
Similarly, if
, then it follows that
. Hence,
. Therefore,
Then, it follows from (1) and (2) that
□
Theorem 4. Let and be two bounded lattices and be two t-norms on , respectively. Then, .
Proof. Assume that . Then,
or . So, ( and ) or ( and ).
Let . In this case, we have that
- (i)
and
or
- (ii)
and .
If , then and . Since , then . Therefore, or . Consequently, .
Similarly, if and , we obtain that .
Therefore, we obtain that
Conversely, let and , . In this case, we obtain that or there exist in such that and . Similarly, we have that or there exist in such that and .
Assume that and . Then . Because , we obtain that or . So, we obtain that or , which is a contradiction. Consequently, it holds that or .
- (i)
If , then . Thus, . So, we have and . Thus, or . Hence, .
- (ii)
Let . Similarly, it is proved that .
As a consequence, we have that
Therefore, it follows from (3) and (4) that
□
Corollary 1. Let and be two bounded lattices and be two t-norms on , respectively. If and , then .
Proof. This is straightforward from Theorems 3 and 4. □
Corollary 2. Let and be two bounded lattices and be two t-norms on , respectively. Then, Proof. If or , then the proof is obvious. Assume that and .
Suppose that and is its element. Then, and . So, we obtain that ( and ) and also we have that ( and ) or ( and ). That is a contradiction. Therefore, . □
Corollary 3. Let and be two bounded lattices and be two t-norms on , respectively. Then, Proof. The proof follows similarly to the one given in Corollary 2. □
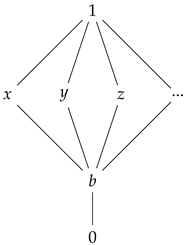
Example 8. Let be the lattice given by following Hasse diagram and consider the lattice given in Example 5.
Let us consider the t-norms by the followingon , respectively. It is easily seen that and . Hence, Example 9. Let be a chain given by the following diagram and consider the t-norm on :
Assume that is a chain given by following diagram and consider the t-norm on :
4. The Lattice
Karaçal and Sağıroğlu [
11] have constructed a lattice by using
T-prime elements in a complete lattice
L and they have suggested a new t-norm on the constructed lattice using Theorem 2 [
11]. In this section, we show that Theorem 2 in [
11] is false by giving some counterexamples. We present a necessary and sufficient condition for the mentioned theorem to be correct.
Definition 9 ([
11])
. Let T be a t-norm on a complete lattice L and . If the set is nonempty, then the infimum of this set is called the of x denoted by . Since the infimum of the empty set is equal to 1, in the case where , then . x is called a if . The set of all T-prime radical elements in L is denoted by . Clearly, . Proposition 6 ([
11])
. Let T be a t-norm on a complete lattice L. Then, for every . Proposition 7 ([
11])
. The set is a complete lattice. Proposition 8. Let be t-norms on a complete lattice L and . Then, is a -subsemilattice of .
Proof. First, we show that
. Let
be arbitrary. Then,
On the other side, since , then . This shows that . Therefore, .
From Proposition 7, we know that
and
are complete lattices (∧-subsemilattices of
L (Proposition 5, Remark 2, [
11])). The fact that infimums on
and
coincide implies that
for any
. It proves that
is a
-subsemilattice of
. □
The notation denotes the restriction of T to .
Theorem 5 (Theorem 2, [
11])
. is an infinitely ∪-distributive t-norm on . Authors in the proof of (Theorem 2, [11]) claimed the following:”… We have that for every by Proposition 6. Thus for …”
But, for any , we obtain that . Thus, unless , this need not imply . Now, we give the following counterexamples to show that Theorem 4.5 is really false.
Example 10. Consider the lattice given in Example 5 and define a t-norm T on L as follows [11]:Then, . Since , we have that T is not closed on . So, it is not a t-norm on . Example 11. Consider the lattice given in Example 3. Then,is a t-norm on L. It is easily seen that and .
. Hence, is not a t-norm on .
By the following, we provide a characterization for the statement in Theorem 5 (Theorem 2, [11]) to be true. Theorem 6. on is a t-norm if and only if .
Proof. Since is a complete lattice, by Proposition 7, for any , we have that and . Thus, if , then, for . Since T is associative, commutative, and monotone in L, it is clear that satisfies these properties in . Finally, using , it holds that is a t-norm on .
Assume that is a t-norm on . Thus, for , we have that . Then, we obtain that . So, it follows that . Therefore, and hence . □