An Interval Observer for a Class of Cyber–Physical Systems with Disturbance

Abstract

This paper investigates the problem of interval estimation for cyber–physical systems with unknown disturbance. In order to realize the interval estimation of cyber–physical systems, two technical methods are adopted. The first one requires the observer dynamic error system to be non-negative, and the second one relaxes this limitation by coordinate transformation. The sufficient conditions are established using both Lyapunov stability and positive system theory. Furthermore, according to the Schur complement, the linear matrix inequality is solved to determine the observer gains. Finally, the effectiveness and feasibility of the designed interval observer are verified by one numerical simulation.

1. Introduction

In the last two decades, there has been a great deal of research in observer design. These results lay a good foundation for the further study of the interval observer (IO), so the research of the IO has received extensive attention in recent years. Ref. [1] first introduced the concept of the IO, and the basic frame of the IO was given. Because there are always unknown but bounded perturbations and uncertainties in real systems, Refs. [2,3] studied two different classes of uncertain biological systems and designed the corresponding IO for each of them. The precondition for the IO to be effective is that the upper and lower error systems are both positive and uniformly bounded. In order to relax this condition, Ref. [4] first applied the coordinate transformation method to the interval estimation for time-varying systems and then [5] introduced this method for time-invariant systems. Under these methods, the design of the IO got more freedom. Since then, some researchers studied the IO design problem for nonlinear uncertain switched systems [6], singular systems [7] and impulse systems [8]. Ref. [9] provided an interval estimation method for discrete-time systems with uncertain inputs. Ref. [10] proposed IOs for nonlinear discrete-time systems. Ref. [11] designed a distributed interval observer for multiple Euler–Lagrange systems. In addition, there were other reports on interval observers, such as [12,13,14] and so on.

A cyber–physical system (CPS) is a typical complex system in an intelligent system. It closely integrates computing elements and physical processes to realize real-time interaction and control [15]. Among them, the main research hotspots of CPSs are state security estimation and state reconstruction under network attacks. In response to the issue of sparse sensor attacks in CPSs, Ref. [16] built a Luenberger switching observer for state estimation. Ref. [17] constructed a new observer to reduce the influence of unknown inputs by means of the gain method. Ref. [18] proposed an elastic attack detection estimator to complete security estimation and attack detection under both false data injection attacks and interference attacks. Ref. [19], based on the time differential equation and uncertainty hybrid time automaton, extended the CPS system model and established the uncertain CPS extended model. Ref. [20] provided an algorithm for building indeterminate finite-state sensors for CPSs, thus restoring the original state under attack. At present, there are few studies on the security estimation of CPSs with nonlinear term and disturbance. And the IO is an effective tool to study the state estimation method for uncertain systems with bounded disturbance. Therefore, applying the IO to such a CPS can effectively address the issue of security estimation.

Based on the above discussion, the problem of IO design for a CPS is investigated in this paper. We mainly use the monotone system method to formulate the framework of the IO; in addition, we employ the coordinate transformation method to address the situation where the error system is not cooperative. This paper is structured as follows: In Section 2, the relevant basic theory and CPS model framework are given. Section 3 gives the design method of the IO for the CPS. In Section 4, we conduct a simulation using MATLAB to illustrate the effectiveness of IO design. Section 5 is the summary of the article.

Notaion: For a matrix $x=\left[x_{ij}\right]\in R^{m\times n}$, $x\ge 0$ means $x_{ij}\ge 0$ for all $i=1,\cdots ,m$ and $j=1,\cdots ,n$. In the case of a matrix $\mathbb{M}\in R^{m\times n}$, ${\mathbb{M}}^{+}$ and ${\mathbb{M}}^{-}$ are defined as ${\mathbb{M}}^{+}=max\left\{\mathbb{M},0\right\},{\mathbb{M}}^{-}=max\left\{-\mathbb{M},0\right\}$ and ${\mathbb{M}}^{+}={\mathbb{M}}^{-}+\mathbb{M}$. Moreover, the matrix $\mathbb{N}\in R^{n\times n}$ is positive (negative) definite and can be expressed as $\mathbb{N}>0(<0)$.

2. Preliminaries

In this paper, a class of CPS models with disturbance is considered as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{x}_{k+1}=A{x}_k+B{u}_k+\Phi \left(x_k\right)+D{\varpi }_k,\hfill \\ y_k=C{x}_k+E{ϵ}_k,\hfill \end{array}\end{array}\right.$$

(1)

where $x_k\in {\mathbb{R}}^{n_x}$ and $y_k\in {\mathbb{R}}^{n_y}$ are the state and output, and $u_k\in {\mathbb{R}}^{n_u}$ denotes the control input. ${\varpi }_k\in {\mathbb{R}}^{n_{\varpi }}$ and ${ϵ}_k\in {\mathbb{R}}^{n_{ϵ}}$ are the unknown process noise and measurement error, and $\Phi \left(x_k\right)\in {\mathbb{R}}^{n_x}$ is a nonlinear function. $A\in {\mathbb{R}}^{n_x\times n_x}$, $B\in {\mathbb{R}}^{n_x\times n_u}$, $C\in {\mathbb{R}}^{n_y\times n_x}$, $D\in {\mathbb{R}}^{n_x\times n_{\varpi }}$ and $E\in {\mathbb{R}}^{n_y\times n_{ϵ}}$ are given constant matrices.

Assumption 1.

The disturbance and measurement error in system (1) are bounded, i.e.,

$${\varpi }_k^{-}\le {\varpi }_k\le {\varpi }_k^{+},{ϵ}_k^{-}\le {ϵ}_k\le {ϵ}_k^{+},$$

(2)

where ${\varpi }_k^{-}$, ${\varpi }_k^{+}$, ${ϵ}_k^{-}$ and ${ϵ}_k^{+}$ are constant vectors.

Assumption 2.

For a function $\Phi :{\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$, there exists a Lipschitz constant α if for any $(x,y_a),(x,y_b)$ of its domain Ω there exists α, such that the following holds:

$$\Vert \Phi (x,y_a)-\Phi (x,y_b)\Vert \le \alpha \Vert y_a-y_b\Vert .$$

(3)

Then, $\Phi (x,y)$ satisfies the Lipschitz continuity condition.

Lemma 1

([21]). If the Lipschitz function $\Phi \left(x\right)$ is globally differentiable, then it can be decomposed into the difference of two globally differentiable Lipschitz functions ${\varphi }_1\left(x\right)$ and ${\varphi }_2\left(x\right)$, and they are two increasing functions with respect to x, such that:

$$\Phi \left(x\right)={\varphi }_1\left(x\right)-{\varphi }_2\left(x\right).$$

(4)

Lemma 2

([21]). For any global Lipschitz function $\Phi \left(x\right)$, there is a global differentiable Lipschitz function $\overline{\Phi }(x_i,x_j)$ such that

$$\begin{array}{cc}\hfill \overline{\Phi }(x,x)& =\Phi \left(x\right),\hfill \\ \hfill {\displaystyle \frac{\partial \overline{\Phi }}{\partial x_i}\ge 0}& {\displaystyle and\frac{\partial \overline{\Phi }}{\partial x_j}\le 0.}\hfill \end{array}$$

From Lemmas 1 and 2, we have upper and lower bound information for the nonlinear Lipschitz function $\Phi (x,x)$:

$$\overline{\Phi }(x^{-},x^{+})\le \Phi (x,x)\le \overline{\Phi }(x^{+},x^{-}).$$

(5)

Lemma 3

([21]). For the global Lipschitz function $\Phi \left(x\right)$ and the associate function $\overline{\Phi }\left(x\right)$ defined in Lemma 2, the variable x satisfies the bounded condition: $x^{-}\le x\le x^{+}$. If ${\displaystyle \frac{\partial \overline{\Phi }}{\partial x}}$ is bounded, then there are matrices ${\psi }_j(j=1,2,3,4)$ such that

$$\left\{\begin{array}{c}\begin{array}{c}\overline{\Phi }(x^{+},x^{-})-\Phi (x,x)\le {\psi }_1{e}^{+}+{\psi }_2{e}^{-},\hfill \\ \overline{\Phi }(x^{-},x^{+})-\Phi (x,x)\le {\psi }_3{e}^{+}+{\psi }_4{e}^{-},\hfill \end{array}\end{array}\right.$$

(6)

where ${\psi }_1$, ${\psi }_2$, ${\psi }_3$ and ${\psi }_4$ are known matrices.

Lemma 4

([22]). There exists a vector g such that $g^{-}\le g\le g^{+}$, for any matrix $N\in {\mathbb{R}}^{n\times n}$, and then:

$$N^{+}{g}^{-}-N^{-}{g}^{+}\le Ng\le N^{+}{g}^{+}-N^{-}{g}^{-}.$$

(7)

Lemma 5

([23]). The following systems

$$\left\{\begin{array}{c}\begin{array}{c}{x}_{k+1}=A{x}_k+\Phi \left(x_k\right),\hfill \\ x_0\ge 0,\hfill \end{array}\end{array}\right.$$

where $A\in {\mathbb{R}}^{n\times n}$ is a non-negative matrix, and the nonlinear function $\Phi \left(x_k\right)\ge 0$. Then, for all $k\ge 0$, we have $x_k\ge 0$.

Lemma 6

([24]). Given a positive constant α and two arbitrary matrices $T,N\in {\mathbb{R}}^{n\times n}$, the matrix $P\ge 0$ and the following inequality holds:

$$T^{T}N+N^{T}T\le \frac{1}{\alpha }{T}^{T}PT+\alpha N^T{P}^{-1}N.$$

(8)

Definition 1.

If there exist positive constants r and b, for the following error system

$$e_{k+1}=f(e_k,u_k,k),$$

with initial conditions $\left|\right|e_0\left|\right|\le r$, and for all $k\ge 0$, we have $\left|\right|e_k\left|\right|\le b$, and then the error system is called uniformly ultimately bounded (UUB).

3. Main Results

3.1. Design of the IO

Based on Section 2, we design the following IO for system (1):

$$\left\{\begin{array}{c}\begin{array}{c}\hfill x_{k+1}^{+}=A{x}_k^{+}+B{u}_k+\overline{\Phi }(x_k^{+},x_k^{-})+{\xi }^{+}+LC(x_k-x_k^{+})+L^{+}{k}^{+},\\ \hfill x_{k+1}^{-}=A{x}_k^{-}+B{u}_k+\overline{\Phi }(x_k^{-},x_k^{+})+{\xi }^{-}+LC(x_k-x_k^{-})+L^{+}{k}^{-},\end{array}\end{array}\right.$$

(9)

where $x_k^{+}$ and $x_k^{-}$ are the estimated upper and lower bounds of the state $x_k$. ${\xi }^{+}=D^{+}{\varpi }^{+}-D^{-}{\varpi }^{-}$, ${\xi }^{-}=D^{+}{\varpi }^{-}-D^{-}{\varpi }^{+}$, $k^{+}=Eϵ-(E^{+}{ϵ}^{-}-E^{-}{ϵ}^{+})$ and $k^{-}=Eϵ-(E^{+}{ϵ}^{+}-E^{-}{ϵ}^{-})$. The specific calculation steps of gain L will be given in the sequel.

Theorem 1.

Suppose that $A-LC$ is non-negative, and the initial condition of $x_k$ satisfies $x_0^{-}\le x_0\le x_0^{+}$, then it holds that

$$x_k^{-}\le x_k\le x_k^{+}.$$

(10)

Proof. 

Denote that $e_x^{+}=x_k^{+}-x_k$ and $e_x^{-}=x_k-x_k^{-}$, and then one obtains the error system:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill e_{k+1}^{+}=& (A-LC)e_k^{+}+\overline{\Phi }(x_k^{+},x_k^{-})-\Phi \left(x_k\right)+e_{\varpi }^{+}+e_{ϵ}^{+},\hfill \\ \hfill e_{k+1}^{-}=& (A-LC)e_k^{-}+\Phi \left(x_k\right)-\overline{\Phi }(x_k^{-},x_k^{+})+e_{\varpi }^{-}+e_{ϵ}^{-},\hfill \end{array}\end{array}\right.$$

(11)

where $e_{\varpi }^{+}={\xi }^{+}-D\varpi$, $e_{\varpi }^{-}=D\varpi -{\xi }^{-}$, $e_{ϵ}^{+}=L^{+}{k}^{+}$ and $e_{ϵ}^{-}=-L^{+}{k}^{-}$. In view of Lemma 4, then $e_{\varpi }^{+}\ge 0$, $e_{\varpi }^{-}\ge 0$,$e_{ϵ}^{+}\ge 0$ and $e_{ϵ}^{-}\ge 0$. Also, according to Lemma 5, we can conclude that

$$\begin{array}{c}\hfill x_k^{-}\le x_k\le x_k^{+},k\ge 0.\end{array}$$

□

Continuing Theorem 1, it is assumed that $A-LC$ is non-negative. Denote ${\delta }_k={\left[\begin{array}{cc}{e_k^{+}}^T& {e_k^{-}}^T\end{array}\right]}^T$, and according to (11), the error system has the following form:

$$\begin{array}{cc}\hfill {\delta }_{k+1}=& H{\delta }_k+\mho +\overline{\varpi }+\overline{ϵ},\hfill \end{array}$$

(12)

where

$$H=\tilde{A}-\tilde{L}\tilde{C},\tilde{A}=diag\{A,A\},$$

$$\tilde{L}=diag\{L,L\},\tilde{C}=diag\{C,C\},$$

$$\mho =\left[\begin{array}{c}\overline{\Phi }(x_k^{+},x_k^{-})-\Phi \left(x_k\right)\\ \Phi \left(x_k\right)-\overline{\Phi }(x_k^{-},x_k^{+})\end{array}\right],$$

$$\overline{\varpi }=\left[\begin{array}{c}{e}_{\varpi }^{+}\\ e_{\varpi }^{-}\end{array}\right]and\overline{ϵ}=\left[\begin{array}{c}{e}_{ϵ}^{+}\\ e_{ϵ}^{-}\end{array}\right].$$

Theorem 2.

Given a set of constants ${\sigma }_i>0(i=1,2,...,6)$ and λ satisfy $0\le \theta \le 1$. Suppose that both Assumptions 1 and 2 hold. If there exists $P>0$ such that

$$\begin{array}{cc}\hfill & \left[\begin{array}{ccc}(\theta -1)P& \sqrt{{\Xi }_1}{H}^T& \sqrt{{\Xi }_2}{\psi }^T\\ \ast & -P^{-1}& 0\\ \ast & \ast & -P^{-1}\end{array}\right]<0,\hfill \end{array}$$

(13)

where

$${\Xi }_1=1+{\sigma }_1+{\sigma }_2+{\sigma }_3,{\Xi }_2=1+\frac{1}{{\sigma }_1}+{\sigma }_4+{\sigma }_5$$

and

$$\psi =\left[\begin{array}{cc}{\psi }_1& {\psi }_2\\ {\psi }_3& {\psi }_4\end{array}\right].$$

Then, system (9) is UUB, i.e., the error system is eventually bounded upper and lower.

Proof. 

Choosing the Lyapunov function $V_k={\delta }_k^{T}P{\delta }_k$, then we derive from $V_{k+1}$ that

$$\begin{array}{cc}\hfill V_{k+1}=& {[H{\delta }_k+\mho +\overline{\varpi }+\overline{ϵ}]}^{T}P[H{\delta }_k+\mho +\overline{\varpi }+\overline{ϵ}]\hfill \\ \hfill =& {\left(H{\delta }_k\right)}^{T}PH{\delta }_k+{\left(H{\delta }_k\right)}^{T}P\mho +{\left(H{\delta }_k\right)}^{T}P\overline{\varpi }+{\left(H{\delta }_k\right)}^{T}P\overline{ϵ}\hfill \\ \hfill & +{(\mho )}^{T}PH\delta +{\left(\overline{\varpi }\right)}^{T}PH\delta +{\left(\overline{ϵ}\right)}^{T}PH\delta +{(\mho )}^{T}P\overline{\varpi }\hfill \\ \hfill & +{\left(\overline{\varpi }\right)}^{T}P\mho +{(\mho )}^{T}P\overline{ϵ}+{\left(\overline{ϵ}\right)}^{T}P\mho +{\left(\overline{\varpi }\right)}^{T}P\overline{ϵ}+{\left(\overline{ϵ}\right)}^{T}P\overline{\varpi }\hfill \\ \hfill & +{(\mho )}^{T}P\mho +{\left(\overline{\varpi }\right)}^{T}P\overline{\varpi }+{\left(\overline{ϵ}\right)}^{T}P\overline{ϵ}.\hfill \end{array}$$

(14)

Define that

$$\begin{array}{cc}\hfill M_1\left(k\right)& ={\left(H{\delta }_k\right)}^{T}P\mho ,M_2\left(k\right)={\left(H{\delta }_k\right)}^{T}P\overline{\varpi },\hfill \\ \hfill M_3\left(k\right)& ={\left(H{\delta }_k\right)}^{T}P\overline{ϵ},M_4\left(k\right)={(\mho )}^{T}P\overline{\varpi },\hfill \\ \hfill M_5\left(k\right)& ={(\mho )}^{T}P\overline{ϵ},M_6\left(k\right)={\left(\overline{\varpi }\right)}^{T}P\overline{ϵ}.\hfill \end{array}$$

(15)

It is derived from Lemma 6 that

$$\begin{array}{cc}\hfill & M_1\left(k\right)+M_1^T\left(k\right)\le {\sigma }_1{\left(G{\delta }_k\right)}^{T}PH{\delta }_k+\frac{1}{{\sigma }_1}{(\mho )}^{T}P\mho ,\hfill \\ \hfill & M_2\left(k\right)+M_2^T\left(k\right)\le {\sigma }_2{\left(H{\delta }_k\right)}^{T}PH{\delta }_k+\frac{1}{{\sigma }_2}{\left(\overline{\varpi }\right)}^{T}P\overline{\varpi },\hfill \\ \hfill & M_3\left(k\right)+M_3^T\left(k\right)\le {\sigma }_3{\left(H{\delta }_k\right)}^{T}PH{\delta }_k+\frac{1}{{\sigma }_3}{\left(\overline{ϵ}\right)}^{T}P\overline{ϵ},\hfill \\ \hfill & M_4\left(k\right)+M_4^T\left(k\right)\le {\sigma }_4{\left(\check{\mho }\right)}^{T}P\check{\mho }+\frac{1}{{\sigma }_4}{\left(\overline{\varpi }\right)}^{T}P\overline{\varpi },\hfill \\ \hfill & M_5\left(k\right)+M_5^T\left(k\right)\le {\sigma }_5{(\mho )}^{T}P\mho +\frac{1}{{\sigma }_5}{\left(\overline{ϵ}\right)}^{T}P\overline{ϵ},\hfill \\ \hfill & M_6\left(k\right)+M_6^T\left(k\right)\le {\sigma }_6{\left(\overline{\varpi }\right)}^{T}P\overline{\varpi }+\frac{1}{{\sigma }_6}{\left(\overline{ϵ}\right)}^{T}P\overline{ϵ}.\hfill \end{array}$$

(16)

Thus,

$$\begin{array}{cc}\hfill \Delta V_k=& V_{k+1}-V_k\hfill \\ \hfill \le & (1+{\sigma }_1+{\sigma }_2+{\sigma }_3){\left(H{\delta }_k\right)}^{T}PH{\delta }_k\hfill \\ \hfill & +(1+\frac{1}{{\sigma }_1}+{\sigma }_4+{\sigma }_5){(\mho )}^{T}P\mho +(1+\frac{1}{{\sigma }_2}+\frac{1}{{\sigma }_4}+{\sigma }_6){\left(\overline{\varpi }\right)}^{T}P\overline{\varpi }\hfill \\ \hfill & +(1+\frac{1}{{\sigma }_3}+\frac{1}{{\sigma }_5}+\frac{1}{{\sigma }_6}){\left(\overline{ϵ}\right)}^{T}P\overline{ϵ}-{\delta }_k^{T}P{\delta }_k.\hfill \end{array}$$

(17)

From Lemma 3, we can deduce that

$${\mho }^{T}P\mho \le {\delta }_k^T{\psi }^{T}P\psi {\delta }_k.$$

(18)

Substituting (18) into (17), then

$$\begin{array}{cc}\hfill \Delta V_k\le & {\delta }_k^T[(1+{\sigma }_1+{\sigma }_2+{\sigma }_3)H^{T}PH+(1+\frac{1}{{\sigma }_1}+{\sigma }_4+{\sigma }_5){\psi }^{T}P\psi -P]{\delta }_k\hfill \\ \hfill & +(1+\frac{1}{{\sigma }_2}+\frac{1}{{\sigma }_4}+{\sigma }_6){\left(\overline{\varpi }\right)}^{T}P\overline{\varpi }+(1+\frac{1}{{\sigma }_3}+\frac{1}{{\sigma }_5}+\frac{1}{{\sigma }_6}){\left(\overline{ϵ}\right)}^{T}P\overline{ϵ}.\hfill \end{array}$$

(19)

Define that

$$\begin{array}{c}\hfill \Delta \left(k\right)=(1+\frac{1}{{\sigma }_2}+\frac{1}{{\sigma }_4}+{\sigma }_6){\left(\overline{\varpi }\right)}^{T}P\overline{\varpi }+(1+\frac{1}{{\sigma }_3}+\frac{1}{{\sigma }_5}+\frac{1}{{\sigma }_6}){\left(\overline{ϵ}\right)}^{T}P\overline{ϵ}.\end{array}$$

(20)

Therefore, we can obtain

$$\begin{array}{cc}\hfill \Delta V_k& \le {\delta }_k^T[(1+{\sigma }_1+{\sigma }_2+{\sigma }_3)H^{T}PH+(1+\frac{1}{{\sigma }_1}+{\sigma }_4+{\sigma }_5){\psi }^{T}P\psi -P]{\delta }_k+\Delta \left(k\right)\hfill \\ \hfill & ={\delta }_k^T(-\lambda P){\delta }_k+\Delta \left(k\right)\hfill \\ \hfill & =-\lambda {\delta }_k^{T}P{\delta }_k+\Delta \left(k\right),\hfill \end{array}$$

(21)

then

$$V_{k+1}-V_k\le -\lambda V_k+\Delta \left(k\right).$$

(22)

According to Assumption 1, letting $\Delta \ge \Delta \left(k\right)$, by iteration, one can obtain

$$\begin{array}{cc}\hfill V_k\le & (1-\lambda )V_{k-1}+\Delta \hfill \\ \hfill \le & {(1-\lambda )}^{k-1}{V}_0+\sum _{i=1}^n{(1-\lambda )}^{i-1}\Delta ,\hfill \end{array}$$

(23)

where $\lambda$ satisfies $0\le \lambda \le 1$, and according to Definition 1, then system (9) is UUB, and system (9) is the interval observer of system (1). □

3.2. IO Design by Coordinates Transformation Method

Under the condition that $A-LC$ is not non-negative, to facilitate the design of the IO, we can adopt the method of coordinate transformation. Let $z_k=M{x}_k$, where $M\in {\mathbb{R}}^{n\times n}$ is invertible, and system (1) can be equivalent to:

$$\left\{\begin{array}{c}\begin{array}{c}{z}_{k+1}=\overline{A}{z}_k+\overline{B}{u}_k+M\overline{\Phi }\left(M^{-1}{z}_k\right)+\overline{D}{\varpi }_k,\hfill \\ y=\overline{C}{z}_k+\overline{E}{ϵ}_k,\hfill \end{array}\end{array}\right.$$

(24)

where $\overline{A}=MA{M}^{-1}$, $\overline{B}=MB$, $\overline{C}=C{M}^{-1}$, $\overline{D}=MD$ and $\overline{E}=E$, and the transformation M is chosen such that $M(\overline{A}-L\overline{C})M^{-1}$ satisfies the non-negative.

Remark 1.

The transformation matrix M can be constructed according to the Sylvester equation, and based on the transformation of the Schur form, so as to obtain T through the inverse substitution. The specific selection process can be referred to in [5].

To facilitate the estimation of the bounds for $\overline{\Phi }\left(x\right)$ by denoting that

$$\left\{\begin{array}{c}\begin{array}{c}\phi (z_k^{+},z_k^{-})=\overline{\Phi }(M_a^{+}{z}_k^{+}-M_a^{-}{z}_k^{-},M_a^{+}{z}_k^{-}-M_a^{-}{z}_k^{+}),\hfill \\ \phi (z_k^{-},z_k^{+})=\overline{\Phi }(M_a^{+}{z}_k^{-}-M_a^{-}{z}_k^{+},M_a^{+}{z}_k^{+}-M_a^{-}{z}_k^{-}),\hfill \end{array}\end{array}\right.$$

(25)

where $z_k^{+}$ and $z_k^{-}$ are defined as the upper and lower bound estimates of the designed IO for $z_k$, and $M_a=M^{-1}$.

According to Lemma 4, the nonlinear function $\overline{\Phi }\left(x\right)$ can satisfy the following inequality

$$\begin{array}{c}\hfill M^{+}\phi (z_k^{-},z_k^{+})-M^{-}\phi (z_k^{+},z_k^{-})\le M\overline{\Phi }\left(M^{-1}{z}_k\right)\le M^{+}\phi (z_k^{+},z_k^{-})-M^{-}\phi (z_k^{-},z_k^{+})\end{array}$$

and define that

$$\begin{array}{cc}\hfill {\overline{\Phi }}_z(z_k^{-},z_k^{+})& =M^{+}\phi (z_k^{-},z_k^{+})-M^{-}\phi (z_k^{+},z_k^{-})\hfill \\ \hfill {\overline{\Phi }}_z(z_k^{+},z_k^{-})& =M^{+}\phi (z_k^{+},z_k^{-})-M^{-}\phi (z_k^{-},z_k^{+}).\hfill \end{array}$$

An IO based on the coordinate transformation of system (12) is given as:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill z_{k+1}^{+}=& \overline{A}{z}_k^{+}+\overline{B}{u}_k+{\overline{\Phi }}_z(z_k^{+},z_k^{-})+{\pi }^{+}+L\overline{C}(z_k-z_k^{+})+L^{+}{h}^{+},\hfill \\ \hfill z_{k+1}^{-}=& \overline{A}{z}_k^{-}+\overline{B}{u}_k+{\overline{\Phi }}_z(z_k^{-},z_k^{+})+{\pi }^{-}+L\overline{C}(z_k-z_k^{-})+L^{+}{h}^{-},\hfill \end{array}\end{array}\right.$$

(26)

where

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\pi }^{+}=& {\overline{D}}^{+}{\varpi }^{+}-{\overline{D}}^{-}{\varpi }^{-},\hfill \\ \hfill {\pi }^{-}=& {\overline{D}}^{+}{\varpi }^{-}-{\overline{D}}^{-}{\varpi }^{+},\hfill \end{array}\end{array}\right.$$

(27)

and

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill h^{+}=& Eϵ-({\overline{E}}^{+}{ϵ}^{-}-{\overline{E}}^{-}{ϵ}^{+}),\hfill \\ \hfill h^{-}=& Eϵ-({\overline{E}}^{+}{ϵ}^{+}-{\overline{E}}^{-}{ϵ}^{-}).\hfill \end{array}\end{array}\right.$$

(28)

Remark 2.

Because the transformation matrix T is invertible and $x_k$ is known to satisfy the initial condition (30), and $x_0$ satisfies $x_0^{-}\le x_0\le x_0^{+}$, we have

$$z_0^{-}\le z_0\le z_0^{+},$$

(29)

where

$$\left\{\begin{array}{c}\begin{array}{c}{z}_0^{+}=M^{+}{x}_0^{-}-M^{-}{x}_0^{+},\hfill \\ z_0^{-}=M^{+}{x}_0^{+}-M^{-}{x}_0^{-}.\hfill \end{array}\end{array}\right.$$

(30)

Remark 3.

The observed values of the system after coordinate transformation meet the requirements of the original system:

$$\left\{\begin{array}{c}\begin{array}{c}{x}_k^{+}=M^{+}{z}_k^{+}-M^{-}{z}_k^{+},\hfill \\ x_k^{-}=M^{+}{z}_k^{-}-M^{-}{z}_k^{+}.\hfill \end{array}\end{array}\right.$$

(31)

The specific proof process can be referred to in [4].

Theorem 3.

If $A-LC$ is not non-negative, we can find a matrix M such that $\overline{A}-L\overline{C}$ in error system (33) is non-negative, and the initial condition of $x_k$ satisfies $x_0^{-}\le x_0\le x_0^{+}$, and then it holds that

$$z_k^{-}\le z_k\le z_k^{+}.$$

(32)

Define that ${\widehat{e}}_k^{+}=z_k^{+}-z_k$ and ${\widehat{e}}_k^{-}=z_k-z_k^{-}$. Therefore, the error system can be derived as:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\widehat{e}}_{k+1}^{+}=& (\overline{A}-L\overline{C}){\widehat{e}}_k^{+}+{\overline{\Phi }}_z(z_k^{+},z_k^{-})-M\overline{\Phi }\left(M^{-1}{z}_k\right)+e_{\overline{\varpi }}^{+}+e_{\overline{ϵ}}^{+},\hfill \\ \hfill {\widehat{e}}_{k+1}^{-}=& (\overline{A}-L\overline{C}){\widehat{e}}_k^{-}+{\overline{\Phi }}_z(z_k^{+},z_k^{-})-M\overline{\Phi }\left(M^{-1}{z}_k\right)+e_{\overline{\varpi }}^{-}+e_{\overline{ϵ}}^{-},\hfill \end{array}\end{array}\right.$$

(33)

where $e_{\overline{\varpi }}^{+}={\pi }^{+}-\overline{D}\varpi$, $e_{\overline{\varpi }}^{-}=\overline{D}\varpi -{\pi }^{-}$, $e_{\overline{ϵ}}^{+}=L^{+}{h}^{+}$ and $e_{\overline{ϵ}}^{-}=-L^{+}{h}^{-}$.

In view of Lemma 4, then $e_{\overline{\varpi }}^{+}\ge 0$, $e_{\overline{\varpi }}^{-}\ge 0$,$e_{\overline{ϵ}}^{+}\ge 0$ and $e_{\overline{ϵ}}^{-}\ge 0$. The initial condition of $x_k$ satisfies $x_0^{-}\le x_0\le x_0^{+}$, and according to Remark 2, we can obtain that the initial condition of $z_k$ satisfies $z_0^{-}\le z_0\le z_0^{+}$. Finally, according to Lemma 5, we can conclude that

$$\begin{array}{c}\hfill z_k^{-}\le z_k\le z_k^{+},k\ge 0.\end{array}$$

The proof of Theorem 3 has finished.

Theorem 3 only provides the IO frame for system (1). In order to make the error system UUB, i.e., system (26) becomes an IO of system (24), the sufficient conditions and specific proof are given below.

Denote ${\zeta }_k={\left[\begin{array}{cc}{\widehat{e}}_k^{+T}& {\widehat{e}}_k^{-T}\end{array}\right]}^T$ according to (33), and the error system has the following form:

$$\begin{array}{cc}\hfill {\zeta }_{k+1}=& H{\zeta }_k+\check{\mho }+\check{\varpi }+\check{ϵ},\hfill \end{array}$$

(34)

where

$$H=\tilde{A}-\tilde{L}\tilde{C},\tilde{A}=diag\{\overline{A},\overline{A}\},$$

$$\tilde{L}=diag\{L,L\},\tilde{C}=diag\{\overline{C},\overline{C}\},$$

$$\check{\mho }=\left[\begin{array}{c}{\overline{\Phi }}_z(z_k^{+},z_k^{-})-M\overline{\Phi }\left(M^{-1}{z}_k\right)\\ M\overline{\Phi }\left(M^{-1}{z}_k\right)-{\overline{\Phi }}_z(z_k^{-},z_k^{+})\end{array}\right],$$

$$\check{\varpi }=\left[\begin{array}{c}{\overline{D}}^{+}{\varpi }^{+}-{\overline{D}}^{-}{\varpi }^{-}-\overline{D}\varpi \\ \overline{D}\varpi -{\overline{D}}^{+}{\varpi }^{-}+{\overline{D}}^{-}{\varpi }^{+}\end{array}\right]and\check{ϵ}=\left[\begin{array}{c}{L}^{+}({\overline{E}}^{+}{ϵ}^{+}-{\overline{E}}^{-}{ϵ}^{-})-L^{+}\overline{E}ϵ\\ L^{+}\overline{E}ϵ-L^{+}({\overline{E}}^{+}{ϵ}^{-}-{\overline{E}}^{-}{ϵ}^{+})\end{array}\right].$$

Theorem 4.

Given a set of constants ${\gamma }_i>0(i=1,2,\dots ,6)$ and λ satisfy $0\le \lambda \le 1$. Suppose that both Assumptions 1 and 2 hold. If there exists $P>0$ such that

$$\begin{array}{cc}\hfill & \left[\begin{array}{ccc}(\lambda -1)P& \sqrt{{\Sigma }_1}{H}^T& \sqrt{{\Sigma }_2}{\psi }^T\\ \ast & -P^{-1}& 0\\ \ast & \ast & -P^{-1}\end{array}\right]<0,\hfill \end{array}$$

(35)

where

$${\Sigma }_1=1+{\gamma }_1+{\gamma }_2+{\gamma }_3,{\Sigma }_2=1+\frac{1}{{\gamma }_1}+{\gamma }_4+{\gamma }_5$$

and

$$\psi =\left[\begin{array}{cc}{\psi }_1& {\psi }_2\\ {\psi }_3& {\psi }_4\end{array}\right].$$

Then, system (26) is UUB, i.e., the error system is eventually upper and lower bounded.

Proof. 

Choosing the Lyapunov function $V_k={\zeta }_k^{T}P{\zeta }_k$, then we derive from $V_{k+1}$ that

$$\begin{array}{cc}\hfill V_{k+1}=& {[H{\zeta }_k+\check{\mho }+\check{\varpi }+\check{ϵ}]}^{T}P[H{\zeta }_k+\check{\mho }+\check{\varpi }+\check{ϵ}]\hfill \\ \hfill =& {\left(H{\zeta }_k\right)}^{T}PH{\zeta }_k+{\left(H{\zeta }_k\right)}^{T}P\check{\mho }+{\left(H{\zeta }_k\right)}^{T}P\check{\varpi }+{\left(H{\zeta }_k\right)}^{T}P\check{ϵ}\hfill \\ \hfill & +{\left(\check{\mho }\right)}^{T}PH\zeta +{\left(\check{\varpi }\right)}^{T}PH\zeta +{\left(\check{ϵ}\right)}^{T}PH\zeta +{\left(\check{\mho }\right)}^{T}P\check{\varpi }\hfill \\ \hfill & +{\left(\check{\varpi }\right)}^{T}P\check{\mho }+{\left(\check{\mho }\right)}^{T}P\check{ϵ}+{\left(\check{ϵ}\right)}^{T}P\check{\mho }+{\left(\check{\varpi }\right)}^{T}P\check{ϵ}+{\left(\check{ϵ}\right)}^{T}P\check{\varpi }\hfill \\ \hfill & +{\left(\check{\mho }\right)}^{T}P\check{\mho }+{\left(\check{\varpi }\right)}^{T}P\check{\varpi }+{\left(\check{ϵ}\right)}^{T}P\check{ϵ}.\hfill \end{array}$$

(36)

Define that

$$\begin{array}{cc}\hfill M_1\left(k\right)& ={\left(H{\zeta }_k\right)}^{T}P\check{\mho },M_2\left(k\right)={\left(H{\zeta }_k\right)}^{T}P\check{\varpi },\hfill \\ \hfill M_3\left(k\right)& ={\left(H{\zeta }_k\right)}^{T}P\check{ϵ},M_4\left(k\right)={\left(\check{\mho }\right)}^{T}P\check{\varpi },\hfill \\ \hfill M_5\left(k\right)& ={\left(\check{\mho }\right)}^{T}P\check{ϵ},M_6\left(k\right)={\left(\check{\varpi }\right)}^{T}P\check{ϵ}.\hfill \end{array}$$

(37)

It is derived from Lemma 6 that

$$\begin{array}{cc}\hfill & M_1\left(k\right)+M_1^T\left(k\right)\le {\gamma }_1{\left(G{\zeta }_k\right)}^{T}PH{\zeta }_k+\frac{1}{{\gamma }_1}{\left(\check{\mho }\right)}^{T}P\check{\mho },\hfill \\ \hfill & M_2\left(k\right)+M_2^T\left(k\right)\le {\gamma }_2{\left(H{\zeta }_k\right)}^{T}PH{\zeta }_k+\frac{1}{{\gamma }_2}{\left(\check{\varpi }\right)}^{T}P\check{\varpi },\hfill \\ \hfill & M_3\left(k\right)+M_3^T\left(k\right)\le {\gamma }_3{\left(H{\zeta }_k\right)}^{T}PH{\zeta }_k+\frac{1}{{\gamma }_3}{\left(\check{ϵ}\right)}^{T}P\check{ϵ},\hfill \\ \hfill & M_4\left(k\right)+M_4^T\left(k\right)\le {\gamma }_4{\left(\check{\mho }\right)}^{T}P\check{\mho }+\frac{1}{{\gamma }_4}{\left(\check{\varpi }\right)}^{T}P\check{\varpi },\hfill \\ \hfill & M_5\left(k\right)+M_5^T\left(k\right)\le {\gamma }_5{\left(\check{\mho }\right)}^{T}P\check{\mho }+\frac{1}{{\gamma }_5}{\left(\check{ϵ}\right)}^{T}P\check{ϵ},\hfill \\ \hfill & M_6\left(k\right)+M_6^T\left(k\right)\le {\gamma }_6{\left(\check{\varpi }\right)}^{T}P\check{\varpi }+\frac{1}{{\gamma }_6}{\left(\check{ϵ}\right)}^{T}P\check{ϵ}.\hfill \end{array}$$

(38)

Thus,

$$\begin{array}{cc}\hfill \Delta V_k=& V_{k+1}-V_k\hfill \\ \hfill \le & (1+{\gamma }_1+{\gamma }_2+{\gamma }_3){\left(H{\zeta }_k\right)}^{T}PH{\zeta }_k\hfill \\ \hfill & +(1+\frac{1}{{\gamma }_1}+{\gamma }_4+{\gamma }_5){\left(\check{\mho }\right)}^{T}P\check{\mho }+(1+\frac{1}{{\gamma }_2}+\frac{1}{{\gamma }_4}+{\gamma }_6){\left(\check{\varpi }\right)}^{T}P\check{\varpi }\hfill \\ \hfill & +(1+\frac{1}{{\gamma }_3}+\frac{1}{{\gamma }_5}+\frac{1}{{\gamma }_6}){\left(\check{ϵ}\right)}^{T}P\check{ϵ}-{\zeta }_k^{T}P{\zeta }_k.\hfill \end{array}$$

(39)

From Lemma 3, we can deduce that

$${\check{\mho }}^{T}P\check{\mho }\le {\zeta }_k^T{\psi }^{T}P\psi {\zeta }_k.$$

(40)

Substituting (40) into (39), then

$$\begin{array}{cc}\hfill \Delta V_k\le & {\zeta }_k^T[(1+{\gamma }_1+{\gamma }_2+{\gamma }_3)H^{T}PH+(1+\frac{1}{{\gamma }_1}+{\gamma }_4+{\gamma }_5){\psi }^{T}P\psi -P]{\zeta }_k\hfill \\ \hfill & +(1+\frac{1}{{\gamma }_2}+\frac{1}{{\gamma }_4}+{\gamma }_6){\left(\check{\varpi }\right)}^{T}P\check{\varpi }+(1+\frac{1}{{\gamma }_3}+\frac{1}{{\gamma }_5}+\frac{1}{{\gamma }_6}){\left(\check{ϵ}\right)}^{T}P\check{ϵ}.\hfill \end{array}$$

(41)

Define that

$$\begin{array}{c}\hfill \Delta \left(k\right)=(1+\frac{1}{{\gamma }_2}+\frac{1}{{\gamma }_4}+{\gamma }_6){\left(\check{\varpi }\right)}^{T}P\check{\varpi }+(1+\frac{1}{{\gamma }_3}+\frac{1}{{\gamma }_5}+\frac{1}{{\gamma }_6}){\left(\check{ϵ}\right)}^{T}P\check{ϵ}.\end{array}$$

(42)

Therefore, we can obtain

$$\begin{array}{cc}\hfill \Delta V_k& \le {\zeta }_k^T[(1+{\gamma }_1+{\gamma }_2+{\gamma }_3)H^{T}PH+(1+\frac{1}{{\gamma }_1}+{\gamma }_4+{\gamma }_5){\psi }^{T}P\psi -P]{\zeta }_k+\Delta \left(k\right)\hfill \\ \hfill & ={\zeta }_k^T(-\lambda P){\zeta }_k+\Delta \left(k\right)\hfill \\ \hfill & =-\lambda V_k+\Delta \left(k\right),\hfill \end{array}$$

(43)

Letting the eigenvalues of P be ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$. $\overline{\alpha }={\left\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right\}}_{max}$, then

$$\begin{array}{cc}\hfill \Delta \left(k\right)\le & (1+\frac{1}{{\gamma }_2}+\frac{1}{{\gamma }_4}+{\gamma }_6){\left(\check{\varpi }\right)}^T\left(\overline{\alpha }I\right)\check{\varpi }+(1+\frac{1}{{\gamma }_3}+\frac{1}{{\gamma }_5}+\frac{1}{{\gamma }_6}){\left(\check{ϵ}\right)}^T\left(\overline{\alpha }I\right)\check{ϵ}\hfill \\ \hfill \le & \overline{\alpha }{\Delta }_1∥\check{\varpi }∥+\overline{\alpha }{\Delta }_1∥\check{ϵ}∥.\hfill \end{array}$$

(44)

where

$$\begin{array}{cc}\hfill & {\Delta }_1=(1+\frac{1}{{\gamma }_2}+\frac{1}{{\gamma }_4}+{\gamma }_6),\hfill \\ \hfill & {\Delta }_2=(1+\frac{1}{{\gamma }_3}+\frac{1}{{\gamma }_5}+\frac{1}{{\gamma }_6}),\hfill \\ \hfill \end{array}$$

according to Assumption 1. We know that $\check{\varpi }$ and $\check{ϵ}$ are bounded; then, let $\Delta =\overline{\alpha }{\Delta }_1∥\check{\varpi }∥+\overline{\alpha }{\Delta }_1∥\check{ϵ}∥$ and plug it into inequality (44).

$$\begin{array}{cc}\hfill V_k\le & (1-\lambda )V_{k-1}+\Delta \hfill \\ \hfill \le & {(1-\lambda )}^{k-1}{V}_0+\sum _{i=1}^k{(1-\lambda )}^{i-1}\Delta ,\hfill \end{array}$$

(45)

If here $\lambda$ satisfies $0\le \lambda \le 1$, then

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}{V}_k=& \underset{k\to \infty }{lim}[{(1-\lambda )}^{k-1}{V}_0+\sum _{i=1}^k{(1-\lambda )}^{i-1}\Delta ]\hfill \\ \hfill =& \underset{k\to \infty }{lim}\sum _{i=1}^k{(1-\lambda )}^{i-1}\Delta \hfill \\ \hfill =& \underset{k\to \infty }{lim}\frac{1-{(1-\lambda )}^n}{1-\lambda }\Delta \hfill \\ \hfill =& \frac{\Delta }{1-\lambda }.\hfill \end{array}$$

(46)

then

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}{V}_k=& \underset{k\to \infty }{lim}{\zeta }_k^{T}P{\zeta }_k\hfill \\ \hfill \le & \underset{k\to \infty }{lim}\overline{\alpha }{\zeta }_k^T{\zeta }_k\hfill \\ \hfill \le & \underset{k\to \infty }{lim}\overline{\alpha }({\widehat{e}}_k^{+2}+{\widehat{e}}_k^{-2})\hfill \\ \hfill \le & \frac{\Delta }{1-\lambda },\hfill \end{array}$$

(47)

so

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}({\widehat{e}}_k^{+2}+{\widehat{e}}_k^{-2})\le & \frac{\Delta }{\overline{\alpha }(1-\lambda )}.\hfill \end{array}$$

(48)

□

According to Definition 1, then system (26) is UUB. Moreover, both the upper and lower errors eventually obtained by the error system are bounded, which completes the proof of Theorem 4.

Remark 4.

The designed IO can be successfully applied to the CPS without attacks, and the bounds of the system states can be reconstructed. Even if there exist attacks in the CPS, the accurate bounds of the system states can still be estimated for the purpose of the security problem.

4. Simulation

In order to verify the effectiveness of the IO design method, this section gives a specific numerical simulation of the CPS. We consider the unmanned ground vehicle system [25], whose dynamic equation can be written as:

$$\dot{x}\left(t\right)=\left[\begin{array}{cc}0& 1\\ 0& -\frac{\mu }{m}\end{array}\right]x\left(t\right)+\left[\begin{array}{c}0\\ \frac{1}{m}\end{array}\right]u\left(t\right),$$

(49)

where $x\left(t\right)=\left[\begin{array}{c}s\left(t\right)\\ \upsilon \left(t\right)\end{array}\right]$ is the state of the car, s is the position of the car and $\upsilon$ is the speed of the car. $\mu$ and m represent the average friction coefficient and mass of the car, respectively. In the experiment, we choose $\mu =0.8$ and $m=1$. At the same time, we consider the existence of certain nonlinear terms in the system, as well as the process noise and measurement errors. The parametric matrix of system (49) after discretization is:

$$A=\left[\begin{array}{cc}1& 0.096\\ 0& 0.923\end{array}\right],B=\left[\begin{array}{c}0.005\\ 0.096\end{array}\right],$$

$$C=\left[\begin{array}{cc}1& 0\end{array}\right],D=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],E=\left[\begin{array}{c}1\end{array}\right].$$

In addition, the disturbance ${\varpi }_k$ and measurement error ${ϵ}_k$ parameters of the system are chosen as:

$${\varpi }_k=\left[\begin{array}{c}0.05+0.05sin\left(k\right)\\ 0.05-0.05cos\left(k\right)\end{array}\right],{ϵ}_k=\left[\begin{array}{c}0.05sin\left(k\right)\end{array}\right].$$

Meanwhile, the nonlinear function $\Phi (x_1,x_2)$ is expressed as:

$$\Phi (x1,x2)=\left[\begin{array}{c}0.05sin{x}_1\\ 0.05cos{x}_2\end{array}\right].$$

The coordinate transformation matrix M and the constants ${\gamma }_i$, $\lambda$ are selected

$$M=\left[\begin{array}{cc}1& -1\\ 1& -2\end{array}\right],$$

$${\gamma }_i=i(i=1,2,3...6),\lambda =0.9,$$

and then P and $\psi$ can be obtained as:

$$P=\left[\begin{array}{cccc}156.23& 0& 0& 0\\ 0& 156.23& 0& 0\\ 0& 0& 156.23& 0\\ 0& 0& 0& 156.23\end{array}\right],\psi =\left[\begin{array}{cccc}2& 0& 1& 0\\ 0& 2& 0& 1\\ 1& 0& 2& 0\\ 0& 1& 0& 2\end{array}\right],$$

thus, L can be obtained by Theorem 3

$$L=\left[\begin{array}{c}0.5038\\ -0.0500\end{array}\right].$$

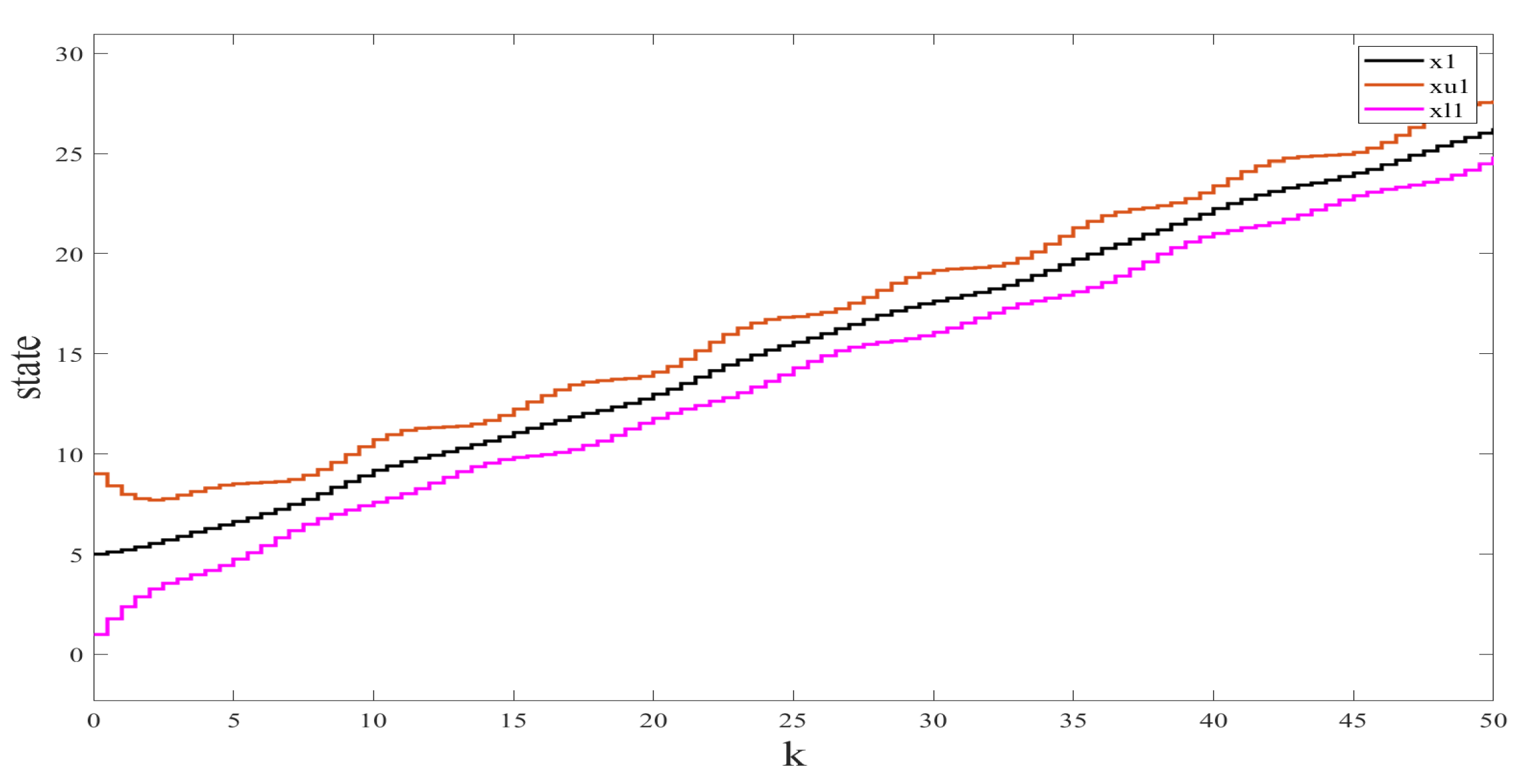
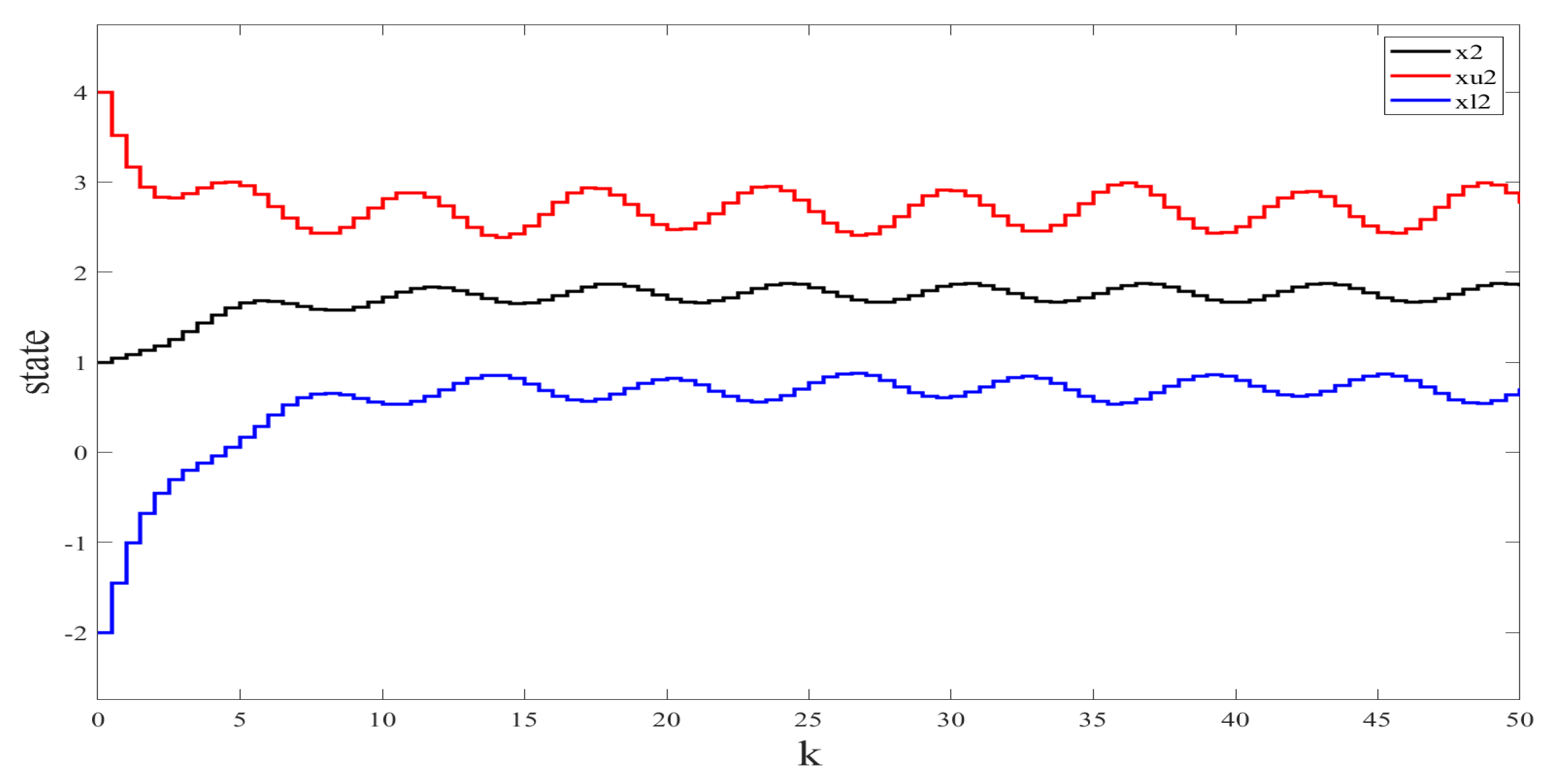
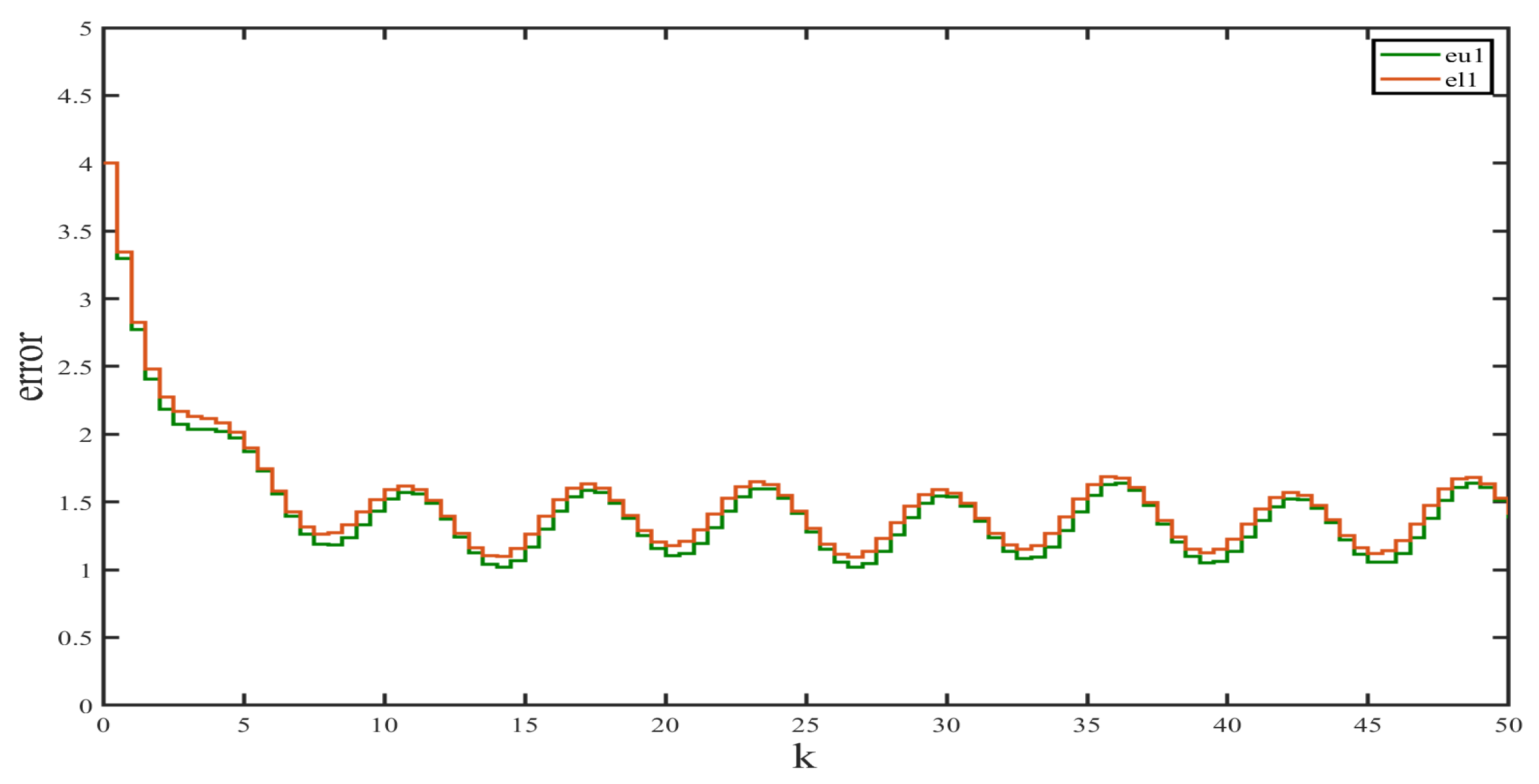
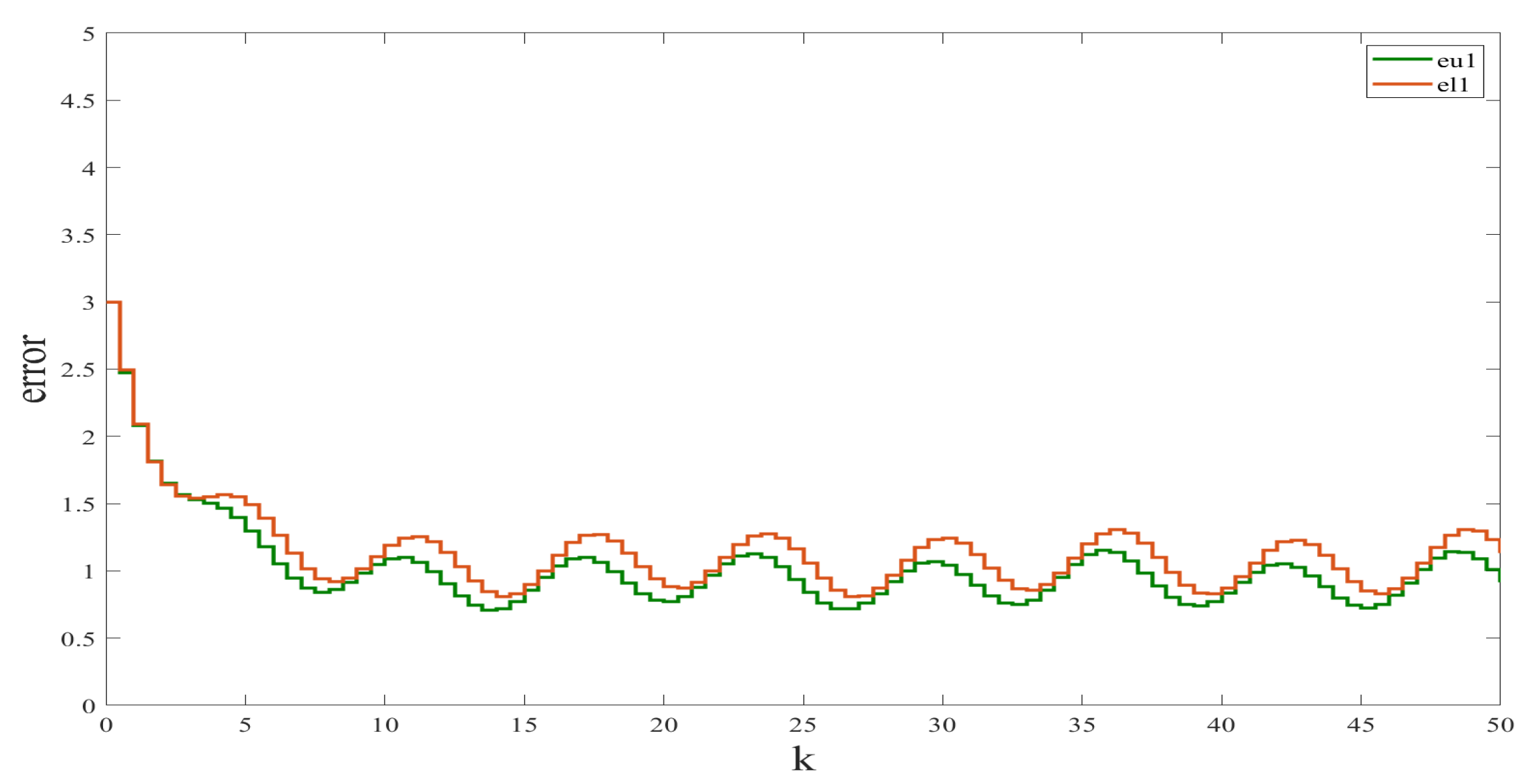
We used the Simulink Toolbox in Matlab to complete the simulation. Figure 1 and Figure 2 show the state and observation trajectories of the system, whose upper and lower bounds of the IO strictly satisfy $x^{-}\le x\le x^{+}$. Figure 3 and Figure 4 illustrate the bounded convergence of the error system, which shows that the error system eventually converges to a bounded value greater than zero. Consequently, it can be inferred that the designed IO can strictly recover the bounds of the original system state. Therefore, we conclude that the designed IO is effective and feasible.

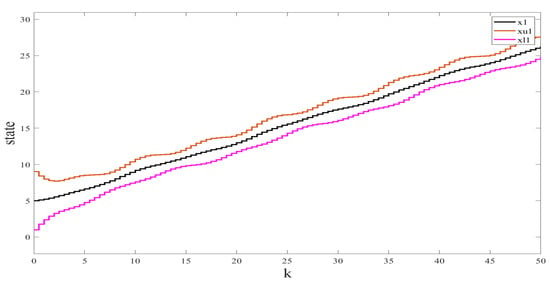
Figure 1. The states $x1$ (position $s\left(t\right)$) of the original system and their interval estimates.

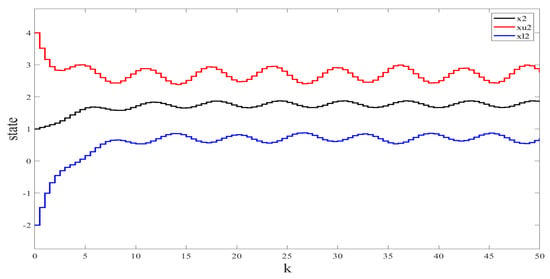
Figure 2. The states $x2$ (speed $\upsilon \left(t\right)$) of the original system and their interval estimates.

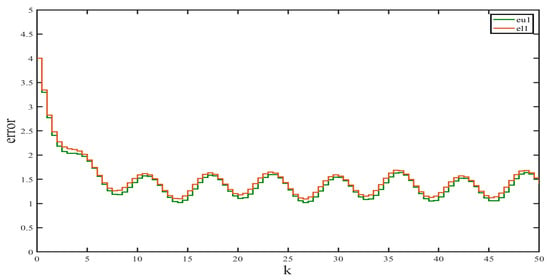
Figure 3. Error in interval estimation of $x1$.

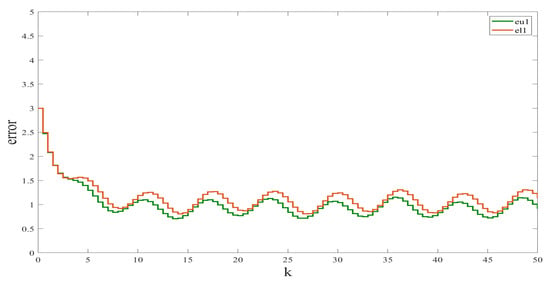
Figure 4. Error in interval estimation of $x2$.

5. Conclusions

This paper presents an IO framework for a class of CPSs with disturbance. According to the state parameters of the original system, the frame of the IO was established based on the positive system theory. For the case that $A-LC$ does not satisfy the non-negative property, the method of coordinate transformation was used to make $A-LC$ non-negative, and the sufficient conditions for the system gain L to be satisfied were also derived. At the end, one example is simulated to verify the validity of the proposed method. Future attempts are verified by introducing interval estimation into the CPS with cyber attacks.