Numerical Solution of Nonlinear Backward Stochastic Volterra Integral Equations
Abstract
1. Introduction
2. Block-Pulse Functions BPFs
- (1)
- Disjointness: The BPFs are disjointed with each other in the interval .
- (2)
- Orthogonality: The BPFs are disjointed with each other in the interval .
- (3)
- The third property is completeness: For every , when , Parseval’s identity holds, that is:
2.1. Function Approximations
2.2. Integration Operational Matrix
3. Stochastic Integration Operational Matrix
4. Implementation in Stochastic Integral Equation
5. General Error Estimate
- (I)
- If , there exists a constant L such that
- (II)
- If , there exists a constant L such that
- (III)
- There exists a constant and L such that, for continuous process , there is an -adapted value.
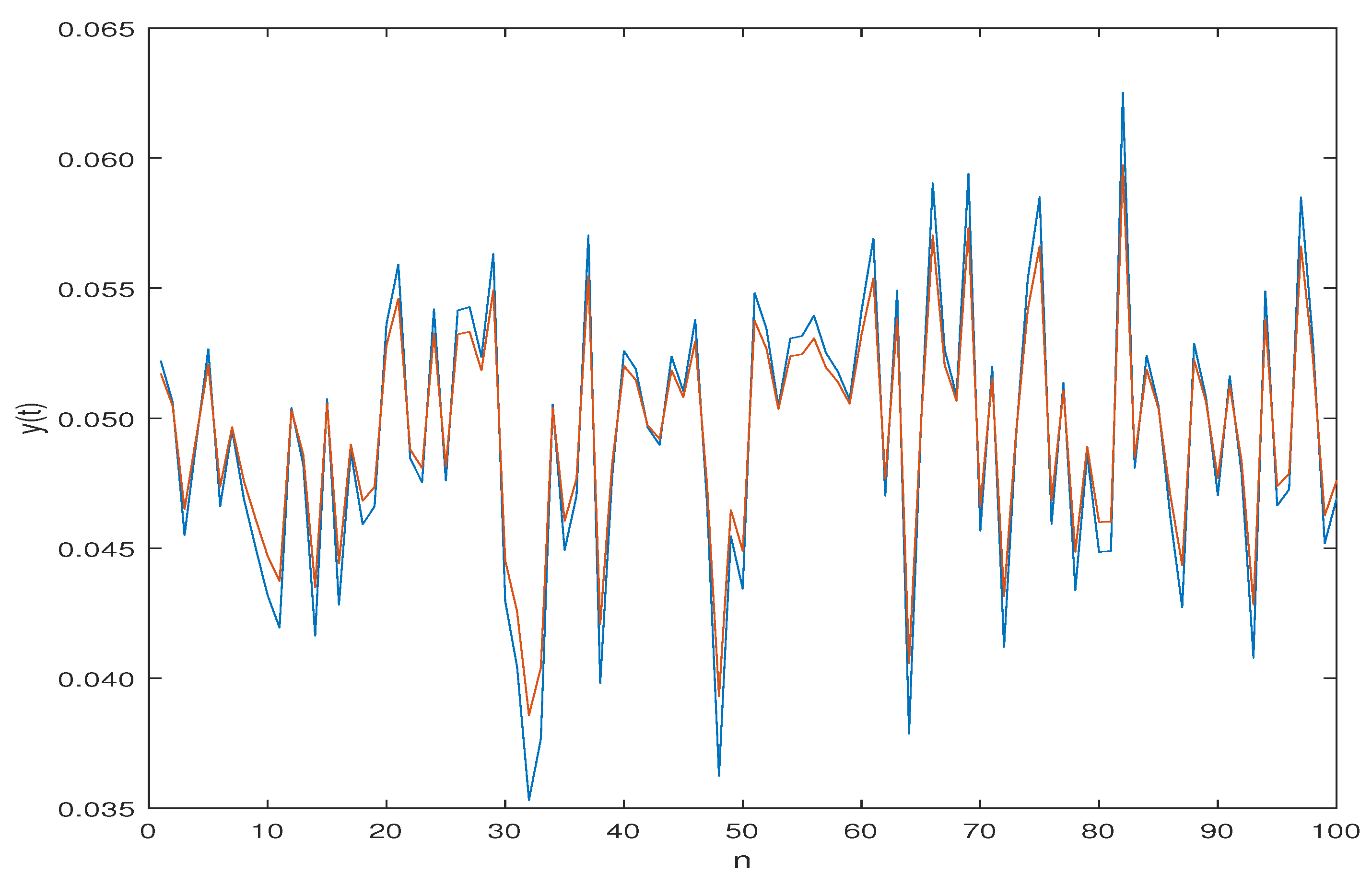
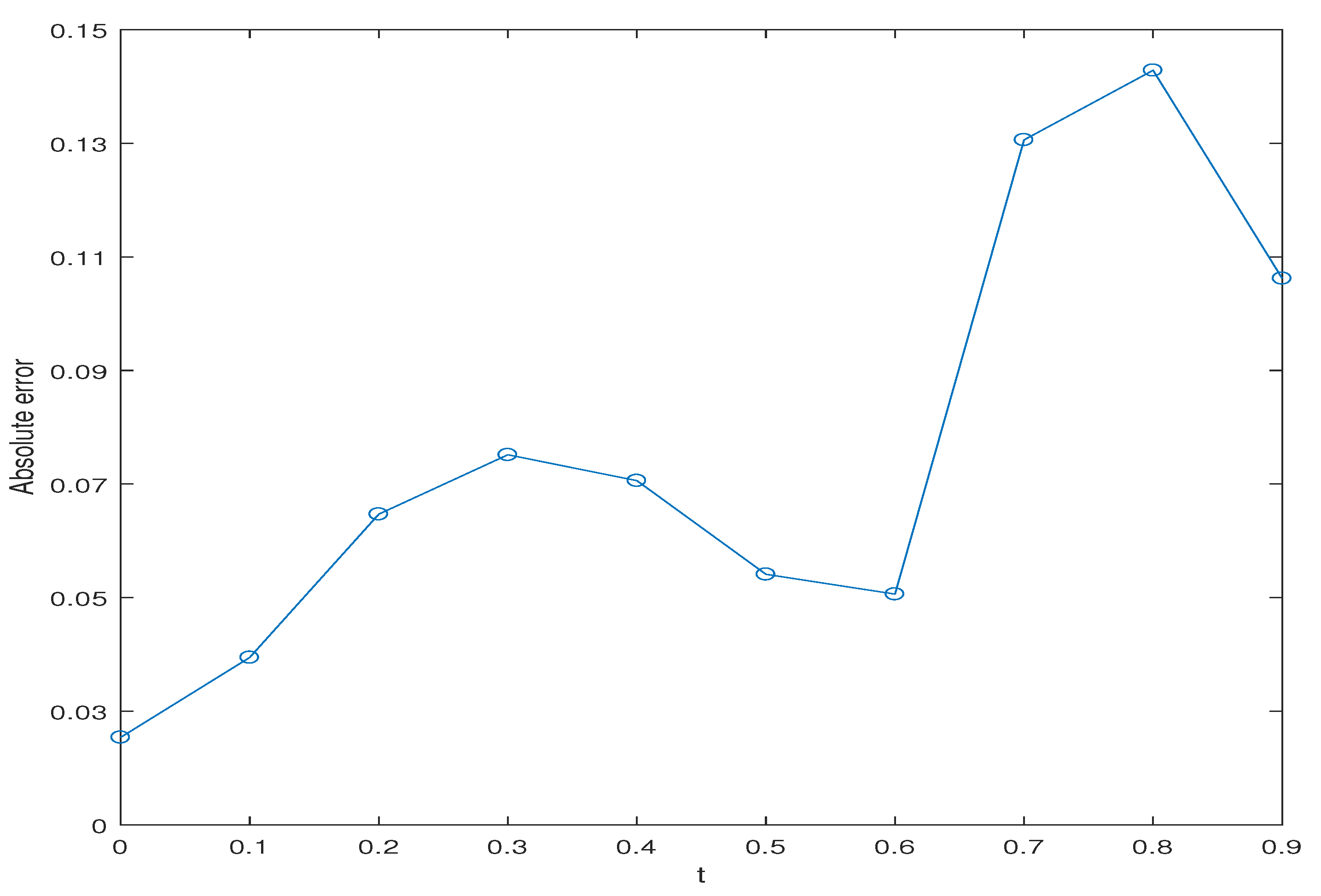
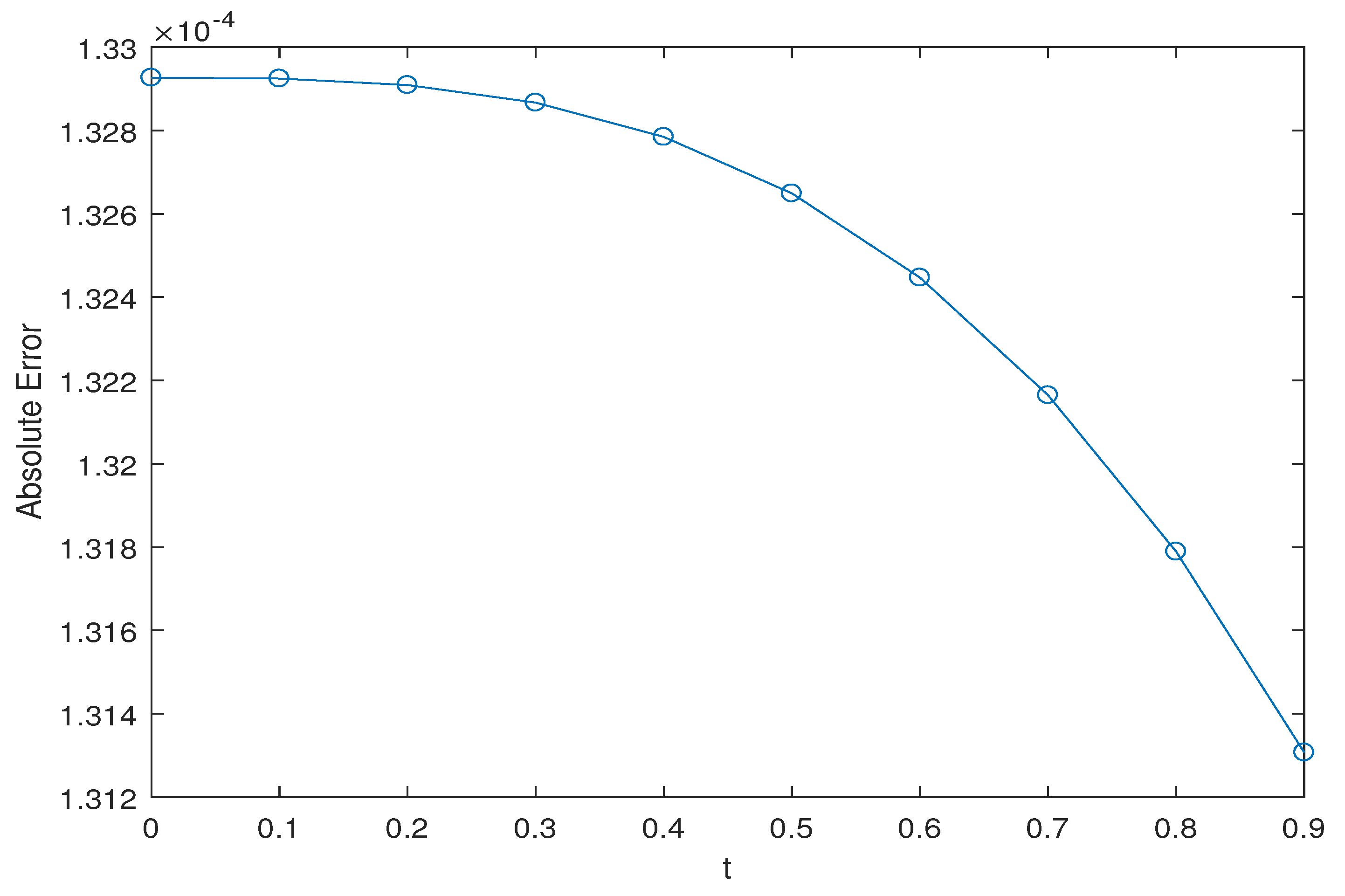
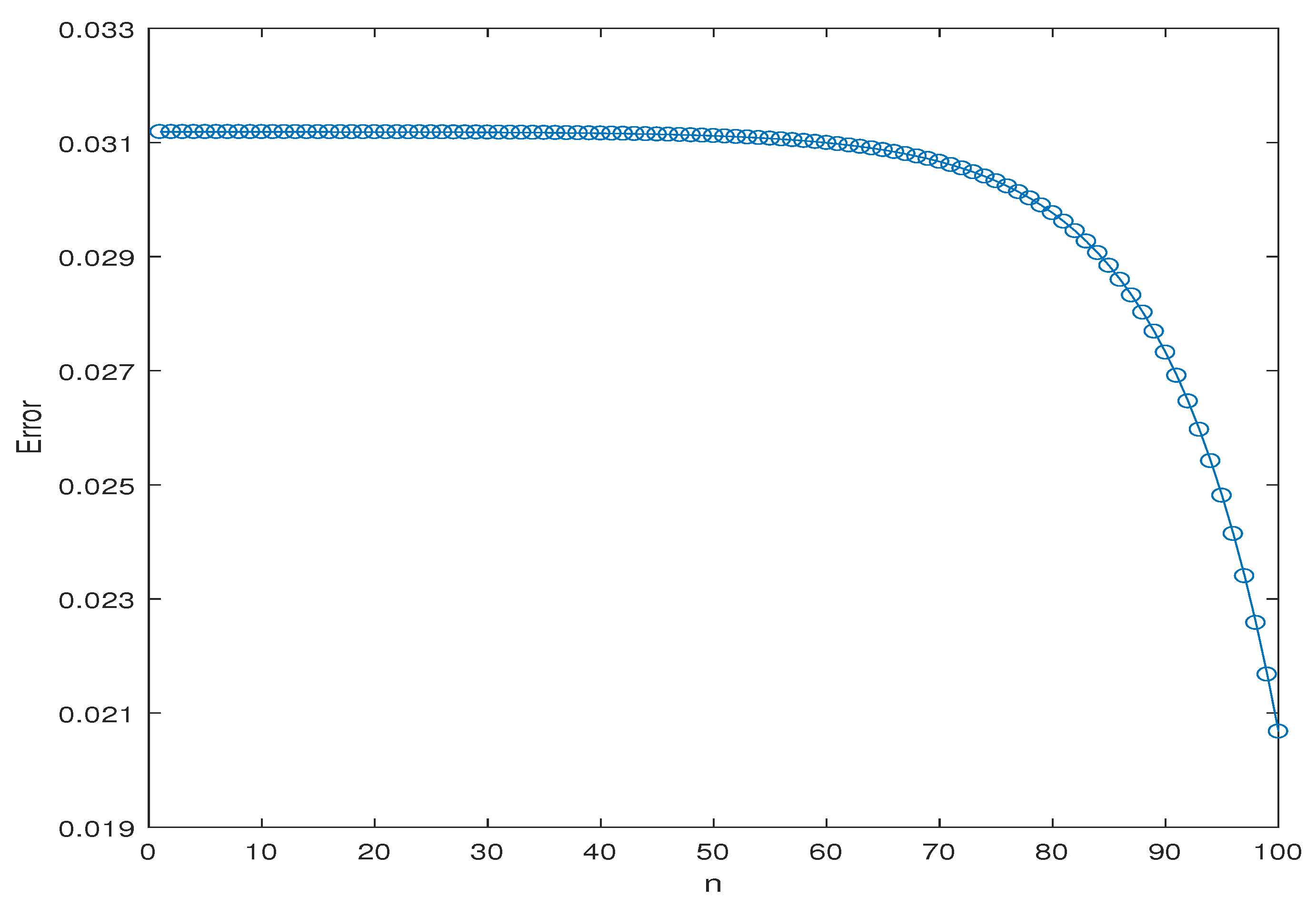
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pardoux, E.; Peng, S.G. Adapted solution of a backward stochastic differential equation. Syst. Control Lett. 1990, 14, 55–61. [Google Scholar] [CrossRef]
- Pardoux, E.; Peng, S.G. Backward stochastic differential equations and quasilinear parabolic partial differential equations. In Stochastic Partial Differential Equations and Their Applications; Springer: Berlin/Heidelberg, Germany, 1992; Volume 176, pp. 200–217. [Google Scholar]
- Shi, Y.; Wang, T. Solvability of general backward stochastic volterra integral equations. J. Korean Math. Soc. 2012, 49, 1301–1321. [Google Scholar] [CrossRef]
- Yong, J. Backward stochastic Volterra integral equations and some related problems. Stoch. Process. Their Appl. 2006, 116, 779–795. [Google Scholar] [CrossRef]
- Yong, J. Well-posedness and regularity of backward stochastic Volterra integral equations. Probab. Theory Relat. Fields 2008, 142, 21–77. [Google Scholar] [CrossRef]
- Wang, H. Extended backward stochastic Volterra integral equations, quasilinear parabolic equations, and Feynman-Kac formula. Stoch. Dyn. 2021, 21, 2150004. [Google Scholar] [CrossRef]
- Pardoux, E.; Peng, S.G. Backward doubly stochastic differential equation and systems of quasilinear SPDEs. Probab. Theory Relat. Fields 1994, 98, 209–227. [Google Scholar] [CrossRef]
- Lin, J. Adapted solution of a backward stochastic nonlinear Volterra integral equation. Stoch. Anal. Appl. 2002, 20, 165–183. [Google Scholar] [CrossRef]
- Aman, A.; N’zi, M. Backward stochastic nonlinear Volterra integral equations with local Lipschitz drift. Prob. Math. Stat. 2005, 25, 105–127. [Google Scholar]
- Karoui, N.E.; Peng, S.; Quenez, M. Backward stochastic differential equations in finance. Math. Financ. 1997, 7, 1–71. [Google Scholar] [CrossRef]
- Yong, J. Continuous-time dynamick risk measures by backward stochastic Volterra integral equations. Appl. Anal. 2007, 86, 1429–1442. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Yong, J. Recursive utility processes, dynamick risk measures and quadratic backward stochastic Volterra integral equations. Appl. Math. Optim. 2021, 84, 145–190. [Google Scholar] [CrossRef]
- Kromer, E.; Overbeck, L. Differentiability of BSIVEs and dynamic capital allocations. Int. J. Theory Appl. Financ. 2017, 20, 1–26. [Google Scholar] [CrossRef]
- Bender, C.; Denk, R. A forward scheme for backward SDEs. Stoch. Process. Their Appl. 2007, 117, 1793–1812. [Google Scholar] [CrossRef]
- Bender, C.; Pokalyuk, S. Discretization of backward stochastic Volterra integral equations, Recent Developments in Computational Finance. Interdiscip. Math. Sci. 2013, 14, 245–278. [Google Scholar]
- Zhang, J. A Numerical scheme for BSDEs. Ann. Appl. Probab. 2004, 14, 459–488. [Google Scholar] [CrossRef]
- Zhang, J. Backward Stochastic Differential Equations: From Linear to Fully Nonlinear Theory; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Popier, A. Backward stochastic Volterra integral equations with jumps in a general filtration. ESAIM Prob. Stats. 2021, 25, 133–203. [Google Scholar] [CrossRef]
- Hu, Y.; Oksendal, B. Linear Volterra backward stochastic integral equations. Stoch. Process. Their Appl. 2019, 129, 626–633. [Google Scholar] [CrossRef]
- Agram, N. Dynamick risk measure for BSVIE with jumps and semimartingale issues. Stoch. Anal. Appl. 2019, 37, 361–376. [Google Scholar] [CrossRef]
- Hamaguchi, Y.; Taguchi, D. Approximations for adapted M-solution of type-II backward stochastic Volterra integral equations. ESAIM Probab. Stat. 2023, 27, 19–79. [Google Scholar] [CrossRef]
- Fu, K.; Zeng, X.; Li, X.; Du, J. A Convolution Method for Numerical Solution of Backward Stochastic Differential Equations Based on the Fractional FFT. Fractal Fract. 2023, 7, 44. [Google Scholar] [CrossRef]
- Maleknejad, K.; Khodabin, M.; Rostami, M. Numerical solution of stochastic Volterra integral equations by a stochastic operational matrix based on block pulse functions. Math. Comput. Model. 2012, 55, 791–800. [Google Scholar] [CrossRef]
- Saffarzadeh, M.; Loghmani, G.B.; Heydari, M. An iterative technique for the numerical solution of nonlinear stochastic Itô-Volterra integral equations. J. Comput. Appl. Math. 2018, 333, 74–86. [Google Scholar] [CrossRef]
- Khan, S.U.; Ali, M.; Ali, I. A spectral collocation method for stochastic Volterra integro-differential equations and its error analysis. Adv. Differ. Equ. 2019, 2019, 161. [Google Scholar] [CrossRef]
- Xie, J.; Huang, Q.; Zhao, F. Numerical solution of nonlinear Volterra-Fredholm-Hammerstein integral equations in two-dimensional spaces based on block pulse functions. J. Comp. Appl. Math. 2017, 317, 565–572. [Google Scholar] [CrossRef]
- Khodabina, M.; Maleknejad, K.; Rostami, M.; Nouri, M. Numerical approach for solving stochastic Volterra-Fredholm integral equations by stochastic operational matrix. Comput. Math. Appl. 2012, 64, 1903–1913. [Google Scholar] [CrossRef][Green Version]
- Maleknejad, K.; Khodabin, M.; Rostami, M. A numerical method for solving m-dimensional stochastic Ito-Volterra integral equations by stochastic operational matrix. Comput. Math. Appl. 2012, 63, 133–143. [Google Scholar] [CrossRef][Green Version]
- Geng, F.Z. Piecewise reproducing kernel-based symmetric collocation approach for linear stationary singularly perturbed problems. AIMS Math. 2020, 5, 6020–6029. [Google Scholar] [CrossRef]
- Ali, I.; Khan, S.U. A Dynamic Competition Analysis of Stochastic Fractional Differential Equation Arising in Finance via Pseudospectral Method. Mathematics 2023, 11, 1328. [Google Scholar] [CrossRef]
- Momendzade, N.; Vahidi, A.R.; Babolian, E. A computational method for solving stochastic Ito-Volterra integral equation with multi-stochastic terms. Math. Sci. 2018, 12, 295–303. [Google Scholar] [CrossRef]
- Maleknejad, K.; Hashemizadeh, E.; Ezzati, R. A new approach to the numerical solution of Volterra integral equations by using Bernstein’s approximation. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 647–655. [Google Scholar] [CrossRef]
- He, J.-H.; Taha, M.H.; Ramadan, M.A.; Moatimid, G.M. Improved Block-Pulse Functions for Numerical Solution of Mixed Volterra-Fredholm Integral Equations. Axioms 2021, 10, 200. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Schaufelberger, W. Block Pulse Functions and Their Applications in Control Systems; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]

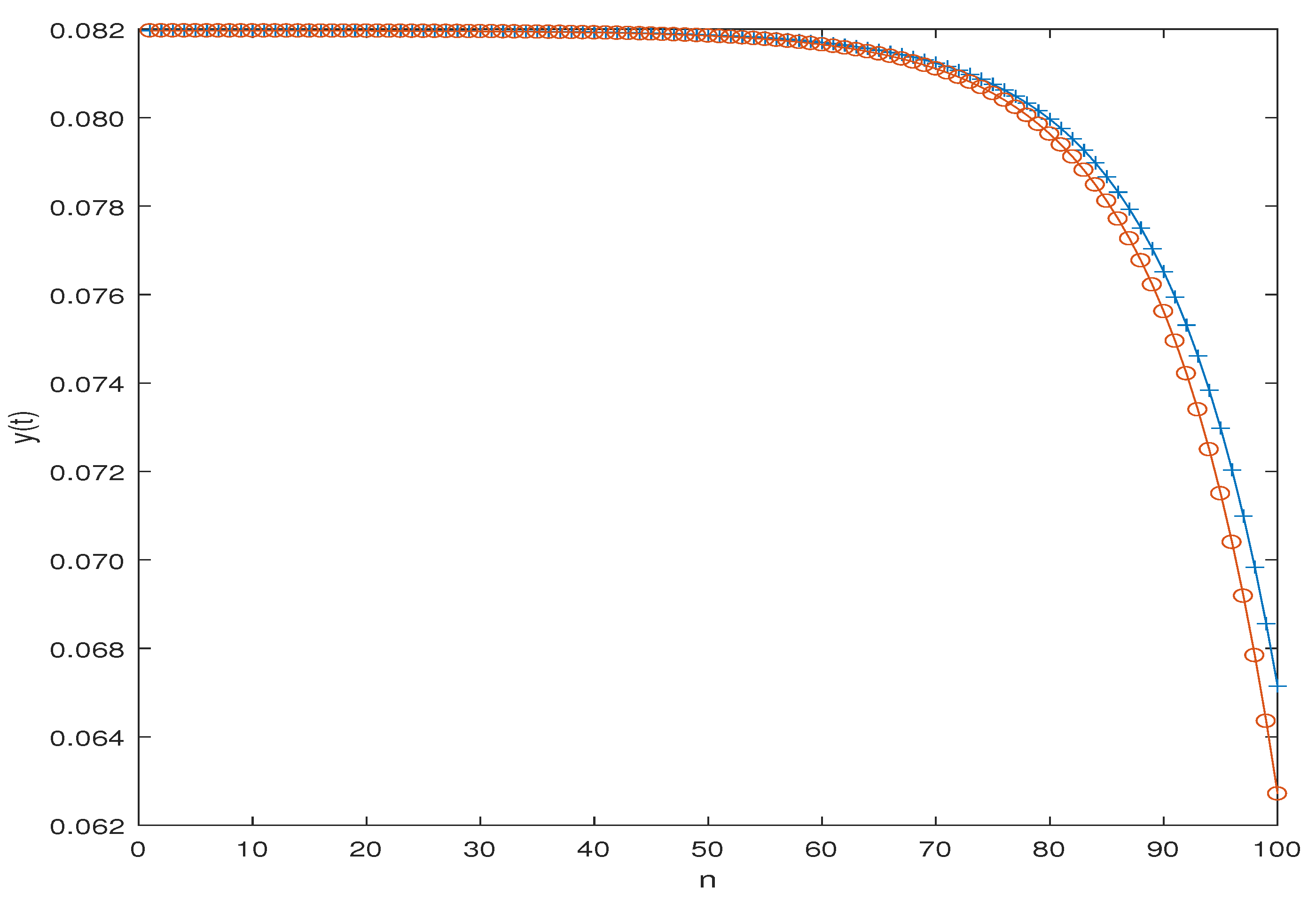
| 95% Confidence Interval for Mean of E | ||||
|---|---|---|---|---|
| Lower | Upper | |||
| 0.1 | 4.7301 | 3.5542 | 3.2465 | 6.0964 |
| 0.2 | 8.0502 | 8.7651 | 6.9504 | 9.3073 |
| 0.3 | 6.4216 | 6.2117 | 5.6333 | 8.7805 |
| 0.4 | 4.2367 | 5.7564 | 3.5854 | 7.8163 |
| 0.5 | 2.5967 | 4.6054 | 1.0986 | 4.4201 |
| 0.6 | 4.6031 | 2.1570 | 3.5834 | 7.2932 |
| 0.7 | 1.4653 | 6.6936 | 1.1032 | 2.1764 |
| 0.8 | 3.4158 | 1.7324 | 2.5766 | 5.0992 |
| 0.9 | 6.7863 | 3.5786 | 5.1752 | 9.9939 |
| 95% Confidence Interval for Mean of E | ||||
|---|---|---|---|---|
| Lower | Upper | |||
| 0.1 | 3.3385 | 4.7213 | 2.0298 | 4.6472 |
| 0.2 | 4.8302 | 4.9320 | 3.8560 | 7.1508 |
| 0.3 | 6.3021 | 7.0513 | 5.6432 | 9.0261 |
| 0.4 | 2.5038 | 1.2407 | 1.0653 | 3.8054 |
| 0.5 | 3.3707 | 1.5796 | 2.223 | 5.3671 |
| 0.6 | 6.1139 | 8.1845 | 6.0452 | 9.7731 |
| 0.7 | 1.2392 | 1.3858 | 1.0902 | 1.5776 |
| 0.8 | 2.1240 | 1.4726 | 1.7162 | 2.532 |
| 0.9 | 2.3683 | 1.6812 | 1.8664 | 2.8703 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samar, M.; Yao, K.E.; Zhu, X. Numerical Solution of Nonlinear Backward Stochastic Volterra Integral Equations. Axioms 2023, 12, 888. https://doi.org/10.3390/axioms12090888
Samar M, Yao KE, Zhu X. Numerical Solution of Nonlinear Backward Stochastic Volterra Integral Equations. Axioms. 2023; 12(9):888. https://doi.org/10.3390/axioms12090888
Chicago/Turabian StyleSamar, Mahvish, Kutorzi Edwin Yao, and Xinzhong Zhu. 2023. "Numerical Solution of Nonlinear Backward Stochastic Volterra Integral Equations" Axioms 12, no. 9: 888. https://doi.org/10.3390/axioms12090888
APA StyleSamar, M., Yao, K. E., & Zhu, X. (2023). Numerical Solution of Nonlinear Backward Stochastic Volterra Integral Equations. Axioms, 12(9), 888. https://doi.org/10.3390/axioms12090888






