Infinite Horizon Irregular Quadratic BSDE and Applications to Quadratic PDE and Epidemic Models with Singular Coefficients
Abstract
:1. Motivation and Introduction
2. Main Result
2.1. Notations
- is the space of -adapted processes Z in such that
- is the space of -adapted processes Z in satisfying
- is the set of -valued, continuous, and -adapted processes Y such that
- represents the Sobolev space consisting of functions u defined on for which both u and its generalized derivatives and belong to .
- is the collection of -valued -measurable random variables with
- denotes the -algebra of predictable sets on .
- For all is a stochastic process that is progressively measurable such that
- There exists two non-random functions and such that, for all, we have, -a.s.:and
- .
- There exists a non-negative random coefficient and a measurable function f such that for every :
- (i)
- and for all most every x, .
- (ii)
- u is a bijective mapping the whole real line to itself.
- (iii)
- The inverse function is both continuously differentiable on and locally in the Sobolev space .
- (iv)
- For any pair of real numbers x and y, there exist positive constants m and M independent on x and y satisfying the following inequalitiesand
- (v)
- Moreover, if f is continuous, then both u and belong to the class .
- 1.
- The stochastic process is progressively measurable and satisfies the integrability condition
- 2.
- For fixed ω and s, the mapping is Lipschitz continuous for a bounded and integrable function f over the whole space .
2.2. Comparison Principle
3. Application to Quadratic Partial Differential Equations
- are uniformly Lipschitz, i.e., there exists a constant such that ,
- The coefficients and b are monotonic with respect to x, meaning that there exists a constant such that, for all and all :and
- The functions and .
- The function is integrable, and is a continuous function such that, for some constant ,
- (i)
- In this section, f is assumed to be continuous only for making sense of the associated semi-linear QPDE, see [22] for more details.
- (ii)
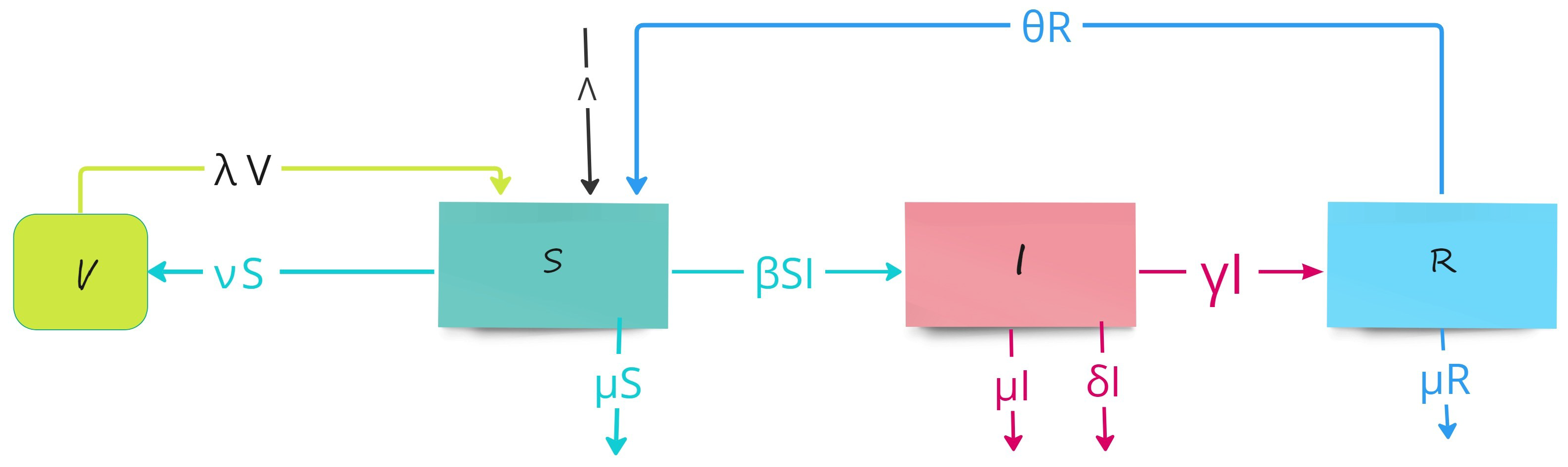
4. Application to Epidemic Models
- is the constant migration rate of the susceptible population.
- represents the transmission rate between S and I at time t.
- denotes the rate at which immunity decreases for vaccinated individuals.
- represents the natural death rate of the S, I, V, and R compartments and .
- represents the proportional coefficient of vaccinated individuals among those susceptible at time t.
- signifies the rate at which recovered individuals lose their immunity and revert to being susceptible.
- is introduced to turn off/on the control in “summer”/“rest of the year”. See below for more details.
- for represents the noise for the suspected, infected, and recovered people, where these parameters can be estimated from the data of the history of the epidemic. The uncertainty comes from the fact that there are infected non-detected and also recovered non-detected. For the vaccination, the uncertainty comes from the imperfect type of vaccination that could be used.
- represents the constant recovery rate for the disease-infected individual.
- is the death rate due to disease.
- : Represents the government’s efforts in border protection (airports and ports to track) as well as awareness campaigns and guidance.
- : Represent the control over the number of vaccinated people
- A four-dimensional diffusion of the formHere, is a positive constant for simplicity.
- A QBSDE with measurable coefficients.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bismut, J.M. Contrôle des Systemes LinéAires Quadratiques: Applications de l’Intégrale Stochastique; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Pardoux, E.; Peng, S. Adapted solution of a backward stochastic differential equation. Syst. Control Lett. 1990, 14, 55–61. [Google Scholar] [CrossRef]
- Pardoux, E. Generalized discontinuous backward stochastic differential equations. In Pitman Research Notes in Mathematics Series; Longman: London, UK, 1997; pp. 207–219. [Google Scholar]
- Pardoux, E.; Zhang, S. Generalized BSDEs and nonlinear Neumann boundary value problems. Probab. Theory Relat. Fields 1998, 110, 535–558. [Google Scholar] [CrossRef]
- Darling, R.W.; Pardoux, E. Backwards SDE with random terminal time and applications to semilinear elliptic PDE. Ann. Probab. 1997, 25, 1135–1159. [Google Scholar] [CrossRef]
- Peng, S. Probabilistic interpretation for systems of quasilinear parabolic partial differential equations. Stochastics Stochastics Rep. 1991, 37, 61–74. [Google Scholar]
- Chen, Z. Existence and uniqueness for BSDE with stopping time. Chin. Sci. Bull. 1998, 43, 96–99. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, B. Infinite time interval BSDEs and the convergence of g-martingales. J. Aust. Math. Soc. 2000, 69, 187–211. [Google Scholar] [CrossRef]
- Rouge, R.; El Karoui, N. Pricing via utility maximization and entropy. Math. Financ. 2000, 10, 259–276. [Google Scholar] [CrossRef]
- El Karoui, N.; Peng, S.; Quenez, M.C. Backward stochastic differential equations in finance. Math. Financ. 1997, 7, 1–71. [Google Scholar] [CrossRef]
- Ankirchner, S.; Fromm, A.; Hu, Y.; Imkeller, P.; Muller, M.; Popier, A.; Dos Reis, G. On cross hedging, BSDE and Malliavin’s calculus. Ann. Appl. Probab. 2005, 15, 1691–1712. [Google Scholar]
- Briand, P.; Confortola, F. Quadratic BSDEs with random terminal time and elliptic PDEs in infinite dimension. Electron. J. Probab. 2008, 13, 1529–1561. [Google Scholar]
- Kobylanski, M. Backward stochastic differential equations and partial differential equations with quadratic growth. Ann. Probab. 2000, 28, 558–602. [Google Scholar] [CrossRef]
- Ekren, I.; Nadtochiy, S. Utility-based pricing and hedging of contingent claims in Almgren-Chriss model with temporary price impact. Math. Financ. 2022, 32, 172–225. [Google Scholar] [CrossRef]
- Dermoune, A.; Hamadène, S.; Ouknine, Y. Backward stochastic differential equation with local time. Stochastics Stoch. Rep. 1999, 66, 103–119. [Google Scholar] [CrossRef]
- Barrieu, P.; El Karoui, N. Monotone stability of quadratic semimartingales with applications to unbounded general quadratic BSDEs. Ann. Probab. 2013, 41, 1831–1863. [Google Scholar] [CrossRef]
- Briand, P.; Hu, Y. BSDE with quadratic growth and unbounded terminal value. Probab. Theory Relat. Fields 2006, 136, 604–618. [Google Scholar] [CrossRef]
- Lepeltier, J.P.; San Martin, J. Existence for BSDE with superlinear-quadratic coefficient. Stochastics Int. J. Probab. Stoch. Process. 1998, 63, 227–240. [Google Scholar] [CrossRef]
- Lepeltier, J.P.; Xu, M. Penalization method for reflected backward stochastic differential equations with one rcll barrier. Stat. Probab. Lett. 2005, 75, 58–66. [Google Scholar] [CrossRef]
- Tevzadze, R. Solvability of backward stochastic differential equations with quadratic growth. Stoch. Process. Their Appl. 2008, 118, 503–515. [Google Scholar] [CrossRef]
- Bahlali, K.; Eddahbi, M.; Ouknine, Y. Solvability of some quadratic BSDEs without exponential moments. Comptes Rendus Mathématiques 2013, 351, 229–233. [Google Scholar] [CrossRef]
- Bahlali, K.; Eddahbi, M.; Ouknine, Y. Quadratic BSDE with L2-terminal data: Krylov’s estimate, Itô-Krylov’s formula and existence results. Ann. Probab. 2017, 45, 2377–2397. [Google Scholar] [CrossRef]
- Zvonkin, A.K. A transformation of the phase space of a diffusion process that removes the drift. Math. USSR-Sb. 1974, 22, 129–149. [Google Scholar] [CrossRef]
- Hamadène, S.; Lepeltier, J.P.; Wu, Z. Infinite horizon reflected backward stochastic differential equations and applications in mixed control and game problems. Probab. Math. Stat. 1999, 19, 211–234. [Google Scholar]
- Peng, S.; Shi, Y. Infinite horizon forward-backward stochastic differential equations. Stoch. Process. Their Appl. 2000, 85, 75–92. [Google Scholar] [CrossRef]
- Freddi, L.; Goreac, D. Infinite horizon optimal control of a SIR epidemic under an ICU constraint. arXiv 2023, arXiv:2306.10513. [Google Scholar]
- Bergomi, L. Stochastic Volatility Modeling; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Cruz, J.; Grossinho, M.; Sevcovic, D.; Udeani, C.I. Linear and Nonlinear Partial Integro-Differential Equations arising from Finance. arXiv 2022, arXiv:2207.11568. [Google Scholar]
- Düring, B.; Jüngel, A. Existence and uniqueness of solutions to a quasilinear parabolic equation with quadratic gradients in financial markets. Nonlinear Anal. Theory Methods Appl. 2005, 62, 519–544. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, H. Forward-backward stochastic differential equations on infinite horizon and quasilinear elliptic PDEs. J. Math. Anal. Appl. 2020, 485, 123791. [Google Scholar] [CrossRef]
- El Karoui, N.; Kapoudjian, C.; Pardoux, E.; Peng, S.; Quenez, M.C. Reflected solutions of backward SDE’s, and related obstacle problems for PDE’s. Ann. Probab. 1997, 25, 702–737. [Google Scholar] [CrossRef]
- Crandall, M.G.; Lions, P.L. Viscosity solutions of Hamilton-Jacobi equations. Trans. Am. Math. Soc. 1983, 277, 1–42. [Google Scholar] [CrossRef]
- Peng, S. Monotonic limit theorem of BSDE and nonlinear decomposition theorem of Doob–Meyer’s type. Probab. Theory Relat. Fields 1999, 113, 473–499. [Google Scholar] [CrossRef]
- Bensoussan, A.; Peng, S. Singular perturbations in optimal control problems. Autom.-Prod. Inform. Ind. 1986, 20, 359–381. [Google Scholar]
- Bensoussan, A. Perturbation Methods in Optimal Control, 1st ed.; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar]
- Sun, G.Q.; Wang, S.F.; Li, M.T.; Li, L.; Zhang, J.; Zhang, W.; Jin, Z.; Feng, G.L. Transmission dynamics of COVID-19 in Wuhan, China: Effects of lockdown and medical resources. Nonlinear Dyn. 2020, 101, 1981–1993. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.B.; Zhang, X.H. The threshold of a deterministic and a stochastic SIQS epidemic model with varying total population size. Appl. Math. Model. 2021, 91, 749–767. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eddahbi, M.; Kebiri, O.; Sene, A. Infinite Horizon Irregular Quadratic BSDE and Applications to Quadratic PDE and Epidemic Models with Singular Coefficients. Axioms 2023, 12, 1068. https://doi.org/10.3390/axioms12121068
Eddahbi M, Kebiri O, Sene A. Infinite Horizon Irregular Quadratic BSDE and Applications to Quadratic PDE and Epidemic Models with Singular Coefficients. Axioms. 2023; 12(12):1068. https://doi.org/10.3390/axioms12121068
Chicago/Turabian StyleEddahbi, Mhamed, Omar Kebiri, and Abou Sene. 2023. "Infinite Horizon Irregular Quadratic BSDE and Applications to Quadratic PDE and Epidemic Models with Singular Coefficients" Axioms 12, no. 12: 1068. https://doi.org/10.3390/axioms12121068
APA StyleEddahbi, M., Kebiri, O., & Sene, A. (2023). Infinite Horizon Irregular Quadratic BSDE and Applications to Quadratic PDE and Epidemic Models with Singular Coefficients. Axioms, 12(12), 1068. https://doi.org/10.3390/axioms12121068





