The Stability Analysis of Linear Systems with Cauchy—Polynomial-Vandermonde Matrices
Abstract
1. Introduction
2. Preliminaries
3. Structured Singular Values
4. Main Results
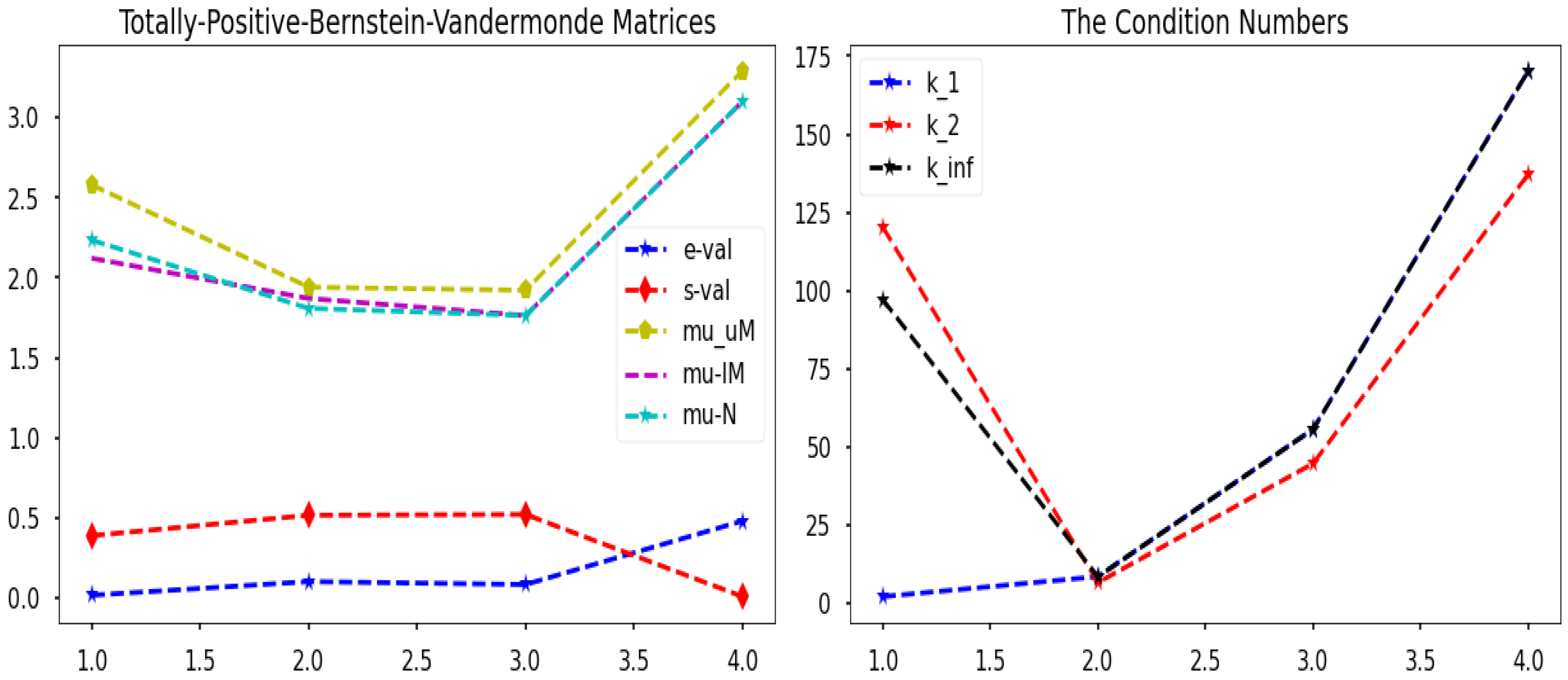
5. Total Positive Bernstein–Vandermonde and Bernstein–Bezoutian Matrices
Spectral Properties of Total Positive Bernstein–Vandermonde and Bernstein–Bezoutian Matrices
6. Cauchy—Polynomial-Vandermonde Matrices (CPV Matrices)
Spectral Properties of Cauchy—Polynomial-Vandermonde Matrices
7. Quasi-Rational Bernstein–Vandermonde Matrices
Spectral Properties of Quasi-Rational Bernstein–Vandermonde Matrices
8. Numerical Testing for Matrices in Higher Dimensions
| Algorithm 1 Approximate perturbation level. |
|
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- James, D.; Ioana, D.; Olga, H.; Plamen, K. Accurate and Efficient Expression Evaluation and Linear Algebra; Acta Numerica; Cambridge University Press: Cambridge, UK, 2008; Volume 10, pp. 87–145. [Google Scholar]
- Fallat, S.M.; Johnson, C.R. Totally Nonnegative Matrices; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Ando, T. Totally Positive Matrices; Cambridge University Press: Cambridge, UK, 2010; p. 181. [Google Scholar]
- Andalib, T.W.; Azizan, N.A.; Halim, H.A. Case Matrices and Connections of Entrepreneurial Career Management Module. Int. J. Entrep. 2019, 23, 1–10. [Google Scholar]
- James, D.; Plamen, K. The accurate and efficient solution of a totally positive generalized Vandermonde linear system. SIAM J. Matrix Anal. Appl. 2005, 27, 142–152. [Google Scholar]
- Koev, P. Accurate eigenvalues and SVDs of totally nonnegative matrices. SIAM J. Matrix Anal. Appl. 2005, 27, 1–23. [Google Scholar] [CrossRef]
- Koev, P. Accurate computations with totally nonnegative matrices. SIAM J. Matrix Anal. Appl. 2007, 29, 731–751. [Google Scholar] [CrossRef]
- Marco, A.; Martı, J.J. A fast and accurate algorithm for solving Bernstein-Vandermonde linear systems. Linear Algebra Its Appl. 2007, 4, 616–628. [Google Scholar] [CrossRef]
- Marco, A.; Martı, J.J. Polynomial least squares fitting in the Bernstein basis. Linear Algebra Its Appl. 2010, 433, 1254–1264. [Google Scholar] [CrossRef]
- Farin, G.E.; Farin, G. Curves and Surfaces for CAGD: A Practical Guide; Morgan Kaufmann: Burlington, MA, USA, 2002. [Google Scholar]
- Farin, G. Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Farin, G.; Hamann, B. Current trends in geometric modeling and selected computational applications. J. Comput. Phys. 1997, 138, 1–15. [Google Scholar] [CrossRef]
- Farin, G.E.; Hansford, D. The Geometry Toolbox for Graphics and Modeling; AK Peters/CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Forrest, A.R. Interactive interpolation and approximation by Bézier polynomials. Comput. J. 1972, 15, 71–79. [Google Scholar] [CrossRef]
- Wolters, H.J.; Farin, G. Geometric curve approximation. Comput. Aided Geom. Des. 1997, 14, 499–513. [Google Scholar] [CrossRef]
- Bini, D.A.; Gemignani, L. Bernstein-bezoutian matrices. Theor. Comput. Sci. 2004, 315, 319–333. [Google Scholar] [CrossRef]
- Brown, W.S. On Euclid’s algorithm and the computation of polynomial greatest common divisors. J. ACM 1971, 18, 478–504. [Google Scholar] [CrossRef]
- Collins, G.E. Subresultants and reduced polynomial remainder sequences. J. ACM 1967, 14, 128–142. [Google Scholar] [CrossRef]
- Bini, D.A.; Gemignani, L. Fast fraction-free triangularization of Bezoutians with applications to sub-resultant chain computation. Linear Algebra Its Appl. 1998, 284, 19–39. [Google Scholar] [CrossRef]
- Barnett, S. A Bezoutian Matrix for Chebyshev Polynomials; University of Bradford, School of Mathematical Sciences: Bradford, UK, 1987. [Google Scholar]
- Gemignani, L. Fast and Stable Computation of the Barycentric Representation of Rational Interpolants. Calcolo 1996, 33, 371–388. [Google Scholar] [CrossRef]
- Gohberg, I.; Olshevsky, V. Fast inversion of Chebyshev-Vandermonde matrices. Numer. Math. 1994, 67, 71–92. [Google Scholar] [CrossRef]
- Kailath, T.; Olshevsky, V. Displacement-structure approach to polynomial Vandermonde and related matrices. Linear Algebra Its Appl. 1997, 261, 49–90. [Google Scholar] [CrossRef]
- Rost, K. Generalized companion matrices and matrix representations for generalized Bezoutians. Linear Algebra Its Appl. 1993, 193, 151–172. [Google Scholar] [CrossRef][Green Version]
- Pan, V. Structured Matrices and Polynomials: Unified Superfast Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Phillips, G.M. Interpolation and Approximation by Polynomials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Junghanns, P.; Oestreich, D. Numerische Lösung des Staudammproblems mit Drainage. Z. Angew. Math. Mech. 1989, 69, 83–92. [Google Scholar] [CrossRef]
- Weideman, J.A.C.; Laurie, D.P. Quadrature rules based on partial fraction expansions. Numer. Algorithms 2000, 24, 159–178. [Google Scholar] [CrossRef]
- Dailey, M.; Dopico, F.M.; Ye, Q. Relative perturbation theory for diagonally dominant matrices. SIAM J. Matrix Anal. Appl. 2014, 35, 1303–1328. [Google Scholar] [CrossRef]
- Dailey, M.; Dopico, F.M.; Ye, Q. A new perturbation bound for the LDU factorization of diagonally dominant matrices. SIAM J. Matrix Anal. Appl. 2014, 35, 904–930. [Google Scholar] [CrossRef][Green Version]
- Demmel, J.; Kahan, W. Accurate singular values of bidiagonal matrices. SIAM J. Sci. Stat. Comput. 1990, 11, 873–912. [Google Scholar] [CrossRef]
- Demmel, J.; Gu, M.; Eisenstat, S.; Slapničar, I.; Veselić, K.; Drmač, Z. Computing the singular value decomposition with high relative accuracy. Linear Algebra Its Appl. 1999, 299, 21–80. [Google Scholar] [CrossRef]
- Demmel, J.; Koev, P. Accurate SVDs of weakly diagonally dominant M-matrices. Numer. Math. 2004, 98, 99–104. [Google Scholar] [CrossRef]
- Dopico, F.M.; Koev, P. Accurate symmetric rank revealing and eigendecompositions of symmetric structured matrices. SIAM J. Matrix Anal. Appl. 2006, 28, 1126–1156. [Google Scholar] [CrossRef]
- Dopico, F.; Koev, P. Perturbation theory for the LDU factorization and accurate computations for diagonally dominant matrices. Numer. Math. 2011, 119, 337–371. [Google Scholar] [CrossRef]
- Arif, M.S.; Abodayeh, K.; Nawaz, Y. Numerical Schemes for Fractional Energy Balance Model of Climate Change with Diffusion Effects. Emerg. Sci. J. 2023, 7, 808–820. [Google Scholar] [CrossRef]
- Boros, T.; Kailath, T.; Olshevsky, V. Fast algorithms for solving Vandermonde and Chebyshev-Vandermonde systems. Stanf. Inf. Syst. Lab. Rep. 1994. [Google Scholar]
- Higham, N.J. Fast solution of Vandermonde-like systems involving orthogonal polynomials. IMA J. Numer. Anal. 1988, 8, 473–486. [Google Scholar] [CrossRef]
- Higham, N.J. Stability analysis of algorithms for solving confluent Vandermonde-like systems. SIAM J. Matrix Anal. Appl. 1990, 11, 23–41. [Google Scholar] [CrossRef][Green Version]
- Kailath, T.; Olshevsky, V. Displacement structure approach to Chebyshev-Vandermonde and related matrices. Integral Equ. Oper. Theory 1995, 22, 65–92. [Google Scholar] [CrossRef]
- Reichel, L.; Opfer, G. Chebyshev-vandermonde systems. Math. Comput. 1991, 57, 703–721. [Google Scholar] [CrossRef]
- Verde-Star, L. Inverses of generalized Vandermonde matrices. J. Math. Anal. Appl. 1988, 131, 341–353. [Google Scholar] [CrossRef]
- Marco, A.; Martínez, J.-J.; Peña, J.M. Accurate bidiagonal decomposition of totally positive Cauchy–Vandermonde matrices and applications. Linear Algebra Its Appl. 2017, 517, 63–84. [Google Scholar] [CrossRef]
- Huang, R.; Chu, D. Relative perturbation analysis for eigenvalues and singular values of totally nonpositive matrices. SIAM J. Matrix Anal. Appl. 2015, 36, 476–495. [Google Scholar] [CrossRef]
- Huang, R.; Chu, D. Computing singular value decompositions of parameterized matrices with total nonpositivity to high relative accuracy. J. Sci. Comput. 2017, 71, 682–711. [Google Scholar] [CrossRef]
- Dopico, F.M.; Molera, J.M.; Moro, J. n orthogonal high relative accuracy algorithm for the symmetric eigenproblem. SIAM J. Matrix Anal. Appl. 2003, 25, 301–351. [Google Scholar] [CrossRef]
- Dopico, F.M.; Koev, P.; Molera, J.M. Implicit standard Jacobi gives high relative accuracy. Numer. Math. 2009, 113, 519–553. [Google Scholar] [CrossRef]
- Huang, R. Rank structure properties of rectangular matrices admitting bidiagonal-type factorizations. Linear Algebra Its Appl. 2015, 465, 1–14. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, R.; Zhu, W.; Liu, J. Accurate solutions of structured generalized Kronecker product linear systems. Numer. Algorithms 2021, 87, 797–818. [Google Scholar] [CrossRef]
- Alfa, A.; Xue, J.; Ye, Q. Accurate computation of the smallest eigenvalue of a diagonally dominant M-matrix. Math. Comput. 2002, 71, 217–236. [Google Scholar] [CrossRef]
- Ye, Q. Computing singular values of diagonally dominant matrices to high relative accuracy. Math. Comput. 2008, 77, 2195–2230. [Google Scholar] [CrossRef]
- Huang, R. A test and bidiagonal factorization for certain sign regular matrices. Linear Algebra Its Appl. 2013, 438, 1240–1251. [Google Scholar] [CrossRef]
- Yang, Z.; Ma, X.-X. Computing eigenvalues of quasi-rational Bernstein-Vandermonde matrices to high relative accuracy. Numer. Linear Algebra Appl. 2022, 29, 2421. [Google Scholar] [CrossRef]
- Ameer, E.; Nazam, M.; Aydi, H.; Arshad, M.; Mlaiki, N. On (Λ, Y, R)-contractions and applications to nonlinear matrix equations. Mathematics 2019, 7, 443. [Google Scholar] [CrossRef]
- Riazat, M.; Azizi, A.; Naderi Soorki, M.; Koochakzadeh, A. Robust Consensus in a Class of Fractional-Order Multi-Agent Systems with Interval Uncertainties Using the Existence Condition of Hermitian Matrices. Axioms 2023, 12, 65. [Google Scholar] [CrossRef]
- Ali, I.; Saleem, M.T. Applications of Orthogonal Polynomials in Simulations of Mass Transfer Diffusion Equation Arising in Food Engineering. Symmetry 2023, 15, 527. [Google Scholar] [CrossRef]
- Pan, V.Y.; Tsigaridas, E.P. Nearly optimal computations with structured matrices. In Proceedings of the 2014 Symposium on Symbolic-Numeric Computation, Shanghai, China, 28–31 July 2014; pp. 21–30. [Google Scholar]
- Guglielmi, N.; Rehman, M.-U.; Kressner, D. A novel iterative method to approximate structured singular values. SIAM J. Matrix Anal. Appl. 2017, 38, 361–386. [Google Scholar] [CrossRef]
- Marco, A.; Martínez, J.-J. Accurate computations with totally positive Bernstein-Vandermonde matrices. Electron. J. Linear Algebra 2013, 26, 357–380. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, R.; Zhu, W. Accurate computations for eigenvalues of products of Cauchy-polynomial-Vandermonde matrices. Numer. Algorithms 2020, 85, 329–351. [Google Scholar] [CrossRef]
- Braatz, R.P.; Young, P.M.; Doyle, J.C.; Morari, M. Computational complexity of μ calculation. IEEE Trans. Autom. Control. 1994, 39, 1000–1002. [Google Scholar] [CrossRef]
- Levin, D. The approximation power of moving least-squares. Math. Comput. 1998, 67, 1517–1531. [Google Scholar] [CrossRef]
- Jabbari, F. Linear System Theory II, Chapter 3: Eigenvalue, Singular Values, Pseudoinverse; The Henry Samueli School of Engineering, University of California: Irvine, CA, USA, 2015; Available online: http://gram.eng.uci.edu/fjabbari/me270b/me270b.html (accessed on 20 August 2023).


| Eigenvalues | Singular Values | ssv (Upper) | ssv (Lower) | ssv (Lower New) |
|---|---|---|---|---|
| Eigenvalues | Singular Values | ssv (Upper) | ssv (Lower) | ssv (Lower New) |
|---|---|---|---|---|
| Eigenvalues | Singular Values | ssv (Upper) | ssv (Lower) | ssv (Lower New) |
|---|---|---|---|---|
| ssv (Upper) | ssv (Lower) | ssv (Lower New) |
|---|---|---|
| n | ssv (Upper) | ssv (Lower) | ssv (Lower New) |
|---|---|---|---|
| 10 | |||
| 15 | |||
| 20 | |||
| 25 | |||
| 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, M.-U.; Alzabut, J.; Fatima, N.; Rasulov, T.H. The Stability Analysis of Linear Systems with Cauchy—Polynomial-Vandermonde Matrices. Axioms 2023, 12, 831. https://doi.org/10.3390/axioms12090831
Rehman M-U, Alzabut J, Fatima N, Rasulov TH. The Stability Analysis of Linear Systems with Cauchy—Polynomial-Vandermonde Matrices. Axioms. 2023; 12(9):831. https://doi.org/10.3390/axioms12090831
Chicago/Turabian StyleRehman, Mutti-Ur, Jehad Alzabut, Nahid Fatima, and Tulkin H. Rasulov. 2023. "The Stability Analysis of Linear Systems with Cauchy—Polynomial-Vandermonde Matrices" Axioms 12, no. 9: 831. https://doi.org/10.3390/axioms12090831
APA StyleRehman, M.-U., Alzabut, J., Fatima, N., & Rasulov, T. H. (2023). The Stability Analysis of Linear Systems with Cauchy—Polynomial-Vandermonde Matrices. Axioms, 12(9), 831. https://doi.org/10.3390/axioms12090831







