Surface Family Pair with Bertrand Pair as Mutual Curvature Lines in Three-Dimensional Lie Group

Abstract

This paper is on deducing the necessary and sufficient conditions of a surface family pair with a Bertrand pair as mutual curvature lines in three-dimensional Lie group $\mathbb{G}$. As a result, the consequence for the ruled surface family pair is also extrapolated. Meanwhile, examples are specified to show the surface family with common Bertrand geodesic curves.

1. Introduction

Geometry and algebra, two important mathematical topics, combine to form Lie groups in two separate ways: first, as groups, and second, as differentiable manifolds. As a result, Lie group substructure should be coherent in a particular way, both geometrically and algebraically. The shared new approach to geometry heavily depends on research into Lie groups. Consequently, there are several study findings on curves and surfaces in three-dimensional Lie group (3-D Lie group) $\mathbb{G}$ [1,2,3,4,5,6].

In recent years, several academics have become interested in creating surface families with characteristic curves, for example, Wang et al. [7] a surface family with a shared geodesic was created. Their work involves defining a spatial curve to represent the surface in an adverse engineering challenge, and it also includes scenarios where the curve could be a geodesic on this surface. In addition to this, their work could be seen as an example of industrial mathematics. Kasap et al. [8] expanded this work by speculating on new complete marching-scale functions. In [9] Using the Dirichlet principle and the Dirichlet approach, Li et al. analyzed the approximate minimal surface together with geodesics and minimized the surface’s area. When constructing surfaces, this approach can be used to obtain materials at the lowest possible cost. Several studies have taken into account the surface family with characteristic curves [10,11,12,13,14].

The symmetry between the curves is an interesting topic for the theory of space curves. The Bertrand curve is one of the more common private curves. If there is a linear relationship between the principal normal vectors of two curves at their corresponding points, the two curves are said to be a Bertrand pair [15]. The helix can be defined as the generalization of the Bertrand curve. Because of its many applications, the helix has drawn the interest of mathematicians and scientists as well. Examples include the clarification of DNA, carbon nan-otubes, nan-osprings, a-helices, the geometrical shaping of linear chained polymers stabilized as helices, and the eigenproblems interpreted for molecular collation(see [16,17]). Additionally, the Bertrand curves provide unique applications of offset curves that computer-aided manufacture (CAM) and computer-aided design (CAD) (see [18,19]).

To our knowledge, however, no more work has been done to develop a surface family pair with a curve pair to be curvature lines in 3-D Lie group $\mathbb{G}$. A surface family pair with a Bertrand pair as mutual curvature lines is designed in this study using a Bertrand pair as curvature lines to fill this demand. The expansion to the family of ruled surfaces is also described. In the meantime, a some examples are utilized to construct the surface family and ruled surface family with common Bertrand curvature lines.

2. Basic Concepts

The Lie group theory is introduced in this section (see [1,2,3,4,5,6]). Let $\mathbb{G}$ be a Lie group with a bi-invariant metric $<,>$, and ∇ be the Levi-Civita connection of $\mathbb{G}$. If $\mathfrak{g}$ indicates the Lie algebra, then, for all a, b, $\mathit{c}\in \mathfrak{g}$, we have

$$<\mathit{a},[\mathit{b},\mathit{c}]>+<\mathit{b},[\mathit{a},\mathit{c}]>=0,$$

and

$${\nabla }_{\mathit{a}}\mathit{b}=\frac{1}{2}[\mathit{a},\mathit{b}].$$

(1)

Let $\mathit{\gamma }:I\subset \mathbb{R}\to \mathbb{G}$ be an arc-length smooth curve and {${\mathit{s}}_1$,${\mathit{s}}_2$,…,${\mathit{s}}_n$} be an orthonormal basis of $\mathfrak{g}$. In this situation, any two vector fields a and b can be written as $\mathit{a}=\stackrel{n}{\underset{i=1}{\Sigma }}{a}_i{\mathit{s}}_i$ and $\mathit{b}=\stackrel{n}{\underset{i=1}{\Sigma }}{b}_i{\mathit{s}}_i$, where $b_i$, $a_i$: $I\to \mathbb{R}$ are regular functions. The Lie bracket of a and b is given by

$$[\mathit{a},\mathit{b}]=\stackrel{n}{\underset{i,i=1}{\Sigma }}{a}_i{b}_j[{\mathit{s}}_i,{\mathit{s}}_j],$$

and the directional derivative of a on the curve $\mathit{\gamma }$ is displayed as follows:

$${\nabla }_{\mathit{t}}\mathit{a}={\mathit{a}}^{\prime }+\frac{1}{2}[\mathit{t},\mathit{a}],$$

(2)

where $\mathit{t}={\mathit{\gamma }}^{\prime }=\frac{d\mathit{\gamma }}{ds}$ and ${\mathit{a}}^{\prime }=\stackrel{n}{\underset{i=1}{\Sigma }}{a}_i^{{}^{\prime }}{\mathit{s}}_i$, where $a_i^{{}^{\prime }}=\frac{d{a}_i}{ds}$. Here “dash” indicates the derivative with respect to the parameter s. It is imperative to note that if a is the left-invariant vector field to the curve then ${\mathit{a}}^{\prime }=$0 (see for details [5,6,7,8]).

Let $\mathit{\alpha }:I\subset \mathbb{R}\to \mathbb{G}$ be a regular unit speed curve in a three-dimensional Lie group $\mathbb{G}$ with the Serret–Frenet apparatus {$\mathit{t}\left(s\right)$, $\mathit{n}\left(s\right)$, $\mathit{b}\left(s\right)$, $\kappa \left(s\right)$, $\tau \left(s\right)\}$. Then, a smooth function ${\tau }_G$, which is a famed Lie torsion, is specified by:

$${\tau }_G\left(s\right)=\frac{1}{2}<\mathit{t},[\mathit{n},\mathit{b}]>,$$

(3)

and

$${\tau }_G\left(s\right)=\frac{1}{2{\kappa }^2\tau }<{\mathit{t}}^{″},[\mathit{t},{\mathit{t}}^{\prime }]>+\frac{1}{4{\kappa }^2\tau }{∥[\mathit{t},{\mathit{t}}^{\prime }]∥}^2.$$

(4)

Proposition 1

([4,5,6]). Let α be an arc-length represented curve in $\mathbb{G}$. Then,

$$\begin{array}{ccc}\hfill [\mathit{b},\mathit{t}]=<[\mathit{b},\mathit{t}],\mathit{n}>\mathit{n}=& & 2{\tau }_G\left(s\right)\mathit{n},\hfill \\ \hfill [\mathit{t},\mathit{n}]=<\mathit{t},[\mathit{n},\mathit{b}]>\mathit{b}=& & 2{\tau }_G\left(s\right)\mathit{b},\hfill \\ \hfill [\mathit{n},\mathit{b}]=<[\mathit{n},\mathit{b}],\mathit{t}>\mathit{t}=& & 2{\tau }_G\left(s\right)\mathit{t}.\hfill \end{array}$$

In view of Equation (2) and Proposition 1, the Serret–Frenet formulae of $\mathit{\alpha }$ in $\mathbb{G}$ are

$${\nabla }_{\mathit{t}}\left(\begin{array}{c}\mathit{t}\hfill \\ \mathit{n}\hfill \\ \mathit{b}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \kappa \hfill & 0\hfill \\ -\kappa \hfill & 0\hfill & \tau -{\tau }_G\hfill \\ 0\hfill & -\left(\tau -{\tau }_G\right)\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\mathit{t}\hfill \\ \mathit{n}\hfill \\ \mathit{b}\hfill \end{array}\right),$$

(5)

where $\mathit{t}={\mathit{\alpha }}^{\prime }\left(s\right),$ $\kappa \left(s\right)=∥{\nabla }_{\mathit{t}}\mathit{t}∥=∥{\mathit{t}}^{\prime }∥$, and $\tau \left(s\right)=∥{\nabla }_{\mathit{t}}\mathit{b}∥-{\tau }_G$.

Remark 1.

Let $\mathbb{G}$ be a three-dimensional Lie group with a bi-invariant metric. Consequently, the subsequent is true [12,13,14]:

(1)

If $\mathbb{G}$ is special unitary group $\mathbb{SU}$(2), then ${\tau }_G=1$;

(2)

If $\mathbb{G}$ is special orthogonal group $\mathbb{SO}$(3), then ${\tau }_G=1/2$;

(3)

If $\mathbb{G}$ is a commutative (Abelian) group, then ${\tau }_G=0$.

Definition 1

([7]). Let $\mathit{\alpha }\left(s\right)$ and $\widehat{\mathit{\alpha }}\left(s\right)$ be two curves in $\mathbb{G}$; $\mathit{n}\left(s\right)$ and $\widehat{\mathit{n}}\left(\widehat{s}\right)$ are principal normal vectors of them, respectively; {$\mathit{\alpha }\left(s\right)$, $\widehat{\mathit{\alpha }}\left(s\right)$} is named a Bertrand pair if $\mathit{n}\left(s\right)$ and $\widehat{\mathit{n}}\left(\widehat{s}\right)$ are linearly dependent at the corresponding points; $\mathit{\alpha }\left(s\right)$ is named the Bertrand mate of $\widehat{\mathit{\alpha }}\left(s\right)$ and

$$\widehat{\mathit{\alpha }}\left(s\right)=\mathit{\alpha }\left(s\right)+f\mathit{n}\left(s\right).$$

(6)

where f is a stationary.

We signalize a surface M in $\mathbb{G}$ by

$$M:\mathit{y}(s,t)=\left(y_1\left(s,t\right),y_2\left(s,t\right),y_3\left(s,t\right)\right),(s,t)\in \mathbb{D}\subseteq {\mathbb{R}}^2.$$

(7)

If ${\mathit{y}}_j(s,t)=\frac{\partial \mathit{y}}{\partial j}$, the isotropic surface normal is

$$\mathit{N}(s,t)={\mathit{y}}_s\wedge {\mathit{y}}_t,$$

(8)

which is orthogonal to each of the vectors ${\mathit{y}}_s$, and ${\mathit{y}}_t$.

Any curve on a surface M can be the line of curvature under the conditions given by the well-known theorem below. We advise the reader to the following for evidence and specifics [20].

Theorem 1

(Monge’s Theorem). A necessary and sufficient condition for a curve on a surface to be a curvature line is that the surface normals along the curve form a developable surface.

3. Main Results

This section presents an approach for creating a surface family pair interpolating a Bertrand pair as mutual curvature lines in $\mathbb{G}$. With this aim, let $\mathit{\alpha }\left(s\right)$ be a unit speed curve; $\widehat{\mathit{\alpha }}\left(s\right)$ is the Bertrand mate of $\mathit{\alpha }\left(s\right)$ and $\{\widehat{\mathit{t}}\left(s\right),\widehat{\mathit{n}}\left(s\right)$, $\widehat{\mathit{b}}\left(s\right)\}$ is the Frenet–Serret frame of $\widehat{\mathit{\alpha }}\left(s\right)$ as in Equation (5). The surface family M interpolating $\mathit{\alpha }\left(s\right)$ can be written as [7]:

$$M:\mathit{y}(s,t)=\mathit{\alpha }\left(s\right)+a(s,t)\mathit{t}\left(s\right)+b(s,t)\mathit{n}(s)+c(s,t\left)\mathit{b}\right(s);0\le t\le T,$$

(9)

and the surface family $\widehat{M}$ interpolating $\widehat{\mathit{\alpha }}\left(s\right)$ is

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=\widehat{\mathit{\alpha }}\left(s\right)+a(s,t)\widehat{\mathit{t}}\left(s\right)+b(s,t)\widehat{\mathit{n}}\left(s\right)+c(s,t)\widehat{\mathit{b}}\left(s\right);0\le t\le T.$$

(10)

Here $a(s,t),$ $b(s,t)$, $c(s,t)$ are all $C^1$ functions and $0\le t_0\le T,0\le s\le L$. If the parameter t is defined as the time, the functions $a(s,t),$ $b(s,t)$ and $c(s,t)$ can then be named as directed marching distances of a point unit in time t in the orientation t, n and b, respectively, and the vector $\mathit{\alpha }\left(s\right)$ is seen as the initial situation of this point.

Our aim is to gain sufficient and necessary conditions for which the specified curve $\mathit{\alpha }\left(s\right)$ is an isoparametric curvature line on M. At first, since the directrix $\mathit{\alpha }\left(s\right)$ is an isoparametric curve on M, there exists a parameter $t=t_0$ such that $\mathit{\alpha }\left(s\right)=\mathit{y}(s,t_0)$; that is, we have:

$$a(s,t_0)=b(s,t_0)=c(s,t_0)=0,$$

and

$$\frac{\partial a(s,t_0)}{\partial s}=\frac{\partial b(s,t_0)}{\partial s}=\frac{\partial c(s,t_0)}{\partial s}=0.$$

Thus, the normal vector field is

$$\mathit{N}(s,t_0):=\frac{\partial \mathit{y}(s,t_0)}{\partial s}\times \frac{\partial \mathit{y}(s,t_0)}{\partial t}=-\frac{\partial c(s,t_0)}{\partial t}\mathit{n}\left(s\right)+\frac{\partial b(s,t_0)}{\partial t}\mathit{b}\left(s\right),$$

(11)

Secondly, let us choose a unit vector

$$\mathit{e}\left(s\right)=\cos \theta \mathit{n}(s)+\sin \theta \mathit{b}(s).$$

(12)

Then, from Equations (11) and (12), we find that $\mathit{e}(s)\parallel \mathit{N}(s,t_0)$ if and only if there exists a function $\lambda \left(s\right)\ne 0$ such that

$$-\frac{\partial c(s,t_0)}{\partial t}=\lambda \left(s\right)\cos \theta ,\frac{\partial b(s,t_0)}{\partial t}=\lambda \left(s\right)\sin \theta .$$

(13)

Differentiating Equation (12) and using the Serret–Frenet formulae, we find

$${\mathit{e}}^{{}^{\prime }}=({\theta }^{{}^{\prime }}+\tau -{\tau }_G){\mathit{e}}^{\perp }-\kappa \cos \theta \mathit{t}.$$

However, via the Rodrigues’ formula, $\mathit{\alpha }=$ $\mathit{\alpha }\left(s\right)$ is a curvature line on $\mathit{y}(s,t)$ if and only if $\frac{d\theta }{ds}+\tau -{\tau }_G=0.$ This means that

$$\theta \left(s\right)={\theta }_0-\underset{s_0}{\overset{s}{\int }}(\tau \left(s\right)-{\tau }_G\left(s\right))ds,$$

(14)

where $s_0$ is the starting value of arc length and ${\theta }_0=\theta \left(s_0\right)$. The functions $\lambda \left(s\right)$ and $\theta \left(s\right)$ are named controlling functions.

Theorem 2.

$\mathit{\alpha }=\mathit{\alpha }\left(s\right)$ is a curvature line on $\mathit{y}(s,t)$ if and only if

$$\left.\begin{array}{c}a(s,t_0)=b(s,t_0)=c(s,t_0)=0,0\le t_0\le T,0\le s\le L,\lambda \left(s\right)\ne 0,\hfill \\ -\frac{\partial c(s,t_0)}{\partial t}=\lambda \left(s\right)\cos \theta ,\frac{\partial b(s,t_0)}{\partial t}=\lambda \left(s\right)\sin \theta .\hfill \end{array}\right\}$$

(15)

Similarly to [8], for the purpose of facilitation and inspection, we also address the case where the marching-scale functions $a(s,t)$, $b(s,t)$ and $c(s,t)$ can be written into two factors:

$$\begin{array}{c}a(s,t)=l\left(s\right)A\left(t\right),\\ b(s,t)=m\left(s\right)B\left(t\right),\\ c(s,t)=n\left(s\right)C\left(t\right)\end{array}$$

(16)

Here $l\left(s\right)$, $m\left(s\right)$ and $n\left(s\right)$ are $C^1$ functions which are not identically vanishing. Then, from Theorem 1, we gain:

Corollary 1.

$\mathit{\alpha }\left(s\right)$ is a curvature line on $\mathit{y}(s,t)$ if and only if

$$\left.\begin{array}{c}A\left(t_0\right)=B\left(t_0\right)=C\left(t_0\right)=0,0\le t_0\le T,0\le s\le L,\lambda \left(s\right)\ne 0,\hfill \\ -n\left(s\right)\frac{dC\left(t_0\right)}{dt}=\lambda \left(s\right)\cos \theta ,m\left(s\right)\frac{dB\left(t_0\right)}{dt}=\lambda \left(s\right)\sin \theta .\hfill \end{array}\right\}$$

(17)

However, we can allow $a(s,t)$, $b(s,t)$ and $c(s,t)$ based only on the parameter t, that is, $l\left(s\right)=m\left(s\right)=n\left(s\right)=1$. Then, we analyze condition (17) according to the different expressions of $\theta \left(s\right)$:

(i)

In the case of $\tau \left(s\right)\ne {\tau }_G\left(s\right)$, $\theta \left(s\right)$ is a non-constant function of variable s and condition (17) can be displayed as

$$\left.\begin{array}{c}A\left(t_0\right)=B\left(t_0\right)=C\left(t_0\right)=0,\\ -\frac{dC\left(t_0\right)}{dt}=\lambda \left(s\right)\cos \theta ,\frac{dB\left(t_0\right)}{dt}=\lambda \left(s\right)\sin \theta ,\end{array}\right\}$$

(18)

(ii)

In the case of $\tau \left(s\right)={\tau }_G\left(s\right)$, that is the curve is a planar curve, $\theta \left(s\right)={\theta }_0$ is a constant and we have

(a)

In the case of ${\theta }_0\ne 0$, condition (17) can be displayed as

$$\left.\begin{array}{c}A\left(t_0\right)=B\left(t_0\right)=C\left(t_0\right)=0,\\ -\frac{dC\left(t_0\right)}{dt}=\lambda \left(s\right)\cos {\theta }_0,\frac{dB\left(t_0\right)}{dt}=\lambda \left(s\right)\sin {\theta }_0.\end{array}\right\}$$

(19)

(b)

In the case of ${\theta }_0=0$, condition (17) can be displayed as

$$\left.\begin{array}{c}A\left(t_0\right)=B\left(t_0\right)=C\left(t_0\right)=0,\\ -\frac{dC\left(t_0\right)}{dt}=\lambda \left(s\right),\frac{dB\left(t_0\right)}{dt}=0,\end{array}\right\}$$

(20)

and from Equation (17) the normal $\mathit{N}(s,t_0)$ (resp. $\mathit{e}(s)$) is coincident with n. In this case, the curve $\mathit{\alpha }=\mathit{\alpha }\left(s\right)$ is not only a curvature line but also a geodesic. Now, we are dealing with and construct some representative examples to verify the method. Additionally, they serve to confirm the correctness of the formulas obtained previously.

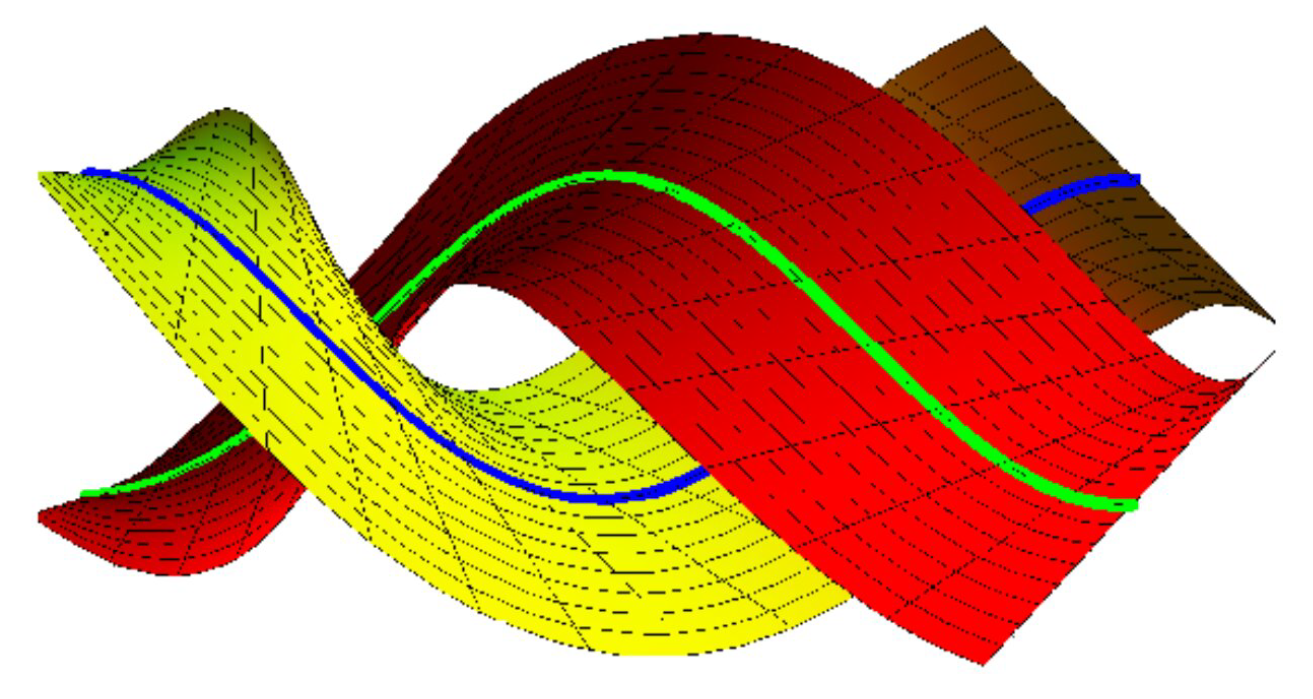
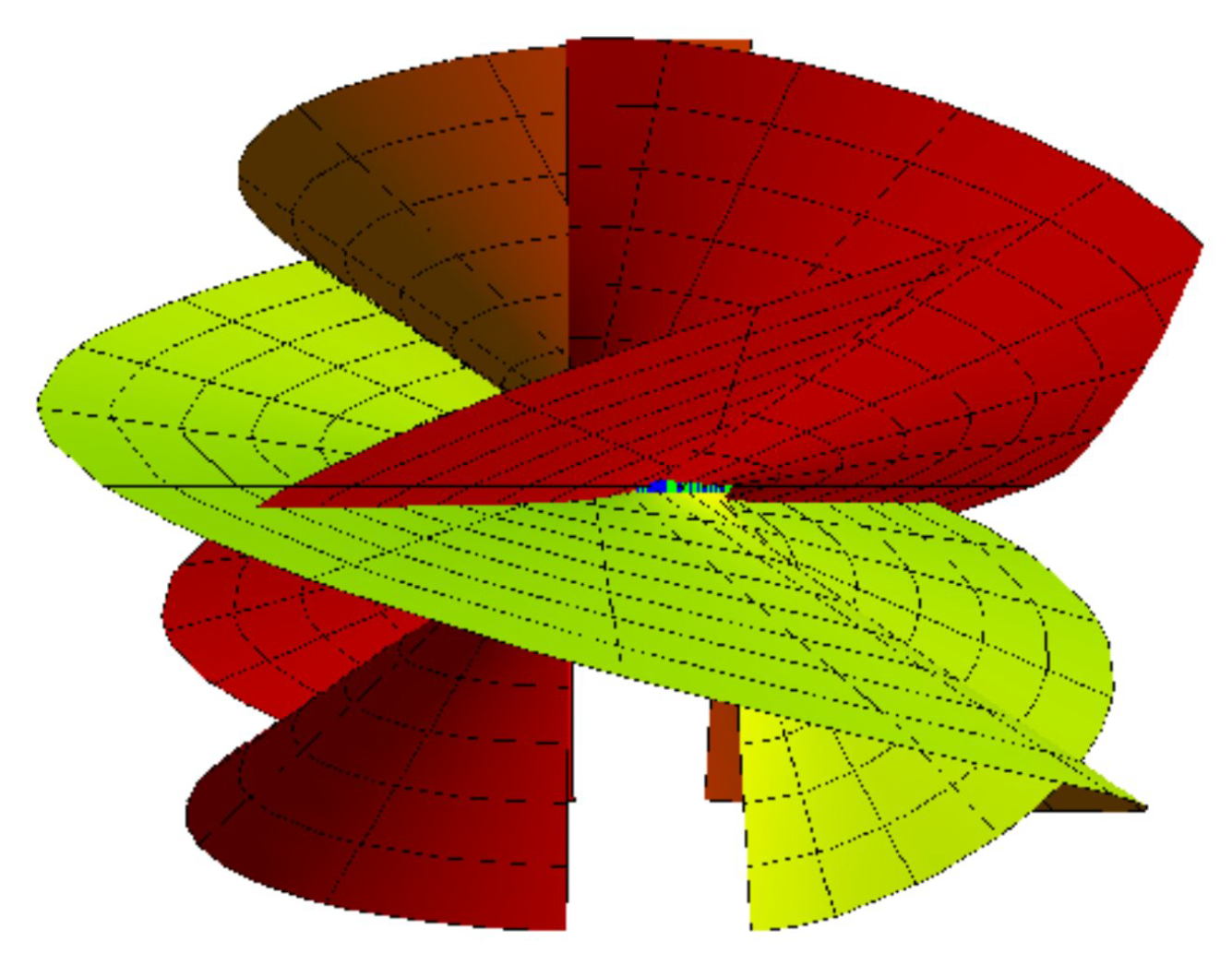
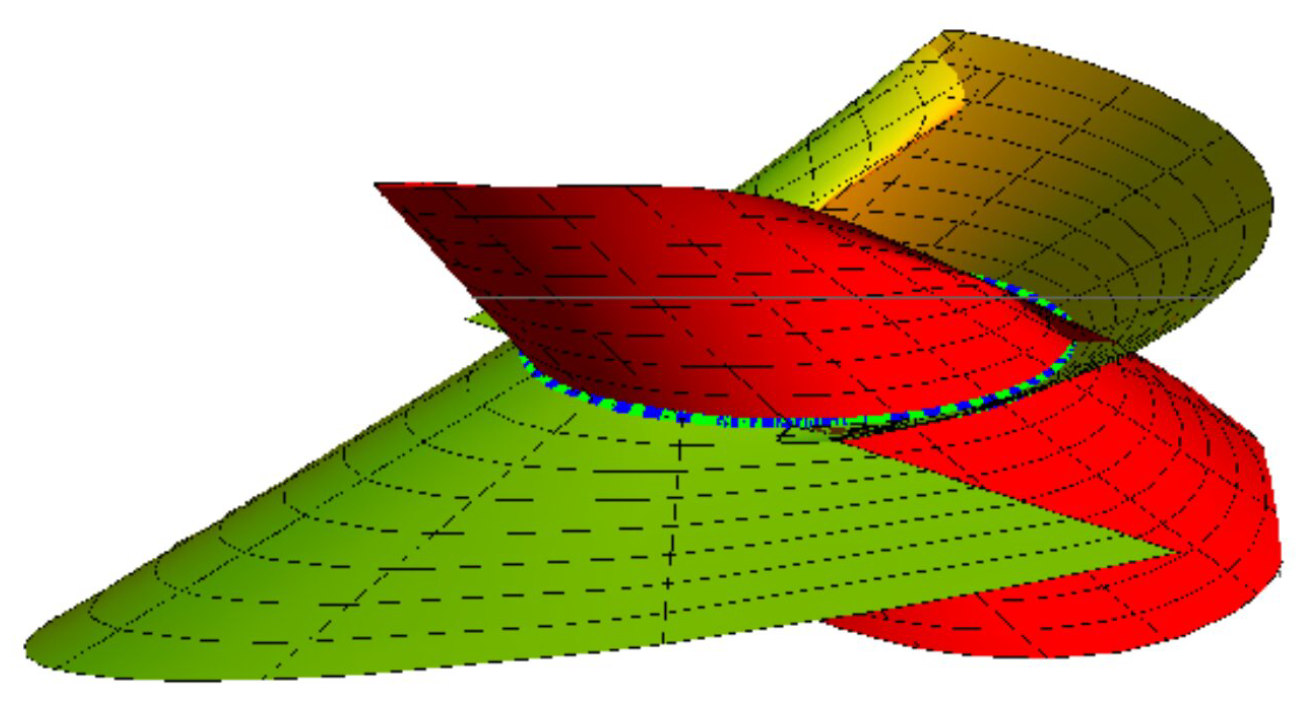
Example 1.

Let $\mathit{\alpha }\left(s\right)$ be a unit speed helix specified by

$$\mathit{\alpha }\left(s\right)=(\frac{1}{\sqrt{2}}\cos s,\frac{1}{\sqrt{2}}\sin s,\frac{s}{\sqrt{2}}),0\le s\le 2\pi .$$

It is clear that

$$\left.\begin{array}{c}\mathit{t}\left(s\right)=\frac{1}{\sqrt{2}}(-\sin s,\cos s,1),\\ \mathit{n}\left(s\right)=(-\cos s,-\sin s,0),\\ \mathit{b}\left(s\right)=\frac{1}{\sqrt{2}}(\sin s,-\cos s,1),\\ \kappa \left(s\right)=\tau \left(s\right)=\frac{1}{\sqrt{2}},{\tau }_G\left(s\right)=0.\end{array}\right\}$$

So, the curve $\mathit{\alpha }\left(s\right)$ is a helix in a commutative group $\mathbb{G}$. Then, $\theta \left(s\right)=-\frac{s}{\sqrt{2}}+{\theta }_0$. If ${\theta }_0=0$, we have $\theta \left(s\right)=-\frac{s}{\sqrt{2}}$. By choosing

$$\begin{array}{ccc}\hfill l\left(s\right)& =& m\left(s\right)=n\left(s\right)=1,\hfill \\ \hfill A\left(t\right)& =& t,B\left(t\right)=-t\lambda \left(s\right)\sin \frac{s}{\sqrt{2}},C\left(t\right)=-t\lambda \left(s\right)\cos \frac{s}{\sqrt{2}},\lambda \left(s\right)\ne 0,\hfill \end{array}$$

and from Equation (9), we attain

$$\begin{array}{ccc}\hfill M& :& \mathit{y}(s,t)=(\frac{1}{\sqrt{2}}\cos s,\frac{1}{\sqrt{2}}\sin s,\frac{s}{\sqrt{2}})+t(1,-\lambda \sin \frac{s}{\sqrt{2}},-\lambda \cos \frac{s}{\sqrt{2}})\hfill \\ & & \times \left(\begin{array}{ccc}-\frac{1}{\sqrt{2}}\sin s& \frac{1}{\sqrt{2}}\cos s& \frac{1}{\sqrt{2}}\\ -\cos s& -\sin s& 0\\ \frac{1}{\sqrt{2}}\sin s& -\frac{1}{\sqrt{2}}\cos s& \frac{1}{\sqrt{2}}\end{array}\right).\hfill \end{array}$$

Hence, the surface family $\widehat{M}$ interpolating $\widehat{\mathit{\alpha }}$ is: let $f=\sqrt{2}$ in Equation (6), we obtain

$$\widehat{\mathit{\alpha }}\left(s\right)=(-\frac{1}{\sqrt{2}}\cos s,-\frac{1}{\sqrt{2}}\sin s,\frac{s}{\sqrt{2}}).$$

The Serret–Frenet vectors of $\widehat{\mathit{\alpha }}\left(s\right)$ are found as

$$\widehat{\mathit{t}}\left(s\right)=\frac{1}{\sqrt{2}}(\sin s,-\cos s,1),\widehat{\mathit{n}}\left(s\right)=(\cos s,\sin s,0),\widehat{\mathit{b}}\left(s\right)=\frac{1}{\sqrt{2}}(-\sin s,\cos s,1).$$

Then, we have

$$\begin{array}{ccc}\hfill \widehat{M}& :& \widehat{\mathit{y}}(s,t)=(-\frac{1}{\sqrt{2}}\cos s,-\frac{1}{\sqrt{2}}\sin s,\frac{s}{\sqrt{2}})+t(1,-\lambda \sin \frac{s}{\sqrt{2}},-\lambda \cos \frac{s}{\sqrt{2}})\hfill \\ & & \times \left(\begin{array}{ccc}\frac{1}{\sqrt{2}}\sin s& -\frac{1}{\sqrt{2}}\cos s& \frac{1}{\sqrt{2}}\\ \cos s& \sin s& 0\\ -\frac{1}{\sqrt{2}}\sin s& \frac{1}{\sqrt{2}}\cos s& \frac{1}{\sqrt{2}}\end{array}\right).\hfill \end{array}$$

Hence, for $\lambda =1$, $-2\le$ $t\le 2$ and $0\le$ $s\le 2\pi$ the corresponding surfaces are shown in Figure 1, where the blue curve represents $\mathit{\alpha }\left(s\right)$, the green curve $\widehat{\mathit{\alpha }}\left(s\right)$.

Example 2.

Let $\mathit{\alpha }\left(s\right)$ be

$$\mathit{\alpha }\left(s\right)=(\cos s,\sin s,0),0\le s\le 2\pi .$$

Then,

$$\mathit{t}\left(s\right)=(-\sin s,\cos s,0),\mathit{n}\left(s\right)=(-\cos s,-\sin s,0),\mathit{b}\left(s\right)=(0,0,1).$$

The curvature of this curve is $\kappa =1$, $\tau =0$ and ${\tau }_G\left(s\right)=\frac{1}{2}$. Thus, the curve $\mathit{\alpha }\left(s\right)$ is a circle in $\mathbb{SO}$(3) and $\theta \left(s\right)=\frac{s}{2}$. By choosing

$$\begin{array}{ccc}\hfill l\left(s\right)& =& m\left(s\right)=n\left(s\right)=1,\hfill \\ \hfill A\left(t\right)& =& t,B\left(t\right)=t\lambda \left(s\right)\sin \frac{s}{2},-C\left(t\right)=t\lambda \left(s\right)\cos \frac{s}{2},\lambda \ne 0,\hfill \end{array}$$

Then,

$$M:\mathit{y}(s,t)=(\cos s,\sin s,0)+t(1,-\lambda \left(s\right)\sin \frac{s}{2},\lambda \cos \frac{s}{2})\left(\begin{array}{ccc}-\sin s& \cos s& 0\\ -\cos s& -\sin s& 0\\ 0& 0& 1\end{array}\right).$$

Let $f=2$ in Equation (6), we get

$$\widehat{\mathit{\alpha }}\left(s\right)=(-\cos s,-\sin s,0),$$

and

$$\widehat{t}\left(s\right)=(\sin s,-\cos s,0),\widehat{n}\left(s\right)=(\cos s,\sin s,0),\widehat{\mathit{b}}\left(s\right)=(0,0,1).$$

Similarly, the surface family $\widehat{M}$ interpolating $\widehat{\mathit{\alpha }}$ is

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=(-\cos s,-\sin s,0)+t(1,-\lambda \left(s\right)\sin \frac{s}{2},\lambda \cos \frac{s}{2})\left(\begin{array}{ccc}\sin s& -\cos s& 0\\ \cos s& \sin s& 0\\ 0& 0& 1\end{array}\right).$$

For $\lambda =1$, $-5\le$ $t\le 5$ and $0\le$ $s\le 2\pi$ thecorresponding surfaces are shown in Figure 2, where the blue curve represents $\mathit{\alpha }\left(s\right)$, the green curve $\widehat{\mathit{\alpha }}\left(s\right)$.

Ruled Surface Family Pair Interpolating Bertrand Pair as Mutual Curvature Lines

Ruled surfaces are simple and mutual surfaces in geometric designs. Suppose $\mathit{y}(s,t)$ is a ruled surface with the directrix $\mathit{\alpha }\left(s\right)$ and $\mathit{\alpha }\left(s\right)$ is also an iso-parametric curve of $\mathit{y}(s,t)$, then there exists $t_0$ such that $\mathit{y}(s,t_0)=\mathit{\alpha }\left(s\right)$. It follows that the surface can be parameterized as

$$M:\mathit{y}(s,t)-\mathit{y}(s,t_0)=(t-t_0)\mathit{e}\left(s\right),0\le s\le L,\mathrm{with}t,t_0\in [0,T],$$

(21)

where $\mathit{e}\left(s\right)$ defines the direction of the rulings. In view of Equation (9), we have

$$(t-t_0)\mathit{e}\left(s\right)=a(s,t)\mathit{t}\left(s\right)+b(s,t)\mathit{n}(s)+c(s,t)\mathit{b}(s),$$

(22)

where $0\le s\le L,$ with $t,t_0\in [0,T]$. In fact, Equation (22) is a system of equations with three unknown functions $a(s,t),$ $b(s,t)$ and $c(s,t)$. The solutions of the above system can be deduced as

$$\begin{array}{c}a(s,t)=(t-t_0)<\mathit{e}\left(s\right),\mathit{t}\left(s\right)>,\\ b(s,t)=(t-t_0)<\mathit{e}\left(s\right),\mathit{n}\left(s\right)>,\\ c(s,t)=(t-t_0)<\mathit{e}\left(s\right),\mathit{b}\left(s\right)>.\end{array}$$

(23)

According to condition (15), if $\mathit{\alpha }\left(s\right)$ is a curvatureline of the surface $\mathit{y}(s,t)$, we have

$$\begin{array}{c}a(s,t)=0,\\ \lambda \left(s\right)\sin \theta =<\mathit{e}\left(s\right),\mathit{n}\left(s\right)>,\\ -\lambda \left(s\right)\cos \theta =<\mathit{e}\left(s\right),\mathit{b}\left(s\right)>.\end{array}$$

(24)

The above equations are simply the necessary and sufficient conditions forwhich $\mathit{y}(s,t)$ is a ruled surface with a directrix $\mathit{\alpha }\left(s\right)$. Suppose at all point on $\mathit{\alpha }\left(s\right)$ the ruling

$$\mathit{e}\left(s\right)=\upsilon \left(s\right)\mathit{t}\left(s\right)+\sigma \left(s\right)\mathit{n}\left(s\right)+\mu \left(s\right)\mathit{b}\left(s\right),$$

then

$$\sigma \left(s\right)=\lambda \left(s\right)\sin \theta ,\mu \left(s\right)=-\lambda \left(s\right)\cos \theta ,$$

that is,

$$\mathit{e}\left(s\right)=\upsilon \left(s\right)\mathit{t}\left(s\right)+\lambda \left(s\right)\sin \theta \mathit{n}\left(s\right)-\lambda \left(s\right)\cos \theta \mathit{b}\left(s\right).$$

Choosing $a(s,t)=t\upsilon \left(s\right)$, $b(s,t)=t\lambda \left(s\right)\sin \theta$ and $c(s,t)=-t\lambda \left(s\right)\cos \theta$, the ruled surface family M with $\mathit{\alpha }\left(s\right)$ can be displayed as

$$\mathit{y}(s,t)=\mathit{\alpha }\left(s\right)+t\upsilon \left(s\right)\mathit{t}\left(s\right)+t\lambda \left(s\right)\left(\sin \theta \mathit{n}\right(s)-\cos \theta \mathit{b}(s\left)\right),0\le s\le L,0\le t\le T.$$

(25)

And, the ruled surface family interpolating $\widehat{\mathit{\alpha }}\left(s\right)$ is

$$\widehat{\mathit{y}}(s,t)=\widehat{\mathit{\alpha }}\left(s\right)+t\upsilon \left(s\right)\widehat{\mathit{t}}\left(s\right)+t\lambda \left(s\right)(\sin \theta \widehat{\mathit{n}}\left(s\right)-\cos \theta \widehat{\mathit{b}}\left(s\right)),0\le s\le L,0\le t\le T.$$

(26)

The functions $\upsilon \left(s\right)$ and $\lambda \left(s\right)$ can control the shape of the surface family M.

Example 3.

In view of Example 1, we have:

(1)

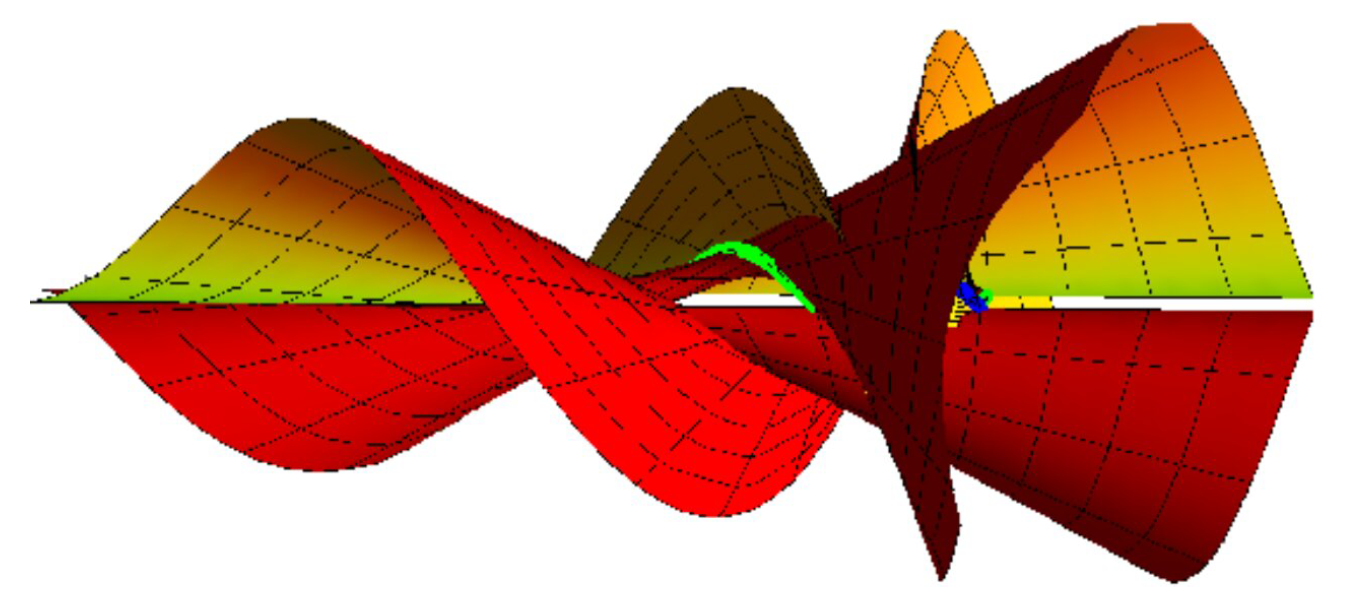
By taking $\upsilon \left(s\right)=\lambda \left(s\right)=s$ the {$\widehat{M}$, M} interpolating {$\widehat{\mathit{\alpha }}\left(s\right)$, $\mathit{\alpha }\left(s\right)$} are (Figure 3):

$$M:\mathit{y}(s,t)=\left(\begin{array}{c}\frac{1}{\sqrt{2}}(\cos s-st\sin s)-st(\sin \frac{s}{2}\sin s+\frac{1}{\sqrt{2}}\cos \frac{s}{2}\cos s)\\ \frac{1}{\sqrt{2}}(\sin s+st\cos s)+st(-\sin \frac{s}{2}\sin s+\frac{1}{\sqrt{2}}\cos \frac{s}{2}\cos s)\\ \frac{s}{\sqrt{2}}(1+t(1-\cos \frac{s}{2}))\end{array}\right),$$

and

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=\left(\begin{array}{c}\frac{1}{\sqrt{2}}(-\cos s+st\sin s)+st(\sin \frac{s}{2}\cos s+\frac{1}{\sqrt{2}}\cos \frac{s}{2}\sin s)\\ -\frac{1}{\sqrt{2}}(\sin s+st\cos s)+st(\sin \frac{s}{2}\sin s-\frac{1}{\sqrt{2}}\cos \frac{s}{2}\cos s)\\ \frac{s}{\sqrt{2}}(1+t(1-\cos \frac{s}{2}))\end{array}\right),$$

where the blue curve represents $\mathit{\alpha }\left(s\right)$, the green curve is $\widehat{\mathit{\alpha }}\left(s\right)$, $-1\le t\le 1$ and $0\le s\le 2\pi$.

(2)

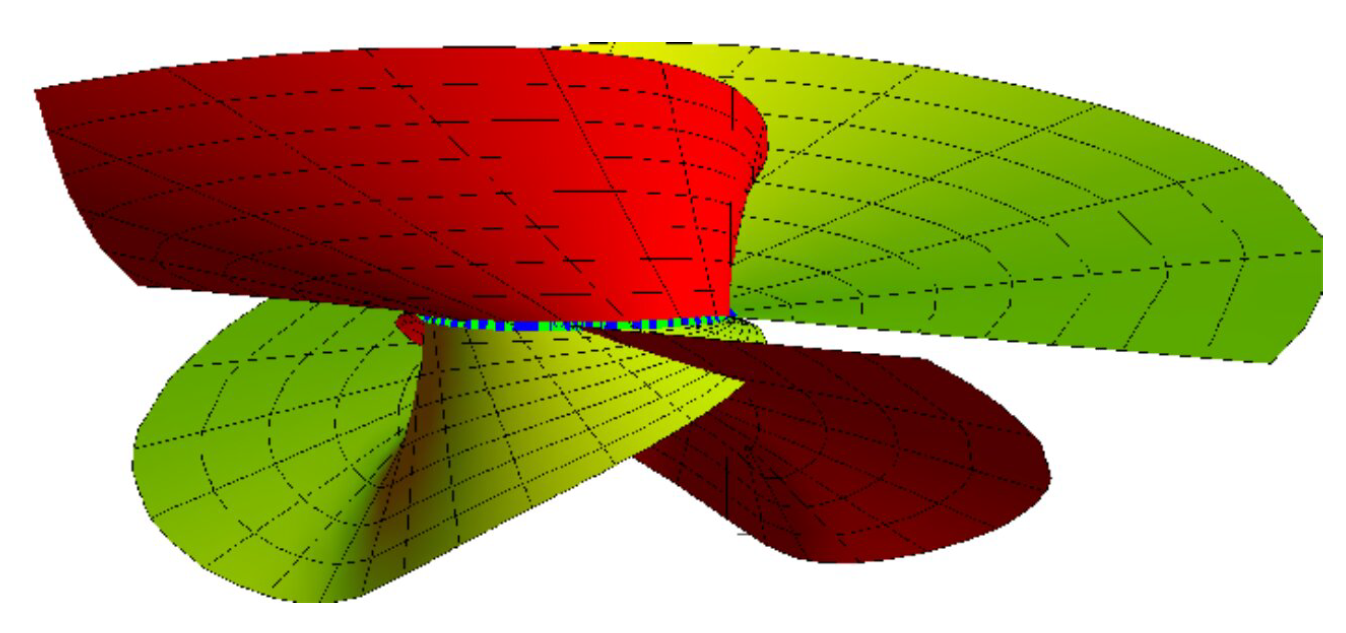
By taking $\upsilon \left(s\right)=\lambda \left(s\right)=\sqrt{s}$ the {$\widehat{M}$, M} with {$\widehat{\mathit{\alpha }}\left(s\right)$, $\mathit{\alpha }\left(s\right)$} as mutual Bertrand-curvature line curves are (Figure 4):

$$M:\mathit{y}(s,t)=\left(\begin{array}{c}\frac{1}{\sqrt{2}}(\cos s-\sqrt{s}t\sin s)-\sqrt{s}t(\sin \frac{s}{2}\sin s+\frac{1}{\sqrt{2}}\cos \frac{s}{2}\cos s)\\ \frac{1}{\sqrt{2}}(\sin s+\sqrt{s}t\cos s)+\sqrt{s}t(-\sin \frac{s}{2}\sin s+\frac{1}{\sqrt{2}}\cos \frac{s}{2}\cos s)\\ \sqrt{\frac{s}{2}}(\sqrt{s}+t(1-\cos \frac{s}{2}))\end{array}\right),$$

and

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=\left(\begin{array}{c}\frac{1}{\sqrt{2}}(-\cos s+\sqrt{s}t\sin s)+\sqrt{s}t(\sin \frac{s}{2}\cos s+\frac{1}{\sqrt{2}}\cos \frac{s}{2}\sin s)\\ -\frac{1}{\sqrt{2}}(\sin s+\sqrt{s}t\cos s)+\sqrt{s}t(\sin \frac{s}{2}\sin s-\frac{1}{\sqrt{2}}\cos \frac{s}{2}\cos s)\\ \sqrt{\frac{s}{2}}(\sqrt{s}+t(1-\cos \frac{s}{2}))\end{array}\right),$$

where the blue curve represents $\mathit{\alpha }\left(s\right)$, the green curve is $\widehat{\mathit{\alpha }}\left(s\right)$, $-1\le t\le 1$ and $0\le s\le 2\pi$.

Example 4.

In view of Example 2, we have:

(1)

By taking $\upsilon \left(s\right)=\lambda \left(s\right)=s$ the {$\widehat{M}$, M} interpolating {$\widehat{\mathit{\alpha }}\left(s\right)$, $\mathit{\alpha }\left(s\right)$} are (Figure 5):

$$M:\mathit{y}(s,t)=\left(\begin{array}{c}(1-st\cos \frac{s}{2})\cos s-st\sin s\\ (1-st\cos \frac{s}{2})\sin s+st\cos a\\ -st\sin \frac{s}{2}\end{array}\right),$$

and

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=\left(\begin{array}{c}-(1-st\cos \frac{s}{2})\cos s+st\sin s\\ -(1-st\cos \frac{s}{2})\sin s-st\cos a\\ -st\sin \frac{s}{2}\end{array}\right),$$

where the blue curve represents $\mathit{\alpha }\left(s\right)$, the green curve is $\widehat{\mathit{\alpha }}\left(s\right)$, $-0.5\le t\le 0.5$ and $0\le s\le 2\pi$

(2)

By taking $\upsilon \left(s\right)=\lambda \left(s\right)=\sqrt{s}$ the {$\widehat{M}$, M} interpolating {$\widehat{\mathit{\alpha }}\left(s\right)$, $\mathit{\alpha }\left(s\right)$} are (Figure 6):

$$M:\mathit{y}(s,t)=\left(\begin{array}{c}(1-\sqrt{s}t\cos \frac{s}{2})\cos s-\sqrt{s}t\sin s\\ (1-\sqrt{s}t\cos \frac{s}{2})\sin s+\sqrt{s}t\cos a\\ -\sqrt{s}t\sin \frac{s}{2}\end{array}\right),$$

and

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=\left(\begin{array}{c}-(1-\sqrt{s}t\cos \frac{s}{2})\cos s+\sqrt{s}t\sin s\\ -(1-\sqrt{s}t\cos \frac{s}{2})\sin s-\sqrt{s}t\cos a\\ -\sqrt{s}t\sin \frac{s}{2}\end{array}\right),$$

where the blue curve represents $\mathit{\alpha }\left(s\right)$, the green curve is $\widehat{\mathit{\alpha }}\left(s\right)$, $-0.5\le t\le 0.5$ and $0\le s\le 2\pi .$

4. Conclusions

In this paper, we considered the problem of how to establish a surface family pair interpolating a Bertrand pair as mutual curvature lines in a three-dimensional Lie group $\mathbb{G}$. The extension to ruled surfaces is also outlined. Meanwhile, some curves are selected to organize the surface family and ruled surface family interpolating the Bertrand pair as mutual curvature lines. An analogue of the problem considered in this paper may be consider for Minkowski 3-space. We will study this problem in the future.