Quantized Control for Local Synchronization of Fractional-Order Neural Networks with Actuator Saturation
Abstract
:1. Introduction
2. Preliminaries
3. Local Synchronization Results
3.1. Main Theorem
3.2. Optimization Algorithms
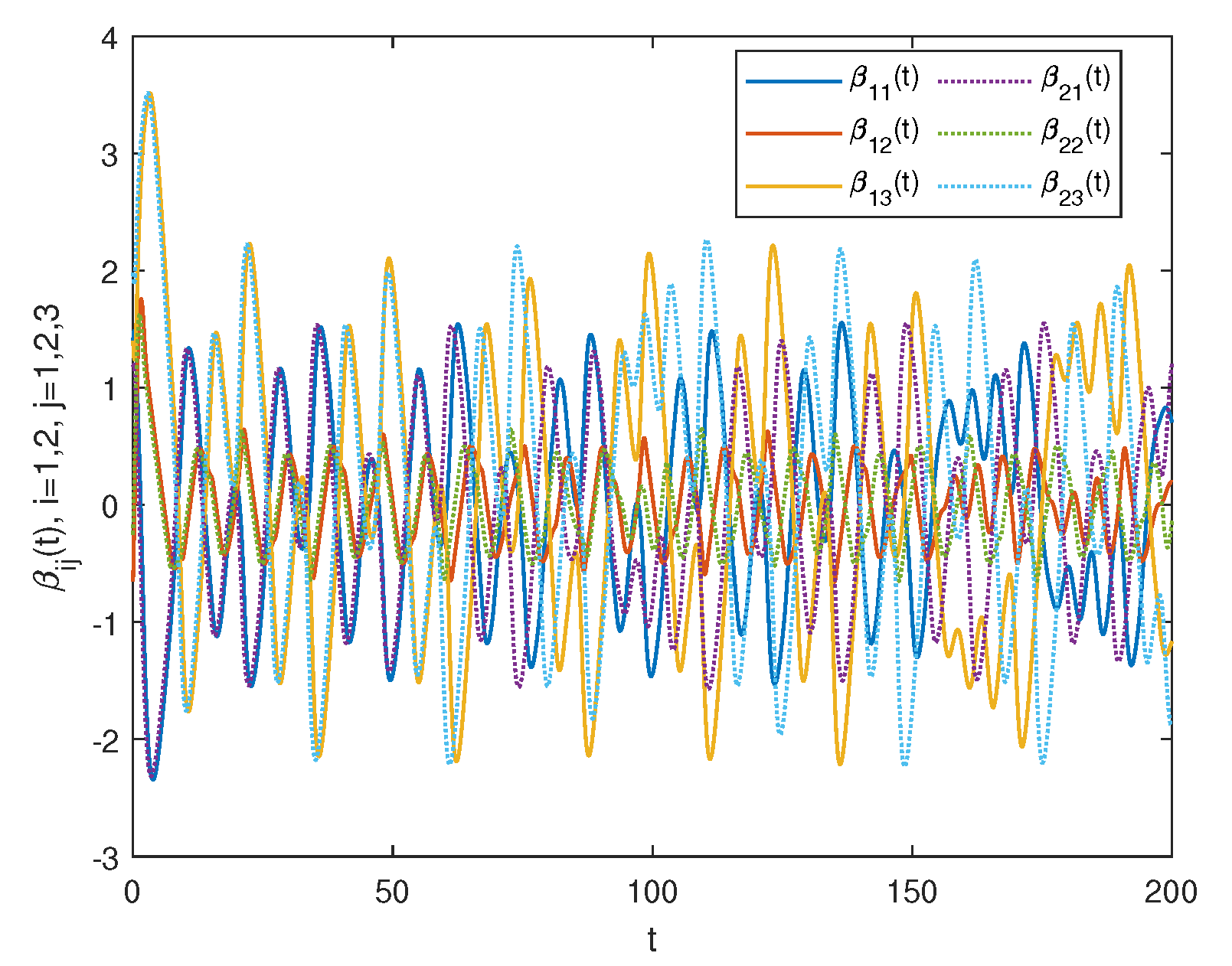
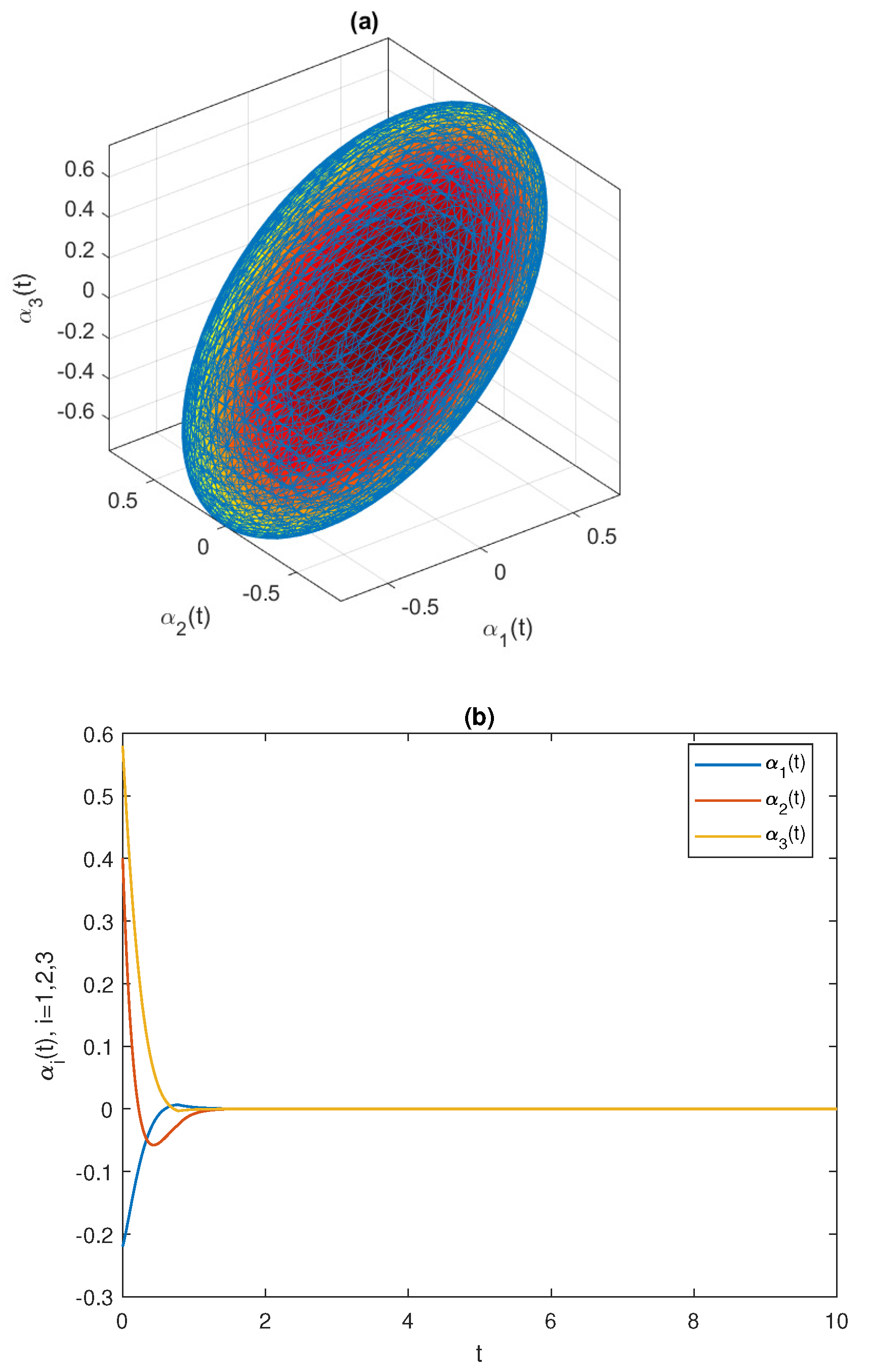
4. Numerical Simulations
4.1. Simulation Based on Algorithm 1
4.2. Simulation Based on Algorithm 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, W.; Luo, T.; Tang, Y.; Du, W.; Tian, Y.; Qian, F. Secure communication based on quantized synchronization of chaotic neural networks under an event-triggered strategy. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3334–3345. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jiang, S.; Ge, M.; Hu, C.; Hu, J. Finite-/fixed-time synchronization of memristor chaotic systems and image encryptio application. IEEE Trans. Circuits Syst. I Reg. Pap. 2021, 68, 4957–4969. [Google Scholar] [CrossRef]
- Chen, H.; Liang, J. Local synchronization of interconnected Boolean networks with stochastic disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 452–463. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Net. 2012, 32, 245–256. [Google Scholar] [CrossRef]
- Sajid, M.; Chaudhary, H.; Kaushik, S. Chaos controllability in non-identical complex fractional order chaotic systems via active complex synchronization technique. Axioms 2023, 12, 530. [Google Scholar] [CrossRef]
- Tural-Polat, S.N. Solution method for systems of nonlinear fractional differential equations using third kind chebyshev wavelets. Axioms 2023, 12, 546. [Google Scholar] [CrossRef]
- Huang, C.; Nie, X.; Zhao, X. Novel bifurcation results for a delayed fractional-order quaternion-valued neural network. Neural Net. 2019, 117, 67–93. [Google Scholar] [CrossRef]
- Chen, L.; Yin, H.; Wu, X. Robust dissipativity and dissipation of a class of fractional-order uncertain linear systems. IET Control Theory Appl. 2019, 13, 1454–1465. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Westerlund, S.; Ekstam, L. Capacitor theory. IEEE Trans. Dielect. Electron. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Hristova, S.; O’Regan, D. Mittag-Leffler-type stability of BAM neural networks modeled by the generalized proportional Riemann-Liouville fractional derivative. Axioms 2023, 12, 588. [Google Scholar] [CrossRef]
- Abdelouahab, M.; Lozi, R.; Chua, L. Memfractance: A mathematical paradigm for circuit elements with memory. Int. J. Bifurc. Chaos 2014, 24, 1430023. [Google Scholar] [CrossRef]
- Lundstrom, B.; Higgs, M.; Spain, W. Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 2008, 11, 1335–1342. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Hu, C.; Jiang, H.; Fan, X. Projective synchronization for fractional neural networks. Neural Net. 2014, 49, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Park, J.; Cao, J.D. Adaptive synchronization of fractional-order output-coupling neural networks via quantized output control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3230–3239. [Google Scholar] [CrossRef]
- Ding, Z.; Zeng, Z.; Wang, L. Robust finite-time stabilization of fractional-order neural networks with discontinuous and continuous activation functions under uncertainty. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1477–1490. [Google Scholar] [CrossRef]
- Yang, Y.; He, Y.; Wu, M. Intermittent control strategy for synchronization of fractional-order neural networks via piecewise Lyapunov function method. J. Franklin Inst. 2019, 356, 4648–4676. [Google Scholar] [CrossRef]
- Song, X.; Man, J.; Song, S. Event-triggered synchronisation of Markovian reaction-diffusion inertial neural networks and its application in image encryption. IET Control Theory Appl. 2020, 14, 2726–2740. [Google Scholar] [CrossRef]
- Zhai, Z.; Yan, H.; Chen, S.; Zhan, X.; Zeng, H. Further results on dissipativity analysis for TS fuzzy systems based on sampled-data control. IEEE Trans. Fuzzy Syst. 2023, 31, 660–668. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Joo, Y. Decentralized H∞ sampled-data fuzzy filter for nonlinear interconnected oscillating systems with uncertain interconnections. IEEE Trans. Fuzzy Syst. 2020, 28, 487–498. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Shen, B. Exponential dynchronization for delayed dynamical networks via intermittent control: Dealing with actuator saturations. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1000–1012. [Google Scholar] [CrossRef]
- Zhou, H.; Tong, S. Adaptive neural network event-triggered output-feedback containment control for nonlinear MASs with input quantization. IEEE Trans. Cybern. 2023. [Google Scholar] [CrossRef] [PubMed]
- Aravind, R.; Balasubramaniam, P. Membership-function-dependent design of quantized fuzzy sampled-data controller for Semi-Markovian jump systems with actuator faults. IEEE Trans. Fuzzy Syst. 2023, 31, 40–52. [Google Scholar] [CrossRef]
- Fu, M.; Xie, L. The sector bound approach to quantized feedback control. IEEE Trans. Autom. Control 2005, 50, 106–111. [Google Scholar]
- Zhang, S.; Yu, Y.; Yu, J. LMI conditions for global stability of fractional-order neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2423–2433. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, J. Global stabilization of fractional-order bidirectional associative memory neural networks with mixed time delays via adaptive feedback control. Int. J. Comput. Math. 2020, 97, 2074–2090. [Google Scholar] [CrossRef]
- Rajchakit, G.; Pratap, A.; Raja, R. Hybrid control scheme for projective lag synchronization of Riemann-Liouville sense fractional order memristive BAM neural networks with mixed delays. Mathematics 2019, 7, 759. [Google Scholar] [CrossRef]
- Rajchakit, G.; Chanthorn, P.; Kaewmesri, P. Global Mittag-Leffler stability and stabilization analysis of fractional-order quaternion-valued memristive neural networks. Mathematics 2020, 8, 42. [Google Scholar] [CrossRef]
- Gomes da Silva, M.; Tarbouriech, S. Anti-windup design with guaranteed region of stability: An LMI-based approach. IEEE Trans. Autom. Control 2005, 50, 1698–1711. [Google Scholar]
- Seuret, A.; Gomes da Silva, M. Taking into account period variations and actuator saturation in sampled-data systems. Syst. Control Lett. 2012, 61, 1286–1293. [Google Scholar] [CrossRef]
- Sang, H.; Zhao, J. Exponential synchronization and L2-gain analysis of delayed chaotic neural networks via intermittent control with actuator saturation. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3722–3734. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Phat, V.N.; Thanh, N.T. New criteria for finite-time stability of nonlinear fractional-order delay systems: A Gronwall inequality approach. Appl. Math. Lett. 2018, 83, 169–175. [Google Scholar] [CrossRef]
- Lazarevic, M.; Spasic, A. Finite-time stability analysis of fractional order time-delay systems: Gronwall approach. Math. Comput. Model. 2009, 49, 475–481. [Google Scholar] [CrossRef]


| 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | |
| 3.0547 | 4.2048 | 5.8199 | 8.1187 | 11.4276 | |
| 0.2694 | 0.4014 | 0.5933 | 0.8725 | 1.2808 | |
| 1.3021 | 1.7813 | 2.4525 | 3.4088 | 4.7876 | |
| 1.4831 | 2.0221 | 2.7740 | 3.8374 | 5.3592 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Li, M. Quantized Control for Local Synchronization of Fractional-Order Neural Networks with Actuator Saturation. Axioms 2023, 12, 815. https://doi.org/10.3390/axioms12090815
Fan S, Li M. Quantized Control for Local Synchronization of Fractional-Order Neural Networks with Actuator Saturation. Axioms. 2023; 12(9):815. https://doi.org/10.3390/axioms12090815
Chicago/Turabian StyleFan, Shuxian, and Meixuan Li. 2023. "Quantized Control for Local Synchronization of Fractional-Order Neural Networks with Actuator Saturation" Axioms 12, no. 9: 815. https://doi.org/10.3390/axioms12090815
APA StyleFan, S., & Li, M. (2023). Quantized Control for Local Synchronization of Fractional-Order Neural Networks with Actuator Saturation. Axioms, 12(9), 815. https://doi.org/10.3390/axioms12090815





