Abstract
Physics-informed neural networks (PINNs) have been widely used to solve partial differential equations in recent years. But studies have shown that there is a gradient pathology in PINNs. That is, there is an imbalance gradient problem in each regularization term during back-propagation, which makes it difficult for neural network models to accurately approximate partial differential equations. Based on the depth-weighted residual neural network and neural attention mechanism, we propose a new mixed-weighted residual block in which the weighted coefficients are chosen autonomously by the optimization algorithm, and one of the transformer networks is replaced by a skip connection. Finally, we test our algorithms with some partial differential equations, such as the non-homogeneous Klein–Gordon equation, the (1+1) advection–diffusion equation, and the Helmholtz equation. Experimental results show that the proposed algorithm significantly improves the numerical accuracy.
1. Introduction
In real life, many problems are represented by partial differential equations (PDEs), such as the advection–diffusion equation, the wave equation, and the Klein–Gordon equation. So, solving the partial differential equations [1,2,3,4] is of great practical significance. Traditional numerical methods: finite volume [5], finite element [6], and finite difference [7] have been very mature in solving partial differential equations. With the rapid development of computers, neural networks have been applied to many fields, such as computer vision, image processing, etc. In recent years, neural networks have been widely used to solve partial differential equations [8,9,10,11].
In the past few years, many neural network algorithms for solving partial differential equations have been proposed. The most representative of which are the physics-informed neural networks (PINNs) [12,13,14]. The PINNs algorithm integrates the control equation into the neural network, and constructs a loss function according to the control equation to constrain the space of the solution so that the final result naturally satisfies the constraints of the control equation. When the loss function tends to zero, we can obtain an approximate solution to the problem. At the same time, many improved and extended algorithms of PINNs have been proposed, such as conservative physics-informed neural networks based on domain decomposition [15], BPINN and UQPINN [16,17] based on uncertainty theory and Bayesian theory, Fourier neural network operators [18] etc. But using the governing equation as a regularization term leads to unstable and erroneous predictions in some cases. In [19], a fundamental failure mode of the stiffness-related physics-informed neural network in gradient flow dynamics is explored. Revealing that in some cases, PINNs have an imbalance gradient problem between the regularization terms during back-propagation. In order to alleviate the problem of unbalanced gradients between the regular terms, inspired by the extended stochastic gradient descent algorithm [20], a learning rate annealing program [19] and an improved fully connected neural network that are elastic for gradient pathology are proposed. At the same time, the convergence speed of the PINNs algorithm is slow and unstable. Based on the Galerkin method, a variational physics-informed neural networks (VPINNs) [21,22] algorithm was proposed. The principle of the VPINNs algorithm is to derive the variational form of partial differential equations based on the Galerkin method, and construct the loss function using the variational form of the partial differential equation. And we can reduce the order of the differential operator through integration by parts, making the problem easier to solve. Moreover, based on the intuitive understanding and prior knowledge of the computational domain, we can adaptively split the computational domain [15] and design the appropriate neural network model on each sub-domain separately to improve numerical accuracy; We only need to specifically deal with the common boundaries of different subdomains to ensure the continuity of the global solution.
In this paper, a mixed-weighted deep residual neural network (M-WDRNN) algorithm based on the decoder–encoder framework in the attention mechanism [23,24] and deep-weighted residual neural network is proposed. M-WDRNN can alleviate the gradient pathology and degradation problems. Moreover, the weighted coefficient of the weighted residual block is used as a trainable parameter to participate in the model training, and the optimal parameter is selected according to the optimization algorithm, which saves the adjustment time of the hyperparameters. Finally, the experimental results show the effectiveness of the algorithm we proposed.
The rest of this article is organized as follows: In Section 2, we describe the problem to be solved, deriving the loss function of PINNs and VPINNs in detail; We describe in detail the structure of a mixed-weighted residual neural network in Section 3; The proposed algorithm is applied to solve PDEs in Section 4, including the advection diffusion equation, the Helmholtz equation, and the Klein–Gordon equation, to demonstrate the performance of the proposed algorithm; Finally, in Section 5, we summarize the contributions and shortcomings of the article, and briefly describe future work.
2. Problem Description
When using neural networks to approximate partial differential equations, PINNs and fully connected neural networks have no essential differences in network structure. The difference between the two is that to construct different loss functions. Compared with fully connected neural networks, PINNs is to incorporate the governing equation into the construction of the loss function. Next, the following equations were considered:
where ℓ, , and represent the differential operator, the boundary operator, and the initial condition, respectively, X denotes the bounded open set. According to Equation (1), we can define PINN’s loss function:
where represent the residual points, boundary points, and initial points, respectively. The parameters represent the weight of residual terms in the loss function, which is used to adjust the weight of the residual terms in the loss function [19]. Although PINNs incorporate the governing equation into the construction of the loss function so that the training results naturally meet the constraints of the governing equation. The training process is unstable, the convergence rate is slow, and it does not necessarily converge. Thus, based on the Galerkin method, variational physics-informed neural networks (VPINNs) [21,22] were proposed, a method that multiplies the residuals of the governing equation with some properly chosen test functions and integrates over the entire computational domain to obtain the variational form of Equation (2):
Further, the loss function:
To reduce convergence time and training costs, variational physics-informed neural networks with domain decomposition (hp-VPINNs) [25] were proposed.
3. Improved Weighted Residual Neural Network
3.1. Weighted Residual Blocks
Many studies [26,27,28] have shown that the performance of neural network models is positively correlated with the number of neural layers in the network. But experimental results show that as the number of layers of neural networks increases, the performance of neural network models not only does not improve but begins to decline. As the number of layers of the network increases, it encounters degradation problems. The deep residual neural network [29] greatly alleviates this problem. On the basis of the residual neural network, we propose a weighted residual neural network in our previous work, compared with the residual neural network. The difference between the two is the difference in the residual block. The output of the hidden layer in the weighted residual block is multiplied by the weighted coefficient and increases the skip connection, relying on the weighted coefficient to dynamically adjust the input to the next neural layer. A simple residual block and a weighted residual block, as shown in Figure 1.
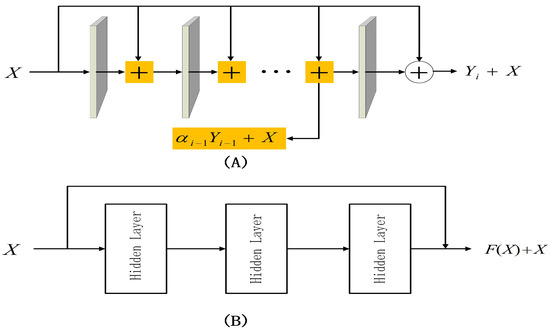
Figure 1.
(A) Weighted residual block, where represents the output of the hidden layer. (B) Residual block.
3.2. Improved Fully Connected Neural Networks
There are two key factors to the success of neural networks: 1. Construct a suitable loss function. Because the neural network algorithm is to transform the problems to be solved into an optimization problem and uses the optimization algorithm to optimize the loss function to obtain the optimal parameters. The construction of the loss function and the appropriate optimization algorithm are very important. 2. Design a special neural network framework. The framework design of the neural network is equally important for solving the problems. For example, convolutional neural networks [30] and residual neural networks [29] are excellent at solving image problems and degradation problems, so appropriate network architectures can be designed according to actual problems. Inspired by neural attention mechanisms applied to computer vision and natural language processing [31], a neural network with a new structure [19] was proposed. Differing from traditional fully connected architectures by introducing two transformer networks that projected input variables into high-dimensional feature spaces. Introduced new weights and biases and improved the network’s ability to represent complex functions. Its forward update rules are as follows:
where represent additional weights and biases, and ⊙ represent activation functions and Hadamard product, respectively. This forward structure results in a certain memory overhead, increases training time, but significantly improves the performance of the model.
3.3. Mixed-Weighted Residual Neural Network
In this section, we consider combining weighted residual neural networks with the forward structure in Section 3.1. At the same time, here, we take the weighted coefficients in the mixed-weighted residual block as trainable parameters to participate in the the model’s training. Eliminating the manual selection of the weighted coefficients. The updated rules for mixed-weighted residual blocks are as follows:
where represent the extra weight and bias in the k + 1-th mixed-weighted residual block and represents the final output from the k-th mixed-weighted residuals block. Here, we replace transformer network V with , and the hidden layer output of the mixed-weighted residual block is given a trainable weight . represents the output of the i-layer in the mixed-weighted residual block, represents the final output of the mixed-weighted residual block, and a simple mixed-weighted residual block is shown in Figure 2.
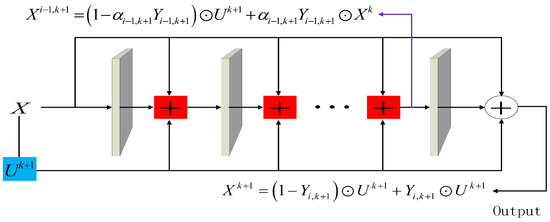
Figure 2.
Mixed-weighted residual block.
4. The Forward and Inverse Problems
In this section, we solve some partial differential equations to test the performance of the algorithm we proposed and build neural network models with different numbers of mixed-weighted residual blocks based on different cases. Adam optimization algorithm [20] is used to optimize the loss function in the following examples.
Example 1.
We first consider the two-dimensional non-homogeneous Poisson equation to test the algorithm we proposed, and the exact solution is shown below:
This example uses five mixed-weighted residuals with three hidden layers to model neural networks. Each with a transformer network, the number of neurons in the hidden layer is 10, and the activation function is . The point-wise error of PINN and M-WDRNN was compared in Figure 3. The root mean square error (RMSE) of PINN and M-WDRNN is , , respectively. During the training process, the loss function values of M-WDRNN and PINN drop to and , respectively. The algorithm we proposed greatly improves the approximation of PINN. The approximation on the boundary is significantly better than that of PINN, and M-WDRNN alleviates the gradient imbalance problem of each regular term in the loss function. We randomly took 1000 inner points and 400 boundary points as training samples in all examples.
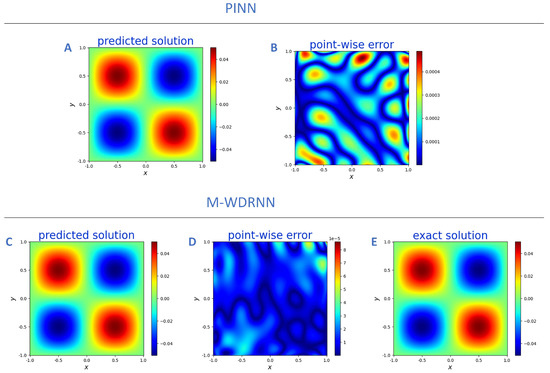
Figure 3.
Top panel: (A) PINN prediction. (B) PINN point-wise error. Bottom panel: (C) M-WDRNN prediction. (D) M-WDRNN point-wise error. (E) exact solution (7).
Example 2.
Here, we apply our proposed algorithm to the problem of the non-homogeneous Klein–Gordon equation:
where Δ represents the Laplace operator, , the parameters the exact solution is expressed as:
In this example, we select three mixed-weighted residuals with three hidden layers to build a neural network. The hidden layer contains 10 neurons. We chose the function as the activation function, the parameters . The exact solution, prediction of the Equation (8) and point-wise error are shown in Figure 4. The maximum point-wise error of PINN and M-WDRNN are and , respectively. Note that the approximation of the PINN algorithm is worse than other regions in the boundary. The M-WDRNN algorithm alleviates this phenomenon and significantly improves the overall approximation.
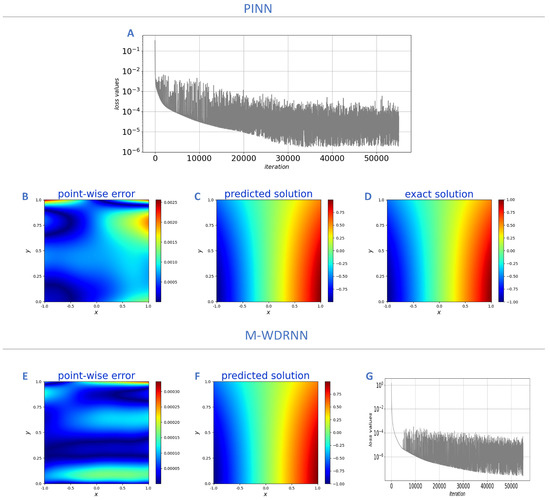
Figure 4.
Top panel: (A) PINN loss values. (B) PINN point-wise error. (C) PINN predicted solution. (D) Exact solution (9). Bottom panel: (E) M-WDRNN point-wise error. (F) M-WDRNN predicted solution. (G) Loss values.
Example 3.
Next, we consider the (1+1) dimensional advection diffusion equation (ADE):
Equation (10) satisfies the following initial condition and boundary condition: where and are the advection coefficient and the diffusion coefficient. The analytical solution to the AD Equation (10) is given in [32] by summing infinite series. We built a neural network model using two mixed-weighted residual blocks with three hidden layers, training samples , and . Since the analytical solution of the equation involves the sum of infinite series, we consider intercepting finite terms as the analytical solution. We use the first 80,000 terms to calculate the analytical solution to Equation (10), and compare the method we propose with other methods. The result is as shown in Figure 5. Compared with other methods, our algorithm is more accurate.
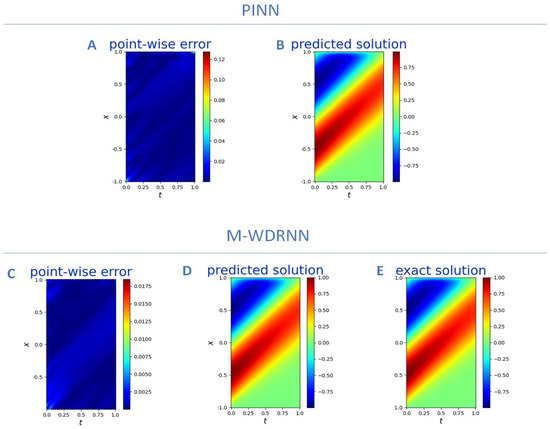
Figure 5.
Top panel: (A) PINN point-wise error. (B) PINN prediction. Bottom panel: (C) M-WDRNN point-wise error. (D) M-WDRNN prediction. (E) Exact solution (10).
Next, we consider solving the inverse problem of the differential equation, that is, the problem of parameter estimation. In contrast to the partial differential forward problem, the inverse problem only requires adding an observational penalty term to the loss function of the forward problems. Here, we assume that the diffusion coefficient is unknown, is initialized by , and 5 data points with measurement error 0.02 are randomly extracted as observations. The PINN algorithm and the M-WDRNN algorithm are used to estimate unknown parameters and approximate the true solution, respectively. Except for the network structure, both maintain the same hyperparameter settings. A comparison of the results of PINN and M-WDRNN is shown in Figure 6. The results show that the M-WDRNN algorithm accurately approximates the exact solution and estimates the unknown parameters . The estimation of PINN is extremely unstable during training, so the approximation error exceeds that of the M-WDRNN algorithm. This shows the effectiveness of the M-WDRNN algorithm for PDE inverse problems.
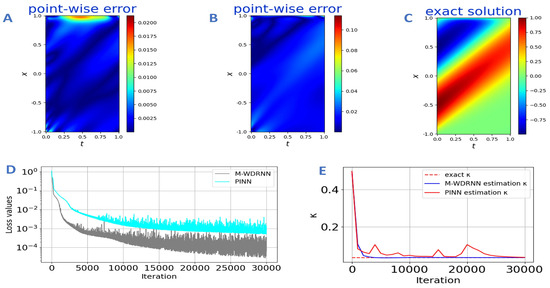
Example 4.
Finally, we consider the Helmholtz equation:
where represents the diffusion coefficient, and the exact solution:
We consider the forward problem. Two mixed-weighted residual blocks with three hidden layers are used to build the network model, the parameters , , . We chose as the activation function, each hidden layer contains 10 neurons. The result is shown in Figure 7. The maximum point-wise error of PINN and M-WDRNN are and , respectively. The RMSE of PINN and M-WDRNN are and , respectively. Both M-WDRNN and PINN successfully fit boundaries and inner domains, but the M-WDRNN algorithm has a more powerful approximation capability.
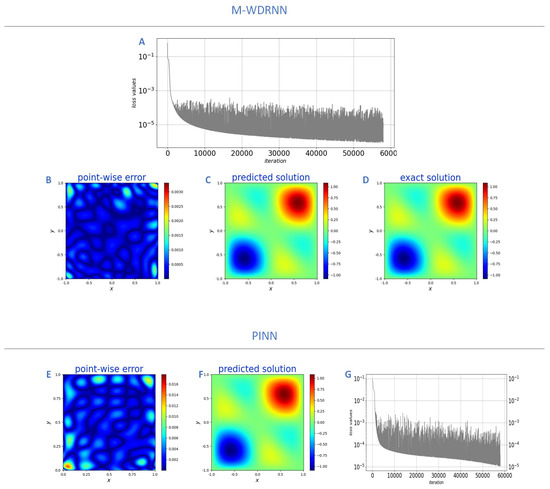
Figure 7.
Top panel: (A) M-WDRNN loss values. (B) M-WDRNN point-wise error. (C) M-WDRNN predicted solution, (D) Exact solution (12). Bottom panel: (E) PINN point-wise error. (F) PINN predicted solution. (G) PINN loss values.
Secondly, we solve the inverse problem of Equation (11), where we assume that the diffusion coefficient is unknown. Randomly select 10 sample points as observation points, and the network model is consistent with the forward problem. As shown in Figure 8, the algorithm we propose can converge quickly with precise values and remain stable during subsequent training, which shows that our algorithm is equally effective for solving inverse problems of differential equations.
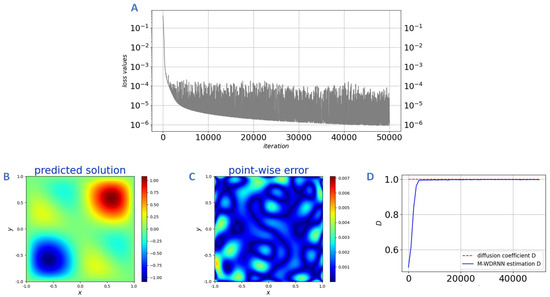
Figure 8.
The inverse problem of the Helmholtz Equation (12). (A) Loss values. (B) Predicted solution. (C) Point-wise error. (D) Diffusion coefficient D.
5. Summary and Discussion
Although PINNs are widely used to solve partial differential equations, gradient pathology makes it difficult for PINNs to accurately approximate solutions to partial differential equations. We propose a new and improved weighted residual neural network based on the deep-weighted residual neural network and attention mechanism. Unlike the improved fully connected neural networks [19], we no longer use two transformer neural networks to participate in the construction of the network. But each residual block adds a transformer neural network to participate in the construction of the network, and a skip connection replaces the other transformer neural network. Based on the numerical experimental results, we can see that the proposed algorithm can alleviate the gradient pathology. It is worth mentioning that in all experiments, we have kept the weights of each penalty term in the loss function unchanged, indicating our algorithm’s the validity. Secondly, we no longer manually select the coefficient of the weighted residual network but take the weighted coefficients in the mixed-weighted residual block as trainable parameters to participate in the training of the model, relying on the network itself and the optimization algorithm to achieve adaptive selection, saving the time of adjusting the network hyperparameters. Finally, the algorithm we propose is equally valid for the inverse problem but is not discussed in further detail.
Author Contributions
J.Z.: Conceptualization, Methodology, Visualization, Writing—Original draft preparation. Y.Y.: Writing—Reviewing and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Guizhou Provincial Science and Technology Projects (No. QKHJC-ZK[2023]YB036), Guizhou Provincial Education Department Higher Education Institution Youth Science Research Projects (QJJ[2022]098), Guizhou Provincial Science and Technology Projects (No. QKHJC-ZK[2021]YB017).
Data Availability Statement
The datasets used or analysed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Zhang, J.; Wang, J. Numerical analysis for Navier-Stokes equations with time fractional derivatives. Appl. Math. Comput. 2018, 336, 481–489. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y. Existence and controllability results for fractional semilinear differential inclusions. Nonlinear Anal. Real. World. Appl. 2011, 12, 3642–3653. [Google Scholar] [CrossRef]
- Si, Y.; Wang, J.; Fečkan, M. Controllability of linear and nonlinear systems governed by Stieltjes differential equations. Appl. Math. Comput. 2020, 376, 1254139. [Google Scholar] [CrossRef]
- Yang, P.; Wang, J.; Fečkan, M. Boundedness, periodicity, and conditional stability of noninstantaneous impulsive evolution equations. Math. Methods Appl. Sci. 2020, 43, 5905–5926. [Google Scholar] [CrossRef]
- Calhoun, D.A.; Helzel, C. A finite volume method for solving parabolic equations on logically cartesian curved surface meshes. SIAM J. Sci. Comput. 2010, 31, 4066–4099. [Google Scholar] [CrossRef]
- Demlow, A. Higher-order finite element methods and pointwise error estimates for elliptic problems on surfaces. SIAM J. Numer. Anal. 2009, 47, 805–827. [Google Scholar] [CrossRef]
- Duo, S.; van Wyk, H.W.; Zhang, Y. A novel and accurate finite difference method for the fractional Laplacian and the fractional Poisson problem. J. Comput. Phys. 2018, 355, 233–252. [Google Scholar] [CrossRef]
- Yu, B. The deep Ritz method: A deep learning-based numerical algorithm for solving variational problems. Commun. Math. Stat. 2018, 6, 1–12. [Google Scholar]
- Berg, J.; Nystrom, K. A unifified deep artifificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2018, 317, 28–41. [Google Scholar] [CrossRef]
- Hayati, M.; Karami, B. Feedforward neural network for solving partial differential equations. J. Appl. Sci. 2007, 7, 2812–2817. [Google Scholar] [CrossRef]
- Yang, Y.; Hou, M.; Luo, J.; Tian, Z. Numerical solution of several kinds of differential equations using block neural network method with improved extreme learning machine algorithm. J. Intell. Fuzzy Syst. 2020, 38, 3445–3461. [Google Scholar] [CrossRef]
- Zhang, D.; Lu, L.; Guo, L.; Karniadakis, G.E. Quantifying total uncertainty in physics-informed neural networks for solving forward and inverse stochastic problems. J. Comput. Phys. 2019, 397, 108850. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, D.; Karniadakis, G.E. Physics-informed generative adversarial networks for stochastic differential equations. SIAM J. Sci. Comput. 2020, 42, A292–A317. [Google Scholar] [CrossRef]
- Meng, X.; Li, Z.; Zhang, D.; Karniadakis, G.E. PPINN: Parareal physicsinformed neural network for time-dependent PDEs. Comput. Methods Appl. Mech. Eng. 2020, 370, 113250. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Yang, L.; Meng, X.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Yang, Y.; Perdikaris, P. Adversarial uncertainty quantification in physics-informed neural networks. J. Comput. Phys. 2019, 394, 136–152. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Neural operator: Graph kernel network for partial differential equations. arXiv 2020, arXiv:2003.03485. [Google Scholar]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and mitigating gradient flow pathologies in physics informed neural networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E. Variational physics-informed neural networks for solving partial differential equations. arXiv 2019, arXiv:1912.00873. [Google Scholar]
- Khodayi-Mehr, R.; Zavlanos, M.M. VarNet: Variational neural networks for the solution of partial differential equations. arXiv 2019, arXiv:1912.07443. [Google Scholar]
- Cho, K.; Van Merrienboer, B.; Gulcehre, C.; Bougares, F.; Schwenk, H.; Bahdanau, D.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar]
- Cho, K.; Van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. In Proceedings of the SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, Doha, Qatar, 25 October 2014; pp. 103–111. [Google Scholar]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Comput. Methods Appl. Mech. Eng. 2021, 374, 113547. [Google Scholar] [CrossRef]
- Ba, J.; Caruana, R. Do deep nets really need to be deep? In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2654–2662. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training very deep networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 2377–2385. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need, ImageNet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems(NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Mojtabi, A.; Deville, M.O. One-dimensional linear advection-diffusion equation: Analytical and finite element solutions. Comput. Fluids 2015, 107, 189–195. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).