Abstract
The evolving customer demands have significantly influenced the operational landscape of agricultural companies, including the transformation of their supply chains. As a response, many organizations are increasingly adopting green supply chain practices. This paper focuses on the initial step of selecting a green supplier, using the case study of the Semberka Company. The objective is to align the company with customer requirements and market trends. Expert decision making, grounded in linguistic values, was employed to facilitate the transformation of these values into fuzzy numbers and subsequently derive rough number boundaries. Ten economic-environmental criteria were identified, and six suppliers were evaluated against these criteria. The fuzzy rough LMAW (Logarithm Methodology of Additive Weights) method was employed to determine the criteria weights, with emphasis placed on the quality criterion. The fuzzy rough MABAC (Multi-Attributive Border Approximation Area Comparison) method was then utilized to rank the suppliers and identify the top performer. The validity of the results was established through validation techniques and sensitivity analysis. This research contributes a novel approach to green supplier selection, employing the powerful tool of fuzzy rough sets. The flexible nature of this approach suggests its potential application in future investigations. The limitation of this study is more complicated calculations for the decision maker. However, this approach is adapted to human thinking and minimizes ambiguity and uncertainty in decision making, and in future research, it is necessary to combine this approach with other methods of multi-criteria analysis.
MSC:
90C29
1. Introduction
In recent years, there has been a growing emphasis on sustainability in various industries, including agriculture and agribusiness. As concerns about environmental degradation, resource scarcity, and social responsibility continue to escalate [1,2,3], the need for sustainable practices in supplier selection becomes increasingly crucial [4,5,6]. Optimizing the selection of green suppliers has become a primary objective for organizations operating in the agricultural sector [7], as it allows them to align their supply chain practices with sustainable development goals [8].
The concept of sustainable sourcing has gained significant attention in recent years due to its potential to mitigate the adverse environmental and social impacts associated with traditional supply chain practices. By adopting sustainable sourcing strategies, organizations can not only reduce their ecological footprint but also contribute to the well-being of local communities and enhance their brand reputation [9]. Therefore, it is crucial to analyze and understand the supplier selection strategies employed in agribusiness to foster sustainable sourcing.
In this study, we propose the integration of a fuzzy rough set with the Logarithm Methodology of Additive Weights (LMAW) and the Multi-attributive Border Approximation Area Comparison (MABAC) as a novel approach to sustainable supplier selection in the agricultural sector. Fuzzy rough sets provide a robust framework for handling imprecise and uncertain data, allowing for a more realistic representation of the complexities and uncertainties inherent in supplier selection processes [10]. The LMAW is employed to assign weights to the evaluation criteria based on their relative importance, capturing the additive nature of decision making [11,12]. Furthermore, MABAC provides a comparative analysis that allows for the ranking and comparison of potential suppliers based on their performance across various criteria [13].
The integration of these methods aims to overcome the limitations of traditional supplier selection approaches, which often fail to consider the multi-dimensional nature of sustainability criteria and the inherent uncertainties in decision making. By incorporating a fuzzy rough set, the LMAW, and MABAC, we can enhance the accuracy and effectiveness of supplier selection, ultimately promoting sustainability in agribusiness.
This research will contribute to the existing body of knowledge by providing a comprehensive evaluation framework that addresses the unique challenges and requirements of sustainable supplier selection in agribusiness. The findings will not only benefit agricultural organizations seeking to optimize their supplier selection processes but also contribute to the broader goal of fostering sustainability within the industry.
The remaining part of this paper is structured as follows: Section 2 provides a literature review on green supplier selection in agribusiness, emphasizing the significance of sustainability criteria and the limitations of traditional approaches. Section 3 outlines the preliminary details of the research methodology. This section elaborates on the integration of fuzzy rough sets, LMAW, and MABAC. Section 4 presents a case study conducted to evaluate potential suppliers. Selection 5 presents the application of selected methods to the case study and obtaining results of which supplier best helps achieve the set goals. In addition, validation and sensitivity analysis of the findings is conducted in this section. A discussion of these findings is in Section 6. Finally, Section 7 concludes the paper by summarizing the key findings, discussing their implications, and suggesting directions for future research.
2. Literature Review
When conducting the literature review, keywords were first defined, i.e., sustainability, economic–ecological criteria, and the choice of suppliers. These keywords were applied using Google Scholar and certain papers were found that were used for the literature review. Papers that did not use these keywords in their abstract were excluded.
Sustainability criteria have garnered significant attention in the agricultural sector, reflecting the growing awareness among organizations of the urgent need to align their supply chain practices with sustainable development goals [14,15,16]. These criteria encompass environmental, social, and economic dimensions [17,18,19], with the overarching objective of reducing ecological footprints [20], ensuring social responsibility [21], and maintaining economic viability [22]. The integration of sustainability criteria into supplier selection processes represents a fundamental shift in the way organizations approach sourcing strategies [23], placing emphasis on responsible and sustainable practices in agribusiness.
Traditionally, supplier selection in the agricultural sector has been primarily driven by economic considerations, such as cost, quality, and delivery performance [24,25,26]. While these factors are undeniably important, they tend to overshadow broader sustainability considerations. The exclusive focus on economic metrics can inadvertently neglect vital environmental and social aspects, leading to adverse environmental impacts, reputational risks, and strained stakeholder relationships [27,28,29]. Furthermore, the subjective nature of qualitative assessments employed in traditional approaches introduces biases and inconsistencies, making it challenging to objectively evaluate suppliers’ sustainability performance [30,31,32,33].
In recent years, a growing body of research [34,35,36,37,38,39,40] has recognized the need to incorporate ecological criteria into green supplier selection in agribusiness. This shift reflects an increased understanding of the environmental challenges faced by the sector and the necessity of integrating environmental considerations into sourcing decisions. Ecological criteria provide a comprehensive framework for assessing suppliers’ environmental impact, resource conservation efforts, and compliance with environmental regulations and standards [41,42,43]. These criteria encompass a wide range of factors, including energy efficiency, waste management, carbon footprint, water usage, and biodiversity conservation [44,45,46,47,48,49,50]. Given the substantial reliance of the agricultural sector on natural resources and its potential to impact ecosystems, the inclusion of ecological criteria is crucial for promoting sustainable practices, reducing environmental degradation, and supporting biodiversity conservation efforts [51].
The literature on green supplier selection in agribusiness underscores the increasing importance of sustainability criteria and the limitations of traditional approaches that primarily prioritize economic factors. The inclusion of ecological criteria in supplier selection has emerged as a crucial component, promoting sustainable sourcing practices and addressing environmental challenges in the agricultural sector [52,53]. However, despite the recognition of sustainability criteria in supplier selection, there remains a notable research gap concerning the integration of economic and ecological dimensions within a cohesive evaluation framework. This research aims to fill this gap by developing an integrated evaluation framework that combines economic and ecological criteria, providing valuable insights and guidance for sustainable supplier selection in agribusiness.
3. Preliminaries
When making decisions, various approaches and methods are utilized. Decision making in situations involving multiple decision makers and criteria is achieved by reconciling their perspectives. To bring decision making closer to human thinking, fuzzy sets are employed. This concept was first introduced by Zadeh [54], providing a solution for decision making when approximate values are available instead of precise values. This approach bridges the gap between decision-making processes and human perception, as it is often challenging to obtain all the necessary information to assign precise ratings. Fuzzy sets allow for the use of linguistic values instead of numerical evaluations [55]. By employing these values, fuzzy sets are utilized to find compromise solutions based on imprecise information [56,57]. These linguistic values do not have precise boundaries; thus, during transformation, they encompass multiple values represented by fuzzy numbers.
Unlike fuzzy sets, a rough set is a means of addressing uncertainty issues without the subjective influence of decision makers [58]. In previous applications, a rough set has proven successful in situations involving imprecision, ambiguity, and uncertainty during decision making [59]. Thus, the use of rough sets is justified when dealing with unclear and inaccessible data.
By combining these two approaches, an attempt is made to leverage the strengths of each [60,61]. A fuzzy rough number is essentially an extension of a rough number, where a rough number is expanded to incorporate fuzzy sets [62]. The procedure is as follows: First, the evaluation of criterion and alternative values is performed using linguistic values. Second, the transformation of these values into fuzzy numbers is carried out using membership functions. Third, individual fuzzy numbers are utilized to conduct rough set operations. Fourth, the steps of the rough set method are applied. Finally, the rough approach is reconciled, and the final result is obtained. The choice of which fuzzy form to use determines the number of rough sets employed. In this research, triangular fuzzy numbers will be used, and based on that, three rough sets will be applied and eventually merged.
By employing this approach, it is necessary to determine the lower and upper bounds of rough sets [63,64]. The lower bound of a rough set is defined as follows:
These values represent the lower bounds for fuzzy numbers (l, m, u). Similarly, the upper bounds of rough sets are defined as follows:
By establishing the lower and upper bounds, fuzzy rough sets are defined as:
This formulation yields rough numbers. When dealing with two sets and rough numbers, i.e., and the basic operations are as follows:
Addition:
Subtraction:
Multiplication:
Division:
Scalar multiplication:
The specificity of these operations is that during Addition and Multiplication operations, operations are performed on the same fuzzy rough numbers, while during Subtraction and Division operations, operations are performed on reciprocal numbers: the first fuzzy rough number of the set with the sixth number of the fuzzy rough set , and the second fuzzy rough of the set with the fifth number of the fuzzy rough set . Operations with all numbers of fuzzy rough sets are performed in the specified manner. The reason for these operations should be found in the fact that the first fuzzy rough should always be smaller than the second, the second more difficult, and whatever numbers these sets have. These operations are applied to existing methods, which will be explained in the following sections.
Before these operations can be applied to certain methods, it is necessary to choose the appropriate methods. The choice of methods used in papers is usually the choice of the authors. It should be noted that all methods have their advantages and disadvantages. When choosing a method for determining the weights of the criteria, the authors Ayan et al. [65] performed an overview of certain methods and determined the advantages and disadvantages of these methods. Thus, these methods must compare criteria in pairs [66,67]; that is, compare criteria in relation to the first or last criteria, and the like. In this paper, the LMAW method will be used, where it is not necessary to compare the criteria, but it is enough to determine the importance of an individual criterion. However, the disadvantage of this method is the application of the Bonferroni aggregator, which complicates the calculation of criteria weights. When choosing the method for ranking the alternative, the MABAC method was chosen. There are several reasons for using this method: ease of use, the development of the fuzzy rough approach in this method, and the acceptance of this method in practice. However, this method also has certain limitations, which is why it is used in the results and validation of the results of this method to make the decision even more certain.
3.1. Fuzzy Rough LMAW Method
The LMAW method has been developed to determine not only the weight of criteria but also the ranking order of alternatives [68]. In this paper, a part of this method responsible for determining the criteria weights will be used. The steps for implementing this method are as follows:
Step 1: Formation of the initial decision matrix. This matrix is constructed by experts who assess the criteria based on linguistic ratings (Table 1). They determine the perceived importance of each criterion.

Table 1.
Linguistic values representing the importance of criteria.
Step 2: Transformation of linguistic values into fuzzy numbers. This is carried out based on the membership function of the fuzzy number (Table 1).
Step 3: Determination of the lower and upper bounds of the rough number for individual fuzzy numbers. This is achieved using the definitions for establishing the lower and upper bounds of rough numbers (Expressions (1)–(6)).
Step 4: Definition of the absolute anti-ideal point. This value is determined based on the minimum value among the fuzzy rough number values. It represents a value that is lower than the minimum value.
Step 5: Definition of the ratio vector. In this step, the values of the fuzzy rough numbers are divided by the absolute anti-ideal point.
Step 6: Determination of the vector of weight coefficients. This step is performed separately for each expert.
Step 7: Calculation of the aggregated vectors of weight coefficients. The calculation of this coefficient is conducted using the Bonferroni aggregator. It is performed by individually calculating the weights for each fuzzy rough number based on the expression:
In this research, the final weights will not be computed as the weights obtained for individual fuzzy rough numbers will be retained. Thus, Step 7 serves as the final step of the fuzzy rough LMAW method.
3.2. Fuzzy Rough MABAC Method
The MABAC method was developed by Pamučar and Ćirović [69]. This method ranks alternatives based on their deviations from the average values. The steps of this method are presented in the paper by Pamučar et al. [59], and here we will provide a brief overview of these steps.
Step 1: Formation of the initial decision matrix. This matrix is formed by experts who assess the alternatives according to observed criteria using linguistic evaluations (Table 2).

Table 2.
Linguistic values for alternative assessment.
Step 2: Transformation of linguistic values from the initial decision matrix into fuzzy numbers. This is done based on the membership function of the fuzzy number (Table 2).
Step 3: Determination of the lower and upper bounds of the rough number for individual fuzzy numbers. This is performed in the same manner as in the fuzzy rough LMAW method.
Step 4: Normalization of the fuzzy rough decision matrix. This is done using the following expressions:
For benefit criteria:
For cost criteria:
Step 5: Weighting the normalized fuzzy rough numbers. This is accomplished using the following expression:
Step 6: Determining the border approximation area matrix (G). This is essentially the geometric mean of the criterion values for individual fuzzy rough number values. It is calculated using the following expression:
Step 7: Calculating the elements of the matrix for the distance of the alternatives from the border approximation area (Q). In this step, the deviation of the weighted normalized fuzzy rough numbers from the values of the border approximation area matrix (G) is calculated.
Step 8: Ranking the alternatives. The ranking of alternatives is done by summing all the deviation values of alternatives from the border approximation area.
The best alternative is the one with the highest value according to the MABAC method, and vice versa.
4. Case Study
The company “Semberka” from Janja is located in the Semberija plain in Bosnia and Herzegovina. The favorable climate and land have influenced intensive agricultural activities in this area. Consequently, it was economically justified to establish processing facilities to obtain a final product, thus completing the agricultural production cycle from farm to table. The “Semberka” company from Janja represents a market-recognized brand that continues to make significant investments in production resources. Its main activity is the production of spices, food additives, and the processing of dried vegetables from its own production. The company places great emphasis on products that meet health, hygiene, and microbiological standards, as evidenced by continuous monitoring of raw materials throughout the entire process, from planting and drying to grinding and mixing according to recipes. In recent years, the company “Semberka” has focused on the production of its branded “Semberski” soups, thereby completing the production process of the factory. Due to increased production and expansion of the product range, there is a need for additional quantities of specific vegetables from other suppliers in the local and wider area. However, the products from these suppliers must meet all the specified quality standards to maintain the quality of the final product and uphold the existing brand.
The company employs several dozen workers whose main activities involve the processing and refinement of a range of dried vegetables. Among these employees are engineers (agriculture, technology, and protection) whose task is to monitor and control the work processes. Due to the need for additional raw material quantities, Semberka decided to conduct research to identify the supplier that best meets their objectives, which is the production of high-quality products with an emphasis on human health. This is due to the increasing number of people turning to a healthy lifestyle in order to improve their quality of life and extend their lifespan. The research was conducted by engaging external experts, professors from the Faculty of Agriculture in Bijeljina, in addition to the company’s own experts. Thus, five experts were involved to assess the suppliers and select the one that best meets the objectives. Among the five experts, the company employed two employees with extensive experience in raw material processing, who are technology engineers, and then three experts, holders of doctoral degrees in agricultural sciences, with years of experience in agricultural activities. This way, two segments were covered, namely raw material processing technology and agricultural production technology.
In order to select the supplier, the task of the experts was to determine the criteria by which the selected suppliers would be evaluated. They decided to apply economic–environmental criteria (Table 3). These criteria aim to choose a green supplier. The economic criteria encompass economic parameters such as costs, quality, production innovation, technological capacities, and delivery. The environmental criteria cover aspects related to environmental management standards, environmental product design, eco-friendly materials, and resource consumption reduction to optimize the production process of the Semberka company. These criteria were selected from existing similar research studies. It is important to note that in practice, there are numerous other criteria, but the experts considered these criteria to be the most suitable for this research.

Table 3.
Criteria for supplier selection.
After selecting the criteria by which to evaluate suppliers, the experts have chosen six suppliers from the Semberija region who would assist them in producing additional and new products. These suppliers will be labeled as S1–S6. In addition to that, these suppliers will help Semberka Company improve its production, which will provide them with an additional quantity of raw materials for future manufacturing. The goal is to select one of these six suppliers with whom Semberka Company will establish partnership relations to mutually enhance their business. Since the criteria and potential suppliers have been selected, the task of the experts was to assess the criteria first using linguistic values (Table 1) and then to evaluate the suppliers using these criteria with linguistic values (Table 2). In order to select the supplier, a fuzzy rough approach will be used, which enables decision-making in the case of imprecise evaluations by applying a fuzzy approach while reducing ambiguity and uncertainty in decision making through a rough approach. This way, a more reliable decision will be made for the decision maker.
5. Results
When selecting a green supplier for Semberka Company’s needs, the weights of the criteria are first determined using expert assessments. In determining the weights of the criteria, the first step is to establish a linguistic assessment of the criteria. This is carried out by having each expert rate the criteria on a scale ranging from absolutely low (AL) to absolutely high (AH). The criteria that are more significant to them will receive higher ratings from the expert. As can be seen from these ratings (Table 4), there is no single criterion that is considered the best by all experts. Therefore, in this case, the ratings are harmonized to obtain a compromise solution. This solution is the one that best reconciles the different assessments.

Table 4.
Initial decision matrix.
After forming the initial linguistic decision matrix, the next step is to transform these linguistic assessments into fuzzy numbers using membership functions (Table 1). The specificity of these fuzzy numbers is that they do not have clear boundaries and the boundaries of individual fuzzy numbers overlap. In this way, imprecise assessments are used to evaluate the weights of the criteria. By transforming linguistic values into fuzzy numbers, a triangular fuzzy number is formed for each value (Table 5).

Table 5.
Initial fuzzy decision matrix.
Then, individual lower and upper bounds of rough numbers are determined based on these numbers. For the first fuzzy number in the first criterion, it looks like this:
It is important to mention that for each expert, the lower and upper bounds are determined by considering the value they provided. To determine the lower bound, all smaller values are compared among that expert and other experts, while for the upper bound, all larger and equal values are considered among that expert and other experts. In this way, these bounds are formed, as shown in Table 6.

Table 6.
Initial fuzzy rough decision matrix for criteria.
By using these rules, lower and upper bounds of rough numbers are determined for all experts and criteria. This forms the initial fuzzy rough decision matrix, which serves as the starting point for applying the fuzzy rough method (Table 6). In this case, the steps of the fuzzy rough LMAW method are applied.
The first step of this method is to define the absolute anti-ideal point. When considering all lower values of the first fuzzy numbers, since these values are the smallest, it can be observed that the minimum value is two (2). Therefore, the value chosen for the absolute anti-ideal point is a value smaller than two. In this example, the value of 1.9 is taken. The next step of this method is to define the relationship vector. In this step, the division of all values in the fuzzy rough decision matrix by the values of the absolute anti-ideal point is performed (Equation (14)). The subsequent step is to determine the vector of weight coefficients. Here, the natural logarithm is calculated for each value, and that value is divided by the natural logarithm of the product of weight coefficient vectors for the corresponding fuzzy numbers and the limits of rough numbers (Table 7).

Table 7.
Matrix of weight coefficient vectors.
Finally, the Bonferroni aggregator is applied to harmonize the weights of the experts. Using this aggregator, the weights of the criteria are obtained, which are used to adjust the initial decision matrix. Based on this approach, weights are obtained where the upper limit of the first fuzzy number cannot be greater than the lower limit of the second fuzzy number, and the upper limit of the second fuzzy number cannot be greater than the lower limit of the third fuzzy number. When examining these results (Table 8), criterion C2 (quality) received the highest weight, followed by criterion C1 (costs), while criterion C8 (environmental product design) received the lowest weight.

Table 8.
Final weights of criteria.
After determining the weights of the criteria, the ranking of alternatives is performed. The first step in the fuzzy rough MABAC method is the same, and the initial decision matrix with linguistic values is formed (Table 9). Then, the transformation of these linguistic values into fuzzy numbers is carried out using the membership function (Table 2).

Table 9.
Initial linguistic decision matrix.
After that, the lower and upper bounds are determined for each fuzzy number and each expert. This is performed in the same way as in the fuzzy rough LMAW method. Then, the aggregate decision matrix is formed by calculating the average values of the lower and upper bounds of the rough numbers, and the initial joint fuzzy rough decision matrix is created (Table 9). This matrix is fundamental for conducting the steps of the fuzzy rough MABAC method. When forming this decision matrix, it is important to ensure that the upper bound of the first fuzzy number is not greater than the lower bound of the second fuzzy number and that the upper bound of the second fuzzy number is not greater than the lower bound of the third fuzzy number. Therefore, where this is the case, adjustments are made to this fuzzy rough decision matrix, so that the upper bound of the first fuzzy number becomes the lower bound of the second fuzzy number, and the upper bound of the second fuzzy number becomes the lower bound of the third fuzzy number. These adjustments are marked in Table 10.

Table 10.
Initial fuzzy rough decision matrix for alternatives.
Once this decision matrix is formed, the steps of the fuzzy rough MABAC method are carried out. The first step is to normalize this initial fuzzy rough decision matrix. Since the linguistic scale is in a form where all criteria are transformed into benefit criteria, normalization is applied for the benefit criteria (Expression (17)). When performing normalization, the minimum value of the lower bound of the first fuzzy number is first identified, followed by the maximum value of the upper bound of the third fuzzy number. For example, for the first supplier, the lower bound of the first fuzzy number will be (2.5 − 2.5)/(9.3 − 2.5) = 0. In this way, the other values of the normalized decision matrix are calculated. The minimum and maximum values for each criterion are taken, and the normalization process is applied.
Then, the weighting of this normalized decision matrix is performed (Expression (19)). Weighting is done by multiplying the normalized values with the corresponding weights and summing them with those weights (Table 11). After that, the border approximation area matrix (g) is formed, which represents the geometric mean value for each boundary of the fuzzy numbers. Then, the values of the weighted decision matrix are subtracted from the values of the border approximation area matrix. For example, the value of the lower bound of the first fuzzy number is subtracted from the value of the border approximation area matrix of the upper bound of the third fuzzy number, the upper bound of the first fuzzy number is subtracted from the lower bound of the third fuzzy number, and so on. In this way, the values of the matrix for the distance of the alternatives from the border approximation area (Q) are calculated.

Table 11.
Weighted values of the normalized decision matrix and border approximation area matrix.
Then, it is necessary to sum up all the values of individual boundaries for all criteria using Expression (8). Finally, the final value of the fuzzy rough MABAC method is obtained by calculating the average value for all boundaries. The results show that supplier S2 achieves the best results (Table 12), making it the first choice for establishing partnerships, followed by supplier S3, while supplier S6 performs the poorest.

Table 12.
Final ranking order of the fuzzy rough MABAC method.
To confirm these results, a validation of the results will be conducted. This validation is performed by using the same weights and the same initial decision matrix while applying other MCDM methods. In this study, the results of the fuzzy rough MABAC method will be compared with the methods: fuzzy rough SAW (Simple Additive Weighting), fuzzy rough ARAS (Additive Ratio Assessment), fuzzy rough CRADIS (compromise ranking of alternatives from distance to ideal solution), and fuzzy rough WPM (Weighted Product Method). The validation results show that the rank order differs between the fuzzy rough ARAS and fuzzy rough WPM methods for suppliers S4 and S5. When examining the results of the fuzzy rough MABAC method, it can be observed that the smallest difference occurs for these two suppliers (Figure 1). This is the reason why the rank order differs between these two methods compared to the fuzzy rough MABAC method. Additionally, these two methods also apply different normalizations. The application of different types of normalization can affect the rank order of alternatives [91,92]. The rank order does not differ from the fuzzy rough MABAC method for the other two methods. Based on these results, the obtained results of the fuzzy rough MABAC method can be confirmed.
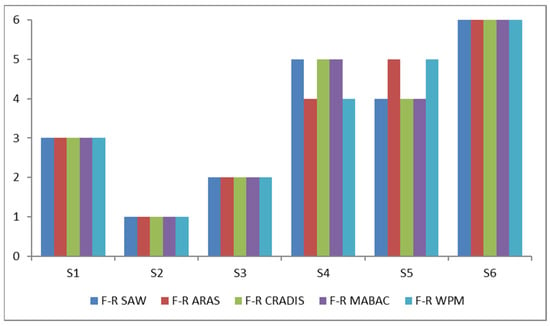
Figure 1.
Validation of the results.
After the validation of the results, a sensitivity analysis will be conducted. This analysis aims to demonstrate the role of individual criteria on the final rank order of alternatives and show how sensitive each supplier is to changes in the weights of individual criteria. This will help identify the areas that each supplier needs to improve in order to perform better in the market. This will be conducted as follows. Each individual criterion will be reduced by 15% until only 10% of the initial criterion value remains [93]. In this way, 6 scenarios for each individual criterion will be applied [94]. Since there are 10 criteria, a total of 60 sensitivity analysis scenarios will be performed.
The results of the sensitivity analysis show that in all scenarios, suppliers S2, S3, and S6 did not change their rank order (Figure 2). Supplier S2 remained in the first position in all scenarios, supplier S3 in the second position, while supplier S6 was consistently ranked last for all criteria. The sensitivity analysis revealed the following: Supplier S4 has poorer indicators than supplier S5 in terms of innovativeness, so in order to be better rated than the other suppliers, this supplier needs to improve the innovativeness of their products and services. Additionally, this analysis showed that supplier S1 has better indicators than supplier S5 in terms of delivery and pollution control. For supplier S5 to be better than supplier S1, they need to adjust their delivery time and improve pollution control in their production because when the weights of these criteria were reduced, supplier S5 had a higher rank than supplier S1. In other cases and scenarios, the rank order of the suppliers remained unchanged.
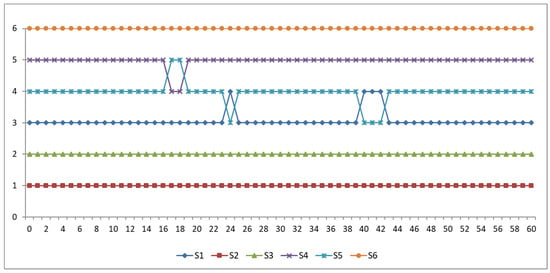
Figure 2.
Sensitivity analysis.
The validations of results and sensitivity analysis have shown that supplier S2 has the best indicators among all suppliers, making it the first choice for establishing partnerships. Following supplier S2, the next choice is supplier S3.
6. Discussion
The growing consumer demand for a healthier lifestyle has triggered a significant transformation in the agro-food industry [95]. Increasingly, customers are seeking out products that promote good health and contribute to environmental preservation. Consequently, ecological criteria have become integral to supplier selection [53], complementing traditional economic considerations. This study focuses on the selection of a green supplier, using the Semberka company as an example. The findings underscore the importance of incorporating ecological criteria into supplier selection processes. In response to the shifting preferences of consumers, companies are prioritizing suppliers that align with eco-friendly practices, showcasing their commitment to sustainability and catering to customer demands.
Integrating ecological criteria into supplier selection offers several advantages [96]. Firstly, it enables companies to contribute to environmental preservation by supporting suppliers that adhere to eco-friendly practices. This not only benefits the planet but also enhances a company’s image and reputation, appealing to eco-conscious consumers. Secondly, choosing green suppliers can lead to the procurement of high-quality products that meet stringent health and safety standards, contributing to consumer satisfaction and trust in the company’s offerings [97]. Moreover, it opens up opportunities for companies to enter new markets or expand their customer base by attracting health-conscious consumers [98]. However, the integration of ecological criteria into supplier selection is not without challenges [99]. Companies may face difficulties in identifying and evaluating suppliers’ eco-friendly practices, particularly when comprehensive and standardized metrics are lacking. Additionally, there may be cost implications associated with sourcing from green suppliers, as environmentally friendly practices often require investments in sustainable technologies or processes. Striking a balance between environmental considerations and economic viability is a key aspect that companies must carefully navigate during the supplier selection process [23].
In the case of the Semberka company, the utilization of ecological criteria in the selection of a green supplier demonstrates a proactive approach to addressing customer demands and aligning with industry trends. This decision allows the company to contribute to sustainable practices and foster a positive impact on the environment [100]. The selection of a green supplier by the Semberka company was facilitated through the innovative application of expert decision making based on linguistic values. Fuzzy sets were employed to accommodate imprecise information, while rough sets addressed ambiguity and uncertainty in the decision-making process. This research utilized the fuzzy rough approach and employed the LMAW and MABAC methods.
The LMAW method was used to determine the criteria weights, with the transformation of linguistic values into fuzzy numbers and subsequent derivation of rough number boundaries being prerequisite steps. The quality criterion emerged as the most significant, while environmental product design received the lowest weight. However, the results indicate that the differences in weights between the selected criteria were not substantial, underscoring the importance of each criterion in the green supplier selection process. The MABAC method, previously adapted for the fuzzy rough approach, was further tailored for ease of use. Care was taken to ensure that the upper boundaries of preceding fuzzy numbers were not greater than the lower boundaries of subsequent fuzzy numbers when determining the rough number boundaries. This adjustment influenced the values in the initial decision matrix, to which the steps of the MABAC method were applied. Sensitivity analysis further demonstrated that even without altering the weights of individual criteria, this supplier consistently displayed the most favorable indicators.
Future research in this field should focus on exploring the long-term effects and outcomes of selecting green suppliers. Investigating the economic benefits, operational efficiency, and customer satisfaction resulting from such supplier selections would provide valuable insights for businesses aiming to incorporate ecological criteria into their decision-making processes.
7. Conclusions
Since many existing studies predominantly focus on either economic or environmental factors, neglecting the need for a comprehensive approach that holistically evaluates suppliers’ performance in both dimensions, there is a gap that needs to be addressed. This research aims to fill that gap by developing an integrated evaluation framework that simultaneously incorporates economic and ecological criteria for green supplier selection. By merging these dimensions, organizations can make informed and sustainable supplier selection decisions that align with their overall sustainability objectives. The development of an integrated evaluation framework holds immense promise for the agricultural sector. It allows organizations to effectively balance economic and ecological considerations in supplier selection, enabling them to identify suppliers that not only meet economic requirements but also demonstrate strong environmental stewardship and social responsibility. This comprehensive approach plays a crucial role in mitigating environmental impacts, supporting biodiversity conservation, and enhancing the overall sustainability of supply chains.
In the case of the Semberka company, this research applied an integrated fuzzy rough approach to solving the problem of selecting a green supplier. This approach was chosen to leverage the advantages offered by fuzzy and rough techniques, enhancing the decision-making process’s reliability and providing decision makers with a safer and more robust framework. To implement this approach, customized versions of the LMAW and MABAC methods were utilized. The fuzzy rough LMAW method was used to determine the criteria weights, with the quality criterion receiving the highest weight. The fuzzy rough MABAC method was then employed to rank suppliers based on the observed criteria. The results indicated that supplier S2 achieved the best performance and was the preferred choice for establishing partnerships. These results were validated and further supported by sensitivity analysis. These results were confirmed through validation, wherein the same weights and initial decision matrix were utilized, employing different MCDM methods.
The advantage of applying the fuzzy rough approach lies in the fact that the combination of these approaches uses the good sides of both approaches. By applying the fuzzy approach, imprecise evaluations of decision making are used, while by applying the rough approach, the influence of subjectivity in decision making is reduced. In addition, the rough approach helps to solve the problem of uncertainty in decision making. Despite this, this approach has limitations. The application of this approach complicates calculations, as it requires transforming linguistic values into fuzzy values and determining rough number boundaries. Moreover, specific operations need to be applied to these numbers. However, despite these challenges, the fuzzy rough approach enhances the decision-making process’s reliability by adapting the research to human thinking, reducing subjectivity in decision making, minimizing ambiguities, and addressing uncertainties. Furthermore, the practical example of selecting a green supplier provided a detailed explanation of this approach. Future research should focus on further applying and developing similar approaches that leverage the fuzzy rough approach. The case study of the Semberka company demonstrates the effectiveness of the fuzzy rough approach in making informed decisions that align with sustainability objectives. The research contributes to the field by addressing the limitations of existing studies and offering a comprehensive framework for green supplier selection. Further research is needed to expand the application of this approach and explore new approaches that build upon it.
Author Contributions
Conceptualization, A.P. and M.N.; methodology, A.P. and S.B.; software, D.B.; validation, A.Š., M.N. and D.B.; formal analysis, A.P.; investigation, M.N.; resources, D.B. and S.B.; data curation, A.P; writing—original draft preparation, A.P.; writing—review and editing, A.Š.; visualization, A.Š.; supervision, M.N. and D.B.; project administration, D.B. and S.B.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| LMAW | Logarithm Methodology of Additive Weights |
| MABAC | Multi-attributive Border Approximation Area Comparison |
| AL | Absolutely low |
| VL | Very low |
| L | Low |
| ML | Medium-low |
| E | Equal |
| MH | Medium-high |
| H | High |
| VH | Very high |
| AH | Absolutely high |
| VB | Very bad |
| B | Bad |
| MB | Medium bad |
| M | Medium |
| MG | Medium good |
| G | Good |
| VG | Very good |
| SAW | Simple Additive Weighting |
| ARAS | Additive Ratio Assessment |
| CRADIS | Compromise ranking of alternatives from distance to ideal solution |
| WPM | Weighted Product Method |
References
- Ali, Q.; Parveen, S.; Yaacob, H.; Zaini, Z.; Sarbini, N.N. COVID-19 and dynamics of environmental awareness, sustainable consumption and social responsibility in Malaysia. Environ. Sci. Pollut. Res. 2021, 28, 56199–56218. [Google Scholar] [CrossRef] [PubMed]
- Dresse, A.; Nielsen, J.B.; Fischhendler, I. From corporate social responsibility to environmental peacebuilding: The case of bauxite mining in Guinea. Resour. Policy 2021, 74, 102290. [Google Scholar] [CrossRef]
- Yasin, R.; Huseynova, A.; Atif, M. Green human resource management, a gateway to employer branding: Mediating role of corporate environmental sustainability and corporate social sustainability. Corp. Soc. Responsib. Environ. Manag. 2022, 30, 369–383. [Google Scholar] [CrossRef]
- Amin-Chaudhry, A.; Young, S.; Afshari, L. Sustainability motivations and challenges in the Australian agribusiness. J. Clean. Prod. 2022, 361, 132229. [Google Scholar] [CrossRef]
- Duan, S.X.; Wibowo, S.; Chong, J. A Multicriteria Analysis Approach for Evaluating the Performance of Agriculture Decision Support Systems for Sustainable Agribusiness. Mathematics 2021, 9, 884. [Google Scholar] [CrossRef]
- Joshi, S.; Singh, R.; Sharma, M. Sustainable Agri-Food Supply Chain Practices: Few Empirical Evidences from a Developing Economy. Glob. Bus. Rev. 2020; in press. [Google Scholar] [CrossRef]
- Trivellas, P.; Malindretos, G.; Reklitis, P. Implications of Green Logistics Management on Sustainable Business and Supply Chain Performance: Evidence from a Survey in the Greek Agri-Food Sector. Sustainability 2020, 12, 10515. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development (A/RES/70/1); UN General Assembly: New York, NY, USA, 2015; Available online: https://sustainabledevelopment.un.org/content/documents/21252030%20Agenda%20for%20Sustainable%20Development%20web.pdf (accessed on 15 June 2023).
- Ghosh, P.; Jha, A.; Sharma, R. Managing carbon footprint for a sustainable supply chain: A systematic literature review. Mod. Supply Chain Res. Appl. 2020, 2, 123–141. [Google Scholar] [CrossRef]
- Ibrahim, H.A.; Zaidan, A.A.; Qahtan, S.; Zaidan, B.B. Sustainability assessment of palm oil industry 4.0 technologies in a circular economy applications based on interval-valued Pythagorean fuzzy rough set-FWZIC and EDAS methods. Appl. Soft Comput. 2023, 136, 110073. [Google Scholar] [CrossRef]
- Božanić, D.K.; Pamučar, D.; Milić, A.; Marinković, D.; Komazec, N. Modification of the Logarithm Methodology of Additive Weights (LMAW) by a Triangular Fuzzy Number and Its Application in Multi-Criteria Decision Making. Axioms 2022, 11, 89. [Google Scholar] [CrossRef]
- Puška, A.; Božanić, D.; Nedeljković, M.; Janošević, M. Green Supplier Selection in an Uncertain Environment in Agriculture Using a Hybrid MCDM Model: Z-Numbers–Fuzzy LMAW–Fuzzy CRADIS Model. Axioms 2022, 11, 427. [Google Scholar] [CrossRef]
- Torkayesh, A.E.; Tirkolaee, E.B.; Bahrini, A.; Pamučar, D.; Khakbaz, A. A Systematic Literature Review of MABAC Method and Applications: An Outlook for Sustainability and Circularity. Informatica 2023, 34, 415–448. [Google Scholar] [CrossRef]
- Lahane, S.; Kant, R.; Shankar, R. Circular supply chain management: A state-of-art review and future opportunities. J. Clean. Prod. 2020, 258, 120859. [Google Scholar] [CrossRef]
- Negra, C.; Remans, R.; Attwood, S.; Jones, S.; Werneck, F.; Smith, A.B. Sustainable agri-food investments require multi-sector co-development of decision tools. Ecol. Indic. 2020, 110, 105851. [Google Scholar] [CrossRef]
- Permatasari, P.; Ilman, A.S.; Tilt, C.A.; Lestari, D.; Islam, S.; Tenrini, R.H.; Rahman, A.B.; Samosir, A.P.; Wardhana, I.W. The Village Fund Program in Indonesia: Measuring the Effectiveness and Alignment to Sustainable Development Goals. Sustainability 2021, 13, 12294. [Google Scholar] [CrossRef]
- Cosenz, F.; Rodrigues, V.P.; Rosati, F. Dynamic Business Modeling for Sustainability: Exploring a System Dynamics Perspective to Develop Sustainable Business Models. Bus. Strategy Environ. 2019, 29, 651–664. [Google Scholar] [CrossRef]
- Da Costa Maynard, D.; Vidigal, M.D.; Farage, P.; Zandonadi, R.P.; Nakano, E.Y.; Botelho, R.B.A. Environmental, Social and Economic Sustainability Indicators Applied to Food Services: A Systematic Review. Sustainability 2020, 12, 1804. [Google Scholar] [CrossRef]
- Osmundsen, T.C.; Amundsen, V.S.; Alexander, K.P.; Asche, F.; Bailey, J.A.; Finstad, B.; Olsen, M.S.; Hernández, K.; Salgado, H. The operationalisation of sustainability: Sustainable aquaculture production as defined by certification schemes. Glob. Environ. Chang. Hum. Policy Dimens. 2020, 60, 102025. [Google Scholar] [CrossRef]
- Alvarado, R.; Ortiz, C.; Jiménez, N.V.L.; Ochoa-Jiménez, D.; Tillaguango, B. Ecological footprint, air quality and research and development: The role of agriculture and international trade. J. Clean. Prod. 2021, 288, 125589. [Google Scholar] [CrossRef]
- Nedeljković, M. Criteria for Sustainable Supplier Selection in Agro-Industrial Complex. West. Balk. J. Agric. Econ. Rural Dev. 2022, 4, 49–64. [Google Scholar] [CrossRef]
- Volkov, A.; Žičkienė, A.; Morkunas, M.; Baležentis, T.; Ribašauskienė, E.; Streimikiene, D. A Multi-Criteria Approach for Assessing the Economic Resilience of Agriculture: The Case of Lithuania. Sustainability 2021, 13, 2370. [Google Scholar] [CrossRef]
- Masoomi, B.; Sahebi, I.G.; Fathi, M.; Yıldırım, F.; Ghorbani, S. Strategic supplier selection for renewable energy supply chain under green capabilities (fuzzy BWM-WASPAS-COPRAS approach). Energy Strategy Rev. 2022, 40, 100815. [Google Scholar] [CrossRef]
- Candemir, A.; Duvaleix-Treguer, S.; Latruffe, L. Agricultural Cooperatives and Farm Sustainability—A Literature Review. J. Econ. Surv. 2021, 35, 1118–1144. [Google Scholar] [CrossRef]
- Jain, N.; Singh, A.K. Sustainable supplier selection criteria classification for Indian iron and steel industry: A fuzzy modified Kano model approach. Int. J. Sustain. Eng. 2019, 13, 17–32. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Mardani, A.; Dashtian, Z.; Soltani, M.; Weber, G. A novel hybrid method using fuzzy decision making and multi-objective programming for sustainable-reliable supplier selection in two-echelon supply chain design. J. Clean. Prod. 2020, 250, 119517. [Google Scholar] [CrossRef]
- Bouwman, T.; Andersson, J.; Giller, K.E. Herbicide Induced Hunger? Conservation Agriculture, Ganyu Labour and Rural Poverty in Central Malawi. J. Dev. Stud. 2020, 57, 244–263. [Google Scholar] [CrossRef]
- Süß, A.; Höse, K.; Götze, U. Sustainability-Oriented Business Model Evaluation—A Literature Review. Sustainability 2021, 13, 10908. [Google Scholar] [CrossRef]
- Yusriadi, Y.; Cahaya, A. Food security systems in rural communities: A qualitative study. Front. Sustain. Food Syst. 2022, 6, 987853. [Google Scholar] [CrossRef]
- Jovčić, S.; Průša, P.; Dobrodolac, M.; Švadlenka, L. A Proposal for a Decision-Making Tool in Third-Party Logistics (3PL) Provider Selection Based on Multi-Criteria Analysis and the Fuzzy Approach. Sustainability 2019, 11, 4236. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, Y.; Zhou, X.S.; Wei, Z. Selection of Agricultural Machinery Based on Improved CRITIC-Entropy Weight and GRA-TOPSIS Method. Processes 2022, 10, 266. [Google Scholar] [CrossRef]
- Ma, L.; Wang, W.; Xie, J.; Zhang, N.; Hu, N.; Wang, Z. Evaluation of product conceptual design based on Pythagorean fuzzy set under big data environment. Sci. Rep. 2022, 12, 22387. [Google Scholar] [CrossRef] [PubMed]
- Rane, N.L.; Choudhary, S. Fuzzy AHP and Fuzzy TOPSIS as an effective and powerful Multi-Criteria Decision-Making (MCDM) method for subjective judgements in selection process. Int. Res. J. Mod. Eng. Technol. Sci. 2023, 5, 3786–3799. [Google Scholar] [CrossRef]
- Baki, R. An Integrated Multi-criteria Structural Equation Model for Green Supplier Selection. Int. J. Precis. Eng. Manuf. Green Technol. 2022, 9, 1063–1076. [Google Scholar] [CrossRef]
- Causil, O.M.M.; Morais, D.C. Multicriteria negotiation model for selecting sustainable suppliers’ problem in the agribusiness. Prod. J. 2023, 33, e20220090. [Google Scholar] [CrossRef]
- Miranda-Ackerman, M.A.; Azzaro-Pantel, C.; Aguilar-Lasserre, A.A.; Bueno-Solano, A.; Arredondo-Soto, K.C. Green Supplier Selection in the Agro-Food Industry with Contract Farming: A Multi-Objective Optimization Approach. Sustainability 2019, 11, 7017. [Google Scholar] [CrossRef]
- Sonar, H.C.; Gunasekaran, A.; Agrawal, S.; Roy, M. Role of lean, agile, resilient, green, and sustainable paradigm in supplier selection. Clean. Logist. Supply Chain 2022, 4, 100059. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, T. A hybrid group decision-making approach involving Pythagorean fuzzy uncertainty for green supplier selection. Int. J. Prod. Econ. 2023, 261, 108875. [Google Scholar] [CrossRef]
- Gergin, R.E.; Peker, İ.; Kısa, A.C.G. Supplier Selection by Integrated IFDEMATEL-IFTOPSIS Method: A Case Study of Automotive Supply Industry. Decis. Mak. Appl. Manag. Eng. 2022, 5, 169–193. [Google Scholar] [CrossRef]
- Durmić, E.; Stević, Ž.; Chatterjee, P.; Vasiljević, M.; Tomašević, M. Sustainable supplier selection using combined FUCOM—Rough SAW model. Rep. Mech. Eng. 2020, 1, 34–43. [Google Scholar] [CrossRef]
- Litvinenko, V.; Bowbrik, I.; Naumov, I.V.; Zaitseva, Z. Global guidelines and requirements for professional competencies of natural resource extraction engineers: Implications for ESG principles and sustainable development goals. J. Clean. Prod. 2022, 338, 130530. [Google Scholar] [CrossRef]
- Shah, N.; Soomro, B.A. Internal green integration and environmental performance: The predictive power of proactive environmental strategy, greening the supplier, and environmental collaboration with the supplier. Bus. Strategy Environ. 2020, 30, 1333–1344. [Google Scholar] [CrossRef]
- Stekelorum, R.; Laguir, I.; Elbaz, J. Can you hear the Eco? From SME environmental responsibility to social requirements in the supply chain. Technol. Forecast. Soc. Chang. 2020, 158, 120169. [Google Scholar] [CrossRef]
- Hu, A.H.; Chen, C.; Huang, L.H.; Chung, M.; Lan, Y.; Chen, Z. Environmental Impact and Carbon Footprint Assessment of Taiwanese Agricultural Products: A Case Study on Taiwanese Dongshan Tea. Energies 2019, 12, 138. [Google Scholar] [CrossRef]
- Raihan, A.; Muhtasim, D.A.; Farhana, S.; Kurasaki, M.; Hasan, A.U.; Paul, A.; Faruk, O. Dynamic Linkages between Environmental Factors and Carbon Emissions in Thailand. Environ. Process. 2023, 10, 5. [Google Scholar] [CrossRef]
- Raihan, A.; Muhtasim, D.A.; Farhana, S.; Pavel, M.I.; Faruk, O.; Kurasaki, M.; Mahmood, A. Nexus between carbon emissions, economic growth, renewable energy use, urbanization, industrialization, technological innovation, and forest area towards achieving environmental sustainability in Bangladesh. Energy Clim. Chang. 2022, 3, 100080. [Google Scholar] [CrossRef]
- Raihan, A.; Tuspekova, A. Dynamic impacts of economic growth, renewable energy use, urbanization, industrialization, tourism, agriculture, and forests on carbon emissions in Turkey. Carbon Res. 2022, 1, 20. [Google Scholar] [CrossRef]
- Walston, L.J.; Barley, T.; Bhandari, I.; Campbell, B.; McCall, J.R.; Hartmann, H.; Dolezal, A.G. Opportunities for agrivoltaic systems to achieve synergistic food-energy-environmental needs and address sustainability goals. Front. Sustain. Food Syst. 2022, 6, 932018. [Google Scholar] [CrossRef]
- Badi, I.; Abdulshahed, A. Sustainability performance measurement for Libyan Iron and Steel Company using Rough AHP. J. Decis. Anal. Intell. Comput. 2021, 1, 22–34. [Google Scholar] [CrossRef]
- Dabic-Miletic, S.; Simic, V. Smart and Sustainable Waste Tire Management: Decision-Making Challenges and Future Directions. Decis. Mak. Adv. 2023, 1, 10–16. [Google Scholar] [CrossRef]
- Mishenin, Y.V.; Yarova, I.; Koblianska, I. Ecologically Harmonized Agricultural Management for Global Food Security; Springer: Singapore, 2021; pp. 29–76. [Google Scholar] [CrossRef]
- Puška, A.; Nedeljković, M.; Stojanović, I.; Božanić, D. Application of Fuzzy TRUST CRADIS Method for Selection of Sustainable Suppliers in Agribusiness. Sustainability 2023, 15, 2578. [Google Scholar] [CrossRef]
- Da Silva, A.R.; Cirani, C.B.S.; Serra, F.a.R.; Pigola, A.; Da Costa, P.R.; Scafuto, I.C.; Ruas, R.L.; Mazieri, M.R. Determining Factors on Green Innovation Adoption: An Empirical Study in Brazilian Agribusiness Firms. Sustainability 2023, 15, 6266. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Riaz, M.; Athar Farid, H.M. Picture fuzzy aggregation approach with application to third-party logistic provider selection process. Rep. Mech. Eng. 2022, 3, 227–236. [Google Scholar] [CrossRef]
- Limboo, B.; Dutta, P. A q-rung orthopair basic probability assignment and its application in medical diagnosis. Decis. Mak. Appl. Manag. Eng. 2022, 5, 290–308. [Google Scholar] [CrossRef]
- Milovanović, V.R.; Aleksić, A.V.; Sokolović, V.S.; Milenkov, M.A. Uncertainty modeling using intuitionistic fuzzy numbers. Mil. Tech. Cour. 2021, 69, 905–929. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Pamučar, D.; Petrović, I.; Ćirović, G. Modification of the Best–Worst and MABAC methods: A novel approach based on interval-valued fuzzy-rough numbers. Expert Syst. Appl. 2018, 91, 89–106. [Google Scholar] [CrossRef]
- Jangid, V.; Kumar, G. A Novel Technique for Solving Two-Person Zero-Sum Matrix Games in a Rough Fuzzy Environment. Yugosl. J. Oper. Res. 2022, 32, 251–278. [Google Scholar] [CrossRef]
- Pamučar, D.S.; Ćirović, G.; Božanić, D. Application of Interval Valued Fuzzy-Rough Numbers in Multi-Criteria Decision Making: The IVFRN-MAIRCA Model. Yugosl. J. Oper. Res. 2019, 29, 221–247. [Google Scholar] [CrossRef]
- Zhu, G.-N.; Ma, J.; Hu, J. Evaluating biological inspiration for biologically inspired design: An integrated DEMATEL-MAIRCA based on fuzzy rough numbers. Int. J. Intell. Syst. 2021, 36, 6032–6065. [Google Scholar] [CrossRef]
- Subha, V.S.; Dhanalakshmi, P. Some similarity measures of rough interval Pythagorean fuzzy sets. J. Fuzzy Ext. Appl. 2020, 1, 304–313. [Google Scholar] [CrossRef]
- Eskandari, S. Rough sets theory and its extensions for attribute reduction: A review. Big Data Comput. Vis. 2021, 1, 96–100. [Google Scholar] [CrossRef]
- Ayan, B.; Abacıoğlu, S.; Basilio, M.P. A Comprehensive Review of the Novel Weighting Methods for Multi-Criteria Decision-Making. Information 2023, 14, 285. [Google Scholar] [CrossRef]
- Alavi, S.; Zeinalnezhad, M.; Mousavi, E. Prioritisation of GPM activities from lean-agile-resilience perspective using fuzzy analytic hierarchy process. J. Fuzzy Ext. Appl. 2022, 3, 263–278. [Google Scholar] [CrossRef]
- Shafi Salimi, P.; Edalatpanah, S.A. Supplier selection using fuzzy AHP method and D-numbers. J. Fuzzy Ext. Appl. 2020, 1, 1–14. [Google Scholar] [CrossRef]
- Pamučar, D.; Žižović, M.; Biswas, S.; Božanić, D. A new logarithm methodology of additive weights (LMAW) for multi-criteria decision-making: Application in logistics. Facta Univ. Ser. Mech. Eng. 2021, 19, 361–380. [Google Scholar] [CrossRef]
- Pamučar, D.; Ćirović, G. The Selection of Transport and Handling Resources in Logistics Centers Using Multi-Attributive Border Approximation Area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
- Yucesan, M.; Mete, S.; Serin, F.; Celik, E.; Gul, M. An Integrated Best-Worst and Interval Type-2 Fuzzy TOPSIS Methodology for Green Supplier Selection. Mathematics 2019, 7, 182. [Google Scholar] [CrossRef]
- Ulutaş, A.; Topal, A.; Bakhat, R. An Application of Fuzzy Integrated Model in Green Supplier Selection. Math. Probl. Eng. 2019, 2019, 4256359. [Google Scholar] [CrossRef]
- Zhang, H.; Cui, Y. A model combining a Bayesian network with a modified genetic algorithm for green supplier selection. Simulation 2019, 95, 1165–1183. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Yildizbasi, A.; Üstünyer, P. Intuitionistic Fuzzy TOPSIS method for green supplier selection problem. Soft Comput. 2020, 24, 2215–2228. [Google Scholar] [CrossRef]
- Gupta, S.; Soni, U.; Kumar, G. Green supplier selection using multi-criterion decision making under fuzzy environment: A case study in automotive industry. Comput. Ind. Eng. 2019, 136, 663–680. [Google Scholar] [CrossRef]
- Phochanikorn, P.; Tan, C. An Integrated Multi-Criteria Decision-Making Model Based on Prospect Theory for Green Supplier Selection under Uncertain Environment: A Case Study of the Thailand Palm Oil Products Industry. Sustainability 2019, 11, 1872. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Pardasani, K.R.; Mardani, A. A novel hesitant fuzzy WASPAS method for assessment of green supplier problem based on exponential information measures. J. Clean. Prod. 2019, 238, 117901. [Google Scholar] [CrossRef]
- Wu, Q.; Zhou, L.; Chen, Y.; Chen, H. An integrated approach to green supplier selection based on the interval type-2 fuzzy best-worst and extended VIKOR methods. Inf. Sci. 2019, 502, 394–417. [Google Scholar] [CrossRef]
- Puška, A.; Nedeljković, M.; Zolfani, S.H.; Pamučar, D. Application of Interval Fuzzy Logic in Selecting a Sustainable Supplier on the Example of Agricultural Production. Symmetry 2021, 13, 774. [Google Scholar] [CrossRef]
- Sachdeva, N.; Shrivastava, A.K.; Chauhan, A. Modeling supplier selection in the era of Industry 4.0. Benchmarking Int. J. 2021, 28, 1809–1836. [Google Scholar] [CrossRef]
- Kannan, D.; Khodaverdi, R.; Olfat, L.; Jafarian, A.; Diabat, A. Integrated fuzzy multi criteria decision making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain. J. Clean. Prod. 2013, 47, 355–367. [Google Scholar] [CrossRef]
- Banaeian, N.; Mobli, H.; Fahimnia, B.; Nielsen, I.; Omid, M. Green supplier selection using fuzzy group decision making methods: A case study from the agri-food industry. Comput. Oper. Res. 2018, 89, 337–347. [Google Scholar] [CrossRef]
- Matić, B.; Jovanovic, S.; Das, D.K.; Zavadskas, E.K.; Stević, Ž.; Sremac, S.; Marinković, M. A New Hybrid MCDM Model: Sustainable Supplier Selection in a Construction Company. Symmetry 2019, 11, 353. [Google Scholar] [CrossRef]
- Forghani, A.; Sadjadi, S.J.; Moghadam, B.H. A supplier selection model in pharmaceutical supply chain using PCA, Z-TOPSIS and MILP: A case study. PLoS ONE 2018, 13, e0201604. [Google Scholar] [CrossRef]
- Liang, R.Q.; Chong, H. A hybrid group decision model for green supplier selection: A case study of megaprojects. Eng. Constr. Archit. Manag. 2019, 26, 1712–1734. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P.; Zavadskas, E.K.; Zolfani, S.H. Integrated QFD-MCDM framework for green supplier selection. J. Clean. Prod. 2017, 142, 3728–3740. [Google Scholar] [CrossRef]
- Liou, J.J.; Chuang, Y.; Zavadskas, E.K.; Tzeng, G. Data-driven hybrid multiple attribute decision-making model for green supplier evaluation and performance improvement. J. Clean. Prod. 2019, 241, 118321. [Google Scholar] [CrossRef]
- Nascimento, D.C.; Alencastro, V.; Quelhas, O.L.G.; Caiado, R.G.G.; Kumar, V.; Rocha-Lona, L.; Tortorella, G.L. Exploring Industry 4.0 technologies to enable circular economy practices in a manufacturing context. J. Manuf. Technol. Manag. 2019, 30, 607–627. [Google Scholar] [CrossRef]
- Chen, Z.; Ming, X.; Zhou, T.; Chang, Y. Sustainable supplier selection for smart supply chain considering internal and external uncertainty: An integrated rough-fuzzy approach. Appl. Soft Comput. 2020, 87, 106004. [Google Scholar] [CrossRef]
- Dev, N.K.; Shankar, R.; Swami, S. Diffusion of green products in industry 4.0: Reverse logistics issues during design of inventory and production planning system. Int. J. Prod. Econ. 2020, 223, 107519. [Google Scholar] [CrossRef]
- Qin, J.; Liu, X.; Pedrycz, W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. Eur. J. Oper. Res. 2017, 258, 626–638. [Google Scholar] [CrossRef]
- Puška, A.; Božanić, D.; Mastilo, Z.; Pamučar, D. Extension of MEREC-CRADIS methods with double normalization-case study selection of electric cars. Soft Comput. 2023, 27, 7097–7113. [Google Scholar] [CrossRef]
- Bari, P.; Karande, P. Ranking of sequencing rules in a job shop scheduling problem with preference selection index approach. J. Decis. Anal. Intell. Comput. 2022, 2, 12–25. [Google Scholar] [CrossRef]
- Mešić, A.; Miškić, S.; Stević, Ž.; Mastilo, Z. Hybrid MCDM Solutions for Evaluation of the Logistics Performance Index of the Western Balkan Countries. Econ. Innov. Econ. Res. J. 2022, 10, 13–34. [Google Scholar] [CrossRef]
- Stojanović, I.; Puška, A.; Selaković, M. A multi-criteria approach to the comparative analysis of the global innovation index on the example of the Western Balkan countries. Econ. Innov. Econ. Res. J. 2022, 10, 9–26. [Google Scholar] [CrossRef]
- Sénquiz-Díaz, C. The Effect of Transport and Logistics on Trade Facilitation and Trade: A PLS-SEM Approach. Econ. Innov. Econ. Res. J. 2021, 9, 11–34. [Google Scholar] [CrossRef]
- Mansory, A.; Nasiri, A.; Mohammadi, N. Proposing an integrated model for evaluation of green and resilient suppliers by path analysis, SWARA and TOPSIS. J. Appl. Res. Ind. Eng. 2021, 8, 129–149. [Google Scholar] [CrossRef]
- Banihashemi, S.A.; Khalilzadeh, M.; Antucheviciene, J.; Edalatpanah, S.A. Identifying and Prioritizing the Challenges and Obstacles of the Green Supply Chain Management in the Construction Industry Using the Fuzzy BWM Method. Buildings 2023, 13, 38. [Google Scholar] [CrossRef]
- Sazegari, S.; Davoodi, S.M.R.; Goli, A. Pricing the green products in a sustainable supply chain with data envelopment analysis approach (case study: Home appliance companies). J. Appl. Res. Ind. Eng. 2022, 9, 165–179. [Google Scholar] [CrossRef]
- Balaei, S.; Mohammadi, N.; Doroudi, H. Designing a hybrid model for the green supply chain in Gilan Steel Industry. Int. J. Res. Ind. Eng. 2023, 12, 73–87. [Google Scholar] [CrossRef]
- Yatribi, T. Factors Affecting Precision Agriculture Adoption: A Systematic Litterature Review. Econ. Innov. Econ. Res. J. 2020, 8, 103–121. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).