Abstract
In this paper we consider examples of complex expansion (cKdV) and perturbation (pKdV) of the Korteweg–de Vries equation (KdV) and show that these equations have a representation in the form of the zero-curvature equation. In this case, we use the Lie algebra of 4-dimensional quadratic nilpotent matrices. Moreover, it is shown that the simplest possible matrix representation of this algebra leads to the possibility of constructing a countable number of conservation laws for these equations.
Keywords:
complexification of the Korteweg–de Vries equation; perturbations of the Korteweg–de Vries equation; zero-curvature equation; conservation laws MSC:
35Q53
1. Introduction
The modern understanding of the integrability of nonlinear equations is based on the method of the inverse scattering problem. This method is applicable when the equation under study admits a representation in the form of consistency conditions for auxiliary linear systems. In particular, the integrability of the equations of field theory 1 + 1 and condensed matter physics is based on the possibility of their representation in the form of the zero-curvature equation [1,2,3]. The most productive interpretation of the zero-curvature equation is achieved if we consider it as a consistency condition for a set of commutating Hamiltonian flows in the dual space with some Lie algebra [3,4,5]. In this case, the corresponding pair of operators is identified with matrix gradients of mutually commutating Hamiltonians with respect to the Lie–Poisson bracket.
The possibility of using this method was found to be relevant, even for classical problems in mechanics related to the motion of a heavy solid body around a stationary point (the Kovalevskaya top). Almost a hundred years later, since Kovalevskaya reduced the problem to hyperelliptic quadratures, Reyman and Semenov-Tian-Shansky found a “natural” Lax representation with a spectral parameter for the Kovalevskaya vertex [6,7]. The method is based on a general group-theoretic approach to integrable systems and uses the Lie algebra so(4).
In 2006, Clarkson, Joshi, and Mazzocco demonstrated an algorithmic method for obtaining Lax pairs for a modified Korteweg–de Vries hierarchy [8]. Thanks to a special reduction under the action of a similarity group, they obtained a proof of isomonodromy for two identical Penlevé hierarchies.
To obtain new Volterra coupled systems and modified Toda field equations in [9,10], the authors used the special quasi-graduated Lie algebras parameterized by some numerical matrices, which are multiparametric deformations of loop algebras, which also generalize a special elliptic algebra so(3). In [11], a new generalized spectral problem with a 5 × 5 matrix for the Ablowitz-Kaup-Newell-Segur type models associated with an extended matrix Lie superalgebra was considered, and a superintegrable hierarchy corresponding to it was constructed.
The purpose of this paper is to apply the Zakharov–Shabat method for constructing various perturbations of the KdV equation using the Lie algebra of nilpotent 4 × 4 matrices and to study the existence of a countable number of conservation laws for the resulting models. In this paper, we continue the study of the kKdV and vKdV equations, for which Lax pairs were constructed, and some exact solutions were found in [12]. The application of the Zakharov–Shabat method allows us not only to integrate such complex equations but also to obtain some additional properties, in particular the presence of a countable number of conservation laws. In addition, the approach used is directly related to the dressing method, which not only allows us to construct new integrable nonlinear equations together with the corresponding auxiliary problems but also to obtain broad classes of exact solutions of the constructed equations, as well as wave functions and variable coefficients of the auxiliary problems.
2. Application of the Zakharov and Shabat Method
The advantage of the Lax method is its elementary character; the method is essentially reduced to the calculation of the conditions of conservation of eigenfunctions. However, after obtaining integrable equations to actually integrate them, it is necessary to develop a technique for solving the inverse spectral problem, which is not always easy. This difficulty was overcome by Zakharov and Shabat [2,13], who demonstrated the possibility of constructing integrable equations together with an explicit indication of the way to calculate their exact solutions by means of the dressing method.
The basic idea of the dressing method is based on the representation of the integral operator on a straight line as a product of two Volterra operators. The method was further developed in [14], where the Riemann–Hilbert problem was introduced into the scheme of the dressing method. The method proved to be applicable both for (1 + 1)-dimensional and (2 + 1)-dimensional (two spatial and one time coordinate) nonlinear equations.
The integration of known non-linear evolution equations (the Korteweg–de Vries equation, the non-linear Schrödinger equation, the Sine–Gordon equation, etc.) [15] is usually based on their representation in the form of a consistency condition for two linear problems
where is a vector function with values in space , which is commonly called auxiliary; and are matrices in this space, parameterized by functions j = 1, ..., N (classical fields) included in the nonlinear equation and by the spectral parameter ξ of , on which they depend meromorphically.
It is well known that relation (1.1) underlies the applicability of the inverse scattering problem to the nonlinear evolution equations, so using the terminology adopted in soliton theory, we will call the scattering operator. The most important feature of the pair of Lax matrix operators is that the time derivative is not included in the operator . Thus, we can consider t as a parameter and investigate the spectral properties of this operator, i.e., investigate solutions of the equation on eigenvalues.
This representation of the integrable equations is called geometric, since the matrix functions , can be interpreted as local coefficients of connectivity in the trivial decomposition , where the space-time plays the role of a base and the auxiliary space plays the role of a layer. Equations (1) and (2) mean that the vector V is covariantly constant, and the condition
shows that the connectivity of , has zero curvature. Therefore, (3) is called the zero-curvature condition. It replaces the Lax-type representation in the modern formalism of the inverse problem method.
Let us apply the Fourier transform to Equations (1) and (2) using the parameter ξ; then, we represent the operators and in the following form
provided that are complex constants, are matrices depending on some functions of the variables x and t and their derivatives with respect to these variables.
The problem is reduced to determining the equations that and must satisfy in order for each solution of system (1) and (2) to satisfy the consistency condition (3), i.e., zero-curvature equation. Substituting (4) and (5) into (3), we obtain the conditions on the matrices . The existence of such conditions requires the commutativity of the matrices and . In this case, the equations always exist but may not be uniquely determined. The following conditions are necessary and sufficient for uniqueness:
- At least one of the numbers is not equal to zero;
- None of is equal to .
If these conditions are satisfied, no new powers of or new prime fractions not contained in and appear in the commutator ; therefore, the commutator can also be decomposed into the same prime fractions as and .
The operators and will be considered as quadratic matrices and is a 4-dimensional vector function. For the convenience of further calculations, let us introduce the basis of four-dimensional Lie algebra matrices in the following form:
Lie algebra is a vector space over some field together with a binary operation , called a Lie bracket, satisfying the following axioms: bilinearity, skew-symmetry
and Jacobi identity
Let us make a table (Table 1) of the results of the commutator [X, Y], where X and Y take values from the set of basis matrices {M, N, L, K, T, U, S, H, E, F}, without making any assumptions about its closure. Further it is used to construct closures of Equation (3).

Table 1.
Table of commutations of the Lie algebra .
2.1. Representation of the Complexification of the Korteweg–de Vries Equation in the Form of the Zero-Curvature Equation
Let us consider a special case of Equation (3), when coefficients of expansion (4) and (5) are square matrices of the fourth order with elements that depend on functions , (“–” means complex conjugation) and their partial derivatives with respect to the variable x. To write Equations (1) and (2), we choose a column vector as an eigenfunction, where T stands for transpose.
The structure of the operator (4) is given in a special way when only two coefficients are non-zero: and is a functional matrix. has the following spectral parameter expansion
where i is the imaginary unit. Let us write using basis (6)
The consistency condition (3) for the system of Equations (1) and (2) must be satisfied for all values of ξ, so the form of the operator cannot be arbitrary. Let us represent in the form
Considering as constant and as functional matrices, determine possible values of powers m and s. The artificial closure (3) is the means by which Wahlquist and Estabrook came to the expression for and in the context of the Korteweg–de Vries equation [16], and it is in this direction that subsequent authors have acted [17,18]. In (3), we equate the coefficients at the same powers of iξ:
…
…
The only equation that contains a derivative with respect to the variable t is equality (13), so it will determine the equation we are looking for; the other equations should identically turn to zero. The coefficient q1 defines the smallest degree s at which the system (9)–(16) is consistent, i.e., s ≥ 1. To make the number of equations as small as possible, consider the limiting case when s = 1.
Comparing the relations of the system (9)–(12), we can note that the values of matrices bk are substituted into the following equations, though bk are not included in these equations themselves but through their derivatives with respect to the variable x; therefore, it is easy to see that m will determine the degree of the highest derivative included in Equation (13).
Consider the case when m = 3. Using the table of commutations of the Lie algebra and the previously defined form (7) , we find, by virtue of Equation (9), a constant matrix commuting with , and in the simplest form
where is some parameter, which for obtaining a special form of the final equation, we assume to by . Equation (10) is similar to Equation (9), but the matrix is a functional matrix and cannot be constant, so we assume .
The coefficient at the first power of iξ depends only on the functions , and is expressed from (11) using the table as follows:
The matrix can be obtained similarly
The value is determined from the overdetermined system of Equations (12) and (16), which gives
The specified structure of the matrices and in the found form ensures that all members of the system (9)–(16) vanish, except for member (13) at (iξ)−1, which gives a matrix with two complex conjugate equations. The requirement that the resulting matrix be equal to zero means that satisfies the equation
The obtained Equation (21) coincides with the complex extension of the Korteweg–de Vries equation (cKdV) [12]. The conducted studies led to the following conclusion.
Theorem 1.
The complexification of the KdV Equation (21) has a zero-curvature operator representation (3) with operators and in the form
where is an unknown complex function and is an imaginary parameter.
2.2. Representation of the Perturbed Korteweg–de Vries Equation in the Form of the Zero-Curvature Equation
Consider the new problem of the consistency of the system (1), (2) with a given operator in the form of a polynomial of the first order by the parameter
Its expansion, we write using the basis matrices (6) in the form
where are some functions and is an arbitrary non-zero constant.
Using the consistency condition (3), let us define the matrix . Let us choose in the form
The representation in the form of a polynomial is considered for even powers of . Let us determine possible values of powers m and s, considering as a constant matrix. To do this, we substitute (24) and (25) into (3) and equate the coefficients at the same powers (iξ) to zero
…
…
Some remarks are necessary here:
- Only one equation contains a derivative with respect to the variable t; this is equality (29), so it will determine the sought relations between the functions and . The other equations should identically turn to zero.
- The coefficient q1 enters Equations (29) and (30) and determines the smallest power s at which the system (29)–(32) is consistent, i.e., s ≥ 0. To make the number of equations the smallest, consider the limiting case where s = 0.
- Comparing relations (26)–(29), we can note that the matrices defined in the upper equations then do not enter into the subsequent relations themselves but their derivatives with respect to the variable x, so it is easy to see that the degree of the highest derivative included in Equation (28) will determine the value of m. Next, consider the case where m = 2.
Now, let us analyze which basis matrices should be part of the expansion of in power of iξ if the highest power is 2:
where are 4 × 4 functional matrices, depending on and . This form of operator transforms the system (26)–(32) into four equalities
where .
Using the representation of in the form (25), we will use the basis matrices (6) and Table 1 to correctly select the suitable commutative matrix b0 in the first equality (34). Suitable elements can be L, E, and F, or a linear combination of . Let us consider each case separately.
(A1) (L): choose, for example,
is an arbitrary parameter; then,
(B1) (E, F): if we choose E and F, they can be taken with different constant multipliers , , which gives
(C1) (): in order for the first commutator of system (34) to become zero with , the condition must be satisfied
Therefore,
where is a constant coefficient.
Cases A, B, and C will be considered separately, but a linear combination of them can also be used. Let us proceed to the analysis of the second equation of the system (34).
(A2). The right part of has the form
and the left part of defines the form of b1. Let us use the table of commutations of the Lie algebra and find the right structure for (38). The matrix b1 should contain the matrix K; then
Comparing (38) and (39), it is easy to see that the expressions are incomparable, so case (A) will not be used further.
(B2). At defined by expression (36), we obtain a diagonal form with two parameters
Consequently, b1 must contain matrices S and H; then, gives
Comparing (40) and (41), we obtain the refined form of and :
(C2). The linear combination in the commutator has the following elements
among which there is a matrix K, which cannot be compensated in (see table), so option (C) is not involved in further study.
In order to compensate the terms of the third equality in system (34) and obtain a meaningful fourth equation, matrices b1 and b2 must depend on the functions Let us complement matrix b1 so that this complement does not affect the commutation in the third equality of system (34). This is possible since
Let us examine all the cases where
will be further defined below. The cases (45) will be considered separately, but their linear combination can also be used.
Let us write an explicit form of the right-hand side of using (44) for the value of without
Since the equality should be fulfilled, and, as can be seen from Table 1, the initial commutator gives matrices only if b2 contains an element proportional to K, given that and the relations between the coefficients of result , in (46) we should additionally put . As a result, the basis part of corresponding to (46) will take the form
The additional part depends on the choice of the right-hand side of (45):
Using Table 1, it is easy to see that there is no basis matrix whose commutator with would allow us to obtain (48), (49) completely, so cases (a) and (b) are not of interest and will not be used further.
Case (c) gives an additional part b23
As a result, (44) and the combination of (47) and (51) give
The fourth equation of the system (34) is not trivial but defines differential relations on the functions and :
Ten basis matrices participate in writing the result and give ten equations, three of which contain derivatives with respect to the variable t at . The remaining seven equalities should give identically zero. Two arbitrary parameters are introduced in the construction of the matrix b2; their number is insufficient to resolve the problem. As was shown in Equation (43), the commutator of with does not give additional elements, so by adding them to matrix b2, we can nullify the superfluous equations. Let b2 take the form
where are unknown functions.
Write out all equations derived from the equality :
Equation (55) determines the coefficients:
The remaining three equalities give equations, two of which coincide
Assuming the parameter , we obtain a system of two differential equations relating the functions and :
The system (56) coincides with the perturbation of the Korteweg–de Vries equation (pKdV) of [12]; hence, an operator representation in the form of the zero-curvature equation is found for it, and the following theorem is proved.
Theorem 2.
The system of Equation (56) has a zero-curvature operator representation (3) with operators and in the form
where are unknown functions, is imaginary parameter, is arbitrary constant, and the matrices have the form (6).
3. Construction of Conservation Laws
An important property of nonlinear evolution equations is the existence of an infinite sequence of local conservation laws. Each of these laws gives, for a class of solutions asymptotically tending to zero at , a conserved value expressed as an integral over the entire space of the corresponding nonlinear polynomial combination of functions and their derivatives.
3.1. Conservation Laws for cKdV
Consider the eigenvalue Equation (1) written for Equation (21), with vector function and operator (22) as a system
Let us reduce the resulting system to a single equation for the function
Let us show that the complexification of the Korteweg–de Vries Equation (21) has an infinite sequence of conservation laws. Let us construct integrals of motion of the form
where are polynomials from the function and their derivatives with respect to x associated with problem (60); we will use the method proposed by Zakharov and Shabat [19]. Integrals of the form (61) are called local polynomial integrals.
Suppose
then, the solution of Equation (60) will take the following form
Theorem 3.
from which follows a polynomial dependence on the functions
,
and their partial derivatives with respect to the variable x.
If changes according to Equation (21) and turns to zero together with its derivatives at
, then
- (1).
- The solution of (60) can be represented in the form (63), where
- (2).
- The functions are defined recurrently by the formulas
Proof of Theorem 3.
Let us write the solution in the form (64) and find the derivatives
Substituting (69) into Equation (60), we obtain a new equation for the function :
After removal of brackets and collecting terms, write
Let us group the terms by decreasing powers of the product :
Let us introduce the following notations in Formula (62) for brevity
Then, the function after performing the operations in Formula (62) will take the form
Let us represent the function in the neighborhood of an infinitely distant point of the -plane as a series expansion in powers of :
where
Substituting the right-hand side of Equality (71) into the equation on (69) and taking into account the properties of the function: , , derived from the representation (71), let us write out terms with different powers of :
The first five equalities contain the incomplete set of terms included in the general equation with power , from which we find (66), (67), and (68). The remaining functions are determined recurrently via Formula (65).
The values of contain no integration operations and all are polynomially expressed in terms of the functions , and their partial derivatives with respect to the variable x. □
Note the interesting properties of the found polynomial functions.
Corollary 1.
- All contain a linear part in the form of higher derivatives of order n–1 from and ; in the recurrence formula it is created by terms .
- In , there are no linear terms with derivatives of order lower than n–1.
- All other terms (except for those highlighted in item (1) of the recurrence Formula (65)) give non-linear terms.
- If we give the functions and a weight coefficient of 1, and the derivatives of the k-th order with respect to the variable x a weight coefficient of , where m is the weight coefficient of f (when functions and their derivatives are multiplied their weights are added), then all the terms of the polynomial have the same weight: .
Proof of Corollary 1.
For the proof, we will use the method of mathematical induction. As the general form of the recurrence Formula (60) shows, the higher terms of the expansion depend on the lower ones, and we need to know at least the first three terms of the expansion (65) in order to use this construction, so in the first step of the method, we perform a formal check for , , .
(I) So, for , obviously, each term and corresponds to weight 1; for , both terms represent a first-order derivative and, therefore, the weight of these terms will coincide and be ; : the first pair as a second-order derivative has weight , in the terms representing the product we add the weights and have total weight 2.
(II) Assume that the hypothesis is true for all the lowest up to and including . Let us show that all terms in the recurrent Formula (64) have the same weight . Let us find the weight of each term:
All terms have an assumed weight . The property is proved. □
Note that in Formulas (65)–(68), there is no explicit dependence on x, t. Obviously, all the quantities are linearly independent (none of them can be expressed in terms of the others), so the quantities are each conserved separately. The polynomials , contain full derivatives; they appear at even powers n and are conserved trivially. Dropping some full derivatives in (65), we obtain that a nontrivial set of conserved quantities for Equation (60) will look like
where the first laws have the form:
This proves the following corollary.
Corollary 2.
The nonlinear partial differential Equation (21) has a countable set of first integrals (72), where the differential polynomials are defined by the recurrent Formula (65). The first integrals of motion are defined by (73) and (74).
3.2. Conservation Laws for pKdV System
Let us construct a countable number of conserved quantities for the system (56). Stages of the algorithm for construction of conservation laws and their justification fully correspond to the previous section, so the presentation of the material is reduced to a demonstration of only qualitatively different moments of their construction.
Let us write the equation for eigenvalues (1) with operator (57) and as a system
Let us reduce this system to a single equation
Theorem 4.
If the functions and
change according to the system of Equation (56) and tend to zero together with their derivatives at
, then
- (1).
- The solution of (76) can be represented as (64).
- (2).
- The functions are determined recurrently by the formulas
Proof of Theorem 4.
Let us reproduce the proof in fragmentary form. Let us use the form (63) of writing the solution and, substituting it into Equation (76), we obtain the equation on :
Replacing with series (64) allows us to group terms with different powers of in equality (80):
This system allows us to find the functions recurrently by sequentially applying Equations (78), (79), (77). □
Formulas (77)–(79) are linearly independent (none of them can be expressed through the others). The polynomials , ,... contain only the full derivatives; they appear at odd powers of of the above system and are trivially conserved. A non-trivial set of conserved quantities for Equation (56) would look like
This proves the following corollary.
Corollary 3.
The nonlinear system of partial differential Equation (56) describing the KdV perturbation has a countable set of first integrals (81)–(83), where the differential polynomials
are defined by the recurrence Formula (77).
The constructed first integrals of the system (56) define the following physical characteristics of the densities of conserved quantities:
- (81)—conservation of mass of the wave process (fully coincides with the first law for the classical soliton in the unperturbed KdV equation);
- (81)—shows the conservation of momentum of interacting functions;
- (82)—conservation of energies (similar terms for the KdV equation are ) with the interaction element of and or their functional connection .
Obviously, if there is no perturbation in the system (56) , the solution is a classical soliton:
The plot of the function corresponding to Formula (84) is shown in Figure 1.
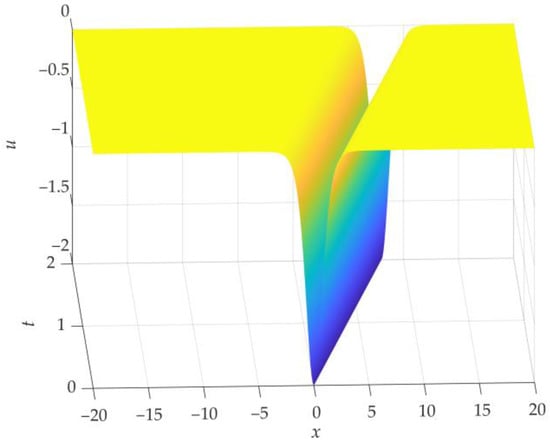
Figure 1.
Classical soliton in the case of zero perturbation according to Formula (84).
The question arises as to whether it is possible to preserve the soliton solution in the perturbed system. This is possible if the perturbation function does not create new terms in the first equality of system (56) other than those created by the soliton itself, i.e., those proportional to .
Corollary 4.
The system of Equation (56) at
describes the interaction of the soliton and the kink
and at
The proof is obtained via simple substitution of these functions.
From Formulas (85) and (86), it follows that when interacting with the kink, the soliton changes the direction of motion and doubles its speed compared to the unperturbed system (84), and when in contact with the hyperbolic secant, it changes the direction of motion and slows down by a factor of two. An illustration of the above is shown in Figure 2, which shows the plots of the corresponding functions according to Formulas (85) and (86).
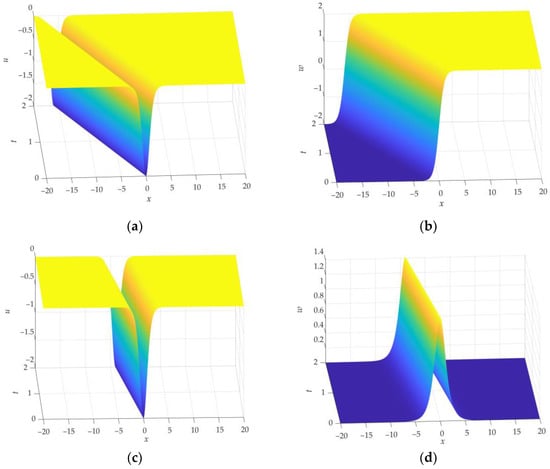
Figure 2.
Soliton solution in the perturbed system. (a,b) Functions and according to Equation (85) at , and using “+” in corresponding equation. (c,d) Functions and according to Equation (86) at , and using “+” in corresponding equation.
Note that similar interactions were considered in [20]. The dynamics of the kinks of the modified Sine-Gordon equation in a model with localized spatial modulation of the periodic potential were studied numerically. Two qualitatively different scenarios of the dynamic behavior of the kink were demonstrated.
We also conducted numerical studies of the possibility of preserving the soliton solution in the perturbed system. A numerical solution was carried out on the basis of finite-difference approximation of the investigated partial differential equations [21]. A numerical study of the system of Equation (56) on the emergence of stable solutions of the kink and soliton, for initial conditions at , corresponding to the form of functions (85) and (86) was performed. The numerical results obtained in this case give a picture of a stable soliton solution and coincide with the analytical solutions shown in Figure 2.
Figure 3 shows numerical solutions of system (56) under other different initial conditions that differ completely or partially from the form of functions (85) and (86). As can be seen from the presented numerical results, a stable soliton solution is not formed in the considered situations.
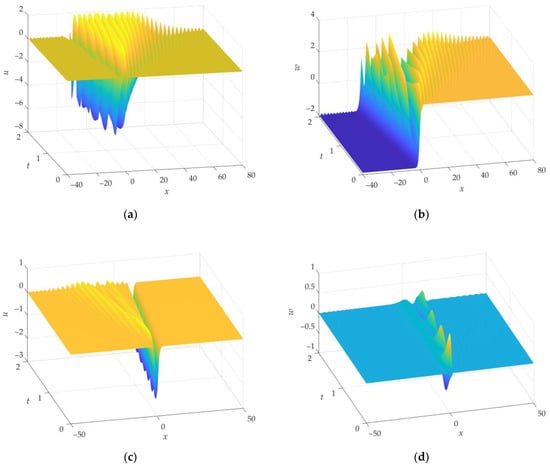
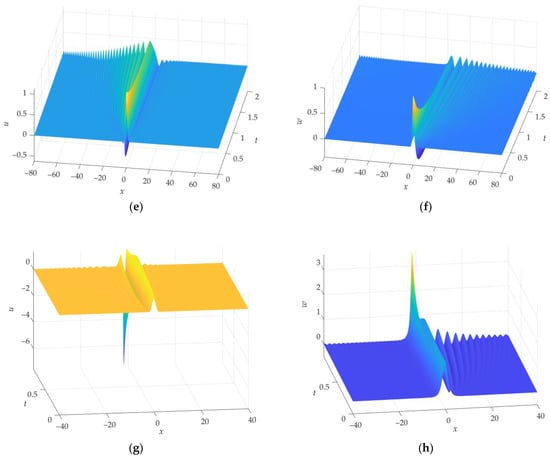
Figure 3.
Numerical solution of the system of Equation (56) under different initial conditions. (a,b) , at . (c,d) , at . (e,f) , at . (g,h) , at .
Thus, numerical simulations confirmed the analytically obtained conclusion that only under the initial conditions corresponding to the analytical solution (85) and (86), the solution splits into a stable soliton and a kink (at ) and into a soliton and a hyperbolic secant (at ). In the perturbed state, the propagation velocities in the soliton-kink and soliton-hyperbolic secant pairs coincide but differ from the velocities in the unperturbed state.
4. Conclusions
Using the zero-curvature operator equation with operators represented as polynomials decomposed by the spectral parameter with the Lie algebra of nilpotent 4 × 4 matrices, perturbations of the KdV equation were constructed, which coincided with the previously obtained cKdV and pKdV equations in [12].
One of the proofs of integrability of nonlinear differential equations is the existence of an infinite number of conserved quantities. The Zakharov–Shabat method allows one, using the equation on eigenvalues, to construct a countable number of conservation laws.
For the cKdV Equation (21), an infinite sequence of polynomial first integrals is found, such that all the terms of the polynomial have the same weight .
A countable set of conservation laws was also constructed for the system (56) describing the KdV perturbation. Comparing expressions (81) and (82) with the KdV conservation laws, it is easy to see that the parts of their structure related to the function coincide exactly. This coincidence suggested that system (56) should have a soliton solution. This led to the search for special perturbations in the form of a kink and a hyperbolic secant, which create the conditions for the appearance of a soliton solution of the form (85) and (86), respectively. Numerical simulations confirmed this conclusion.
The system (56) has an applied significance, since it describes the interaction of soliton and kink, soliton and hyperbolic secant, which is widespread in modeling wave phenomena in various real systems (see Refs. [22,23,24] and the literature therein). Of particular importance in the model is the presence of the parameter μ. By varying this parameter, one can strengthen or weaken the presence of the perturbation w(x,t) and observe the mutual influence of the functions u(x,t) and w(x,t).
Further development of these studies will be the construction of n-soliton solutions.
Author Contributions
Conceptualization, T.V.R.; methodology, T.V.R.; validation, R.G.Z.; visualization, A.R.Z.; formal analysis, A.R.Z. and R.G.Z.; investigation, T.V.R.; writing—original draft preparation, T.V.R.; writing—review and editing, A.R.Z. and R.G.Z.; project administration, A.R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by North-Caucasus Center for Mathematical Research under agreement No 075-02-2023-938 with the Ministry of Science and Higher Education of the Russian Federation.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Faddeev, L.D.; Takhtajan, L.A. Hamiltonian Methods in the Theory of Solitons; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Zakharov, V.E.; Shabat, A.B. A scheme for integrating the nonlinear equations of mathematical physics by the method of the inverse scattering problem. I. Funct. Anal. Its Appl. 1974, 8, 226–235. [Google Scholar] [CrossRef]
- Newell, A.C. Solitons in Mathematics and Physics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1985. [Google Scholar]
- Flaschka, H.; Newell, A.C.; Ratiu, T. Kac–Moody Lie algebras and soliton equations. II. Lax equations associated with . Physica D 1983, 9, 303–323. [Google Scholar]
- Holod, P. Integrable Hamiltonian Systems on the Orbits of Affine Lie Groups and Periodical Problem for the Modified Korteweg-deVries Equation; Preprint ITP-82-144; Institute for Theoretical Physics: Kyiv, Ukraine, 1982. (In Russian) [Google Scholar]
- Bobenko, A.I.; Reyman, A.G.; Semenov-Tian-Shansky, M.A. The Kowalewski top 99 years later: A Lax pair, generalizations and explicit solutions. Commun. Math. Phys. 1989, 122, 321–354. [Google Scholar] [CrossRef]
- Reyman, A.G.; Semenov-Tian-Shansky, M.A. A new integrable case of the motion of the 4-dimensional rigid body. Commun. Math. Phys. 1986, 105, 461–472. [Google Scholar] [CrossRef]
- Clarkson, P.A.; Joshi, N.; Mazzocco, M. The Lax pair for the mKdV hierarchy. Séminaire et Congrès 2006, 14, 53–64. [Google Scholar]
- Skrypnyk, T.V. Quasigraded Lie algebras and modified Toda field equations. Symmetry Integr. Geom. Methods Appl. 2006, 2, 043. [Google Scholar] [CrossRef]
- Skrypnyk, T.V. Deformations of loop algebras and integrable systems: Hierarchies of integrable equations. J. Math. Phys. 2004, 45, 4578–4595. [Google Scholar] [CrossRef]
- Hu, B.; Ma, W.-X.; Xia, T.; Zhang, L. Nonlinear integrable couplings of a generalized super Ablowitz-Kaup-Newell-Segur hierarchy and its super bi-Hamiltonian structures. Math. Methods Appl. Sci. 2018, 41, 1565–1577. [Google Scholar] [CrossRef]
- Redkina, T.V.; Zakinyan, A.R.; Zakinyan, R.G.; Surneva, O.B. Hierarchies of the Korteweg– de Vries equation related to complex expansion and perturbation. Axioms 2023, 12, 371. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Integration of nonlinear equations of mathematical physics by the method of inverse scattering. II. Funct. Anal. Appl. 1979, 13, 166–174. [Google Scholar] [CrossRef]
- Zakharov, V.E. Benney equations and quasiclassical approximation in the method of the inverse problem. Funct. Anal. Appl. 1980, 14, 89–98. [Google Scholar] [CrossRef]
- Takhtadzhyan, L.A.; Faddeev, L.D. Simple connection between the geometric and the Hamiltonian representations of integrable nonlinear equations. J. Math. Sci. 1985, 28, 800–806. [Google Scholar] [CrossRef]
- Wahlquist, H.D.; Estabrook, F.B. Prolongation structures of nonlinear evolution equations. J. Math. Phys. 1975, 16, 1–7. [Google Scholar] [CrossRef]
- Dodd, R.K.; Eilbeck, J.C.; Gibbon, J.D.; Morris, H.C. Solitons and Nonlinear Wave Equations; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Calogero, F.; Degasperis, A. Spectral Transform and Solitons I; North Holland: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Novikov, S.P.; Manakov, S.V.; Pitaevskii, L.P.; Zakharov, V.E. Theory of Soliton, the Inverse Scattering Method; Plenum: New York, NY, USA, 1984. [Google Scholar]
- Ekomasov, E.G.; Gumerov, A.M. Collective influence of impurities on the dynamics of kinks of modified sine-Gordon equation. Comput. Res. Model. 2013, 5, 403–412. [Google Scholar] [CrossRef]
- Zabusky, N.J.; Kruskal, M.D. Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef]
- Saifullah, S.; Fatima, N.; Abdelmohsen, S.A.M.; Alanazi, M.M.; Ahmad, S.; Baleanu, D. Analysis of a conformable generalized geophysical KdV equation with Coriolis effect. Alexandria Eng. J. 2023, 73, 651–663. [Google Scholar] [CrossRef]
- Lü, X.; Chen, S.-J. N-soliton solutions and associated integrability for a novel (2+1)-dimensional generalized KdV equation. Chaos Solitons Fractals 2023, 169, 113291. [Google Scholar] [CrossRef]
- Saifullah, S.; Ahmad, S.; Alyami, M.A.; Inc, M. Analysis of interaction of lump solutions with kink-soliton solutions of the generalized perturbed KdV equation using Hirota-bilinear approach. Phys. Lett. A 2022, 454, 128503. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).