Abstract
In the present study, two effective methods, the Exp-function method and He’s frequency formulation, are employed to investigate the dynamic behaviors of the (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation, which is used widely to describe the incompressible fluid. A variety of the wave structures, including the dark wave, bright-dark wave and periodic wave solutions, are successfully constructed. Compared with the results attained by the methods, the obtained solutions are all new and have not been presented in the other literature. The diverse wave structures of the solutions are presented through numerical results in the form of three-dimensional plots and two-dimensional curves. It reveals that the proposed methods are powerful and straightforward, which are expected to be helpful for the study of travelling-wave theory in fluid.
Keywords:
Exp-function method; He’s frequency formulation; solitary solutions; periodic wave solution MSC:
35Q35; 35Q51
1. Introduction
Exploration of the exact solutions of the partial differential equations (PDEs) has obtained wide attention from scientists and mathematicians. Until now, some effective approaches thus far are: the auxiliary equation mapping method [1,2], Wang’s Bäcklund transformation based method [3,4], the modified extended direct algebraic method [5,6], Sardar subequation method [7,8], variational method [9,10], trial equation method [11,12], logarithmic transformation [13] and so on. As is common knowledge, the fluid, as a phase of matter including liquid, gas and plasma, is considered to be one of the most common substances in nature. Significant research on fluids has provided an important guide for the design of related industries. Additionally, there are many famous partial–differential equations available to model fluid characteristics. In this paper, we consider the famous (3+1)-dimensional Boiti–Leon–Manna–Pempinelli (BLMP) equation, which is provided by [14,15]:
where is a well-known function that is used widely in the liquid engendering and incompressible liquid. Additionally, many scholars have made outstanding contributions to the solution of Equation (1). MelikeKaplan used the transformed rational function to construct different types of analytical solutions [16]. In [17], Mohamed R. Ali et al, obtained the lump solutions and mixed solution involving lump waves and solitons by the bilinear method and symbolic computation. Tang et al. found the periodic wave solutions for Equation (1) via the extended homoclinic test approach [18]. Additionally, the double-periodic soliton solutions are constructed by Liu in [19]. The sine Gordon expansion method and the extended tanh function method are used to seek the new soliton solutions in [20]. Mohammad Najafi et al. studied the problem via the semi-inverse method [21]. The Hirota’s bilinear algorithm is applied to seek the lump solutions by Ahmad M.Alenezi in [22]. Considering the importance of Equation (1) in the field of fluids, and being encouraged by recent research results, we aim to construct abundant exact solutions of Equation (1) by the Exp-function method (EFM) and He’s frequency formulation (HFF). The structure of this paper is as follows. In Section 2, we will provide a brief introduction to the EFM and HFF. In Section 3, the EFM and HFF are used to find the exact solutions and the behaviors of the different solutions are presented by the three-dimensional and two-dimensional contours. The physical explanation of the different solutions are provided in Section 4. The conclusion is presented in Section 5.
2. The Two Methods
Considering the general nonlinear FDEs as:
Introducing the following transformation:
where , , , are all non-zero constant. using Equation (3), the nonlinear PDE of Equation (2) can be reduced into the ODE as:
2.1. The EFM
The EFM is a powerful tool to construct the abundant traveling wave solutions of the studied equation. In this section, we will provide a brief introduction to the EFM [23,24,25,26,27]. Its primary steps are presented as follows:
Assuming the solution of Equation (4) with the form as:
where u, p, s, g are positive integers that can be determined later, , are unknown constants.
Taking Equation (5) into Equation (4) and balancing the linear term of highest and lowest orders, respectively, we can determine the u, p, s, g.
Then, substituting the obtained results into Equation (4), setting the coefficients of to be zero, we can determine the coefficients and . With this, we can obtain the exact solutions of Equation (2) via Equation (3).
2.2. The HFF
The HFF [28,29,30], which was first proposed by Chinese mathematician Ji-Huan He, is a powerful tool to seek the periodic solution.
Considering Equation (4) with the form as:
In Equation (6), is a function of . Here, the periodic solution of Equation (6) can be assumed as:
where represents angular frequency. In the view of He’s frequency formulation [31,32], the amplitude–frequency relationship of Equation (7) can be determined via one step, which is:
With this, we can obtain the periodic wave solution of Equation (1).
3. Applications
In order to obtain the abundant solutions, the following transformation is introduced:
In Equation (9), , , and are non-zero real numbers, and there is . With the help of Equation (9), Equation (1) becomes an ordinary differential equation, which is:
Additionally, there are , and .
Integrating Equation (10) once, with respect to , and setting the integral constant to be zero, yields:
which is:
3.1. Application of the EFM
Based on the EFM, we assume the solution of Equation (12) with the form as:
which can be expressed as:
Putting Equation (14) into Equation (12) and balancing the linear term of highest order and in Equation (12) with the highest order nonlinear term, we obtain:
By balancing the highest order of Exp-function in Equations (15) and (16), it yields:
which leads to:
In the same way, we balance the linear term of lowest order in Equation (12), there is:
Balancing the lowest order of Exp-function in Equations (19) and (20), there is:
which results in:
For simplicity, we set , and , Equation (14) can be written as:
Taking Equation (23) into Equation (12), we can obtain the following form:
where
Letting the coefficients of to be zero, we obtain:
Solving the above systems, we obtain the following three families:
Family 1
Set 1:, , , , , , .
Therefore, we can get the first exact traveling wave solution (dark-wave solution Form 1) as:
Here, , , and are free parameters. If we select , , = 0, the behavior of solution is plotted in Figure 1.
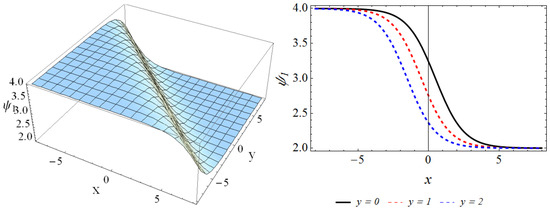
Figure 1.
The 3D plot and 2D curve of the solution for , , , when , .
Set 2:, , , , , , .
Furthermore, we can obtain the second exact traveling solution (bright-dark wave solution) as:
where , , and are free parameters. By selecting , , , the propagation of solution is described in Figure 2.
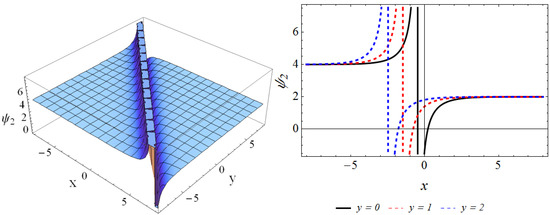
Figure 2.
The 3D plot and 2D curve of the solution for , , , when , .
Family 2
Set 3:, , , , , , .
Next, we can obtain the third exact traveling wave solution (dark-solitary wave solution Form 2):
where , , and are free parameters. The performance of the solution is presented in Figure 3 for , , .
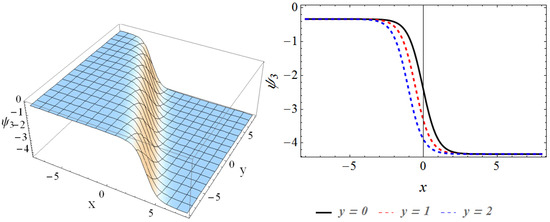
Figure 3.
The 3D plot and 2D curve of the solution for , , , when , .
Set 4:, , , , , , .
Then, we can obtain the fourth exact traveling wave solution (bright-dark wave solution) as:
where , , and are free parameters. We plot the behavior of the solution in Figure 4 with , , .
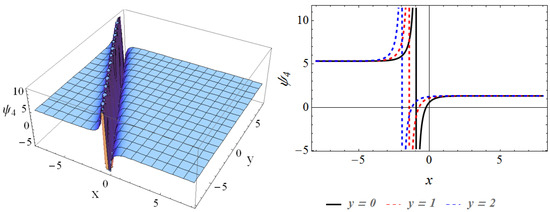
Figure 4.
The 3D plot and 2D curve of the solution for , , , when , .
Family 3
Set 5:, , , , , , .
Next, we can get the fifth exact traveling wave solution (kinky bright-dark solitary wave solution Form 1) as:
Here, the , , and are free parameters. The solution is presented in Figure 5 by using , , .
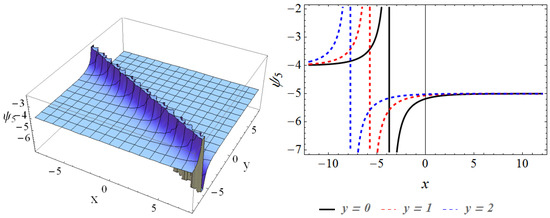
Figure 5.
The 3D plot and 2D curve of the solution for , , , when , .
Set 6:, , , , , , .
Finally, we can get the sixth exact traveling wave solution (bright-dark wave solution) as
where , , and are free parameters. In this case, the contour of solution is illustrated in Figure 6 by selecting , , .
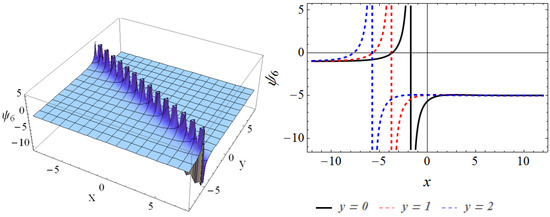
Figure 6.
The 3D plot and 2D curve of the solution for , , , when , .
3.2. Application of the HFF
In the view of Equation (12), we cannot solve it directly by the HFF. Here, we can make a transformation as:
So Equation (12) becomes:
Which is
From which, we obtain
The periodic solution of Equation (32) is supposed with the form as:
Based on the HFF, the amplitude frequency relationship can be easily determined as:
With this, the periodic solution of Equation (32) can be obtained as:
In the view of Equation (31), we obtain:
Thus, the periodic wave solution of Equation (1) can be obtained as:
Set 7:
By using , , , , , = 0, the performances of Equation (39) are described in Figure 7.
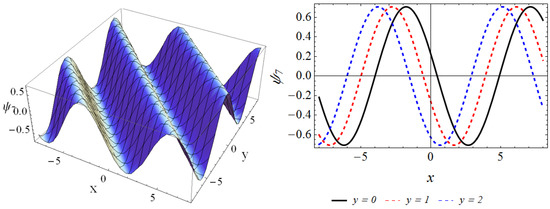
Figure 7.
The 3D plot and 2D curve of the solution when , .
4. Physical Explanation
This section provides the physical explanation of the results in Section 3. Figure 1 describes the contours of the solution in the region , for , . It can be seen that the wave is the dark-solitary wave. The behaviors of are presented in Figure 2 through the three-dimensional contour and two-dimensional curve, where we can discover that the wave contour is the bright-dark wave. Figure 3 depicts the solution of in the domain , at , . By comparing Figure 3 with Figure 1, Figure 3 is similar with Figure 1, which is also the dark-solitary wave. We describe the performances of in Figure 4 for , in the interval , , which is the bright-dark wave in Figure 2. Figure 5 and Figure 6 illustrate the solutions and , respectively. By comparing them with Figure 2 and Figure 4, we find that although Figure 5 and Figure 6 are somewhat similar to Figure 2 and Figure 4, they are still the bright-dark solitary wave. The behaviors of the solution are plotted in Figure 7. It can be observed that the wave contour is a perfect periodic wave.
5. Conclusions and Future Recommendation
The (3+1)-dimensional BLMP equation that describes the incompressible fluid is investigated in this study. Two effective techniques, namely the EFM and HFF, are successfully applied to construct the abundant traveling wave solutions. Seven sets of the traveling wave solutions like the bright-dark wave, dark wave and periodic wave solutions are obtained. As we've seen from [14,15,16,17,18,19,20,21,22], the results disclosed in this work are all new, which can extend the study of the exact solutions of the (3+1)-dimensional BLMP equation. Finally, the solutions are all illustrated through the three-dimensional contours and two-dimensional curves. The results show that the proposed methods are concise and effective, which, in turn, are expected to be helpful for the study of nonlinear equations arising in physics.
Fractal and Fractional calculus has seen many advancements over the past years, and we have found that many classical models in current physics are being analyzed via this calculus [33,34,35,36,37,38,39]. Applying the Fractal and Fractional calculus to Equation (1) and extracting the exact solutions are the focus of future research.
Author Contributions
Conceptualization, K.-J.W.; methodology, K.-J.W.; writing—original draft preparation, K.-J.W.; supervision, K.-J.W.; writing—review and editing, Y.-N.C.; data curation, Y.-N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Key Programs of Universities in Henan Province of China (22A140006), Program of Henan Polytechnic University (B2018-40), the Innovative Scientists and Technicians Team of Henan Provincial High Education (21IRTSTHN016).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
This work does not have any conflict of interest.
Notation and Abbreviations
| PDEs | partial differential equations |
| EFM | Exp-function method |
| HFF | He’s frequency formulation |
| BLMP | Boiti–Leon–Manna–Pempinelli |
References
- Akram, G.; Sarfraz, M. Multiple optical soliton solutions for CGL equation with Kerr law nonlinearity via extended modified auxiliary equation mapping method. Optik 2021, 242, 167258. [Google Scholar] [CrossRef]
- Cheemaa, N.; Seadawy, A.R.; Chen, S. More general families of exact solitary wave solutions of the nonlinear Schrödinger equation with their applications in nonlinear optics. Eur. Phys. J. Plus 2018, 133, 547. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H. Diverse optical solitons to the nonlinear Schrödinger equation via two novel techniques. Eur. Phys. J. Plus 2023, 138, 74. [Google Scholar] [CrossRef]
- Wang, K.J.; Si, J.; Wang, G.D.; Shi, F. A new fractal modified Benjamin-Bona-Mahony equation: Its generalized variational principle and abundant exact solutions. Fractals 2023. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.; Lu, D.; Wang, J. Travelling wave solutions of generalized coupled Zakharov–Kuznetsov and dispersive long wave equations. Results Phys. 2016, 6, 1136–1145. [Google Scholar] [CrossRef]
- Soliman, A.A. The modified extended direct algebraic method for solving nonlinear partial differential equations. Int. J. Nonlinear Sci. 2008, 6, 136–144. [Google Scholar]
- Asjad, M.I.; Munawar, N.; Muhammad, T.; Hamoud, A.A.; Emadifar, H.; Hamasalh, F.K.; Azizi, H.; Khademi, M. Traveling wave solutions to the Boussinesq equation via Sardar sub-equation technique. AIMS Math. 2022, 7, 11134–11149. [Google Scholar]
- Onder, I.; Secer, A.; Ozisik, M.; Bayram, M. On the optical soliton solutions of Kundu-Mukherjee-Naskar equation via two different analytical methods. Optik 2022, 257, 168761. [Google Scholar] [CrossRef]
- Wang, K.J. Diverse wave structures to the modified Benjamin-Bona-Mahony equation in the optical illusions field. Mod. Phys. Lett. B 2023, 37, 2350012. [Google Scholar] [CrossRef]
- Wang, K.-J.; Shi, F.; Wang, G.-D. Abundant soliton structures to the (2+1)-dimensional Heisenberg ferromagnetic spin chain dynamical model. Adv. Math. Phys. 2023, 2023, 4348758. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons of Biswas-Arshed equation by trial equation technique. Optik 2019, 182, 876–883. [Google Scholar] [CrossRef]
- Ekici, M.; Sonmezoglu, A.; Biswas, A.; Belic, M.R. Optical solitons in (2+1)-Dimensions with Kundu-Mukherjee-Naskar equation by extended trial function scheme. Chin. J. Phys. 2019, 57, 72–77. [Google Scholar] [CrossRef]
- Özkan, Y.S.; Yaşar, E.; Seadawy, A.R. On the multi-waves, interaction and Peregrine-like rational solutions of perturbed Radhakrishnan–Kundu–Lakshmanan equation. Phys. Scr. 2020, 95, 085205. [Google Scholar] [CrossRef]
- Duan, X.; Lu, J. The exact solutions for the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Results Phys. 2021, 21, 103820. [Google Scholar] [CrossRef]
- Yel, G.; Aktürk, T. A new approach to (3+ 1) dimensional Boiti–Leon–Manna–Pempinelli equation. Appl. Math. Nonlinear Sci. 2020, 5, 309–316. [Google Scholar] [CrossRef]
- Kaplan, M. Two different systematic techniques to find analytical solutions of the (2+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Chin. J. Phys. 2018, 56, 2523–2530. [Google Scholar] [CrossRef]
- Ali, M.R.; Ma, W.X. New exact solutions of nonlinear (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Adv. Math. Phys. 2019, 2019, 9801638. [Google Scholar] [CrossRef]
- Tang, Y.; Zai, W. New periodic-wave solutions for (2+1)- and (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equations. Nonlinear Dyn. 2015, 81, 249–255. [Google Scholar] [CrossRef]
- Liu, J.G. Double-periodic soliton solutions for the (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation in incompressible fluid. Comput. Math. Appl. 2018, 75, 3604–3613. [Google Scholar] [CrossRef]
- Ali, K.K.; Mehanna, M.S. On some new soliton solutions of (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation using two different methods. Arab. J. Basic Appl. Sci. 2021, 28, 234–243. [Google Scholar] [CrossRef]
- Najafi, M.N.S.A.M. New exact solutions to the integrable (2+1) and (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equations. Chin. Phys. C 2013, 37, 010201. [Google Scholar]
- Alenezi, A.M. Lump solutions of nonlinear (3+1)-dimensional for nonlinear partial differential equations. Partial. Differ. Equ. Appl. Math. 2020, 2, 100008. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Zulfiqar, A.; Ahmad, J. Soliton solutions of fractional modified unstable Schrödinger equation using Exp-function method. Results Phys. 2020, 19, 103476. [Google Scholar] [CrossRef]
- Wu, X.H.B.; He, J.H. Exp-function method and its application to nonlinear equations. Chaos Solitons Fractals 2008, 38, 903–910. [Google Scholar]
- Ellahi, R.; Mohyud-Din, S.T.; Khan, U. Exact traveling wave solutions of fractional order Boussinesq-like equations by applying Exp-function method. Results Phys. 2018, 8, 114–120. [Google Scholar]
- Wu, X.H.B.; He, J.H. Solitary solutions, periodic solutions and compacton-like solutions using the Exp-function method. Comput. Math. Appl. 2007, 54, 966–986. [Google Scholar] [CrossRef]
- He, J.H. The simplest approach to nonlinear oscillators. Results Phys. 2019, 15, 102546. [Google Scholar] [CrossRef]
- He, J.H. The simpler, the better: Analytical methods for nonlinear oscillators and fractional oscillators. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 1252–1260. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Salas, A.H.; Alharthi, M.R.; El-Tantawy, S.A. Galerkin method, ansatz method, and He’s frequency formulation for modeling the forced damped parametric driven pendulum oscillators. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 1426–1445. [Google Scholar] [CrossRef]
- He, J.H. Variational principle and periodic solution of the Kundu–Mukherjee–Naskar equation. Results Phys. 2020, 17, 103031. [Google Scholar] [CrossRef]
- Wang, K.; Si, J. Dynamic properties of the attachment oscillator arising in the nanophysics. Open Phys. 2023, 21, 20220214. [Google Scholar] [CrossRef]
- İlhan, E.; Kıymaz, İ.O. A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 171–188. [Google Scholar] [CrossRef]
- Wang, K.L. Exact travelling wave solution for the fractal Riemann wave model arising in ocean science. Fractals 2022, 30, 2250143. [Google Scholar] [CrossRef]
- Singh, J. Analysis of fractional blood alcohol model with composite fractional derivative. Chaos Solitons Fractals 2020, 140, 110127. [Google Scholar] [CrossRef]
- Wang, K.-J.; Shi, F.; Si, J.; Liu, J.-H.; Wang, G.-D. Non-differentiable exact solutions of the local fractional Zakharov-Kuznetsov equation on the Cantor sets. Fractals 2023, 31, 2350028. [Google Scholar] [CrossRef]
- He, J.H.; Ji, F.Y. Two-scale mathematics and fractional calculus for thermodynamics. Therm. Sci. 2019, 23, 2131–2133. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H.; Si, J.; Shi, F.; Wang, G.-D. N-soliton, breather, lump solutions and diverse travelling wave solutions of the fractional (2+1)-dimensional Boussinesq equation. Fractals 2023, 31, 2350023. [Google Scholar] [CrossRef]
- He, C.H.; Liu, C.; He, J.H.; Gepreel, K.A. Low frequency property of a fractal vibration model for a concrete beam. Fractals 2021, 29, 2150117. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).