UAV Path Planning Based on an Improved Chimp Optimization Algorithm
Abstract
1. Introduction
- (1)
- We established 3D environment models for UAV trajectory planning, covering different terrains or buildings such as plains, mountains, hills, and human engineering.
- (2)
- The path length, flight altitude, and angle loss during the flight of UAVs were considered, which constituted the comprehensive evaluation index of path planning. The cubic spline interpolation method is used to smooth the trajectory of UAVs to solve the problem of low accuracy of interpolation points in B-spline curves [39].
- (3)
- TRS-ChOA: To solve the 3D UAV path planning problem, we propose an enhanced version of the original ChOA based on differential evolution, improved reverse learning, and similarity preference weights.
- (4)
- The optimization performance of TRS-ChOA is verified by the benchmark test function and the CEC2017 complex test function.
- (5)
- Several well-known meta-heuristic methods are compared with the proposed TRS-ChOA in different 3D environments.
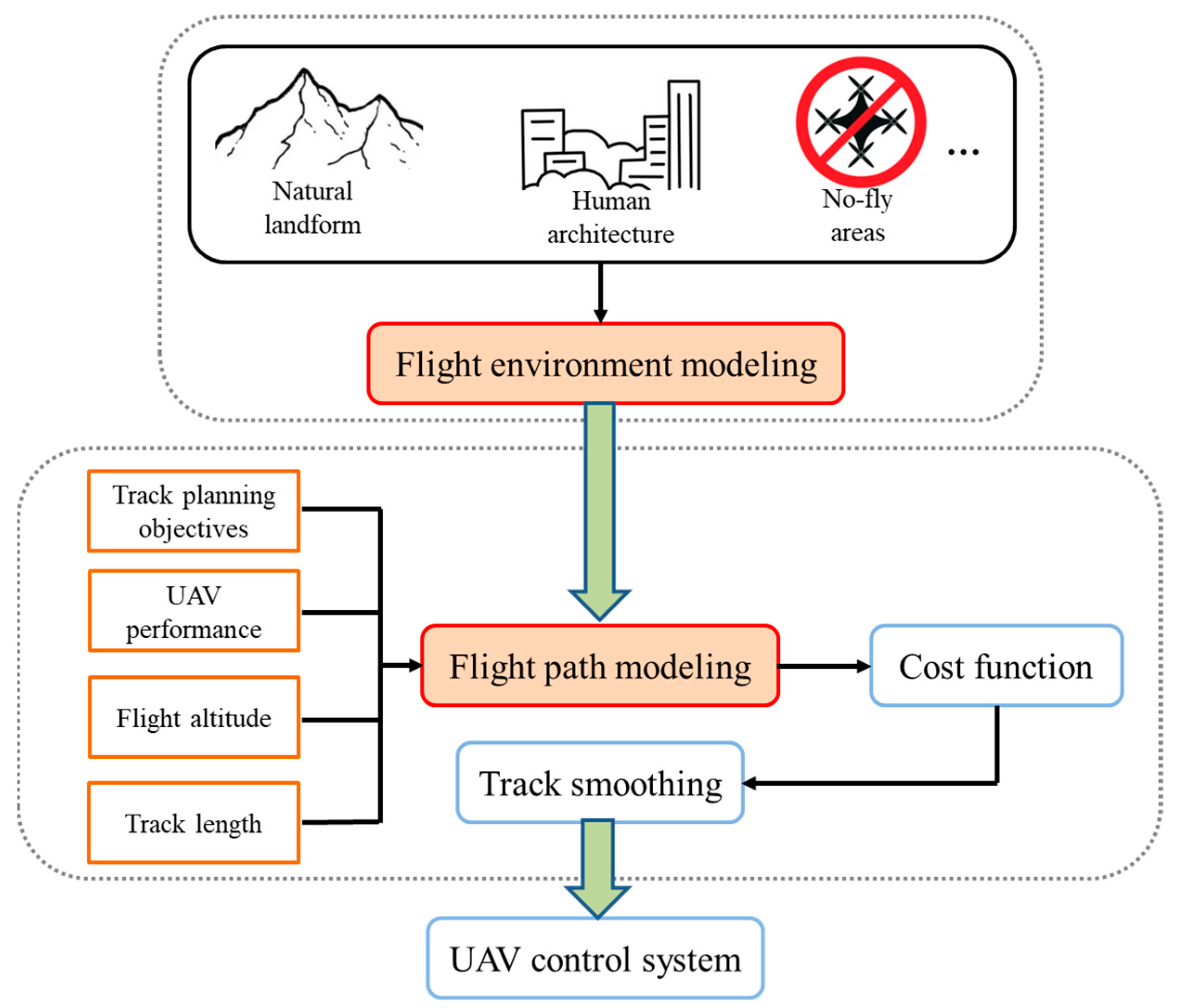
2. UAV Path Planning Problem Model
2.1. Background
2.2. Environmental Model
2.3. Track Model
3. Chimp Optimization Algorithm (ChOA)
3.1. Driving and Chasing the Prey
3.2. Attacking Method
4. Improved Chimp Optimization Algorithm (TRS-ChOA)
4.1. The Differential Evolution
| Algorithm 1 (The DE Algorithm) |
| 1. Generate the initial population xi (i = 1, 2, …, N) 2. Evaluate the fitness of each individual in xi 3. while (t < T) 4. for i = 1 to N do 5. Select uniform randomly r1 ≠ r2 ≠ r3 ≠ i 6. jrand = randint(1, n) 7. for j = 1 to d do 8. if randrealj [0, 1) > CR or j == jrand then 9. vi(j) = x* (j) + F × (xr2 (j) − xr3 (j)) 10. else 11. vi(j) = xi(j) 12. end if 13. end for 14. end for 15. Evaluate the offspring vi 16. if vi is better than Xi then 17. Update individual i, xi = vi 18. if vi is better than x* then 19. Update best individual, x* = vi 20. end if 21. end if 22. end while |
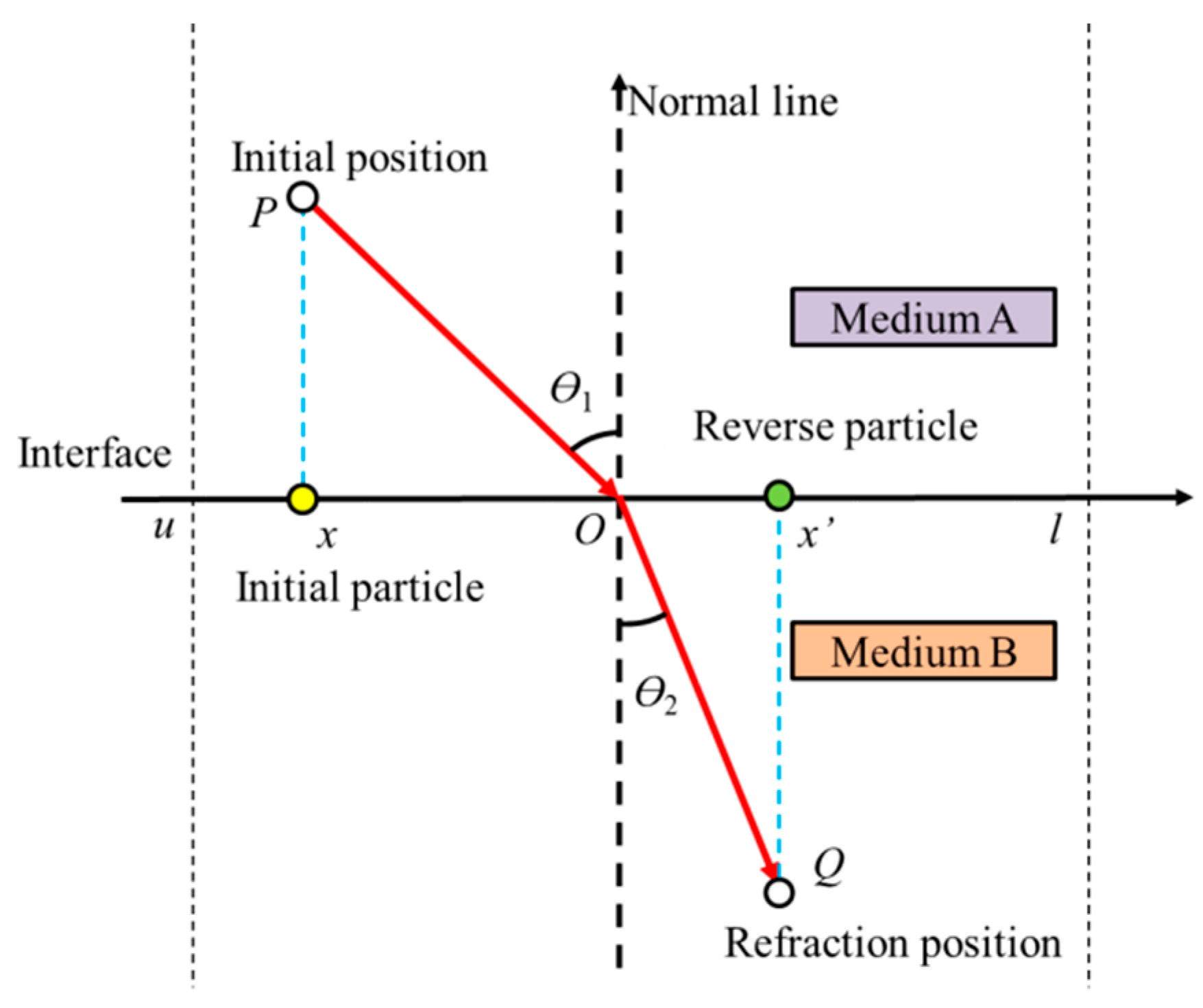
4.2. Improved Reverse Learning
4.3. Similarity Preference Weight
4.4. TRS-ChOA Pseudocode
| Algorithm 2 (TRS-ChOA Algorithm) |
| 1. Generate the initial population xi (i = 1, 2, …, N) 2. Initialize f, m, a and c |
| 3. Divide chimps randomly into independent groups 4. Calculate the fitness of each chimp 5. xAttacker = the best search agent 6. xChaser = the second-best search agent 7. xBarrier = the third-best search agent 8. xDriver = the fourth-best search agent |
| 9. while (t < T) 10. for i = 1 to N do 11. Extract the chimp’s group 12. Use its group strategy to update f, m, c, a and d |
| 13. Select uniform randomly r1 ≠ r2 ≠ i 14. Update α by the Equation (25), jrand = randint(1,n), p = randreal(0,1), μ = randreal(0,1) 15. for j = 1 to d do 16. if p ≤ α then 17. if randrealj[0,1) ≤ CR or j == jrand then 18. vi(j) = randchoice{xAttacker (j), xChaser (j), xBarrier (j), xDriver (j)} + F × (xr1(j) – xr2(j)) 19. else 20. vi(j) = Chaotic_value 21. end if 22. else if p > α then 23. if randrealj [0,1) ≤ 0.5 then 24. vi(j)= xAttacker (j) – a × d 25. else 26. Update the position of the current search agent using the Equation (34) 27. end if 28. end if 29. end for 30. end for 31. Calculate the reverse position of each chimp by Equation (31) 32. Update high-quality individuals by Equation (32) 33. Ranking chimp individuals by fitness value |
| 34. Update xAttacker, xDriver, xBarrier, xChaser 35. t = t + 1 36. end while 37. return xAttacker |
4.5. Time Complexity Analysis of TRS-ChOA
- (1)
- The time complexity after combining with differential evolution is represented as O (N × d), so the time complexity of the algorithm becomes O (N × d × T + N × d) = O (N × d × T) after it is introduced;
- (2)
- The time complexity of using improved reverse learning to update the position of the population is O (N × d × T), However, this is a juxtaposed loop, so the time complexity of the algorithm is O (N × d × T + N × d × T) = O (N × d × T).
- (3)
- Assuming that the time required to introduce the similarity preference weight is t, then the time complexity of the algorithm is O (N × d × T + t) = O (N × d × T)
5. TRS-ChOA Optimized Performance Test
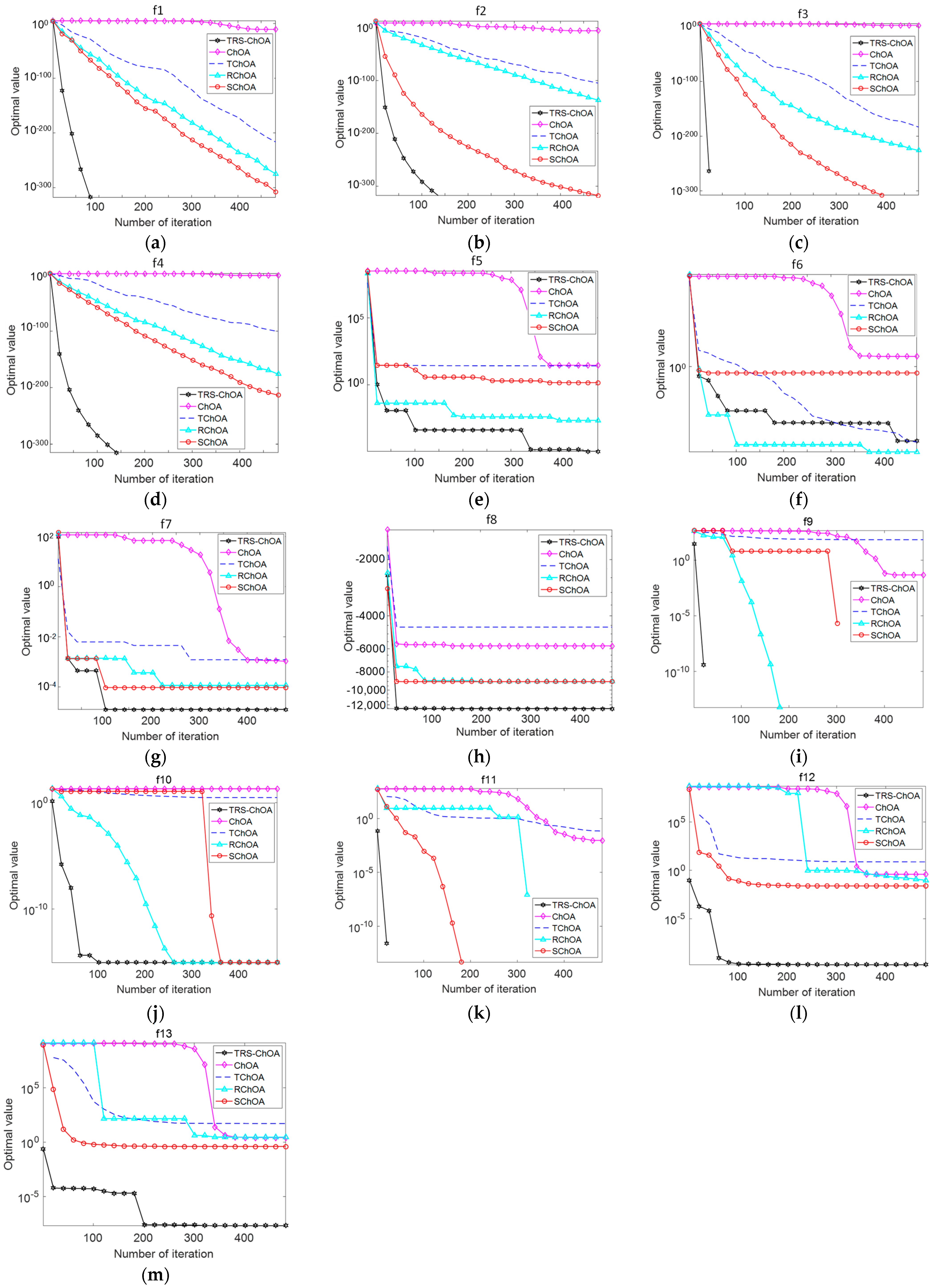
5.1. Benchmark Function Test
5.2. Wilcoxon Rank-Sum Test
5.3. CEC2017 Function Test
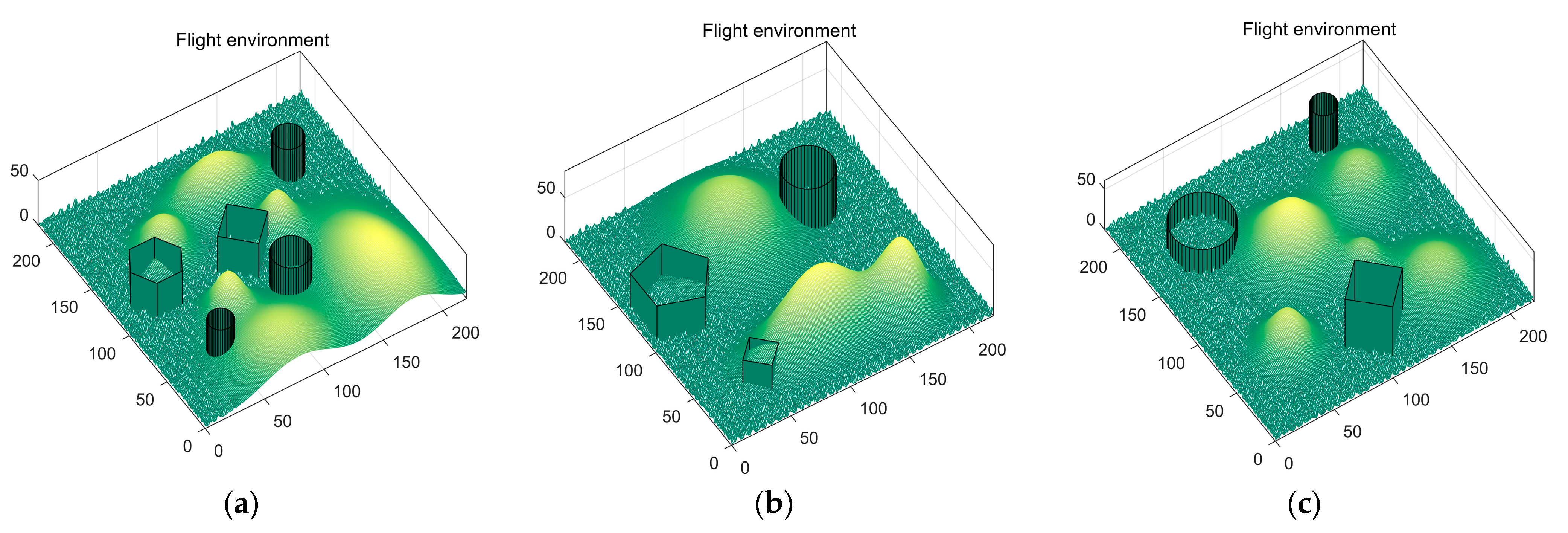
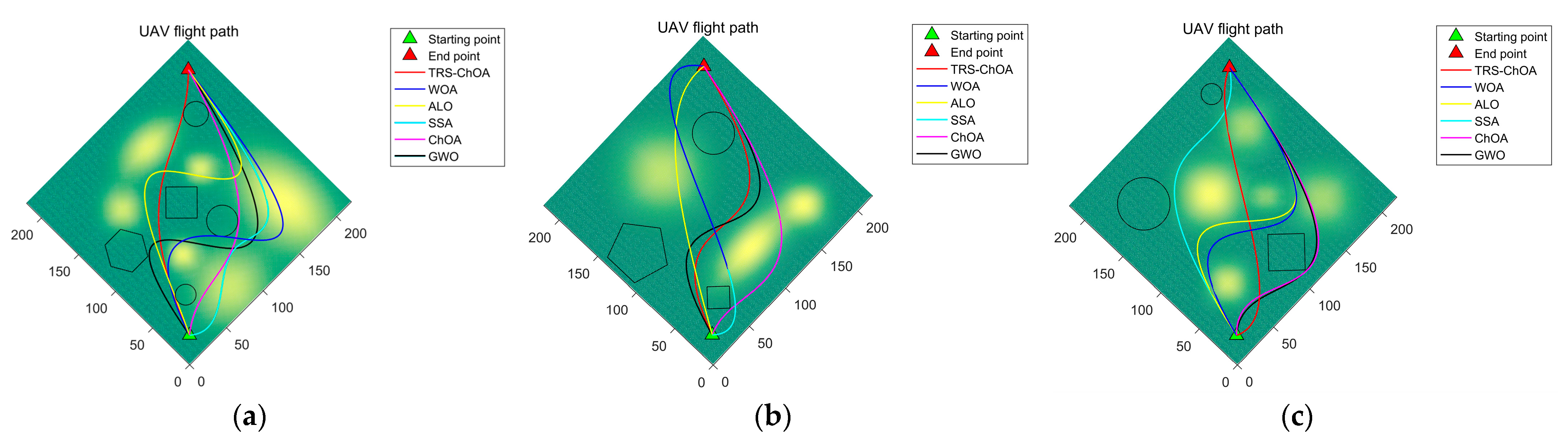
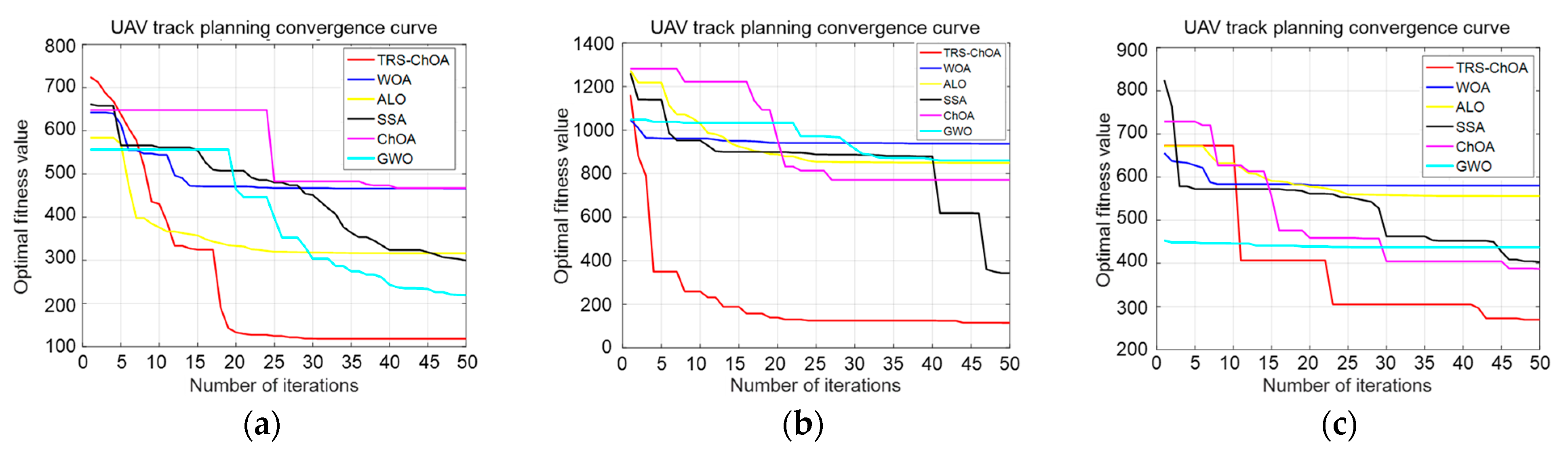
6. UAV Path Planning Test
6.1. Parameter Settings
6.2. Simulation Experiment and Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, B.; Li, Y.; Zhang, R.; Fu, Q. Review on the technological development and application of UAV systems. Chin. J. Electron. 2020, 29, 199–207. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Ren, H.; Zhao, Y.; Xiao, W.; Hu, Z. A review of UAV monitoring in mining areas: Current status and future perspectives. Int. J. Coal Sci. Technol. 2019, 6, 320–333. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, Z.; Liu, Y. Survey on computational-intelligence-based UAV path planning. Knowl.-Based Syst. 2018, 158, 54–64. [Google Scholar] [CrossRef]
- Shin, J.-J.; Bang, H. UAV path planning under dynamic threats using an improved PSO algorithm. Int. J. Aerosp. Eng. 2020, 2020, 8820284. [Google Scholar] [CrossRef]
- Liu, W.; Zheng, Z.; Cai, K.-Y. Bi-level programming based real-time path planning for unmanned aerial vehicles. Knowl.-Based Syst. 2013, 44, 34–47. [Google Scholar] [CrossRef]
- Lu, N.; Zhou, Y.; Shi, C.; Cheng, N.; Cai, L.; Li, B. Planning while flying: A measurement-aided dynamic planning of drone small cells. IEEE Internet Things J. 2018, 6, 2693–2705. [Google Scholar] [CrossRef]
- Lluvia, I.; Lazkano, E.; Ansuategi, A. Active mapping and robot exploration: A survey. Sensors 2021, 21, 2445. [Google Scholar] [CrossRef]
- Munoz, P.; Rodriguez-Moreno, M. Improving efficiency in any-angle path-planning algorithms. In Proceedings of the 2012 6th IEEE International Conference Intelligent Systems, Sofia, Bulgaria, 6–8 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 213–218. [Google Scholar]
- Choset, H.; Lynch, K.M.; Hutchinson, S.; Kantor, G.A.; Burgard, W. Principles of Robot Motion: Theory, Algorithms, and Implementations; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Kim, J.; Kim, S.; Choo, Y. Stealth path planning for a high speed torpedo-shaped autonomous underwater vehicle to approach a target ship. Cyber-Phys. Syst. 2018, 4, 1–16. [Google Scholar] [CrossRef]
- Pettie, S. A new approach to all-pairs shortest paths on real-weighted graphs. Theor. Comput. Sci. 2004, 312, 47–74. [Google Scholar] [CrossRef]
- Nash, A.; Daniel, K.; Koenig, S.; Felner, A. Theta*: Any-angle path planning on grids. AAAI 2007, 7, 1177–1183. [Google Scholar]
- Kim, J. Fast Path Planning of Autonomous Vehicles in 3D Environments. Appl. Sci. 2022, 12, 4014. [Google Scholar] [CrossRef]
- Fulcher, J. Computational intelligence: An introduction. In Computational Intelligence: A Compendium; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–78. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN′95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 210–214. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Poudel, S.; Arafat, M.Y.; Moh, S. Bio-Inspired Optimization-Based Path Planning Algorithms in Unmanned Aerial Vehicles: A Survey. Sensors 2023, 23, 3051. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Labonté, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2012, 9, 132–141. [Google Scholar] [CrossRef]
- Wen, X.; Ruan, Y.; Li, Y.; Xia, H.; Zhang, R.; Wang, C.; Liu, W.; Jiang, X. Improved genetic algorithm based 3-D deployment of UAVs. J. Commun. Netw. 2022, 24, 223–231. [Google Scholar] [CrossRef]
- Guan, Y.; Gao, M.; Bai, Y. Double-ant colony based UAV path planning algorithm. In Proceedings of the 2019 11th International Conference on Machine Learning and Computing, Zhuhai, China, 22–24 February 2019; pp. 258–262. [Google Scholar]
- Chai, X.; Zheng, Z.; Xiao, J.; Yan, L.; Qu, B.; Wen, P.; Wang, H.; Zhou, Y.; Sun, H. Multi-strategy fusion differential evolution algorithm for UAV path planning in complex environment. Aerosp. Sci. Technol. 2022, 121, 107287. [Google Scholar] [CrossRef]
- Zhang, R.; Li, S.; Ding, Y.; Qin, X.; Xia, Q. UAV Path Planning Algorithm Based on Improved Harris Hawks Optimization. Sensors 2022, 22, 5232. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Zhao, X.; Hao, J. A novel UAV path planning algorithm based on double-dynamic biogeography-based learning particle swarm optimization. Mob. Inf. Syst. 2022, 2022, 8519708. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhang, J.; Zhong, M. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning. Knowl.-Based Syst. 2020, 194, 105530. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Yu, X.; Li, C.; Zhou, J. A constrained differential evolution algorithm to solve UAV path planning in disaster scenarios. Knowl.-Based Syst. 2020, 204, 106209. [Google Scholar] [CrossRef]
- Jiang, W.; Lyu, Y.; Li, Y.; Guo, Y.; Zhang, W. UAV path planning and collision avoidance in 3D environments based on POMPD and improved grey wolf optimizer. Aerosp. Sci. Technol. 2022, 121, 107314. [Google Scholar] [CrossRef]
- Du, N.; Zhou, Y.; Deng, W.; Luo, Q. Improved chimp optimization algorithm for three-dimensional path planning problem. Multimed. Tools Appl. 2022, 81, 27397–27422. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Kaur, M.; Kaur, R.; Singh, N.; Dhiman, G. Schoa: A newly fusion of sine and cosine with chimp optimization algorithm for hls of datapaths in digital filters and engineering applications. Eng. Comput. 2021, 38, 975–1003. [Google Scholar] [CrossRef]
- Hu, T.; Khishe, M.; Mohammadi, M.; Parvizi, G.-R.; Karim, S.H.T.; Rashid, T.A. Real-time COVID-19 diagnosis from X-Ray images using deep CNN and extreme learning machines stabilized by chimp optimization algorithm. Biomed. Signal Process Control 2021, 68, 102764. [Google Scholar] [CrossRef] [PubMed]
- Houssein, E.H.; Emam, M.M.; Ali, A.A. An efficient multilevel thresholding segmentation method for thermography breast cancer imaging based on improved chimp optimization algorithm. Expert Syst. Appl. 2021, 185, 115651. [Google Scholar] [CrossRef]
- Thompson, S.E.; Patel, R.V. Formulation of joint trajectories for industrial robots using B-splines. IEEE Trans. Ind. Electron. 1987, IE-34, 192–199. [Google Scholar] [CrossRef]
- Tisdale, J.; Kim, Z.; Hedrick, J.K. Autonomous UAV path planning and estimation. IEEE Robot. Autom. Mag. 2009, 16, 35–42. [Google Scholar] [CrossRef]
- Lv, Z.; Yang, L.; He, Y.; Liu, Z.; Han, Z. 3D environment modeling with height dimension reduction and path planning for UAV. In Proceedings of the 2017 9th International Conference on Modelling, Identification and Control (ICMIC), Kunming, China, 10–12 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 734–739. [Google Scholar]
- Hussain, A.; Muhammad, Y.S.; Nauman Sajid, M.; Hussain, I.; Mohamd Shoukry, A.; Gani, S. Genetic algorithm for traveling salesman problem with modified cycle crossover operator. Comput. Intell. Neurosci. 2017, 2017, 7430125. [Google Scholar] [CrossRef]
- Ergezer, H.; Leblebicioğlu, K. 3D path planning for multiple UAVs for maximum information collection. J. Intell. Robot. Syst. 2014, 73, 737–762. [Google Scholar] [CrossRef]
- Besada-Portas, E.; de la Torre, L.; de la Cruz, J.M.; de Andrés-Toro, B. Evolutionary trajectory planner for multiple UAVs in realistic scenarios. IEEE Trans. Robot. 2010, 26, 619–634. [Google Scholar] [CrossRef]
- McKinley, S.; Levine, M. Cubic spline interpolation. Coll. Redw. 1998, 45, 1049–1060. [Google Scholar]
- Brest, J.; Zumer, V.; Maucec, M.S. Self-adaptive differential evolution algorithm in constrained real-parameter optimization. In Proceedings of the 2006 IEEE international conference on evolutionary computation, Vancouver, BC, Canada, 16–21 July 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 215–222. [Google Scholar]
- Gong, W.; Cai, Z.; Ling, C.X. DE/BBO: A hybrid differential evolution with biogeography-based optimization for global numerical optimization. Soft Comput. 2010, 15, 645–665. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Technical Report; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Auger, A. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization. KanGAL Rep. 2005, 2005005, 2005. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]

| Algorithm | Parameters Setting | Reference |
|---|---|---|
| GWO | r1 ∈ [0, 1], r2 ∈ [0, 1] | [17] |
| SSA | proportion of discoverers: 20% proportion of scouter: 10% alert threshold: 0.7 | [19] |
| WOA | b = 1, r1 ∈ [0, 1], r2 ∈ [0, 1], l ∈ [−1, 1], p ∈ [0, 1] | [20] |
| ALO | w = 1, t ≤ 0.1 T w = 2, t > 0.1 T w = 3, t > 0.5 T w = 4, t > 0.75 T w = 5, t > 0.9 T w = 6, t > 0.95 T | [21] |
| ChOA | r1 ∈ [0, 1], r2 ∈ [0, 1], m = chaos (3,1,1) | [35] |
| TRS-ChOA | F ∈ [0, 1], CR = 0.1, k ∈ [0, 1], σ = 2.5 | Section 4 of this article |
| Fun No. | Name | Range | Dim | Optimal Value | Function Type |
|---|---|---|---|---|---|
| f1 | Sphere Function | [−100, 100] | 30, 500, 1000 | 0 | Single-modal |
| f2 | Schwefel’s problem 2.22 | [−10, 10] | 30, 500, 1000 | 0 | Single-modal |
| f3 | Schwefel’s problem 1.2 | [−100, 100] | 30, 500, 1000 | 0 | Single-modal |
| f4 | Schwefel’s problem 2.21 | [−100, 100] | 30, 500, 1000 | 0 | Single-modal |
| f5 | Generalized Rosenbrock’s Function | [−30, 30] | 30, 500, 1000 | 0 | Single-modal |
| f6 | Step Function | [−100, 100] | 30, 500, 1000 | 0 | Single-modal |
| f7 | Quartic Function | [−1.28, 1.28] | 30, 500, 1000 | 0 | Single-modal |
| f8 | Generalized Schwefel’s problem 2.26 | [−500, 500] | 30, 500, 1000 | 12,569.5 | Multi-modal |
| f9 | Generalized Rastrigin’s Function. | [−5.12, 5.12] | 30, 500, 1000 | 0 | Multi-modal |
| f10 | Ackley’sFunction | [−32, 32] | 30, 500, 1000 | 0 | Multi-modal |
| f11 | Generalized Criewank’s Function | [−600, 600] | 30, 500, 1000 | 0 | Multi-modal |
| f12 | Generalized Penalized Function 1 | [−50, 50] | 30, 500, 1000 | 0 | Fixed multi-modal |
| f13 | Generalized Penalized Function 2 | [−50, 50] | 30, 500, 1000 | 0 | Fixed multi-modal |
| Fun No. | Dim | ChOA | TChOA | RChOA | SChOA | TRS-ChOA | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | ||
| f1 | d = 30 | 1.69 × 10−21 | 4.76 × 10−21 | 1.70 × 10−215 | 4.95 × 10−214 | 1.46 × 10−243 | 1.53 × 10−240 | 1.76 × 10−300 | 8.66 × 10−298 | 0 | 0 |
| d = 500 | 2.03 × 10−22 | 3.61 × 10−22 | 5.69 × 10−168 | 6.42 × 10−174 | 3.58 × 10−233 | 1.76 × 10−230 | 2.20 × 10−301 | 6.33 × 10−300 | 0 | 0 | |
| d = 1000 | 7.84 × 10−16 | 4.38 × 10−17 | 3.77 × 10−164 | 4.29 × 10−150 | 1.25 × 10−200 | 9.23 × 10−203 | 6.53 × 10−276 | 4.85 × 10−280 | 0 | 0 | |
| f2 | d = 30 | 2.13 × 10−15 | 1.41 × 10−15 | 1.13 × 10−78 | 5.74 × 10−77 | 3.38 × 10−112 | 3.14 × 10−103 | 4.49 × 10−326 | 2.47 × 10−341 | 0 | 0 |
| d = 500 | 3.74 × 10−15 | 1.89 × 10−14 | 4.81 × 10−82 | 5.11 × 10−85 | 6.52 × 10−105 | 4.32 × 10−105 | 7.55 × 10−317 | 4.35 × 10−377 | 0 | 0 | |
| d = 1000 | 6.51 × 10−15 | 7.03 × 10-−9 | 7.64 × 10−77 | 3.58 × 10−77 | 2.78 × 10−67 | 7.53 × 10−69 | 4.89 × 10−300 | 3.14 × 10−305 | 0 | 0 | |
| f3 | d = 30 | 5.15 × 101 | 2.90 × 101 | 3.50 × 10−167 | 1.22 × 10−165 | 4.33 × 10−214 | 8.64 × 10−213 | 0 | 0 | 0 | 0 |
| d = 500 | 2.82 × 101 | 7.26 × 101 | 2.21 × 10−154 | 1.97 × 10−148 | 4.67 × 10−212 | 6.38 × 10−213 | 6.47 × 10−303 | 4.54 × 10−302 | 0 | 0 | |
| d = 1000 | 4.15 × 101 | 3.91 × 101 | 5.30 × 10−144 | 1.79 × 10−139 | 3.55 × 10−210 | 7.24 × 10−218 | 6.52 × 10−170 | 6.09 × 10−175 | 0 | 0 | |
| f4 | d = 30 | 4.92 × 10−1 | 2.34 × 10−1 | 1.36 × 10−81 | 1.93 × 10−80 | 3.72 × 10−141 | 3.69 × 10−151 | 3.36 × 10−184 | 2.36 × 10−185 | 0 | 0 |
| d = 500 | 4.57 × 10−1 | 1.99 × 10−1 | 2.14 × 10−56 | 4.31 × 10−67 | 3.11 × 10−110 | 2.76 × 10−133 | 3.52 × 10−217 | 8.12 × 10−142 | 0 | 0 | |
| d = 1000 | 8.44 × 100 | 7.34 × 100 | 3.42 × 10−40 | 2.66 × 10−42 | 1.52 × 10−86 | 3.74 × 10−76 | 4.16 × 10−182 | 3.81 × 10−163 | 0 | 0 | |
| f5 | d = 30 | 2.90 × 101 | 4.25 × 101 | 1.33 × 101 | 1.04 × 101 | 2.82 × 10−2 | 1.76 × 10−1 | 2.88 × 101 | 1.29 × 101 | 2.64 × 10−4 | 8.62 × 10−4 |
| d = 500 | 4.36 × 101 | 1.69 × 101 | 4.22 × 102 | 1.67 × 101 | 4.66 × 10−1 | 1.80 × 10−1 | 2.69 × 101 | 3.58 × 100 | 2.15 × 10−5 | 8.33 × 10−5 | |
| d = 1000 | 8.92 × 102 | 4.53 × 102 | 1.73 × 102 | 6.51 × 101 | 2.06 × 101 | 4.69 × 100 | 1.18 × 102 | 2.39 × 101 | 3.05 × 10−5 | 6.69 × 10−4 | |
| f6 | d = 30 | 3.53 × 101 | 3.05 × 100 | 8.24 × 10−4 | 5.56 × 10−4 | 3.62 × 10−5 | 1.51 × 10−5 | 1.33 × 100 | 7.39 × 10−1 | 1.37 × 10−4 | 6.12 × 10−4 |
| d = 500 | 4.31 × 100 | 4.81 × 100 | 7.96 × 10−2 | 4.81 × 10−2 | 3.69 × 10−5 | 1.71 × 10−4 | 1.57 × 100 | 6.63 × 10−1 | 1.47 × 10−2 | 5.77 × 10−3 | |
| d = 1000 | 6.37 × 101 | 4.22 × 101 | 1.67 × 10−3 | 4.10 × 10−2 | 9.04 × 10−4 | 2.58 × 10−2 | 7.33 × 101 | 1.09 × 100 | 1.55 × 10−2 | 7.04 × 10−2 | |
| f7 | d = 30 | 1.82 × 10−3 | 6.88 × 10−4 | 2.55 × 10−2 | 3.41 × 10−2 | 2.13 × 10−3 | 1.46 × 10−3 | 5.38 × 10−4 | 1.91 × 10−4 | 4.77 × 10−7 | 9.28 × 10−8 |
| d = 500 | 2.03 × 10−3 | 5.16 × 10−4 | 2.18 × 10−2 | 3.63 × 10−2 | 4.30 × 10−4 | 3.87 × 10−4 | 4.01 × 10−3 | 3.19 × 10−3 | 4.35 × 10−6 | 7.81 × 10−8 | |
| d = 1000 | 1.66 × 10−2 | 6.09 × 10−2 | 8.25 × 10−1 | 4.52 × 10−1 | 1.94 × 10−3 | 8.33 × 10−2 | 6.13 × 10−3 | 5.46 × 10−1 | 5.72 × 10−6 | 3.20 × 10−5 | |
| f8 | d = 30 | −5734.36 | 8.95 × 10−9 | −5498.63 | 3.21 × 102 | −10340.06 | 2.21 × 103 | −8334.31 | 6.26 × 102 | −12,567.28 | 2.53 × 10−10 |
| d = 500 | −5529.71 | 6.34 × 10−8 | −5736.44 | 2.73 × 102 | −10649.63 | 2.08 × 102 | −8221.50 | 5.90 × 102 | −12,496.63 | 4.10 × 10−10 | |
| d = 1000 | −6017.87 | 3.65 × 10−5 | −4396.07 | 8.60 × 103 | −8774.59 | 6.77 × 102 | −8005.19 | 2.53 × 103 | −12,195.10 | 2.74 × 10−9 | |
| f9 | d = 30 | 1.37 × 101 | 6.11 × 102 | 8.07 × 101 | 2.88 × 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| d = 500 | 1.63 × 101 | 6.40 × 102 | 7.46 × 101 | 3.00 × 100 | 0 | 0 | 0 | 0 | 0 | 0 | |
| d = 1000 | 2.70 × 102 | 8.39 × 100 | 3.98 × 102 | 5.14 × 100 | 7.57 × 10−279 | 9.41 × 10−278 | 7.03 × 10−131 | 3.72 × 10−110 | 0 | 0 | |
| f10 | d = 30 | 2.00 × 101 | 9.03 × 10−14 | 5.89 × 100 | 3.86 × 10−1 | 4.34 × 10−15 | 3.97 × 10−11 | 1.60 × 10−12 | 7.11 × 10−16 | 8.88 × 10−14 | 0 |
| d = 500 | 3.12 × 101 | 6.51 × 10−13 | 5.53 × 100 | 4.02 × 10−1 | 4.22 × 10−12 | 2.67 × 10−8 | 3.07 × 10−11 | 2.97 × 10−15 | 6.93 × 10−14 | 0 | |
| d = 1000 | 4.73 × 101 | 7.73 × 10−4 | 8.14 × 101 | 7.50 × 10−2 | 5.96 × 10−13 | 7.51 × 10−8 | 8.46 × 10−7 | 5.29 × 10−10 | 5.00 × 10−13 | 1.37 × 10−12 | |
| f11 | d = 30 | 4.42 × 10−2 | 3.97 × 10−12 | 4.45 × 10−1 | 3.24 × 10−2 | 1.61 × 10−216 | 1.62 × 10−223 | 0 | 0 | 0 | 0 |
| d = 500 | 4.90 × 10−3 | 3.62 × 10−11 | 4.73 × 10−2 | 1.88 × 10−2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| d = 1000 | 2.26 × 10−3 | 4.74 × 10−11 | 5.30 × 10−2 | 4.09 × 10−2 | 2.73 × 10−10 | 2.11 × 10−10 | 6.16 × 10−14 | 8.40 × 10−15 | 3.71 × 10−13 | 6.11 × 10−16 | |
| f12 | d = 30 | 4.68 × 10−1 | 1.60 × 10−11 | 1.41 × 101 | 3.17 × 100 | 9.29 × 10−2 | 7.76 × 10−2 | 9.02 × 10−3 | 5.12 × 10−2 | 6.07 × 10−6 | 8.36 × 10−13 |
| d = 500 | 3.90 × 10−1 | 4.25 × 10−10 | 2.68 × 101 | 5.33 × 100 | 6.75 × 10−2 | 5.77 × 10−1 | 4.57 × 10−2 | 8.16 × 10−2 | 9.12 × 10−6 | 6.31 × 10−12 | |
| d = 1000 | 9.57 × 100 | 7.75 × 10−8 | 4.69 × 102 | 8.01 × 101 | 5.10 × 10−2 | 9.69 × 10−2 | 3.88 × 10−3 | 1.90 × 10−2 | 5.17 × 10−6 | 6.21 × 10−12 | |
| f13 | d = 30 | 2.71 × 100 | 1.66 × 10−13 | 2.25 × 101 | 3.37 × 101 | 5.48 × 10−1 | 2.82 × 10−6 | 2.85 × 10−1 | 7.45 × 10−9 | 1.93 × 10−4 | 5.65 × 10−17 |
| d = 500 | 6.24 × 100 | 3.57 × 10−12 | 3.06 × 101 | 5.65 × 101 | 3.98 × 10−1 | 2.17 × 10−5 | 1.74 × 100 | 8.61 × 10−5 | 2.01 × 10−4 | 4.85 × 10−15 | |
| d = 1000 | 4.82 × 100 | 3.07 × 10−10 | 6.44 × 101 | 6.00 × 101 | 4.32 × 10−1 | 2.73 × 10−1 | 9.38 × 100 | 1.00 × 10−3 | 2.13 × 10−4 | 9.32 × 10−14 | |
| Fun No. | ChOA (P1) | TChOA (P2) | RChOA (P3) | SChOA (P4) |
|---|---|---|---|---|
| f1 | 8.01 × 10−14 | 8.01 × 10−14 | 8.01 × 10−14 | 8.01 × 10−14 |
| f2 | 1.83 × 10−15 | 1.83 × 10−15 | 1.83 × 10−15 | 1.83 × 10−15 |
| f2 | 3.16 × 10−13 | 3.16 × 10−13 | 3.16 × 10−13 | 3.16 × 10−13 |
| f2 | 3.02 × 10−16 | 3.16 × 10−13 | 3.16 × 10−13 | 3.16 × 10−13 |
| f3 | 2.03 × 10−7 | 4.73 × 10−12 | 5.80 × 10−15 | 1.01 × 10−17 |
| f4 | 1.86 × 10−12 | 8.66 × 10−14 | 2.64 × 10−15 | 1.83 × 10−17 |
| f5 | 3.09 × 10−9 | 1.71 × 10−10 | 1.83 × 10−11 | 1.83 × 10−11 |
| f6 | 7.77 × 10−13 | NaN | 1.12 × 10−13 | 1.83 × 10−13 |
| f7 | 1.64 × 10−14 | 9.53 × 10−17 | 7.07 × 10−18 | 1.01 × 10−17 |
| f8 | 2.65 × 10−18 | 7.08 × 10−12 | 0.91 × 10−6 | 9.54 × 10−18 |
| f9 | 3.31 × 10−20 | 3.31 × 10−20 | NaN | 8.97 × 10−7 |
| f10 | 3.31 × 10−20 | 3.43 × 10−13 | 6.45 × 10−15 | NaN |
| f11 | 3.31 × 10−20 | 3.31 × 10−20 | 3.27 × 10−6 | NaN |
| f12 | 7.10 × 10−9 | 1.46 × 10−12 | 7.06 × 10−18 | 7.79 × 10−12 |
| f13 | 1.58 × 10−12 | 1.62 × 10−13 | 4.44 × 10−15 | 2.38 × 10−10 |
| +/=/― | 13/0/0 | 12/1/0 | 11/1/1 | 11/2/0 |
| Fun No. | Dim | Function Type | Range | Optimal Value |
|---|---|---|---|---|
| CEC01 | 10, 50 | UF (Uni-modal Function) | [−100, 100] | 100 |
| CEC02 | 10, 50 | UF | [−100, 100] | 200 |
| CEC03 | 10, 50 | SMF (Simple Multimodal Functions) | [−100, 100] | 300 |
| CEC04 | 10, 50 | SMF | [−100, 100] | 400 |
| CEC05 | 10, 50 | SMF | [−100, 100] | 500 |
| CEC06 | 10, 50 | SMF | [−100, 100] | 600 |
| CEC07 | 10, 50 | SMF | [−100, 100] | 700 |
| CEC08 | 10, 50 | SMF | [−100, 100] | 800 |
| CEC09 | 10, 50 | SMF | [−100, 100] | 900 |
| CEC10 | 10, 50 | HF (Hybrid Function) | [−100, 100] | 1000 |
| CEC11 | 10, 50 | HF | [−100, 100] | 1100 |
| CEC12 | 10, 50 | HF | [−100, 100] | 1200 |
| CEC13 | 10, 50 | HF | [−100, 100] | 1300 |
| CEC14 | 10, 50 | HF | [−100, 100] | 1400 |
| CEC15 | 10, 50 | HF | [−100, 100] | 1500 |
| CEC16 | 10, 50 | HF | [−100, 100] | 1600 |
| CEC17 | 10, 50 | HF | [−100, 100] | 1700 |
| CEC18 | 10, 50 | HF | [−100, 100] | 1800 |
| CEC19 | 10, 50 | HF | [−100, 100] | 1900 |
| CEC20 | 10, 50 | CF (Composition Function) | [−100, 100] | 2000 |
| CEC21 | 10, 50 | CF | [−100, 100] | 2100 |
| CEC22 | 10, 50 | CF | [−100, 100] | 2200 |
| CEC23 | 10, 50 | CF | [−100, 100] | 2300 |
| CEC24 | 10, 50 | CF | [−100, 100] | 2400 |
| CEC25 | 10, 50 | CF | [−100, 100] | 2500 |
| CEC26 | 10, 50 | CF | [−100, 100] | 2600 |
| CEC27 | 10, 50 | CF | [−100, 100] | 2700 |
| CEC28 | 10, 50 | CF | [−100, 100] | 2800 |
| CEC29 | 10, 50 | CF | [−100, 100] | 2900 |
| Fun No. | Dim | ChOA | SSA | GWO | WOA | TRS-ChOA | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | ||
| CEC1 | d = 10 | 2.32 × 102 | 7.39 × 101 | 8.47 × 102 | 2.15 × 102 | 1.36 × 102 | 3.13 × 101 | 5.78 × 102 | 2.62 × 100 | 1.14 × 102 | 1.59 × 100 |
| d = 50 | 4.52 × 102 | 2.31 × 102 | 3.62 × 103 | 4.22 × 102 | 2.37 × 102 | 1.16 × 102 | 7.40 × 102 | 1.72 × 102 | 1.32 × 102 | 6.21 × 101 | |
| CEC2 | d = 10 | 9.70 × 102 | 5.46 × 100 | 6.53 × 102 | 1.59 × 101 | 3.35 × 102 | 4.61 × 101 | 4.41 × 102 | 3.84 × 10−1 | 3.51 × 102 | 4.32 × 100 |
| d = 50 | 6.94 × 102 | 2.40 × 102 | 5.39 × 102 | 3.11 × 102 | 4.02 × 102 | 4.11 × 102 | 5.37 × 102 | 3.78 × 101 | 3.77 × 102 | 1.60 × 100 | |
| CEC3 | d = 10 | 4.80 × 102 | 1.13 × 102 | 4.85 × 102 | 1.97 × 101 | 3.32 × 102 | 4.44 × 102 | 1.00 × 103 | 6.93 × 102 | 3.28 × 102 | 6.55 × 10−1 |
| d = 50 | 6.40 × 102 | 3.27 × 102 | 2.66 × 103 | 5.64 × 102 | 5.49 × 102 | 3.13 × 101 | 7.46 × 102 | 2.86 × 102 | 4.09 × 102 | 9.85 × 100 | |
| CEC4 | d = 10 | 4.51 × 102 | 4.75 × 10−2 | 4.22 × 102 | 9.53 × 10−2 | 3.69 × 102 | 1.35 × 101 | 4.36 × 102 | 4.30 × 10−2 | 4.02 × 102 | 4.28 × 10−2 |
| d = 50 | 4.89 × 102 | 5.77 × 10−1 | 6.35 × 102 | 4.91 × 10−1 | 4.62 × 102 | 4.62 × 101 | 5.76 × 102 | 2.73 × 101 | 4.55 × 102 | 4.58 × 10−1 | |
| CEC5 | d = 10 | 6.44 × 102 | 1.14 × 100 | 5.14 × 102 | 3.24 × 100 | 5.75 × 102 | 1.33 × 101 | 6.44 × 102 | 1.26 × 100 | 5.26 × 102 | 6.82 × 10−1 |
| d = 50 | 6.97 × 102 | 4.03 × 100 | 5.96 × 102 | 1.95 × 101 | 5.20 × 102 | 4.67 × 10−2 | 5.76 × 102 | 2.73 × 101 | 5.19 × 102 | 2.73 × 10−2 | |
| CEC6 | d = 10 | 6.37 × 102 | 2.99 × 101 | 6.47 × 102 | 6.21 × 101 | 6.01 × 102 | 1.35 × 10−1 | 6.72 × 102 | 6.72 × 10−2 | 6.22 × 102 | 1.24 × 100 |
| d = 50 | 6.84 × 102 | 3.62 × 101 | 6.72 × 102 | 2.51 × 101 | 6.49 × 102 | 5.23 × 10−1 | 6.94 × 102 | 5.26 × 100 | 6.43 × 102 | 7.30 × 100 | |
| CEC7 | d = 10 | 7.66 × 102 | 5.39 × 101 | 8.06 × 102 | 3.67 × 100 | 7.15 × 102 | 6.59 × 10−3 | 8.21 × 102 | 3.00 × 101 | 7.04 × 102 | 6.39 × 10−1 |
| d = 50 | 8.04 × 102 | 1.41 × 101 | 2.93 × 103 | 4.80 × 101 | 8.01 × 102 | 3.57 × 100 | 1.53 × 103 | 5.12 × 101 | 7.87 × 102 | 0 | |
| CEC8 | d = 10 | 2.41 × 103 | 9.41 × 101 | 1.19 × 103 | 9.13 × 101 | 9.36 × 102 | 5.43 × 101 | 9.77 × 102 | 1.84 × 102 | 9.04 × 102 | 4.32 × 101 |
| d = 50 | 1.47 × 103 | 6.27 × 102 | 1.65 × 103 | 2.41 × 102 | 1.79 × 103 | 1.75 × 102 | 1.01 × 103 | 3.17 × 102 | 1.23 × 103 | 8.02 × 101 | |
| CEC9 | d = 10 | 1.91 × 103 | 3.72 × 102 | 3.37 × 103 | 8.44 × 101 | 2.85 × 103 | 9.62 × 10−1 | 1.38 × 103 | 3.16 × 102 | 9.44 × 103 | 7.06 × 10−3 |
| d = 50 | 3.34 × 103 | 8.00 × 102 | 4.17 × 103 | 1.94 × 102 | 1.45 × 103 | 1.16 × 101 | 3.93 × 103 | 2.40 × 102 | 9.65 × 103 | 1.00 × 101 | |
| CEC10 | d = 10 | 5.34 × 102 | 7.01 × 102 | 2.63 × 103 | 2.61 × 102 | 9.10 × 102 | 8.21 × 100 | 5.20 × 103 | 7.46 × 100 | 1.03 × 103 | 3.13 × 100 |
| d = 50 | 7.99 × 102 | 8.96 × 102 | 9.13 × 102 | 1.36 × 102 | 1.81 × 103 | 1.96 × 102 | 3.18 × 103 | 2.17 × 102 | 1.08 × 103 | 4.32 × 100 | |
| CEC11 | d = 10 | 1.00 × 103 | 2.85 × 101 | 1.39 × 103 | 3.59 × 101 | 1.13 × 103 | 3.85 × 101 | 1.28 × 103 | 7.62 × 100 | 1.11 × 103 | 2.25 × 100 |
| d = 50 | 1.41 × 104 | 4.28 × 102 | 2.77 × 103 | 2.99 × 101 | 4.31 × 103 | 3.38 × 102 | 7.19 × 103 | 2.85 × 102 | 1.30 × 103 | 7.36 × 100 | |
| CEC12 | d = 10 | 3.45 × 103 | 2.09 × 101 | 2.07 × 103 | 8.00 × 100 | 2.96 × 103 | 4.45 × 101 | 1.84 × 103 | 4.51 × 102 | 1.54 × 103 | 7.31 × 10−1 |
| d = 50 | 4.06 × 103 | 5.23 × 101 | 2.62 × 103 | 1.36 × 102 | 1.49 × 103 | 5.27 × 102 | 1.78 × 103 | 2.81 × 102 | 2.19 × 103 | 4.85 × 100 | |
| CEC13 | d = 10 | 1.30 × 103 | 3.60 × 101 | 1.42 × 103 | 7.62 × 100 | 1.33 × 103 | 1.57 × 101 | 6.55 × 103 | 1.98 × 103 | 1.35 × 103 | 1.43 × 101 |
| d = 50 | 1.01 × 104 | 1.44 × 102 | 2.58 × 103 | 1.01 × 102 | 1.34 × 103 | 1.83 × 102 | 7.01 × 103 | 7.46 × 102 | 1.28 × 103 | 1.20 × 102 | |
| CEC14 | d = 10 | 3.79 × 103 | 2.16 × 100 | 1.71 × 103 | 1.56 × 102 | 1.64 × 103 | 2.27 × 102 | 8.84 × 103 | 2.48 × 102 | 1.63 × 103 | 5.57 × 100 |
| d = 50 | 2.95 × 103 | 7.02 × 101 | 3.26 × 103 | 3.71 × 102 | 1.89 × 103 | 1.23 × 102 | 1.07 × 104 | 5.05 × 102 | 1.57 × 103 | 8.23 × 100 | |
| CEC15 | d = 10 | 2.44 × 103 | 8.15 × 102 | 2.25 × 103 | 5.61 × 102 | 5.49 × 103 | 7.61 × 101 | 1.74 × 103 | 3.46 × 101 | 1.68 × 103 | 2.17 × 101 |
| d = 50 | 3.76 × 103 | 1.54 × 102 | 3.77 × 103 | 9.99 × 101 | 6.25 × 103 | 8.09 × 100 | 1.99 × 103 | 2.27 × 102 | 1.39 × 103 | 4.44 × 100 | |
| CEC16 | d = 10 | 1.85 × 103 | 5.07 × 101 | 2.50 × 103 | 5.57 × 101 | 1.71 × 103 | 7.33 × 10−1 | 1.77 × 103 | 1.65 × 101 | 1.66 × 103 | 6.59 × 10−1 |
| d = 50 | 1.90 × 103 | 4.39 × 101 | 3.98 × 103 | 4.35 × 101 | 1.61 × 103 | 4.82 × 100 | 5.28 × 103 | 6.92 × 102 | 1.60 × 103 | 4.78 × 100 | |
| CEC17 | d = 10 | 2.02 × 103 | 3.18 × 101 | 2.03 × 103 | 5.70 × 101 | 1.73 × 103 | 1.17 × 100 | 1.79 × 103 | 6.83 × 100 | 1.72 × 103 | 1.08 × 100 |
| d = 50 | 1.87 × 103 | 4.67 × 101 | 3.77 × 103 | 9.92 × 101 | 3.13 × 103 | 5.60 × 102 | 4.46 × 103 | 4.30 × 102 | 1.83 × 103 | 6.85 × 101 | |
| CEC18 | d = 10 | 3.23 × 103 | 1.78 × 101 | 1.90 × 103 | 1.06 × 102 | 1.86 × 103 | 3.27 × 102 | 1.54 × 103 | 2.12 × 102 | 1.88 × 103 | 1.25 × 101 |
| d = 50 | 1.45 × 103 | 5.14 × 102 | 3.26 × 103 | 2.29 × 101 | 2.39 × 103 | 4.38 × 102 | 2.36 × 103 | 7.03 × 102 | 2.06 × 103 | 1.73 × 101 | |
| CEC19 | d = 10 | 1.46 × 103 | 3.69 × 102 | 4.24 × 103 | 4.50 × 102 | 3.12 × 103 | 1.05 × 102 | 3.18 × 103 | 2.37 × 102 | 2.27 × 103 | 1.01 × 102 |
| d = 50 | 3.36 × 103 | 4.05 × 102 | 5.38 × 103 | 7.82 × 101 | 2.76 × 103 | 9.47 × 100 | 3.37 × 103 | 9.15 × 101 | 2.69 × 103 | 5.05 × 100 | |
| CEC20 | d = 10 | 4.06 × 103 | 2.70 × 100 | 2.41 × 103 | 2.55 × 102 | 2.63 × 103 | 2.94 × 101 | 1.53 × 104 | 2.40 × 103 | 2.28 × 103 | 2.31 × 100 |
| d = 50 | 3.00 × 103 | 7.18 × 101 | 5.75 × 103 | 9.57 × 100 | 4.79 × 103 | 2.70 × 102 | 5.18 × 103 | 2.17 × 102 | 2.89 × 103 | 8.86 × 100 | |
| CEC21 | d = 10 | 2.33 × 103 | 1.28 × 102 | 2.37 × 103 | 4.09 × 102 | 2.10 × 103 | 3.12 × 10−1 | 2.18 × 103 | 9.06 × 100 | 2.03 × 103 | 5.31 × 100 |
| d = 50 | 2.94 × 103 | 5.05 × 101 | 2.63 × 103 | 5.33 × 102 | 2.64 × 103 | 1.50 × 102 | 2.88 × 103 | 3.54 × 101 | 2.15 × 103 | 3.51 × 101 | |
| CEC22 | d = 10 | 2.41 × 103 | 6.22 × 101 | 2.88 × 103 | 2.68 × 101 | 2.29 × 103 | 2.84 × 101 | 2.32 × 103 | 2.49 × 101 | 2.18 × 103 | 1.97 × 101 |
| d = 50 | 8.29 × 103 | 8.13 × 102 | 1.09 × 104 | 3.87 × 102 | 2.31 × 103 | 7.52 × 101 | 1.60 × 104 | 3.83 × 102 | 2.28 × 103 | 5.36 × 101 | |
| CEC23 | d = 10 | 2.67 × 103 | 4.28 × 101 | 2.59 × 103 | 3.06 × 102 | 2.63 × 103 | 0 | 2.69 × 103 | 7.35 × 100 | 2.37 × 103 | 4.28 × 101 |
| d = 50 | 4.13 × 103 | 1.59 × 102 | 2.90 × 103 | 5.17 × 102 | 2.64 × 103 | 4.48 × 10−1 | 3.64 × 103 | 1.25 × 102 | 2.29 × 103 | 4.11 × 101 | |
| CEC24 | d = 10 | 2.64 × 103 | 3.22 × 101 | 2.73 × 103 | 6.85 × 101 | 2.29 × 103 | 2.38 × 100 | 2.73 × 103 | 8.76 × 100 | 2.46 × 103 | 2.02 × 100 |
| d = 50 | 3.77 × 103 | 2.65 × 101 | 2.99 × 103 | 8.36 × 101 | 2.68 × 103 | 6.69 × 10−1 | 3.50 × 103 | 3.29 × 102 | 2.43 × 103 | 1.99 × 10−1 | |
| CEC25 | d = 10 | 3.36 × 103 | 2.45 × 102 | 1.03 × 104 | 4.42 × 102 | 2.90 × 103 | 1.53 × 102 | 4.45 × 103 | 5.55 × 102 | 2.64 × 103 | 1.45 × 102 |
| d = 50 | 6.63 × 103 | 2.52 × 101 | 9.13 × 103 | 3.57 × 102 | 3.18 × 103 | 3.41 × 102 | 6.29 × 103 | 8.12 × 101 | 3.02 × 103 | 2.21 × 101 | |
| CEC26 | d = 10 | 4.69 × 103 | 1.58 × 103 | 3.89 × 103 | 2.29 × 102 | 4.45 × 103 | 1.91 × 102 | 4.84 × 103 | 6.35 × 100 | 3.50 × 103 | 4.75 × 100 |
| d = 50 | 3.08 × 103 | 9.14 × 102 | 4.03 × 103 | 1.57 × 102 | 4.62 × 103 | 2.16 × 102 | 3.98 × 103 | 9.50 × 102 | 2.94 × 103 | 1.38 × 102 | |
| CEC27 | d = 10 | 4.30 × 103 | 3.28 × 102 | 2.29 × 103 | 1.11 × 102 | 3.18 × 103 | 4.14 × 101 | 5.52 × 103 | 3.08 × 102 | 3.18 × 103 | 2.20 × 102 |
| d = 50 | 3.01 × 103 | 5.24 × 101 | 3.53 × 103 | 3.34 × 102 | 2.89 × 103 | 1.54 × 102 | 7.85 × 103 | 1.25 × 102 | 3.04 × 103 | 4.00 × 101 | |
| CEC28 | d = 10 | 3.44 × 103 | 4.37 × 102 | 4.88 × 103 | 1.20 × 102 | 3.19 × 103 | 2.40 × 102 | 6.07 × 103 | 1.37 × 102 | 2.99 × 103 | 7.49 × 101 |
| d = 50 | 5.96 × 103 | 2.27 × 100 | 6.79 × 103 | 6.17 × 101 | 3.91 × 103 | 2.87 × 102 | 9.38 × 103 | 3.08 × 102 | 3.37 × 103 | 1.56 × 100 | |
| CEC29 | d = 10 | 2.82 × 103 | 8.13 × 102 | 3.11 × 103 | 3.18 × 102 | 2.27 × 103 | 1.50 × 102 | 4.58 × 103 | 9.71 × 101 | 3.10 × 103 | 7.58 × 101 |
| d = 50 | 2.76 × 103 | 3.03 × 102 | 4.35 × 103 | 6.07 × 102 | 1.14 × 104 | 3.62 × 103 | 6.61 × 103 | 7.49 × 102 | 3.18 × 103 | 2.74 × 102 | |
| 3D Environment | Threat Areas | Parameters | Value | |||||
|---|---|---|---|---|---|---|---|---|
| Model 1 | mountains | Central coordinate | [80,25] | [70,80] | [175,45] | [140,125] | [60,150] | [120,175] |
| height | 40 | 40 | 50 | 40 | 40 | 45 | ||
| Slope in the X direction | 40 | 15 | 35 | 15 | 20 | 35 | ||
| Slope in the Y direction | 40 | 15 | 60 | 15 | 20 | 20 | ||
| buildings | Central coordinate | [35,120] | [105,115] | |||||
| height | 40 | 40 | ||||||
| Apothem | 15 | 15 | ||||||
| Side length | 30 | 15 | ||||||
| Radar areas | Central coordinate | [45,50] | [120,75] | [175,165] | ||||
| height | 40 | 40 | 40 | |||||
| radius | 10 | 15 | 12 | |||||
| Model 2 | mountains | Central coordinate | [100,160] | [170,40] | [105,50] | |||
| height | 60 | 70 | 80 | |||||
| Slope in the X direction | 40 | 20 | 45 | |||||
| Slope in the Y direction | 40 | 20 | 20 | |||||
| buildings | Central coordinate | [30,125] | [50,40] | |||||
| height | 40 | 30 | ||||||
| Apothem | 24 | 10 | ||||||
| Side length | 34.87 | 20 | ||||||
| Radar areas | Central coordinate | [160,150] | ||||||
| height | 50 | |||||||
| radius | 20 | |||||||
| Model 3 | mountains | Central coordinate | [50,60] | [130,100] | [135,90] | [170,150] | [170,50] | |
| height | 40 | 40 | 50 | 40 | 40 | |||
| Slope in the X direction | 40 | 15 | 60 | 15 | 20 | |||
| Slope in the Y direction | 40 | 15 | 35 | 15 | 20 | |||
| buildings | Central coordinate | [110,40] | ||||||
| height | 60 | |||||||
| Apothem | 17.3 | |||||||
| Side length | 34.6 | |||||||
| Radar areas | Central coordinate | [50,170] | [170,195] | |||||
| height | 30 | 50 | ||||||
| radius | 25 | 10 | ||||||
| 3D Model | Path Length | Longest | Shortest | Mean | |
|---|---|---|---|---|---|
| Algorithm | |||||
| Environment 1 | WOA | 410.32 | 284.73 | 390.27 | |
| ALO | 399.76 | 363.45 | 374.18 | ||
| SSA | 341.25 | 295.07 | 318.08 | ||
| ChOA | 292.08 | 259.62 | 283.24 | ||
| GWO | 406.91 | 372.94 | 381.06 | ||
| TRS-ChOA | 286.40 | 251.79 | 263.29 | ||
| Environment 2 | WOA | 354.61 | 293.55 | 318.46 | |
| ALO | 317.42 | 261.00 | 284.72 | ||
| SSA | 320.08 | 294.18 | 315.65 | ||
| ChOA | 327.10 | 281.38 | 304.01 | ||
| GWO | 321.94 | 300.25 | 309.19 | ||
| TRS-ChOA | 297.36 | 274.82 | 279.56 | ||
| Environment 3 | WOA | 352.47 | 312.29 | 338.97 | |
| ALO | 354.12 | 347.53 | 350.68 | ||
| SSA | 297.74 | 263.80 | 285.88 | ||
| ChOA | 333.26 | 304.91 | 317.93 | ||
| GWO | 324.59 | 299.47 | 313.93 | ||
| TRS-ChOA | 284.06 | 262.56 | 267.71 | ||
| 3D Model | Fitness Value | Optimal | Worst | Mean | |
|---|---|---|---|---|---|
| Algorithm | |||||
| Environment 1 | WOA | 464.13 | 487.51 | 477.19 | |
| ALO | 300.00 | 364.74 | 311.42 | ||
| SSA | 287.85 | 329.99 | 300.61 | ||
| ChOA | 463.11 | 490.07 | 476.08 | ||
| GWO | 198.65 | 347.61 | 224.93 | ||
| TRS-ChOA | 113.60 | 152.79 | 115.37 | ||
| Environment 2 | WOA | 392.64 | 985.06 | 937.40 | |
| ALO | 435.29 | 908.31 | 850.31 | ||
| SSA | 224.57 | 678.34 | 343.06 | ||
| ChOA | 339.15 | 852.38 | 771.56 | ||
| GWO | 455.74 | 890.00 | 860.67 | ||
| TRS-ChOA | 119.48 | 481.90 | 125.04 | ||
| Environment 3 | WOA | 314.60 | 869.75 | 573.51 | |
| ALO | 428.00 | 589.91 | 560.29 | ||
| SSA | 365.77 | 714.70 | 401.57 | ||
| ChOA | 316.49 | 462.39 | 385.48 | ||
| GWO | 293.68 | 613.44 | 442.83 | ||
| TRS-ChOA | 250.84 | 419.56 | 268.16 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; He, Q.; Zhang, D. UAV Path Planning Based on an Improved Chimp Optimization Algorithm. Axioms 2023, 12, 702. https://doi.org/10.3390/axioms12070702
Chen Q, He Q, Zhang D. UAV Path Planning Based on an Improved Chimp Optimization Algorithm. Axioms. 2023; 12(7):702. https://doi.org/10.3390/axioms12070702
Chicago/Turabian StyleChen, Qinglong, Qing He, and Damin Zhang. 2023. "UAV Path Planning Based on an Improved Chimp Optimization Algorithm" Axioms 12, no. 7: 702. https://doi.org/10.3390/axioms12070702
APA StyleChen, Q., He, Q., & Zhang, D. (2023). UAV Path Planning Based on an Improved Chimp Optimization Algorithm. Axioms, 12(7), 702. https://doi.org/10.3390/axioms12070702






