Simulation Analysis of a Novel Digital Pump with Direct Recycling of Hydraulic Energy

Abstract

There is a permanent and strong need for energy recovery to improve the efficiency of the hydraulic system in the field of the construction machinery. In addition, the digital pump will become powerful and versatile by employing different configurations and intelligent control of the flow distribution valves. Considering this case, we have proposed a novel digital pump in which every plunger is equipped with two flow distribution valves. By controlling these two valves, external hydraulic energy can be directly reused without other components. Based on the structure and working principle of the digital pump, the mathematical model is established and three working modes are detailed. To verify the feasibility and correctness of control methods, a performance simulation testing platform including a digital pump, load module, hydraulic energy to be recovered, and controller module was developed in AMESim R15 software. The pressure, flow rate, and torque simulations of the digital pump in three working modes were carried out. The simulation results have shown that the digital pump not only can be used as an ordinary pump but also has the function of recovery and immediate reutilization of another hydraulic energy. Meanwhile, the corresponding variable displacement control strategy is effective and the positive torque required to drive the digital pump can be reduced, which verified the energy-saving of this scheme. The ideas and contents in this paper can offer significant references for energy conservation technology of various engineering machineries and the intensive study of digital hydraulics.

1. Introduction

Fluid transmission technology with its advantage of high power density is widely applied in agriculture, transport machinery, construction machinery, aerospace, and marine [1]. However, with the concept of industrial green development gradually becoming mainstream, fluid transmission technology has the characteristics of high energy consumption, and high carbon emissions can no longer meet the needs of environmentally friendly development [2,3,4]. According to statistics from the U.S. Department of Energy have shown that the average efficiency of fluid transmission systems is only 22% [5]. If the efficiency of the fluid transmission system is improved by 1%, the economic benefit is about $26 billion [6]. Therefore, improving the efficiency of fluid transmission systems in various application fields has been a popular research topic and many researchers have contributed to it, such as [7,8,9,10,11]. Construction machinery plays an extremely important role in infrastructure construction and national economic development, but it also has the disadvantages of lower efficiency and higher fuel consumption due to the fluid transmission system. Energy recovery is a very effective method to increase the efficiency of construction machinery and has received extensive attention and studies by academia [12,13]. Zheng Sun et al. proposed a novel swashplate plunger energy recovery device for seawater reverse osmosis systems, using a hollow plunger with side openings only for pressure exchange. After optimizing the design parameters using numerical simulations and theoretical calculations, the efficiency of the device can reach 96% [14]. X. Liang et al. described an energy regeneration system for a hydraulic crane, and the testing outcomes display that this system can recover and reuse wasted energy to achieve the goal of enhancing energy utilization [15]. A new auxiliary hydraulic circuit containing a hydraulic transformer was proposed by Hung Ho et al., which can cause the transformer and cylinder to operate under appropriate conditions with the directional controlled valves and designed controllers, and the final simulation results showed that the energy-saving effect is obvious [16]. Tianliang Lin et al. investigated two kinds of energy regeneration systems that can recycle the potential energy of the hybrid hydraulic excavator by conducting co-simulation of AMESim version 4.2.1 and MATLAB version 7.1 software, and the simulation data indicate that the accumulator-motor-generator energy regeneration system can recover 41% of the potential energy when the boom is lowered [17]. Daniel Boehm et al. brought forward a high-power differential cylinder for the excavator system to realize the integration of the boom drive and the reutilization of the potential energy generated by the lowering of the boom. The test results demonstrate that the installed power of the prototype engine is lowered by 25% and the lifting speed and slewing accelerations of the boom are heightened by 80% [18]. Thompson et al. proposed a simple swing energy recovery system that employs an accumulator, constant displacement hydraulic motor, and control valves. The simulations show that the energy consumed by the swing system can be reduced by 48% and the total energy consumption of the excavator can be abated by 17% [19].

Digital hydraulics is a newer branch of hydraulic transmission technology and has become a research hotspot because of its high efficiency and flexible control. Many studies have shown that digital hydraulics can significantly improve the performance of the entire hydraulic system and reduce energy consumption and loss to the greatest extent [20,21]. Azzam et al. applied a digital pump instead of a conventional variable pump to a tandem hydraulic hybrid drivetrain and performed simulation tests using MATLAB/Simscape, and the total efficiency was improved by at least 8% to 25% [22]. Minav et al. studied electro-hydraulic reprocessing methods for recycling potential energy from a fork truck. The key of the proposed setups is the direct hydraulic energy storage device composed of the accumulator and digital hydraulic valves [23]. Matthew Green et al. proposed the “DEXTER” project in which a Digital Displacement Pump (DDP) was installed in the excavator, and the comparison testing between the modified excavator and the standard excavator showed that the productivity and energy-saving rate were significantly improved under certain mode [24]. John Hutcheson et al. utilized the digital displacement pump motor as a controlling element to directly control the motion of the actuator. Without throttling loss, the digital displacement system saved 1.1–10.8 times of energy through the comparison of their simulation outcomes [25]. Jill Macpherson et al. carried out a backward-facing simulation on an 18-ton excavator with the bus system architecture. The energy recycling capacity is raised by the digital displacement pump-motor, and it is confirmed that the simulated fuel saving is 53% to 58% [26]. M. Pellegri et al. introduced the multi-service digital displacement pump to the excavator, which allows dynamic distribution of the pump displacement under different pressure levels. The eventual testing results proved that the energy consumption is downgraded by more than 30% through comparing with the benchmark excavator [27].

According to the above pieces of research, the energy recovery system adopting traditional hydraulic or digital hydraulic components can significantly increase the efficiency of these types of mechanical equipment; however, there are some obvious disadvantages such as the complex structure of the hydraulic system, too many energy conversions. Given that the digital pump is capable of various free and brilliant flow distributions by the active control of flow distribution valves, a new type of direct energy recycling digital pump (DERDP) is proposed in this article, which can realize the direct and efficient recycling of hydraulic energy and enhance the energy utilization. The rest of this paper is organized as below: Section 2 exhibits the structure and mathematic model of the proposed DERDP. In the following Section 3, the working principles and corresponding control methods of the three operating modes of the digital pump are presented in detail. Section 4 gives an overview of the simulation and testing platform for the DERDP in AMESim software. The simulation curves of three working modes are compared and analyzed respectively in Section 5. Finally, the conclusions are obtained and the future works are discussed.

2. Structure and Mathematic Model of DERDP

2.1. Structure of DERDP

The structure and components of the DERDP with five plungers are shown in Figure 1a. It can be seen that DERDP is mainly composed of a plunger pair, eccentric wheel, and flow distribution valve groups and has three oil ports, such as suction port, energy recovery port, and pressure port. The eccentric wheel driven by a motor rotates and pushes the piston to achieve the reciprocating motion, which makes the volume of the sealed plunger chamber formed by the plunger pair change. Each plunger pair is equipped with a flow distribution valve group that includes a suction valve (SV), an energy recovery valve (ERV), and a check valve (CV). When the SV is energized, the corresponding sealed plunger chamber has a direct connection to the suction port, thus hydraulic oil can flow freely between the sealed plunger chamber and the tank pass through the suction port. By opening the ERV, the external high-pressure oil runs through the energy recovery port and enters the sealed plunger chamber. The plunger is forced to move and help the eccentric wheel work under high-pressure oil, which realizes the direct recycling of hydraulic energy. The CV connecting to the pressure port is used to prevent the high-pressure oil of the hydraulic system from flowing into the sealed plunger chamber. For the convenience of application, the Simplified graphic symbol of DERDP is defined in Figure 1b.

2.2. Mathematical Model of DERDP

The kernel of the energy recovery function of the DERDP is to accomplish the expected flow assignment for the radial plunger pump with the flow distribution valve, and therefore the mathematical modeling work is divided into two parts. The first part is about the radial plunger pump and the second part concerns the flow distribution valve.

2.2.1. Motion Characteristics of Radial Plunger Pump

The five plungers of the radial plunger pump are uniformly distributed along the circumference of the eccentric wheel, as shown in Figure 2a. As these plungers are completely consistent, the whole radial plunger pump is simplified as the reciprocating motion of one plunger under the eccentric wheel. The major parameters of the eccentric wheel and plunger pair are annotated in Figure 2b.

The plunger is always crushed against the working surface of the eccentric wheel due to the spring, hence the displacement expression of the plunger is obtained as below:

$$x=L+L\left(\mathit{cos}(\theta -\beta )\right)$$

(1)

where $L$ and $\theta$ are the eccentric distance and angular displacement of the eccentric wheel respectively, $x$ represents the plunger displacement. The angular displacement $\theta$ can be created by multiplying the angular velocity $\omega$ of the eccentric distance by time $t;$ $\beta$ is the included angle between the plunger axis and horizontal line.

$$\theta =\omega t$$

(2)

By substituting the equation of the angular velocity $\omega$ into Equation (1), we can find:

$$x=L+L\left(\mathit{cos}(\omega t-\beta )\right)$$

(3)

By calculating a derivative of the plunger displacement Equation (3); the plunger velocity $V$ is achieved as follows:

$$V=\dot{x}=-L\omega \mathit{sin}\left(\omega t-\beta \right)$$

(4)

According to the velocity and area of the plunger, the output flow rate of this plunger pair can be determined by using the following equation:

$$Q=V·A=-\frac{{\pi d}^2}{8}L\omega \mathit{sin}\left(\omega t-\beta \right)$$

(5)

In Equation (5), $d$ is the diameter of the plunger. The pressure variation characteristics in the plunger chamber can also be derived:

$$V_p=V_{dead}+\left(L_p-x\right)A$$

(6)

where $V_p$ is the volume in the plunger chamber; $V_{dead}$ is the dead volume of the plunger chamber; $L_p$ is the cylinder length.

$$\frac{dp}{dt}=\frac{{\beta }_e}{V_{dead}+\left(L_p-x\right)A}\left(Q_v+Q_{leak}-VA\right)$$

(7)

In Equation (7), ${\beta }_e$ is the effective bulk modulus of oil containing 1% air. The fluid viscous friction $F_v$ during plunger motion can also be modeled as follows [28]:

$$F_v=\frac{2\pi R_{cyl}\left(l_c+x\right)\mu v_p}{R_{cyl}-\frac{d}{2}}$$

(8)

where $l_c$ is the contact length between the plunger; $R_{cyl}$ is the bore diameter of the cylinder.

2.2.2. Leakage Characteristics

Leakage flow between the volume chamber and the plunger surface is divided into Couette and Poiseuille flow [29], which is shown in Equation (7):

$$Q_{leak}=Q_{co}+Q_{po}$$

(9)

where $Q_{leak}$ is the leakage flow rate; $Q_{co}$ is the Couette flow, and $Q_{po}$ is the Poiseuille flow. The mathematical expressions of both flow models are referred to in the literature [30] and are shown in the following equations:

$$Q_{co}=\pi \frac{d}{2}V\left(R_{cyl}-\frac{d}{2}\right)$$

(10)

$$Q_{po}=\frac{{{\pi R}_{cyl}∆P\left(R_{cyl}-\frac{d}{2}\right)}^3}{6\mu \left(x+l_c\right)}$$

(11)

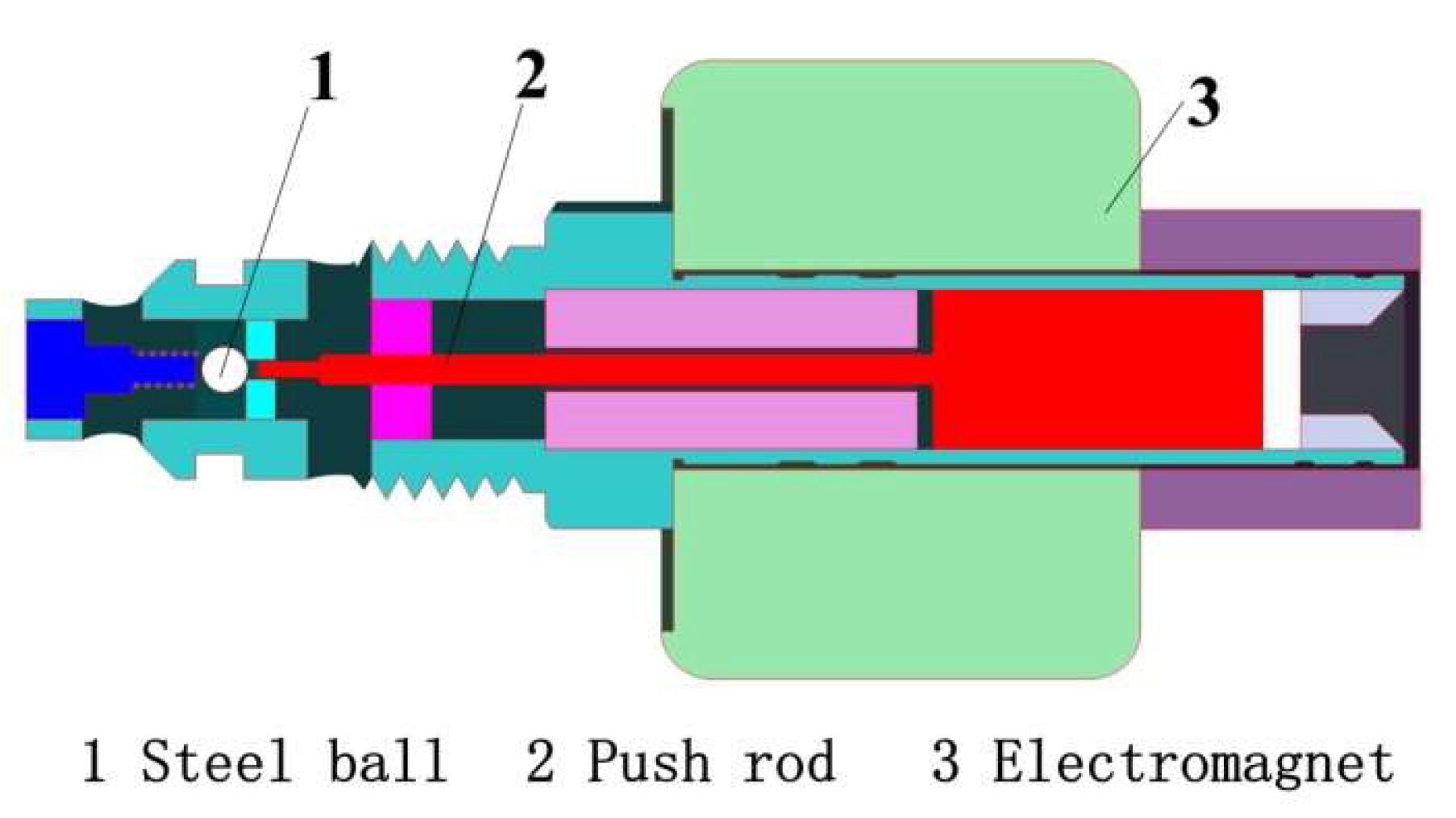
2.2.3. Flow Distribution Valve

In order to achieve the flow distribution of the plunger chamber very quickly with higher accuracy, a high-speed on-off valve is selected to serve as the flow distribution valve. The high-speed on-off valve used in this study is a two-position two-way ball valve, as shown in Figure 3. The response time of this high-speed on-off valve can reach ms-level because of special mechanical design. This research focuses on the energy recovery control of the digital pump and therefore the flow distribution valve is treated to a first-order system. The relationship between spool displacement and input control voltage is revealed below:

$$\frac{\mathrm{X}\left(\mathrm{s}\right)}{\mathrm{U}\left(\mathrm{s}\right)}=\frac{\mathrm{k}}{\mathrm{T}\mathrm{s}+1}$$

(12)

where $\mathrm{X}\left(\mathrm{s}\right)$ and $\mathrm{U}\left(\mathrm{s}\right)$ reflect the Laplace transformation of the ball spool displacement and control voltage separately. The $\mathrm{T}$ is the time constant of the first-order system and k is displacement amplification factor. The flow rate $Q_v$ through the high-speed on-off valve can be described by the following equation:

$$Q_v=C_d{A}_v\sqrt{\frac{2\left(∆p\right)}{\rho }}$$

(13)

where $C_d$ is the flow coefficient, $A_v$ is the valve port through-flow area, and $∆p$ is the differential pressure between the inlet and outlet of the valve. The $\rho$ represents the density of the oil. The dynamics equation of the spool can be derived as:

$$m_v\ddot{x_v}=F_e-F_{ss}-F_f-F_{ft}-F_{fs}$$

(14)

where $m_v$ represents the equivalent total mass of the spool; $x_v$ is the displacement of the spool; $F_e$ is the electromagnetic force; $F_{ss}$ is the elastic force generated by the compression of the spring; $F_f$ is the frictional force, $F_{ft}$, $F_{fs}$ are the transient and steady-state hydrodynamic forces, respectively. $F_e$, $F_{ss}$, $F_{ft}$, and $F_{fs}$ can be represented by the following equation [31]:

$$F_e=\frac{1}{2}\times I^2\times \frac{d{L}_v}{d\delta }$$

(15)

$$F_{ss}=K\left(x_{v0}+x_v\right)$$

(16)

$$F_{fs}=C_d{C}_v{A}_v\cos \alpha \mathsf{\Delta }p$$

(17)

$$F_{ft}=C_d\omega l\sqrt{2\rho \mathsf{\Delta }p}{\dot{x}}_v$$

(18)

On expression, $I$ and $L_v$ represent the current and inductance of the coil; $\delta$ represents the air gap of the electromagnetic part; $K$ is the coefficient of stiffness of the spring; $x_{v0}$ is the initial compression of the spring; $C_v$ is the velocity coefficient of the valve port; $d_v$ is the diameter of the valve seat; α represents the conical spool jet angle; $l$ is the damping length. $\omega$ represent the area gradient.

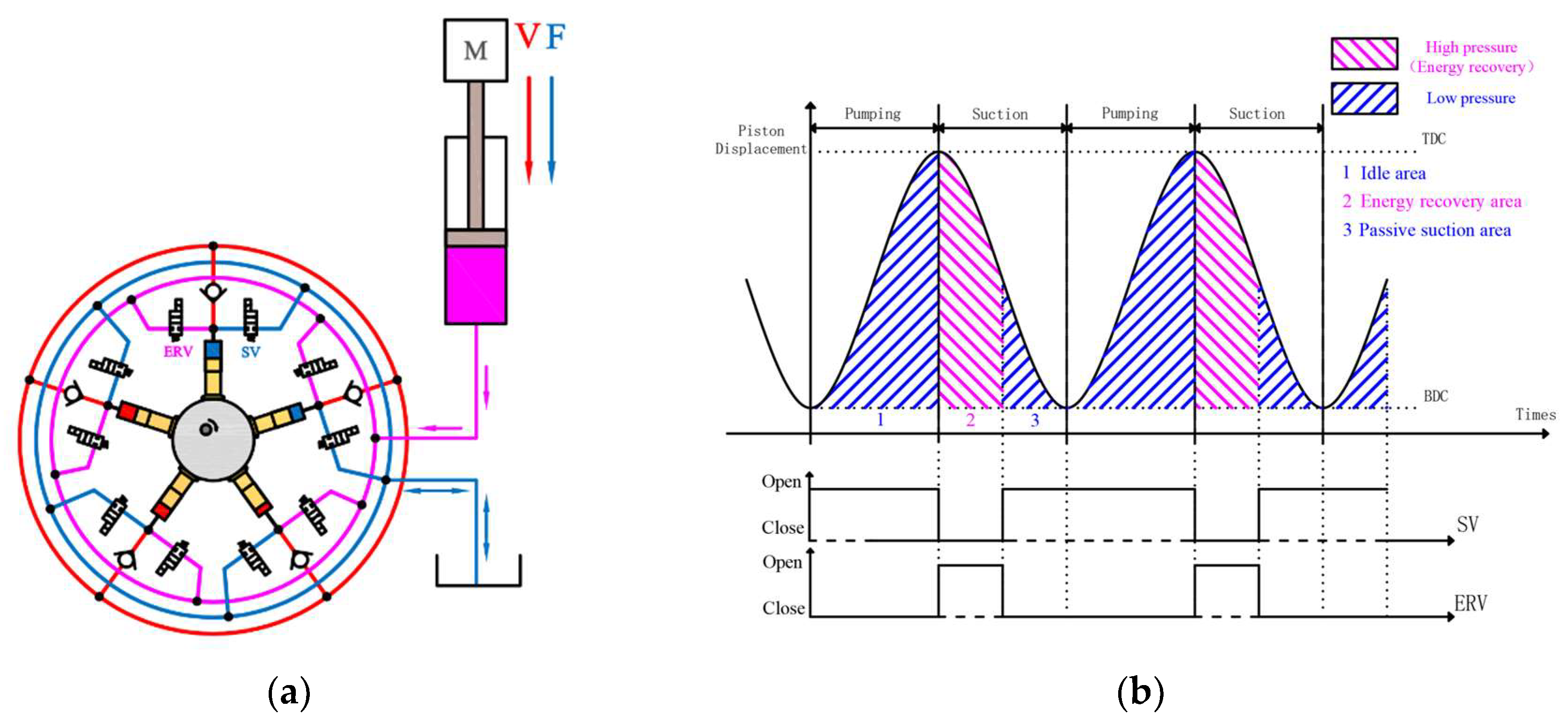
3. Working Modes of DERDP

By controlling the SV and ERV of every plunger pair, three different working modes of DERDP including the pump mode (PM), the energy recycling mode (ERM), and the direct reuse mode (DRM) can be accomplished. For demonstration purposes, the hydraulic cylinder is selected as a controlled plant of the DERDP. The working principles and control strategies of three operating modes are introduced in detail as follows:

3.1. Pump Mode (PM)

As shown in Figure 4a, the suction port and the pressure port are connected with the tank and the hydraulic cylinder individually in the pump mode of DERDP, and the energy recovery port is not used. Under the drive of the motor, the DERDP sucks hydraulic oil from the tank and squeezes the compressed hydraulic oil into the hydraulic cylinder to lift the load. In PM, the control strategy of the SV and ERV is described in Figure 4b. As you can see from this chart, the ERV is kept off all the time and the SV is always open at the suction stage of the plunger. According to the desired displacement, the SV is switched off at a certain position of the pumping stage. The longer the close time of the SV is the larger displacement the DERDP has. By this means, the rising speed of the hydraulic cylinder can be effectively adjusted. In brief, the DERDP in pump mode provides the same function as the normal digital pump.

3.2. Energy Recycling Mode (ERM)

The working principle of DERDP in energy recycling mode is s shown in Figure 5a. Compared with PM, the energy recovery port is employed to import the hydraulic energy that is transformed from the potential energy of the load, while the pressure port is idle. The imported hydraulic energy enables the plunger and eccentric wheel to move, which achieves the goal of the hydraulic energy recovery. The Figure 5b reveals the control method of these two valves in the process of energy recovery. When the plunger is at the pumping stage, the SV has been put on opening and the sealed plunger chamber is in a state of low pressure. When the energy recovery function of DERDP is in demand and the plunger enters the suction stage, the ERV is turned on. At the opening moment of the ERV, the SV is closed as quickly as possible to raise the pressure of the sealed plunger chamber. That is, the SV and ERV cannot keep open at the same time. To sum up, DERDP in energy recycling mode is similar to a digital hydraulic motor. The variable displacement of the ‘motor’ is completed by adjusting the opening time of the EVR.

3.3. Direct Reuse Mode (DRM)

The direct reuse mode of DERDP is essentially a combination of pump mode and energy recycling mode. For the convenience of describing the operating principle of DRM, two hydraulic cylinders are employed in Figure 6a. The left hydraulic cylinder connecting with the pressure port receives the hydraulic energy from DERDP and makes the load move up against gravity. The other one has a downward movement under gravity and pours hydraulic energy into the DERDP through the energy recovery port. In this way, the potential energy of the load on the right is regenerated to propel the eccentric wheel to work similar to an electric motor. If recovered hydraulic energy is less than that of elevating the load, electric energy is consumed by an electric motor to fill the energy gap. Figure 6b represents the switch status of the SV and the ERV when hydraulic energy is directly reused. It is easy to see that the plunger chamber is at high pressure during the portion of the pumping and suction stages due to the continuous shutdown of the SV. Of course, the ERV is also opened at the suction stage to permit high-pressure hydraulic oil into the DERDP. The pumping and suction stages perform the compression of the hydraulic oil and energy liberation of high-pressure oil, respectively, thus these two stages caused by the reciprocating motion of the plunger have been fully utilized.

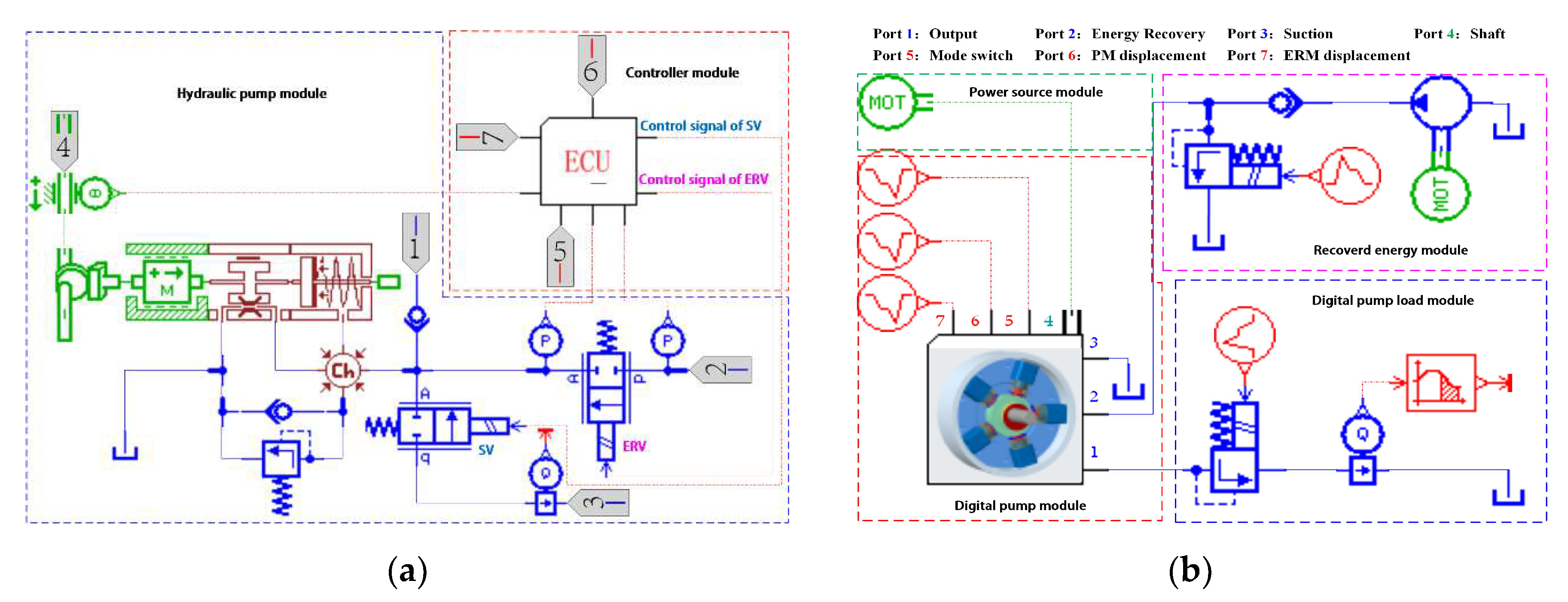
4. Simulation Modeling of DERDP

According to the structure and three working modes of DERDP described previously, it can be found that the modeling of DERDP touches on various disciplines such as hydraulics, mechanics, electrics, and so on. As a modeling and simulation platform for complex systems involving multi-disciplinary fields, users can build up a sophisticated system model with the aid of the AMESim software more conveniently and quickly. Therefore, the powerful AMESim software is selected as the modeling and simulation tools to verify the effectiveness of the new digital pump proposed by this paper, which makes full use of the mature hydraulic library, mechanical library, and signal control library offered by this software.

The DERDP investigated in this paper has five identical plunger modules and therefore, the foundation and core of the entire pump is the modeling of the single plunger module that is shown in Figure 7a. The AMESim model of the single plunger module includes two main parts: a hydraulic plunger part and a controller part. The hydraulic plunger part is established for the simulation of the plunger pairs, eccentric wheel, and flow distribution valve group. Judging by various operating conditions, the controller part is used to generate the control signals for the SV and ERV. On the basis of the single plunger modeling, the performance simulation test system for the DERDP is accomplished as shown in Figure 7b. This system is composed mainly of a power source module, DERDP module, load module, and recovered energy module. In the load module, a proportional relief valve is controlled to regulate the working pressure of the DERDP. A hydraulic power source with adjustable pressure in the recovered energy module is designed to offer the outside hydraulic energy to the DERDP when the energy recycling and direct reuse modes are utilized. The parameters of the DERDP model are entirely consistent with the experimental prototype that is reconstructed from a radial plunger pump, as listed in

Table 1. Main design parameters of DERDP.

Parameter	Value	Unit
Pump angular speed	1000	rpm
Chamber length	25.1	mm
Eccentric radius	31	mm
Eccentricity	3.8	mm
Flow coefficient	0.7
Piston diameter	10	mm
Dead volume of piston	0.08	cm3
SV response time	3	ms
ERV response time	3	ms

.

5. Simulation Analysis

To test the validity of the three working modes and control methods of DERDP, three different simulation scenarios were carried out by the earlier-established AMESim model. The first simulation is implemented to imitate the different variable displacement conditions in the pump mode, and the pump displacement factor (PDF) is changed from 1.0 to 0.2. In the energy recycling mode, the DERDP is running in hydraulic motor working condition in nature. Therefore, the displacement of the DERDP is represented with a motor displacement factor (MDF) that has the same value as the PDF. The pump mode and energy recycling mode are successively executed in the pumping and suction stages in direct reuse mode, so these two displacement parameters both need to be set. To lower the simulation difficulty caused by simultaneous changes of two displacement parameters, the PDF is set to a constant value of 1.0 and the MDF rises from 0.2 to 1.0 at an interval of 0.2.

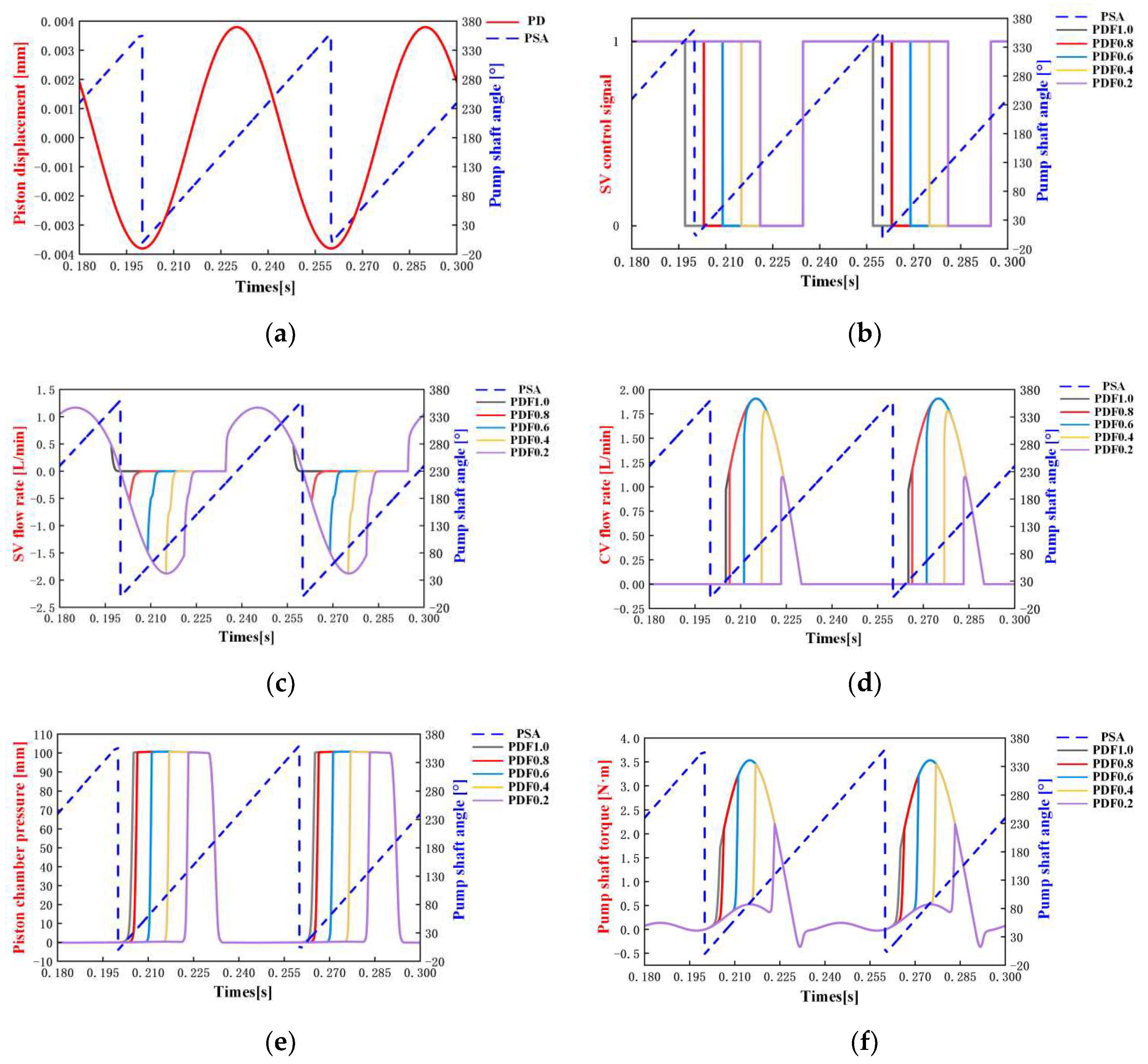
5.1. The Simulation of the DERDP in PM

The comparison between pump shaft angle (PSA) and piston displacement (PD) is shown in Figure 8a. As this picture shows, the plunger comes to the bottom dead center (BDC) when the PSA is 0°. With the increase of the PSA, the plunger moves up under the eccentric wheel. When the PSA is equal to 180°, the plunger reaches the top dead center (TDC). Moving from BDC to TDC, the plunger is at the pumping stroke and squeezes the hydraulic oil into the pressure port. As the PSA increases from 180°to 360°, the plunger has a movement from TDC to BDC and falls into the suction stroke. During the working process of the plunger, the suction stroke and pumping stroke come in swift alternation.

The control signals of SV under five pump displacement factors (PDF) are 1.0, 0.8, 0.6, 0.4, and 0.2 are illustrated in Figure 8b. The PDF 1.0 indicates that the SV will remain closed at the pumping stroke of the plunger and the DERDP has the maximum displacement. The open time of the SV at the pumping stroke increases with the PDF, which makes the displacement of the DERDP smaller and smaller. Conversely, the control signal for the SV is always set to 1 at the suction stroke for allowing hydraulic oil into the plunger chamber. It can also be found clearly that the open and close signals for the SV with the PDF 1.0 both occur in advance to compensate for the dynamic response time of the SV.

Figure 8c,d show the flow rate variation curve of the SV and CV respectively. When the PDF is set to one, as shown in the picture, the flow rate of the SV at the pumping stroke leaves zero. If the PDF is less than one, a negative flow rate representing the opposite oil flow direction will appear. Furthermore, the smaller the PDF is, the greater the hydraulic oil flows from the plunger chamber into the tank. At the suction stroke, the flow rate curves of the SV with different PDFs are almost exactly the same by reason of the invariant control signal. As you can see from Figure 8b–d, the output flow rate passing through the CV at the pumping stroke diminishes gradually with the decrease of the PDF, and the flow rates of the SV and CV are complementary. Owing to blocking fluid backflow of the CV, the flow rate comes down to zero at the suction stroke.

The plunger chamber pressure and pump shaft torque with pump shaft angle is demonstrated in Figure 8e,f. The maximum pressure of 100 bar in the plunger chamber is influenced by the setting of the relief pressure of the relief valve connected to the plunger chamber. The high-pressure duration of the plunger chamber becomes much longer along with the bigger PDF. Accordingly, the torque propelling the eccentric wheel has the same changing tendency as the results of the CV flow rate. As described earlier, it can be concluded that different displacement operating of the DERDP used as a pump can be achieved by employing the control method of the SV exhibited in Figure 8b.

5.2. The Simulation of the DERDP in ERM

Figure 9 displays the working characteristics of the DERDP in ERM with different motor displacement factor (MDF). The corresponding relationship between the PSA and the PD, as shown in Figure 9a, is entirely consistent with that of the pump mode. There are two ports used except the pressure port in ERM, which keeps the flow rate of the CV at zero. The control signal and flow rate of the ERV are displayed in Figure 9c,d respectively. From these two figures, the recovery process of external hydraulic energy mainly utilizes the suction stroke in which the PSA increases from 180° to 360°. For various MDFs, the opening signals of the ERV all start at 180° and the working time of the ERV increases as the desired displacement. The flow rate curve of the ERV has a similar outline as a sinusoid as a result of the sinusoidal motion of the plunger. The ratio of the area occupied by the flow rate curve of ERV to the entire sinusoidal scales up as the MDF is greatly increased. From the analysis of the ERM working principle of the DERDP, the opening signals of the SV and the ERV are mutually exclusive, in other words, these two valves cannot open simultaneously. Moreover, the opening of the SV just follows the closing of the ERV, which can be explained by careful contrast of Figure 9c,e. The flow rate curves of the SV and the ERV with the same MDF form a complete sinusoid together. From Figure 9e, we also understand that the SV is always in the open state during the pumping stroke so the plunger chamber is filled with hydraulic oil. The variations of the plunger chamber pressure and pump shaft torque are presented in Figure 9g,h. Unlike the PM, the high-pressure state of the plunger chamber arises within the suction stroke. In this situation, the plunger has to travel to the eccentric wheel, which brings about a negative torque shown in Figure 9h. The negative torque implies that the external hydraulic energy is recovered and transmuted into mechanical energy. The periods of high pressure and negative torque also expand in proportion to the MDF, which can achieve more energy recovery.

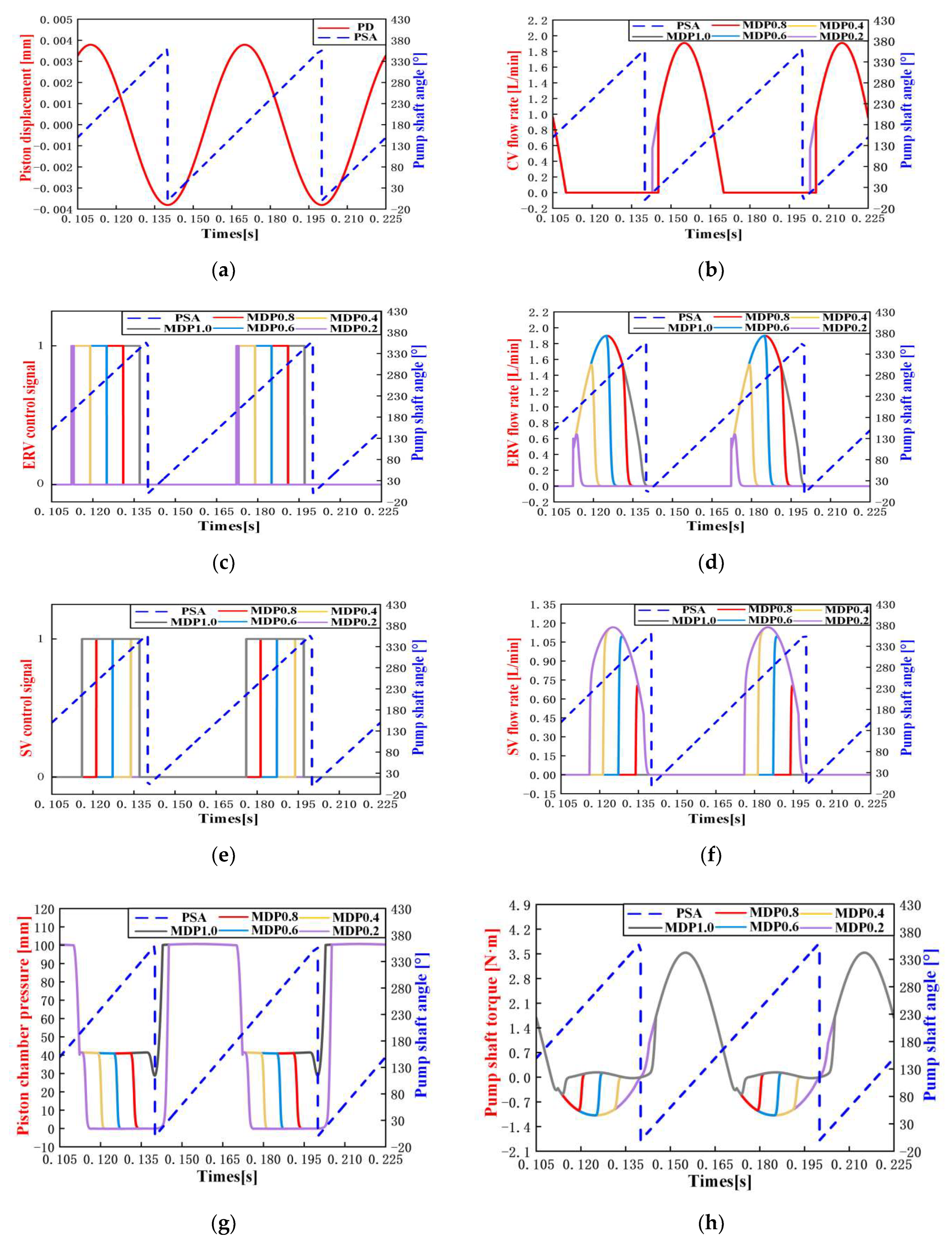
5.3. The Simulation of the DERDP in DRM

There are two displacements needing to be simultaneously treated when the DERDP works in the DRM. One is the pump displacement at the pumping stroke, and the other is the motor displacement at the suction stroke. To facilitate the analysis, the pump displacement is supposed as an invariable value and the motor displacement will gradually increase. Namely, the PDF is one and the MDF goes up from 0.2 to 1.0 with a step size of 0.2. The simulation results of the DERDP with the above condition are described in Figure 8. As seen in Figure 10b, the flow rate curves of the CV with different MDF are on the whole the same on account of the constant PDF. The closing of the SV in the pumping stroke that is shown in Figure 10e has positive evidence that the PDF is always 1.0. The influences of the MDF on the control signal and flow rate changes of the ERV and SV in the DRM are revealed in Figure 10c–f, which is consistent with that of the ERM. It can be seen from Figure 10g that the most note-worthy feature of the DERDP in DRM is the high pressure of the plunger chamber in both strokes. When the MDF is small, the pressure of the plunger chamber during the suction stroke first varies from 100 bar to 40 bar, then drops to 0 bar. The 100 bar and 40 bar are individually decided by the set points of the load pressure and energy recovery pressure. If the MDF is the maximum size, the plunger chamber will continuously keep a high pressure in the entire suction stroke. Figure 10h reports the changing trend of the shaft torque during the whole working process of the plunger. The shaft torque is positive for compressing the hydraulic oil when the PSA ascends from 0° to 180°. The negative shaft torque appearing between 180° and 360° denotes that the mechanical energy converted from the external hydraulic energy has been output and can be exploited by the other plunger motion.

To understand all the differences more clearly before and after external hydraulic energy recovery, a comparative simulation has been implemented with PDF 1.0 and MDF 0.6. From Figure 11a,b, the plunger initiates the pumping stroke, and the energy recovery function is activated after 0.4 s. According to the control signals of the ERV and the SV displayed in Figure 11c, these two valves have to rotate in an effort to reclaim the hydraulic energy. In Figure 11d, the flow rate of the ERV raised at 0.43 s and finally was restricted to zero for the closing of the ERV. The next flow rate curve is that of the SV, which will last until the end of the suction stroke. The impact of the energy recovery on the working condition of the plunger also is reflected in the pressure and torque variations in Figure 11e,f.

6. Conclusions

In this paper, a new digital pump with high-capacity direct energy recovery is proposed in order to achieve further energy savings in fluid transmission systems and reduce fuel consumption in construction machinery while simplifying the complex structure of the energy recovery system. Firstly, the structure of DERDP and the working principle of three operating modes (PM, ERM, and DRM) are described. The corresponding control strategies are also shown. A detailed simulation model of the DERDP is established based on AMESim to study the variable displacement working conditions of the DERDP in PM, ERM, and DRM. The simulation results prove that the DERDP can be used as a common digital pump and has also been treated as a critical energy conversion component of the hydraulic energy recovery system. The corresponding variable displacement control strategies are also effective.

• When DERDP is in PM, only PDF can be controlled to realize the control of output flow and the control input energy of DERDP, which is used as a digital pump.
• As the DERDP is switched to ERM, the energy recovery function is activated. External hydraulic energy is allowed to be recovered and converted into mechanical energy. The period of the negative torque of DERDP expands proportionally to the MDF, i.e., increasing the MDF allows for more energy recovered.
• In the case that DERDP is in DRM, both PDF and MDF can be adjusted. The positive torque required to drive the DERDP decreases as the PDF reduces, and the operation of increasing the MDF also has this effect. The negative torque generated by the direct reuse process of DERDP can contribute to helping other plungers’ movement. Therefore, the energy required to drive the DERDP will be reduced.

To obtain more detailed experimental data and verify simulation results, the experiment test platform for the DERDP is being designed and built. Moreover, the research work on the DERDP applied to the boom potential energy recovery of the hydraulic excavator also is underway in our laboratory.