Abstract
In this study, we investigated a novel asymptotic stabilization control method for a fractional-order HIV-1 infection model. First, we constructed a mathematical model of the fractional-order HIV-1 infection using the state-space equations of Caputo fractional calculus. Subsequently, a new control strategy was designed for the fractional-order HIV-1 infection model, and the corresponding asymptotic stabilization criterion was proposed by combining a novel vector Lyapunov function with the M-matrix method. Additionally, we incorporated a time delay, which was generated by the interaction between different variables in the actual system, into the fractional-order HIV-1 infection model, forming a system with a time delay. Based on the vector Lyapunov function associated with the M-matrix measure and Razumikhin interpretation, a control strategy was developed for the fractional-order HIV-1 infection model with a time delay. Finally, we show the results of two numerical simulations of the fractional-order HIV-1 infection model, with and without time delay, to illustrate the accuracy, usefulness, and universality of the proposed measure in our paper.
1. Introduction
AIDS is known as “Super Cancer” and the “Plague of the Century” [1,2,3]; according to the new AIDS data released by the WHO Global Health Watch, there have been 78 million HIV patients and there are currently 39 million HIV patients around the world. The culprit of this tragedy is HIV-1 [4,5,6]. When the virus develops to a certain extent, it destroys the body’s immune system. The initial infection period can develop into AIDS after about 10 to 15 years. HIV-1 can be mixed with blood in a variety of ways, such as a blood transfusion, the sharing of contaminated needles, unprotected sexual intercourse, childbirth, and breastfeeding. After HIV-1 infection, CD4+ T lymphocytes in the body become the primary molecule of infection. Long-term infection of HIV-1 will cause the failure of the CD4+ T cell bank, then affect the immune response of the body, and finally form acquired immunodeficiency syndrome [7,8]. The establishment of a dynamic model of HIV-1 infection based on HIV-1 can effectively inhibit the spread of infectious diseases and lay a foundation for an in-depth understanding of the virus content in the human body and its evolution over time [9,10]. The study of this dynamic characteristic is of great significance for the further understanding of AIDS and the development of AIDS prevention and a control scheme [11,12,13].
The modeling of physical systems is a hot topic in current research. For example, some studies investigated the identification of parameters of an anomalous diffusion model based on measurements or modeling of heat distribution in porous aluminum using fractional differential equations [14,15]. Up to now, this has been a very effective way to use mathematical models to describe the dynamic process of virus infection [16,17]. A reasonable mathematical model combined with the HIV-1 infection mechanism can provide a theoretical basis for studying the dynamic changes of HIV-1 in vivo, which can help people to understand the pathogenesis and transmission pattern of HIV-1, and thus, theoretically develop drugs and antiviral treatment programs to better prevent and control the transmission of HIV-1 [18,19]. Mathematical modeling and analysis of viral kinetics with humoral immunity can help to design therapeutic strategies and provide insights into the evaluation of antiviral drug therapies, and it is believed that only a deeper understanding of the immune responses can lead to the development of a safe and effective HIV-1 vaccine. In [20], the researchers pointed out that humoral immunity plays an important role in overall human immunity and studied the kinetics of the viral model with cellular and humoral immune responses. Furthermore, [21,22,23,24] referred to the immune mechanism used against the disease as cellular immunity, and the immune mechanism of antibody cells that attack the virus was called humoral immunity. Many researchers believe that antibody cells play a vital role in the immune response against the virus. However, in most viral infections, the immune response is primarily mediated by non-specific and rapidly acting cytotoxic T cells (CTLs). These cells, along with specific immune components, such as cytotoxic T lymphocytes and antibody cells, target the virus and trigger an immune response in the body. This immune response plays a crucial role in eliminating the virus and inhibiting the progression of the disease. At present, the research on HIV-1 is mainly focused on its pathogenic mechanism, and the analysis of its pathogenic mechanism is of great significance for an in-depth understanding of its pathogenic mechanism and the development of effective anti-HIV-1 drugs.
Fractional derivatives are a hot topic that has been developed in recent years, and it is widely used in many disciplines [25,26,27,28,29,30], such as in mathematics [31,32], computer engineering [33], financial systems [34], and especially in the biological field [35]. At present, many mathematical workers and applied scientists are trying to use this model to simulate biological phenomena in complex network systems [36,37,38,39,40]. Researchers have found that biological cell membranes have fractional electron conductivity, and thus, it can be classified as a fractional model. Currently, there were also numerous studies that focused on studying the fractional-order HIV infection process [41,42,43,44], which has become a research hotspot. In addition, studies showed that a biological model based on fractional derivatives has better performance than a traditional integer model [45,46]. Therefore, we focused on a fractional-order HIV-1 infection model. Among the research on general fractional-order HIV-1 infection models, stabilization control is the most critical issue. However, since the stability analysis measure for the integer-order system is not able to be directly put into use in a fractional-order system, stability estimates and stabilization control for the fractional form pose difficulties during the study of such issues. Moreover, there have been few significant studies on the puzzle of gradual near-stability estimates and asymptotic stabilization. Additionally, in an actual HIV-1 infection model, the time delay is a significant factor. However, the introduction of a time delay greatly increases the system complexity, and thus, it has rarely been considered in previous research.
In this study, motivated by the challenges mentioned above, we surveyed asymptotic stabilization control of a fractional-order HIV-1 infection model by applying a novel measure, that is, a vector Lyapunov function associated with an M-matrix measure. There are two foremost innovation points regarding this study. On the one hand, we considered the time delay between different variables of a fractional-order HIV-1 infection model to construct a model that incorporated a time delay. On the other hand, we applied the novel measure to design an asymptotically stabilized control strategy for an open-loop fractional-order HIV-1 infection model. This technique can solve fractional-order cases, either with or without time delay.
2. Preliminaries
Definition 1
([47]). The Caputo fractional-order derivative is defined as follows:
where is any integrable function; if , one has
Then, we considered the following fractional-order system:
where is the state of Equation (3), and satisfies the condition and the local Lipschitz continuity condition.
Definition 2
([48]). The solution of Equation (3) is called stable if for any there exists such that for every and representing the initial time, we have
The solution of Equation (3) is called asymptotically stable if it is stable and there exists such that whenever
Lemma 1
([47]). Let be a differentiable vector function. Then, for any time instant the following inequality holds:
Lemma 2
([49]). Let be an equilibrium point for the fractional-order system (Equation (3)) if there is a Lyapunov function and functions satisfying
where the fractional-order operator
then the equilibrium point of a fractional-order system is asymptotically stable.
Definition 3
([50]). A realn×n matrix is an if the element and if all of its principal minor determinants are positive.
Lemma 3
([50]). If is an there exists a diagonal matrix with elements such that the matrix
is positive definite.
For the above biological and virological descriptions, it is very appropriate to use a fractional-order model to construct the kinetic process of HIV-1 infection, and the specific fractional-order HIV-1 infection model is shown below [51]:
where are the densities of uninfected target cells (DUTCs), infected target cells (ITCs), and the free virus (FV), respectively, at time is the infection rate of uninfected cells by the virus. is the constant rate that the uninfected cells are restored, and the uninfected cells are infected at a rate of and die at a rate of is the constant rate of each producing HIV-1 particle, and is the per capita rate. The density represents the concentration of CTL cells, where CTL kills infected cells at a rate of and perish at a rate of CTL cells multiply at a rate of and die at a rate of
Lemma 4
([51]). For the fractional-order HIV-1 infection model (Equation (9)), the state variable is non-negatively invariant, where the non-negative invariant compact set is given as
3. Main Results
First of all, from the fractional-order HIV-1 infection model (Equation (9)), we assumed that were the equilibrium points of the system. Then, on the basis of [51], we obtained the following equilibrium points:
where
Then, to make the analysis clearer, we moved the equilibrium point to the origin. We set and thus, the following equations were obtained:
3.1. Stabilization Control of the Fractional-Order HIV-1 Infection Model
Then, we converted the fractional-order HIV-1 infection model (Equation (13)) into a matrix form as follows:
where is the state of the system and is a differentiable vector, the function represents the linear part:
and describes the nonlinear part:
A series of controllers were added to the system as follows:
where
and represent the control gain, then the system can be rewritten to give
Then, we have
where
Theorem 1.
If the following inequality holds and the following matrix is an then the fractional-order HIV-1 infection model (Equation (13)) is asymptotically stable:
Proof of Theorem 1.
According to (Equation (11)), we have that the equilibrium point of the fractional-order HIV-1 infection model is
Then, we choose the following vector Lyapunov function of the system:
where
Then, the following inequality can be derived:
where can be selected as the following forms:
From (Equations (24)–(26)), we have
where
Then, taking the fractional derivative of the sub-Lyapunov function and according to Lemma 4, we have
Then, it can be converted into the following form:
where
According to Lemma 2, we can obtain that the controlled fractional-order HIV-1 infection model (Equation (14)) is asymptotically stable, which completes the proof. □
3.2. Stabilization Control of the Fractional-Order HIV-1 Infection Model with a Time Delay
The fractional-order HIV-1 infection model must inevitably be affected by a time delay in practical situations, and the generation of such a time delay is most likely to occur in the process of the interaction between different variables. To make the modeling more realistic, we added a time delay to the parts of the state-space equations where the different variables interact. The revised mathematical model is shown below:
where
A controller was added to the system (Equation (33)) as follows:
where
Assumption 1.
According to the Razumikhin interpretation [47], we considered that there is a continuous non-decreasing function for such that
Theorem 2.
Assume that the controlled fractional-order HIV-1 infection model satisfies Assumption 1 and Equation (21). In addition, the following matrix is an Then, the controlled fractional-order HIV-1 infection model with a time delay (Equation (35)) is asymptotically stable.
Proof of Theorem 2.
Choosing the same vector Lyapunov function of the system:
we can also obtain the following inequality:
According to the conditions in Assumption 1 and (Equation (37)), we selected the function to be
where satisfies . Then, taking the fractional derivative of the sub-Lyapunov function and according to Lemma 4, we have
According to (Equations (40)–(42)), this can be converted into the following form:
Then, it can be converted into the following form:
where
According to Lemma 2, we can obtain that the controlled fractional-order HIV-1 infection model (Equation (35)) is asymptotically stable, which completes the proof. □
4. Numerical Simulation
In this section, we give the results of the numerical simulation of the fractional-order HIV-1 infection model, which verified the effectiveness and feasibility of the proposed method through the time responses. According to the setting of the structural parameters of the fractional-order HIV-1 infection model in the actual situation [51], the structural parameters of the fractional-order HIV-1 infection model were set to the values shown in Table 1.

Table 1.
The structural parameters of the fractional-order HIV-1 infection model.
Then, according to the control strategy in Theorem 1, the control gain could be set to
Then, according to (Equation (29)), we had
Obviously, it can be determined via a calculation that is an In order to verify the effectiveness of the proposed control strategy, the time responses of different fractional orders are shown in the figures below (Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10).
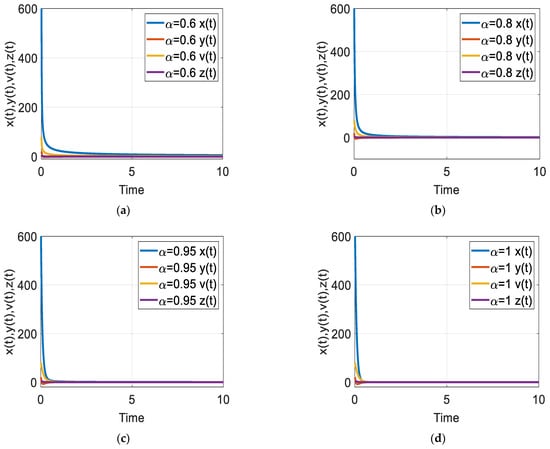
Figure 1.
Time response of the fractional-order HIV-1 infection model with control when . Each subfigures (a–d) represent the time response of the system in a different fractional order.
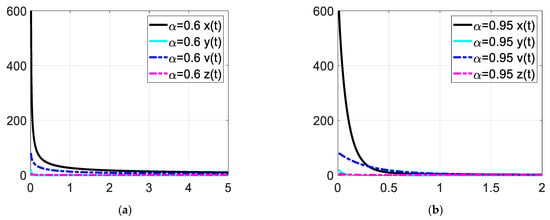
Figure 2.
Enlarged view of the time response at low time values. Each subfigures (a,b) represent the time response of the system in a different fractional order.
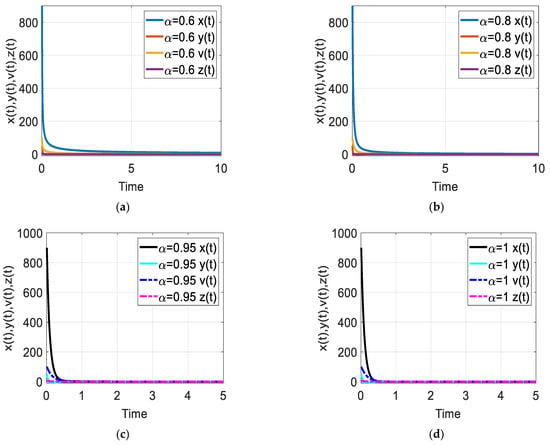
Figure 3.
Time response of the fractional-order HIV-1 infection model with control when . Each subfigures (a–d) represent the time response of the system in a different fractional order.
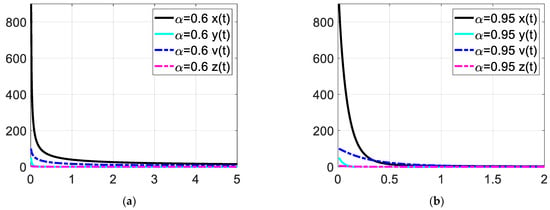
Figure 4.
Enlarged view of the time response at low time values. Each subfigures (a,b) represent the time response of the system in a different fractional order.
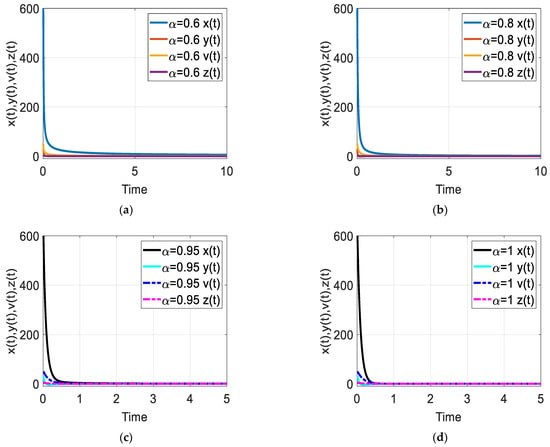
Figure 5.
Time response of the fractional-order HIV-1 infection model with control when . Each subfigures (a–d) represent the time response of the system in a different fractional order.
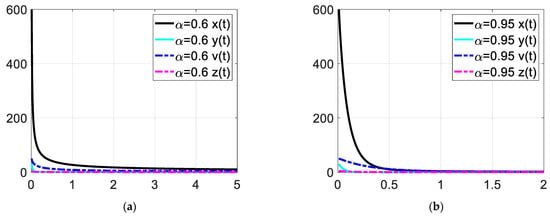
Figure 6.
Enlarged view of the time response at low time values. Each subfigures (a,b) represent the time response of the system in a different fractional order.
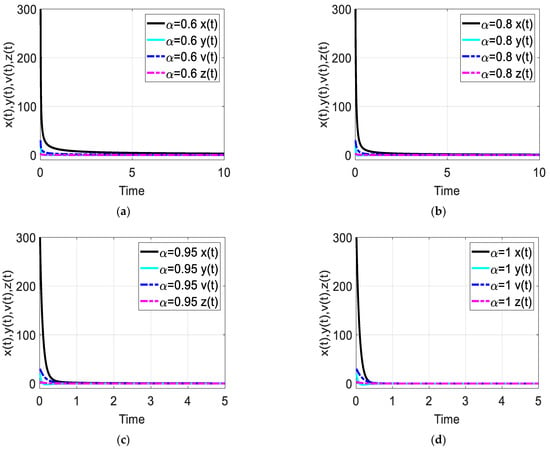
Figure 7.
Time response of the fractional-order HIV-1 infection model with control when . Each subfigures (a–d) represent the time response of the system in a different fractional order.
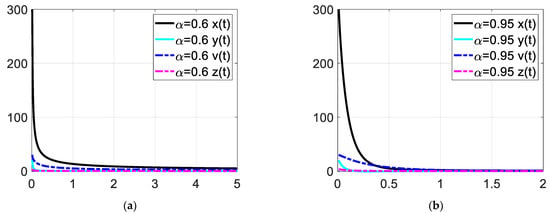
Figure 8.
Enlarged view of the time response at low time values. Each subfigures (a,b) represent the time response of the system in a different fractional order.
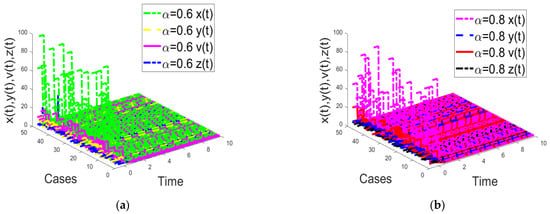
Figure 9.
Time response of the fractional-order HIV-1 infection model with a time delay when . Each subfigures (a,b) represent the time response of the system in a different fractional order.
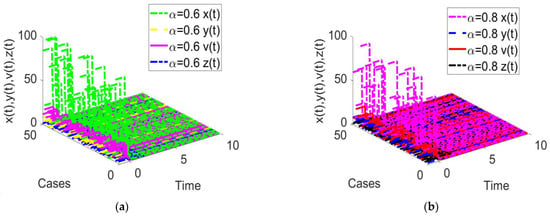
Figure 10.
Time response of the fractional-order HIV-1 infection model with a time delay when . Each subfigures (a,b) represent the time response of the system in a different fractional order.
In light of the time responses, we were able to draw the conclusion that the controlled fractional-order HIV-1 infection model could quickly converge and had almost no overshoot. This showed that our control strategy was effective and had a fast control rate and high control accuracy. Then, we conducted control strategy verification experiments on the controlled fractional-order HIV-1 infection model with a time delay. The structural parameter values are shown in Table 2.

Table 2.
The structural parameters of the fractional-order HIV-1 infection model with a time delay.
According to (Equation (41)) and the control strategy in Theorem 2, could be selected as 1.5, and the control gain could be set to
Then, according to (Equation (43)), we had
Obviously, it can be determined via a calculation that is an Then, for the purpose of further expounding on the universality of our new control strategy, 50 groups of initial values were selected arbitrarily. The state curves of the controlled fractional-order HIV-1 infection model with a time delay are demonstrated below.
From the time responses, the same result could be obtained. Without loss of generality, another time delay was selected randomly, and 50 groups of initial values were also chosen; the corresponding state curves of the controlled fractional-order HIV-1 infection model with a time delay are demonstrated below.
From the time responses, the same result could be obtained. To further verify the robustness of our control strategy, a larger time delay of was set, and the corresponding state curves of the controlled fractional-order HIV-1 infection model with a time delay are demonstrated below.
The same conclusion could be clearly obtained, as shown from the time responses in Figure 11.
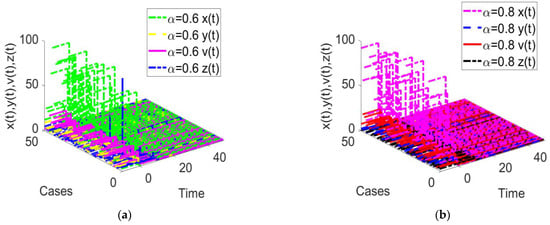
Figure 11.
Time response of the fractional-order HIV-1 infection model with a time delay when . Each subfigures (a,b) represent the time response of the system in a different fractional order.
5. Conclusions
In summary, we first applied a combination of a vector Lyapunov function and the M-matrix measure to a fractional-order HIV-1 infection model. Also, we conducted asymptotic stabilization control to design two new control strategies for situations with or without a time delay. At the same time, we proposed a corresponding asymptotic stabilization criterion. The experimental consequences clearly revealed that our proposed measure had outstanding effectiveness and universality for fractional-order HIV-1 infection models. When different initial values and time delays were selected, the controlled system could always achieve asymptotic stability. This method is helpful for revealing the infection process of HIV-1 and provides a new theoretical basis for controlling the infection rate of the virus. However, in this study, we only analyzed the case of a constant delay and did not consider a fluctuating delay. Therefore, in future work, we will focus on the case with a variable time lag.
Author Contributions
Conceptualization, Z.L.; methodology, Z.L.; validation, Z.L. and Z.Z.; writing—original draft preparation, Z.L.; writing—review and editing, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by China Postdoctoral Science Special Foundation (Grant Number: 2021TQ0102), National Natural Science Foundation of China (Grant Number: 62203158), Changsha Natural Science Foundation (Grant Number: kq2202175) and National Natural Science Foundation of Hunan Province (Grant Number: 2023JJ40182).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- González, S.F.; Martín, G.J. The neuropathogenesis of AIDS. Nat. Rev. Immunol. 2005, 5, 6981. [Google Scholar]
- Cantara, W.A.; Pathirage, C.; Hatterschide, J.; Olson, E.D.; Musier-Forsyth, K. Phosphomimetic S207D Lysyl–tRNA synthetase binds HIV-1 5′ UTR in an open conformation and increases RNA dynamics. Viruses 2022, 14, 1556. [Google Scholar] [CrossRef] [PubMed]
- AlShamrani, N.H.; Alshaikh, M.A.; Elaiw, A.M.; Hattaf, K. Dynamics of HIV-1/HTLV-I Co-Infection Model with Humoral Immunity and Cellular Infection. Viruses 2022, 14, 1719. [Google Scholar] [CrossRef]
- Ramya, R.; Maheswari, M.C.; Krishnan, K. Modified HIV-1 infection model with delay in saturated CTL immune response. Commun. Math. Biol. Neurosci. 2022, 2022, 77. [Google Scholar]
- Gumbs, S.B.; Berdenis van Berlekom, A.; Kübler, R.; Schipper, P.J.; Gharu, L.; Boks, M.P.; Ormel, P.R.; Wensing, A.M.; de Witte, L.D.; Nijhuis, M. Characterization of HIV-1 infection in microglia-containing human cerebral organoids. Viruses 2022, 14, 829. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Zankharia, U.; Vladimirova, O.; Yi, Y.; Collman, R.G.; Lieberman, P.M. Epigenetic Landscape of HIV-1 Infection in Primary Human Macrophage. J. Virol. 2022, 96, e00162-22. [Google Scholar] [CrossRef]
- Wang, J.; Qin, C.; Chen, Y.; Wang, X. Hopf bifurcation in a CTL-inclusive HIV-1 infection model with two time delays. Math. Biosci. Eng. 2019, 16, 2587–2612. [Google Scholar]
- Ahmad, S.; Ullah, A.; Partohaghighi, M.; Saifullah, S.; Akgül, A.; Jarad, F. Oscillatory and complex behaviour of Caputo-Fabrizio fractional order HIV-1 infection model. AIMS Math. 2021, 7, 4778–4792. [Google Scholar] [CrossRef]
- Shrivastava, S.; Ray, R.M.; Holguin, L.; Echavarria, L.; Grepo, N.; Scott, T.A.; Burnett, J.; Morris, K.V. Exosome-mediated stable epigenetic repression of HIV-1. Nat. Commun. 2021, 12, 5541. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Aljahdali, A.K.; Hobiny, A.D. Dynamical Properties of Discrete-Time HTLV-I and HIV-1 within-Host Coinfection Model. Axioms 2023, 12, 201. [Google Scholar] [CrossRef]
- Pradeesh, M.; Manivannan, A.; Lakshmanan, S.; Rihan, F.A.; Mani, P. Dynamical Analysis of Posttreatment HIV-1 Infection Model. Complexity 2022, 2022, 9752628. [Google Scholar] [CrossRef]
- Liu, X.L.; Zhu, C.C. A Non-Standard Finite Difference Scheme for a Diffusive HIV-1 Infection Model with Immune Response and Intracellular Delay. Axioms 2022, 11, 129. [Google Scholar] [CrossRef]
- Dubey, P.; Dubey, U.S.; Dubey, B. Modeling the role of acquired immune responseand antiretroviral therapy in the dynamics of HIV infection. Math. Comput. Simul. 2018, 144, 120–137. [Google Scholar] [CrossRef]
- Brociek, R.; Wajda, A.; Słota, D. Comparison of heuristic algorithms in identification of parameters of anomalous diffusion model based on measurements from sensors. Sensors 2023, 23, 1722. [Google Scholar] [CrossRef]
- Brociek, R.; Słota, D.; Król, M.; Matula, G.; Kwaśny, W. Modeling of heat distribution in porous aluminum using fractional differential equation. Fractal Fract. 2017, 1, 17. [Google Scholar] [CrossRef]
- Abbas, S.; Tyagi, S.; Kumar, P.; Ertürk, V.S.; Momani, S. Stability and bifurcation analysis of a fractional-order model of cell-to-cell spread of HIV-1 with a discrete time delay. Math. Methods Appl. Sci. 2022, 45, 7081–7095. [Google Scholar] [CrossRef]
- Naik, P.A.; Owolabi, K.M.; Yavuz, M.; Zu, J. Chaotic dynamics of a fractional order HIV-1 model involving AIDS-related cancer cells. Chaos Solitons Fractals 2020, 140, 110272. [Google Scholar] [CrossRef]
- Wu, Y.; Ahmad, S.; Ullah, A.; Shah, K. Study of the fractional-order HIV-1 infection model with uncertainty in initial data. Math. Probl. Eng. 2022, 2022, 7286460. [Google Scholar] [CrossRef]
- Arafa AA, M.; Rida, S.Z.; Khalil, M. A fractional-order model of HIV infection: Numerical solution and comparisons with data of patients. Int. J. Biomath. 2014, 7, 1450036. [Google Scholar] [CrossRef]
- Virgin, H.W.; Walker, B.D. Immunology and the elusive AIDS vaccine. Nature 2010, 464, 224–231. [Google Scholar] [CrossRef]
- Rong, L.B.; Gilchrist, M.A.; Feng, Z.L.; Perelson, A.S. Modeling within-host HIV-1 dynamics and the evolution of drug resistance: Trade-offs between viral enzyme function and drug susceptibility. J. Theor. Biol. 2007, 247, 804–818. [Google Scholar] [CrossRef]
- Shu, H.Y.; Wang, L.; Watmough, J. Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL immune responses. SIAM J. Appl. Math. 2013, 73, 1280–1302. [Google Scholar] [CrossRef]
- Lv, C.F.; Huang, L.H.; Yuan, Z.H. Global stability for an HIV-1 infection model with Beddington-De Angelis incidence rate and CTL immune response. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 121–127. [Google Scholar] [CrossRef]
- Li, M.Y.; Shu, H.Y. Multiple Stable Periodic Oscillations in a Mathematical Model of CTL Response to HTLV-I Infection. Bull. Math. Biol. 2011, 73, 1774–1793. [Google Scholar] [CrossRef] [PubMed]
- Zhe, Z.; Ushio, T.; Jing, Z.; Wang, Y. A novel asymptotic stability condition for a delayed distributed order nonlinear composite system with uncertain fractional order. J. Frankl. Inst. 2022, 359, 10986–11006. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Cheng, F.; Liu, F.; Ding, C. Dynamic analysis of a novel time-lag four-dimensional fractional-order financial system. Asian J. Control. 2021, 23, 536–547. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Zhang, J.; Zhang, H.; Ai, Z.; Liu, K.; Liu, F. Asymptotic stabilization control of fractional-order memristor-based neural networks system via combining vector Lyapunov function with M-matrix. IEEE Trans. Syst. Man Cybern. Syst. 2022, 53, 1734–1747. [Google Scholar] [CrossRef]
- Zhe, Z.; Yaonan, W.; Jing, Z.; Ai, Z.; Cheng, F.; Liu, F. Novel fractional-order decentralized control for nonlinear fractional-order composite systems with time delays. ISA Trans. 2022, 128, 230–242. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Ai, Z.; Cheng, F.; Liu, F. A novel general stability criterion of time-delay fractional-order nonlinear systems based on WILL Deduction Method. Math. Comput. Simul. 2020, 178, 328–344. [Google Scholar] [CrossRef]
- Zhang, Z.; Ai, Z.; Zhang, J.; Cheng, F.; Liu, F.; Ding, C. A general stability criterion for multidimensional fractional-order network systems based on whole oscillation principle for small fractional-order operators. Chaos Solitons Fractals 2020, 131, 109506. [Google Scholar] [CrossRef]
- Chefnaj, N.; Taqbibt, A.; Hilal, K.; Melliani, S.; Kajouni, A. Boundary Value Problems for Differential Equations Involving the Generalized Caputo-Fabrizio Fractional Derivative in λ-Metric Space. Turk. J. Sci. 2023, 8, 24–36. [Google Scholar]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar] [CrossRef]
- Bayrak, M.A.; Demir, A. On the challenge of identifying space dependent coefficient in spacetime fractional diffusion equations by fractional scaling transformations method. Turk. J. Sci. 2022, 7, 132–145. [Google Scholar]
- Dokuyucu, M.A. Analysis of a novel finance chaotic model via ABC fractional derivative. Numer. Methods Partial. Differ. Equ. 2021, 37, 1583–1590. [Google Scholar] [CrossRef]
- İlhan, E. Analysis of the spread of Hookworm infection with Caputo-Fabrizio fractional derivative. Turk. J. Sci. 2022, 7, 43–52. [Google Scholar]
- Liu, D.; Li, T.; Wang, Y. Adaptive Dual Synchronization of Fractional-Order Chaotic System with Uncertain Parameters. Mathematics 2022, 10, 470. [Google Scholar] [CrossRef]
- Nuez-Perez, J.C.; Adeyemi, V.A.; Sandoval-Ibarra, Y.; Perez-Pinal, F.-J.; Tlelo-Cuautle, E. Maximizing the Chaotic Behavior of Fractional Order Chen System by Evolutionary Algorithms. Mathematics 2021, 9, 1194. [Google Scholar] [CrossRef]
- Alesemi, M.; Iqbal, N.; Botmart, T. Novel Analysis of the Fractional-Order System of Non-Linear Partial Differential Equations with the Exponential-Decay Kernel. Mathematics 2022, 10, 615. [Google Scholar] [CrossRef]
- Motorga, R.; Murean, V.; Ungurean, M.L.; Abrudean, M.; Vălean, H.; Clitan, I. Artificial Intelligence in Fractional-Order Systems Approximation with High Performances: Application in Modelling of an Isotopic Separation Process. Mathematics 2022, 10, 1459. [Google Scholar] [CrossRef]
- Ding, Q.; Abba, O.A.; Jahanshahi, H.; Alassafi, M.O.; Huang, W.H. Dynamical Investigation, Electronic Circuit Realization and Emulation of a Fractional-Order Chaotic Three-Echelon Supply Chain System. Mathematics 2022, 10, 625. [Google Scholar] [CrossRef]
- Culshaw, R.V.; Ruan, S. A delay-di erential equation model of HIV infection of CD4 T-cells. Math. Biosci. 2000, 165, 27–39. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Ye, H. A fractional-order differential equation model of HIV infection of CD4+ T-cells. Math. Comput. Model. 2009, 50, 386–392. [Google Scholar] [CrossRef]
- Yan, Y.; Kou, C. Stability analysis for a fractional differential model of HIV infection of CD4+ T-cells with time delay. Math. Comput. Simul. 2012, 82, 1572–1585. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D. A new fractional analysis on the interaction of HIV with CD4+ T-cells. Chaos Solitons Fractals 2018, 113, 221–229. [Google Scholar] [CrossRef]
- Cole, K.S. Electric conductance of biological systems//Cold Spring Harbor symposia on quantitative biology. Cold Spring Harb. Lab. Press 1933, 1, 107–116. [Google Scholar] [CrossRef]
- Anastasio, T.J. The fractional-order dynamics of brainstem vestibulo-oculomotor neurons. Biol. Cybern. 1994, 72, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Zhou, X.F.; Zhang, Z.; Liu, S. Lyapunov method for nonlinear fractional differential systems with delay. Nonlinear Dyn. 2015, 82, 1015–1025. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag–Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Siljak, D.D. Decentralized Control of Complex Systems; Courier Corporation: North Chelmsford, MA, USA, 2011. [Google Scholar]
- Azoz, S.; Hussien, F.; Abdelsamea, H. Analysis of a fractional order HIV-1 infection model with saturated immune response. Assiut Univ. J. Multidiscip. Sci. Res. 2023, 52, 23–47. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).