A Novel Non-Ferrous Metals Price Forecast Model Based on LSTM and Multivariate Mode Decomposition
Abstract
1. Introduction
1.1. Background
1.2. Related Literature
1.2.1. Single Model Based Prediction
1.2.2. Fusion Model Based Prediction
1.3. Research Organization
2. Fundamental Method
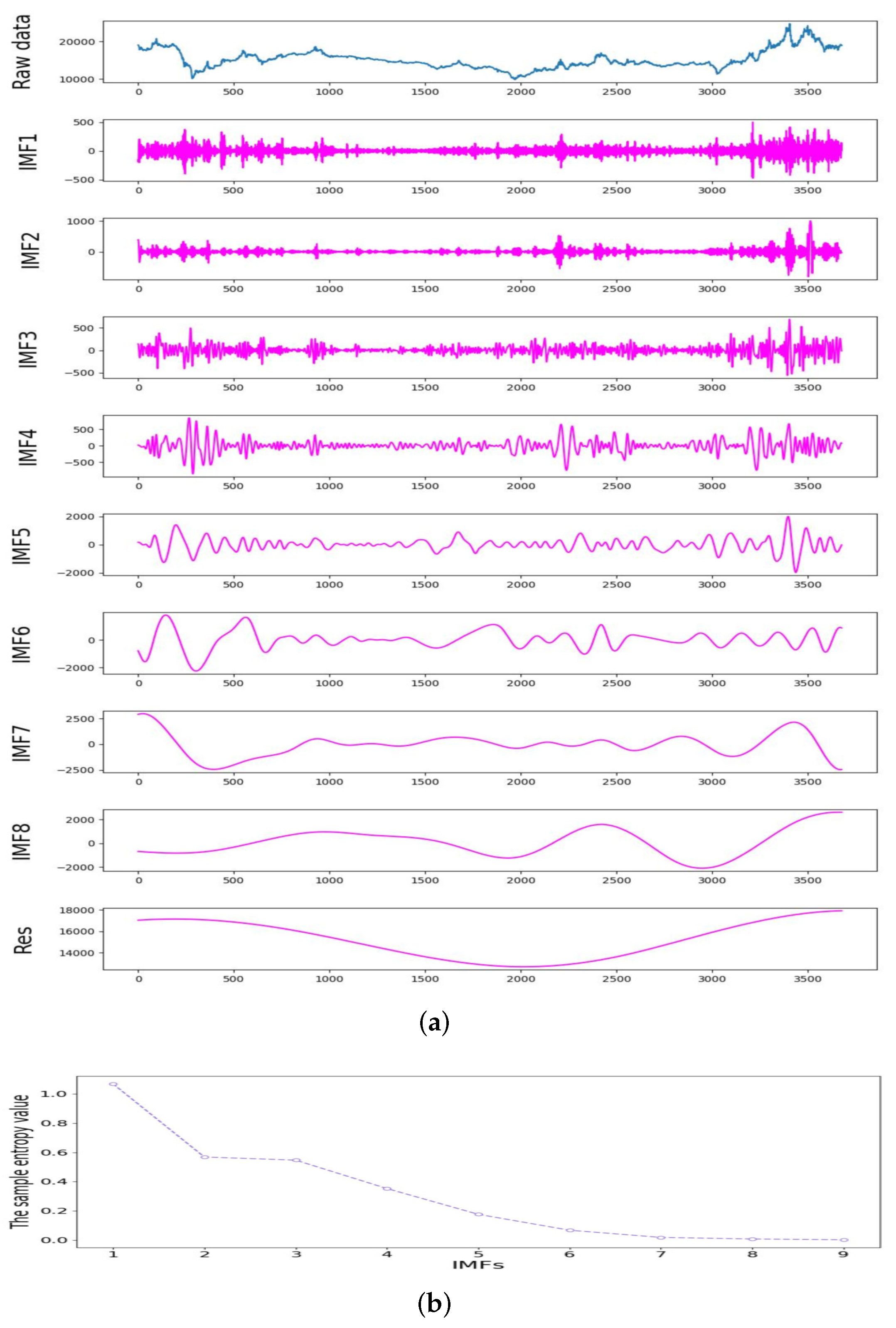
2.1. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise
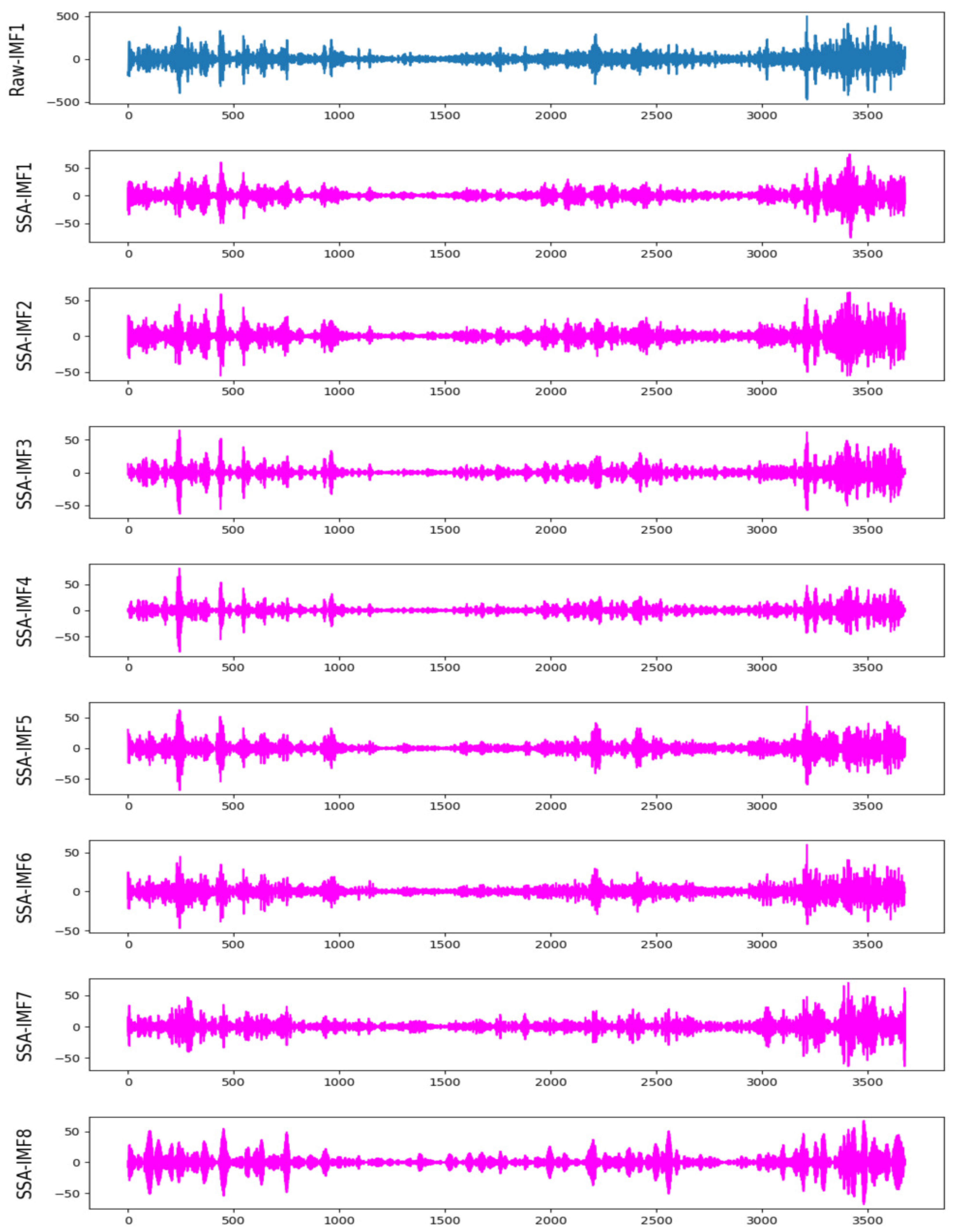
2.2. Singular Spectrum Analysis
- (a)
- Transfer into a time series by diagonal averaging:where .
- (b)
- The sum of all the reconstructed sequences should be equal to the original sequence, i.e.,
2.3. Sample Entropy
2.4. Sparrow Search Algorithm
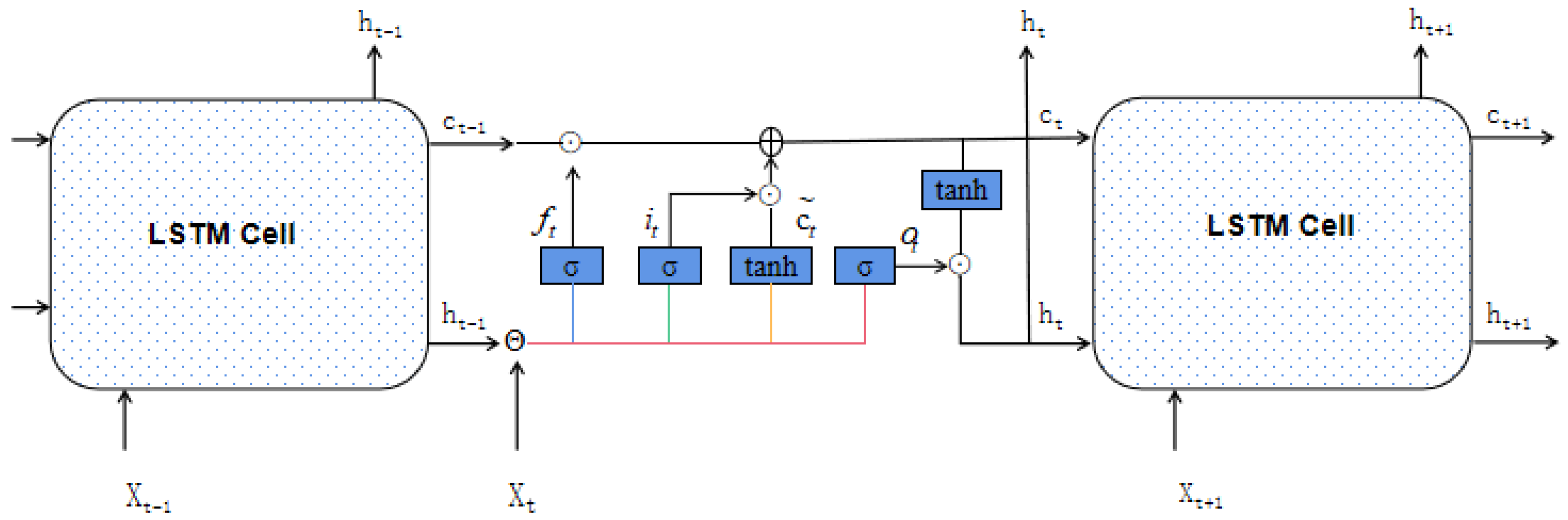
2.5. LSTM Network
3. The Proposed Method
3.1. Multivariate Mode Decomposition
| Algorithm 1: Dual-stage decomposition |
Input: The original non-ferrous metal price. Output: Several IMFs and a residual. Step 1: Apply CEEMDAN algorithm to decompose original price series into several IMFs and a residual, namely IMF1, IMF2, …, IMFX and Res. The specific decomposition process is referred to Section 2.1. Step 2: Compute the sample entropy of each subsequence. The specific calculation process is referred to Section 2.3. Step 3: Select the subsequence IMFX with maximum sample entropy, and apply SSA algorithm to decompose it into several SSA-IMFs. The specific decomposition process is referred to Section 2.2. |
3.2. Metals Price Forecast
| Algorithm 2: Non-ferrous metal price forecast based on LSTM network |
Input: All subsequence of original non-ferrous metal price. Output: The forecast result of non-ferrous metal price. Training stage Step 1: For each subsequence, normalize the dataset as well as divide it into training dataset and testing dataset. Step 2: Set the time step, namely the former 21 points predict the 22th point. Step 3: Build LSTM network and set its parameters, including network structure, optimizer, learning rate, loss function, the number of iteration and batchsize. Among them, the number of hidden neurons and learning rate are optimized by sparrow search algorithm. Step 4: Train LSTM network. Prediction stage Step 5: Apply the trained model to predict, then make the inverse normalization about forecast results. Step 6: Sum the forecast result of each subsequence as the final predicted value. |
4. Experiments Study
4.1. Data Description
4.2. Evaluation Criteria of Performance
4.3. Related Parameters
4.4. Empirical Results and Analysis
4.4.1. Multivariate Mode Decomposition Results
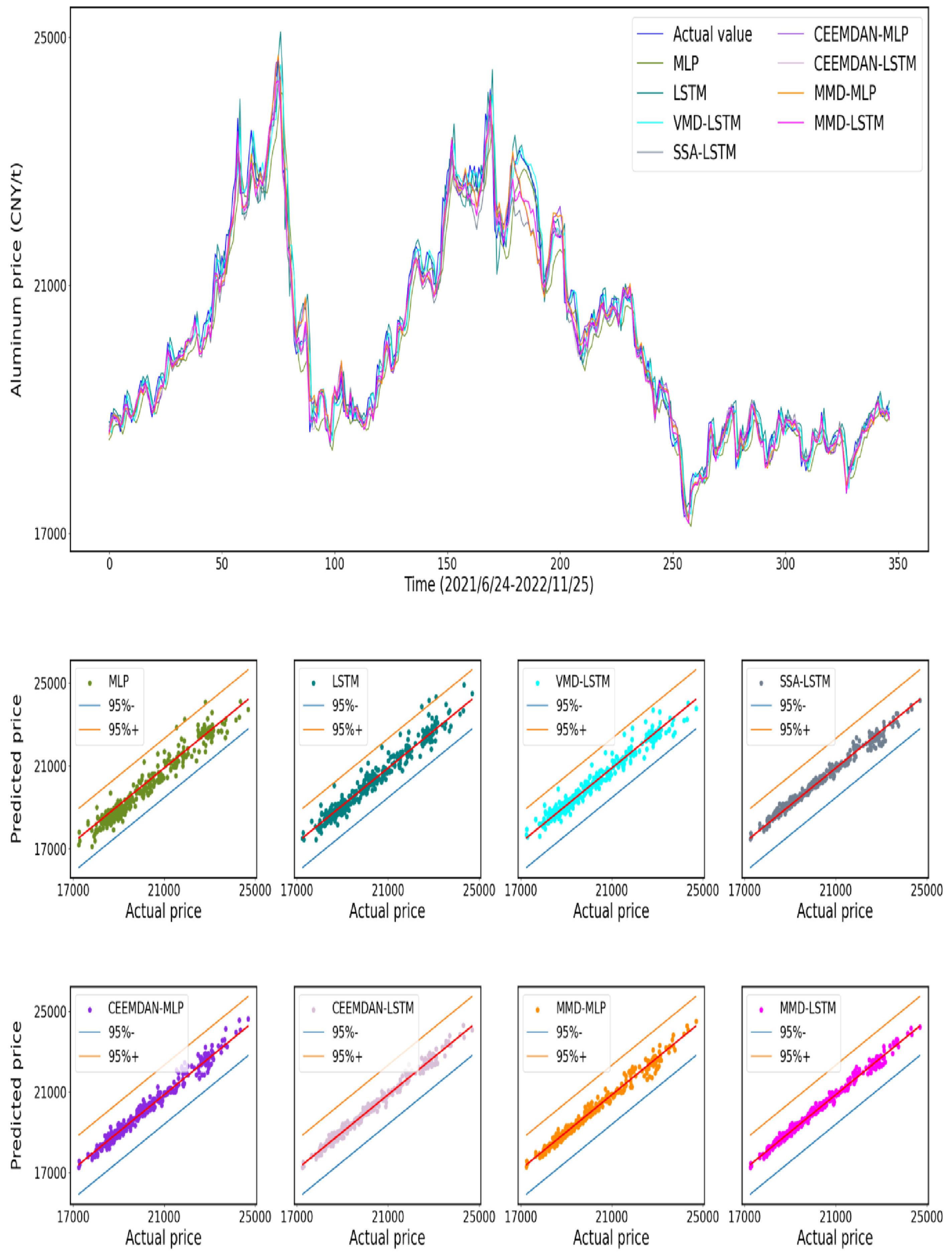
4.4.2. Analysis of Forecast Results
4.4.3. Analysis of Statistics
5. Conclusions
6. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SD | Standard Deviation |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| ARIMA | Autoregressive Integrated Moving Average |
| GARCH | Generalized Autoregressive Conditional Heteroskedasticity |
| ANN | Artificial Neural Network |
| MLP | Multi-Layer Perceptron |
| CNN | Convolutional Neural Network |
| ELM | Extreme Learning Machine |
| SVM | Support Vector Machine |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| SSO | Sparrow Search Optimization |
| SSA | Singular Spectrum Analysis |
| MMD | Multivariate Mode Decomposition |
| EMD | Empirical Mode Decomposition |
| EEMD | Ensemble Empirical Mode Decomposition |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
Appendix A
| Metals | Models | RMSE | MAE | MAPE(%) | |
|---|---|---|---|---|---|
| Copper | MLP | 1111.9553 | 903.2919 | 1.3233 | 0.9389 |
| LSTM | 836.6295 | 633.7231 | 0.9452 | 0.9654 | |
| VMD-LSTM | 740.8218 | 555.5603 | 0.8238 | 0.9665 | |
| SSA-LSTM | 764.3102 | 545.408 | 0.8217 | 0.9711 | |
| CEEMDAN-MLP | 537.9811 | 423.3759 | 0.6307 | 0.9856 | |
| CEEMDAN-LSTM | 524.3169 | 411.9391 | 0.6101 | 0.9864 | |
| MMD-MLP | 443.2475 | 357.9791 | 0.5306 | 0.9902 | |
| MMD-LSTM | 435.5633 | 352.4775 | 0.5167 | 0.9906 | |
| Zinc | MLP | 463.8865 | 334.9679 | 1.3571 | 0.9127 |
| LSTM | 429.8289 | 299.0934 | 1.2194 | 0.9251 | |
| VMD-LSTM | 407.9518 | 282.3788 | 1.1504 | 0.9325 | |
| SSA-LSTM | 256.5028 | 189.0633 | 0.7684 | 0.9733 | |
| CEEMDAN-MLP | 268.7251 | 204.0592 | 0.8297 | 0.9707 | |
| CEEMDAN-LSTM | 250.2042 | 188.0501 | 0.7693 | 0.9746 | |
| MMD-MLP | 239.2537 | 181.464 | 0.7374 | 0.9767 | |
| MMD-LSTM | 209.4423 | 153.0592 | 0.6266 | 0.9822 |
| Non-Ferrous Metals | Models | Wilcoxon Signed-Rank Test | |
|---|---|---|---|
| W = 100 | p-Value | ||
| Copper | MLP | 0 | 0.000000 |
| LSTM | 0 | 0.000002 | |
| VMD-LSTM | 22 | 0.000372 | |
| SSA-LSTM | 43 | 0.000905 | |
| CEEMDAN-MLP | 56 | 0.002495 | |
| CEEMDAN-LSTM | 81 | 0.008776 | |
| MMD-MLP | 134 | 0.077883 | |
| Zinc | MLP | 0 | 0.000000 |
| LSTM | 73 | 0.007916 | |
| VMD-LSTM | 56 | 0.002537 | |
| SSA-LSTM | 15 | 0.000153 | |
| CEEMDAN-MLP | 0 | 0.000000 | |
| CEEMDAN-LSTM | 57 | 0.004081 | |
| MMD-MLP | 23 | 0.000420 | |
Appendix B
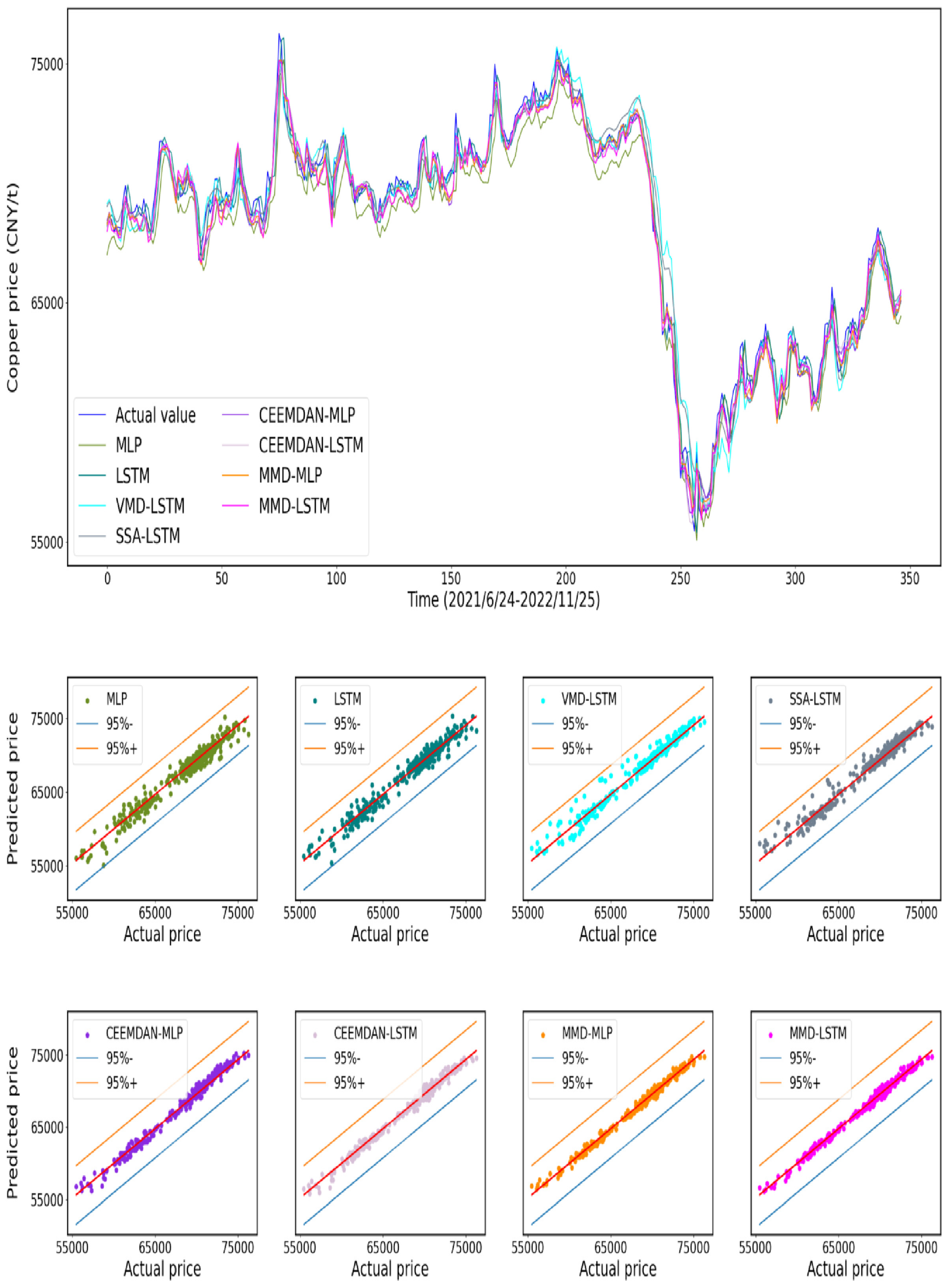
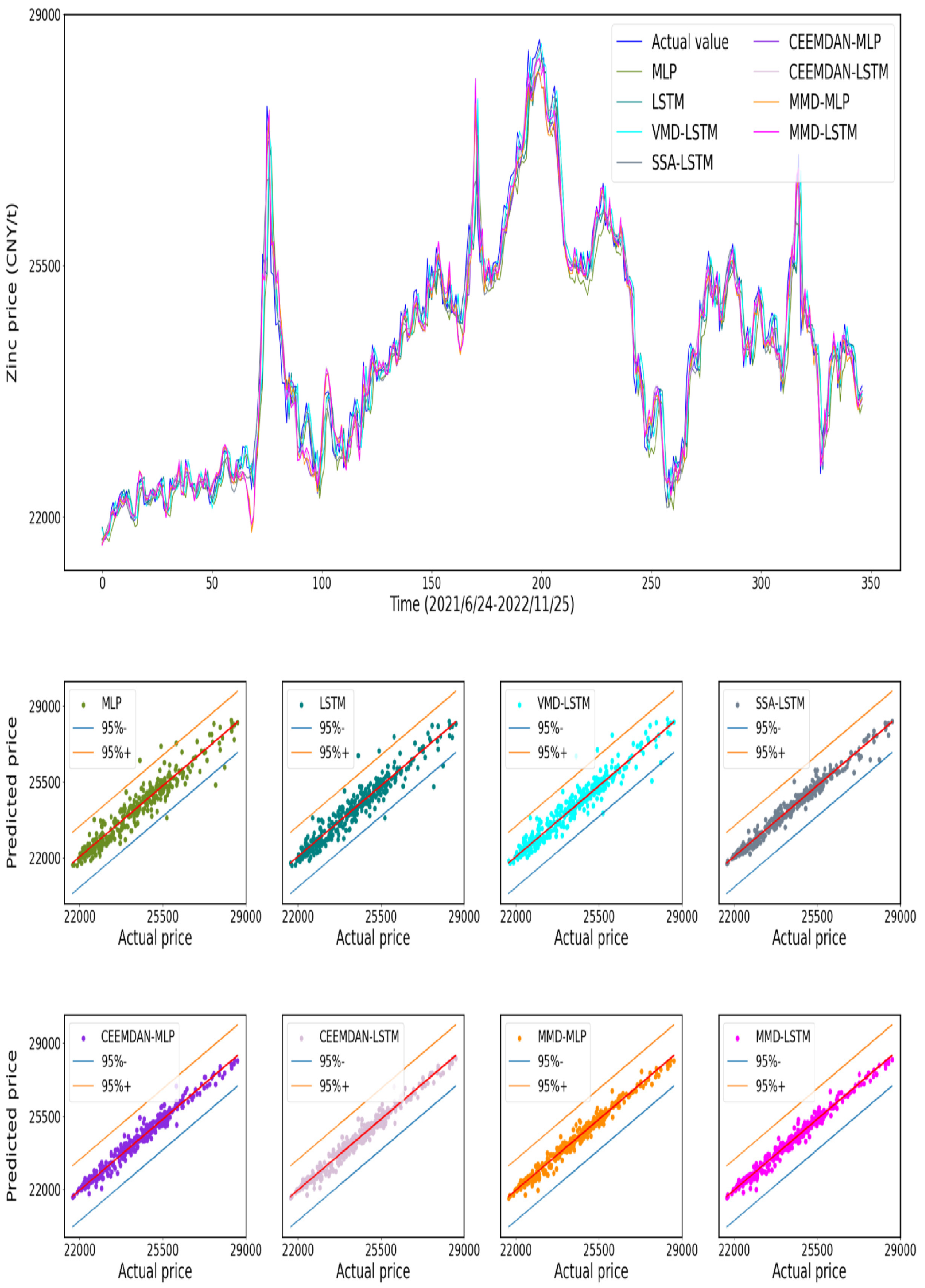
References
- Ron, A.; Bhattarai, S.; Coibion, O. Commodity-price comovement and global economic activity. J. Monet. Econ. 2020, 112, 41–56. [Google Scholar]
- Gil, C. Algorithmic Strategies for Precious Metals Price Forecasting. Mathematics 2022, 10, 1134. [Google Scholar]
- Garcĺa, D.; Kristjanpoller, W. An adaptive forecasting approach for copper price volatility through hybrid and non-hybrid models. Appl. Soft Comput. 2019, 74, 466–478. [Google Scholar] [CrossRef]
- Gillian, D.; Lenihan, H. An assessment of time series methods in metal price forecasting. Resour. Policy 2005, 30, 208–217. [Google Scholar]
- Sungdo, K.; Min, M.B.; Joo, B.S. Data depth based support vector machines for predicting corporate bankruptcy. Appl. Intell. 2018, 48, 791–804. [Google Scholar]
- Yusheng, H.; Gao, Y.; Gan, Y.; Ye, M. A new financial data forecasting model using genetic algorithm and long short-term memory network. Neurocomputing 2021, 425, 207–218. [Google Scholar]
- Yunlei, Y.; Yang, W.; Muzhou, H.; Lou, J.; Xie, X. Solving Emden-Fowler Equations Using Improved Extreme Learning Machine Algorithm Based on Block Legendre Basis Neural Network. Neural Process. Lett. 2023, 1–20. [Google Scholar]
- Liu, C.; Hu, Z.; Li, Y.; Liu, S. Forecasting copper prices by decision tree learning. Resour. Policy 2017, 52, 427–434. [Google Scholar] [CrossRef]
- Pinyi, Z.; Ci, B. Deep belief network for gold price forecasting. Resour. Policy 2020, 69, 101806. [Google Scholar]
- Chen, Y.; Wang, D.; Kai, C.; Pan, C.; Yu, Y.; Hou, M. Prediction of safety parameters of pressurized water reactor based on feature fusion neural network. Ann. Nucl. Energy 2022, 166, 108803. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, M.; Zhou, H.; Yan, F. A multi-model fusion based non-ferrous metal price forecasting. Resour. Policy 2022, 77, 102714. [Google Scholar] [CrossRef]
- Dehghani, H.; Bogdanovic, D. Copper price estimation using bat algorithm. Resour. Policy 2018, 55, 55–61. [Google Scholar] [CrossRef]
- Bilin, S.; Maolin, L.; Yu, Z.; Genqing, B. Nickel Price Forecast Based on the LSTM Neural Network Optimized by the Improved PSO Algorithm. Math. Probl. Eng. 2019, 2019, 1934796. [Google Scholar]
- Roslindar, Y.S.; Zakaria, R. ARIMA and Symmetric GARCH-type Models in Forecasting Malaysia Gold Price. J. Phys. Conf. Ser. 2019, 1366, 012126. [Google Scholar]
- Hou, M.; Liu, T.; Yang, Y.; Hao, Z.; Hongjuan, L.; Xiugui, Y.; Xinge, L. A new hybrid constructive neural network method for impacting and its application on tungsten price prediction. Appl. Intell. 2017, 47, 28–43. [Google Scholar]
- Andrés, V.; Werner, K. Gold Volatility Prediction using a CNN-LSTM approach. Expert Syst. Appl. 2020, 157, 113481. [Google Scholar]
- Hu, Y.; Ni, J.; Wen, L. A hybrid deep learning approach by integrating LSTM-ANN networks with GARCH model for copper price volatility prediction. Phys. A Stat. Mech. Its Appl. 2020, 557, 124907. [Google Scholar] [CrossRef]
- Chu, Z.; Muhammad, S.N.; Tian, P.; Hua, L.; Ji, C. An evolutionary robust solar radiation prediction model based on WT-CEEMDAN and IASO-optimized outlier robust extreme learning machine. Appl. Energy 2022, 322, 119518. [Google Scholar]
- Wang, J.; Li, X. A combined neural network model for commodity price forecasting with SSA. Soft Comput. 2018, 22, 5323–5333. [Google Scholar] [CrossRef]
- Zhou, S.; Lai, K.K.; Yen, J. A dynamic meta-learning rate-based model for gold market forecasting. Expert Syst. Appl. 2012, 39, 6168–6173. [Google Scholar] [CrossRef]
- Ming, L.; Yang, S.; Cheng, C. The double nature of the price of gold-A quantitative analysis based on Ensemble Empirical Mode Decomposition. Resour. Policy 2016, 47, 125–131. [Google Scholar] [CrossRef]
- Wen, F.; Yang, X.; Gong, X.; Lai, K.K. Multi-Scale Volatility Feature Analysis and Prediction of Gold Price. Int. J. Inf. Technol. Decis. Mak. 2017, 16, 205–223. [Google Scholar] [CrossRef]
- Lahmiri, S. Long memory in international financial markets trends and short movements during 2008 financial crisis based on variational mode decomposition and detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2015, 437, 130–138. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Huang, K.; Gui, W. Non-ferrous metals price forecasting based on variational mode decomposition and LSTM network. Knowl. Based Syst. 2019, 188, 105006. [Google Scholar] [CrossRef]
- Feite, Z.; Zhehao, H.; Changhong, Z. Carbon price forecasting based on CEEMDAN and LSTM. Appl. Energy 2022, 311, 118601. [Google Scholar]
- Wei, S.; Wang, X.; Tan, B. Multi-step wind speed forecasting based on a hybrid decomposition technique and an improved back-propagation neural network. Environ. Sci. Pollut. Res. 2022, 49, 684–699. [Google Scholar]
- Zhaohua, W.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. Complementary ensemble empirical mode decom-position: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Peng, D.; Xiu, N.; Yu, J. Global Optimality Condition and Fixed Point Continuation Algorithm for Non-Lipschitz lp Regularized Matrix Minimization. Sci. China Math. 2018, 61, 1139–1152. [Google Scholar] [CrossRef]
- Yan, X.; Weihan, W.; Chang, M. Research on financial assets transaction prediction model based on LSTM neural network. Neural. Comput. Appl. 2020, 33, 257–270. [Google Scholar] [CrossRef]
- Cao, X.; Fekan, M.; Shen, D.; Wang, J. Iterative learning control for multi-agent systems with impulsive consensus tracking. Nonlinear Anal. Model. 2021, 26, 130–150. [Google Scholar] [CrossRef]
- Yu, C.; Zhao, Y.; Qi, X.; Ma, H.; Wang, C. LLR: Learning learning rates by LSTM for training neural networks. Neurocomputing 2020, 394, 41–50. [Google Scholar] [CrossRef]
- He, Q.; Wang, Y. Reparameterized full-waveform inversion using deep neural networks. Geophysics 2021, 86, 1–13. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Li, Y.; Fan, C.; Li, Y.; Wu, Q.; Ming, Y. Improving deep neural network with multiple parametric exponential linear units. Neurocomputing 2018, 301, 11–24. [Google Scholar] [CrossRef]
- Hou, M.; Lv, W.; Kong, M.; Li, R.; Liu, Z.; Wang, D.; Wang, J.; Chen, Y. Efficient predictor of pressurized water reactor safety parameters by topological information embedded convolutional neural network. Ann. Nucl. Energy. 2023, 192, 110004. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, J.; Zhang, Z.; Wei, D.; Yin, L. Short-term PV power forecasting based on time series expansion and high-order fuzzy cognitive maps. Appl. Soft Comput. 2023, 135, 110037. [Google Scholar] [CrossRef]
- Li, M.-W.; Xu, D.-Y.; Jing, G.; Hong, W.-C. A hybrid approach for forecasting ship motion using CNN-GRU-AM and GCWOA. Appl. Soft Comput. 2022, 114, 108084. [Google Scholar] [CrossRef]

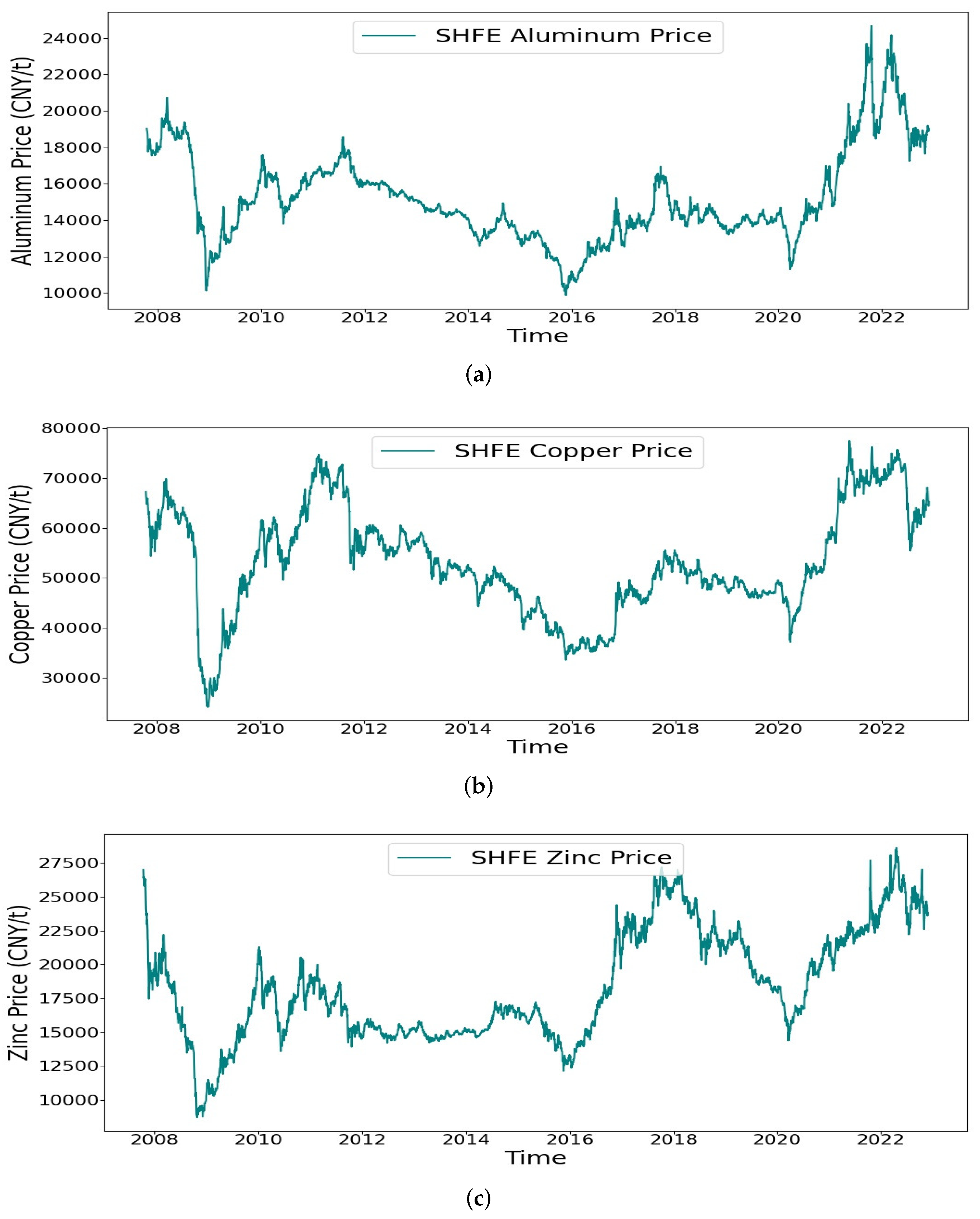
| Related Parameters | Value | Description |
|---|---|---|
| Validation split | 0.1 | The proportion of a training set used to validate during training. |
| Shuffle | True | Whether to randomly disrupt the order of input samples during training. |
| Epochs | 100 | How many times that a complete dataset passes the neural network once and returns during training. |
| Batch size | 16 | The number of samples contained in each batch when performing gradient descent. |
| Cells | 32 | The number of neurons in the hidden layer. |
| Activation | SeLU | The activation function for connected layer. |
| Optimizer | Nadam | The optimization method, here its loss is MSE. |
| Callbacks | / | ReduceLROnPlateau and EarlyStopping mechanisms of Keras are used for improvement. |
| Patience | 20,30 | The epochs for the model to perform the callbacks operations, one-tenth of the total epochs for reducing learning rate and a half for the early stop. |
| Models | RMSE | MAE | MAPE(%) | |
|---|---|---|---|---|
| MLP | 405.5379 | 312.0251 | 1.5204 | 0.9415 |
| LSTM | 362.5705 | 258.0344 | 1.2651 | 0.9532 |
| VMD-LSTM | 317.6078 | 223.8584 | 1.1006 | 0.9641 |
| SSA-LSTM | 280.2321 | 198.3769 | 0.9435 | 0.9721 |
| CEEMDAN-MLP | 244.8113 | 184.1368 | 0.8947 | 0.9786 |
| CEEMDAN-LSTM | 219.5632 | 163.7091 | 0.7903 | 0.9828 |
| MMD-MLP | 223.7218 | 164.3561 | 0.7953 | 0.9822 |
| MMD-LSTM | 195.6278 | 141.2734 | 0.6779 | 0.9863 |
| Non-Ferrous Metals | Models | Wilcoxon Signed-Rank Test | |
|---|---|---|---|
| W = 100 | p-Value | ||
| Aluminum | MLP | 0 | 0.000000 |
| LSTM | 0 | 0.000000 | |
| VMD-LSTM | 0 | 0.000002 | |
| SSA-LSTM | 48 | 0.00100 | |
| CEEMDAN-MLP | 22 | 0.000327 | |
| CEEMDAN-LSTM | 57 | 0.004319 | |
| MMD-MLP | 22 | 0.000131 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yang, Y.; Chen, Y.; Huang, J. A Novel Non-Ferrous Metals Price Forecast Model Based on LSTM and Multivariate Mode Decomposition. Axioms 2023, 12, 670. https://doi.org/10.3390/axioms12070670
Li Z, Yang Y, Chen Y, Huang J. A Novel Non-Ferrous Metals Price Forecast Model Based on LSTM and Multivariate Mode Decomposition. Axioms. 2023; 12(7):670. https://doi.org/10.3390/axioms12070670
Chicago/Turabian StyleLi, Zhanglong, Yunlei Yang, Yinghao Chen, and Jizhao Huang. 2023. "A Novel Non-Ferrous Metals Price Forecast Model Based on LSTM and Multivariate Mode Decomposition" Axioms 12, no. 7: 670. https://doi.org/10.3390/axioms12070670
APA StyleLi, Z., Yang, Y., Chen, Y., & Huang, J. (2023). A Novel Non-Ferrous Metals Price Forecast Model Based on LSTM and Multivariate Mode Decomposition. Axioms, 12(7), 670. https://doi.org/10.3390/axioms12070670






