In this section, a min–max algorithm is proposed to look for a subset of the robust vector equilibrium flows.
3.1. Description of the Algorithm
In this subsection, we construct an optimization problem whose solution is equivalent to the the robust vector equilibrium flow. For
, we define:
.
Proposition 1. Let be a feasible flow. The following statements are equivalent.
- (i)
is a robust vector equilibrium;
- (ii)
There exists such that it is a saddle-point of the problem, denoted as follows:
and is equal to zero. Proof. Firstly, we prove the implication
. Since
, it suffices to prove
for all
, i.e.,
. Hence, for every
,
, we consider the following term:
If for some , then by Definition 2, one has or and so . If , for some , , and hence, . By the above cases, one has for all .
Conversely, if (ii) is satisfied, is a saddle-point and . If for every , some one has , then and so . Consequently, is a robust vector equilibrium. □
Now, a min–max algorithm is proposed to solve problem (
2). In our algorithm, we select different steps for the two variables
y and
, which is different from one proposed in [
22]. In addition, we extend the search directions of the algorithm to make the search faster and more suitable for different needs. Thus, our algorithm is an improvement of that in [
22].
Direction set: The set D consist of finite unit vectors which can span . Here, in order to reduce the computational cost, we only consider some directions in D. For example, when , in this paper, let , , .
Step length: Let initial step and , . Let . If iteration is successful, i.e., for all (), then the next step length value ; if the iteration is unsuccessful, then .
Remark 2. It is worth noting that computations for and in Algorithm 1 are based on Algorithm 2.
| Algorithm 1: Min–max algorithm (Algorithm 1). |
![Axioms 12 00662 i001 Axioms 12 00662 i001]() |
| Algorithm 2: Algorithm 2 . |
![Axioms 12 00662 i002 Axioms 12 00662 i002]() |
3.2. Comparison with Other Methods
In this subsection, we will give three numerical examples to show the comparison with that of [
22]. In these numerical examples, both Algorithm 1 and the algorithm proposed in [
22] start from the same set of initial points. To make a fair comparison, all test problems are run five times to reduce the impact of randomness.
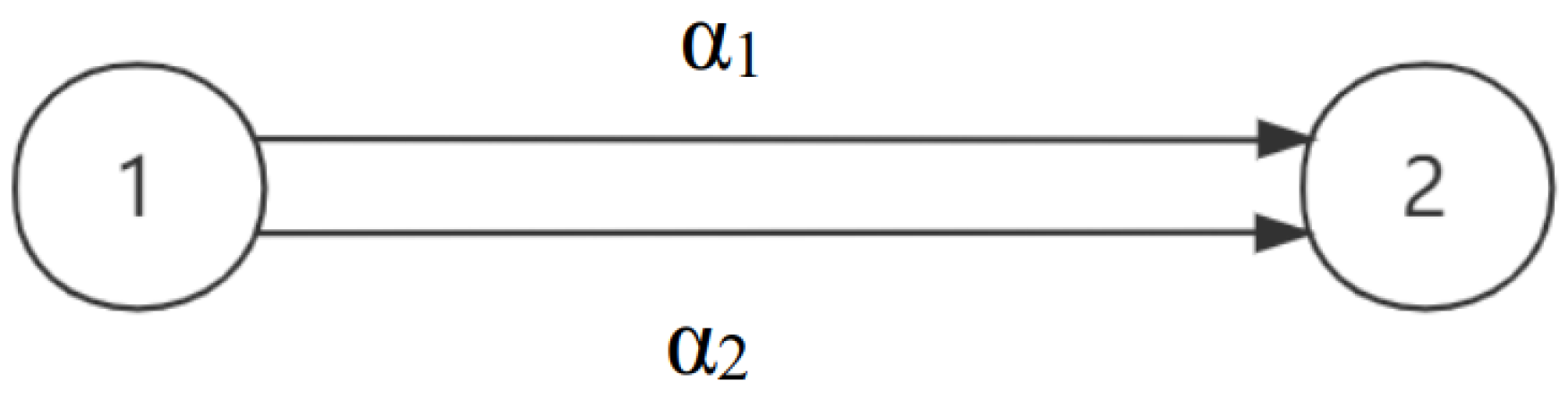
Remark 3. There is a step calculation method in reference [22]—if the iteration is successful: , , where is the largest step size; if iteration is unsuccessful: . Compared with the step calculation method in reference [22], the step calculation method presented in Algorithm 1 has better performance, since Algorithm 1 selects different step size for different variables and extends the search directions. What is more, Algorithm 1 requires neither gradient information nor redundant parameters. Example 2. Consider a network problem depicted in
Figure 1, where
. There are two criteria: travel time and travel cost. The cost functions of arcs and constraints of paths are given as bellow:
,
,
.
Then, we have:
where
and
. Initial feasible flows and a subset of the robust vector equilibrium flows are obtained in
. The results are shown in
Table 1. However, if we use step calculational method in [
22], then it takes 25.68 s and the obtain the same robust vector equilibrium flows with our algorithm.
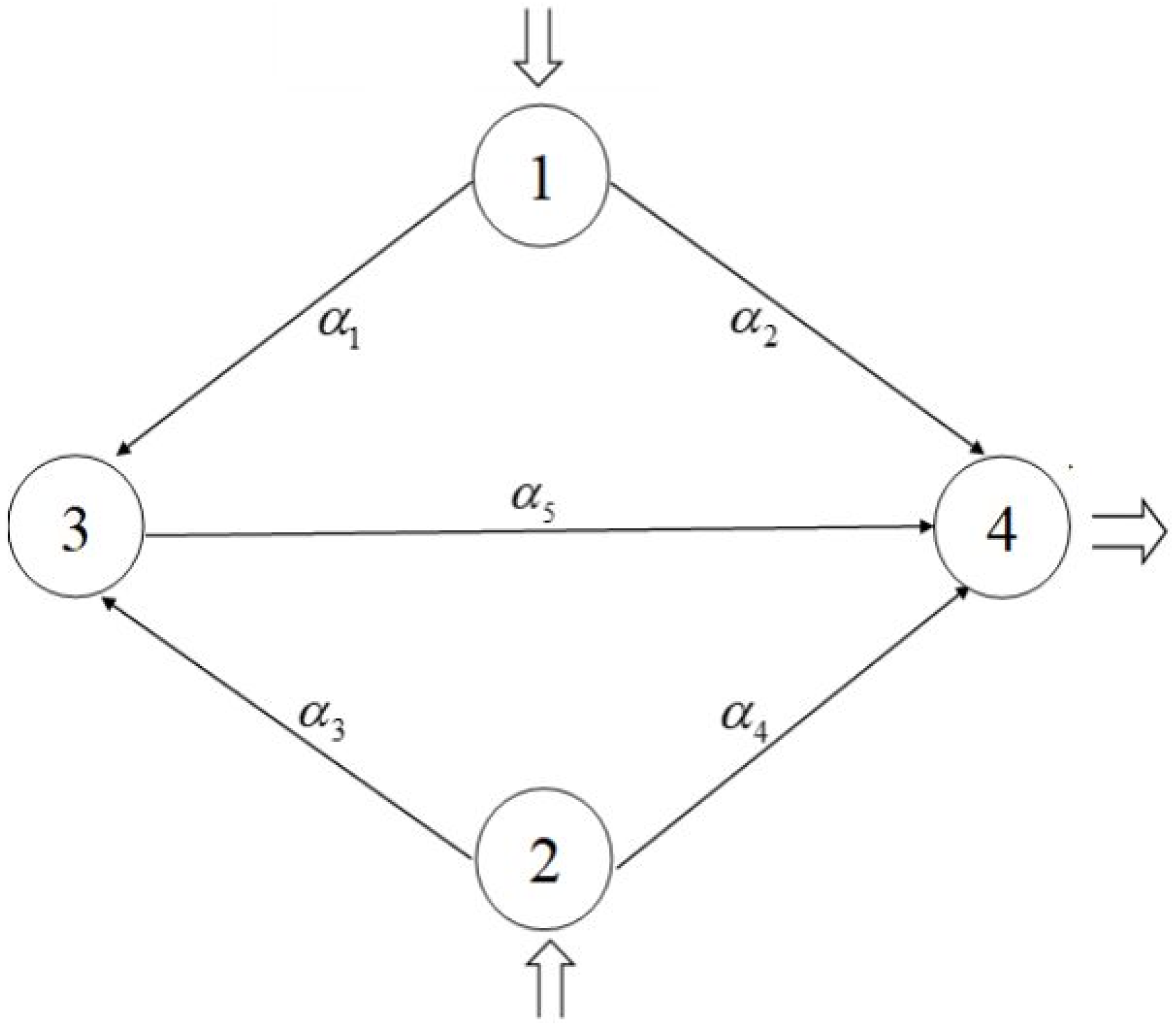
Example 3. Consider the network problem depicted in Figure 2, where , , and there are two O-D pairs, . . There are two criteria: travel time and travel cost. Constrains of paths are given as follows: The cost functions of arcs are defined as follows:
Then, we have:
where
. Initial feasible flows and a subset of the robust vector equilibrium flows are obtained in
. The results are shown in
Table 2. The time cost of Algorithm 1 is
lower than that of the step calculation method in [
22].
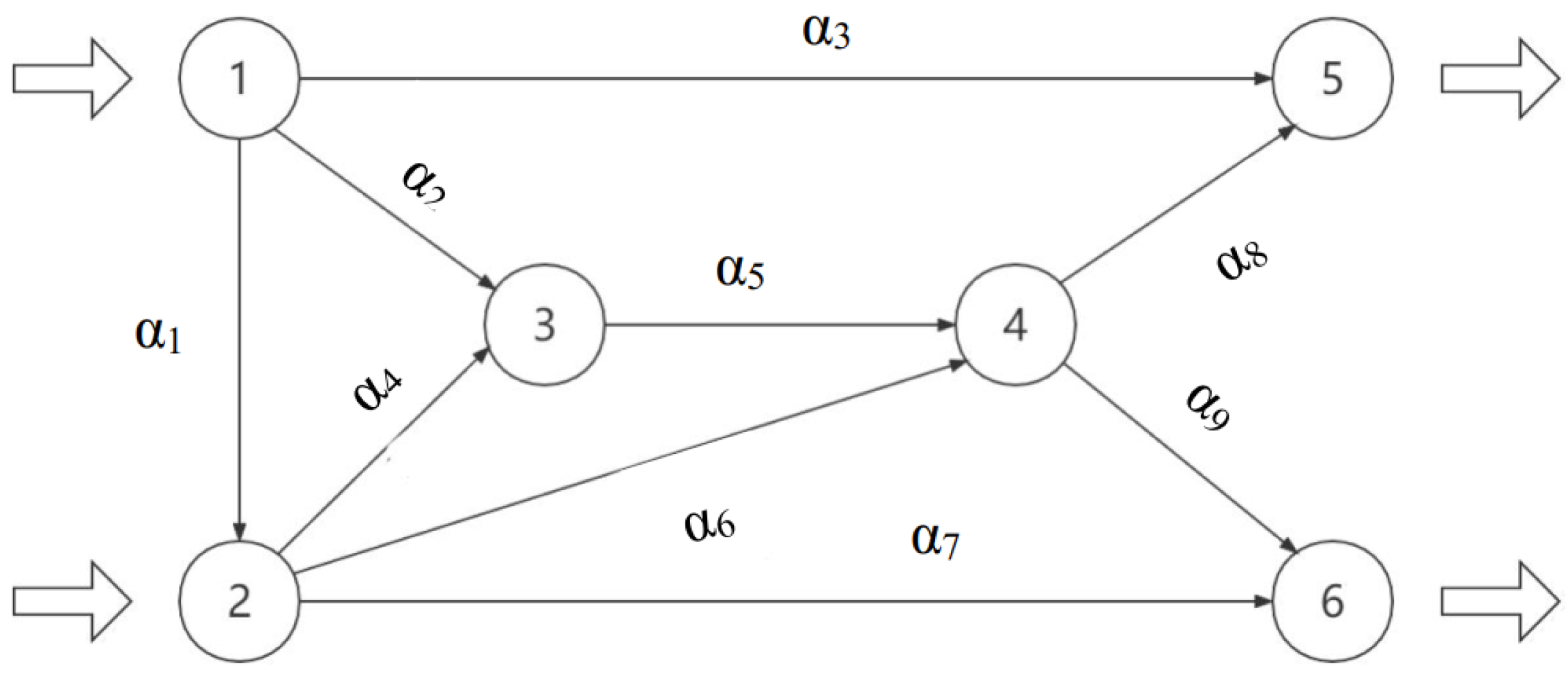
Example 4. Consider the network problem depicted in Figure 3, where , with two criteria: travel time and travel cost. , where , , , , , and . The constrains of paths and cost functions are given as follows:
where
denotes the flow on arc
. Then we have
where
. Initial feasible flows and a subset of the robust vector equilibrium flows are obtained in
s. The results are shown in
Table 3. The algorithm proposed in [
22] obtains the same robust vector equilibrium flows, but its time cost is 548.32 s.