On the Optimal Input Rate in Queues with Batch Service
Abstract
1. Introduction
- If the number of customers in the system is less than a, then the server is idle;
- If the number of customers in the waiting line is between the two thresholds a and b, then they are all served as soon as the previous batch leaves the queue;
- Otherwise, a group of b customers is selected for service.
- There are at least a customers in the queue;
- There are less than a customers in the queue but their measured average waiting time is greater than or equal to the waiting time tolerance T.
2. Materials and Methods
2.1. The Queue
2.2. A Deeper Insight into the Roots of the Characteristic Equation
2.3. Analysis of the Equivalent Birth–Death Process
3. Optimal Input Rate for Batch Services
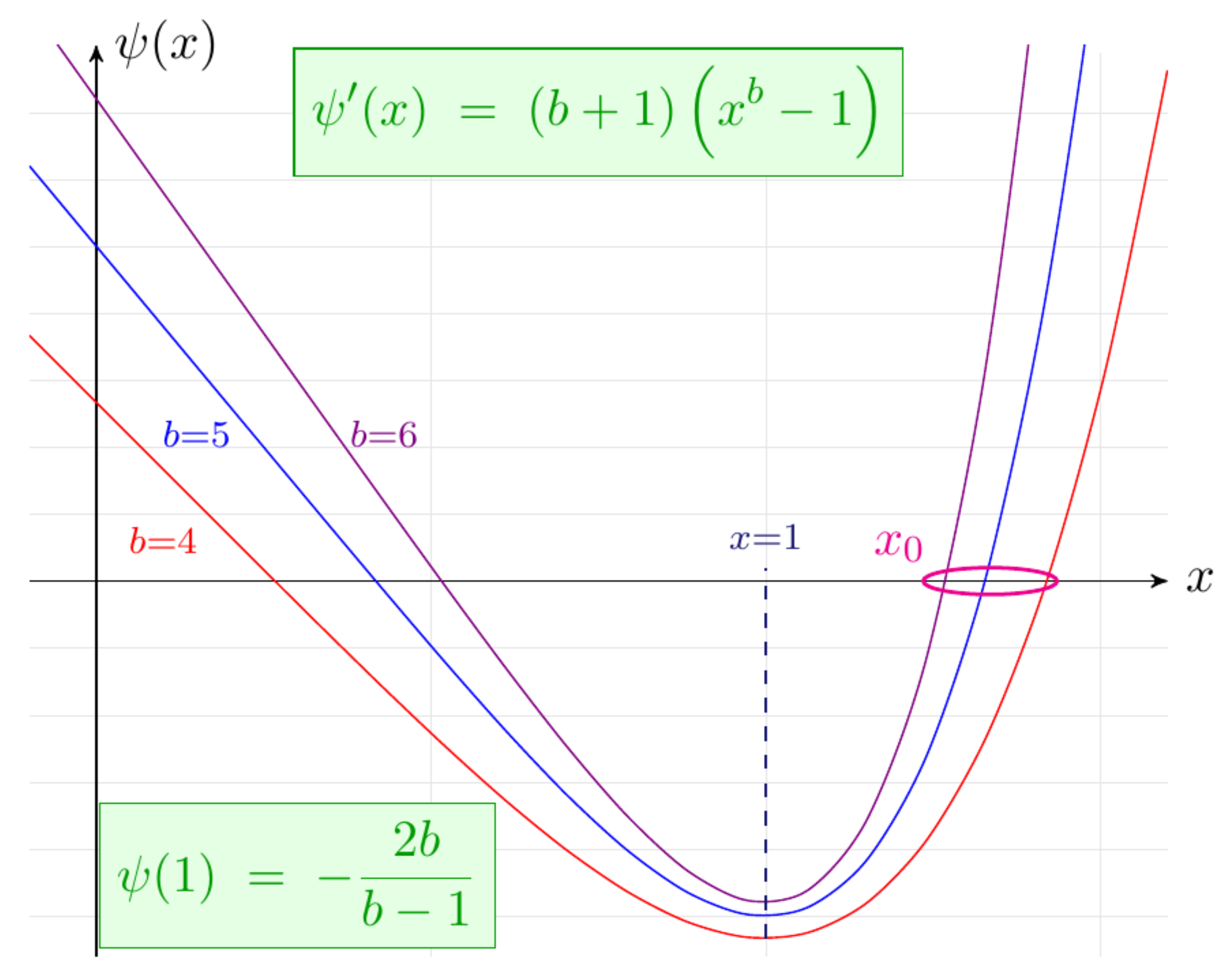
3.1. Condition for the Existence of an Optimal Arrival Rate
3.2. Calculation of the Optimal Rate
3.3. Approximate Expression for the Optimal Input Rate
4. Discussion
4.1. Numerical Validation of the First Order Approximation
4.2. Evaluation of the Optimal Rate and Corresponding Sojourn Time
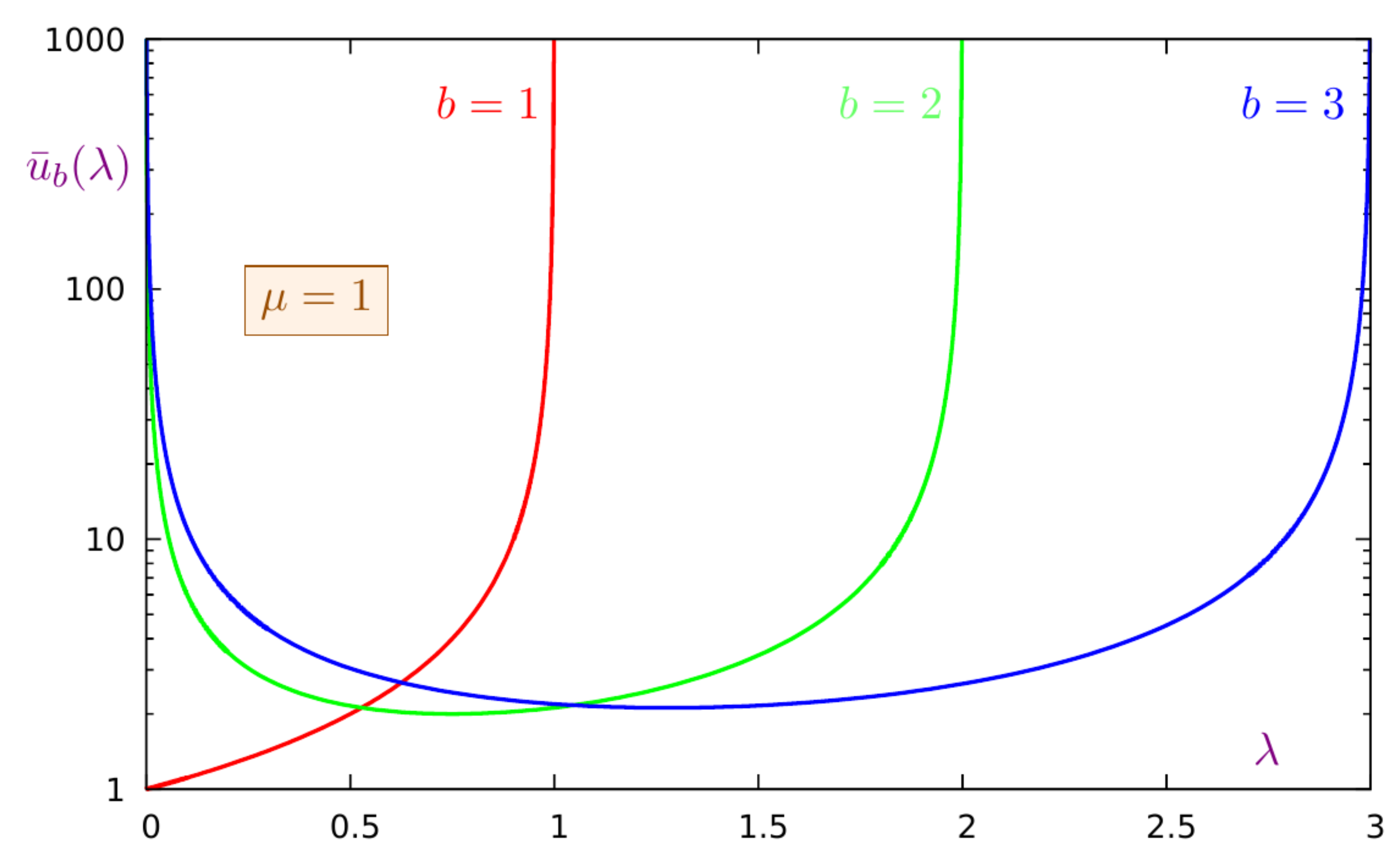
- The shape of the curve is quite flat around its minimum; indeed, even significant deviations in lead to small variations in the sojourn time, as shown in the first lines of the table. In practice, this implies a high stability of the system even in case of variations in the input rate;
- In spite of the fact that as (i.e., ), the increments in become increasingly smaller as b goes to .
4.3. Optimal Sojourn Time with Respect to Other Queue Parameters
4.4. Final Remarks and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brockmeyer, E.; Halstrøm, H.; Erlang, A.; Jensen, A. The Life and Works of A.K. Erlang; Academy of Technical Sciences, Copenhagen Telephone Comp.: Copenhagen, Denmark, 1948. [Google Scholar]
- Bychkov, I.; Kazakov, A.; Lempert, A.; Zharkov, M. Modeling of Railway Stations Based on Queuing Networks. Appl. Sci. 2021, 11, 2425. [Google Scholar] [CrossRef]
- Lee, H.; Choi, E.K.; Min, K.A.; Bae, E.; Lee, H.; Lee, J. Physician-Customized Strategies for Reducing Outpatient Waiting Time in South Korea Using Queueing Theory and Probabilistic Metamodels. Int. J. Environ. Res. Public Health 2022, 19, 2073. [Google Scholar] [CrossRef]
- Li, L.; Guo, M.; Ma, L.; Mao, H.; Guan, Q. Online Workload Allocation via Fog-Fog-Cloud Cooperation to Reduce IoT Task Service Delay. Sensors 2019, 19, 3830. [Google Scholar] [CrossRef]
- Andonov, V.; Poryazov, S.; Otsetova, A.; Saranova, E. A Queue in Overall Telecommunication System with Quality of Service Guarantees. In Future Access Enablers for Ubiquitous and Intelligent Infrastructures; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 243–262. [Google Scholar] [CrossRef]
- Gold, H.; Tran-Gia, P. Performance analysis of a batch service queue arising out of manufacturing system modelling. Queueing Syst. 1993, 14, 413–426. [Google Scholar] [CrossRef]
- Wu, K. Classifications for batch service queues in production systems. In Proceedings of the 2014 IEEE International Conference on Automation Science and Engineering (CASE), New Taipei, Taiwan, 18–22 August 2014; pp. 698–703. [Google Scholar]
- Chang, W. Bulk queue model for computer system analysis. IBM J. Res. Dev. 1974, 18, 370–372. [Google Scholar] [CrossRef]
- Santhi, K.; Saravanan, R.D. Performance analysis of cloud computing bulk service using queueing models. Int. J. Appl. Eng. Res. 2017, 12, 6487–6492. [Google Scholar]
- Balbo, G.; Vigliotti, M.G. On the analysis of a M/M/1 queue with bulk services. Comput. J. 2015, 58, 57–74. [Google Scholar] [CrossRef]
- Gupta, G.K.; Banerjee, A. Steady state analysis of system size-based balking in M/Mb/1 queue. Int. J. Math. Oper. Res. 2019, 14, 319–337. [Google Scholar] [CrossRef]
- Bailey, N.T.J. On queueing processes with bulk service. J. R. Stat. Soc. Ser. B Methodol. 1954, 16, 80–87. [Google Scholar] [CrossRef]
- Downton, F. Waiting time in bulk service queues. J. R. Stat. Soc. Ser. B Methodol. 1955, 17, 256–261. [Google Scholar] [CrossRef]
- Neuts, M.F. A general class of bulk queues with Poisson input. Ann. Stat. 1967, 38, 759–770. [Google Scholar] [CrossRef]
- Bagchi, T.P.; Templeton, J.G.C. Finite waiting space bulk queueing systems. J. Eng. Math. 1973, 7, 313–317. [Google Scholar] [CrossRef]
- Deb, R.K.; Serfozo, R.F. Optimal control of batch service queues. Adv. Appl. Probab. 1973, 5, 340–361. [Google Scholar] [CrossRef]
- Chaudhry, M.L.; Templeton, J.G.C. A First Course in Bulk Queues; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Gross, D.; Shortle, J.F.; Thompson, J.M.; Harris, C.M. Fundamentals of Queueing Theory; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kleinrock, L. Queueing Systems: Volume I-Theory; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Krishna Reddy, G.V.; Anitha, R. Markovian bulk service queue with delayed vacations. Comput. Oper. Res. 1998, 25, 1159–1166. [Google Scholar] [CrossRef]
- Holman, D.F.; Chaudhry, M.L.; Ghosal, A. Some results for the general bulk service queueing system. Bull. Aust. Math. Soc. 1981, 23, 161–179. [Google Scholar] [CrossRef]
- Economou, A. An alternative model for queueing systems with single arrivals, batch services and customer coalescence. Queueing Syst 2002, 40, 407–432. [Google Scholar] [CrossRef]
- Deena Merit, C.K.; Haridass, M. Analysis of flexible batch service queueing system to constrict waiting time of customers. Math. Probl. Eng. 2021, 2021, 16. [Google Scholar]
- Krishnamoorthy, A.; Joshua, A.N.; Vishnevsky, V. Analysis of a k-Stage Bulk Service Queuing System with Accessible Batches for Service. Mathematics 2021, 9, 559. [Google Scholar] [CrossRef]
- Barbhuiya, F.P.; Gupta, U.C. A difference equation approach for analysing a batch service queue with the batch renewal arrival process. J. Differ. Equ. Appl. 2019, 25, 233–242. [Google Scholar] [CrossRef]
- Stankevich, E.; Tananko, I.; Pagano, M. Analysis of Open Queueing Networks with Batch Services. In Information Technologies and Mathematical Modelling. Queueing Theory and Applications; Dudin, A., Nazarov, A., Moiseev, A., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 40–51. [Google Scholar]
- Krishnamoorthy, A.; Ushakumari, P.V. A queueing system with single arrival bulk service and single departure. Math. Comput. Modelling 2000, 31, 99–108. [Google Scholar] [CrossRef]
- Bountali, O.; Economou, A. Equilibrium joining strategies in batch service queueing systems. Eur. J. Oper. Res. 2017, 260, 1142–1151. [Google Scholar] [CrossRef]
- Stankevich, E.; Tananko, I.; Pagano, M. Optimization of Open Queuing Networks with Batch Services. Mathematics 2022, 10, 3027. [Google Scholar] [CrossRef]
- Smirnov, V.I. A Course of Higher Mathematics; Volume I Elementary Calculus; International Series of Monographs in Pure and Applied Mathematics; Pergamon Press: Oxford, UK, 1964. [Google Scholar]

| b | RE (%) | ||
|---|---|---|---|
| 4 | 1.419552 | 1.376310 | 3.04613 |
| 5 | 1.327085 | 1.301048 | 1.96194 |
| 6 | 1.268258 | 1.250874 | 1.37074 |
| 7 | 1.227461 | 1.215034 | 1.01239 |
| 8 | 1.197479 | 1.188155 | 0.77859 |
| 9 | 1.174502 | 1.167249 | 0.617527 |
| 10 | 1.156327 | 1.150524 | 0.501826 |
| 20 | 1.076636 | 1.075262 | 0.127612 |
| 30 | 1.050775 | 1.050175 | 0.057092 |
| 40 | 1.037966 | 1.037631 | 0.0322264 |
| 60 | 1.025235 | 1.025087 | 0.0143748 |
| 80 | 1.018898 | 1.018816 | 0.00810094 |
| 100 | 1.015105 | 1.015052 | 0.00519053 |
| 200 | 1.007539 | 1.007526 | 0.00130072 |
| 300 | 1.005023 | 1.005017 | 0.0005786 |
| 400 | 1.003766 | 1.003763 | 0.000325619 |
| 500 | 1.003013 | 1.003010 | 0.000208465 |
| 600 | 1.002510 | 1.002509 | 0.000144804 |
| 700 | 1.002151 | 1.002150 | 0.000106408 |
| 800 | 1.001882 | 1.001882 | |
| 900 | 1.001673 | 1.001672 | |
| 1000 | 1.001506 | 1.001505 |
| b | RE (%) | RE (%) | ||||
|---|---|---|---|---|---|---|
| 2 | 0.7500 | 0.8961 | 19.4839 | 2.0000 | 2.0407 | 2.0328 |
| 3 | 1.2768 | 1.4046 | 10.0058 | 2.1165 | 2.1309 | 0.6803 |
| 4 | 1.7965 | 1.9168 | 6.6928 | 2.1617 | 2.1689 | 0.3372 |
| 5 | 2.3146 | 2.4307 | 5.0175 | 2.1850 | 2.1894 | 0.2008 |
| 6 | 2.8320 | 2.9455 | 4.009 | 2.1991 | 2.2020 | 0.1332 |
| 7 | 3.3491 | 3.4609 | 3.3371 | 2.2084 | 2.2105 | 0.0947 |
| 8 | 3.8662 | 3.9766 | 2.857 | 2.2151 | 2.2166 | 0.0708 |
| 9 | 4.3831 | 4.4926 | 2.4976 | 2.2200 | 2.2212 | 0.0549 |
| 10 | 4.9001 | 5.0088 | 2.2182 | 2.2238 | 2.2248 | 0.0439 |
| 20 | 10.0689 | 10.1742 | 1.0460 | 2.2394 | 2.2397 | 0.0103 |
| 30 | 15.2376 | 15.3419 | 0.6841 | 2.2441 | 2.2442 | 0.0045 |
| 40 | 20.4064 | 20.5101 | 0.5083 | 2.2463 | 2.2464 | 0.0025 |
| 60 | 30.7440 | 30.8472 | 0.3357 | 2.2485 | 2.2485 | 0.0011 |
| 80 | 41.0817 | 41.1846 | 0.2506 | 2.24955 | 2.24957 | |
| 100 | 51.4194 | 51.5223 | 0.1999 | 2.25018 | 2.25019 | |
| 200 | 103.108 | 103.210 | 0.0994 | 2.25141 | 2.25141 | |
| 300 | 154.796 | 154.899 | 0.0661 | 2.25182 | 2.25182 | |
| 400 | 206.485 | 206.587 | 0.0496 | 2.25202 | 2.25202 | |
| 500 | 258.173 | 258.275 | 0.0396 | 2.25214 | 2.25214 | |
| 600 | 309.862 | 309.964 | 0.0330 | 2.25222 | 2.25222 | |
| 700 | 361.550 | 361.652 | 0.0283 | 2.25228 | 2.25228 | |
| 800 | 413.234 | 413.341 | 0.0248 | 2.25232 | 2.25232 | |
| 900 | 464.927 | 465.029 | 0.0220 | 2.25235 | 2.25235 | |
| 1000 | 516.616 | 516.718 | 0.0198 | 2.25238 | 2.25238 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pagano, M.; Tananko, I.; Stankevich, E. On the Optimal Input Rate in Queues with Batch Service. Axioms 2023, 12, 656. https://doi.org/10.3390/axioms12070656
Pagano M, Tananko I, Stankevich E. On the Optimal Input Rate in Queues with Batch Service. Axioms. 2023; 12(7):656. https://doi.org/10.3390/axioms12070656
Chicago/Turabian StylePagano, Michele, Igor Tananko, and Elena Stankevich. 2023. "On the Optimal Input Rate in Queues with Batch Service" Axioms 12, no. 7: 656. https://doi.org/10.3390/axioms12070656
APA StylePagano, M., Tananko, I., & Stankevich, E. (2023). On the Optimal Input Rate in Queues with Batch Service. Axioms, 12(7), 656. https://doi.org/10.3390/axioms12070656






