Abstract
This paper considers a 1D time-domain inverse scattering problem for the Helmholtz equation in which penetrable scatterers are to be determined from boundary measurements of the scattering data. It is formulated as a coefficient identification problem for a wave equation. Using the Laplace transform, the inverse problem is converted into an overdetermined nonlinear system of partial differential equations. To solve this system, a Carleman weighted objective functional, which is proved to be strictly convex in an arbitrary set in a Hilbert space, is constructed. An alternating minimization algorithm is used to minimize the Carleman weighted objective functional. Numerical results are presented to illustrate the performance of the proposed algorithm.
Keywords:
inverse medium scattering problem; Carleman estimates; Carleman weighted objective functional; alternating minimization; numerics MSC:
35R30; 35L05; 78A46
1. Introduction
Scattering theory of waves is concerned with the effect scatterers have on incident waves [1]. There are two kinds of problems in the scattering theory. Forward scattering problems aim to determine the scattered waves, which are generated when incident waves interact with known scatterers. Inverse scattering problems (ISPs) aim to detect and identify scatterers from knowledge of the scattered wave(s) generated by one or multiple incident waves. The identification of scatterers is based on their geometrical or/and physical properties. Scatterers can be categorized as penetrable or impenetrable. Penetrable scatterers allow waves to penetrate and are characterized by both physical properties (such as the refractive index or permittivity) and geometrical properties (such as location and shape). By contrast, impenetrable scatterers (which are also called obstacles) do not allow waves to penetrate and are usually characterized by geometrical properties. ISPs are also divided into two types: inverse medium scattering problems and inverse obstacle scattering problems. The former aim to determine physical properties (which in turn provide information about geometrical properties) of penetrable scatterers, whereas the latter aim to determine the geometrical properties of impenetrable scatterers.
ISPs play a central role in many technologies such as ground-penetrating radar (GPR), microwave imaging, ultrasound imaging, and seismic imaging; see, e.g., [2,3,4,5,6] and the references therein. These technologies are used in various applications. GPR is an effective tool for detecting buried objects such as landmines, underground structures, or archaeological sites [5]. Ultrasound is widely used as a medical imaging tool. Recent research has shown the potential of microwaves in detecting breast tumors or brain strokes [7,8,9,10,11]. Seismic imaging is used for geophysical explorations [12].
In this paper, we are interested in inverse medium scattering problems for the Helmholtz equation in the time domain, which can be stated as follows. Let be a convex bounded domain in with a piecewise-smooth boundary . We denote by the lateral boundary of , i.e., . Consider a coefficient function which satisfies the following conditions:
for some given constants and such that . Here, denotes Hölder spaces, where is an integer and . Consider the following Cauchy problem:
The coefficient represents a physical property of the medium (including the scatterers) in which the waves propagate. For electromagnetic waves, it represents the dielectric constant, whereas for acoustic waves, it represents the refractive index. Here, is normalized so that its value in the background medium, i.e., in , equals 1. The state function represents the wave (or one component of the wave) propagating in the medium. The function represents the source of the wave. In this work, we assume that the source is located outside of the domain , i.e.,
The inverse medium scattering problem is stated as a coefficient identification problem as follows:
CIP: Suppose that conditions (1)–(4) are satisfied. Determine the coefficient for , from the boundary data:
where is the outward unit normal vector of Ω.
Remark 1.
1. In practice, the Neumann data, i.e., , are usually not measured. However, if the Dirichlet data, i.e., , are measured on the whole boundary , we can compute by solving the initial value problem (2) and (3) in
2. In computation, the infinite time interval in (5) can be replaced by a finite interval . The reason is that the incident wave is usually excited for a short period of time. Therefore, the wave function u is usually too small to be useful after some finite time. Moreover, in the numerical method we discuss in this paper, data at large time instants are essentially eliminated when a Laplace transform is used. The infinite interval is used for the convenience of theoretical analysis only.
In this work, we assume that the CIP with noiseless data has a unique solution. Our investigation is devoted to numerical methods for solving it. The most common numerical methods for solving this inverse problem use the least-squares minimization approach. These methods find an approximation of the coefficient by minimizing a least-squares objective functional. Due to the nonlinearity of the CIP, the objective functional is nonconvex. Therefore, a good initial guess is usually needed for the convergence of gradient-based iterative optimization methods to the global minimizer of the objective functional.
We consider in this paper a numerical method for solving the above CIP without requiring a good initial guess. The idea of this method is to transform the CIP into a system of nonlinear partial differential equations with overdetermined boundary conditions. To solve the resulting nonlinear system, we minimize a Carleman weighted objective functional which can be proved to be strictly convex in an arbitrary domain if the Carleman weight chosen is sufficiently large. The approach of convexification using Carleman weighted objective functional was introduced by Klibanov in the 1990s and then expanded to several inverse problems by himself and his collaborators; see, e.g., [13,14,15,16,17,18,19]. This paper extends the method we developed in our previous work [14]. The novel contributions of the current paper include the following: (1) A new first-order PDE system is obtained instead of a second-order system as in [14]; (2) the convexity of the discrete Carleman weighted objective functional is proved; and (3) we propose an alternating minimization method to solve the Carleman weighted objective functional instead of the steepest gradient algorithm used in [14]. The advantages of the proposed method include the following:
- Unlike the least-squares approach, the proposed method does not require a good first guess. Indeed, it was demonstrated through numerical examples in our previous work [14] that the least-squares method failed to converge at initial guesses at which the convexification method was able to provide a reasonably good approximation of the coefficient.
- Compared to our previous work [14] and the above references in the convexification approach, each minimization sub-problem in our proposed method has a much smaller number of variables than the original nonlinear system. Consequently, the sub-problems can be solved more quickly. We observed in our numerical tests that the alternating minimization method converges much faster than the steepest descent method.
As another interesting approach for solving ISPs that has received a lot of attention in the last year, we refer to various deep learning-based methods; see, e.g., [20,21,22,23,24] for an incomplete list of recent works focusing on this direction. Some results for microwave imaging data for medical applications have been reported in [25,26,27]. Numerical results of this approach appear promising, although the mathematical foundation of deep learning is still to be investigated.
The rest of the paper is organized as follows. In Section 2 we describe the transformation from the CIP into a nonlinear system of coupled partial differential equations. In Section 3 we describe the Carleman weighted objective functional and the alternating minimization algorithm. Section 4 is devoted to the discretized problems and its convexity. Numerical examples are presented in Section 5. Finally, we make some concluding remarks in Section 6.
2. Transformation of the CIP into a Nonlinear System
We first transform the CIP into a nonlinear system of coupled partial differential equations using the method described in our previous work [14]. For that purpose, we use the Laplace transform:
where s is referred to as the pseudofrequency. Let be a positive constant depending only on such that the Laplace transforms of u and its derivatives converge absolutely for all . It follows from (2) and (4) that satisfies the equation
For appropriate choices of the source function f, we can prove that for ; see Theorem 3.1 of [28]. In this work, we assume that the source function is chosen such that for . We define a new vector-valued function as
From (7) we obtain
Equation (9) provides an explicit way to compute the coefficient if is known. Unfortunately, both functions c and are unknown in this equation. However, since the right-hand side of (9) does not depend on s, we can eliminate the unknown function by differentiating (9) with respect to s. Denoting by , we obtain the following integral differential equation for q:
In addition, q satisfies the following boundary condition:
with and being the Laplace transforms of and , respectively.
We note that Equation (10) is not easy to solve. Using the same approach as in our previous work [14], we represent the function as a series with respect to an orthonormal basis of . For this purpose, we consider Laguerre polynomials [29]:
It can be verified that the set , where , is an orthonormal basis in . We then approximate the function as follows.
where N is a sufficiently large integer. The choice of N will be discussed in our numerical examples presented in Section 5. Substituting the truncated series (12) into (10), we approximate the coefficients , by the solution of the following equation:
Multiplying both sides of (13) by , integrating over , and using the orthonormality of in , we obtain the following system of coupled nonlinear equations:
where the numbers , , are given by
3. Carleman Weighted Objective Functional and Alternating Minimization Algorithm
We note that the unknown functions , in system (14) and (15) are coupled. Moreover, this system is overdetermined. Therefore, direct methods for solving this system are not applicable. To overcome this difficulty, we convert the above system into a minimization problem. For simplicity of notation, we denote by . We approximate the solution of (14) and (15) by minimizing the following objective functional:
in the set
where R is a given positive constant. In (16), is a Carleman weight function. The key idea of adding this weight function to the objective functional J is to make it convex in the set G. The choice of the weight function depends on the geometry of the domain . We will discuss the choice of this function in our numerical examples.
To minimize the objective functional J in (16), we use a proximal block alternating minimization method. This method updates the unknown functions , alternatively; see, e.g., [30,31,32,33]. The algorithm is described as follows.
The sequence obtained by the alternating minimization satisfies the following square summable property.
Lemma 1.
Let , be obtained by Algorithm 1. Then:
| Algorithm 1: Proximal block alternating minimization algorithm for minimizing the objective functional . |
|
Proof.
Since is the minimizer of , it follows from (18) that . This inequality implies that
Hence,
Taking the sum of inequality (19) for , we obtain
Thus,
The proof is complete. □
Remark 2.
The global convergence of the alternating minimization algorithm has been proved for objective functionals which satisfy the so-called Kurdyka–Lojasiewicz (KL) property. One case in which this KL property is satisfied is when the objective functional is locally strongly convex; see, e.g., [34,35]. In the case , as we will prove in Theorem 1, the objective functional in (16) is strongly convex in an arbitrary given set. Therefore, the global convergence of the alternating minimization follows.
4. Discretized Objective Functional and Convexity in 1D
In this section, we consider the discretized version of the objective functional in (16) in 1D. Our focus in this section is to prove the convexity of the discretized version of J in an arbitrary domain in an appropriate Hilbert space. Although results concerning the convexity of continuous Carleman weighted objective functionals associated with second-order elliptic systems have been reported [14], this appears to be the first time that the convexity for the discretized objective functional for the first-order system (14) is proved. The multi-dimensional case is still open.
In the following, let . In this 1D problem, we denote the spatial variable by x instead of . The objective functional J can be rewritten as
Consider a partition of the interval into M sub-intervals by a uniform set of grid points with grid size . Denote by an approximate value of , . In the following we use Q to represent the matrix . The objective functional J is replaced by the following discrete version:
where and is given by
To simplify the notation, we define the following bilinear function:
for two matrices and .
The boundary condition (15) can be rewritten as
The minimization problem now becomes a finite dimensional problem in which the unknown matrix Q belongs to the set of real matrices of sizes . In the following, we consider the standard Frobenius norm of matrices in defined by
We also consider the norm in :
We also use to denote the Frobenius inner product of two matrices in .
For each positive constant R, we define the set in as
where , with
As we mentioned in Section 2, the choice of the Carleman weight function for the convexity of the objective functional J (or ) depends on the domain . In this 1D case, we can choose , where is a positive constant referred to as the Carleman weight coefficient. With this choice, we can prove that the objective functional is convex in the domain for any fixed radius R given that the Carleman weight coefficient chosen is large enough. To prove this property, we need the following estimate, which can be considered as a discrete Carleman estimate. Its proof is presented in Appendix A.
Lemma 2.
Let , be scalar values in with . Then, for , , , , the following estimate holds:
Now we are ready to state and prove the convexity of the objective functional .
Theorem 1.
Let R be an arbitrary positive number. Then, there exists a sufficiently large positive number depending only on the parameters such that the objective functional defined by (23) is strongly convex on for all . More precisely, there exists a constant such that for arbitrary matrices , the following estimate holds:
where is the gradient of .
Proof.
It follows from (24) that
Since is bilinear, it follows that
Hence,
where . Thus,
Substituting this equality into (23), we obtain
Since the last two terms of (30) are quadratic functions of and the first term on the right-hand side is a linear function of , we have
Hence,
Now we estimate the right-hand side of (31). First, we have
Using the Cauchy–Schwarz inequality, we have
Substituting this inequality into (32), we obtain
Since Q, are in , there exists a constant depending only on R, , h, and such that
It follows from Lemma 2 that
The proof is complete. □
5. Numerical Implementation and Examples
In this section we describe details of our numerical implementation of the proposed algorithm.
5.1. Generating Simulated Data
In this work, we tested the proposed algorithm using simulated data. To generate these data, we solved the forward problem (2) and (3) in a bounded interval such that . The source function was chosen as , where . The total wave function was rewritten as , where is the incident wave and is the scattered wave. The incident wave was given by the following formula:
As in [14], we also used the absorbing boundary condition to approximate the boundary conditions at the endpoints and . The forward problem was then rewritten as follows:
In the numerical examples presented below, we chose , , , and . The waveform of the incident wave was chosen to be
where and . The constant A was used as the normalization factor. Problem (38)–(40) was solved by an explicit finite difference scheme with a uniform grid in both the x and t directions with step sizes of and . This results in 141 grid points in space and 2001 points in time.
In order to simulate noisy measurements, we added additive noise of (in the norm) to the simulated data.
5.2. Numerical Examples of the CIP
In the following examples, the parameters were chosen as follows. The pseudofrequencies were with step size . The number of Laguerre’s functions was . The Carleman weight coefficient was chosen to be . The proximal coefficient L was . These parameters were chosen numerically for the best reconstruction of one simulated dataset, then they were fixed for all other examples. We have observed in numerical tests that a larger number of Laguerre’s functions do not necessarily result in substantially more accurate reconstruction results. The possible reason is due to the fact that the objective functional is quite insensitive to changes in the high-frequency modes near the minimizer.
We also remark that the data associated with large pseudofrequencies are dominated by that at low pseudofrequencies. This is due to the exponential decaying nature of the Laplace transform. Therefore, the interval of the pseudofrequencies chosen should not be too large.
Example 1.
In the first example, we considered a smooth coefficient in the following form:
The reconstructed coefficient is depicted in Figure 1 together with the exact coefficient. We can see that the algorithm was able to reconstruct the coefficient quite accurately. The largest error is near , which is near the “back” of the scattered. We note that the source illuminates the scatterer from the left. As a result, the measured signal at is stronger than that at That made the reconstruction on the left side of the scatterer easier to reconstruct.
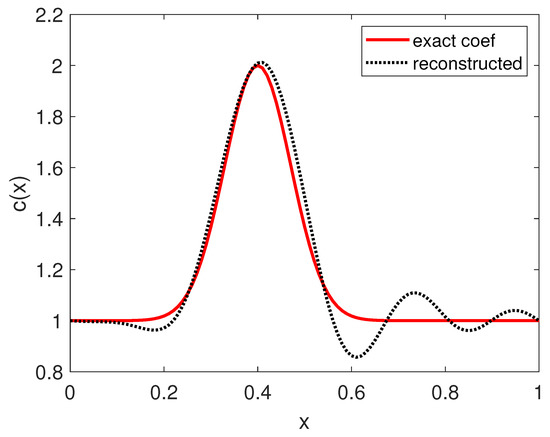
Figure 1.
Reconstruction of the coefficient in Example 1. The data were measured at and .
Example 2.
In the second example, we tested the algorithm for a more challenging smooth function . More precisely, is a combination of two Gaussian peaks. Its formula is given by
The reconstructed coefficient is depicted in Figure 2. Although the reconstruction is not as accurate as in Example 1, it still captured the main peaks of the coefficient function. The largest peak was reconstructed with a relative error of approximately 17% (2.5 vs. 3) and the second peak was reconstructed with a relative error of approximately 15% (1.7 vs. 2).
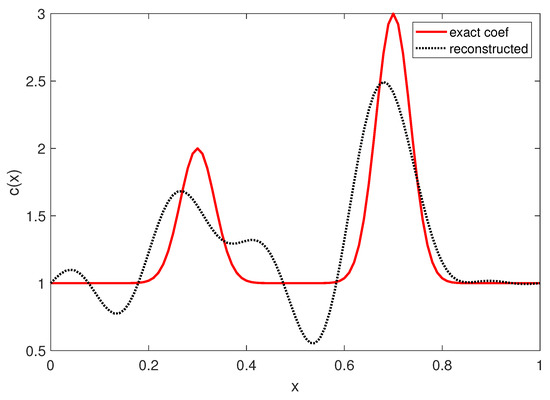
Figure 2.
Reconstruction of the coefficient in Example 2. The data were measured at and .
Example 3.
Finally, we tested the algorithm for a piecewise constant coefficient with large and small peaks. The coefficient was given as
where is the characteristic function of interval .
The reconstructed coefficient is depicted in Figure 3. As we can see, the algorithm was still able to reconstruct the peaks of the coefficient, with a relative error of approximately 10%, even though the quantitative values are not so accurate. This is a very challenging example which mimics the case when a “weak” object and a “strong” object are in the same medium. In this case, it is usually difficult to reconstruct the weaker target. To see the effect of the number of Laguerre’s functions on the reconstruction accuracy in this challenging example, we also tested using 20 Laguerre’s functions but the result (not shown in the figure) was not really improved.
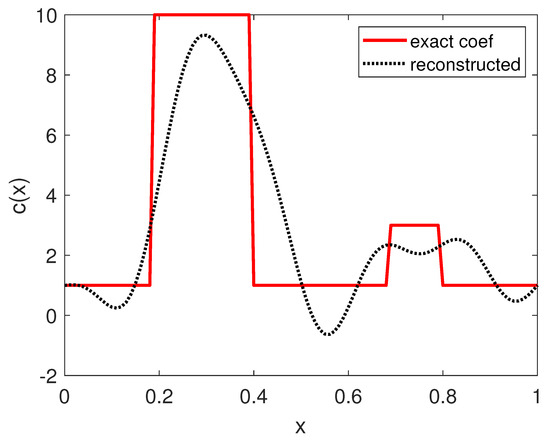
Figure 3.
Reconstruction of the coefficient in Example 3. The data were measured at and .
Concerning computational cost, the algorithm was set to run for 2000 iterations, which took approximately 5 min on a Lenovo Thinkpad X1 Yoga laptop computer with an Intel i7 1.8 GHz processor with four cores (but only one was used in the computation).
6. Conclusions
In this paper we combined the Carleman weighted convexification method with an alternating minimization method for solving a 1D inverse medium scattering problem. The convexity of the Carleman weighted objective functional was proved in the discrete setting, which was actually used in the optimization algorithm. The global convergence of the alternating minimization was shown. Numerical examples indicated that the proposed algorithm was able to provide a good solution without requiring a good first guess. If more accurate results are expected, we can use locally convergent gradient-based methods with the result of the proposed algorithm as an initial guess to refine the reconstruction.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The author is grateful to the constructive comments and suggestions from the referees.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Proof of Lemma 2.
The proof follows the same approach as in [36], Lemma 3.1. Let . Then . Hence,
Taking the sum for , we obtain
Since , it follows that
Hence,
The proof is complete. □
References
- Colton, D.; Kress, R. Inverse Acoustic and Electromagnetic Scattering Theory, 3rd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Ammari, H. An Introduction to Mathematics of Emerging Biomedical Imaging; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Baum, C. Detection and Identification of Visually Obscured Targets; Taylor and Francis: Philadelphia, PA, USA, 1998. [Google Scholar]
- Buchanan, J.L.; Gilbert, R.P.; Wirgin, A.; Xu, Y.S. Marine Acoustics: Direct and Inverse Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2004. [Google Scholar]
- Daniels, D.J. Ground Penetrating Radar; The Institute of Electrical Engineers: London, UK, 2004. [Google Scholar]
- Pastorino, M. Microwave Imaging; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Ireland, D.; Bialkowski, M. Microwave heat imaging for stroke detection. Prog. Electromagn. Res. M 2011, 21, 163–175. [Google Scholar] [CrossRef]
- Nikolova, N.K. Microwave imaging for breast cancer. IEEE Microw. Mag. 2011, 12, 78–94. [Google Scholar] [CrossRef]
- Persson, M.; Fhager, A.; Trefna, H.D.; Yu, Y.; McKelvey, T.; Pegenius, G.; Karlsson, J.E.; Elam, M. Microwave-Based Stroke Diagnosis Making Global Prehospital Thrombolytic Treatment Possible. IEEE Trans. Biomed. Eng. 2014, 61, 2806–2817. [Google Scholar] [CrossRef]
- Scapaticci, R.; Tobon, J.; Bellizzi, G.; Vipiana, F.; Crocco, L. Design and Numerical Characterization of a Low-Complexity Microwave Device for Brain Stroke Monitoring. IEEE Trans. Antennas Propag. 2018, 66, 7328–7338. [Google Scholar] [CrossRef]
- Tournier, P.H.; Aliferis, I.; Bonazzoli, M.; de Buhan, M.; Darbas, M.; Dolean, V.; Hecht, F.; Jolivet, P.; Kanfoud, I.E.; Migliaccio, C.; et al. Microwave tomographic imaging of cerebrovascular accidents by using high-performance computing. Parallel Comput. 2019, 85, 88–97. [Google Scholar] [CrossRef]
- Yilmaz, O. Seismic Data Imaging; Society of Exploration Geophysicists: Tulsa, OK, USA, 1987. [Google Scholar]
- Klibanov, M.V.; Ioussoupova, O.V. Uniform strict convexity of a cost functional for three-dimensional inverse scattering problem. SIAM J. Math. Anal. 1995, 26, 147–179. [Google Scholar] [CrossRef]
- Klibanov, M.V.; Thành, N.T. Recovering dielectric constants of explosives via a globally strictly convex cost functional. SIAM J. Appl. Math. 2015, 75, 518–537. [Google Scholar] [CrossRef]
- Klibanov, M.V.; Kolesov, A.E. Convexification of a 3-D coefficient inverse scattering problem. Comput. Math. Appl. 2019, 77, 1681–1702. [Google Scholar] [CrossRef]
- Klibanov, M.V.; Kolesov, A.E.; Nguyen, L.; Sullivan, A. Globally strictly convex cost functional for a 1-D inverse medium scattering problem with experimental data. SIAM J. Appl. Math. 2017, 77, 1733–1755. [Google Scholar] [CrossRef]
- Klibanov, M.V.; Nguyen, D.L.; Nguyen, L.H.; Liu, H. A globally convergent numerical method for a 3D coefficient inverse problem with a single measurement of multi-frequency data. Inverse Probl. Imaging 2018, 12, 493–523. [Google Scholar] [CrossRef]
- Kolesov, A.E.; Klibanov, M.V.; Nguyen, L.H.; Nguyen, D.L.; Thành, N.T. Single measurement experimental data for an inverse medium problem inverted by a multi-frequency globally convergent numerical method. Appl. Numer. Math. 2017, 120, 176–196. [Google Scholar] [CrossRef]
- Nguyen, D.L.; Klibanov, M.V.; Nguyen, L.H.; Fiddy, M.A. Imaging of buried objects from multi-frequency experimental data using a globally convergent inversion method. J. Inverse Ill-Posed Probl. 2018, 26, 501–522. [Google Scholar] [CrossRef]
- Chen, X.; Wei, Z.; Li, M.; Rocca, P. A review of deep learning approaches for inverse scattering problems. Prog. Electromagn. Res. 2020, 167, 67–81. [Google Scholar] [CrossRef]
- Fan, Y.; Ying, L. Solving Inverse Wave Scattering with Deep Learning. arXiv 2019, arXiv:1911.13202. [Google Scholar] [CrossRef]
- Khoo, Y.; Ying, L. SwitchNet: A Neural Network Model for Forward and Inverse Scattering Problems. SIAM J. Sci. Comput. 2019, 41, A3182–A3201. [Google Scholar] [CrossRef]
- Xu, K.; Darve, E. Physics Constrained Learning for Data-driven Inverse Modeling from Sparse Observations. J. Comput. Phys. 2022, 453, 110938. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, X. Deep-Learning Schemes for Full-Wave Nonlinear Inverse Scattering Problems. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1849–1860. [Google Scholar] [CrossRef]
- Ambrosanio, M.; Franceschini, S.; Pascazio, V.; Baselice, F. An End-to-End Deep Learning Approach for Quantitative Microwave Breast Imaging in Real-Time Applications. Bioengineering 2022, 9, 651. [Google Scholar] [CrossRef]
- Dachena, C.; Fedeli, A.; Fanti, A.; Lodi, M.B.; Fumera, G.; Pastorino, M.; Randazzo, A. Microwave Medical Imaging of the Human Neck using a Neural-Networks-Based Inversion Procedure: A Phantom Study. In Proceedings of the 2023 17th European Conference on Antennas and Propagation (EuCAP), Florence, Italy, 26–31 March 2023; pp. 1–5. [Google Scholar]
- Salucci, M.; Polo, A.; Vrba, J. Multi-Step Learning-by-Examples Strategy for Real-Time Brain Stroke Microwave Scattering Data Inversion. Electronics 2021, 10, 95. [Google Scholar] [CrossRef]
- Thành, N.T.; Beilina, L.; Klibanov, M.V.; Fiddy, M.A. Imaging of Buried Objects from Experimental Backscattering Time-Dependent Measurements Using a Globally Convergent Inverse Algorithm. SIAM J. Imaging Sci. 2015, 8, 757–786. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards Applied Mathematics Series; U.S. Government Printing Office: Washington, DC, USA, 1964; Volume 55. [Google Scholar]
- Beck, A. On the convergence of alternating minimization for convex programming with applications to iteratively reweighted least squares and decomposition schemes. SIAM J. Optim. 2015, 25, 185–209. [Google Scholar] [CrossRef]
- Grippo, L.; Sciandrone, M. Globally convergent block-coordinate techniques for unconstrained optimization. Optim. Methods Softw. 1999, 10, 587–637. [Google Scholar] [CrossRef]
- Tupitsa, N.; Dvurechensky, P.; Gasnikov, A.; Guminov, S. Alternating minimization methods for strongly convex optimization. J. Inverse Ill-Posed Probl. 2021, 29, 721–739. [Google Scholar] [CrossRef]
- Wright, S.J. Coordinate descent algorithms. Math. Program. 2015, 151, 3–34. [Google Scholar] [CrossRef]
- Attouch, H.; Bolte, J.; Redont, P.; Soubeyran, A. Proximal alternating minimization and projection methods for nonconvex problems: An approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res. 2010, 35, 438–457. [Google Scholar] [CrossRef]
- Xu, Y.; Yin, W. A Block Coordinate Descent Method for Regularized Multiconvex Optimization with Applications to Nonnegative Tensor Factorization and Completion. SIAM J. Imaging Sci. 2013, 6, 1758–1789. [Google Scholar] [CrossRef]
- Thành, N.T. Convexity of a discrete Carleman weighted objective functional in an inverse medium scattering problem. J. Inv. Ill-Posed Probl. 2020, 30, 485–493. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).