Stability Results for the Darboux Problem of Conformable Partial Differential Equations
Abstract
1. Introduction
- Existence and uniqueness of the solution: We provide a rigorous proof of the existence and uniqueness of the solution for the DPCDEs.
- UHRS of the DPCDEs: Our study delves into the UHRS of the DPCDEs. We explore the behavior and stability characteristics of solutions to the DPCDEs under perturbations, taking into account the principles and methodologies established in the UHRS framework.
2. Basic Definitions and Tools
3. Stability Results
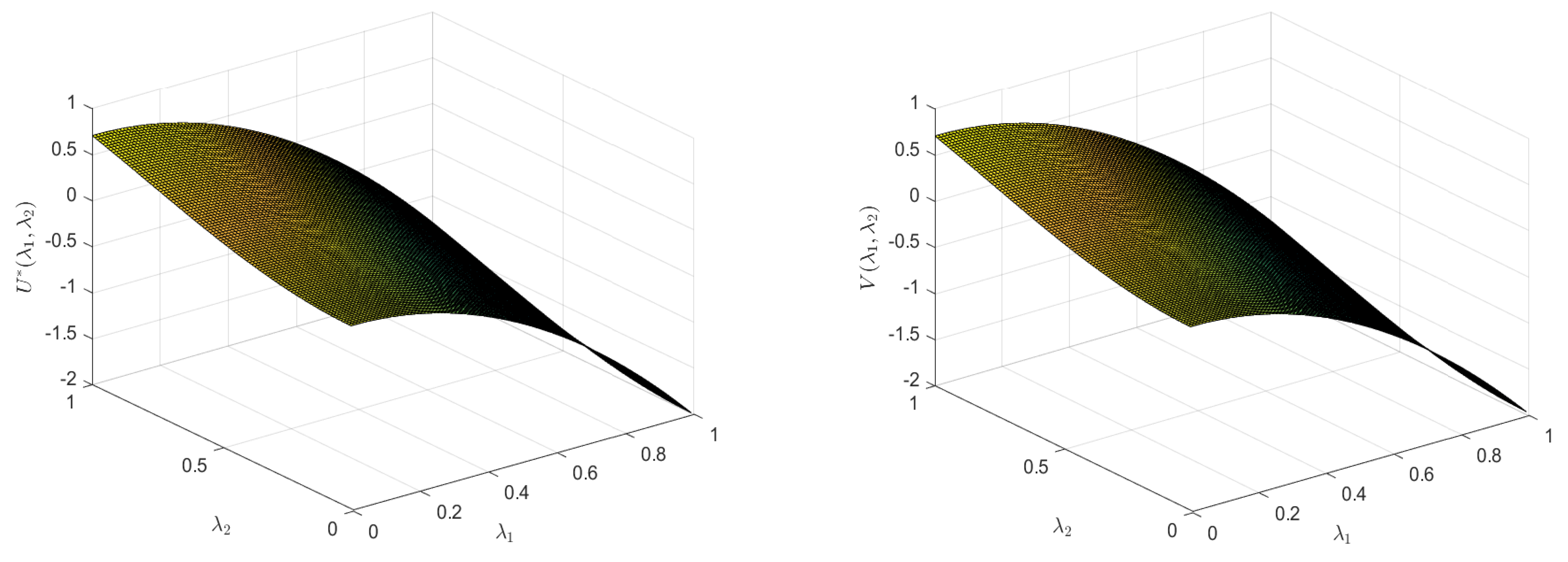
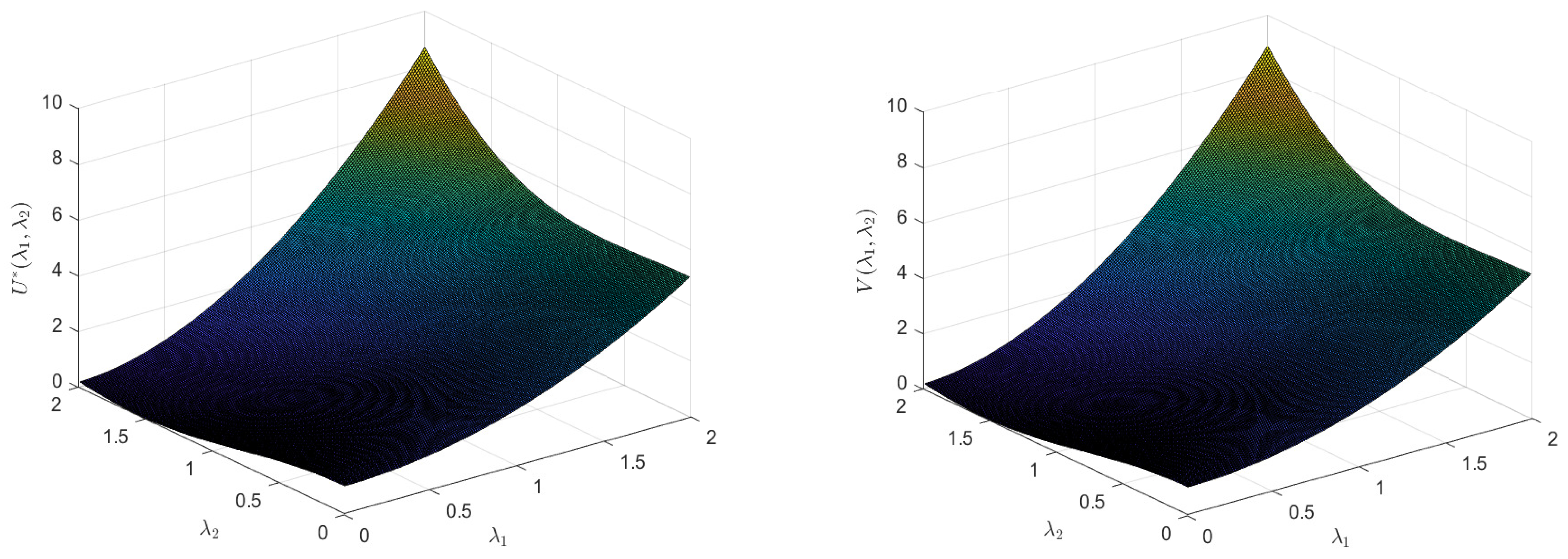
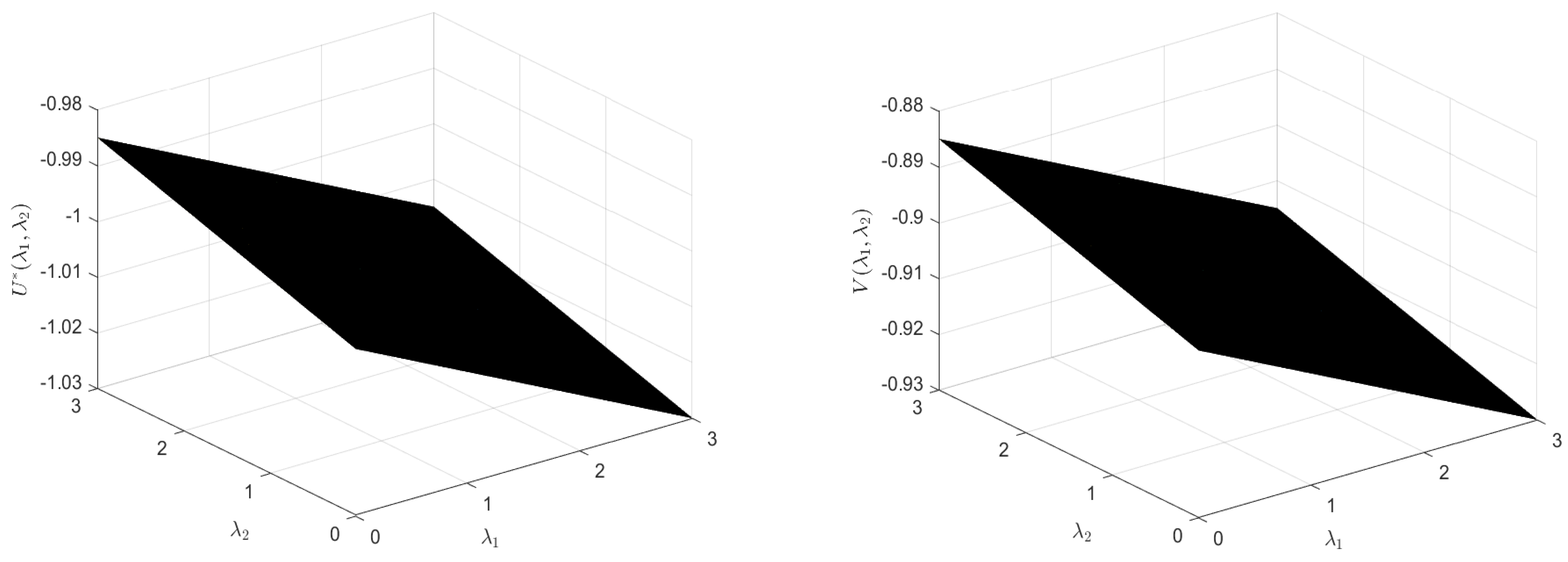
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atanackovic, T.M.; Pilipovic, S.; Stankovic, B.; Zorica, D. Fractional Calculus with Applications in Mechanics; Wiley-ISTE: London, UK; Hoboken, NJ, USA, 2014. [Google Scholar]
- Baleanu, D.; Machado, J.A.; Luo, A.C. Fractional Dynamics and Control; Springer Science and Business Media: New York, NY, USA, 2011. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Azouz, F.; Boucenna, D.; Ben Makhlouf, A.; Mchiri, L.; Benchaabane, A. Controllability of Differential Systems with the General Conformable Derivative. Complexity 2021, 2021, 2817092. [Google Scholar] [CrossRef]
- Hyder, A.A.; Soliman, A.H. An extended Kudryashov technique for solving stochastic nonlinear models with generalized conformable derivatives. Commun. Nonlinear Sci. Numer. Simul. 2021, 97, 105730. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Liu, R. The Existence of Solution of Diffusion Equation with the General Conformable Derivative. J. Funct. Spaces 2020, 2020, 3965269. [Google Scholar] [CrossRef]
- Ben Makhlouf, A.; El-Hady, E.; Boulaaras, S.; Hammami, M.A. Stability analysis for differential equations of the general conformable type. Complexity 2022, 2022, 7283252. [Google Scholar] [CrossRef]
- Ulam, S.M. A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics; No. 8 Interscience Publishers: New Yor, NY, USA; London, UK, 1960. [Google Scholar]
- Hyers, D.H. On the stability of the linear functional equation. Proc. Nat. Acad. Sci. USA 1941, 27, 222–224. [Google Scholar] [CrossRef]
- Rassias, T.M. On the stability of linear mappings in Banach spaces. Proc. Am. Math. Soc. 1978, 72, 297–300. [Google Scholar] [CrossRef]
- Hyers, D.H.; Isac, G.; Rassias Th, M. Stability of Functional Equations in Several Variables; Birkhauser: Boston, MA, USA, 1998. [Google Scholar]
- Jung, S.M. Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis; Hadronic Press: Palm Harbor, FL, USA, 2001. [Google Scholar]
- Jung, S.-M. Hyers-Ulam stability of linear differential equations of first order. Appl. Math. Lett. 2004, 17, 1135–1140. [Google Scholar] [CrossRef]
- Lungu, N.; Ciplea, S.A. Ulam-Hyers-Rassias stability of pseudoparabolic partial differential equations. Carpathian J. Math. 2015, 31, 233–240. [Google Scholar] [CrossRef]
- Shikhare, P.U.; Kucche, K.D. Existence, Uniqueness and Ulam Stabilities for Nonlinear Hyperbolic Partial Integrodifferential Equations. Int. J. Appl. Comput. Math. 2019, 5, 156. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, W.; Sheng, J.; Li, R. Ulam’s stability for some linear conformable fractional differential equations. Adv. Differ. Equations 2020, 2020, 251. [Google Scholar] [CrossRef]
- El-hady, E.; Ben Makhlouf, A. A novel stability analysis for the Darboux problem of partial differential equations via fixed point theory. AIMS Math. 2021, 6, 12894–12901. [Google Scholar] [CrossRef]
- Mchiri, L.; Ben Makhlouf, A.; Rguigui, H. Ulam–Hyers stability of pantograph fractional stochastic differential equations. Math. Methods Appl. Sci. 2023, 46, 4134–4144. [Google Scholar] [CrossRef]
- Kahouli, O.; Ben Makhlouf, A.; Mchiri, L.; Rguigui, H. Hyers–Ulam stability for a class of Hadamard fractional Itô–Doob stochastic integral equations. Chaos Solitons Fractals 2023, 166, 112918. [Google Scholar] [CrossRef]
- Houas, M.; Martinez, F.; Samei, M.E.; Kaabar, M.K.A. Uniqueness and Ulam-Hyers–Rassias stability results for sequential fractional pantograph q-differential equations. J. Inequalities Appl. 2022, 2022, 93. [Google Scholar] [CrossRef]
- Alzabut, J.; Selvam, A.G.M.; Dhineshbabu, R.; Kaabar, M.K.A. The existence, uniqueness, and stability analysis of the discrete fractional three-point boundary value problem for the elastic beam equation. Symmetry 2021, 13, 789. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Zhao, D.; Luo, M. General conformable fractional derivative and its physical interpretation. Calcolo 2015, 54, 903–917. [Google Scholar] [CrossRef]
- Guzman, P.M.; Langton, G.; Bittencurt, L.M.L.M.; Medina, J.; Valdes, J.E.N. A New Definition of a fractional derivative of local type. J. Math. Anal. 2018, 9, 88–98. [Google Scholar]
- Valdes, J.E.N.; GuzmÁNPM, L.L.M. Some New Results on Nonconformable Fractional Calculus. Adv. Dyn. Syst. Appl. 2018, 13, 167–175. [Google Scholar]
- Guzmán, P.M.; Lugo, L.M.; Valdes, J.E.N.; Vivas-Cortez, M. On a New Generalized Integral Operator and Certain Operating Properties. Axioms 2020, 9, 69. [Google Scholar] [CrossRef]
- Martínez, F.; Valdes, J.E.N. Towards a Non-conformable Fractional Calculus of n-Variables. J. Math. Appl. 2020, 43, 87–98. [Google Scholar] [CrossRef]
- Fleitas, A.; Valdes, J.E.N.; Rodríguez, J.M.; Sigarreta, J.M. Note on the generalized conformable derivative. Revista UMA 2021, 62, 443–457. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Lugo, L.M.; Valdes, J.E.N.; Samei, M.E. A Multi-Index Generalized Derivative Some Introductory Notes. Appl. Math. Inf. Sci. 2022, 16, 883–890. [Google Scholar]
- Inc, M.; Yusuf, A.; Aliyu, A.I.; Baleanu, D. Soliton solutions and stability analysis for some conformable nonlinear partial differential equations in mathematical physics. Opt. Quantum Electron. 2018, 50, 190. [Google Scholar] [CrossRef]
- Martinez, F.; Martinez, I.; Kaabar, M.K.A.; Paredes, S. Solving systems of conformable linear differential equations via the conformable exponential matrix. Ain Shams Eng. J. 2021, 12, 4075–4080. [Google Scholar] [CrossRef]
- Martinez, F.; Martinez, I.; Kaabar, M.K.A.; Paredes, S. Novel results on conformable Bessel functions. Nonlinear Eng. 2022, 11, 6–12. [Google Scholar] [CrossRef]
- Awadalla, M.; Subramanian, M.; Abuasbeh, K.; Manigandan, M. On the Generalized Liouville–Caputo Type Fractional Differential Equations Supplemented with Katugampola Integral Boundary Conditions. Symmetry 2022, 14, 2273. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghania, R.; Mchiri, L.; Rhaima, M.; Hannabou, M.; Ben Makhlouf, A. Stability Results for the Darboux Problem of Conformable Partial Differential Equations. Axioms 2023, 12, 640. https://doi.org/10.3390/axioms12070640
Ghania R, Mchiri L, Rhaima M, Hannabou M, Ben Makhlouf A. Stability Results for the Darboux Problem of Conformable Partial Differential Equations. Axioms. 2023; 12(7):640. https://doi.org/10.3390/axioms12070640
Chicago/Turabian StyleGhania, Rebiai, Lassaad Mchiri, Mohamed Rhaima, Mohamed Hannabou, and Abdellatif Ben Makhlouf. 2023. "Stability Results for the Darboux Problem of Conformable Partial Differential Equations" Axioms 12, no. 7: 640. https://doi.org/10.3390/axioms12070640
APA StyleGhania, R., Mchiri, L., Rhaima, M., Hannabou, M., & Ben Makhlouf, A. (2023). Stability Results for the Darboux Problem of Conformable Partial Differential Equations. Axioms, 12(7), 640. https://doi.org/10.3390/axioms12070640






