Outer Topology Network Synchronization Using Chaotic Nodes with Hidden Attractors
Abstract
1. Introduction
2. Complex Dynamical Networks
3. Master Stability Function
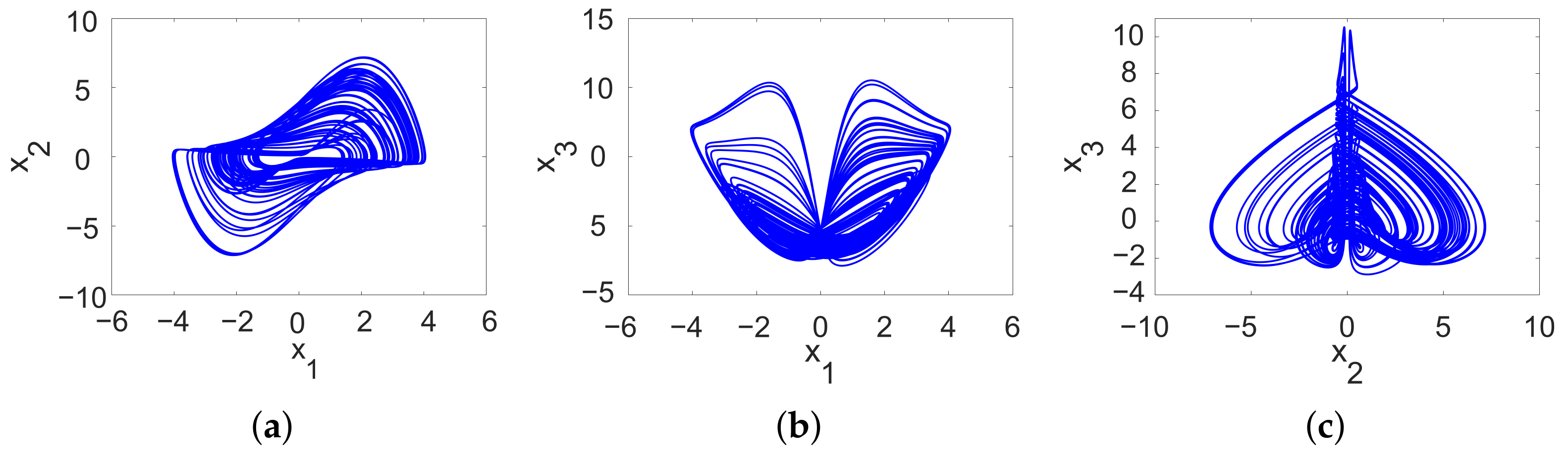
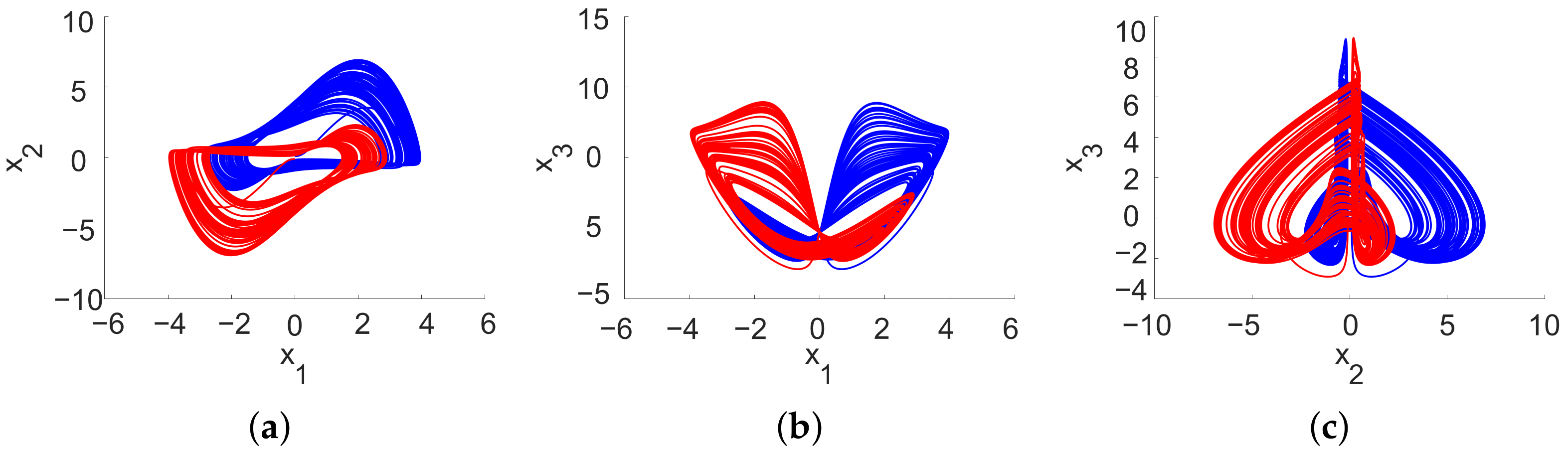
4. Chaotic Node
5. Synchronization of Inner and Outer Coupling Topologies
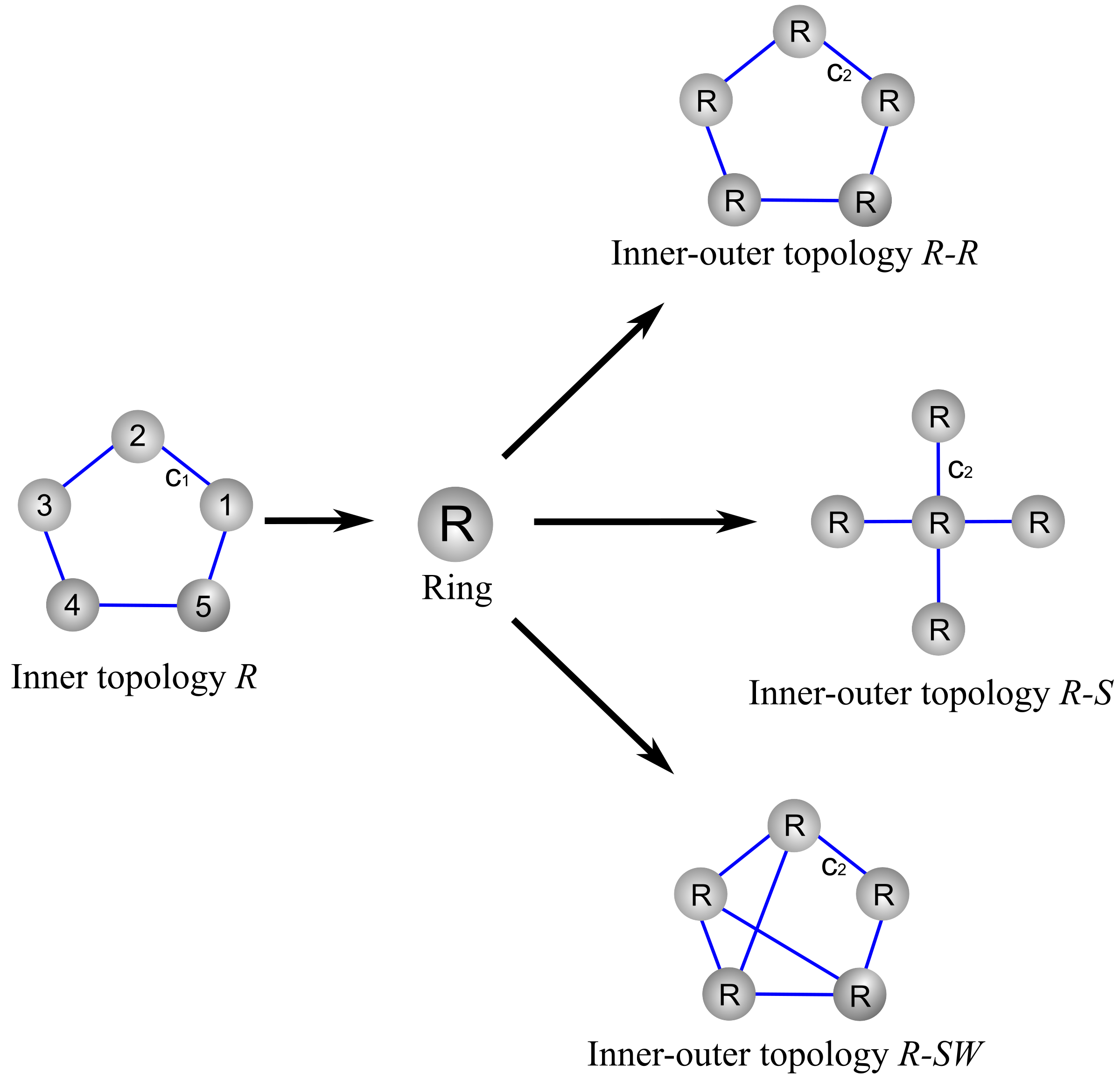
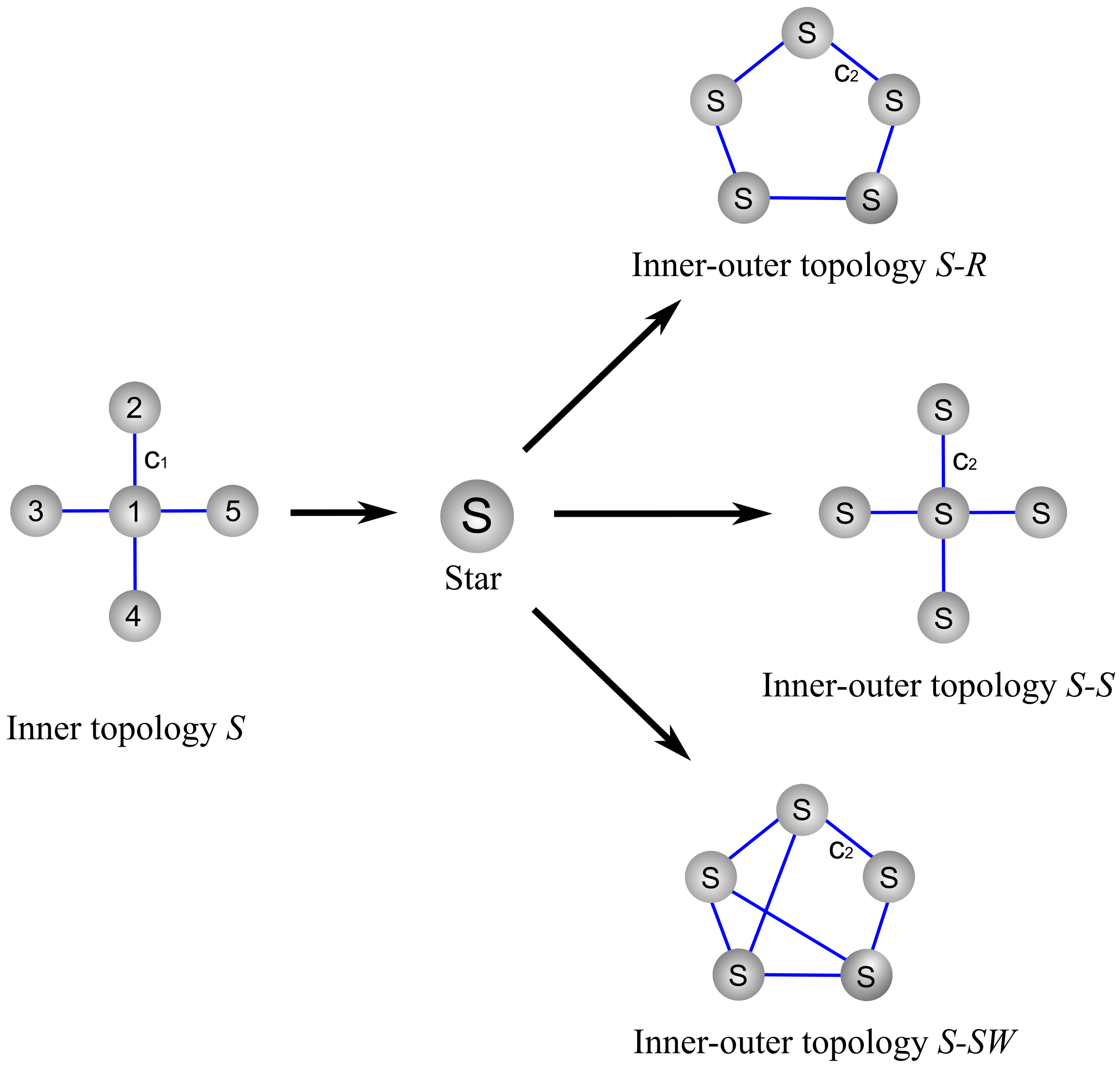
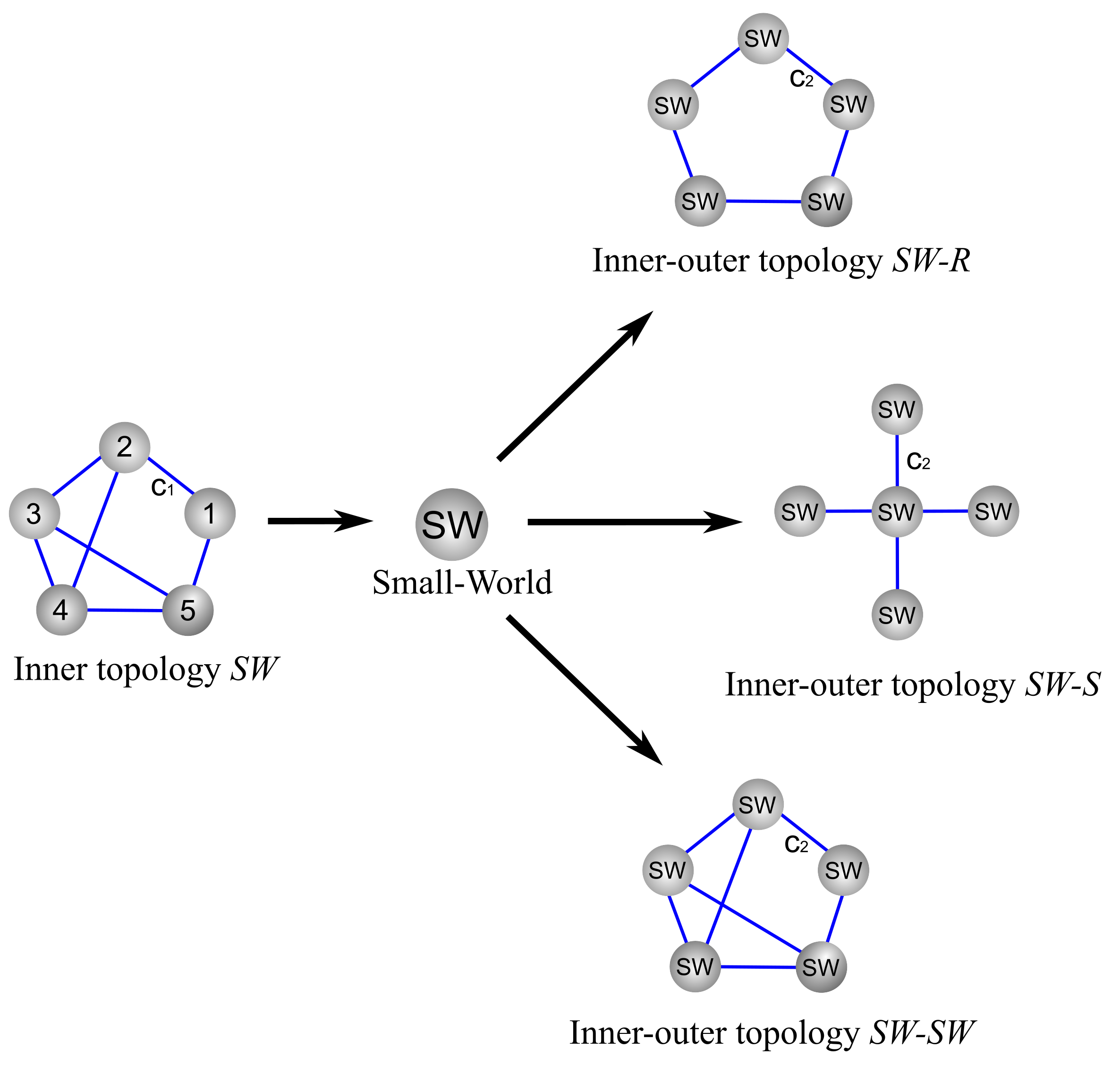
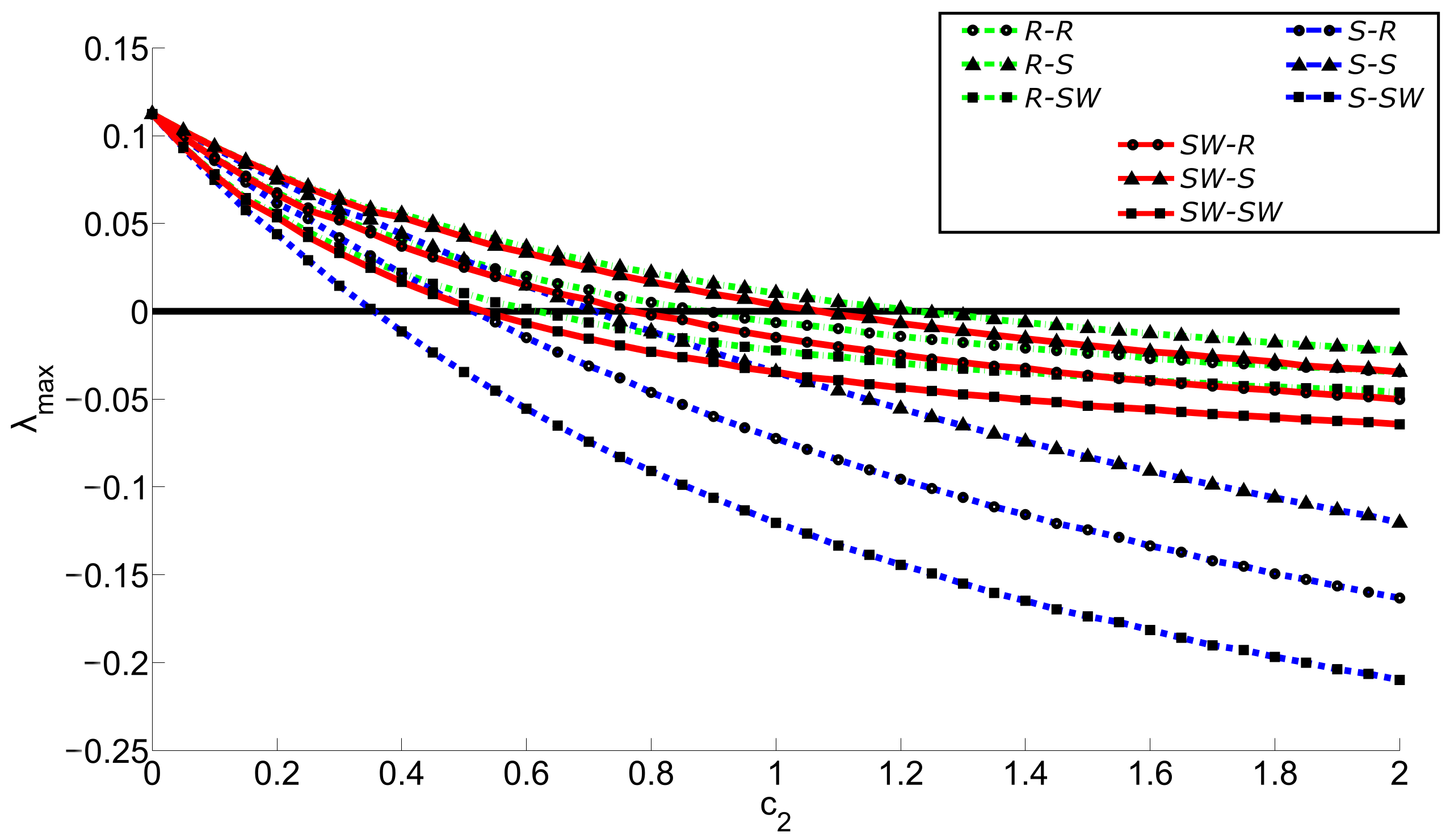
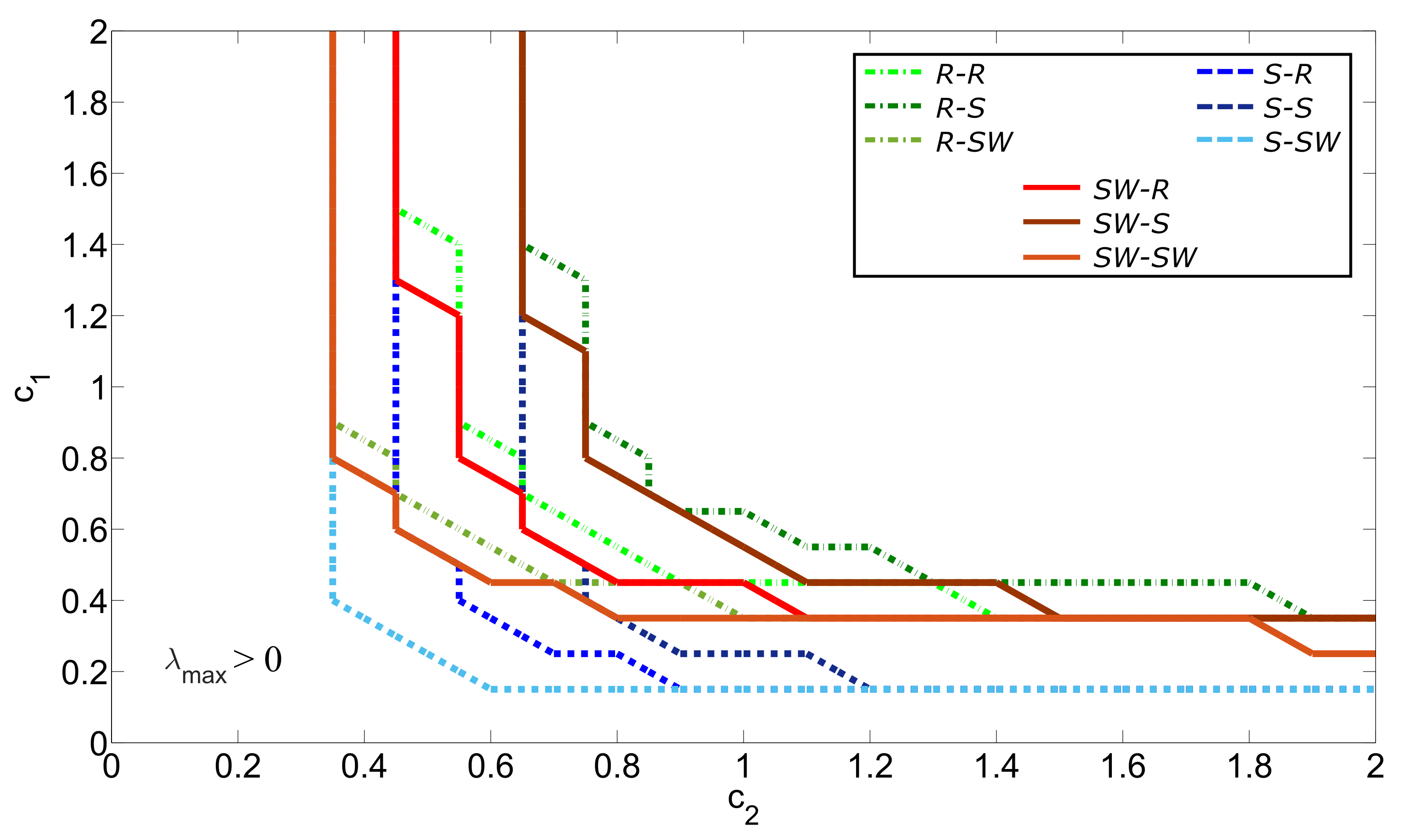
5.1. Inner Topologies of the Ring, Star, and Small-World Networks Synchronization
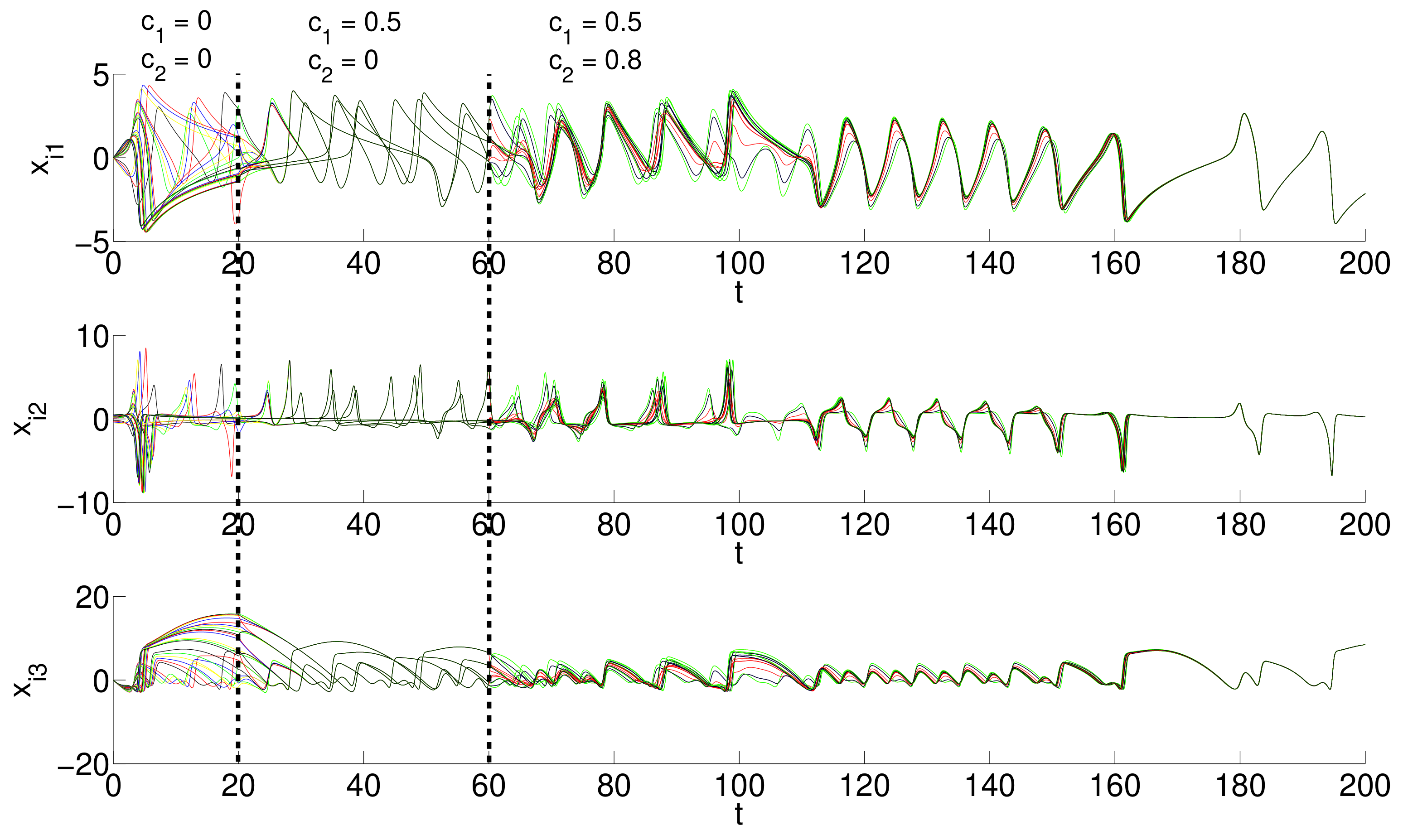
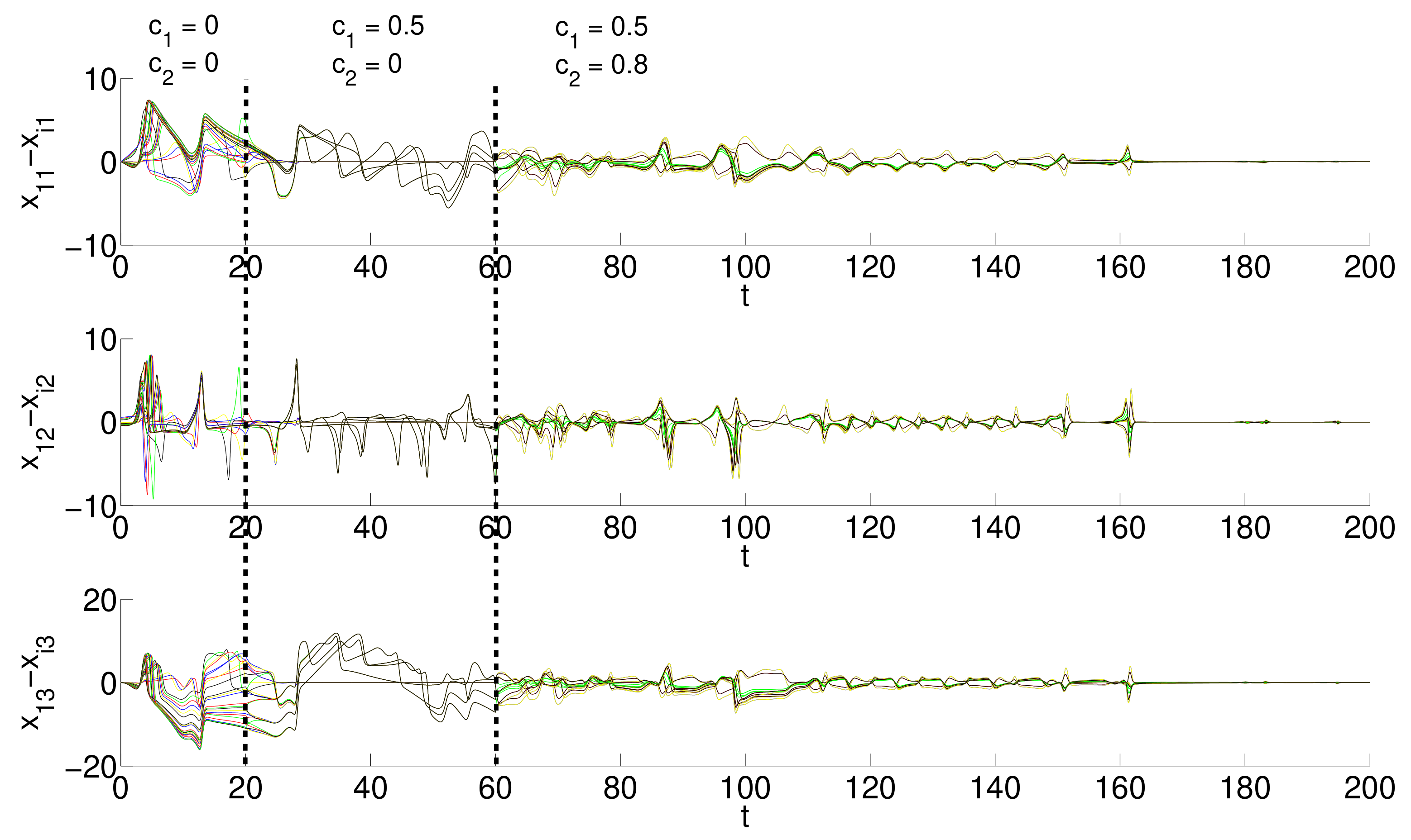
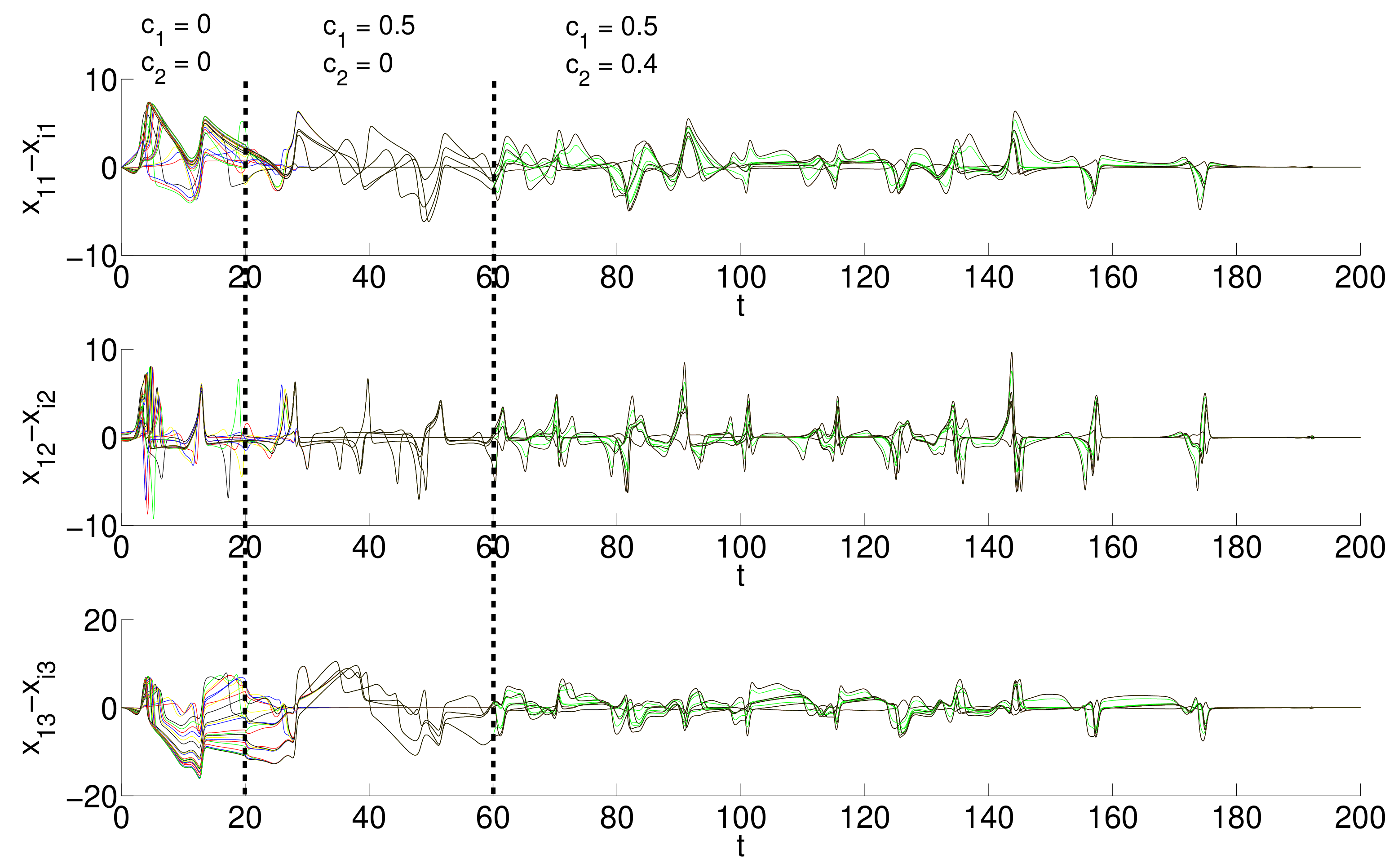
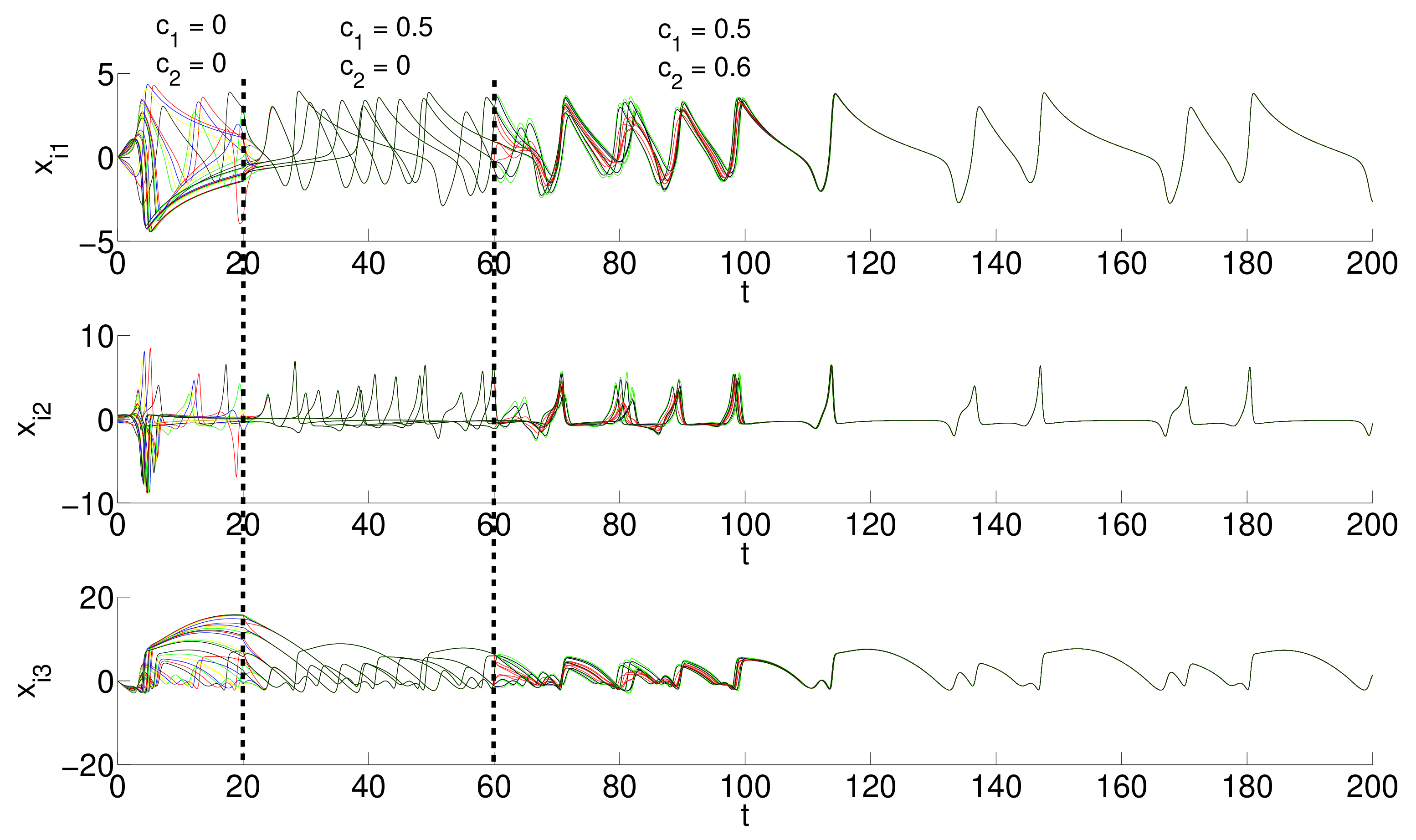
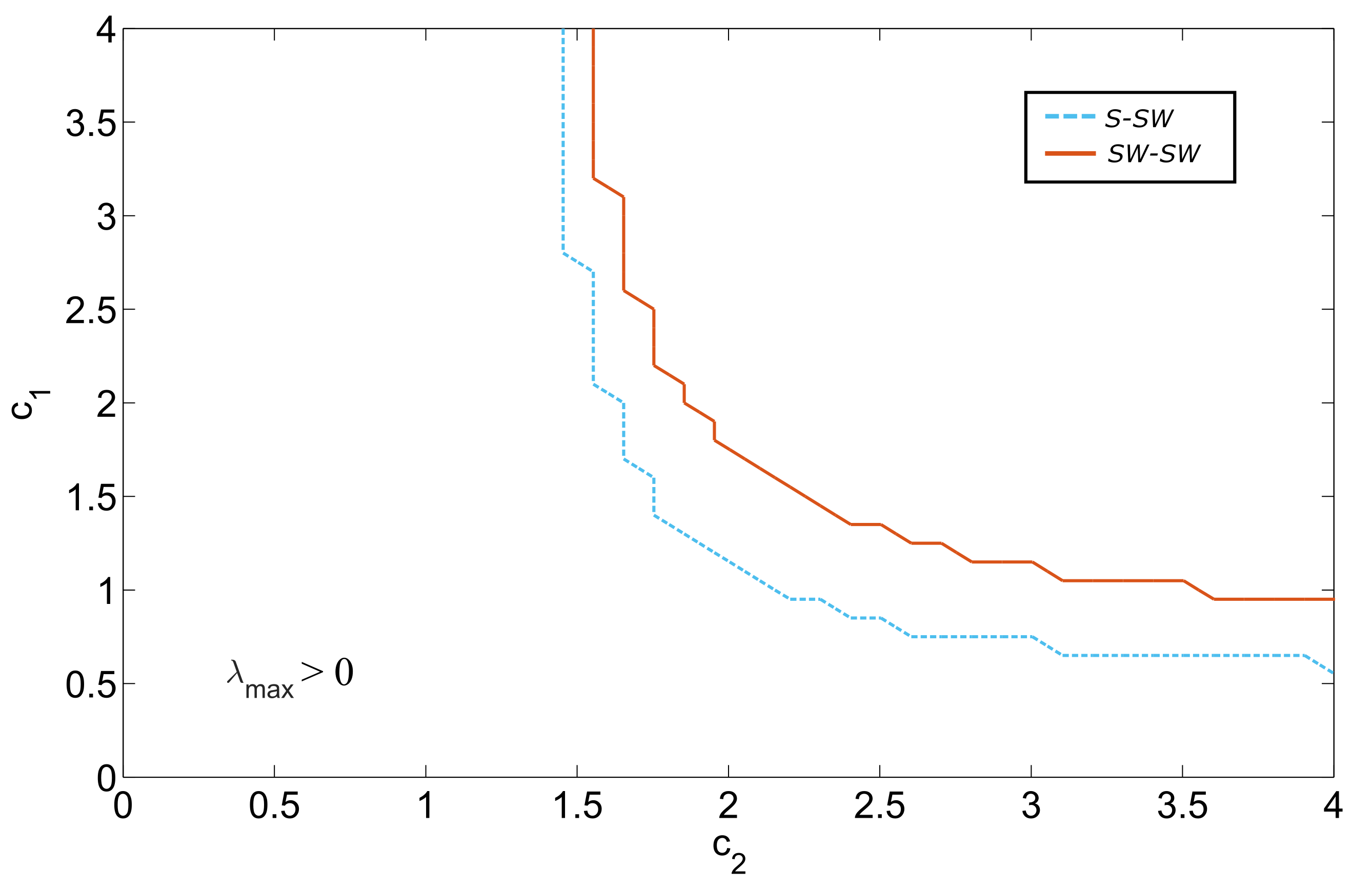
5.2. Outer Topology of Ring, Star, and Small-World Networks Synchronization
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pikovsky, A.; Rosenblum, M.; Kurths, J. A universal concept in nonlinear sciences. Self 2001, 2, 3. [Google Scholar]
- Blasius, B.; Huppert, A.; Stone, L. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 1999, 399, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1999, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Zambrano-Serrano, E.; Munoz-Pacheco, J.M.; Anzo-Hernández, A.; Félix-Beltrán, O.G.; Guevara-Flores, D.K. Synchronization of a cluster of β-cells based on a small-world network and its electronic experimental verification. Eur. Phys. J. Spec. Top. 2022, 231, 1035–1047. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López Gutiérrez, R.M.; Cruz-Hernández, C.; Martinez-Clark, R. Small-World Outer Synchronization of Small-World Chaotic Networks. J. Comput. Nonlinear Dyn. 2018, 13, 101008. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López Gutiérrez, R.M.; Méndez-Ramírez, R.; Cardoza-Avendaño, L.; Cruz-Hernández, C. Dynamic coupling in small-world outer synchronization of chaotic networks. Phys. D Nonlinear Phenom. 2021, 423, 132928. [Google Scholar] [CrossRef]
- Sun, J.; Bollt, E.M.; Porter, M.A.; Dawkins, M.S. A mathematical model for the dynamics and synchronization of cows. Phys. D 2011, 240, 1497–1509. [Google Scholar] [CrossRef]
- Bowen, T.A.; Zhivun, E.; Wickenbrock, A.; Dumont, V.; Bale, S.D.; Pankow, C.; Dobler, G.; Wurtele, J.S.; Budker, D. A network of magnetometers for multi-scale urban science and informatics. Geosci. Instrum. Methods Data Syst. 2019, 8, 129–138. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Zou, C.; Wei, X.; Zhang, Q.; Liu, Y. Synchronization of chemical reaction networks based on DNA strand displacement circuits. IEEE Access 2018, 6, 20584–20595. [Google Scholar] [CrossRef]
- Lü, L.; Zhang, F.; Zou, C. Finite-time synchronization in the laser network based on sliding mode control technology. Optik 2021, 225, 165605. [Google Scholar] [CrossRef]
- Lü, L.; Zhao, L. Finite-time synchronisation transmission of quantum signals between Jaynes-Cummings models based on coupling technology. Opt. Quantum Electron. 2023, 55, 145. [Google Scholar] [CrossRef]
- López-Mancilla, D.; López-Cahuich, G.; Posadas-Castillo, C.; Castañeda, C.E.; García-López, J.H.; Vázquez-Gutiérrez, J.L.; Tlelo-Cuautle, E. Synchronization of complex networks of identical and nonidentical chaotic systems via model-matching control. PLoS ONE 2019, 14, e0216349. [Google Scholar] [CrossRef]
- Strogatz, S.H. Sync: How Order Emerges from Chaos in the Universe, Nature, and Daily Life, 1st ed.; Hachette: Westport, CO, USA, 2003. [Google Scholar]
- Sun, W.; Yan, Z.Z.; Chen, S.H.; Lü, J.H. Outer synchronization of complex networks by impulse. Commun. Theor. Phys. 2011, 56, 885. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Sun, W. Adaptive outer synchronization and topology identification between two complex dynamical networks with time-varying delay and disturbance. IMA J. Math. Control. Inf. 2019, 36, 949–961. [Google Scholar] [CrossRef]
- Kuznetsov, N.V. Theory of Hidden Oscillations and Stability of Control Systems. J. Comput. Syst. Sci. Int. 2020, 59, 647–668. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Synchronization in small-world dynamical networks. Int. J. Bifurc. Chaos 2002, 12, 187–192. [Google Scholar] [CrossRef]
- Wang, X.F. Complex networks: Topology, dynamics and synchronization. Int. J. Bifurc. Chaos 2002, 12, 885–916. [Google Scholar] [CrossRef]
- Pecora, L.M.; Caroll, T.L. Master Stability Functions for Synchronized Coupled Systems. Phys. Rev. Lett. 1997, 80, 2109–2112. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Jafari, S.; Kapitaniak, T. Coexistence of hidden chaotic attractors in a novel no-equilibrium system. Nonlinear Dyn. 2017, 87, 2001–2010. [Google Scholar] [CrossRef]
- Reyes-De la Cruz, D.; Méndez-Ramírez, R.; Arellano-Delgado, A.; Cruz-Hernández, C. Electronic Implementation of a Deterministic Small-World Network: Synchronization and Communication. Entropy 2023, 25, 709. [Google Scholar] [CrossRef] [PubMed]
- Cetina-Denis, J.J.; Lopéz-Gutiérrez, R.M.; Cruz-Hernández, C.; Arellano-Delgado, A. Design of a Chaotic Trajectory Generator Algorithm for Mobile Robots. Appl. Sci. 2022, 12, 2587. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Barabási, A.-L. The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Dorogovtsev, S.N.; Mendes, J.F.; Dorogovtsev, S.N. Evolution of Networks: From Biological Nets to the Internet and WWW; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Newman, M.E.J.; Watts, D.J. Scaling and percolation in the small-world network model. Phys. Rev. E 1999, 60, 7332–7342. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López-Gutiérrez, R.M.; Murillo-Escobar, M.A.; Posadas-Castillo, C. Master—Slave Outer Synchronization in Different Inner—Outer Coupling Network Topologies. Entropy 2023, 25, 707. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villalobos-Aranda, C.A.; Arellano-Delgado, A.; Zambrano-Serrano, E.; Pliego-Jiménez, J.; Cruz-Hernández, C. Outer Topology Network Synchronization Using Chaotic Nodes with Hidden Attractors. Axioms 2023, 12, 634. https://doi.org/10.3390/axioms12070634
Villalobos-Aranda CA, Arellano-Delgado A, Zambrano-Serrano E, Pliego-Jiménez J, Cruz-Hernández C. Outer Topology Network Synchronization Using Chaotic Nodes with Hidden Attractors. Axioms. 2023; 12(7):634. https://doi.org/10.3390/axioms12070634
Chicago/Turabian StyleVillalobos-Aranda, Carlos Andrés, Adrian Arellano-Delgado, Ernesto Zambrano-Serrano, Javier Pliego-Jiménez, and César Cruz-Hernández. 2023. "Outer Topology Network Synchronization Using Chaotic Nodes with Hidden Attractors" Axioms 12, no. 7: 634. https://doi.org/10.3390/axioms12070634
APA StyleVillalobos-Aranda, C. A., Arellano-Delgado, A., Zambrano-Serrano, E., Pliego-Jiménez, J., & Cruz-Hernández, C. (2023). Outer Topology Network Synchronization Using Chaotic Nodes with Hidden Attractors. Axioms, 12(7), 634. https://doi.org/10.3390/axioms12070634






