Abstract
The emergence of SARS-CoV-2 virus mutations is a pressing concern in the context of the COVID-19 pandemic. In this paper, a Susceptible–Infected–Recovered (SIR) compartmental model has been formulated in terms of cellular automata and ordinary differential equations to simulate the transmission dynamics of a virus. This model accounts for the potential of new virus mutations to create additional infections of a multi-strain disease while also considering the impact of vaccination on disease control within a population. The basic reproduction number of the disease is derived, and the effect of virus mutations and vaccination rates is evaluated on a population over five years. The results of numerical simulations demonstrate the significant role of maintaining high vaccination rates in controlling the spread of the virus, even when assuming that all variants have similar illness characteristics and that a single shot of vaccine provides complete and lifelong protection against all strains. The findings underscore the necessity for countries to implement a consistent and high-level vaccination plan as soon as vaccines become available in order to mitigate the impact of a pandemic effectively. In conclusion, this study highlights the importance of taking into account the potential impact of virus mutations for controlling the COVID-19 pandemic. Furthermore, it emphasizes the critical role of vaccination in limiting the spread of the virus, and emphasizes the need to implement and maintain high vaccination rates as part of a comprehensive approach to managing the ongoing pandemic.
MSC:
92D30
1. Introduction
The COVID-19 pandemic is an ongoing global public health crisis, which has been further complicated by the emergence of several mutations in the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). These variants have distinct genetic profiles and exhibit varying clinical and epidemiological features. In March 2020, the D614G mutation, characterized by increased infectivity, became the predominant strain worldwide, replacing the strain reported in Wuhan [1]. In September 2020, a new variant, known as Cluster-5 or FVI-spike, emerged from mink farms in Denmark, resulting in the culling of approximately 17 million animals [2].
In December 2020, a variant of concern, SARS-CoV-2 VOC 202012/01, was identified in the United Kingdom. Preliminary reports suggested that this variant had increased transmissibility and mortality risk [3,4]. It has since been reported in over 62 countries [4]. In the same month, a new strain, 501Y.V2, was identified in South Africa, replacing the original strain in some provinces. Studies have demonstrated that this variant has higher viral loads, increased transmissibility, and reduced vaccine efficacy [3,5,6].
Another variant, named P.1, emerged in Brazil in November 2020, causing a second wave of infections in the country [7]. Recently, the Omicron variant was identified, and it has quickly become the predominant strain globally [8]. Notably, several new mutations have been detected in the spike protein of the virus, which is the primary target of current COVID-19 vaccines. The Beta, Gamma, and Delta variants have shown increased transmissibility and may be associated with higher rates of hospitalization and mortality [9].
The emergence and spread of these SARS-CoV-2 variants underscore the urgent need for continued surveillance and research to understand their clinical and epidemiological impact. Effective management of this pandemic requires a coordinated global response, including widespread vaccination and public health measures, such as physical distancing, wearing masks, and avoiding large gatherings. Furthermore, ongoing monitoring and genomic sequencing of the virus will be crucial in identifying new variants and developing strategies to combat their spread. Furthermore, without serious research on modelling such crises, control strategies aimed at combating mutating viruses or variations would inevitably fall short [10].
Hence, it is crucial for epidemiological modelling to account for novel variants of a disease in order to comprehend the dynamics of disease spread and furnish comprehensive solutions to public health officials. The necessity of a multidisciplinary approach for studying and managing virus variants usually begins with the use of mathematical modeling and differential equations, aiming to establish a framework for analyzing the interplay between viral mutations, transmission dynamics, and their impact on population-level infection patterns [11]. Within the ambit of this paper, we propose a disease transmission model that involves viral infection via human contact. This model accommodates the spontaneous emergence of new virus variants during the infection process, while also accounting for a spectrum of vaccination rates as a measure of disease control.
Previous works presented multi-strain disease models for a variety of objectives. In general, there is a need to assess the transmissibility of a new mutation, and whether this new mutation will be the majority of cases, invading a population and becoming endemic. Diseases transmitted both directly and environmentally [12], considering an age-structured model [13], formulated for mean-field and pair approximation approaches [14], and considering Malaria [15] and COVID-19 [16] are a few examples of multi-strain disease studies. Consider two strains of the same pathogen. If one strain in a host population may limit the growth or presence of another strain, we have competitive exclusion, which has also been taken into account due to important implications for disease dynamics and control strategies [15,17]. For example, if a highly infectious strain of a pathogen is introduced into a population that is already infected with a less infectious strain of the same pathogen, the highly infectious strain may outcompete the less infectious strain and become dominant. This could result in a more severe disease outbreak and potentially make control efforts more difficult.
In spite of the concerted efforts made by these models to generalize the outcomes across multiple strains prevalent in a population, the complexity of mathematical analysis directly corresponds to the number of strains involved. In the study conducted by Breban et al. [12], the stability of equilibria and the determination of the basic reproduction number were derived for multiple strains; however, the discussion was limited to the consideration of only two strains. Several other scholarly works have investigated scenarios involving two [17,18,19] and three [20] strains. Furthermore, certain studies have focused on evaluating the process by which the most successful strain would dominate the entire human population, thereby incorporating an evolutionary aspect into the investigation [13,15]. Consequently, there is a demand for a flexible model that accommodates the presence of any necessary number of strains, while simultaneously enabling a comprehensive mathematical analysis of the basic reproduction number.
The present model is constructed utilizing Probabilistic Cellular Automata (PCA) and Ordinary Differential Equations (ODE) within the framework of the Susceptible–Infected–Recovered (SIR) compartmental model. The use of cellular automata has been documented in the literature as a viable tool for simulating COVID-19 [21,22,23], as well as variations of compartmental models, particularly the Susceptible–Exposed–Infected–Recovered (SEIR) model, which accounts for an exposed state before infection [24,25,26]. Indeed, compartmental models have been tailored to meet specific research needs, such as the investigation of the impact of the COVID-19 pandemic on healthcare systems utilizing states related to hospitalized individuals [23,26]; the assessment of the influence of migrant-exposed individuals in predicting COVID-19 trends [27]; the use of separate asymptomatic and symptomatic infected states to study the effects of social isolation [22,23,28]; the propagation of two SARS-CoV-2 strains, separating the respective exposed and infected states [18]; and even the study of an elementary cellular automaton evolution for a visible representation of important features of the protein of SARS-CoV-2 [29]. Furthermore, PCA and ODE have been employed in tandem to compare the pairwise approach for modelling the contact between individuals (PCA) to the mean-field concept of ODE, with ODE representing a mean-field approximation for PCA [14,30,31].
In summary, cellular automata possess specific constraints that researchers must consider. These models operate under the assumption of cellular homogeneity, neglecting subtle variations and individual-level heterogeneity, thereby potentially compromising their accuracy in capturing the intricate intricacies of real-world scenarios. Additionally, they may encounter difficulties when incorporating evolving population structures and behavioral adaptations during disease outbreaks. Nonetheless, despite these limitations, which are also prevalent in alternative mathematical and computational methodologies, cellular automata continue to hold significance in the study of disease propagation dynamics, serving as valuable complements to other epidemiological modelling approaches.
A broad range of mutation and vaccination rates are taken into account, yielding numerous scenarios. The compartmental model consists of three states: susceptible, infected, and recovered (for the cases with zero viral mutations). During the process of infection, the virus has a chance of to undergo a mutation, thus producing a new strain and a distinct type of infected state. With the PCA and ODE models described, the basic reproduction number is derived from ODE using the next-generation matrix process [32,33].
The model has been formulated based on specific assumptions, consisting of the homogeneity of disease features across all viral variants, the probability of reinfection among individuals who have already recuperated from the disease by contracting new strains, the administration of single-dose vaccines that guarantee durable immunity against all viral variants, immediate onset of immunity post-inoculation, and a consistent and abundant supply of vaccines. Therefore, this paper presents a numerical exercise that showcases the effectiveness of achieving elevated vaccination rates in mitigating disease burden and preventing the emergence of forthcoming variants that may pose a significant risk to public health.
2. Methods
The probabilistic cellular automaton is structured on a square lattice with side n. The lattice consists of cells that represent individuals in one of the disease states. In the context where only a single viral strain exists within the population, an individual in the susceptible state may undergo infection with a probability of per time step. Following infection, the individual has a probability of recovering and transitioning to a recovered state with a probability of , as well as a probability of experiencing fatality due to the disease with a probability of per time step. Furthermore, a recovered individual may experience natural death with a probability of . In the event of fatality, a susceptible individual replaces the deceased member to ensure a constant population size.
The probability of individuals becoming infected is a function of their neighborhood. Each individual is connected to C neighbors located within a Moore radius r per time step. The neighborhood alters at each time step, with C connections being randomly established using the following procedure. An individual has a likelihood of establishing a connection to a cell in layer i, with the probability . By layer i, consider the cells that are at a Chebyshev distance of i. A random cell from this layer is selected, and C connections are established. Subsequently, the number of infected neighbors determines the probability of an individual being infected, given by , where k is a parameter associated with the disease’s infectivity. This approach has been employed in several previous works, such as [22,23,31]. When multiple disease strains are present in the population, the number of infected neighbors is counted separately, and the likelihood of becoming infected with each disease type is determined randomly to prevent any prioritization. It is assumed that an individual may only contract one strain of the disease at a time.
The introduction of new mutations into a model leads to the addition of new states. For example, in the case where two strains are circulating within a population, represents the state of individuals susceptible to all strains, while and denote the states of individuals susceptible to all strains except strain 1 and strain 2, respectively. These states represent individuals who have previously recovered from either strain 1 or strain 2. Infected individuals of strain 1 and strain 2 are denoted as and , respectively. Recovered individuals are represented by the state .
To illustrate the possible transitions between states, Figure 1 depicts a transition state diagram for a single strain, shown in blue with dark arrows, as well as the possibilities when three strains are present within the population, shown in light red with grey arrows. For instance, individuals who have recovered from strain 1 may become infected with either strain 2 or strain 3, and consequently, transition to either or , respectively. In the event of individual mortality, replacement occurs with individuals who are susceptible to all strains and are represented by the state . This mechanism maintains a constant population size.
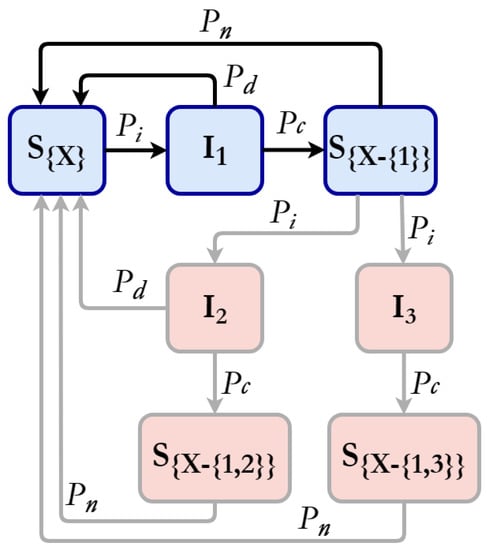
Figure 1.
Probabilistic state transition diagram. In blue, the case for a single strain of SARS-CoV-2 that confers immunity to this strain when cured. We have few examples of transitions in light red with light grey lines, such as an individual recovered from strain 1 being infected by strains 2 or 3 with respective possibilities of cure and death.
When vaccination is implemented in the population, susceptible individuals of any type are vaccinated per time step. Following vaccination, individuals become immune to the disease and are henceforth impervious to infection. The only possible state transition is the occurrence of natural death, whereby the decreased individual is replaced by an individual of the susceptible state .
The model was implemented using the C programming language and is available upon request to the author.
The ODE Model
Here, we propose an exercise to construct an ODE model from the PCA model in a systematic manner. Subsequently, we derive the basic reproduction number for a few cases, and extend it to the general scenario.
Let us begin by considering the case with a single variant. In this scenario, the ODE model can be expressed as follows:
where is the infection rate constant; p is the vaccination rate constant; b is the recovering rate constant; c is the death rate constant due to the disease; and e is the death rate constant due to other causes.
As in the PCA model, here the total number of individuals is also constant, because , then . Moreover, , p, b, c, e can be estimated from simulations, since the ODE model is a mean-field approximation. Based on [31], the expressions that link these models are
where
- is the increase in due to new infection cases from per time step;
- and are the increase in V due to vaccination of and per time step;
- is the increase in due to recovering of per time step;
- is the increase in related to death by the disease of ;
- and are the increase in due to deaths from another cause of and V per time step.
In this system, the disease-free equilibrium (DFE) corresponds to a stationary solution satisfying represented by . This point in the state space is of a particular interest since it is used to calculate the basic reproduction number using the next-generation matrix [33] method. From Equation (1), the infectious subsystem is given by
For this subsystem, the Jacobian matrix in the disease-free equilibrium is
Then, the Jacobian matrix is decomposed as , where T is the transmission part, containing the production of new infected, and is the transition part, containing changes in the states [32], only for the infected states. With these matrices, we calculate the dominant eigenvalue (spectral radius) of the matrix . Therefore,
and
The eingenvalue of is . Then, is given by
as analyzed in [31] for the case . If , the disease is endemic, and thus present in the permanent regime of the system; if , the disease is simply extinguished from the population.
If we consider two variants in the population, the ODE system presented in Equation (1) can be expanded to
where the new constants are as the infection rate of , generating an infected individual , and as the infection rate of , generating an infected individual . The total number of individuals is also constant, because , then . Note that and . From the individuals that are cured from the disease, part is recovered only for strain one, and part is recovered for both strains; the same is true for individuals. The new estimations of the constant rates from PCA are
with the new expressions being as the increase in due to new infection cases from per time step; is the increase in due to new infection cases from per time step; is the increase in due to new infection cases from per time step; is the increase in V due to vaccination of per time step; is the increase in V due to vaccination of per time step; is the increase in V due to vaccination of per time step; is the increase in due to recovering of previously cured from strain two per time step; is the increase in due to recovering of per time step; is the increase in due to recovering of previously cured from strain one per time step; is the increase in related to death by the disease of ; and is the increase in due to deaths from another cause of per time step.
In this system with two variants, the disease-free equilibrium (DFE) corresponds to a stationary solution satisfying represented by . From Equation (8), the infectious subsystem is given by
For this subsystem, the Jacobian matrix in the disease-free equilibrium , is
Decomposing the Jacobian matrix as ,
and
The eingenvalues of are: and . Then, is given by
Expanding the system to more than two strains can become laborious. However, due to the calculation by next-generation matrix, the basic reproduction number will always have the form presented before. Therefore, considering strains in the population, we have
In the next section, the results are presented.
3. Results
The cellular automata is configured with a square lattice of size , and 1,000,000 cells. At the beginning of the simulation, the states are homogeneously distributed over the lattice. To compare PCA and ODE models with one variant, one simulation in PCA is run with , , , , , , and vaccinations per time step (from time step ). After the system reaches the permanent regime, Equation (2) is used to estimate ODE constant rates. Figure 2 contains the time evolution of the PCA and ODE approaches.
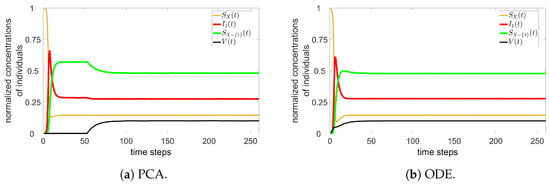
Figure 2.
PCA (a) and ODE (b) simulations for one variant.
For two variants, a PCA simulation is run with , , , , , , , and vaccinations per time step (from time step ). From PCA, the ODE approach with two variants is simulated using the constant rates from Equation (9). Figure 3 contains the time evolution of the PCA and ODE approaches.
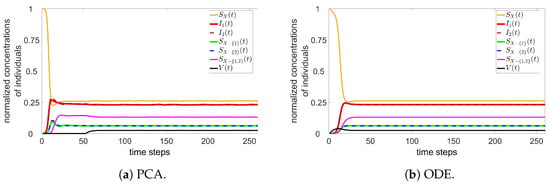
Figure 3.
PCA (a) and ODE (b) simulations for two variants.
Note that there is a good agreement between the approaches. Other parameters have been tested, always returning such similar results for PCA and ODE.
If we assume that a single time step of the simulation corresponds to one week of real time, and if the average duration during which an infected individual can spread the virus is roughly three weeks, we can estimate the probability of cure as . Additionally, we consider the probability of an infected individual dying from COVID-19 as 1%, denoted as [34,35,36]. Given the life expectancy of Brazil, which is approximately 76.3 years [37], we assume . To achieve an value within the range of , we adjust the values of , , and [36,38,39].
A summary of the variables and parameters of the PCA and ODE models is presented in Table 1.

Table 1.
Description of variables and parameters used for PCA and ODE models. * Note that C, r, and k were chosen to have an value within the range of ; we adjust the values to , , and .
Prior to analyzing the impact of mutations, Figure 4 presents the temporal evolution of the normalized cumulative deaths resulting from the disease, as a function of two key variables, k and vaccine efficacy (Figure 4a and Figure 4b, respectively). The vaccine efficacy utilized in all subsequent simulations is fixed at 100%; nevertheless, this figure enables consideration of two additional scenarios corresponding to lower vaccine efficacies. It is noteworthy that as k increases, so does the total number of deaths. The increase in deaths from to highlights how even a minor increase in k may significantly impact disease transmission as a result of increased mutational frequency. The simulations were executed under the conditions of vaccinations per time step, , , and , except where indicated otherwise.
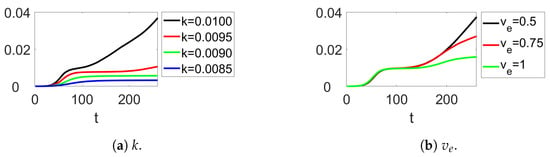
Figure 4.
Time evolution of the normalized accumulated number of deaths due to disease in function of (a) k and (b) the vaccine efficacy .
Once the parameters have been defined, it becomes feasible to assess the mutation and vaccination rates and generate simulation scenarios for the COVID-19 pandemic over a period of five years. The model posits that the mutation leading to the emergence of a new disease variant occurs during the infection process. In particular, when an individual is infected, there exists a probability that a new strain and disease variations may arise. Given that the vaccines were not immediately available, we assume that non-infected individuals are vaccinated per time step after 52 time steps of the simulation have elapsed. Consequently, it becomes possible to evaluate the impact of the values of and on the course of the pandemic’s evolution.
In order to accomplish this objective, we have conducted ten simulations for a duration of 260 time steps, encompassing all possible combinations of and within the range of and 30,000, resulting in a total of 12,000 simulations. Our analysis has primarily centered on five outputs, namely:
- The number of successful strains by the conclusion of the simulation. Specifically, those strains that have caused more than 1000 cases will be considered in the final results.
- The average number of new infection cases per time step at the end of the five-year simulation period will be calculated across all strains.
- The total number of deaths caused by all strains during the simulation.
- The duration of the pandemic, measured in weeks, specifically the time taken for zero cases per time step to occur.
- The basic reproduction number at the conclusion of the five-year simulation period.
These results, in function of and , are graphically represented in Figure 5. Notably, our findings underscore that a low vaccination rate coupled with a high mutation frequency results in a significant increase in multiple epidemiological metrics, including the number of successful mutations, the average count of new cases five years following the commencement of the pandemic, the total mortality rate, and the time required for the disease to be eradicated. However, it is pertinent to mention that the duration of the simulation was limited to 260 time steps, and hence the plateau depicted in Figure 5d signifies that the disease was not eradicated by the end of the simulation period.
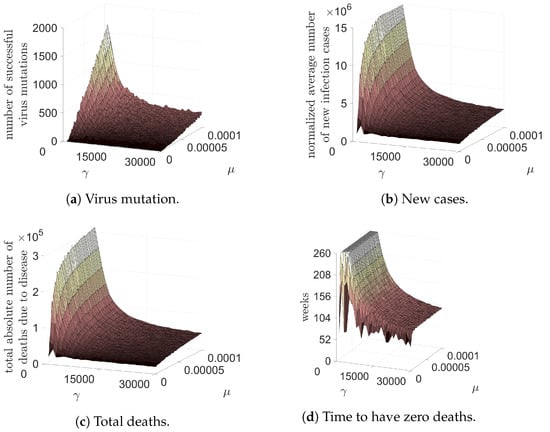
Figure 5.
Four variables in function of the mutation rate of the SARS-CoV-2 and vaccination rate: the number of successful virus mutations; normalized average number of new infection cases per time step after five years from the beginning of pandemic; total number of deaths in five years; and the time, in weeks, to have zero deaths due to COVID-19 pandemic.
The final result to be presented pertains to the basic reproduction number at the culmination of the five-year period. As depicted in Figure 6, is illustrated as a function of the vaccination rate and mutation, utilizing the average value for the last ten temporal steps. It is noteworthy that for a vaccination rate exceeding 5000 vaccinations per week, the contagion will no longer disseminate within the population beyond a five-year span. This is an important result, substantiating that persistent and uninterrupted vaccination measures can culminate in the eradication of an epidemic.
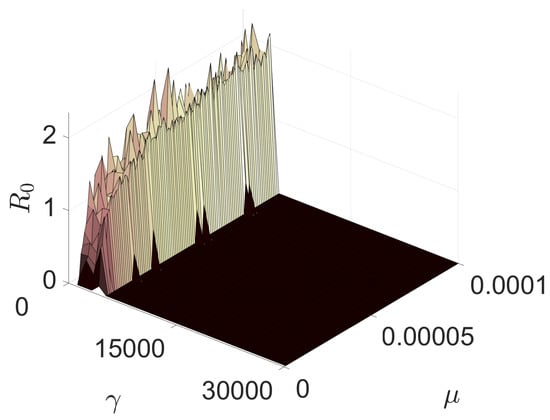
Figure 6.
Basic reproduction number in function of the mutation rate and vaccination rate.
In conclusion, our study underscores the importance of vaccination rates in controlling the spread of disease, particularly in the context of high mutation frequency. The simulation results highlight the significant impact of low vaccination rates and high mutation frequency on various epidemiological metrics, and the importance of maintaining sustained vaccination efforts in controlling the spread of disease.
4. Discussion
In the present study, a novel model has been proposed that utilizes probabilistic cellular automata and ordinary differential equations to simulate the transmission dynamics of a virus that may generate several active strains within the host population due to mutations. The basic reproduction number of the disease has been derived by employing the next-generation matrix process. Moreover, a vaccination strategy has been evaluated to mitigate the epidemic and confront the virus mutations over a period of five years. Although the model entails some strong assumptions, the findings underscore the critical significance of a consistent and comprehensive vaccination plan in curtailing the emergence of new mutations and ultimately eradicating the pandemic.
In this study, the COVID-19 pandemic served as a reference point for investigating a novel multi-strain disease model. Notably, the PCA flexibility, which is endorsed by the ODE approach, obviates the problem of high-dimensional analytical analysis commonly encountered in other publications in the field, where typically two [17,19] or three [20] strains are considered. The model presented herein is transferable to pathogenic diseases exhibiting drug resistance [17,40]. Although the model assumes equal epidemiological characteristics for all strains, the calculated basic reproduction number can be applied to strains possessing diverse transmissibility, illness severity, and mortality.
The world has undergone a considerable experience in combating the COVID-19 pandemic. Since December 2019, numerous mutations of the SARS-CoV-2 virus have dominated populations both locally and globally, exhibiting rapid dispersion, even during periods of lower international travel. The results presented herein exhibit two positive outcomes: vaccination reduces the number of successful SARS-CoV-2 mutations, and the incidence of COVID-19 cases and deaths decreased within the considered period, irrespective of the mutation rate. Additionally, Figure 5d illustrates a remarkable finding: regardless of the virus’s mutation rate, vaccinating 30,000 individuals (in our lattice) per time step (week) can end the pandemic within a year of vaccine availability. Since vaccination commenced after one year in the simulation (52 weeks), the pandemic could be over by March 2022, for all mutation rates. However, the pandemic’s end could be postponed by lower vaccine efficacy, individuals refusing to vaccinate in some countries, and mutations that evade vaccines. The significance of an early vaccination program has been substantiated in prior studies [20]. Furthermore, multi-strain models that incorporate vaccination strategies, assuming a two-dose regimen for achieving complete immunity, have demonstrated that one strain tends to prevail, ultimately leading to disease eradication when a substantial proportion of the population has received both vaccine shots, as outlined in the chosen parameters [16].
According to a recent study conducted by Oliveira et al. [41], the pandemic in Brazil could be effectively terminated within a year if a vaccination rate of 14 million individuals per week was achieved from the vaccine availability. Notably, the study’s findings were predicated upon the administration of a vaccine with a 50% efficacy rate, specifically Sinovac Biotech’s Coronavac, which was initially employed in Brazil’s vaccination campaign. In the current study, we have considered the use of a vaccine with a 100% efficacy rate, and our calculations have been based on a weekly dose administration of 30,000, which translates to 6 million doses for a population of approximately 200 million people in Brazil. It is imperative to acknowledge that this difference in the efficacy of the vaccine and the corresponding dose administration may affect the estimated timeline for terminating the pandemic.
Funding
This research was funded by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), grant number #440025/2020-6.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Conflicts of Interest
The author declares no conflict of interest.
References
- Korber, B.; Fischer, W.M.; Gnanakaran, S.; Yoon, H.; Theiler, J.; Abfalterer, W.; Hengartner, N.; Giorgi, E.E.; Bhattacharya, T.; Foley, B.; et al. Tracking Changes in SARS-CoV-2 Spike: Evidence that D614G Increases Infectivity of the COVID-19 Virus. Cell 2020, 182, 812–827.e19. [Google Scholar] [CrossRef] [PubMed]
- Koopmans, M. SARS-CoV-2 and the human-animal interface: Outbreaks on mink farms. Lancet Infect. Dis. 2021, 21, 18–19. [Google Scholar] [CrossRef]
- WHO. Disease Outbreak News—SARS-Cov-2 Variants; World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- OPAS. Atualização Epidemiológica: Variantes de SARS-CoV-2 nas Américas; Organização Pan-Americana da Saúde: Washington, DC, USA, 2021. [Google Scholar]
- Zucman, N.; Uhel, F.; Descamps, D.; Roux, D.; Ricard, J.D. Severe reinfection with South African SARS-CoV-2 variant 501Y.V2: A case report. Clin. Infect. Dis. 2021, ciab129. [Google Scholar] [CrossRef]
- Fontanet, A.; Autran, B.; Lina, B.; Kieny, M.P.; Karim, S.S.A.; Sridhar, D. SARS-CoV-2 variants and ending the COVID-19 pandemic. Lancet 2021, 6736, 19–21. [Google Scholar] [CrossRef]
- Naveca, F.; Souza, V.; Costa, C. COVID-19 epidemic in the Brazilian state of Amazonas was driven by long-term persistence of endemic SARS-CoV-2 lineages and the recent emergence of the new Variant of Concern P.1. Preprint 2021, 1–21. [Google Scholar] [CrossRef]
- WHO. Classification of Omicron (B.1.1.529): SARS-CoV-2 Variant of Concern; World Health Organization: Geneva, Switzerland, 2022. [Google Scholar]
- WHO. Tracking SARS-CoV-2 Variants; World Health Organization: Geneva, Switzerland, 2023. [Google Scholar]
- Elmouki, I.; Zhong, L.; Jraifi, A.; Darouichi, A. Optimal Control: Application and Applicability in Times of Pandemics. In Integrated Science of Global Epidemics; Rezaei, N., Ed.; Springer International Publishing: Cham, Switzerland, 2023; pp. 191–210. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Cot, C.; de Hoffer, A.; Hohenegger, S.; Sannino, F.; Vatani, S. Epidemiological theory of virus variants. Phys. A Stat. Mech. Its Appl. 2022, 596. [Google Scholar] [CrossRef]
- Breban, R.; Drake, J.M.; Rohani, P. A general multi-strain model with environmental transmission: Invasion conditions for the disease-free and endemic states. J. Theor. Biol. 2010, 264, 729–736. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Z.; Li, X.; Martcheva, M. Multi-strain persistence induced by host age structure. J. Math. Anal. Appl. 2012, 391, 595–612. [Google Scholar] [CrossRef]
- Wang, R.H.; Jin, Z.; Liu, Q.X. The evolutionary dynamics of a spatial multi-strain host-pathogen system with cross-immunity. Nonlinear Anal. Hybrid Syst. 2012, 6, 741–753. [Google Scholar] [CrossRef]
- Dang, Y.X.; Li, X.Z.; Martcheva, M. Competitive exclusion in a multi-strain immuno-epidemiological influenza model with environmental transmission. J. Biol. Dyn. 2016, 10, 416–456. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.C.; Liu, C.T. A Stochastic Multi-Strain SIR Model with Two-Dose Vaccination Rate. Mathematics 2022, 10, 1804. [Google Scholar] [CrossRef]
- Zheng, T.; Nie, L.F.; Teng, Z.; Luo, Y. Competitive exclusion in a multi-strain malaria transmission model with incubation period. Chaos Solitons Fractals 2020, 131, 109545. [Google Scholar] [CrossRef]
- Khyar, O.; Allali, K. Global dynamics of a multi-strain SEIR epidemic model with general incidence rates: Application to COVID-19 pandemic. Nonlinear Dyn. 2020, 102, 489–509. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Z.C.; Ruan, S. Dynamics of a time-periodic two-strain SIS epidemic model with diffusion and latent period. Nonlinear Anal. Real World Appl. 2020, 51, 102966. [Google Scholar] [CrossRef]
- Yaagoub, Z.; Allali, K. Global Stability of Multi-Strain SEIR Epidemic Model with Vaccination Strategy. Math. Comput. Appl. 2023, 28, 9. [Google Scholar] [CrossRef]
- Medrek, M.; Pastuszak, Z. Numerical simulation of the novel coronavirus spreading. Expert Syst. Appl. 2021, 166, 114109. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, L.H.; Gandini, D.M.; Schimit, P.H. The influence of immune individuals in disease spread evaluated by cellular automaton and genetic algorithm. Comput. Methods Programs Biomed. 2020, 196, 105707. [Google Scholar] [CrossRef]
- Schimit, P.H.T. A model based on cellular automata to estimate the social isolation impact on COVID-19 spreading in Brazil. Comput. Methods Programs Biomed. 2021, 200, 105832. [Google Scholar] [CrossRef] [PubMed]
- Hou, C.; Chen, J.; Zhou, Y.; Hua, L.; Yuan, J.; He, S.; Guo, Y.; Zhang, S.; Jia, Q.; Zhao, C.; et al. The effectiveness of the quarantine of Wuhan city against the Corona Virus Disease 2019 (COVID-19): Well-Mixed SEIR model analysis. J. Med. Virol. 2020, 92, 841–848. [Google Scholar] [CrossRef]
- Huang, R.; Liu, M.; Ding, Y. Spatial-temporal distribution of COVID-19 in China and its prediction: A data-driven modeling analysis. J. Infect. Dev. Ctries. 2020, 14, 246–253. [Google Scholar] [CrossRef]
- Lyra, W.; do Nascimento, J.D.; Belkhiria, J.; de Almeida, L.; Chrispim, P.P.M.; de Andrade, I. COVID-19 pandemics modeling with modified determinist SEIR, social distancing, and age stratification. The effect of vertical confinement and release in Brazil. PLoS ONE 2020, 15, e0237627. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef]
- Arcede, J.P.; Caga-anan, R.L.; Mentuda, C.Q.; Mammeri, Y. Accounting for Symptomatic and Asymptomatic in a SEIR-type model of COVID-19. Math. Model. Nat. Phenom. 2020, 15, 34. [Google Scholar] [CrossRef]
- Souza, L.F.; Filho, T.M.R.; Moret, M.A. Relating SARS-CoV-2 variants using cellular automata imaging. Sci. Rep. 2022, 12, 10297. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, L.; Chimara, H.; Chaui-Berlinck, J. Big cities: Shelters for contagious diseases. Ecol. Model. 2006, 197, 258–262. [Google Scholar] [CrossRef]
- Schimit, P.H.T.; Monteiro, L.H.A. On the basic reproduction number and the topological properties of the contact network: An epidemiological study in mainly locally connected cellular automata. Ecol. Model. 2009, 220, 1034–1042. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- Van Den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Faculty of Medicine, School of Public Health, Imperial College London: London, UK, 2020; pp. 3–20. [Google Scholar] [CrossRef]
- Hu, Z.; Song, C.; Xu, C.; Jin, G.; Chen, Y.; Xu, X.; Ma, H.; Chen, W.; Lin, Y.; Zheng, Y.; et al. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing, China. medRxiv 2020, 63, 706–711. [Google Scholar] [CrossRef]
- Singhal, T. Review on COVID19 disease so far. Indian J. Pediatr. 2020, 87, 281–286. [Google Scholar] [CrossRef]
- IBGE. Tábuas Completas de Mortalidade; Instituto Brasileiro de Geografia e Estatística: Rio de Janeiro, Brazil, 2021. [Google Scholar]
- Gostic, K.M.; Gomez, A.C.; Mummah, R.O.; Kucharski, A.J.; Lloyd-Smith, J.O. Estimated effectiveness of symptom and risk screening to prevent the spread of COVID-19. eLife 2020, 9, e55570. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Liu, Q.; Yang, Z.; Liao, J.; Yang, K.; Bai, W.; Lu, X.; Zhang, W. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV. J. Evid.-Based Med. 2020, 13, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Meehan, M.T.; Cocks, D.G.; Trauer, J.M.; McBryde, E.S. Coupled, multi-strain epidemic models of mutating pathogens. Math. Biosci. 2018, 296, 82–92. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, R.; Xavier, C.; Vieira, V.; Reis, R.; Quintela, B.; Rocha, B.; Santos, R. Nota Técnica 04—Como um Esquema Sólido de Vacinação Pode Controlar a Pandemia de COVID-19 no Brasil? Nota Técnica from Universidade Federal de Juiz de Fora; Universidade Federal de São João del Rey: São João del Rei, Brazil, 2021; pp. 1–9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).