Abstract
Analyzing the co-variability between the Hilbert regressor and the scalar output variable is crucial in functional statistics. In this contribution, the kernel smoothing of the Relative Error Regression (RE-regression) is used to resolve this problem. Precisely, we use the relative square error to establish an estimator of the Hilbertian regression. As asymptotic results, the Hilbertian observations are assumed to be quasi-associated, and we demonstrate the almost complete consistency of the constructed estimator. The feasibility of this Hilbertian model as a predictor in functional time series data is discussed. Moreover, we give some practical ideas for selecting the smoothing parameter based on the bootstrap procedure. Finally, an empirical investigation is performed to examine the behavior of the RE-regression estimation and its superiority in practice.
Keywords:
complete convergence (a.co.); relative error regression; nonparametric prediction; kernel method; bandwidth parameter; functional data; financial time series; quasi-associated process MSC:
62R20; 62G05; 62G08
1. Introduction
This paper focuses on nonparametric prediction in Hilbertian statistics, which is an intriguing area of research within nonparametric Hilbertian statistics. Various approaches exist for modeling the relationship between the input Hilbertian variable and the output real variable. Typically, this relationship is modeled through a regression model, where the regression operators are estimated using the least square error. However, this rule is not relevant for some practical cases. Instead, we consider in this paper the relative square error. The primary advantage of this regression is the possibility of reducing the effect of the outliers. This kind of relative error is used as a performance measure in many practical situations, namely in time series forecasting. The literature on the subject of nonparametric analysis is limited. Most existing works consider a parametric approach. In particular, Narula and Wellington [1] were the first to investigate the use of the relative square error in the estimation method. For practical purposes, relative regression has been applied in areas such as medicine by Chatfield [2] and financial data by Chen et al. [3]. Yang and Ye [4] considered the estimation by RE-regression in multiplicative regression models. Jones et al. [5] also focused on the use of this model but with the nonparametric estimation method and stated the convergence of the local linear estimator obtained by the relative error as a loss function. The RE-regression estimation has been deeply studied for time series data in the last few years, specifically by Mechab and Laksaci [6] for the quasi-associated time series, and Attouch et al. [7] for the spatial process. The nonparametric Hilbertian RE-regression was first developed by Demongeot et al. [8], who focused on strong consistency and gave the asymptotic law of the RE-regression. To summarize, functional statistics is an attractive subject in mathematical statistics; the reader may refer to some survey papers, such as [9,10,11,12,13,14,15], for recent advances and trends in functional data analysis and/or functional time series analysis.
In this article, we focus on the Hilbertian RE-regression for weak functional time series data. In particular, the correlation of our observations is modeled by using the quasi-association assumption. This correlation includes many important Hilbertian time series cases, such as the linear and Gaussian processes, as well as positive and negative associated processes. Our ambition in this contribution is to build a new Hilbertian predictor in the Hilbertian time series. This predictor is defined as the ratio of the first and the second inverted conditional moments. We use this explicit expression to construct two estimators based on the kernel smoothing and/or k-Neighbors Number (kNN). We prove a strong consistency of the constructed estimator, which provides good mathematical support for its use in practice. Thus, treating the functional RE-regression by the kNN method under quasi-associated assumption is a great theoretical development which requires nonstandard mathematical tools and techniques. On the one hand, it is well known that the establishment of the asymptotic property in the kNN method is more difficult than the classical kernel estimation due to the random feature of the bandwidth parameter. On the other hand, our weak structure of the functional time series data requires additional techniques and mathematical tools alternative to those used in the mixing case. Clearly, this theoretical development is very useful in practice because the kNN estimator is more accurate than the kernel method and the quasi-association structure is sufficiently weak to cover a large class of functional time series data. Furthermore, the applicability of this estimator is highlighted by giving some selection procedures to determine the parameters involved in the estimator. Then, real data are used to emphasize the superiority and impact of this contribution in practice.
This paper is organized as follows. We introduce the estimation algorithms in Section 2. The required conditions, as well as the main asymptotic results, are demonstrated in Section 3. We discuss some selectors for the smoothing parameter in Section 4. The constructed estimator’s performance over the artificial data is evaluated in Section 5. Finally, we state our conclusion in Section 6 and demonstrate proofs of the technical results in the Appendix A.
2. The Re-Regression Model and Its Estimation
As discussed in the introduction, we aim to evaluate the relationship between an exogenous Hilbertian variable X and a real endogenous variable Y. Specifically, the variables belong in . The set constitutes a separable Hilbert space. We assume that the norm in is associated with the inner product . Furthermore, we define on a complete orthonormal basis . In addition, we suppose that Y is strictly positive, and we suppose that the Hilbertian operators and exist and are, almost surely, finite. The RE-regression is defined by
By differentiating with respect to , we prove that
Clearly, the RE-regression is a good alternative to the traditional regression, in the sense that, the traditional regression, based on the least square error, treats all variables with equal weight. This is inadequate when the observations contain some outliers. Thus, the traditional regression can lead to irrelevant results in the presence of outliers. Thus, the main advantage of the RE-regression compared to the traditional regression is the possibility to reduce the effect of the outliers (see Equation (1)). So, we can say that the robustness feature is one of the main advantages of the RE-regression. Additionally, unlike the classical robust regression (the M-egression), the RE-regression is very easy to implement in practice. It has an explicit definition based on the ratio of the first and the second inverted conditional moments (see Equation (2)).
Now, consider strictly stationary observations, as copies of a couple . The Hilbertian time series framework of the present contribution is carried out using the quasi-association setting (see Douge [16] for the definition of the Hilbert space). We use the kernel estimators of the inverse moments and as conditional expectations of (), given , to estimate by
where is a positive sequence of real numbers, and K is a real-function so-called kernel. The choice of is the determining issue of the applicability of the estimator . A common solution is to utilize kernel smoothing with the kNN estimation, for which
where
where is an open ball of radius centered x. In , the smoothing parameter is the number k. Once again, the selection of k is crucial.
3. The Consistency of the Kernel Estimator
We demonstrate the almost complete convergence of to at the fixed point x in . Hereafter, is the given neighborhood of x, and are strictly positive constants. In the sequel, we put , and , and we denote this by
where . Moreover, we assume the following conditions:
- (D1)
- For all , and .
- (D2)
- For all ,
- (D3)
- The covariance coefficient is , such that
- (D4)
- K is the Lipschitzian kernel function, which has as support and satisfies the following:
- (D5)
- The endogenous variable Y gives:
- (D6)
- For all ,
- (D7)
- There exist and
- Brief comment on the conditions: Note that the required conditions stated above are standard in the context of Hilbertian time series analysis. Such conditions explore the fundamental axes of this contribution. The functional path of the data is explored through the condition (D1), the nonparametric nature of the model is characterized by (D2), and the correlation degree of the Hilbertian time series is explored by conditions (D3) and (D6). The principal parameters used in the estimator, namely the kernel and the bandwidth parameter, are explored through the conditions, (D4), (D5), and (D6). Such conditions are of a technical nature. They allow for retaining the usual convergence rate in nonparametric Hilbertian time series analysis.
Theorem 1.
Based on the conditions (D1)–(D7), we get
where .
Proof of Theorem 1.
Firstly, we write
where
We use a basic decomposition (see Demongeot et al. [8] to deduce that Theorem 1 is a consequence result of the below lemmas). □
Lemma 1.
Using the conditions (D1) and (D3)–(D7), we get
and
Lemma 2.
Under conditions (D1),(D2), (D4), and (D7), we get
and
Corollary 1.
Using the conditions of Theorem 1, we obtain
Next, to prove the consistency of , we adopt the following postulates:
- (K1)
- has a bounded derivative on ;
- (K2)
- The function , such thatwhere , are positive and bounded functions, and is an invertible function;
- (K3)
- There exist and such that
Theorem 2.
Under conditions (D1)–(D6) and (K1)–(K3), we have
Proof of Theorem 2.
Similarly to Theorem 1, write
where
and we define, for a sequence , such that , , and . Using standard evidence (see Bouzebda et al. [17] ), we deduce that Theorem 2 is the outcome of Theorem 1 and the two lemmas below. □
Lemma 3.
Under the conditions of Theorem 2, we have
Lemma 4.
Based on the conditions of Theorem 2, we obtain
Corollary 2.
Using the conditions of Theorem 2, we get
and
4. Smoothing Parameter Selection
The applicability of the estimator is related to the selection of the parameters used for the construction of the estimator . In particular, the bandwidth parameter has a decisive effect on the implementation of this regression in practice. In the literature on nonparametric regression analysis, there are several ways to achieve this issue. In this paper, we adopt two approaches common in classical regression to the relative one. The two selections are the cross-validation rule and the bootstrap algorithm.
4.1. Leave-One-Out Cross-Validation Principle
In classical regression, the leave-one-out cross-validation rule is obtained using the mean square error. This criterion has been employed for predicting Hilbertian time series by several authors in the past (see Feraty and View [18] for some references). The leave-one-out cross-validation rule is easy to execute and has shown good behavior in practice. However, it is a relatively time-consuming rule. We overcome this inconvenience by reducing the cardinal of the optimization set of the rule. Thus, we adopt this rule for this kind of regression analysis. Specifically, we consider some subset of smoothing parameters (resp. number of the neighborhood) (resp. ), and we select the best bandwidth parameter as follows.
or
where (resp. ) is the leave-out-one estimator of (resp. ). The latter is calculated without the observation . It is worth noting that the efficiency of this estimator is also linked to the determination of the subset , where the rule (7) is optimized. Often, we distinguish two cases, the local case and the global case. In the local one, the subset is defined with respect to the number of neighborhoods near the location point. For the global case, the subset is the quantile of the vector distance between the Hilbertian regressors. The choice of is easier, and it suffices to take as a subset of a positive integer. This selection procedure has shown good behavior in practice, but there is no theoretical result concerning its asymptotic optimality. This will be a significant prospect for the future.
4.2. Bootstrap Approach
In addition to the leave-one-out cross-validation rule, the bootstrap method constitutes another important selection method. The principle of the latter is based on the plug-in estimation of the quadratic error. In the rest of this subsection, we describe the principal steps of this selection procedure.
- Step 1.
- We choose an arbitrary bandwidth (resp. ), and we calculate (resp. ).
- Step 2.
- We estimate (resp. ).
- Step 3.
- We create a sample of residual (resp. ) from the distributionwhere is the Dirac measure (see Hardle and Marron [19] for more details).
- Step 4.
- We reconstruct the sample (resp.
- Step 5.
- We use the sample to calculate and to calculate .
- Step 6.
- We repeat the previous steps times and put (resp. ), the estimators, at the replication r.
- Step 7.
- We select h (resp. k) according to the criteriaand
Once again, the choice of the subset (resp. ) and the pilot bandwidth (resp. ) have a significant impact on the performance of the estimator. It will be very interesting to combine both approaches in order to benefit from the advantage of both selections. However, the time cost of this idea is very important.
5. Computational Study
5.1. Empirical Analysis
As a theoretical contribution, we wish in this empirical analysis to inspect the easy implementation of the built estimator in practice. As the determination of is the principal challenge of the computation ability of , we compared in this computational study the two selections discussed in the previous section. For this purpose, we conducted an empirical analysis based on artificial data generated through the following nonparametric regression
where is known regression operator r and sequence of independent random variable generated from a Gaussian distribution . The model, in (9), shows the relationship between an endogenous and exogenous variable.
On the other hand, in order to prospect the dependency of the data, we generated the Hilbertian regressor by using the Hilbertian GARCH process through dgp.fgarch from the R-package rockchalk. We plotted, in Figure 1, a sample of the exogenous curves .
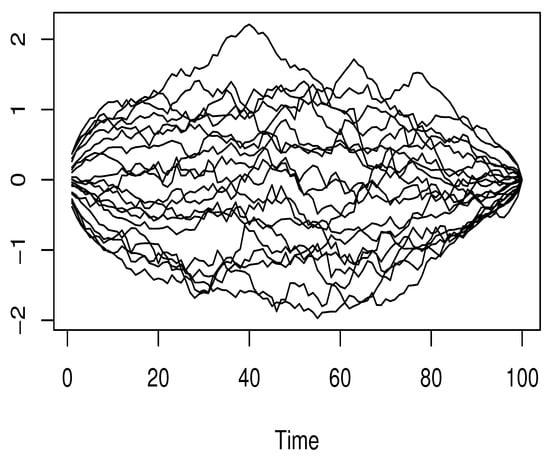
Figure 1.
Displayed is a sample of the functional curves.
The endogenous variable Y was generated by
For this empirical analysis, we compared the two selectors (7) and (8) with the mixed one obtained by using the optimal h of the rule (7) as the pilot bandwidth in the bootstrap procedure (8). For a fair comparison between the three algorithms, we optimized over the same subset . We selected the optimal h for the three selectors, and the subset of the quantiles of the vector distance between the Hilbertian curves observations of (the order of the quantiles was . Finally, based on a quadratic kernel on , the estimator was computed, and we utilized the metric associated with the PCA definition based on the first eigenfunctions of the empirical covariance operator associated with the greatest eigenvalues (see Ferraty and Vieu [18]).
The efficiency of the estimation method was evaluated by plotting the true response value versus the predicted values . In addition, we used the relative error defined by
to evaluate the performance of this simulation study, which performed over 150 replications. The prediction results are depicted in Figure 2.
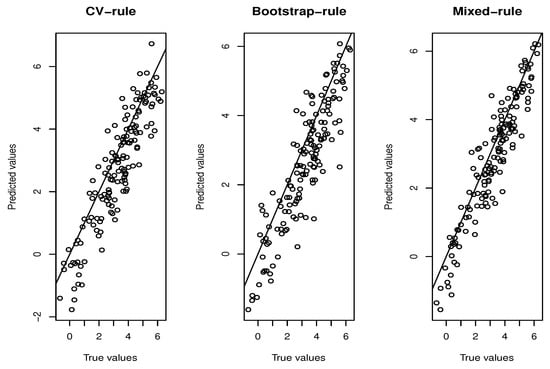
Figure 2.
Prediction results.
It shows clearly that the of the relative regression was very easy to implement in practice, and both selection algorithms had satisfactory behaviors. Typically the mixed approach performed better compared to the two separate approaches. It had an . On the other hand, the cross-validation rule had a small superiority () over the bootstrap approach ) in this case. Of course, this small superiority was justified by the fact that the efficiency of the bootstrap approach was based on the pilot bandwidth parameter , whereas the cross-validation rule was strongly linked to the relative error loss function.
5.2. A Real Data Application
We devote this paragraph to the real application of the RE-regression as a predictor. Our ambition is to emphasize the robustness of this new regression. To do this, we compared it to the classical regression defined by the conditional expectation. For this purpose, we considered physics data corresponding to the monthly number of sunspots in the years 1749–2021. These data were available at the website of WDC-SILSO, Royal Observatory of Belgium, Brussels, http://www.sidc.be (accessed on 1 April 2023). The prediction of sunspots is very useful in real life. It can be used to forecast the space weather, assess the state of the ionosphere, and define the appropriate conditions of radio shortwave propagation or satellite communications. It is worth noting that these kinds of data can be viewed as a continuous time process, which is the principal source of a Hilbertian time series by cutting the continuous trajectory into small intervals with fixed larger intervals. To fix these ideas, we plotted the initial data in Figure 3.
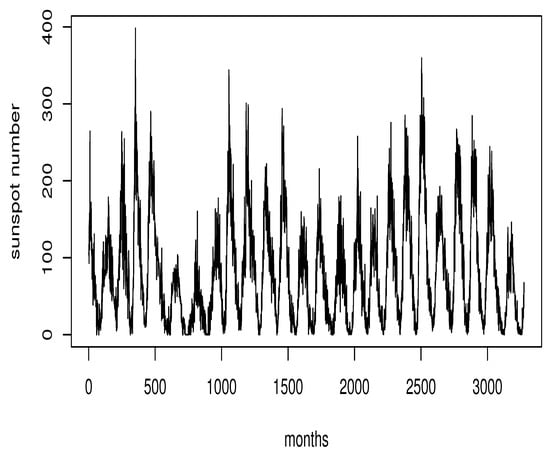
Figure 3.
Initial data.
To predict the value of a sunspot in the future, given its past observations in a continuous path, we use the whole data set, as a real-valued process in continuous time. We then constructed, from , n Hilbertian variables , where
Thus, our objective was to predict , knowing and . At this stage, was the predictor of . In this computational study, we aimed to forecast the sunspot number one year ahead, given the observation of the past years. Thus, we fixed on month j in 1, …, 12, and computed the estimator by the sample , with as the sunspot number of jth months in the th year, and we repeated this estimation procedure for all .
As the main feature of the RE-regression is its insensitivity to the outliers, we examined this property by detecting the number of outliers in each prediction step j. To do this, we used a MAD-Median rule (see Wilcox and Rand [20]). Specifically, the MAD-Median rule considers an observation as an outlier if
where M and MAD are the medians of , and respectively, and (with one degree of freedom). Table 1 summarizes the number of outliers for each step j.

Table 1.
Number of outliers with respect to j.
Both estimators and
were simulated using the quadratic kernel , where
and norm
was associated with the PCA-metric with . The cross-validation rule (7) is used to choose the smoothing parameter h. Figure 4 shows the prediction results, where we drew two curves showing the predicted values (the dashed curve for the relative regression and the point curve for the classical regression) and the observed values (solid curve).
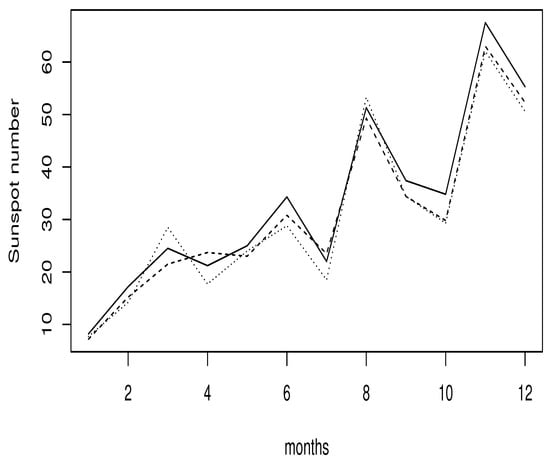
Figure 4.
Comparison of the prediction result.
Figure 4 shows that performed better in terms of the prediction results compared to . Even though both predictors had good behavior, the ASE of the relative regression (2.09) was smaller than the classical regression, which was equal to 2.87.
6. Conclusions
In the current contribution, we focused on the kernel estimation of the RE-regression when the observations exhibited quasi-associated autocorrelation. It constituted a new predictor in the Hilbertian time series, an alternative to classical regression based on conditional expectation. Clearly, this new estimator increased the robustness of the classical regression because it reduced the effect of the largest variables. Therefore, it made this Hilbertian model insensitive to the outlier observations; this is the main feature of this kind of regression. We provided in this contribution two rules to select the bandwidth parameter. The first was based on adapting the cross-validation rule to the relative error loss function. The second was obtained by the adaptation of the wild bootstrap algorithm. The simulation experiment highlighted the applicability of both selectors in practice. In addition to these features, the present work opened an important number of questions for the future. First, establishing the asymptotic distribution of the present estimator allows extending the applicability of this model to other applied issues in statistics. The second natural prospect focuses on the treatment of some alternative Hilbertian time series, including the ergodic case, the spatial case, and the -mixing case, among others. It will also be very interesting to study another type of data (missing, censored, …) or another estimation method, such as the kNN, local linear method, …, etc.
Author Contributions
The authors contributed approximately equally to this work. Formal analysis, F.A.; Validation, Z.C.E. and Z.K.; Writing—review & editing, I.M.A., A.L. and M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research project was funded by the Deanship of Scientific Research, Princess Nourah bint Abdulrahman University, through the Program of Research Project Funding after Publication, grant No. (43-PRFA-P-25).
Data Availability Statement
The data used in this study are available through the link http://www.sidc.be (accessed on 1 April 2023).
Acknowledgments
The authors would like to thank the Associate Editor and the referees for their very valuable comments and suggestions which led to a considerable improvement of the manuscript. The authors also thank and extend their appreciation to the Deanship of Scientific Research, Princess Nourah bint Abdulrahman University for funding this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this appendix, we briefly give the proof of preliminary results; the proofs of Lemmas 3 and 4 are omitted, as they can be obtained straightforwardly through the adaptation of the proof of Bouzebda et al. [17].
Proof of Lemma 1.
Clearly, the proof of both terms is very similar. So, we will focus only in the first one. In fact, the difficulty in this kind of proof comes from the fact that the quantity is not bounded. So, to deal with this problem, the truncation method is used to define
Then, the desired result is a consequence of
and
We start by proving (A3). For this, we write
with
Observe that,
The key tool for proving (A3) is the application of Kallabis and Newmann’s inequality (see [21], p. 2). We apply this inequality on Yi. It requires evaluating asymptotically two quantities: and , for all and
Concerning the variance term, we write
Note that the above formula has two terms. For the and under (D5), we obtain
Then, we use
to deduce that
Now, we need to examine the covariance term. To do that, we use the techniques of Massry to obtain the decomposition:
Note that is a positive sequence of real number integers, which tends to infinity as .
We use the second part of (D5) to obtain
Therefore,
Since the observations are quasi-associated, and the kernel K is bounded, based on the Lipschitz, we obtain
Then, by (A5) and (A6), we obtain
Putting , we obtain
Combining together results (A4) and (A7), we show that
We evaluate the covariance term
To do that, we treat the following cases:
- The first case is ; based on the definition of quasi-association, we obtainOn the other hand, we haveFurthermore, taking a -power of (A9) and a -power of (A10), we get for
- The second one is where . In this case, we have
So, we are in a position for Kallabis and Newmann’s inequality for the variable , where
It allows us to have
Choosing the adequately leads to achieving the proof of (A3).
Next, to prove (A1), use Holder’s inequality to write that
Since , which allows us to obtain
We use Markov’s inequality to obtain the last claimed result (A2). Hence, for all
Then,
Use the definition of to achieve the proof of the lemma. □
Proof of Lemma 2.
Once again, the focus is on the first statement’s proof; the second statement is obtained in the same way. In fact, the proof of both results uses the stationarity of the couples . Therefore, we write
The conditions (D2) and (D4) imply
Hence,
□
Proof of Corollary 1.
Clearly, we can obtain that
So,
Consequently,
□
References
- Narula, S.C.; Wellington, J.F. Prediction, linear regression and the minimum sum of relative errors. Technometrics 1977, 19, 185–190. [Google Scholar] [CrossRef]
- Chatfield, C. The joys of consulting. Significance 2007, 4, 33–36. [Google Scholar] [CrossRef]
- Chen, K.; Guo, S.; Lin, Y.; Ying, Z. Least absolute relative error estimation. J. Am. Statist. Assoc. 2010, 105, 1104–1112. [Google Scholar] [CrossRef]
- Yang, Y.; Ye, F. General relative error criterion and M-estimation. Front. Math. China 2013, 8, 695–715. [Google Scholar] [CrossRef]
- Jones, M.C.; Park, H.; Shin, K.-I.; Vines, S.K.; Jeong, S.-O. Relative error prediction via kernel regression smoothers. J. Stat. Plan. Inference 2008, 138, 2887–2898. [Google Scholar] [CrossRef]
- Mechab, W.; Laksaci, A. Nonparametric relative regression for associated random variables. Metron 2016, 74, 75–97. [Google Scholar] [CrossRef]
- Attouch, M.; Laksaci, A.; Messabihi, N. Nonparametric RE-regression for spatial random variables. Stat. Pap. 2017, 58, 987–1008. [Google Scholar] [CrossRef]
- Demongeot, J.; Hamie, A.; Laksaci, A.; Rachdi, M. Relative-error prediction in nonparametric functional statistics: Theory and practice. J. Multivar. Anal. 2016, 146, 261–268. [Google Scholar] [CrossRef]
- Cuevas, A. A partial overview of the theory of statistics with functional data. J. Stat. Plan. Inference 2014, 147, 1–23. [Google Scholar] [CrossRef]
- Goia, A.; Vieu, P. An introduction to recent advances in high/infinite dimensional statistics. J. Multivar. Anal. 2016, 146, 1–6. [Google Scholar] [CrossRef]
- Ling, N.; Vieu, P. Nonparametric modelling for functional data: Selected survey and tracks for future. Statistics 2018, 52, 934–949. [Google Scholar] [CrossRef]
- Aneiros, G.; Cao, R.; Fraiman, R.; Genest, C.; Vieu, P. Recent advances in functional data analysis and high-dimensional statistics. J. Multivar. Anal. 2019, 170, 3–9. [Google Scholar] [CrossRef]
- Aneiros, G.; Horova, I.; Hušková, M.; Vieu, P. On functional data analysis and related topics. J. Multivar. Anal. 2022, 189, 3–9. [Google Scholar] [CrossRef]
- Chowdhury, J.; Chaudhuri, P. Convergence rates for kernel regression in infinite-dimensional spaces. Ann. Inst. Stat. Math. 2020, 72, 471–509. [Google Scholar] [CrossRef]
- Li, B.; Song, J. Dimension reduction for functional data based on weak conditional moments. Ann. Stat. 2022, 50, 107–128. [Google Scholar] [CrossRef]
- Douge, L. Théorèmes limites pour des variables quasi-associées hilbertiennes. Ann. L’Isup 2010, 54, 51–60. [Google Scholar]
- Bouzebda, S.; Laksaci, A.; Mohammedi, M. The k-nearest neighbors method in single index regression model for functional quasi-associated time series data. Rev. Mat. Complut. 2023, 36, 361–391. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis; Springer Series in Statistics; Theory and Practice; Springer: New York, NY, USA, 2006. [Google Scholar]
- Hardle, W.; Marron, J.S. Bootstrap simultaneous error bars for nonparametric regression. Ann. Stat. 1991, 16, 1696–1708. [Google Scholar] [CrossRef]
- Wilcox, R. Introduction to Robust Estimation and Hypothesis Testing; Elsevier Academic Press: Burlington, MA, USA, 2005. [Google Scholar]
- Kallabis, R.S.; Neumann, M.H. An exponential inequality under weak dependence. Bernoulli 2006, 12, 333–335. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).