1. Introduction
Non-convex optimization is a type of mathematical optimization problem in which the objective function to be optimized is not convex. Unlike convex optimization problems, non-convex problems can have multiple local optima, which can make it difficult to find the global optimum. Non-convex optimization has many applications in various fields, including finance (portfolio optimization, risk management, and option pricing) [
1,
2,
3], computer vision (image segmentation, object recognition) [
4,
5], signal processing (compressed sensing, channel estimation, and equalization) [
6,
7,
8], engineering (control systems, optimization of structures) [
9,
10], machine learning [
11,
12,
13,
14], and damage characterization [
15] based on deep neural networks and the YUKI algorithm [
16].
To solve non-convex optimization problems, two broad classes of techniques have been developed: deterministic and stochastic methods [
17]. Deterministic methods include gradient-based methods, which rely on computing gradients of the objective function, and which can be sensitive to the choice of initialization and can converge to local optima. On the other hand, stochastic methods use randomness to explore the search space and can be less sensitive to initialization and more likely to find the global optimum.
Several reasons make stochastic methods more appropriate for non-convex optimization problems. Stochastic methods avoid getting stuck in local optima or saddle points, as they explore the search space more thoroughly. Additionally, complex non-convex optimization problems often have a large number of variables, making gradient-based methods computationally expensive. In contrast, stochastic methods can scale better to high-dimensional problems. Stochastic methods can also be more robust to noise and uncertainty in the problem formulation.
Scientific studies have shown the effectiveness of stochastic methods in solving non-convex optimization problems. One of the most widely studied deterministic methods that has been extended with random perturbations is gradient descent. For example, a study by Pogu and Souza de Cursi (1994) [
18] compared the performance of deterministic gradient descent and stochastic gradient descent on a variety of non-convex optimization problems and found that stochastic gradient descent was more robust and could converge to better solutions. Another study by Mandt et al. (2016) [
19] investigated the use of random perturbations in the context of Bayesian optimization and found that it could lead to better exploration of the search space and improved optimization performance. In addition to stochastic gradient descent, other deterministic methods have also been extended with random perturbations. For example, a study by Nesterov and Spokoiny (2017) [
20] proposed a variant of the conjugate gradient method that adds random noise to the search direction at each iteration and showed that it could improve the convergence rate and solution quality compared to the standard conjugate gradient method. Another study by Songtao Lu et al. (2019) [
21] proposed a variant of the projected gradient descent method that added random perturbations to the method, and they demonstrated its effectiveness in solving non-convex optimization problems.
We consider non-convex optimization problems with linear equality or inequality constraints of the form
where
is a continuously differentiable function,
A is an
matrix with rank
m,
b is an
m-vector, and the lower and upper bound vectors,
and
, may contain some infinite components; and
where
,
, and
is a continuously differentiable, non-convex objective function.
One possible numerical method to solve problem (
1) is the conditional gradient with bisection (CGB) method. This method generates a sequence of feasible points
, starting with an initial feasible point
. A new feasible point
is obtained from
for each
, using an operator
(details can be found in
Section 3). The iterations can be expressed as follows:
In this paper, we present a new approach for solving large-scale non-convex optimization problems by using a modified version of the conditional gradient algorithm that incorporates stochastic perturbations. The main contribution of this paper is to propose the RPCGB algorithm, which is an extension of a method previously presented in [
22] that was designed for small- and medium-scale problems. The RPCGB algorithm was developed to deal with large-scale global optimization problems and aims to determine the global optimum.
This method involves replacing the sequence of vectors
with a sequence of random vectors
, and the iterations are modified as follows:
where
is a random variable that is chosen appropriately, which is commonly known as the stochastic perturbation. It is important that the sequence
converges to zero at a rate slow enough to avoid the sequence
convergence to local minima. For more details, refer to
Section 4.
The paper is structured as follows:
Section 3 revisits the principle of the conditional gradient with bisection method, while
Section 4 provides details on the random perturbation of the CGB method. Notations are introduced in
Section 2, and in
Section 5, the results of numerical experiments for non-convex optimization tests with linear constraints are presented for large-scale problems.
4. RPCGB Method
From [
23], when it comes to objective functions that are non-convex, optimization algorithms based on gradients (CGB) cannot guarantee the discovery of the global minimum. Convex functions are the only ones for which CGB methods can find the global minimum. To deal with this issue, we suggest utilizing a suitable random perturbation method. Next, we will demonstrate how RPCGB can converge to a global minimum for non-convex optimization problems.
The sequence of real numbers
is replaced by a sequence of random variables
involving a random perturbation
of the deterministic iteration (
7). We have
;
where
satisfies Step 7 in the conditional gradient algorithm (Algorithm 1), and
Equation (
9) can be considered a perturbation of the upward direction
, which is substituted with a new direction
. As a result, iterations (
9) become:
In the literature [
18,
26,
27], general properties can be found to select a sequence suitable for perturbation
. Typically, perturbations that satisfy these features are produced using sequences of Gaussian laws.
We define a random vector and use the symbols and to represent its cumulative distribution function and probability density function, respectively.
The conditional probability density function of
is represented by
, and the conditional cumulative distribution function is designated as
|
.
We define a sequence of n-dimensional random vectors . Additionally, we also take into account , a decreasing sequence of positive real numbers that steadily approaches 0, where is less than or equal to 1.
We suppose that
is a decreasing function defined on
such that
For simplicity, let
and
where
Z is a random variable.
The procedure generates a sequence
By construction, this sequence is increasing and upper-bounded by
Thus, there exists
V ≤
such that
Lemma 1. Let and if is given by (12). Then, there exists such thatwhere . Proof. Let for
Since
it can be deduced from (
2) that
is non-empty and has a strictly positive measure.
If for any the result is immediate, since we have on
Let us assume that there exists such that For we have and
for any
and, since the sequence
is increasing, we also have
Letting
we have from (
13)
However, the Markov chain produces
By the conditional probability rule,
Taking (
10) into account, we have
Relation (
5) shows that
and (
11) yields
□
The following result, which follows from Borel–Catelli’s lemma (as described in [
18], for example), is a consequence of the global convergence:
Lemma 2. Let be a increasing sequence, upper-bounded by . Then, there exists V such that for . Assume that there exists such that, for any , there is a sequence of strictly positive real numbers , such that Then almost surely.
Proof. For instance, see [
18,
28]. □
Theorem 1. Assuming belongs to M, and letting , let the sequence be non-increasing, and Then almost surely.
Proof. Since the sequence
is non increasing,
Thus, Equation (
15) shows that
We can conclude that almost surely by applying Lemmas 1 and 2. □
Theorem 2. Let be defined by (12) and bywhere , , and t is the iteration number. If , then for large enough, almost surely. Proof. For
, such that
we have
furthermore, as per the previous Theorem 2, it can be deduced that
V is almost surely equal to
. □
5. Numerical Results
In this section, we present numerical results of six examples implemented using the CGB method and the perturbed RPCGB method. Our aim is to compare the performance of these two algorithms.
We begin by applying the algorithm to the initial value, which is . At each step , is known, and we calculate .
denotes the number of perturbations. When , the method used is the conditional gradient with bisection, without any perturbations (unperturbed conditional gradient with bisection method).
The Gaussian variates used in our experiments are generated using regular generator calls. Specifically, we use
The definitions of the methods listed in the tables are as follows:
- (i)
“CGB”, the method of conditional gradient and bisection;
- (ii)
“RPCGB”, the method of random perturbation of conditional gradient and bisection.
The proposed RPCGB algorithm is implemented using the MATLAB programming language. We evaluate the performance of the RPCGB method and compare it with the CGB method for high-dimensional problems. We test the efficacy of these algorithms on several problems [
29,
30,
31,
32] with linear constraints, using predetermined feasible starting points
. The results are presented in
Table 1,
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6 and
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6, where
n denotes the dimension of the problem under consideration and
represents the number of constraints. The reported test results include the optimal value
and the number of iterations
.
The optimal line search process of CGB and RPCGB is found using the bisection method with . We terminate the iterative process when either the best solution (global solution) is found or the maximum number of iterations has been reached.
All algorithms were run on a TOSHIBA Intel(R) Core(TM) CPU running at 2.40 GHz with 6 GB of RAM, a Core i7 processor, and the 64-bit Windows 7 Professional operating system. The “CPU” column in the table displays the mean CPU time for one run in seconds.
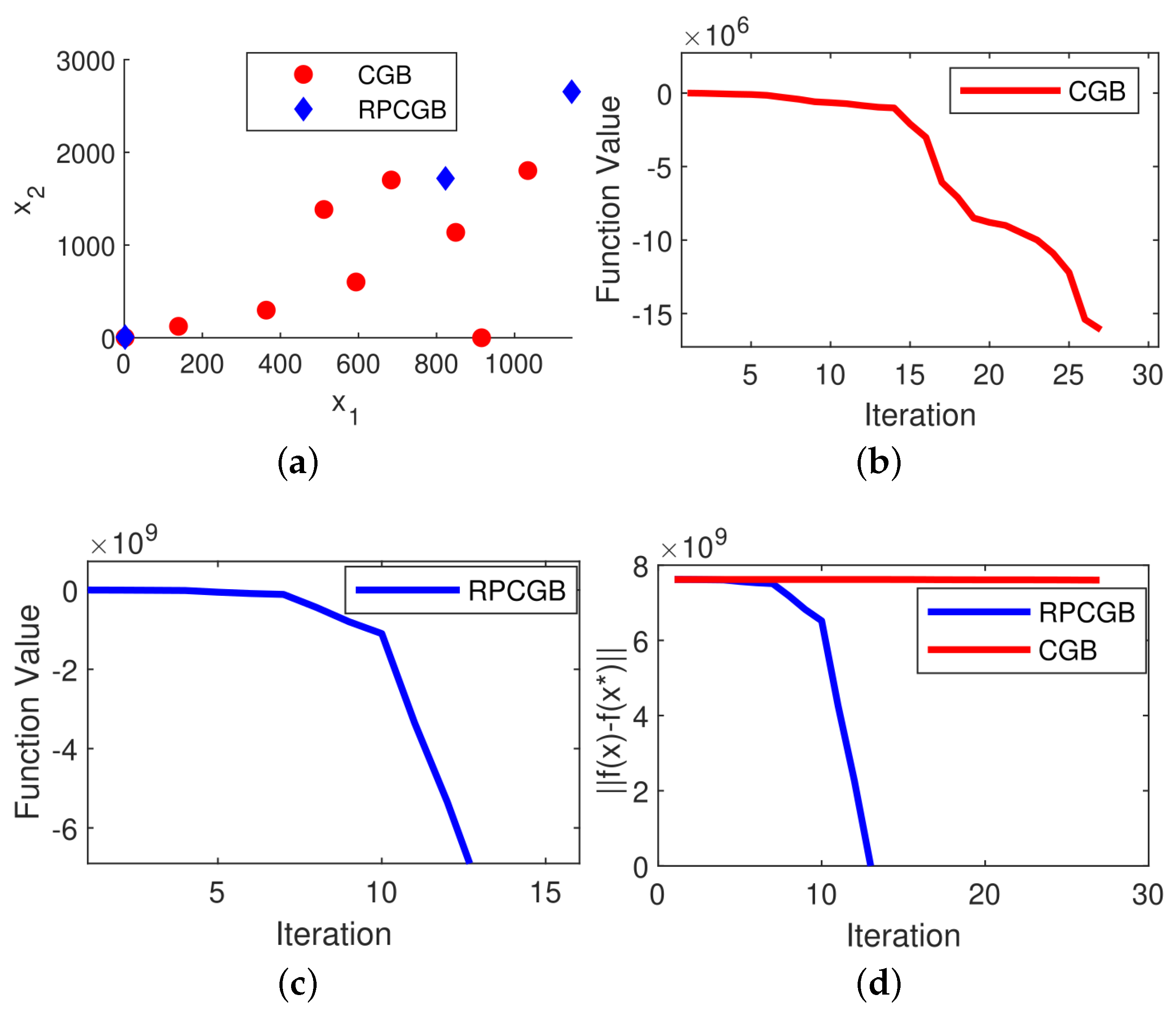
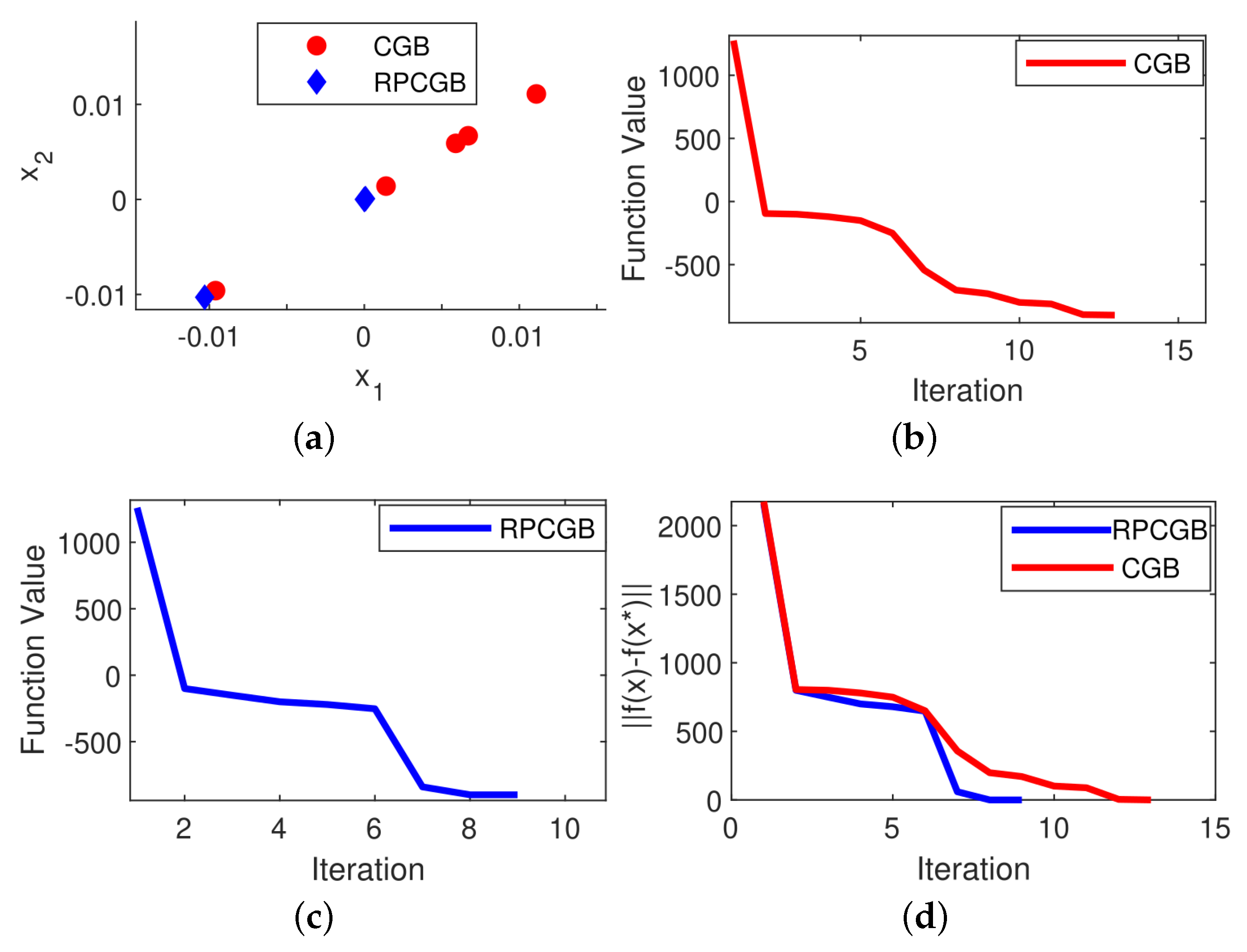
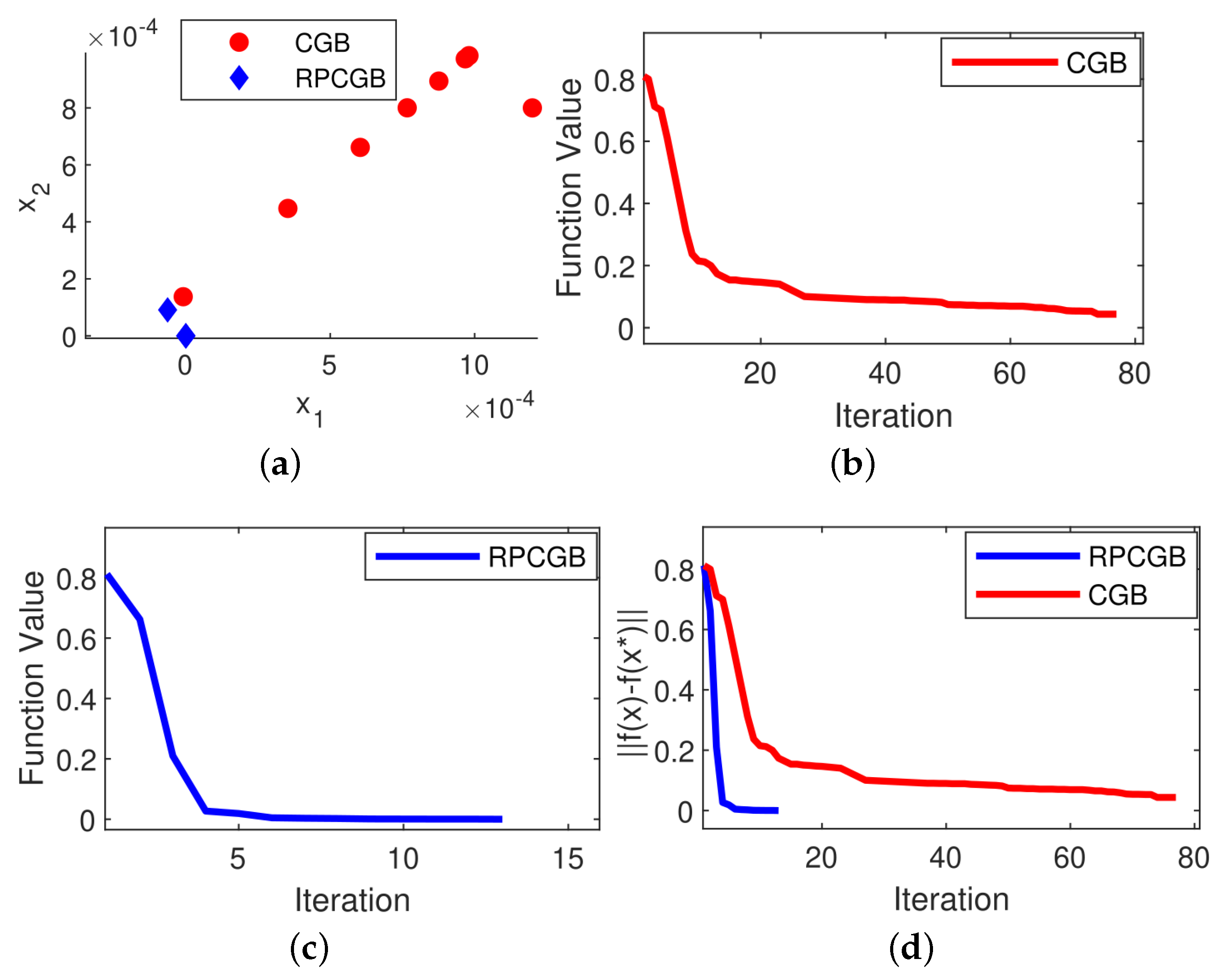
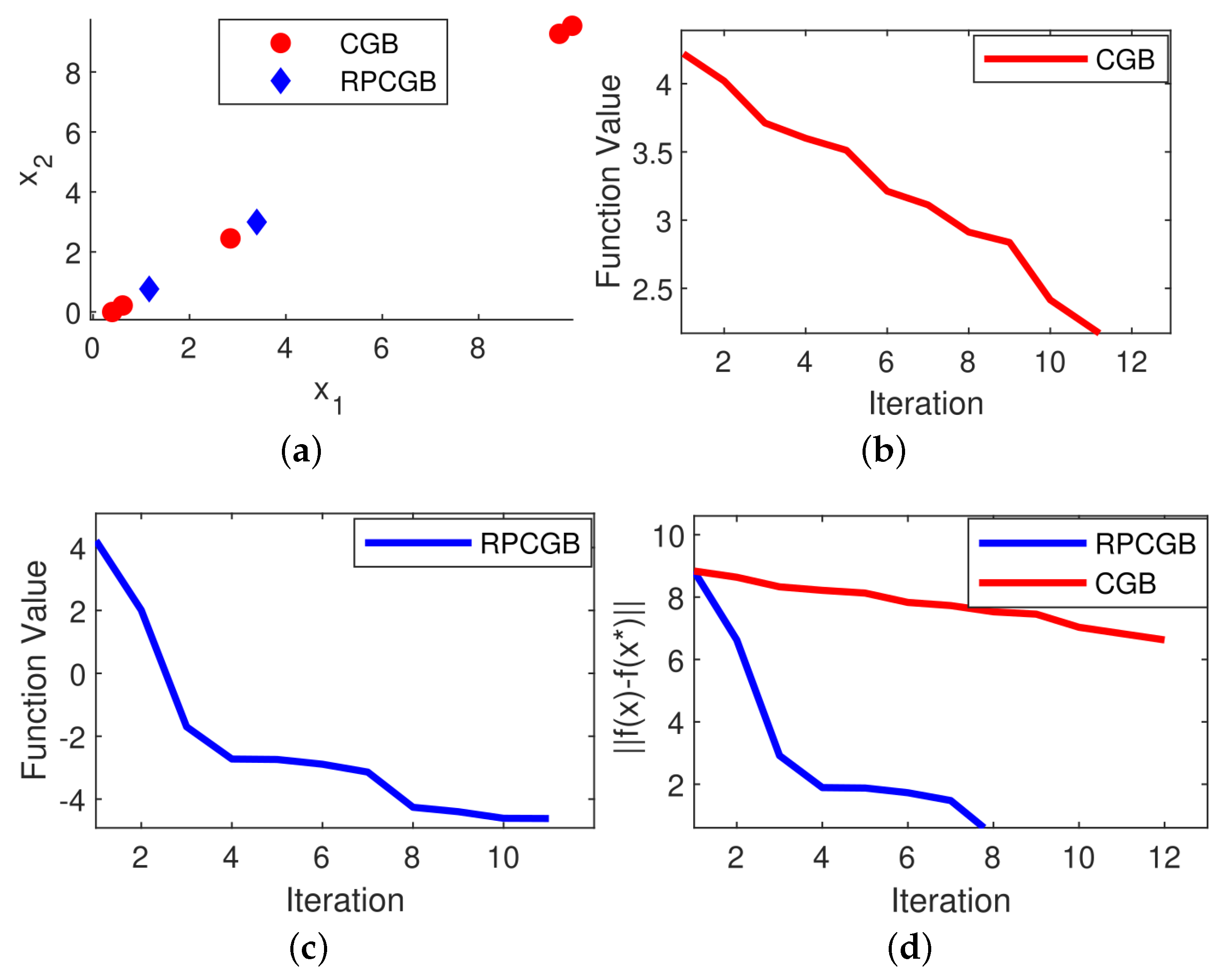
Problem 1. The Neumaier 3 Problem (NF3) is a mathematical optimization problem introduced by Arnold Neumaier in 2003 (see [29]). The problem is defined as follows: Problem 2. The Cosine Mixture Problem (CM) is an optimization problem introduced by Breiman and Cutler in 1993 (see [29]). The problem is defined as follows: Problem 3. The Inverted Cosine Wave Function or the Cosine Mixture with Exponential Decay Problem. This is a commonly used benchmark problem in global optimization and was introduced by Price et al. in 2006 (see [30]). The problem is defined as follows: Problem 4. The Epistatic Michalewicz Problem (EM) is a type of optimization problem commonly used as a benchmark in evolutionary computation and optimization. It was introduced by Michalewicz in 1996 (see [29]). The problem is defined as follows: Problem 5. The problem is a mathematical optimization problem used in global optimization which comes from [32] and is defined as follows: Problem 6. Rastrigin’s function is a non-convex, multi-modal function commonly used as a benchmark problem in optimization. It was introduced by Rastrigin in 1974 (see [31]) and is defined as: To gain a deeper understanding of the effect of the modifications on the proposed algorithm, we utilized a scatter plot that illustrates the distribution of the algorithm’s solutions in two dimensions for both the CGB and RPCGB algorithms. The goal was to generate scatter plots to depict the distribution of solutions in a 2D space for all problems when using two variables (
n = 2). However, we found that for Problems 1 to 3, we were able to obtain the optimal solution value using only one iteration, which made the creation of a scatter plot unnecessary in this case. Thus, we generated a scatter plot of the solution distribution for the case of
n = 900. This allowed us to effectively illustrate the distribution of solutions using scatter plots. In each algorithm, the scatter plot was generated at the first iteration and continued up to the limit of the required number of iterations to reach the solution. After analyzing
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
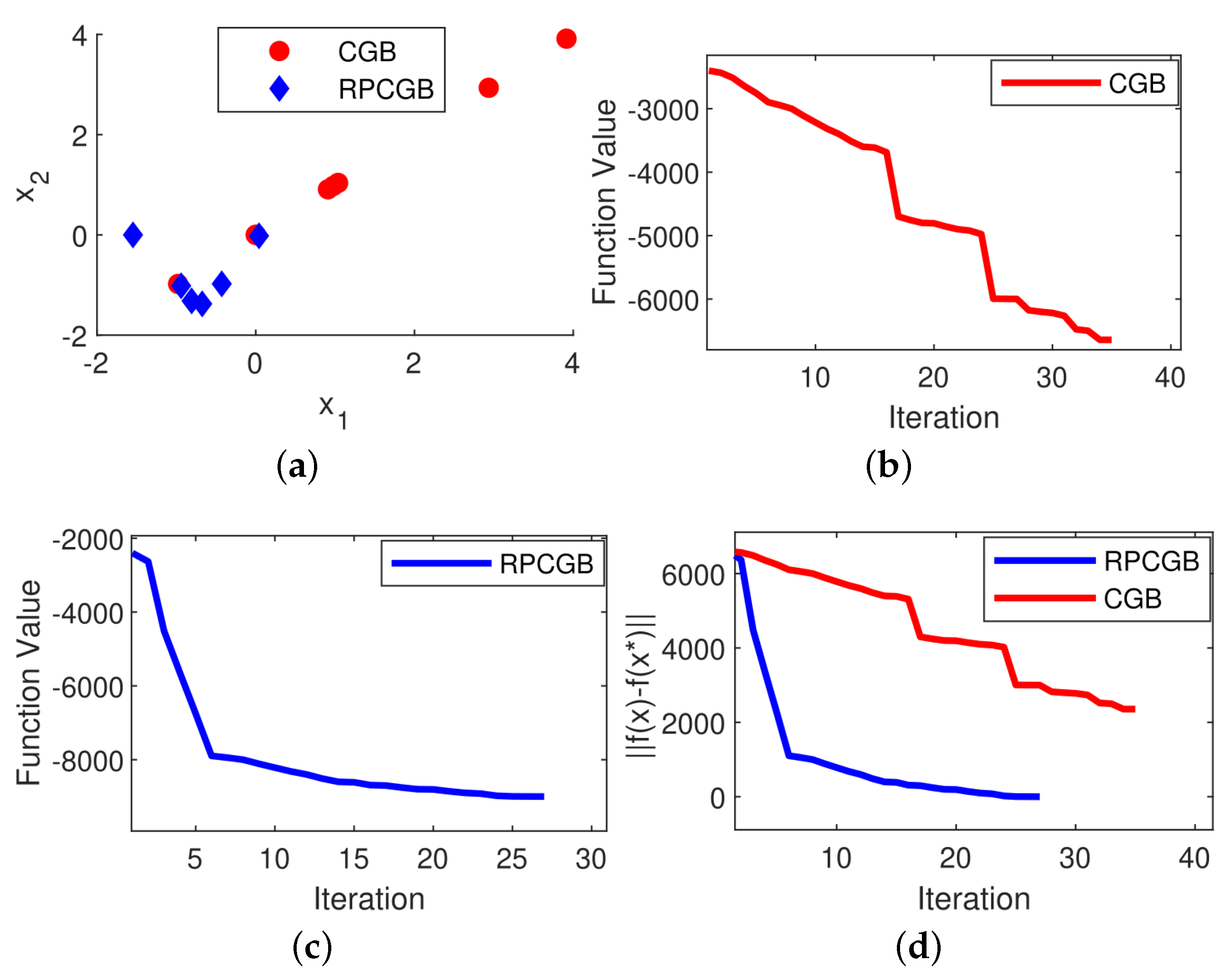
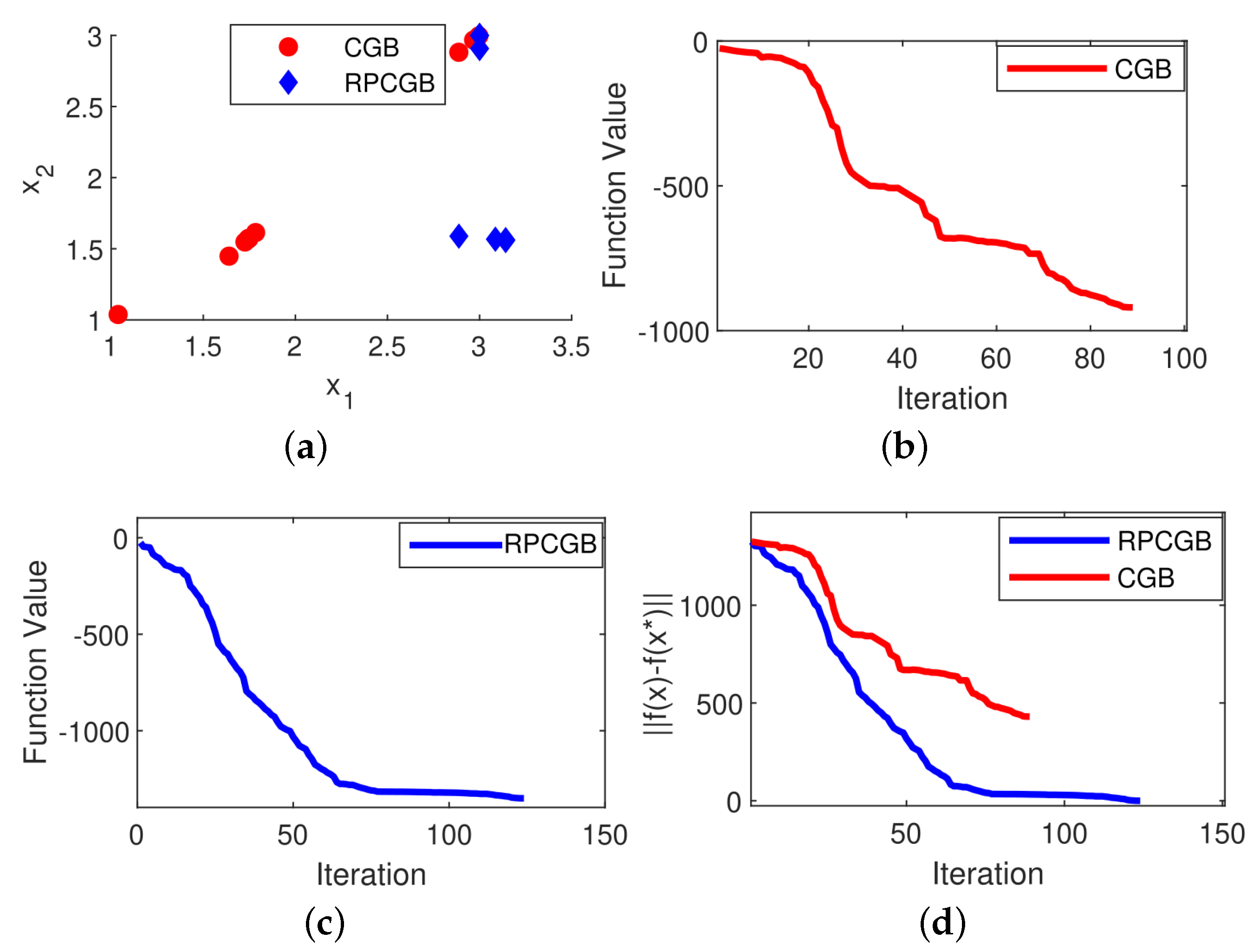
Figure 6, we concluded that the modified algorithm exhibited a more tightly clustered solution distribution in the scatter plot compared to the original algorithm.
We also present in
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 the results of plotting the objective function values in each iteration and the convergence performance for the CGB and RPCGB methods with 9000 variables. The plots (
d) show that the proposed algorithm performs better than the CGB algorithm, with the majority of cases showing that the suggested algorithm achieves convergence in fewer iterations than the CGB algorithm. However, there is an exception observed in Problem 4, as presented in
Figure 4, where the CGB algorithm stops early. This demonstrates that the convergence behavior of optimization algorithms can vary based on the problem being solved. It is worth noting that both algorithms terminated their execution before the 30th iteration, which is because a stopping criterion of approximately
was met. The algorithms cease their iterations upon reaching the optimal solution (the local or global solution) or upon reaching the maximum number of iterations. We observe that the random perturbation has a significant effect on the convergence. This suggests that the changes made to the algorithm led to an improvement in its performance.
The results presented in
Table 1,
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6 demonstrate that the CGB algorithm is capable of obtaining global solutions in certain instances regardless of the number of dimensions, such as Problem 2 (see
Table 2). However, in some cases, the CGB algorithm fails to obtain global solutions as the number of dimensions increases, as seen in Problem 3 (see
Table 3). In contrast, our RPCGB algorithm can obtain a global solution for all cases, and the computational results indicate that it performs effectively for these high-dimensional problems. These results also indicate that, for larger-dimensions problems, the CGB method necessitates a greater number of iterations to finalize the optimization process, whereas the RPCGB method does not, as evidenced by Problem 5. This difference can be explained by the
parameter, which denotes the number of perturbations. If the number of perturbations is raised, then the number of iterations needed to achieve the optimal solution is reduced.
When analyzing the obtained results, it is evident that the perturbed conditional gradient method with bisection algorithm (RPCGB) performs well compared to the conditional gradient algorithm (CGB).
6. Conclusions
In this work, we generalized the RPCGB method to solve large-scale non-convex optimization problems. The algorithms mentioned in this paper, specifically the conditional gradient algorithm, are commonly used optimization techniques for solving convex optimization problems. However, in the case of non-convex optimization problems, these algorithms may converge to a local minimum instead of the global minimum. To overcome this problem, the proposed approach introduces a random perturbation to the optimization problem. Specifically, at each iteration of the algorithm, a random perturbation is added to the operator, which allows the algorithm to escape from local minima and explore the search space more effectively. The bisection algorithm is used to find the optimal step size along the search direction. It involves solving a one-dimensional optimization problem to find the step size that minimizes the objective function. By combining these two algorithms with the random perturbation approach, the proposed method is able to efficiently explore the search space for large-scale non-convex optimization problems under linear constraints and reach a global minimum. The tuning of the parameters and is related to the main difficulty in applying random perturbation in practice.
The RPCGB algorithm has the ability to solve various problems, such as control systems, as well as optimization problems in machine learning, robotics, and image reconstruction. There are problems that contain a part that is not smooth. Therefore, in the future, we plan to use the random perturbation of the conditional subgradient method with bisection algorithm to solve non-convex, non-smooth (non-differentiable) programming under linear constraints. Additionally, we intend to use the perturbed conditional gradient method to address non-convex optimization problems in support vector machines (SVM).