Settlement of a Foundation on an Unsaturated Sandy Base Taking Vibrocreep into Account
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ter-Martirosyan, A.Z.; Sobolev, E.S. Safe performance of bases of buildings and structures under dynamic impacts. Vestn. MGSU 2017, 12, 537–544. [Google Scholar] [CrossRef]
- Chernov, Y.T. Design of buildings and structures exposed to dynamic influences. Ind. Civ. Eng. 2018, 4, 73–77. [Google Scholar]
- Savinov, O.A. Modern Designs of Foundations for Machines and Their Analysis; Leningrad, Stroyizdat: Moscow, Russia, 1979; 200p. [Google Scholar]
- Ma, L. Study on abnormal vibration caused by foundation settlement of a 650MW unit. J. Phys. Conf. Ser. 2021, 1748, 062032. [Google Scholar] [CrossRef]
- Barkan, D.D. Dynamics of Foundations; McGraw-Hill Book Co.: New York, NY, USA, 1948; 411p. [Google Scholar]
- Barkan, D.D. Dynamics of Bases and Foundations; McGraw-Hill Book Co.: New York, NY, USA, 1962; 434p. [Google Scholar]
- Pyatetsky, V.M.; Alexandrov, B.K.; Savinov, O.A. Modern Computer Designed Foundations and Their Automated Design; Stroyizdat: Moscow, Russia, 1993; 415p. [Google Scholar]
- Ivanov, P.L. Soils and Bases of Hydraulic Structures. Mechanics of Soils: Textbook for Hydraulic Engineering Specialties of Universities; Higher School: Moscow, Russia, 1991; 447p. [Google Scholar]
- Krasnikov, N.D. Dynamic Properties of Soils and Methods of Their Determination; Leningrad, Stroyizdat: Moscow, Russia, 1970; 240p. [Google Scholar]
- Ilyichev, V.A.; Mangushev, R.A. (Eds.) Handbook of Geotechnics. Foundations, Foundations, and Underground Structures; ASV Publishing House: Moscow, Russia, 2016; 1040p. [Google Scholar]
- Shebunyaev, A.N. Review of the results of studies on the effect of vibrations on physical and mechanical properties of sandy soils. Eng. Constr. Bull. Casp. Sea 2022, 3, 15–22. [Google Scholar] [CrossRef]
- Voznesensky, E.A. Dynamic Instability of Soils, 2nd ed.; Leningrad, Stroyizdat: Moscow, Russia, 2014; 264p. [Google Scholar]
- Ilyichev, V.A.; Kerchman, V.I.; Rubin, B.I.; Piatetsky, V.M. Experimental study of sand soil vibrocreeping. In Proceedings of the International Symposium on Soil under Cyclic and Transient Loading, Swansea, UK, 7–11 January 1980; Volume 1, pp. 239–245. [Google Scholar]
- Bogolyubchik, V.S.; Goldstein, M.N.; Khain, V.Y. Experimental field studies of vibrocreep of sandy and sandy loam foundations. Dynamics of foundations, foundations, and underground structures. In Proceedings of the 4th All-Union Conference, Tashkent, Uzbekistan, 16–18 November 1977; pp. 192–195. [Google Scholar]
- Bogolyubchik, V.S.; Khain, V.Y. Flute Tests of Sand to Study Vibrocreep. In The Collection “Voprosy Geotehniki” № 22; Dnepropetrovsk Institute of Railway Transport Engineers Named after L.M. Kaganovich: Dnepropetrovsk, Ukraine, 1973. [Google Scholar]
- Hain, V.Y. Study of the Time Dependence of Vibrocreep of a Sand Foundation Model. NTL, Subpart, B., Issue 6, № 215; Moscow, Russia, 1975. [Google Scholar]
- Gil, D.F.; Mendoza, C.C.; Vásquez-Varela, L.R.; Cano, S. Physical Model of Shallow Foundation under Dynamic Loads on Sands. Infrastructures 2022, 7, 147. [Google Scholar] [CrossRef]
- Al-kaream, K.; Fattah, M.; Khaled, Z. Effect of the mode of vibration on the response of machine foundation on sand. In Proceedings of the IOP Conference Series: Materials Science and Engineering, 4th International Conference on Buildings, Construction and Environmental Engineering, Istanbul, Turkey, 7–9 October 2019; Volume 737. [Google Scholar] [CrossRef]
- Wang, J.; Qi, H.; Lin, Z.; Tang, Y. Analysis of Dynamic Deformation Response of Closely Spaced Square Footings on Geogrid-Reinforced Sand under Cyclic Loading. Sustainability 2023, 15, 438. [Google Scholar] [CrossRef]
- Casagrande, A.; Shannon, W.L. Research on stress deformation and strength characteristics of soils and soft rocks under transient loading. Harv. Soil Mech. Ser. 1948, 31. [Google Scholar]
- Seed, H.B.; Lee, K.L. Liquefaction of saturated sands during cyclic loading. J. Soil Mech. Found. Div. ASCE 1966, 92, 105–134. [Google Scholar] [CrossRef]
- Lee, K.L.; Focht, J. Liquefaction potential at the Ekofisk tank in the North Sea. J. Geotech. Eng. Div. ASCE 1975, 101, 1–18. [Google Scholar] [CrossRef]
- Chaney, R.C.; Fang, H.Y. Response of non-saturated soil to cyclic loading. In Proceedings of the International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, MO, USA, 26 April–3 May 1981; Volume 2, p. 643. [Google Scholar]
- Khosla, V.K.; Singh, R.D. Influence of number of cycles on strain. Can. Geotech. J. 1978, 15, 584–592. [Google Scholar] [CrossRef]
- Ter-Martirosyan, A.Z. Interaction of Foundations with the Base under Cyclic and Vibration Influences Taking into Account Rheological Properties of Soils; NRU MGSU: Moscow, Russia, 2010; 190p. [Google Scholar]
- Ter-Martirosyan, A.Z.; Sobolev, E.S. Long-term vibration laboratory tests of sandy soils. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1015, 012051. [Google Scholar] [CrossRef]
- Sobolev, E.S. Creep and Vibrocreep of Sandy Soils of Foundations of Buildings and Structures; NRU MGSU: Moscow, Russia, 2014; 150p. [Google Scholar]
- Ter-Martirosyan, A.Z. Interaction of Foundations of Buildings and Structures with Saturated Foundations Taking into Account Nonlinear and Rheological Properties of Soils; NRU MGSU: Moscow, Russia, 2016; 324p. [Google Scholar]
- Ter-Martirosyan, Z.; Sobolev, E.; Ter-Martirosyan, A. Rheological Properties of Sandy Soils. Adv. Mater. Res. 2014, 1073–1076, 1673–1679. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Lin, L.; Li, T.; Yin, J. Experimental Study on the Monotonic and Cyclic Behaviour of Carbonate Sand in the South China Sea. KSCE J. Civ. Eng. 2021, 25, 3254–3263. [Google Scholar] [CrossRef]
- Poblete, M.; Wichtmann, T.; Niemunis, A.; Triantafyllidis, T. Accumulation of residual deformations due to cyclic loading with multidimensional strain loops. In Proceedings of the Fifth International Conference on Earthquake Geotechnical Engineering, Santiago, Chile, 9–14 January 2011. [Google Scholar]
- Kafle, B.; Wuttke, F. Response of Shallow Foundation Under Coupled Cyclic Loading For Unsaturated Sand at Large Number of Cycles. Jpn. Geotech. Soc. Spec. Publ. 2019, 7, 525–530. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Z.; Wang, Z.; Chen, Q.; Ma, D. Critical Dynamic Stress and Cumulative Plastic Deformation of Calcareous Sand Filler Based on Shakedown Theory. J. Mar. Sci. Eng. 2023, 11, 195. [Google Scholar] [CrossRef]
- Jianhong, Y.; Haiyilati, Y.; Cao, M.; Zuo, D.; Chai, X. Creep characteristics of calcareous coral sand in the South China Sea. Acta Geotech. 2022, 17, 5133–5155. [Google Scholar] [CrossRef]
- Dong-Ning, D.; Lai-Gui, W.; Zhang, X.; Shu-Kun, Z. Study on sand particles creep model and open pit mine landslide mechanism caused by sand fatigue liquefaction. In Proceedings of the IOP Conference Series: Earth and Environmental Science, 3rd International Conference on Advances in Energy, Environment and Chemical Engineering, Chengdu, China, 26–28 May 2017; Volume 69. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Z.; Liu, Z.; Nie, G. Post-Cyclic Drained Shear Behaviour of Fujian Sand under Various Loading Conditions. J. Mar. Sci. Eng. 2022, 10, 1499. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L. Experimental Study on Dynamic Parameters of Calcareous Sand Subgrade under Long-Term Cyclic Loading. J. Mar. Sci. Eng. 2022, 10, 1806. [Google Scholar] [CrossRef]
- Kumar, A.; Azizi, A.; Toll, D. The Influence of Cyclic Loading Frequency on the Response of an Unsaturated Railway Formation Soil. Geo-Congr. 2022, 2022, 274–283. [Google Scholar] [CrossRef]
- Song, D.; Liu, H.; Sun, Q. Significance of Determination Methods on Shear Modulus Measurements of Fujian Sand in Cyclic Triaxial Testing. Appl. Sci. 2022, 12, 8690. [Google Scholar] [CrossRef]
- Ma, W.; Qin, Y.; Gao, F.; Wu, Q. Experimental Study of the Dynamic Shear Modulus of Saturated Coral Sand under Complex Consolidation Conditions. J. Mar. Sci. Eng. 2023, 11, 214. [Google Scholar] [CrossRef]
- Xia, P.; Shao, L.; Deng, W.; Zeng, C. Evolution Prediction of Hysteresis Behaviour of Sand under Cyclic Loading. Processes 2022, 10, 879. [Google Scholar] [CrossRef]
- Vivek, P.; Ghosh, P. Dynamic interaction of two nearby machine foundations on homogeneous soil. In Proceedings of the GeoCongress 2012. State of the Art and Practice in Geotechnical Engineering, Oakland, CA, USA, 25–29 March 2012; pp. 21–30. [Google Scholar]
- Wichtmann, T.; Niemunis, A.; Triantafyllidis, T. Differential settlements due to cyclic loading and their effect on the lifetime of structures. In Proceedings of the 3rd International Conference on Lifetime Oriented Design Concepts, Freiburg, Germany, 12–14 November 2007. [Google Scholar]
- Wuttke, F.; Schmidt, H.G.; Zabel, V.; Kafle, B.; Stade, I. Vibration Induced Building Settlement Assessment and Calculation. In Proceedings of the 8th International Conference on Structural Dynamics EURODYN, Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Yi, F. Procedure to evaluate seismic settlement in dry sand based on shear wave velocity. In Proceedings of the 9th U.S. National and 10th Canadian Conference on Earthquake Engineering (9USN/10CCEE), Toronto, ON, Canada, 25–29 July 2010. [Google Scholar] [CrossRef]
- Yi, F. Procedures to evaluate seismic settlement of dry sand based on CPT data, an update. In Proceedings of the 5th International Symposium on Cone Penetration Testing, Bologna, Italy, 8–10 June 2022; ISBN 9781003308829. [Google Scholar]
- Pradel, D. Procedure to Evaluate Earthquake-Induced Settlements in Dry Sandy Soils. J. Geotech. Geoenviron. Eng. 1998, 124, 364–368. [Google Scholar] [CrossRef]
- Sobolev, E.; Morev, D. The industrial buildings settlement foundations calculation made taking into account the soils vibro-creep. IOP Conf. Ser. Mater. Sci. Eng. 2019, 698, 022038. [Google Scholar] [CrossRef]
- Geniev, G.A.; Estrin, M.I. Dynamics of Plastic and Loose Medium. TsNIISK im. V.A. Kucherenko; Stroyizdat: Moscow, Russia, 1972; 216p. [Google Scholar]
- Ter-Martirosyan, Z.G.; Ter-Martirosyan, A.Z.; Sobolev, E.S. Creep and vibrocreep of sandy soils. J. Eng. Res. 2014, 5–6, 24–28. [Google Scholar]
- Zhang, B.; Chen, K.; Hu, X.; Zhang, X.; Luo, G. Deformation constitutive model of subgrade soil under intermittent cyclic loading. Sci. Rep. Nat. Publ. Group 2023, 13, 301. [Google Scholar] [CrossRef]
- Ukhov, S.B.; Semenov, V.V.; Znamensky, V.V.; Ter-Martirosyan, Z.G.; Chernyshev, S.N. Mechanics of Soils, Bases, and Foundations—Textbook; ASV Publishing House: Moscow, Russia, 2005; 528p. [Google Scholar]
- Mei, C. Mathematical Analysis in Engineering: How to Use the Basic Tools; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Ter-Martirosyan, Z.G.; Ter-Martirosyan, A.Z. Mechanics of Soils in High-Rise Construction with Exploitable Underground Parts—Textbook; ASV Publishing House: Moscow, Russia, 2020; 946p. [Google Scholar]
- Dacorogna, B.; Tanteri, C. Mathematical Analysis for Engineers; Imperial College Press: London, UK, 2012. [Google Scholar]
- Maxfield, B. Engineering with Mathcad: Using Mathcad to Create and Organize Your Engineering Calculations; Butterworth-Heinemann: London, UK, 2006. [Google Scholar]
- Vick, B. Applied Engineering Mathematics; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Kerchman, V.I. Taking account of vibrocreep of sandy soils when designing foundations, accepting dynamic impacts. Dynamics of foundations, foundations, and underground structures. In Proceedings of the 4th All-Union Conference, Tashkent, Uzbekistan, 16–18 November 1977; pp. 205–207. [Google Scholar]
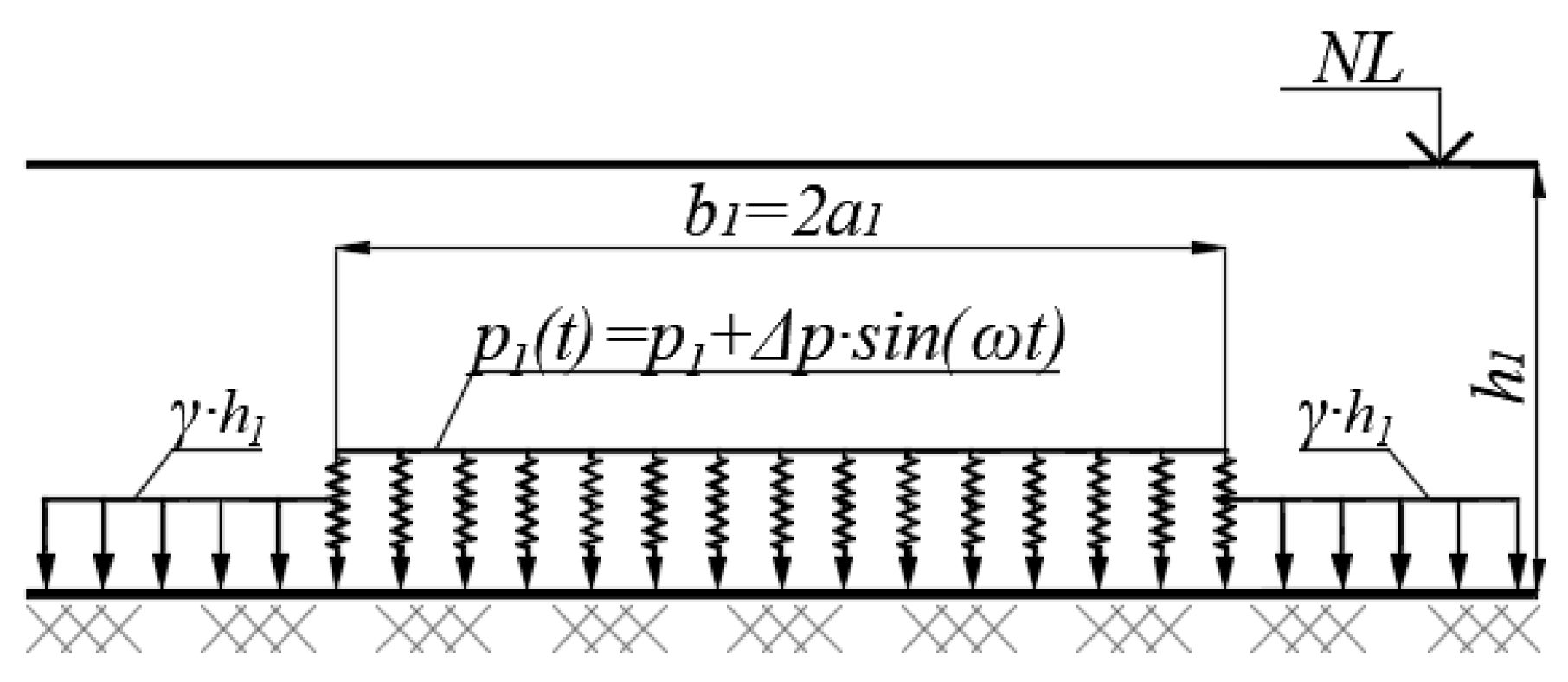
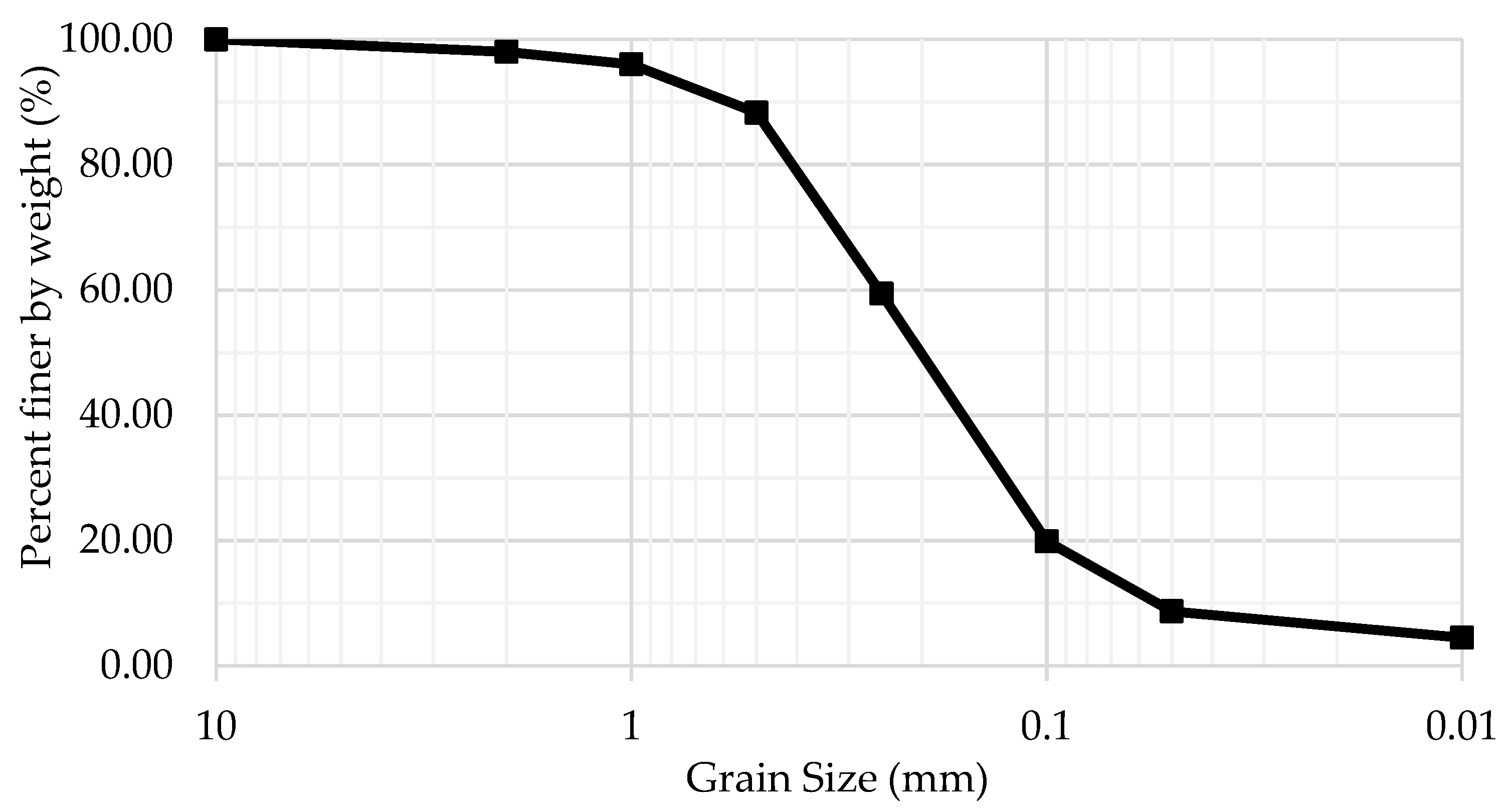

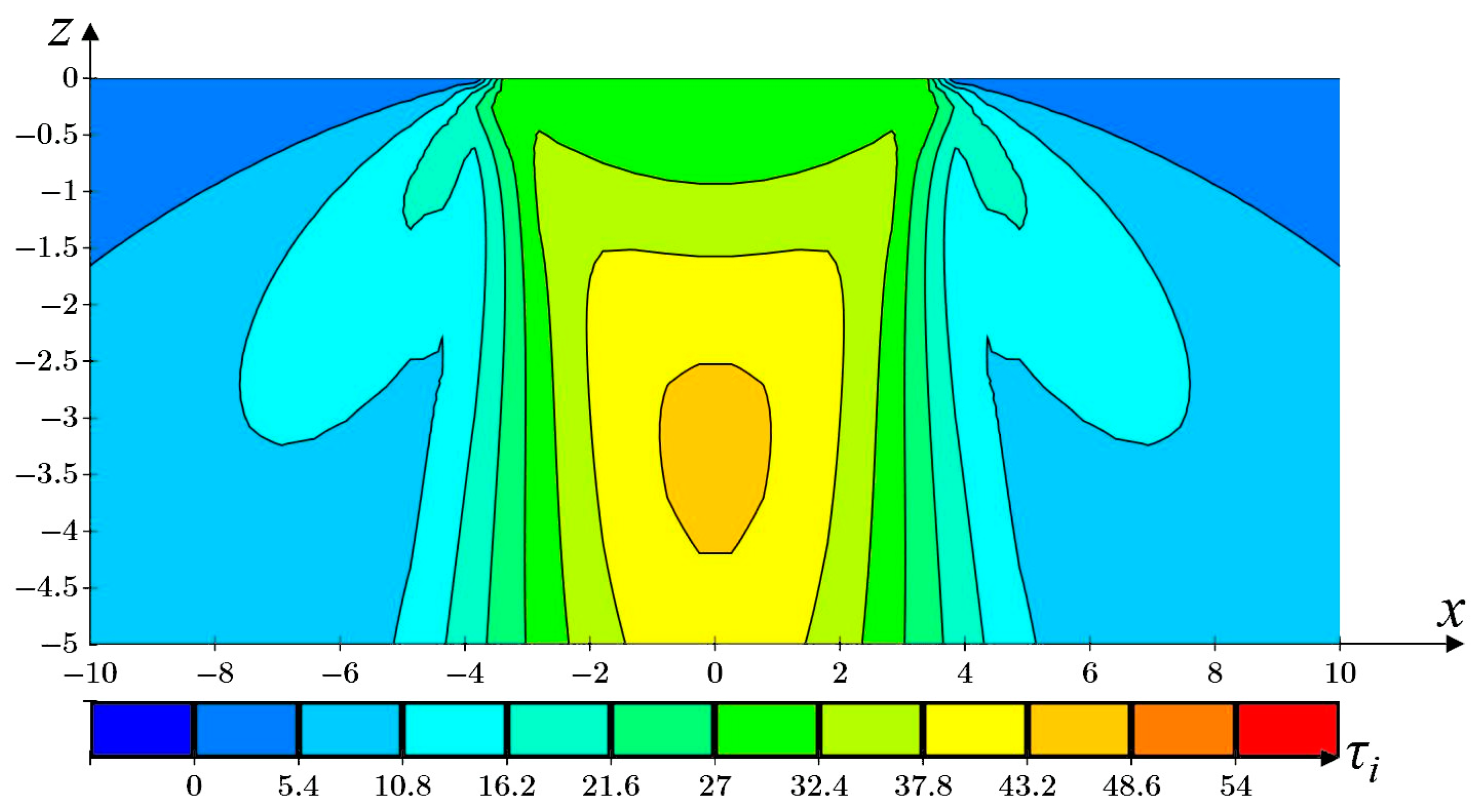
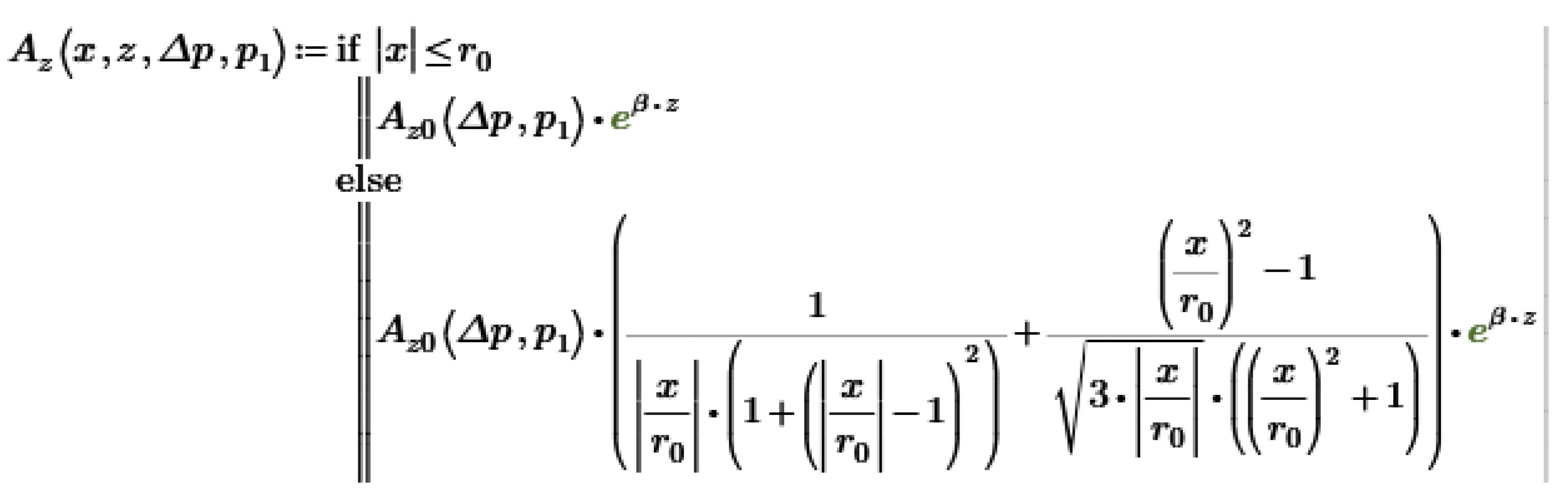
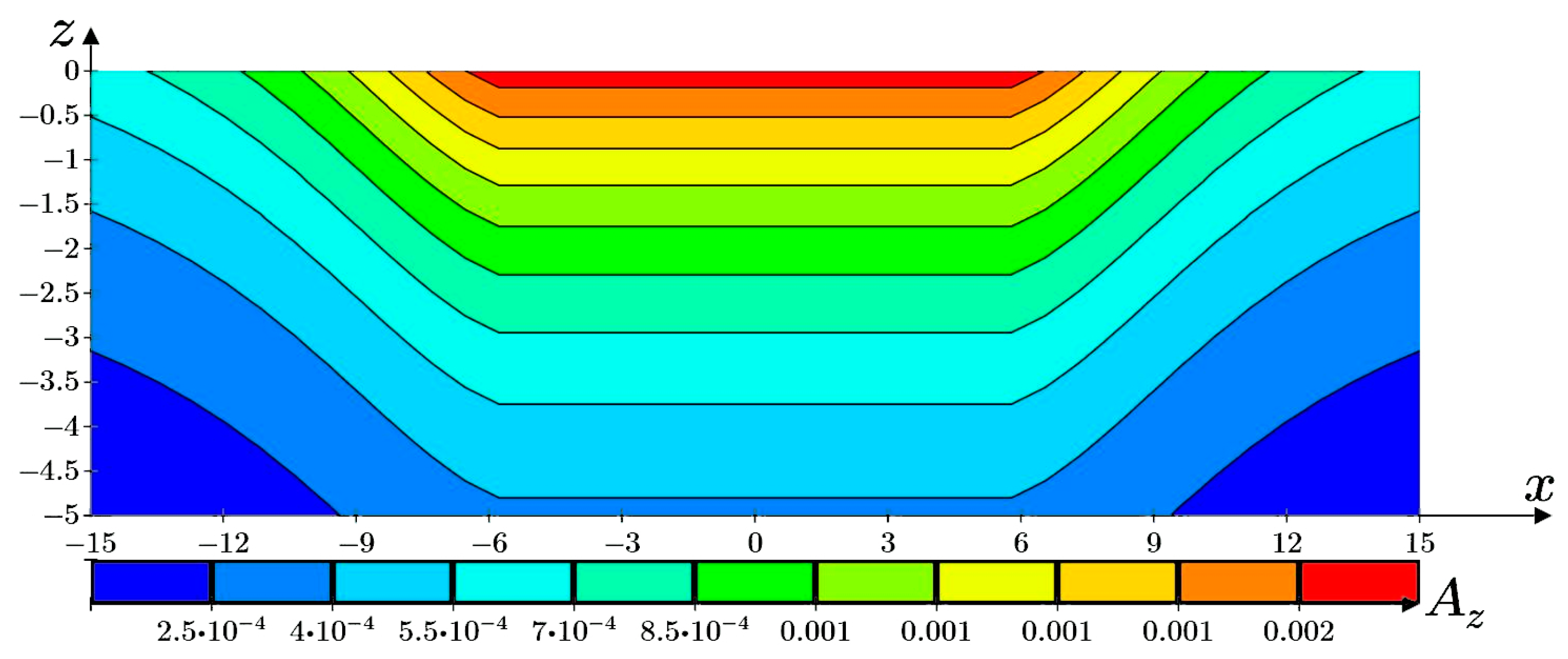


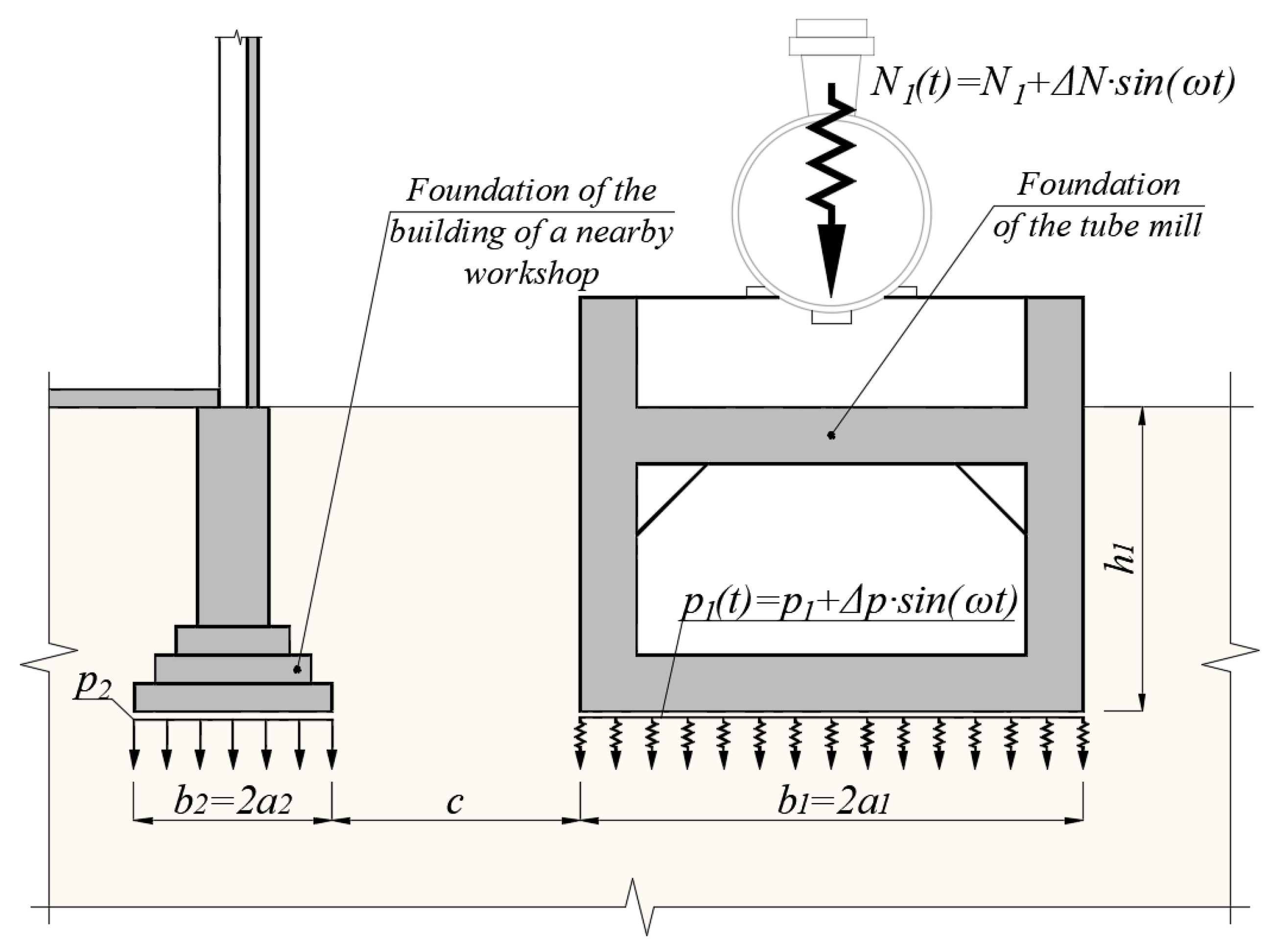
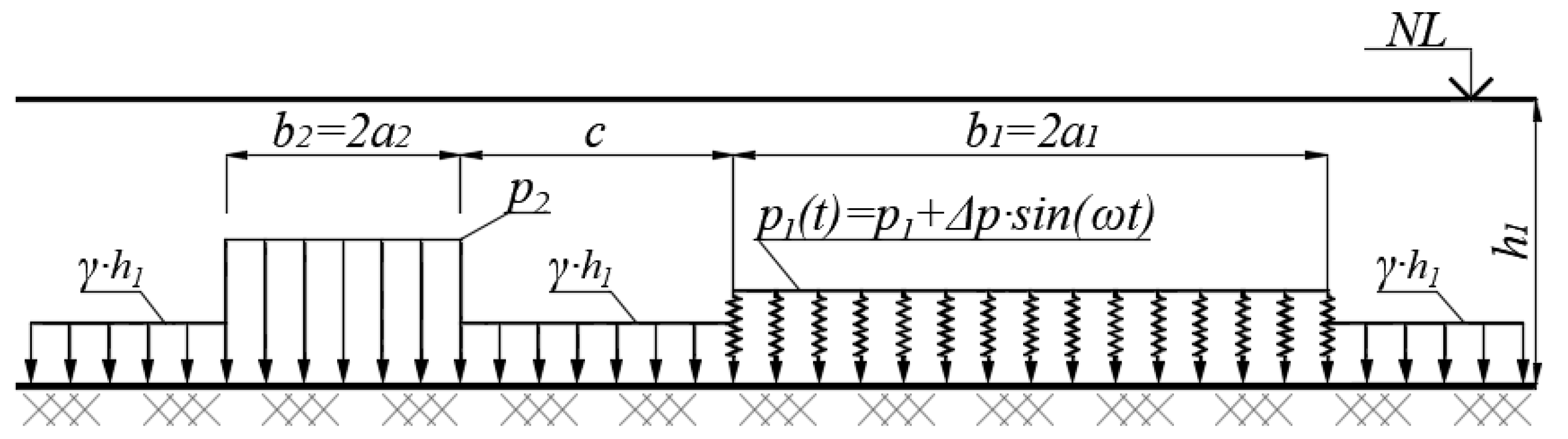
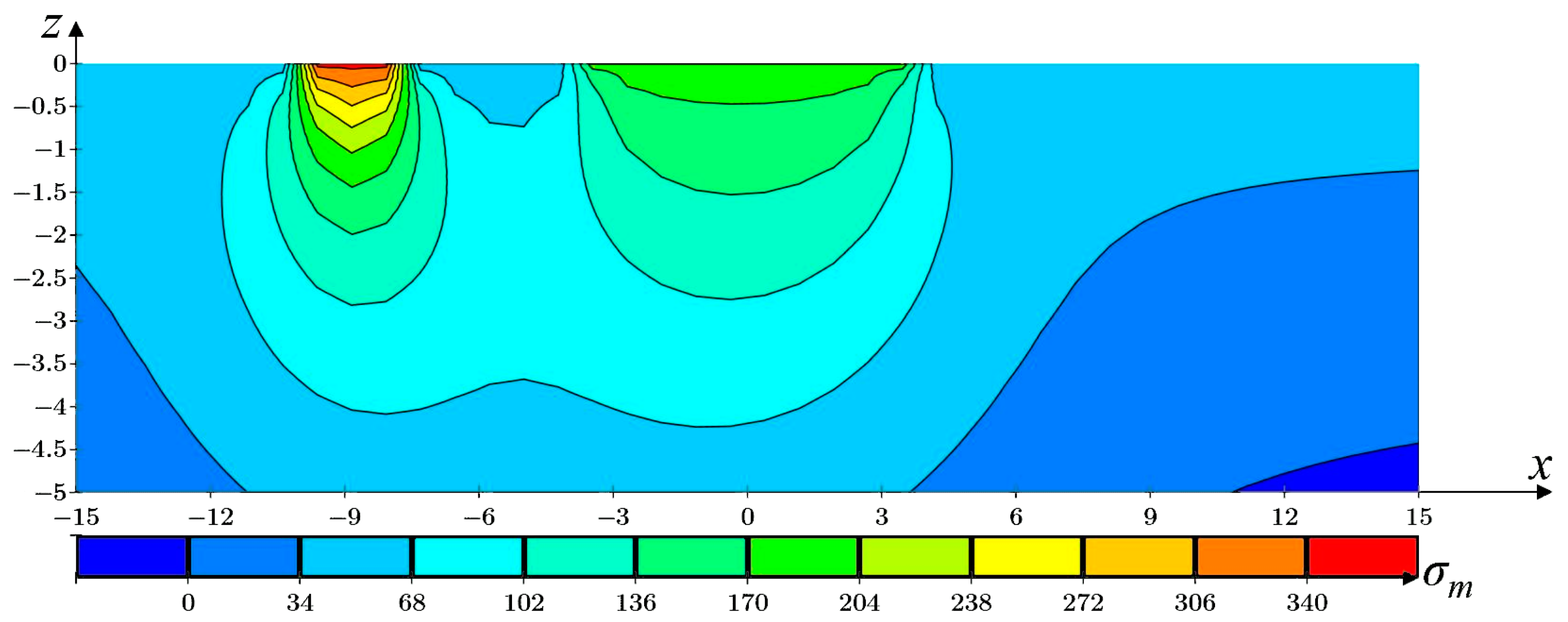
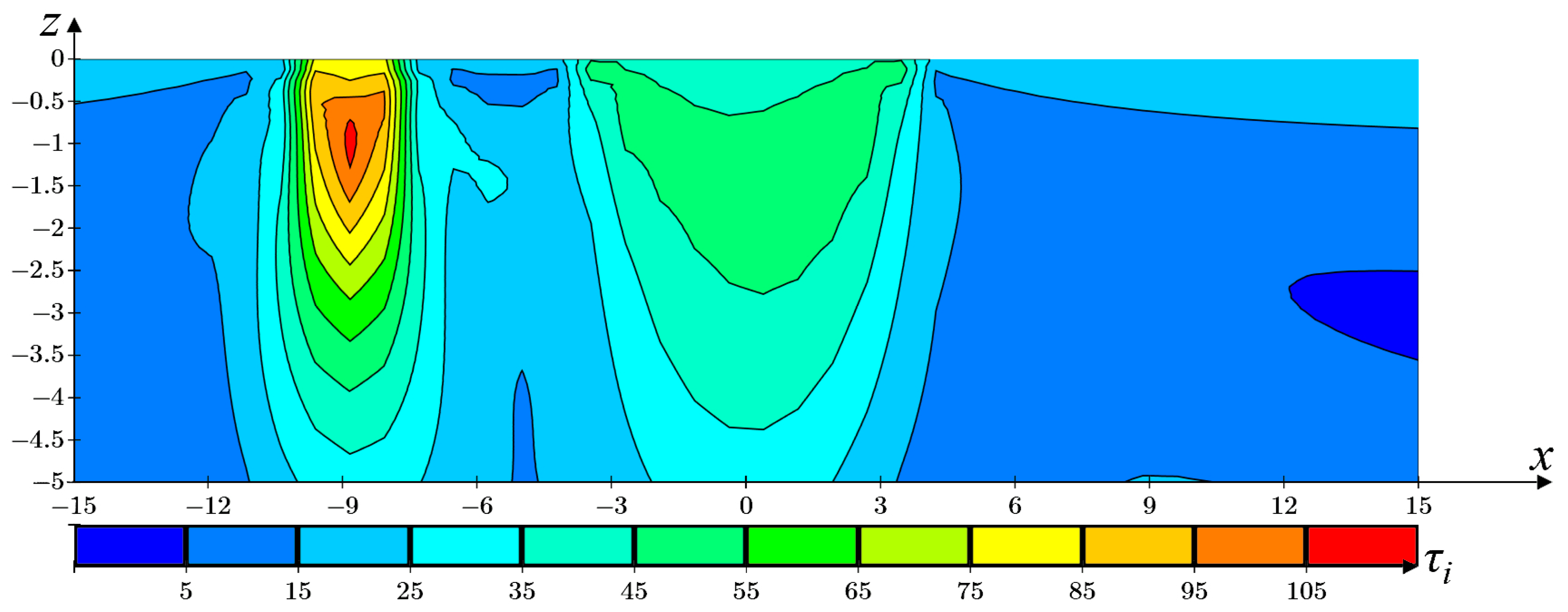
 )—p1 = 160 kPa, ∆p = 10 kPa; (
)—p1 = 160 kPa, ∆p = 10 kPa; ( )—p1 = 160 kPa, ∆p = 20 kPa; (
)—p1 = 160 kPa, ∆p = 20 kPa; ( )—p1 = 160 kPa, ∆p = 30 kPa; (
)—p1 = 160 kPa, ∆p = 30 kPa; ( )—p1 = 200 kPa, ∆p = 10 kPa; (
)—p1 = 200 kPa, ∆p = 10 kPa; ( )—p1 = 200 kPa, ∆p = 20 kPa; (
)—p1 = 200 kPa, ∆p = 20 kPa; ( )—p1 = 200 kPa, ∆p = 30 kPa; (
)—p1 = 200 kPa, ∆p = 30 kPa; ( )—p1 = 240 kPa, ∆p = 10 kPa; (
)—p1 = 240 kPa, ∆p = 10 kPa; ( )—p1 = 240 kPa, ∆p = 20 kPa; (
)—p1 = 240 kPa, ∆p = 20 kPa; ( )—p1 = 240 kPa, ∆p = 30 kPa.
)—p1 = 240 kPa, ∆p = 30 kPa.
 )—p1 = 160 kPa, ∆p = 10 kPa; (
)—p1 = 160 kPa, ∆p = 10 kPa; ( )—p1 = 160 kPa, ∆p = 20 kPa; (
)—p1 = 160 kPa, ∆p = 20 kPa; ( )—p1 = 160 kPa, ∆p = 30 kPa; (
)—p1 = 160 kPa, ∆p = 30 kPa; ( )—p1 = 200 kPa, ∆p = 10 kPa; (
)—p1 = 200 kPa, ∆p = 10 kPa; ( )—p1 = 200 kPa, ∆p = 20 kPa; (
)—p1 = 200 kPa, ∆p = 20 kPa; ( )—p1 = 200 kPa, ∆p = 30 kPa; (
)—p1 = 200 kPa, ∆p = 30 kPa; ( )—p1 = 240 kPa, ∆p = 10 kPa; (
)—p1 = 240 kPa, ∆p = 10 kPa; ( )—p1 = 240 kPa, ∆p = 20 kPa; (
)—p1 = 240 kPa, ∆p = 20 kPa; ( )—p1 = 240 kPa, ∆p = 30 kPa.
)—p1 = 240 kPa, ∆p = 30 kPa.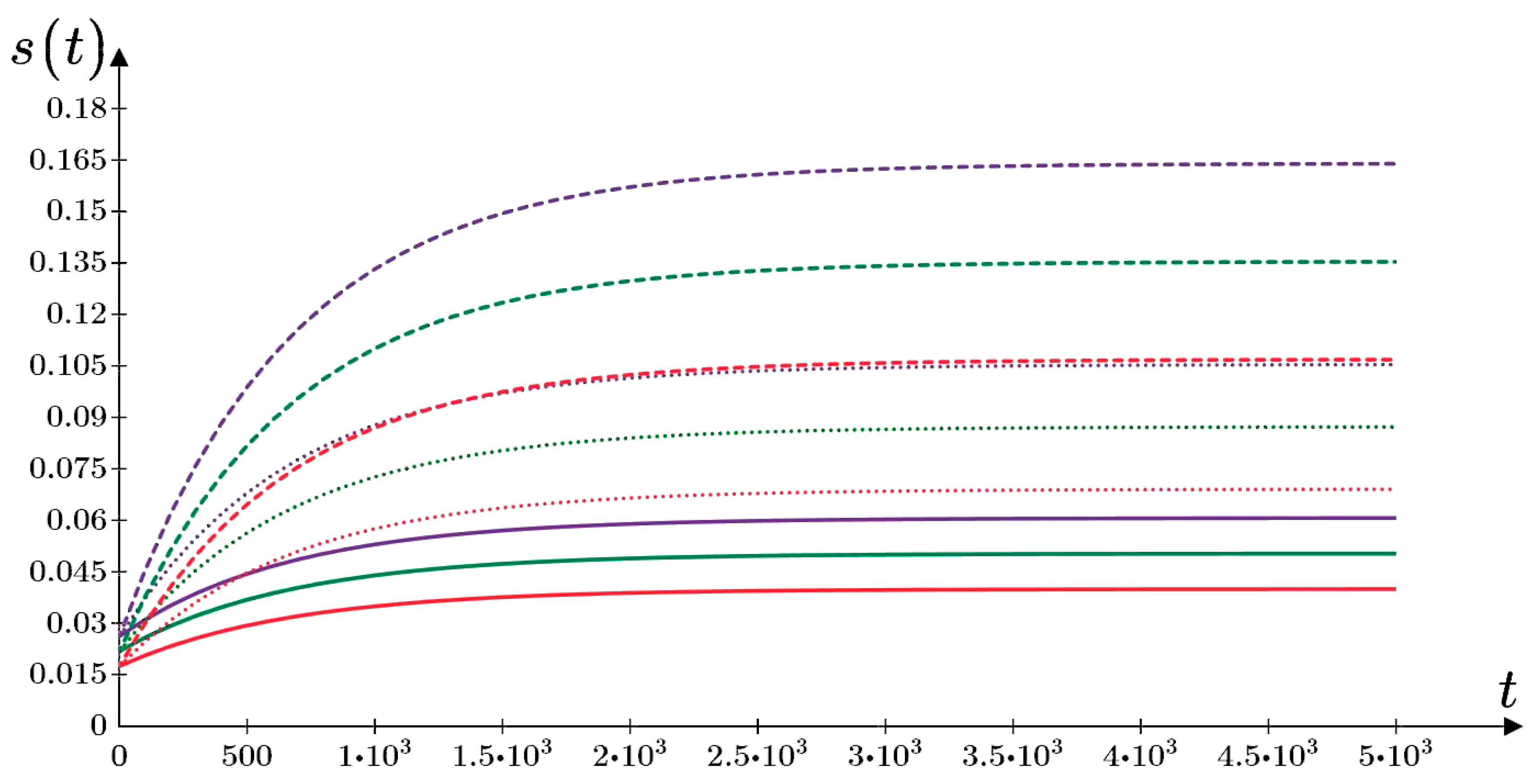
 )—p1 = 80 kPa; (
)—p1 = 80 kPa; ( )—p1 = 120 kPa; (
)—p1 = 120 kPa; ( )—p1 = 160 kPa; (
)—p1 = 160 kPa; ( )—p1 = 200 kPa; (
)—p1 = 200 kPa; ( )—p1 = 240 kPa.
)—p1 = 240 kPa.
 )—p1 = 80 kPa; (
)—p1 = 80 kPa; ( )—p1 = 120 kPa; (
)—p1 = 120 kPa; ( )—p1 = 160 kPa; (
)—p1 = 160 kPa; ( )—p1 = 200 kPa; (
)—p1 = 200 kPa; ( )—p1 = 240 kPa.
)—p1 = 240 kPa.
 )—p2 = 160 kPa; (
)—p2 = 160 kPa; ( )—p2 = 240 kPa; (
)—p2 = 240 kPa; ( )—p2 = 320 kPa.
)—p2 = 320 kPa.
 )—p2 = 160 kPa; (
)—p2 = 160 kPa; ( )—p2 = 240 kPa; (
)—p2 = 240 kPa; ( )—p2 = 320 kPa.
)—p2 = 320 kPa.
 )—p2 = 160 kPa; (
)—p2 = 160 kPa; ( )—p2 = 200 kPa; (
)—p2 = 200 kPa; ( )—p2 = 240 kPa; (
)—p2 = 240 kPa; ( )—p2 = 280 kPa; (
)—p2 = 280 kPa; ( )—p2 = 320 kPa.
)—p2 = 320 kPa.
 )—p2 = 160 kPa; (
)—p2 = 160 kPa; ( )—p2 = 200 kPa; (
)—p2 = 200 kPa; ( )—p2 = 240 kPa; (
)—p2 = 240 kPa; ( )—p2 = 280 kPa; (
)—p2 = 280 kPa; ( )—p2 = 320 kPa.
)—p2 = 320 kPa.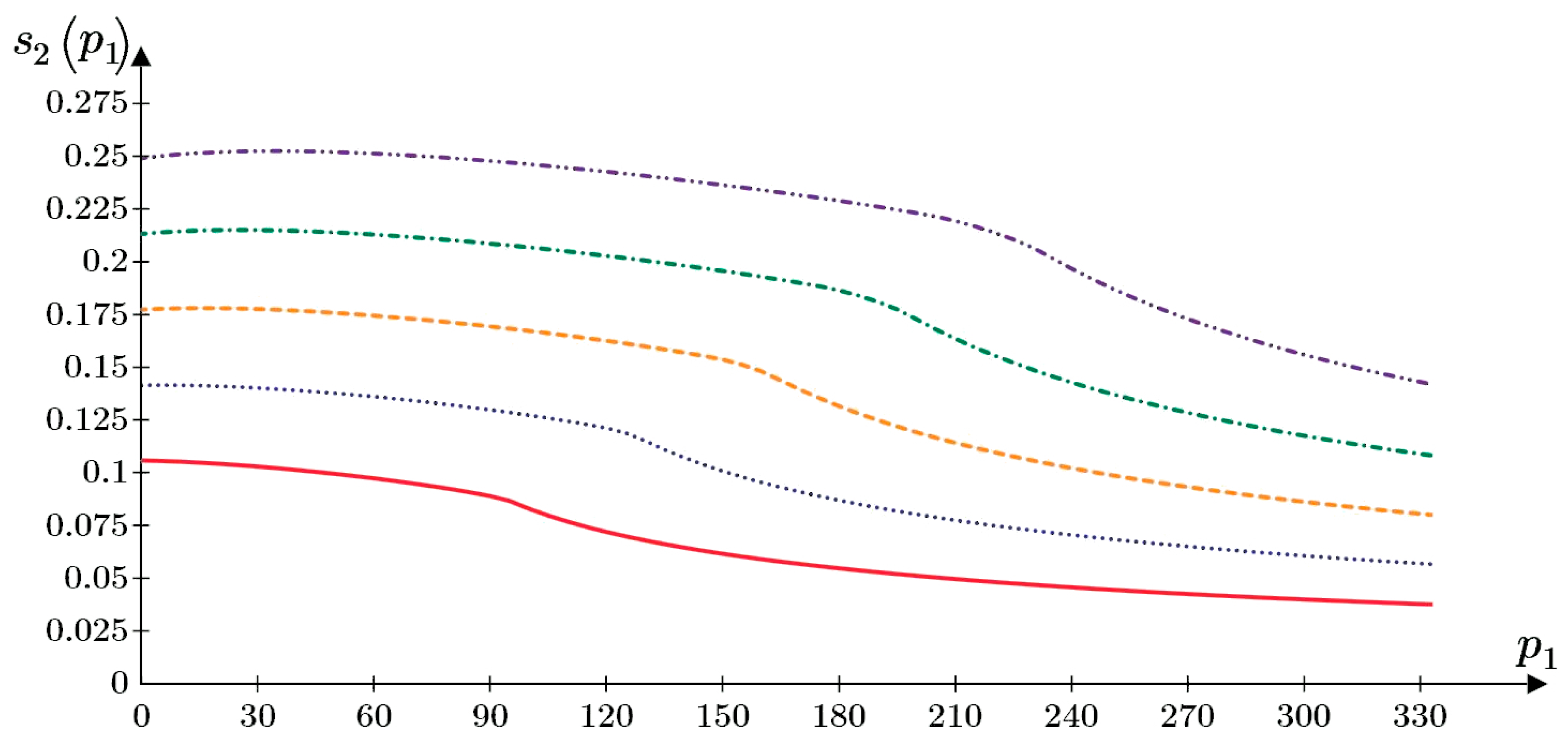
 )—p1 = 160 kPa; (
)—p1 = 160 kPa; ( )—p1 = 200 kPa; (
)—p1 = 200 kPa; ( )—p1 = 240 kPa; (
)—p1 = 240 kPa; ( )—p1 = 280 kPa; (
)—p1 = 280 kPa; ( )—p1 = 320 kPa.
)—p1 = 320 kPa.
 )—p1 = 160 kPa; (
)—p1 = 160 kPa; ( )—p1 = 200 kPa; (
)—p1 = 200 kPa; ( )—p1 = 240 kPa; (
)—p1 = 240 kPa; ( )—p1 = 280 kPa; (
)—p1 = 280 kPa; ( )—p1 = 320 kPa.
)—p1 = 320 kPa.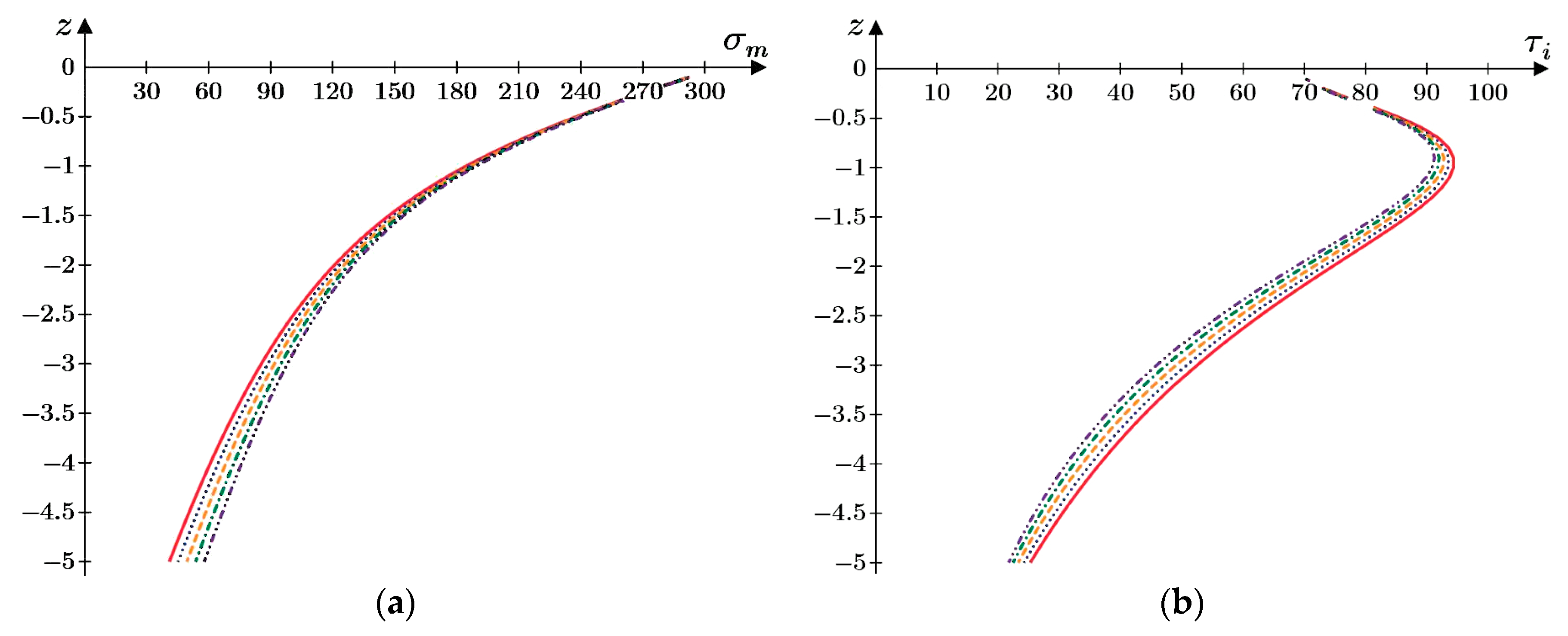
 )—p2 = 160 kPa; (
)—p2 = 160 kPa; ( )—p2 = 200 kPa; (
)—p2 = 200 kPa; ( )—p2 = 240 kPa; (
)—p2 = 240 kPa; ( )—p2 = 280 kPa; (
)—p2 = 280 kPa; ( )—p2 = 320 kPa.
)—p2 = 320 kPa.
 )—p2 = 160 kPa; (
)—p2 = 160 kPa; ( )—p2 = 200 kPa; (
)—p2 = 200 kPa; ( )—p2 = 240 kPa; (
)—p2 = 240 kPa; ( )—p2 = 280 kPa; (
)—p2 = 280 kPa; ( )—p2 = 320 kPa.
)—p2 = 320 kPa.
 )—c = 0.0 m; (
)—c = 0.0 m; ( )—c = 0.5 m; (
)—c = 0.5 m; ( )—c = 1.0 m; (
)—c = 1.0 m; ( )—c = 1.5 m; (
)—c = 1.5 m; ( )—c = 2.0 m.
)—c = 2.0 m.
 )—c = 0.0 m; (
)—c = 0.0 m; ( )—c = 0.5 m; (
)—c = 0.5 m; ( )—c = 1.0 m; (
)—c = 1.0 m; ( )—c = 1.5 m; (
)—c = 1.5 m; ( )—c = 2.0 m.
)—c = 2.0 m.
 )—p1 = 160 kPa; (
)—p1 = 160 kPa; ( )—p1 = 200 kPa; (
)—p1 = 200 kPa; ( )—p1 = 240 kPa; (
)—p1 = 240 kPa; ( )—p1 = 280 kPa; (
)—p1 = 280 kPa; ( )—p1 = 320 kPa.
)—p1 = 320 kPa.
 )—p1 = 160 kPa; (
)—p1 = 160 kPa; ( )—p1 = 200 kPa; (
)—p1 = 200 kPa; ( )—p1 = 240 kPa; (
)—p1 = 240 kPa; ( )—p1 = 280 kPa; (
)—p1 = 280 kPa; ( )—p1 = 320 kPa.
)—p1 = 320 kPa.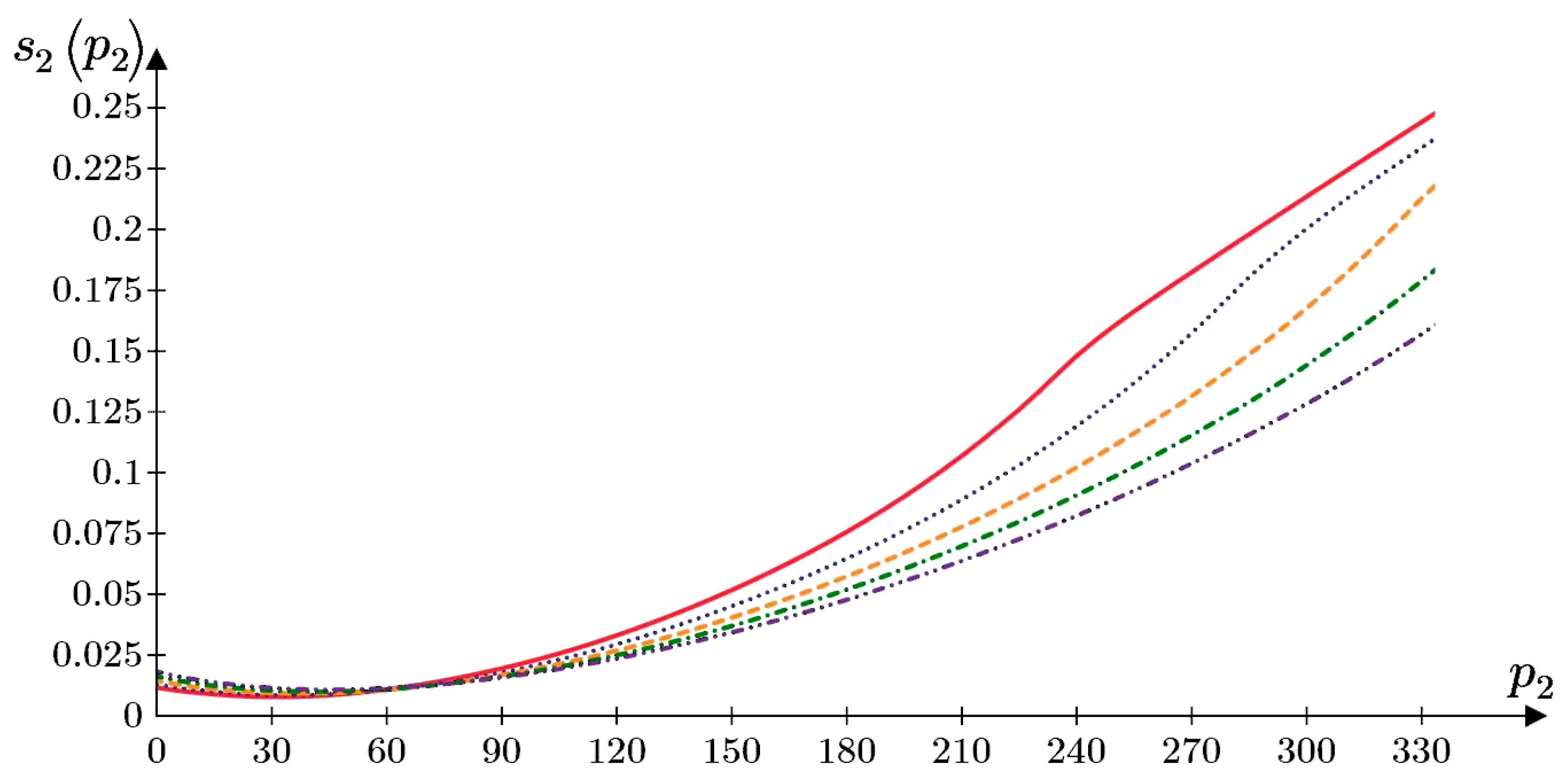
 )—h1 = 1.0 m; (
)—h1 = 1.0 m; ( )—h1 = 2.0 m; (
)—h1 = 2.0 m; ( )—h1 = 3.0 m; (
)—h1 = 3.0 m; ( )—h1 = 4.0 m; (
)—h1 = 4.0 m; ( )—h1 = 5.0 m.
)—h1 = 5.0 m.
 )—h1 = 1.0 m; (
)—h1 = 1.0 m; ( )—h1 = 2.0 m; (
)—h1 = 2.0 m; ( )—h1 = 3.0 m; (
)—h1 = 3.0 m; ( )—h1 = 4.0 m; (
)—h1 = 4.0 m; ( )—h1 = 5.0 m.
)—h1 = 5.0 m.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ter-Martirosyan, A.Z.; Shebunyaev, A.N.; Sobolev, E.S. Settlement of a Foundation on an Unsaturated Sandy Base Taking Vibrocreep into Account. Axioms 2023, 12, 594. https://doi.org/10.3390/axioms12060594
Ter-Martirosyan AZ, Shebunyaev AN, Sobolev ES. Settlement of a Foundation on an Unsaturated Sandy Base Taking Vibrocreep into Account. Axioms. 2023; 12(6):594. https://doi.org/10.3390/axioms12060594
Chicago/Turabian StyleTer-Martirosyan, Armen Z., Alexander N. Shebunyaev, and Evgeny S. Sobolev. 2023. "Settlement of a Foundation on an Unsaturated Sandy Base Taking Vibrocreep into Account" Axioms 12, no. 6: 594. https://doi.org/10.3390/axioms12060594
APA StyleTer-Martirosyan, A. Z., Shebunyaev, A. N., & Sobolev, E. S. (2023). Settlement of a Foundation on an Unsaturated Sandy Base Taking Vibrocreep into Account. Axioms, 12(6), 594. https://doi.org/10.3390/axioms12060594






