Abstract
This article proposes a family of non-standard methods coupled with compact finite differences to numerically integrate the non-linear Burgers’ equation. Firstly, a family of non-standard methods is derived to deal with a system of ordinary differential equations (ODEs) arising from the semi-discretization of initial-boundary value partial differential equations (PDEs). Further, a method of this family is considered as a special case and coupled with a fourth-order compact finite difference resulting in a combined numerical scheme to solve initial-boundary value PDEs. The combined scheme has first-order accuracy in time and fourth-order accuracy in space. Some basic characteristics of the scheme are analysed and a section concerning the numerical experiments is presented demonstrating the good performance of the combined numerical scheme.
Keywords:
non-standard numerical scheme; compact finite difference method; Von Neumann stability analysis MSC:
65L05; 65L20; 65M06; 65M12
1. Introduction
Differential equations are used in the mathematical modelling of physical phenomena based on rate of change of quantities [1,2,3,4] and very few of them can be solved analytically. Usually, in the absence of known analytical solutions, approximations of the true solution are obtained by applying an appropriate numerical method according to the nature of the given problem. Non-linear partial differential equations (PDEs) are considered a class of challenging problems, and researchers have tried to develop numerical codes to solve them accurately and efficiently. Obtaining accurate and efficient numerical approximations of the true solution of a given differential equation is an ongoing research topic. In this regard, the development and modification of new and existing efficient numerical code has been considered to provide accurate numerical approximations of the true solution. Many different approaches, including finite difference, finite element, finite volume and spectral method, are available to numerically solve a given PDE. However, the finite difference approach is still considered a fundamental approach for solving PDEs which occur frequently in various physical fields, such as fluid mechanics, quantum mechanics, electromagnetism, etc. In order to obtain high-order accurate approximations using the finite difference approach, a stencil based on a large number of grid points is required. A common drawback of this approach is the need to include more equations for grid points near and at the boundaries. An alternative approach to overcome this difficulty, that is, not to enlarge the stencil size is the compact finite difference approach. In this approach, values of the derivative of a function at some grid points are used where the function has already been evaluated. It seems that these type of methods have been known for almost 55 years. For instance, some of the these types of code were reported by Collatz [5]. In this article, we proposed a non-standard combined numerical scheme based on the compact finite difference method, possessing some additional advantages for integrating the well-known non-linear Burgers’ equation given by
subject to the following initial and boundary conditions, respectively,
and
where and v are the velocity, spatial coordinate, time and kinematic viscosity, respectively, whereas , are known functions. Equation (1) shows that convection-, diffusion- and time-dependent terms are present in the equation.
Equation (1) was first introduced by H. Bateman in 1915 [6] and later in 1948 by a Dutch physicist J M Burgers to mathematically model turbulence [7]. Burgers was an active researcher in the field of fluid mechanics and to honour his contributions, this equation was termed the Burgers’ equation. The first analytical treatment of the one-dimensional Burgers’ equation was proposed by Bateman [6]. In general, for specific initial and boundary conditions, the problem in eq1 can be treated analytically. More precisely, in the gas dynamics Holf [8] and Cole [9] proved independently that for any initial condition the problem can be reduced to form of a linear homogeneous heat equation that can be treated analytically. Thus, the exact solution of Burgers’ equation can be written in the form of a Fourier series which is difficult to handle analytically; therefore, it is important to have stable and efficient numerical methods to deal with these types of problems. For a good reference to the exact solution of the one-dimensional Burgers’ equation, one can consult the survey by Benton et al. [10].
Many researchers have proposed numerical schemes to numerically solve (1). Zhang et al. [11] discussed its numerical solution by applying two-step predictor–corrector method, known as MacCormack method in combination with compact finite difference method for spatial discretization. M. Sari et al. [12] numerically solved the one-dimensional Burgers’ equation using a sixth-order compact finite difference method in combination with low storage third-order total variation diminishing Runge–Kutta scheme. Gao et al. [13] proposed a numerical scheme by employing a high-accuracy mutli-quadratic quasi-interpolation to approximate the spatial derivatives and a first-order accurate forward difference method for the temporal derivative. For more details on existing numerical schemes to solve Burgers’ equation, one can consult [14,15,16,17,18,19,20] and the references cited therein. In the scientific literature, other types of Burgers’ equation have been addressed, for instance, Hadhoud et al. [21] proposed non-polynomial B-spline and shifted Jacobi spectral collocation methods for solving time-fractional non-linear coupled Burgers’ equations, and the local fractional two-dimensional Burgers-type equations was addressed in Yang et al. [22].
To obtain the numerical solution to Equation (1) using a compact finite difference approach, researchers have used explicit Runge–Kutta-type or linear multi-step methods for advancing the integration process in the time direction. Due to the small stability region of explicit RK methods, a small step size is required to obtain a reliable approximation to the true solution. This increases the computational cost and in some cases due to the very small grid size, round off errors may arise resulting in an unrealistic solution. In order to use linear multi-step methods, the user needs the starting values to begin the integration process. For this, the user needs to use appropriate codes as starters; for instance, RK methods. To obtain a reliable approximation to the true solution of a given problem with a large grid size, an implicit RK method could be sufficient. However, when using implicit RK methods, the user needs to solve a system of equations at each step of the integration due to the implicit nature of the code. To provide an alternative to these codes, we propose a class of unconventional explicit unconditionally stable numerical codes to accurately and efficiently integrate a given problem. Many authors have proposed these type of methods [23,24,25,26,27]. In this regard, we first present the derivation of the family of non-standard methods to integrate systems of ODEs arising in the semi-discretization of initial-boundary values of a Burgers’ equation and analyse its basic characteristics, i.e., order of accuracy and linear stability analysis. Then, by considering this family of methods and coupling them with a fourth-order compact finite difference scheme, a novel combined compact numerical scheme is obtained to deal with the initial-boundary value problem given in Equation (1).
The rest of the article is organized as follows: Section 2 concerns the development of a class of time marching numerical schemes and the basic characteristics. In Section 3, we recall the fourth-order compact finite difference method used with an explicit numerical time marching scheme presented in Section 4 as a combined numerical scheme. The Von Neumann stability analysis of the scheme is carried out in Section 5. Section 6 discusses the numerical experiments carried out by applying the combined numerical scheme, while Section 7 draws some conclusions of the present work.
2. Development of the Explicit Numerical Schemes
The semi-discretization of Equation (1) with regard to the space variable results in a system of first-order ODEs can be written as
where In order to develop the numerical schemes, we consider the scalar case of the above system, for .
Firstly, the interval was discretize into k subintervals of equal length as . We termed the step size and the approximate solution at as . Let us assume the following approximation to the true solution to the problem at point as
where and are arbitrary constants. The type of methods was initially proposed by J.D. Lambert [28]. A difference operator is linked with Equation (6)
Using the Taylor series to expand around the point , we obtain
To obtain the first-order numerical schemes and avoid the second derivative, the coefficient of in (8) must vanish. Equating the coefficient of equal to zero, we obtain given by
provided that
Using and taking arbitrarily in Equation (6), a one-parameter family of numerical schemes is obtained as
This is a new one-parameter class of explicit numerical schemes for solving the system (5).
2.1. Special Cases
By putting different values for the free parameter , we obtain a different numerical scheme.
- If we let , the well-known method of Fatunla [29] is obtained as a special case
- Let , we obtain
- Let , we obtain
2.2. Basic Characteristics of the Numerical Scheme
This section concerns the basic characteristics [30,31,32] of the proposed scheme (9), including the order of accuracy and linear stability analysis. Note from the derivation that the scheme has first-order accuracy and its linear stability analysis was carried out by applying it to the Dahlquist test equation given by
Theorem 1.
The numerical scheme given in (9) is -stable [33] for
Proof.
Considering the proposed numerical scheme (9) and applying it to the Dahlquist test equation, we obtain
which may be simplified as
Now consider the stability function
where For a stable numerical scheme, we must have
It is easy to verify that for and , the numerical scheme (9) is -stable [33]. Further, we also note that
Hence, the proposed class of methods is also -stable [33] for □
3. Compact Finite Difference Method
Compact finite differences have additional advantages over conventional finite differences as they provide higher accuracy in the approximation with a smaller stencil size. In the present article, we considered fourth-order compact finite differences in order to approximate the spatial derivatives from Equation (1). Here we recall a fourth-order compact finite difference method and for more details on this type of method, one can consult [34,35,36,37] and the references cited therein.
The space variable is discretized into N equal subintervals of equal length , where
Consider a fourth-order compact finite difference scheme for discretizing the first spacial derivative from (1) at the interior nodes
where the prime mark denotes the derivative with respect to the space variable and the following one-sided boundary scheme to obtain approximations at boundary points given by
for , and
for .
The above equations can be written in matrix form
Solving the above system of equations, we can obtain approximations to the first-order space derivatives at the discrete points of interest.
Similarly, in order to approximate the second spacial derivative appearing in the equation, we consider the following fourth-order compact finite difference scheme given by:
For interior nodes
For boundary points we have:
for and
for .
The complete matrix system for a tri-diagonal fourth-order compact scheme to approximate the second derivative can be written as follows
Solving the above system of equations, one can obtain an approximation to the second-order space derivatives from the equation at the discrete points of interest.
4. The Proposed Combined Numerical Scheme and Its Accuracy
The proposed combined numerical scheme for solving Equation (1) can be written as
Note that in the numerical scheme, we used
In order to implement the combined numerical scheme, the spatial derivatives are approximated using fourth-order compact finite difference methods and the non-standard numerical scheme (9) will act as a time marching scheme.
In this way, the proposed combined numerical scheme has first-order accuracy in time and fourth-order accuracy in space.
5. Von Neumann Stability Analysis
In this section, we carried out Von Neumann stability analysis on the proposed numerical scheme (21).
Theorem 2.
The proposed combined numerical scheme (21) is unconditionally stable for
Proof.
Considering the linearized form of Equation (1) with , Equation (1) can be rewritten as
and the combined numerical numerical scheme becomes
Note that for approximating the first space derivative using fourth-order compact scheme, the matrices A and B are triangular and both possesses the property
where
Let be the solution to (23),
where is the wave number.
This leads to
which may be simplified as
Thus,
Now, consider
this becomes
which may be simplified as
Thus, the approximation of the first derivative is
Putting the values of and B, we obtain
For approximating the second derivative, consider
where
Similarly,
Thus, we have
For the numerical scheme to be stable, we must have
Consider
where
For scheme to be stable, the following condition must be satisfied
where
considering
Thus,
Here, and This leads to
This implies that
Hence, the proposed combined numerical scheme (21) is unconditionally stable. □
6. Numerical Experiments
In this section, we evaluated the performance of the proposed combined numerical scheme (21) for solving the Burgers’ equation (1), subject to the following initial, boundary conditions and exact solution [11].
Test problem
Consider the problem
subject to the initial and boundary conditions given by
The exact solution of the problem is given by
The Table 1 represents the different notations denote the numerical schemes considered in this article.

Table 1.
Notation for different schemes.
In Table 2, the absolute errors are presented for by applying the new scheme for and . This demonstrates that the new scheme accurately integrates the given problem.

Table 2.
Comparison of the new scheme and analytical solution at time .
Table 3 presents a comparison of the absolute errors produced by the new scheme and conventional scheme 1 for and . It is evident from the data that the new scheme performs better in terms of accuracy.

Table 3.
Conventional scheme 1 versus New scheme.
As the new scheme has first-order accuracy in time, in Table 4 we present a comparison of the numerical results obtained from the new scheme and classical scheme for the values and . The numerical data given in Table 4 shows the good performance of the new scheme compared to classical scheme.

Table 4.
Comparison of the new scheme with classical scheme at time .
Table 5 shows the rate of convergence (ROC) of the new scheme in the space direction for the values and . Table 5 shows that the ROC agrees with the theoretical order of convergence of the new scheme in the space direction.

Table 5.
-error and ROC.
In Table 6, we have presented a comparison of the new scheme with existing approaches [16,38] in terms of -error for values , , , , , and . The data given in Table 6 demonstrate the better performance of the new scheme.

Table 6.
Comparison with different approaches at time .
Next, Table 7 displays the better performance of the new scheme in comparison with an existing scheme [39] in terms of accuracy using values .

Table 7.
Comparison of the new scheme with an existing scheme at time .
Table 8 presents the numerical data concerning -error and -error for different values of v for , , and . Table 8 shows that the new scheme produces very accurate approximations to the true solution of the given test problem.

Table 8.
The maximum absolute error and -error at time .
Table 9 shows a comparison between the absolute errors in the application of the new scheme and conventional scheme 2. The numerical data support the better performance of the new scheme. Note that the new scheme integrates the given problem with fewer function evaluations than the conventional scheme 2.

Table 9.
Comparison of the new scheme versus the conventional scheme 2 at time .
Table 10 shows the ROC of the new scheme in the time direction for values and . Table 10 shows that the ROC agrees with the theoretical order of convergence of the new scheme in the time direction.

Table 10.
-error and ROC.
The Figure 1 shows the numerical and analytical solutions for different values of v using values , and . It is evident that the physical behaviour of the numerical solution agrees with the physical behaviour of the analytical solution for various values of parameter v.
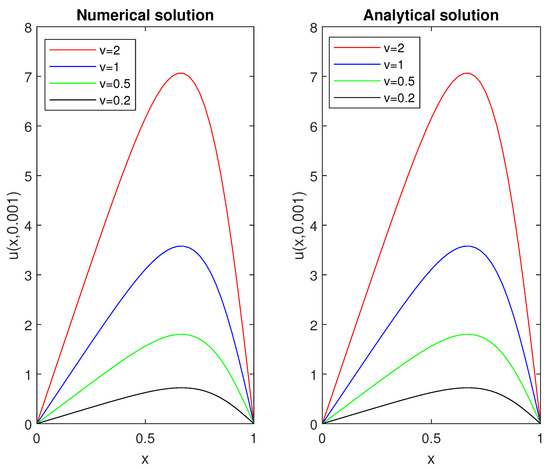
Figure 1.
Numerical and analytical solutions to the problem for different values of v at .
The numerical solution is plotted against the exact solution for different values of T. The Figure 2 shows that the physical behaviour of both solutions is similar. The plot is drawn using the values , , and .
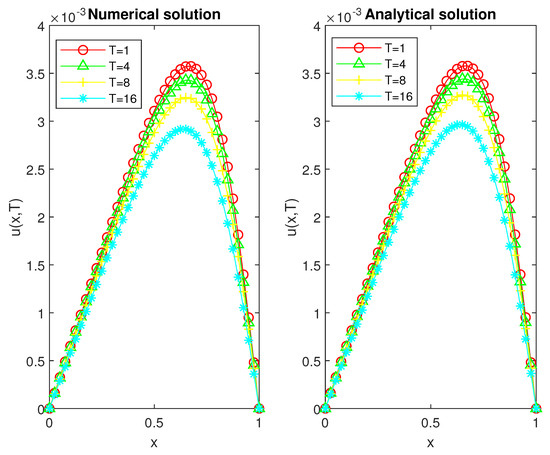
Figure 2.
Numerical versus analytical solutions for different values of T.
7. Conclusions
In this article, we considered a combined numerical scheme based on a family of non-standard numerical schemes coupled with a compact finite difference method to solve the one-dimensional Burgers’ equation. Firstly, a family of non-standard numerical schemes was developed by considering a non-standard approximation to the true solution of a given problem and then combining it with a fourth-order compact finite difference method to obtain an efficient unconditionally stable numerical scheme. The basic characteristics of the proposed numerical scheme were discussed and numerical experiments were carried out by applying the proposed numerical scheme to the Burgers’ equation. The presented numerical results indicate the good performance of the proposed numerical scheme.
Author Contributions
K.K.: Conceptualization; Development, Analysis and Implementation of numerical scheme; Writing—original draft. G.S.: Conceptualization; Supervision; Review and editing of original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No data is associated with this article.
Acknowledgments
We would like to thank the anonymous reviewers for their constructive comments that greatly improved the original manuscript. Komalpreet Kaur would like to thank I.K. Gujral Punjab Technical University Jalandhar, Punjab (India) for providing the research facilities for the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lyu, W.; Wang, Z.-A. Logistic damping effect in chemotaxis models with density-suppressed motility. Adv. Nonlinear Anal. 2022, 12, 336–355. [Google Scholar] [CrossRef]
- Lyu, W.; Wang, Z.-A. Global classical solutions for a class of reaction-diffusion system with density-suppressed motility. Electron. Res. Arch. 2022, 30, 995–1015. [Google Scholar] [CrossRef]
- Jin, H.-Y.; Wang, Z.-A. Asymptotic dynamics of the one-dimensional attraction-repulsion Keller-Segel model. Math. Methods Appl. Sci. 2015, 38, 444–457. [Google Scholar] [CrossRef]
- Xie, X.L.; Wang, T.F.; Zhang, W. Existence of solutions for the (p,q)-Laplacian equation with nonlocal choquard reaction. Appl. Math. Lett. 2023, 135, 108418. [Google Scholar] [CrossRef]
- Collatz, L. The Numerical Treatment of Differential Equations, 1st ed.; Springer: New York, NY, USA, 1966. [Google Scholar]
- Bateman, H. Some recent reseacher on the motion of fluids. Mon. Weather Rev. 1915, 43, 163–170. [Google Scholar] [CrossRef]
- Burgers, J.M. Mathematics examples illustrating relations occuring in the theory of turbulent fluid motion. Trans. R Neth. Acad. Sci. Amst. 1939, 17, 1–53. [Google Scholar]
- Hopf, E. The Partial Differential Equation ut + uux = uxx. Pure Appl. Math. 1950, 3, 201. [Google Scholar] [CrossRef]
- Cole, J.D. On a Quasi-Linear Parabolic equation occuring in Aerodynamics. Q. Appl. Math. 1951, 9, 225–236. [Google Scholar] [CrossRef]
- Benton, E.; Platzman, G.W. A table of solutions of the one-dimensional Burgers’ equations. Q. Appl. Math. 1972, 30, 195–212. [Google Scholar] [CrossRef]
- Zhang, P.G.; Wang, J.P. A predictor-corrector compact finite difference scheme for Burgers’ equation. Appl. Math. Comput. 2012, 219, 892–898. [Google Scholar] [CrossRef]
- Sari, M.; Gurarslan, G. A sixth-order compact finite difference scheme to numerical solution of Burgers’ equation. Appl. Math. Comput. 2009, 208, 475–483. [Google Scholar] [CrossRef]
- Gao, F.; Chi, C. Numerical solution of non-linear Burgers’ equation using high accuracy multi-quadric quasi interpolation. Appl. Math. Comput. 2014, 229, 414–421. [Google Scholar]
- Hassanian, I.A.; Salama, A.A.; Hosham, H.A. Fourth-order finite difference method for solving Burgers’ equation. Appl. Math. Comput. 2005, 170, 892–898. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Zhang, L. A class of high-order compact difference schemes for solving the Burgers’ equation. Appl. Math. Comput. 2019, 358, 394–417. [Google Scholar] [CrossRef]
- Mittal, R.C.; Jain, R.K. Numerical solution of non-linear Burgers’ equation with modified cubic b-splines collocation method. Appl. Math. Comput. 2012, 358, 7839–7855. [Google Scholar]
- Gulsu, M. A finite difference approach for solution of Burgers’ equation. Appl. Math. Comput. 2006, 175, 1245–1255. [Google Scholar] [CrossRef]
- Campos, M.D.; Romao, E.C. A high-order finite-difference scheme with a linearization technique for solving of three-dimensional Burgers’ equation. Comput. Model. Eng. Sci. 2014, 103, 139–154. [Google Scholar]
- Jiang, H.; Xu, D.; Qiu, W.; Zhou, J. An ADI compact difference for the two-dimensional semilinear time fractional mobile-immobile equation. Comput. Appl. Math. 2020, 39, 287. [Google Scholar] [CrossRef]
- Wang, Y.M. A high order compact difference method for fractional sub-diffusion equations with variable coefficients and nonhomogeneous Neumann boundary conditions. Comput. Appl. Math. 2019, 39, 13. [Google Scholar] [CrossRef]
- Hadhoud, A.R.; Srivastava, H.M.; Rageh, A.A.M. Non-polynomial B-spline and shifted Jacobi spectral collocation techniques to solve time-fractional nonlinear coupled Burgers’ equations numerically. Adv. Differ. Equ. 2021, 2021, 439. [Google Scholar] [CrossRef]
- Yang, X.-J.; Gao, F.; Srivastava, H.M. Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations. Comput. Math. Appl. 2017, 73, 203–210. [Google Scholar] [CrossRef]
- Ramos, H. A non-standard explicit numerical scheme for initial value problems. Appl. Math. Comput. 2007, 189, 710–718. [Google Scholar]
- Ramos, H.; Singh, G.; Kanwar, V.; Bhatia, S. An embedded 3(2) pair of nonlinear of methods for solving first order initial-value ordinary differential systems. Numer. Algorithms 2017, 75, 509–529. [Google Scholar] [CrossRef]
- Ramos, H.; Singh, G.; Kanwar, V.; Bhatia, S. Solving first-order initial-value problems by using an explicit non-standard A-stable one-step method in variable step-size formulation. Appl. Math. Comput. 2015, 268, 796–805. [Google Scholar] [CrossRef]
- Ramos, H.; Singh, G.; Kanwar, V.; Bhatia, S. An efficient variable step-size rational Falkner-type method for solving the special second-order IVP. Appl. Math. Comput. 2016, 291, 39–51. [Google Scholar] [CrossRef]
- Brezinski, C. Intégration des systèmes différentiels à l’aide du ρ-algorithme. C. R. Acad. Sci. Paris 1974, 278 A, 875–878. [Google Scholar]
- Lambert, J.D.; Shaw, B. On the numerical solution of y′ = f(x, y) by a class of formulae based on rational approximation. Math. Comput. 1965, 19, 456–462. [Google Scholar] [CrossRef]
- Fatunla, S.O. Non-linear Multi-step Methods for Initial Value Problems. Comput. Math Appl. 1982, 3, 231–239. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, J.; Shi, W.; Huo, Y.; Ren, Z.; He, D. Resonance and bifurcation of fractional quintic Mathieu-Duffing system. Chaos 2023, 33, 023131. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.L.; Wang, Q.Y.; Li, Y.B.; Li, Y.D.; Fan, Y.L. A general linear free energy relationship for predicting partition coefficients of neutral organic compounds. Chemosphere 2020, 247, 125869. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Hu, J.; Zhao, Y.; Ghosh, B.K. Finite-time observer based tracking control of uncertain heterogeneous underwater vehicles using adaptive sliding mode approach. Neurocomputing 2022, 481, 322–332. [Google Scholar] [CrossRef]
- Butcher, J.C. The Numerical Methods for Ordinary Differential Equations, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Zhao, J. Highly accurate compact mixed methods for two point boundary value problems. Appl. Math. Comput. 2017, 188, 1402–1418. [Google Scholar] [CrossRef]
- Tyler, G.J. Analysis and Implementation of High-Order Compact Finite Difference Schemes. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2007. [Google Scholar]
- Mehra, M.; Patel, K.S. A suite of Compact Finite Difference Schemes. ACM Trans. Math. Softw. 2017, 44, 1–31. [Google Scholar] [CrossRef]
- Rahman, K.; Helil, N.; Yimin, R. Some New Semi-Implicit Finite Difference Schemes for Numerical Solution of Burgers Equation. In Proceedings of the International Conference on Computer Application and System Modeling, Taiyuan, China, 22–24 October 2010; pp. 414–455. [Google Scholar]
- Grashlan, G.; Sari, M. Numerical solutions of linear and nonlinear diffusion equations by a differential quadrature method (DQM). Int. J. Numer. Methods Biomed. Eng. 2011, 27, 69–77. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).