On the Applications of the Generalized Littlewood Theorem Concerning Integrals of the Logarithm of Analytical Functions to Elliptic Functions

Abstract

Recently, we have established and used the generalized Littlewood theorem concerning contour integrals of the logarithm of analytical function to obtain new criteria equivalent to the Riemann hypothesis. Later, the same theorem was applied to calculate certain infinite sums and study the properties of zeroes of a few analytical functions. In this study, we apply this approach to elliptic functions of Jacobi and Weierstrass. Numerous sums over inverse powers of zeroes and poles are calculated, including some results for the Jacobi elliptic functions sn(z, k) and others understood as functions of the index k. The consideration of the case of the derivative of the Weierstrass rho-function, ${\wp }_z(z{,}_{}\tau )$, leads to quite easy and transparent proof of numerous equalities between the sums over inverse powers of the lattice points $m+n\tau$ and “demi-lattice” points $m+1/2+n\tau$, $m+(n+1/2)\tau$, $m+1/2+(n+1/2)\tau$. We also prove theorems showing that, in most cases, fundamental parallelograms contain exactly one simple zero for the first derivative ${\theta }_1\prime (z|\tau )$ of the elliptic theta-function and the Weierstrass $\zeta$-function, and that far from the origin of coordinates such zeroes of the $\zeta$-function tend to the positions of the simple poles of this function.

1. Introduction

The generalized Littlewood theorem concerning contour integrals of the logarithm of analytic function is the following statement [1,2]:

Theorem 1.

(The generalized Littlewood theorem). Let C denote the rectangle bounded by the lines $x=X_1{,}_{}x=X_2{,}_{}y=Y_1{,}_{}y=Y_2$, where  $X_1<X_2{,}_{}{Y}_1<Y_2$ and let f(z) be analytic and non-zero on C and meromorphic inside it, and let also g(z) be analytic on C and meromorphic inside it. Let F(z) = ln(f(z)) be the logarithm defined as follows: we start with a particular determination of  $x=X_2$, and obtain the value at other points by continuous variation along y = const from  $\ln (X_2+iy)$. If, however, this path would cross a zero or pole of f(z), we take F(z) to be  $F(z\pm i0)$ according to whether we approach the path from above or below. Let also  $\tilde{F}(z)=\ln (f(z))$ be the logarithm defined by continuous variation along any smooth curve fully lying inside the contour which avoids all poles and zeroes of f(z) and starts from the same particular determination on  $x=X_2$. Suppose that the poles and zeroes of the functions f(z), g(z) do not coincide.

Then, 

$${\displaystyle \underset{C}{\int }F(z)g(z)dz}=2\pi i\left({\displaystyle \sum _{{\rho }_g}res(g({\rho }_g)\cdot \tilde{F}({\rho }_g))-{\displaystyle \sum _{{\rho }_f^0}{\displaystyle \underset{X_1+i{Y}_{\rho }^0}{\overset{X_{\rho }^0+i{Y}_{\rho }^0}{\int }}g(z)dz}+{\displaystyle \sum _{{\rho }_f^{pole}}{\displaystyle \underset{X_1+i{Y}_{\rho }^{pole}}{\overset{X_{\rho }^{pole}+i{Y}_{\rho }^{pole}}{\int }}g(z)dz}}}}\right),$$

(1)

where the sum is over all  ${\rho }_g$ which are poles of the function g(z) lying inside C, all ${\rho }_f^0=X_{\rho }^0+Y_{\rho }^0$ which are zeroes of the function f(z) both counted taking into account their multiplicities (that is the corresponding term is multiplied by m for a zero of the order m) and which lie inside C, and all ${\rho }_f^{pol}=X_{\rho }^{pol}+Y_{\rho }^{pol}$ which are poles of the function f(z) counted taking into account their multiplicities and which lie inside C. The assumption is that all relevant integrals on the right-hand side of the equality exist.

The proof of this theorem [2] is very close to the proof of the standard Littlewood theorem corresponding to the case g(z) = 1, see, e.g., [3]. The application of this theorem is especially interesting for certain particular cases when the contour integral ${\displaystyle \underset{C}{\overset{}{\int }}F(z)g(z)dz}$ disappears (tends to zero) if the contour tends to infinity, that is when $X_1,Y_1\to -\infty$, $X_2,Y_2\to +\infty$ (more precisely, when we can find some sequence of the contours C_j tending to infinity and such, that the contour integral tends to zero, see below). This means that Equation (1) takes the form

$${\displaystyle \sum _{{\rho }_f^0}{\displaystyle \underset{-\infty +i{Y}_{\rho }^0}{\overset{X_{\rho }^0+i{Y}_{\rho }^0}{\int }}g(z)dz}}-{\displaystyle \sum _{{\rho }_f^{pol}}{\displaystyle \underset{-\infty +i{Y}_{\rho }^{pole}}{\overset{X_{\rho }^{pole}+i{Y}_{\rho }^{pole}}{\int }}g(z)dz}}={\displaystyle \sum _{{\rho }_g}^{}res(g({\rho }_g)\cdot F({\rho }_g))}$$

(2)

Earlier, this approach was used by us to analyze some properties of the zeroes of the Riemann zeta-function (see, e.g., [4] for a general discussion of this function)—in particular, to establish a number of theorems equivalent to the Riemann hypothesis [1,2,5,6] (Some of these results were recently included in the corresponding chapter of the Encyclopedia of Mathematics and its Applications [7]). In Ref. [8], we discuss the use of the generalized Littlewood theorem to calculate many infinite sums over integers and to study the properties of zeroes of some analytical functions, such as incomplete Riemann and gamma functions and polygamma functions.

In the present paper, which is closely related to [8], we apply the same approach to calculate certain sums over powers of zeroes for different elliptic functions, which are studied because of their high importance in mathematics and physics, see, e.g., [9,10,11,12,13,14,15]. These functions are fertile ground for our approach based on the generalized Littlewood theorem, and, to the best of the author’s knowledge, similar questions were never systematically studied. At the same time, such information can be really useful for a better understanding of the general properties and behavior of elliptic functions, as this takes place for many other analytic functions including not only the aforementioned Riemann zeta-function, see references above, but also, e.g., degenerate hypergeometric function and Bessel functions [16,17], polygamma and related functions [8,18], Hurwitz zeta-function [8], and many others. Moreover, we may say that the elliptic functions are the natural “starting point” and prototype for all such research because, in a sense, the logarithms of theta-functions are simply defined via the sums over inverse powers of their zeroes, and the Weierstrass zeta-function can also be defined via the sums over inverse powers of its poles (minus 1/z term), see below.

2. Sums over Powers of Zeroes of Elliptic Theta-Functions

Whenever possible, for the references concerning standard formulae pertinent to elliptical functions, we will mostly cite “encyclopedia-like” Ref. [9]. First, we need to give the necessary definitions and specify a notation used, especially because, unfortunately, different notations and conventions still co-exist in the elliptic functions research field. We define four theta-functions as follows

$${\theta }_1(z{,}_{}q)={\theta }_1(z|\tau )=2{\displaystyle \sum _{k=0}^{\infty }{(-1)}^k{q}^{{(k+1/2)}^2}\sin ((2k+1)z)}$$

(3a)

$${\theta }_2(z{,}_{}q)={\theta }_2(z|\tau )=2{\displaystyle \sum _{k=0}^{\infty }{q}^{{(k+1/2)}^2}\cos ((2k+1)z)}$$

(3b)

$${\theta }_3(z{,}_{}q)={\theta }_3(z|\tau )=1+2{\displaystyle \sum _{k=0}^{\infty }{q}^{k^2}\cos (2kz)}$$

(3c)

$${\theta }_4(z{,}_{}q)={\theta }_4(z|\tau )=1+2{\displaystyle \sum _{k=0}^{\infty }{(-1)}^k{q}^{k^2}\cos (2kz)}.$$

(3d)

Here, $q=e^{i\pi \tau }$ (it is named a nome), and $\mathrm{Im}\tau >0$. As functions of z for any fixed $\tau$, they are entire and $2\pi$-periodic, and they are quasiperiodic on the lattice formed by the points $z_{m,n}=(m+n\tau )\pi$—the following relations hold:

$${\theta }_1(z+(m+n\tau )\pi |\tau )={(-1)}^{m+n}{q}^{-n^2}{e}^{-2inz}{\theta }_1(z|\tau ),$$

(4)

and similarly for other theta-functions.

These properties and those defined by asymptotic (the quasi-periodicity condition (4)) guarantee that for large |z| the theta-function is at most O(exp(C|z|²) with some constant C; hence, we have the disappearance of the contour integrals ${\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{{(z-a)}^k}\ln ({\theta }_j(z))dz}$ for j = 1, 2, 3, 4 and k = 4, 5… in the limit of infinitely large contours. The location of zeroes ${\rho }_i$, which all are simple, for these functions, also is well known. Namely, the functions ${\theta }_j(z|\tau )$ for j = 1, 2, 3, 4 have zeroes at the points $(m+n\tau )\pi$, $(m+1/2+n\tau )\pi$, $(m+1/2+(n+1/2)\tau )\pi$, and $(m+(n+1/2)\tau )\pi$ respectively [9]. Here and below, in the combination $m+n\tau$ both m and n are positive or negative integers or zero: $m{,}_{}n\in Z$. We will not always repeat this statement.

In light of the generalized Littlewood theorem, the aforementioned known location of zeroes immediately defines the Taylor expansion of the theta-functions. We have [9]: ${\theta }_1(\pi z|\tau )=\pi z{\theta }_1\prime (0|\tau )\exp (-{\displaystyle \sum _{j=1}^{\infty }\frac{1}{2j}{\delta }_{2j}{z}^{2j})}$, ${\theta }_2(\pi z|\tau )={\theta }_2(0|\tau )\exp (-{\displaystyle \sum _{j=1}^{\infty }\frac{1}{2j}{\alpha }_{2j}{z}^{2j})}$, ${\theta }_3(\pi z|\tau )={\theta }_3(0|\tau )\exp (-{\displaystyle \sum _{j=1}^{\infty }\frac{1}{2j}{\beta }_{2j}{z}^{2j})}$, ${\theta }_4(\pi z|\tau )={\theta }_3(0|\tau )\exp (-{\displaystyle \sum _{j=1}^{\infty }\frac{1}{2j}{\gamma }_{2j}{z}^{2j})}$ (that is ${\theta }_1(\pi z|\tau )=\pi z{\theta }_1\prime (0|\tau )(1-\frac{{\delta }_2}{2}{z}^2-(\frac{{\delta }_4}{4}-\frac{{\delta }_2^2}{8})z^4+O(z^6))$, etc.), where:

$${\delta }_{2j}(\tau )={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{\begin{array}{l}m=-\infty \\ |m|+|n|\ne 0\end{array}}^{\infty }\frac{1}{{(m+n\tau )}^{2j}}}},$$

(5a)

$${\alpha }_{2j}(\tau )={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+\frac{1}{2}+n\tau )}^{2j}}}},$$

(5b)

$${\beta }_{2j}(\tau )={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+\frac{1}{2}+(n+\frac{1}{2})\tau )}^{2j}}}},$$

(5c)

$${\gamma }_{2j}(\tau )={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+(n+\frac{1}{2})\tau )}^{2j}}}}.$$

(5d)

The order of summation is important for these sums if j = 1, see below. Here and below, the prime sign for the function means the differentiation with respect to the first argument.

From these formulae, we obtain the Taylor expansions of the logarithms in some vicinity of zero, like, e.g.,

$$\ln [{\theta }_1(\pi z|\tau )/(\pi z{\theta }_1\prime (0|\tau ))]=-{\displaystyle \sum _{j=1}^{\infty }\frac{1}{2j}{\delta }_{2j}{z}^{2j}},$$

(6)

or $\ln [{\theta }_2(\pi z|\tau )/({\theta }_2(0|\tau )]=-{\displaystyle \sum _{j=1}^{\infty }\frac{1}{2j}{\alpha }_{2j}{z}^{2j}}$, etc. It is also useful to note for the future that

$${\delta }_2=-\frac{{\pi }^2{\theta }_1‴(0|\tau )}{3{\theta }_1\prime (0|\tau )},$$

(7)

which immediately follows from the Taylor series of ${\theta }_1(\pi z|\tau )$ given above.

Based on Taylor expansions of this type, and using the generalized Liitlewood theorem, we immediately “solve” (actually there is nothing to solve, this is more a definition) the problem of finding all sums ${\displaystyle \sum _{{\rho }_i}^{}\frac{1}{{({\rho }_i-a)}^n}}$, $n\ge 2$, over zeroes of theta-functions, which we illustrate with the function ${\theta }_1(\pi z|\tau )$:

Proposition 1.

Let integer  $n\ge 2$ and a be an arbitrary complex number not coinciding with  $m+n\tau$. Then 

$${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau -a)}^n}}}=-\frac{1}{(n-1)!}\frac{d^n}{d{z}^n}(\ln ({\theta }_1(\pi z|\tau )){|}_{\pi z=a}.$$

(8)

For n = 2 the order of summation is important.

Proof. 

For $n\ge 3$ this is the immediate direct consequence of Equation (2) given the aforementioned asymptotic of $\ln {\theta }_1(\pi z|\tau )$. For n = 2, we cannot use Equation (2), but we can integrate Equation (8) with n = 3 from a = 0 to a to get ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau -a)}^2}}}=-\frac{d^2}{d{z}^2}\ln ({\theta }_1(\pi z|\tau )){|}_{\pi z=a}+Const$. The constant here is equal to zero, as shows the case a = 0: ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau )}^2}}}=-\frac{d^2}{d{z}^2}\ln ({\theta }_1(\pi z|\tau )){|}_{z=0}={\delta }_2(\tau )$. This is just a definition with the appropriate order of the summation. □

Remark 1.

1. Note that equations for the case$n\ge 4$ can be obtained just by repetitive differentiation of the equation for n = 3 with respect to a. This is valid for all similar equations occurring below, and we will not repeat this anymore.

2. The case n = 2 deserves further discussion. We already said that the asymptotic of the theta-function does not enable to claim that the integrals ${\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{{(z-a/\pi )}^3}\ln ({\theta }_j(\pi z|\tau ))dz}$ tend to zero when the contours C_i tend to infinity. On the other hand, the conditionally converged sums ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau -a)}^2}}}$ can be calculated, but the result depends on the order of summation: for example, Eisenstein himself already showed that [19]

$${\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{\begin{array}{l}n=-\infty \\ |m|+|n|\ne 0\end{array}}^{\infty }\frac{1}{{(m+n\tau )}^2}}}={\delta }_2(\tau )-\frac{2\pi i}{\tau }.$$

(9)

This means that some sequence of the contours C_j tending to infinity, and such that $\lim {\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{{(z-a/\pi )}^3}\ln ({\theta }_j(\pi z|\tau ))dz}$, exists, do can be constructed, but this is not easy. Fortunately, today we have quite recent results of Romik and Scherer [20]. They studied the importance of the summation order for the Eisenstein series ${\delta }_2$ and Weierstrass ℘-function. In particular, from their results, it follows that if the contours C_j are rectangles with the vertices $\pm j\pm i\cdot h\cdot j$ (here h is an arbitrary real positive constant, integer j tends to infinity, and  $i=\sqrt{-1}$), then the following limit exists: ${\lim }_{j\to \infty }{\displaystyle \sum _{\begin{array}{l}(m,n)\in C_j\\ |m|+|n|\ne 0\end{array}}^{}\frac{1}{{(m+n\tau )}^2}}={\delta }_2(\tau )-\frac{4}{\tau }{\tanh }^{-1}(h\tau )$. (See [16] for original formulation; here ${\tanh }^{-1}(h\tau )$ means the inverse function and not $1/\tanh (h\tau )$). The case $h\to 0$ corresponds to the ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau )}^2}}}$ summation, while the case $h\to \infty$ corresponds to the ${\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }\frac{1}{{(m+n\tau )}^2}}}$ summation order.

Remark 2.

The Taylor expansions given above, albeit quite standard, are circular because they contain the values of  ${\theta }_2(0,q){,}_{}{\theta }_3(0,q){,}_{}{\theta }_4(0,q)$ or ${\theta }_1\prime (0,q)$ (note the Jacobi identity  ${\theta }_1\prime (0,q)={\theta }_2(0,q){\theta }_3(0,q){\theta }_4(0,q)$ [9]), which actually should be determined from the “real” Taylor expansions. Fortunately, this question is not relevant for our central questing concerning the sums over zeroes of the functions at hand, but unfortunately, there are no known ways to determine these values apart from the direct use of the definitions given by Equation (3). For some particular values of q (or $\tau$) and functions  ${\theta }_j(0,q)$, especially  ${\theta }_3(0,q)$, these values are known, for example,  ${\theta }_3(0,e^{-\pi })={\pi }^{1/4}{\mathsf{\Gamma }}^{-1}(3/4)$,  ${\theta }_3(0,e^{-\sqrt{3}\pi })={\pi }^{-1}{\mathsf{\Gamma }}^{3/2}(4/3)2^{-2/3}{3}^{13/18}$, etc.; see [21,22,23] and references cited therein, especially those on the Ramanujan lost notebook.

Note also that the numbers ${\alpha }_{2j}{,}_{}{\beta }_{2j}{,}_{}{\gamma }_{2j}{,}_{}{\delta }_{2j}$ are interrelated with each other in a known fashion, and that all numbers ${\delta }_{2j}$  can be expressed via ${\delta }_2$ and ${\delta }_4$ [9,12], see also below.

Finally, we also would like to note that, in light of Taylor expansions such as Equation (6), theta-functions are truly the most “fundamental” object for the generalized Littlewood theorem applications: their logarithms are expressed exactly via the sums over the powers of zeroes.

The question concerning the corresponding sums of the derivatives of the theta-functions can be put forward and solved in the same fashion.

Proposition 1a.

Let  ${\rho }_i$ be zeroes of the function  $\frac{d^l}{d{z}^l}{\theta }_1(z|\tau )$ (j = 1, 2, 3, 4 and l = 1, 2, 3… having order k_i, and a be an arbitrary complex number not coinciding with any  ${\rho }_i$. Then for integer  $n\ge 3$

$${\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{({\rho }_i-a)}^n}}=-\frac{1}{(n-1)!}\frac{d^n}{d{z}^n}(\ln (\frac{d^l}{d{z}^l}{\theta }_j(z|\tau )){|}_{z=a}$$

(10)

At least for the case l = 1, it is more interesting to consider the logarithmical derivative of the theta-functions rather than their simple derivatives. We have $\frac{d}{dz}\ln {\theta }_j(z|\tau )=\frac{{\theta }_j\prime (z|\tau )}{{\theta }_j(z|\tau )}$ so that this function has simple poles at the points coinciding with zeroes of ${\theta }_j(z|\tau )$, which location is well known, and zeroes coinciding with the zeroes of ${\theta }_j\prime (z|\tau )$ function. At the same time, the asymptotic of this logarithmic derivative, which is for large |z| is O(|z|), enables to consider smaller powers of zeroes. We have the following proposition.

Proposition 1b.

Let  ${\rho }_i^{zero,j}$ be zeroes of the function  ${\theta }_j\prime (z|\tau )$ having order k_i (j = 1, 2, 3, 4). Let also  ${\rho }_i^{pole,j}$ be simple zeroes of the function  ${\theta }_j(z|\tau )$, and let a be an arbitrary complex number not coinciding with any  ${\rho }_i^{zero,j}$,  ${\rho }_i^{pole,j}$. Then

$${\lim }_{N\to \infty }{\displaystyle \sum _{|{\rho }_i^{zero,j}|<N,|{\rho }_i^{pole,j}|<N}^{}(-\frac{k_i}{{({\rho }_i^{zero,j}-a)}^2}+\frac{1}{{({\rho }_i^{pole,j}-a)}^2}})=\frac{d^2}{d{z}^2}\ln \frac{\theta {\prime }_j(z|\tau )}{{\theta }_j(z|\tau )}{|}_{z=a},$$

(11)

and for integer $n\ge 3$

$$-{\displaystyle \sum _{{\rho }_i^{zero,j}}^{}\frac{k_i}{{({\rho }_i^{zero,j}-a)}^n}}+{\displaystyle \sum _{{\rho }_i^{pole,j}}^{}\frac{1}{{({\rho }_i^{pole,j}-a)}^n}}=\frac{d^n}{d{z}^n}\ln \frac{\theta {\prime }_j(z|\tau )}{{\theta }_j(z|\tau )}{|}_{z=a}.$$

(12)

Furthermore, Equation (11) can be reformulated as follows. Let us for any positive real h define $S_{lh,j}(a):={\displaystyle \sum _{(l-1)h\le \mathrm{Im}({\rho }_i)<lh}^{}\frac{k_i}{{({\rho }_i^{zero,j}-a)}^2}}$, $l\in Z$ and let $S_j(a):={\lim }_{h\to 0}{\displaystyle \sum _{l=-\infty }^{\infty }{S}_{lh,j}(a)}$. Then for j = 1 $S_1(a)={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau -a)}^2}}}-\frac{d^2}{d{z}^2}\ln \frac{\theta {\prime }_1(z|\tau )}{{\theta }_1(z|\tau )}{|}_{z=a}$, where the order of summation is important, and similarly for other theta-functions with the corresponding replacement in the term ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau -a)}^2}}}$ taking in account the location of zeroes of these functions.

In particular, for zeroes of the function ${\theta }_1\prime (\pi z|\tau )$, we have: $S_1(0)=\frac{3}{2}{\delta }_2$, ${\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{\rho }_i^4}}=5{\delta }_4+2{\delta }_2^2$, ${\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{\rho }_i^6}}=7{\delta }_6+6{\delta }_2{\delta }_4+2{\delta }_2^3$, etc. For zeroes of the function ${\theta }_2\prime (\pi z|\tau )$ we have: $S_2(0)={\alpha }_2-2\frac{{\alpha }_4}{{\alpha }_2}$, ${\displaystyle \sum _{{\rho }_i}^{}\prime \frac{k_i}{{\rho }_i^4}}={\alpha }_4-4\frac{{\alpha }_6}{{\alpha }_2}+2\frac{{\alpha }_4^2}{{\alpha }_2^2}$, etc. Here, the prime sign means that zero at z = 0 should be excluded during the summing). The same formulae hold for the functions ${\theta }_3\prime (\pi z|\tau )$, ${\theta }_4\prime (\pi z|\tau )$ but ${\alpha }_{2j}$ should be replaced via ${\beta }_{2j}$, ${\gamma }_{2j}$ respectively.

Proof. 

For n = 3, 4, 5…, the proposition immediately follows from Equation (2) applied to the contour integrals ${\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{{(z-a)}^{n+1}}\ln \frac{{\theta }_j\prime (z|\tau )}{{\theta }_j(z|\tau )}dz}$. For applications at a = 0 we use Taylor expansion (6) and similar. We have $\ln {\theta }_1(\pi z|\tau )=\ln ({\theta }_1\prime (\pi z|\tau )+\ln z-{\displaystyle \sum _{j=1}^{\infty }\frac{1}{2j}{\delta }_{2j}{z}^{2j}}$ thus $z\frac{d}{dz}\ln {\theta }_1(\pi z|\tau )=\mathrm{l}-{\displaystyle \sum _{j=1}^{\infty }{\delta }_{2j}{z}^{2j}}$, so that

$$\begin{gathered} \ln [z\frac{d}{dz}\ln {\theta }_1(\pi z|\tau )]=-{\delta }_2{z}^2-{\delta }_4{z}^4-{\delta }_6{z}^6-\frac{1}{2}{\delta }_2^2{z}^4-{\delta }_2{\delta }_4{z}^6-\frac{1}{3}{\delta }_2^3{z}^6+O(z^8)= \\ -{\delta }_2{z}^2-({\delta }_4+\frac{1}{2}{\delta }_2^2)z^4-({\delta }_6+{\delta }_2{\delta }_4+\frac{1}{3}{\delta }_2^3)z^6+O(z^8), \end{gathered}$$

and the Proposition statements follow. For example, for n = 6 we have $-\frac{1}{6}{\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{\rho }_i^6}}+\frac{1}{6}{\delta }_6=-{\delta }_6-{\delta }_2{\delta }_4-\frac{1}{3}{\delta }_2^3$ so that ${\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{\rho }_i^6}}=7{\delta }_6+6{\delta }_2{\delta }_4+2{\delta }_2^3$.

Similarly, $\ln {\theta }_2(\pi z|\tau )=\ln ({\theta }_2(\pi z|\tau )-{\displaystyle \sum _{j=1}^{\infty }\frac{1}{2j}{\alpha }_{2j}{z}^{2j}}$ thus $\frac{d}{dz}\ln {\theta }_2(\pi z|\tau )=-{\displaystyle \sum _{j=1}^{\infty }{\alpha }_{2j}{z}^{2j-1}}$ and $-\frac{1}{{\alpha }_{2}z}\frac{d}{dz}\ln {\theta }_2(\pi z|\tau )={\displaystyle \sum _{j=1}^{\infty }\frac{{\alpha }_{2j}}{{\alpha }_2}{z}^{2j-2}}$. This leads to $\ln (-\frac{1}{{\alpha }_{2}z}\frac{d}{dz}[\ln {\theta }_2(\pi z|\tau )])=\frac{{\alpha }_4}{{\alpha }_2}{z}^2+(\frac{{\alpha }_6}{{\alpha }_2}-\frac{{\alpha }_4^2}{2{\alpha }_2^2})z^4+O(z^6)$, and the Proposition statements follow.

The case n = 2 requires more caution because, as we have already stated in Remark 1, the result of the summation depends on the order of the summation. Thus, we select the sequence of the contours C_j as stated in Remark 1. The value of the contour integrals tends to zero anyway (it does so for any sequence of the contours tending to infinity), but with this choice of C_j, we have the well-defined order of the summation. In the limit $h\to 0$, we obtain for the sum over powers of zeroes the value of S(a) defined in the Proposition statement, and for the sum over poles, the ordered sum ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau -a)}^2}}}$, or similar for other theta-functions. □

For clarity of presentation, let us now briefly state the main results of this section. We see, that due to the Taylor expansion (6) and similar, logarithms of elliptic theta-functions can be defined via the sums of inverse powers of their zeroes, which, of course, makes the task of the determination of these same sums with the help of the generalized Littlewood Theorem 1 trivial (or “superfluous”). Nevertheless, in our opinion, the question does not look so simple already for the “non-central” sums such as ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau -a)}^n}}}$—see Equation (8) and similar. This theorem proves also to be quite useful to study similar sums for derivatives, usual and logarithmical ones, of the elliptic theta-functions.

3. Sums over Powers of Zeroes of Weierstrass $\mathit{\sigma }$- and $\mathit{\zeta }$-Function and Its Derivatives

3.1. Weierstrass $\sigma$-Function

Weierstrass $\sigma$-function is defined as [9]

$$\sigma (z|\mathsf{\Lambda })=z{\displaystyle \prod _{\omega \in \mathsf{\Lambda }/\left\{0\right\}}^{\infty }(1-\frac{z}{\omega })\exp (}\frac{z}{\omega }+\frac{z^2}{2{\omega }^2}),$$

(13)

where $\mathsf{\Lambda }$ is the lattice formed by points $m{\omega }_1+n{\omega }_2$, $m{,}_{}n\in Z$, and $\mathrm{Im}({\omega }_2/{\omega }_1)>0$. We have, by definition, $\zeta (z|\mathsf{\Lambda })=\frac{d}{dz}(\ln \sigma (z|\mathsf{\Lambda }))$, $\rho (z|\mathsf{\Lambda })=-\frac{d\zeta (z|\mathsf{\Lambda })}{dz}$, ${\rho }_z(z|\mathsf{\Lambda })=\frac{d\rho (z|\mathsf{\Lambda })}{dz}$. Below we will use the notation $\sigma (z|\mathsf{\Lambda })$, $\zeta (z|\mathsf{\Lambda })$, etc., if an arbitrary lattice is using; if ${\omega }_1=1$, we shall write $\sigma (z{,}_{}\tau )$, $\zeta (z{,}_{}\tau )$, etc., Sometimes, when this cannot lead to misunderstanding, we omit $\tau$ and write simply $\sigma (z)$, $\zeta (z)$.

From the definition it is clear that $\sigma (z|\mathsf{\Lambda })$ function is an entire function having simple zeroes at the lattice points, hence the question of the sums over its zeroes coincides with the same question for the function ${\theta }_1(\frac{\pi z}{{\omega }_1}|\tau )$ with the appropriate ${\omega }_1{,}_{}\tau$.

3.2. Weierstrass $\zeta$-Function

However, the question concerning the sums over powers of zeroes becomes quite relevant for the function $\zeta (z|\mathsf{\Lambda })$. This function evidently has simple poles at the lattice points, but it also has zeroes. For further analysis, let us select a lattice $m+n\tau$ (the general case is just the rescaling). The following Laurent expansion is well known (and evident from the definition) [9]:

$$\zeta (z{,}_{}\tau )=\frac{1}{z}-{\displaystyle \sum _{k=2}^{\infty }{\delta }_{2k}(\tau )z^{2k-1}},$$

(14)

where ${\delta }_{2k}(\tau )$ are Eisenstein series defined above by Equation (5a). To simplify the notation, below we will omit $\tau$ when writing ${\delta }_{2k}(\tau )$. Thus $z\zeta (z,\tau )=1-{\displaystyle \sum _{k=2}^{\infty }{\delta }_{2k}{z}^{2k}}$ and

$$\ln (z\zeta (z{,}_{}\tau ))=-{\delta }_4{z}^4-{\delta }_6{z}^6-({\delta }_8+\frac{1}{2}{\delta }_4^2)z^8+O(z^{10}).$$

(15)

The quasi-periodicity conditions read $\zeta (z+2{\omega }_j{,}_{}\tau )=\zeta (z{,}_{}\tau )+2\zeta ({\omega }_j{,}_{}\tau )$, j = 1, 2, 3 and ${\omega }_3=-{\omega }_1-{\omega }_2$ [9], which means that for large |z| the asymptotic of $\ln |\zeta (z)|$ does not exceed O(ln|z|). Correspondingly, the generalized Littlewood theorem can be applied even to the integrals ${\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{{(z-a)}^2}\ln \zeta (z{,}_{}\tau )dz}$, which gives the following proposition (compare with analogous statements for polygamma functions in [8]).

Proposition 2.

Let  ${\rho }_i^{pole}=m+n\tau$ be simple poles of $\zeta (z,\tau )$,  $m{,}_{}n\in Z$, and ${\rho }_j^{zero}$ be zeroes of the function  $\zeta (z,\tau )$ having order k_j. Let a be an arbitrary complex number not equal to any ${\rho }_i^{pole}$ or ${\rho }_j^{zero}$. Then,

$${\lim }_{N\to \infty }{\displaystyle \sum _{|{\rho }_i^{zero}|<N,|{\rho }_j^{pole}|<N}^{}(-\frac{k_i}{{\rho }_j^{zero}-a}+\frac{1}{{\rho }_i^{pole}-a})}=\frac{d}{dz}\ln \zeta (z,\tau ){|}_{z=a}.$$

(16)

This proposition attests “how many” there are zeroes of the Weierstrass zeta-function: they are able to “compensate” the formal sums ${\displaystyle \sum _{}^{}{\displaystyle \sum _{}^{}\frac{1}{m+n\tau -a}}}$ over 2D lattice. Qualitative behavior of such zeroes became clear if we will look into the limit of the function $\zeta (z,\tau )$ when $\tau \to i\infty$: $\zeta (z)=\pi \cot (\pi z)+\frac{{\pi }^2}{3}z$. For large |z| zeroes approach the lattice points (and poles) $m+n\tau$, see the theorems below.

In an analogous fashion, we have the following propositions.

Proposition 3.

With the same notation as in the Proposition 2, we have:

$${\lim }_{N\to \infty }{\displaystyle \sum _{|{\rho }_i^{zero}<N|,|{\rho }_i^{pole}<N|}^{\infty }(-\frac{k_i}{{({\rho }_i^{zero}-a)}^2}+\frac{1}{{({\rho }_i^{pole}-a)}^2})}=\frac{d^2}{d{z}^2}\ln (\zeta (z,\tau )){|}_{z=a},$$

(17)

and for n = 3, 4, …

$$-{\displaystyle \sum _{{\rho }_i^{zero}}^{}\frac{k_i}{{({\rho }_i^{zero}-a)}^{{}^n}}}+{\displaystyle \sum _{{\rho }_j^{pole}}^{}\frac{1}{{({\rho }_j^{pole}-a)}^n}}=\frac{1}{(n-1)!}\frac{d^n}{d{z}^n}(\ln \zeta (z,\tau )){|}_{z=a}.$$

(18)

Furthermore, Equation (17) can be reformulated as follows. Let us for any positive real h define $S_{lh}(a):={\displaystyle \sum _{(l-1)h\le \mathrm{Im}({\rho }_i)<lh}^{}\frac{k_i}{{({\rho }_i^{zero}-a)}^2}}$, $l\in Z$, and let $S(a):={\lim }_{h\to 0}{\displaystyle \sum _{l=-\infty }^{\infty }{S}_{lh}(a)}$. Then $S(a)={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(m+n\tau -a)}^2}}}-\frac{d^2}{d{z}^2}\ln \zeta (z,\tau ){|}_{z=a}$, where the order of summation is important. In particular, $S(0)={\delta }_2$, ${\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{({\rho }_i^{zero})}^4}}=5{\delta }_4$, ${\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{({\rho }_i^{zero})}^6}}=7{\delta }_6$, ${\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{({\rho }_i^{zero})}^8}}=9{\delta }_8+4{\delta }_4^2$, etc.

Proof. 

For n = 3, 4, 5…, the proposition immediately follows from Equation (2) applied to the contour integrals ${\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{{(z-a)}^{n+1}}\ln \zeta (z{,}_{}\tau )dz}$. For application at a = 0 we use Taylor expansion (15). For example, from the consideration of ${\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{z^9}\ln (z\zeta (z{,}_{}\tau ))dz}$, we have $-\frac{1}{8}{\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{({\rho }_i^{zero})}^8}}+\frac{1}{8}{\delta }_8=-{\delta }_8-\frac{1}{2}{\delta }_4^2$, whence ${\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{({\rho }_i^{zero})}^8}}=9{\delta }_8+4{\delta }_4^2$.

The case n = 2 requires more caution because, as we have already stated in Remark 1, the result of the summation depends on the order of the summation. Further consideration is exactly the same as during the proof of the Proposition 1b. □

The standard procedure of finding the subsequent terms in the expansion (15) from (14) easily enables us to establish the formulae to find the sums over larger powers of zeroes.

Let us finish this discussion with the following theorems. For greater generality, we formulate the first of them for solutions of the equation $\zeta (z,\tau )=h$ where h is an arbitrary complex number.

Theorem 2.

Let C_MN be a parallelogram with the vortices at the points 1, 2, 3, 4 having the coordinates  $M+\delta +N\tau +\tau \delta$,  $M+1+\delta +N\tau +\tau \delta$,  $M+1+\delta +(N+1)\tau +\tau \delta$ and  $M+\delta +(N+1)\tau +\tau \delta$ respectively; see  Figure 1. Here,  $M{,}_{}N\in Z$,  $\mathrm{Im}\tau \ne 0$, and  $\delta$ is an arbitrary complex number with  $0<\left|\delta \right|<1$. Let us first the following take place: if both  ${\eta }_1:=\zeta (1/2,\tau )$ and  ${\eta }_2:=\zeta (\tau /2,\tau )$ are not equal to zero than  $\mathrm{Im}({\eta }_2/{\eta }_1)\ne 0$; or either  ${\eta }_1=0$, or  ${\eta }_2=0$. Then:

(i) 

There exist such values of M₀, N₀ that for all   $|M|\ge M_0$, $|N|\ge N_0$ each parallelogram C_MN contains one and only one simple root of the equation $\zeta (z,\tau )=h$, where h is an arbitrary complex number.

If both ${\eta }_1\ne 0$ and ${\eta }_2\ne 0$ but $\mathrm{Im}({\eta }_2/{\eta }_1)=0$, then;

(ii) 

For any M we can find such value of N₀, depending on M, that each parallelogram $C_{M_{1}N}$ with $|N|\ge N_0$ and $|M_1|\le M$ contains one and only one simple root of the equation $\zeta (z,\tau )=h$, and;

(iii) 

For any N we can find such value of M₀, depending on N, that each parallelogram $C_{M{N}_1}$ with $|M|\ge M_0$ and $|N_1|\le N$ contains only one simple root of the equation $\zeta (z,\tau )=h$.

Figure 1. Parallelogram C_MN used for the proof of Theorems 2–4. The coordinates of points 1 and 3 are indicated explicitly, and the “vectors” (complex numbers) $\overrightarrow{1}{,}_{}\overrightarrow{\tau }$ forming the lattice are shown.

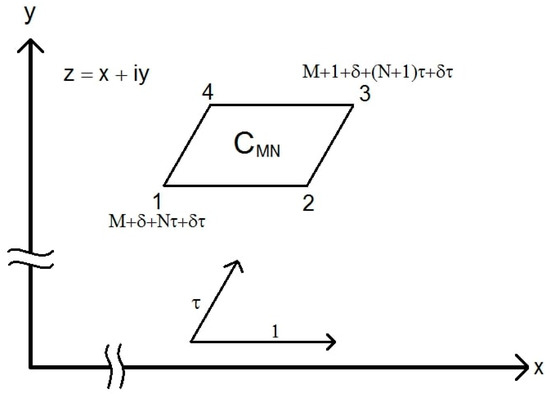
Figure 1. Parallelogram C_MN used for the proof of Theorems 2–4. The coordinates of points 1 and 3 are indicated explicitly, and the “vectors” (complex numbers) $\overrightarrow{1}{,}_{}\overrightarrow{\tau }$ forming the lattice are shown.

Proof. 

First, we note that both ${\eta }_1{,}_{}{\eta }_2$ cannot be simultaneously equal to zero because $\zeta (z,\tau )$ is not a double-periodic function. The theorem is a simple application of the argument Principle, see, e.g., [3], which states that if the function f(z) is meromorphic inside and on some contour C, and has no poles or zeroes on C, then $\frac{1}{2\pi i}{\displaystyle \underset{C_{MN}}{\overset{}{\int }}\frac{f\prime (z)}{f(z)}dz}=Z-P$, where Z is the number of zeroes of the function f(z) inside the contour, and P is the number of poles there. Both Z and P are counted considering their orders.

Let us estimate the contour integral ${\displaystyle \underset{C_{MN}}{\overset{}{\int }}\frac{(\zeta (z{,}_{}\tau )-h)\prime }{\zeta (z{,}_{}\tau )-h}dz}$$={\displaystyle \underset{C_{MN}}{\overset{}{\int }}\frac{-\wp (z{,}_{}\tau )}{\zeta (z{,}_{}\tau )-h}dz}$, which we consider separately for two pairs of opposite sides of the contour. For horizontal sides 1–2 and 3–4, see Figure 1, we have, due to the quasi-periodicity condition of the Weierstrass zeta-function: $\zeta (z,\tau )-h=\zeta (z_0{,}_{}\tau )-h+2N{\eta }_1+2M{\eta }_2$ and

$\zeta (z,\tau )-h=\zeta (z_0{,}_{}\tau )-h+2N{\eta }_1+2(M+1){\eta }_2$ respectively; here,$z_0\in [\delta {,}_{}1+\delta ]$. Function $\wp (z{,}_{}\tau )$ is double-periodic, and the contour C₀₀ is so chosen that on its border there are no poles of this function, thus for our contour C_MN, $|\wp (z{,}_{}\tau )|$ is bounded. There are also no poles of the function $\zeta (z,\tau )$ on the border of the contour C₀₀; hence, both real and imaginary parts of $\zeta (z_0,\tau )-h$ are bounded as well.

If ${\eta }_1\ne 0$, ${\eta }_2\ne 0$ and $\mathrm{Im}({\eta }_2/{\eta }_1)\ne 0$, the angle $\phi$ between the “vectors” (complex numbers) ${\eta }_1{,}_{}{\eta }_2$ is not equal to 0 or $\pi$, and we have $|2N{\eta }_1+2M{\eta }_2|=\sqrt{|2N{\eta }_1+2M\cos \phi {\eta }_2{|}^2+4M^2{\sin }^2\phi }\ge 2|M\sin \phi |$ and $|2N{\eta }_1+2M{\eta }_2|=\sqrt{|2N\cos \phi {\eta }_1+2M{\eta }_2{|}^2+4N^2{\sin }^2\phi }\ge 2|N\sin \phi |$. Thus, independently on N this module can be made as large as we please by the choice of sufficiently large M, and independently on M this module can be made as large as we please by the choice of sufficiently large N. The same is evidently valid for the modules of $|\zeta (z_0,\tau )-h+2N{\eta }_1+2M{\eta }_2|$ and $|\zeta (z_0,\tau )-h+2N{\eta }_1+2(M+1){\eta }_2|$. Thus for sufficiently large M and N we can make the joint contribution of the sides 1-2 and 3-4 to the value of $\frac{1}{2\pi }{\displaystyle \underset{C_{MN}}{\overset{}{\int }}|\frac{-\wp (z{,}_{}\tau )}{\zeta (z{,}_{}\tau )-h}||dz}|$ less than, say 0.1 (Of course, $|{\displaystyle \underset{C_{MN}}{\overset{}{\int }}\frac{-\wp (z{,}_{}\tau )}{\zeta (z{,}_{}\tau )-h}dz}|\le$${\displaystyle \underset{C_{MN}}{\overset{}{\int }}|\frac{-\wp (z{,}_{}\tau )}{\zeta (z{,}_{}\tau )-h}||dz}|$).

Similarly, we can make the joint contribution of the sides 2-3 and 4-1 to the value of $\frac{1}{2\pi }{\displaystyle \underset{C_{MN}}{\overset{}{\int }}|\frac{-\wp (z{,}_{}\tau )}{\zeta (z{,}_{}\tau )-h}|dz}$ also less than 0.1. Thus, we see that the total value of the contour integral is made less than 0.2, that is it is equal to zero. By construction, each our contour C_MN contains exactly one simple pole of the function $\zeta (z,\tau )-h$, viz. at the point $M+1+(N+1)\tau$, hence due to the argument principle it contains exactly one simple zero of this function.

If ${\eta }_1=0$ or ${\eta }_2=0$, then instead of $|\zeta (z_0,\tau )-h+2N{\eta }_1+2M{\eta }_2|$, we get simply $|\zeta (z_0,\tau )-h+2M{\eta }_2|$ or $|\zeta (z_0,\tau )-h+2N{\eta }_1|$; hence, all the abovesaid remains correct.

Now, let the ratio ${\eta }_1/{\eta }_2=a$ be real. Then we get $|\zeta (z_0,\tau )-h+(2Na+2M){\eta }_2|$, so that we can find infinitely many pairs N, M with arbitrary large modules for which $|(2Na+2M){\eta }_2|$ is very small—or simply equal to zero if a is rational. Thus, we need to fix the value of N (or M)—and then, of course, we still can find the value of M₀ (or N₀) such that for any $|M|\ge M_0$ and $|N_1|\le N$ (or $|N|\ge N_0$ and $|M_1|\le M$), the value of $|\zeta (z_0,\tau )-h+(2Na+2M){\eta }_2|$ is as large as we please. This proves (ii) and (iii). Finally, note that we used a simple extension of the argument principle: if zero is located exactly on the contour, it contributes ½ to the contour integral value. This possibility is also excluded by our consideration. □

Remark 3.

Apparently, there is no fundamental reason why a ratio  ${\eta }_1/{\eta }_2=a$ cannot be real. However, this is easy to indicate an important case where it cannot indeed. This is the situation when  $\tau$ is purely imaginary—simply because than  ${\eta }_1$ is real while  ${\eta }_2$ is purely imaginary. The only remaining possibility that  ${\eta }_1=0$ or  ${\eta }_2=0$ is excluded because according to the Legendre relation  $-{\eta }_1+{\eta }_2\tau =\pi i$ [9], in such a case we would have correspondingly either ${\eta }_2=\pi i/\tau$—hence real, or  ${\eta }_1=-\pi i$—hence purely imaginary.

A similar theorem can be even more easily proven for the roots of the equation $g(z):=\zeta (z,\tau )-P_n(z)=0$, where P_n(z) is an arbitrary polynomial of the n-th power ($n\ge 2$)—simply because then the asymptotic of $\frac{g\prime (z)}{g(z)}=\frac{-\wp (z,\tau )-P{\prime }_n(z)}{\zeta (z,\tau )-P_n(z)}$ for large |z| is O(1/|z|). We will not consider here this general case but will limit ourselves with the following more interesting (in our opinion) case concerning the location of zeroes of the derivatives of the theta-function ${\theta }_1\prime (\pi z|\tau )$.

Theorem 3.

Let C_MN be the same parallelogram as in Theorem 2. Let the following take place: if both  ${\kappa }_1:=\zeta (1/2,\tau )-\nu /2$ and  ${\kappa }_2:=\zeta (\tau /2,\tau )-\nu /2$ are not equal to zero then  $\mathrm{Im}({\kappa }_2/{\kappa }_1)\ne 0$; or either  ${\kappa }_1=0$, or  ${\kappa }_2=0$, but these two relations do not hold simultaneously; here  $\nu =-\frac{{\pi }^2}{3}\frac{{\theta }_1‴(0|\tau )}{{\theta }_1\prime (0|\tau )}={\delta }_2(\tau )$, where ${\theta }_1(z|\tau )$ is theta-function and  ${\delta }_2(\tau )$ is defined in Equation (5a). Then:

(i) 

There exist such values of M₀, N₀ that for all $|M|\ge M_0$, $|N|\ge N_0$ each parallelogram C_MN contains one and only one simple zero of the derivative ${\theta }_1\prime (\pi z|\tau )$.

If both ${\kappa }_1\ne 0$ and ${\kappa }_2\ne 0$ but $\mathrm{Im}({\kappa }_2/{\kappa }_1)=0$, then;

(ii) 

For any M we can find such value of N₀, depending on M, that each parallelogram $C_{M_{1}N}$ with $|N|\ge N_0$ and $|M_1|\le M$ contains one and only one simple zero of the derivative ${\theta }_1\prime (\pi z|\tau )$, and;

(iii) 

For any N we can find such value of M₀, depending on N, that each parallelogram $C_{M{N}_1}$ with $|M|\ge M_0$ and $|N_1|\le N$ contains only one simple zero of the derivative ${\theta }_1\prime (\pi z|\tau )$.

Proof. 

The differentiation of Equation (6) gives $\frac{\pi {\theta }_1\prime (\pi z|\tau )}{{\theta }_1(\pi z|\tau )}-\frac{1}{z}=-{\displaystyle \sum _{j=1}^{\infty }{\delta }_{2j}(\tau )z^{2j-1}}$ so that, comparing this with the Taylor development (14), we have $\frac{\pi {\theta }_1\prime (\pi z|\tau )}{{\theta }_1(\pi z|\tau )}=\zeta (z{,}_{}\tau )-{\delta }_2(\tau )z$. Thus, zeroes of the derivative of the first theta-function are the solutions of the equation $\zeta (z{,}_{}\tau )-{\delta }_2(\tau )z=0$. To simplify the notation below we use $\nu :={\delta }_2(\tau )=-\frac{{\pi }^2{\theta }_1\prime \prime \prime (0|\tau )}{3{\theta }_1\prime (0|\tau )}$ (see Equation (7)). To analyze these solutions, we consider the contour integral $\frac{1}{2\pi i}{\displaystyle \underset{C_{MN}}{\overset{}{\int }}\frac{-\wp (z{,}_{}\tau )-\nu }{\zeta (z{,}_{}\tau )-\nu z}dz}$ in the same manner as during the proof of the Theorem 2. Again, we begin with the analysis of the contribution of the sides 1-2 and 3-4. The nominator is similarly bounded, and in the denominator we have for the side 1-2:

$\zeta (z{,}_{}\tau )-vz=\zeta (z_0{,}_{}\tau )-v{z}_0+2N{\eta }_1+2M{\eta }_2-Nv-M\tau v=$$\zeta (z_0{,}_{}\tau )-\nu z_0+2N({\eta }_1-\nu /2)+2M({\eta }_2-\tau \nu /2)$, $z_0\in [\delta {,}_{}1+\delta ]$. If both numbers ${\eta }_1-\nu /2{,}_{}{\eta }_2-\tau \nu /2$ are not equal to zero and $\mathrm{Im}[({\eta }_1-\nu /2)/({\eta }_2-\tau \nu /2)]\ne 0$, we repeat mutatis mutandi the proof of Theorem 2, and similarly if one (but not both) of these numbers is equal to zero. For the case when both these numbers are not equal to zero while $\mathrm{Im}[({\eta }_1-\nu /2)/({\eta }_2-\tau \nu /2)]=0$, the statements similar to the equivalent case of Theorem 2 are proven also similar to Theorem 2. □

Now let us prove the following theorem which gives more precise results than Theorems 2 and 3. We do not search for the most general conditions.

Theorem 4

Let C_MN be the same parallelogram as in Theorem 2, and another notation also follows this Theorem. Let both ${\eta }_1:=\zeta (1/2,\tau )$ and ${\eta }_2:=\zeta (\tau /2,\tau )$ be not equal to zero and $\mathrm{Im}({\eta }_2/{\eta }_1)\ne 0$. Then, there exist such values of M₀, N₀ that when $|M|\ge M_0$ and $|N|\ge N_0$, and |M| or |N|, or both, tend to infinity, the value of $|{\rho }_{zero}-{\rho }_{pole}|$ tend to zero.

If ${\eta }_2=0$, then for any M₀ there exists such value of N₀, depending on M₀, that for any $|M|\le M_0$ and $|N|\ge N_0$ the value of $|{\rho }_{zero}-{\rho }_{pole}|$ tend to zero when N tends to infinity.

If ${\eta }_1=0$, then for any N₀ there exists such value of M₀, depending on N₀, that for any $|N|\le N_0$ and $|M|\ge M_0$ the value of $|{\rho }_{zero}-{\rho }_{pole}|$ tend to zero when M tends to infinity.

Here ${\rho }_{pole}{,}_{}{\rho }_{zero}$ are simple pole and zero of the function $\zeta (z{,}_{}\tau )$ belonging to the parallelogram C_MN.

Proof. 

Now we consider the contour integral $\frac{1}{2\pi i}{\displaystyle \underset{C_{MN}}{\overset{}{\int }}z\frac{\zeta \prime (z{,}_{}\tau )}{\zeta (z{,}_{}\tau )}dz}$ which, by the Cauchy residue theorem and the properties of poles and zeroes of the function $\zeta (z{,}_{}\tau )$ established in the Theorem 2, is equal to ${\rho }_{zero}-{\rho }_{pole}$. For the horizontal sides of the rectangle C_MN we have the following contribution to the contour integral value: ${\displaystyle \underset{1}{\overset{2}{\int }}z\frac{\zeta \prime (z{,}_{}\tau )}{\zeta (z{,}_{}\tau )}dz}$$-{\displaystyle \underset{3}{\overset{4}{\int }}z\frac{\zeta \prime (z{,}_{}\tau )}{\zeta (z{,}_{}\tau )}dz}=$$-{\displaystyle \underset{\delta }{\overset{1+\delta }{\int }}\wp (z)[\frac{z+M+N\tau }{\zeta (z{,}_{}\tau )+2M{\eta }_2+2N{\eta }_1}-\frac{z+M+(N+1)\tau }{\zeta (z{,}_{}\tau )+2M{\eta }_2+(2N+2){\eta }_1}]dz}$. Here we used the periodicity and quasi-periodicity conditions. This integral is evidently equal to $-{\displaystyle \underset{\delta }{\overset{1+\delta }{\int }}\wp (z)[\frac{2{\eta }_{1}z+2{\eta }_{1}M-\zeta (z{,}_{}\tau )\tau -2M{\eta }_2\tau }{(\zeta (z{,}_{}\tau )+2N{\eta }_1+2M{\eta }_2)(\zeta (z{,}_{}\tau )+2M{\eta }_2+(2N+2){\eta }_1)}]dz}=$$-{\displaystyle \underset{\delta }{\overset{1+\delta }{\int }}\wp (z)[\frac{2{\eta }_{1}z-2\pi iM-\zeta (z{,}_{}\tau )\tau }{(\zeta (z{,}_{}\tau )+2N{\eta }_1+2M{\eta }_2)(\zeta (z{,}_{}\tau )+2M{\eta }_2+(2N+2){\eta }_1)}]dz}$, we used the condition $-{\eta }_1+{\eta }_2\tau =\pi i$.

$\zeta (z{,}_{}\tau )$ is bounded, thus now if ${\eta }_{1{,}_{}}{\eta }_2\ne 0$ and $\mathrm{Im}({\eta }_2/{\eta }_1)\ne 0$, we definitely can select M₀, N₀ in such a manner that for all $|M|\ge M_0$, $|N|\ge N_0$ the module of the denominator is strictly positive and larger than ${(2|M\sin \phi |-a)}^2$ and ${(2|N\sin \phi |-a)}^2$; see the proof of the Theorem 2. Thus when |M| or |N|, or both, tend to infinity, the value of the integral tends to zero because the value of the nominator module does not exceed b|M| and ℘(z) is bounded. Here, a and b are some appropriate positive constants not depending on |M| or |N|. This proves the main statement of the theorem, for the consideration of the contribution of non-horizontal sides of the contour to the contour integral value is estimated quite similarly.

If, however, ${\eta }_2=0$, we do not have the O(|M|²) behavior of the denominator. In such a case, we need to limit the values of |M| and consider only $|M|\le M_0$—then the integral still tends to zero when |N| tends to infinity. If ${\eta }_1=0$, we have a similar situation when considering the contributions of the non-horizontal sides of the parallelogram. □

Similar theorems can be formulated for the roots of the equation $\zeta (z)=h$ and the values of the derivative ${\theta }_1\prime (z|\tau )$. We will not do this here. The mathematical meaning of all these theorems is transparent: due to the quasi-periodicity conditions, for large |z| the function $\zeta (z)$”typically” has a large O(|z|) module (apart from some “degenerate” cases which are clear from the Theorems), and thus the (relatively) small values of $|\zeta (z)|$ can be attained only in some close vicinity of a simple pole.

3.3. Weierstrass ℘-Function and Its Derivatives

We have the same consideration for the Weierstrass ℘-function, which has poles of the second order at the lattice points and Taylor expansion [9]

$$\wp (z{,}_{}\tau )=-\frac{d}{dz}\zeta (z{,}_{}\tau )=\frac{1}{z^2}+{\displaystyle \sum _{k=2}^{\infty }(2k-1){\delta }_{2k}{z}^{2k-2}}$$

(19)

hence $z^2\wp (z{,}_{}\tau )=1+{\displaystyle \sum _{k=2}^{\infty }(2k-1){\delta }_{2k}{z}^{2k}}$ and

$$\ln (z^2\wp (z{,}_{}\tau ))=3{\delta }_4{z}^4+5{\delta }_6{z}^6+(7{\delta }_8-\frac{9}{2}{\delta }_4^2)z^8+O(z^{10}).$$

(20)

This is a double periodic function, thus already the integrals ${\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{{(z-a)}^2}\ln \wp (z{,}_{}\tau )dz}$ tend to zero for infinitely large contours.

Note, that contrary to the zeroes of the Weierstrass $\zeta$-function, where the author is unaware of the detailed studies of zeroes, the question concerning the location of the zeroes of the Weierstrass ℘-function received attention [24,25].

We have the following Proposition.

Proposition 4.

Let  ${\rho }_i^{pole}=m+n\tau$, where $m{,}_{}n\in Z$, be second order poles of the $\wp (z,\tau )$ function, and ${\rho }_j^{zero}$ be simple zeroes of this function; the latter can be written as  ${\rho }_j^{zero}=\pm {\rho }_0+m+n\tau$, where  ${\rho }_0$ belongs to the first fundamental parallelogram [24,25]. Let a be an arbitrary complex number not equal to any pole or zero of the function $\wp (z,\tau )$. Than

$${\lim }_{N\to \infty }{\displaystyle \sum _{|{\rho }_i^{zero}|<N,|{\rho }_j^{pole}|<N}^{}(-\frac{1}{{\rho }_j^{zero}-a}+\frac{2}{{\rho }_i^{pole}-a})}=\frac{d}{dz}\ln \wp (z,\tau ){|}_{z=a},$$

(21)

$${\lim }_{N\to \infty }{\displaystyle \sum _{|{\rho }_i^{zero}|<N,|{\rho }_j^{pole}|<N}^{}(-\frac{1}{{({\rho }_j^{zero}-a)}^2}+\frac{2}{{({\rho }_i^{pole}-a)}^2})}=\frac{d^2}{d{z}^2}\ln \wp (z,\tau ){|}_{z=a},$$

(22)

and for n = 3, 4, 5…

$$-{\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{({\rho }_i^{zero}-a)}^{{}^n}}}+{\displaystyle \sum _{{\rho }_j}^{}\frac{2}{{({\rho }_j^{pole}-a)}^n}}=\frac{1}{(n-1)!}\frac{d^n}{d{z}^n}\ln \wp (a,\tau ).$$

(23)

Furthermore, Equation (22) can be formulated as follows:

$$\begin{array}{l}{\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }(\frac{1}{{(m+n\tau -{\rho }_o-a)}^2}}}+\frac{1}{{(m+n\tau +{\rho }_0-a)}^2})=\\ {\displaystyle \sum _{n=-\infty }^{n=\infty }{\displaystyle \sum _{m=-\infty }^{m=\infty }\frac{2}{{(m+n\tau -a)}^2}}}-\frac{d^2}{d{z}^2}(\ln \wp (z,\tau )){|}_{z=a}\end{array}$$

where the order of summation is important.

In particular,  ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }(\frac{1}{{(m+n\tau -{\rho }_0)}^2}}+\frac{1}{{(m+n\tau +{\rho }_0)}^2})}=2{\delta }_2$ (again, the order of summation is important), ${\displaystyle \sum _{{\rho }_i}^{}\frac{1}{{({\rho }_i^{zero})}^4}}=-10{\delta }_4$, ${\displaystyle \sum _{{\rho }_i}^{}\frac{1}{{({\rho }_i^{zero})}^6}}=-28{\delta }_6$, ${\displaystyle \sum _{{\rho }_i}^{}\frac{1}{{({\rho }_i^{zero})}^8}}=-54{\delta }_8+36{\delta }_4^2$, etc.

Proof. 

First, we note that all zeroes here are simple [24,25], so we omit coefficients k_i. Then the proof is absolutely similar to that of Propositions 2 and 3. For example, from the consideration of ${\displaystyle \underset{C_i}{\overset{}{\int }}\frac{1}{z^9}\ln (z^2\wp (z{,}_{}\tau ))dz}$, we have $-\frac{1}{8}{\displaystyle \sum _{{\rho }_i}^{}\frac{k_i}{{({\rho }_i^{zero})}^8}}+\frac{2}{8}{\delta }_8=7{\delta }_8-\frac{9}{2}{\delta }_4^2$, whence ${\displaystyle \sum _{{\rho }_i}^{}\frac{1}{{({\rho }_i^{zero})}^8}}=-54{\delta }_8+36{\delta }_4^2$. We have the term $\frac{2}{8}{\delta }_8$ rather than $\frac{1}{8}{\delta }_8$ in the l.h.s. here because the function has the poles of the second order at the lattice points.

For n = 2 we apply the same sequence of the contours C_j as in Proposition 3. Now, due to the fact that all zeroes of the function have the form ${\rho }_j^{zero}=\pm {\rho }_0+m+n\tau$ [24,25], we need not the same construction of S_lh as was used before, but can write the order of summation as this is done in the Proposition statement. □

The standard procedure of finding the subsequent terms in the expansion (20) from (19) easily enables us to establish the formulae to find the sums over larger powers of zeroes.

In the same fashion, by finding the Laurent expansions of the derivatives $\frac{d^n}{d{z}^n}\zeta (z,\tau )$ starting from Equation (14) and then forming the corresponding Laurent expansions of $\frac{d^k}{d{z}^k}\ln [\frac{d^n}{d{z}^n}\zeta (z,\tau )]$, the questions concerning the sum of zeroes of these derivatives can be elucidated.

We do not analyze this situation in full here and limit ourselves with the case of n = 2, that is the case of $\wp \prime (z{,}_{}\tau )={\wp }_z(z{,}_{}\tau )$ function. Due to the well-known $\frac{d^2}{d{z}^2}\zeta (z{,}_{}\tau )=-\wp \prime (z)=-2\sqrt{(\wp (z)-e_1)(\wp (z)-e_2)(\wp (z)-e_3)}$ [9], where $e_1=\wp (1/2)$, $e_2=\wp (\tau /2)$, $e_3=\wp (1/2+\tau /2)$, we see that this function has a special status: it has poles of the third order at the lattice points $m+n\tau$ and simple zeroes at the points of the “demi-lattices” $m+1/2+n\tau$, $m+1/2+(n+1/2)\tau$ and $m+(n+1/2)\tau$. Clearly, from Equation (19) $\wp \prime (z{,}_{}\tau )=-\frac{2}{z^3}+{\displaystyle \sum _{k=0}^{\infty }(2k+3)(2k+2){\delta }_{2k+4}{z}^{2k+1}}$, $\ln (-\frac{z^3}{2}\wp \prime (z{,}_{}\tau ))=\ln (1-{\displaystyle \sum _{k=0}^{\infty }(2k+3)(k+1){\delta }_{2k+4}{z}^{2k+4}})$—and its Taylor expansion can be used for the search of the corresponding sums and, in such a manner, the relations between ${\alpha }_{2j}{,}_{}{\beta }_{2j}{,}_{}{\gamma }_{2j}$ and ${\delta }_{2j}$. Already from $\ln (-\frac{z^3}{2}\wp \prime (z{,}_{}\tau ))=-3{\delta }_4{z}^4-10{\delta }_6{z}^6-(21{\delta }_8+\frac{9}{2}{\delta }_4^2)z^8+O(z^{10})$, applying Equation (2), we obtain

$$3{\delta }_2={\alpha }_2+{\beta }_2+{\gamma }_2,$$

(24a)

$$15{\delta }_4={\alpha }_4+{\beta }_4+{\gamma }_4,$$

(24b)

$$63{\delta }_6={\alpha }_6+{\beta }_6+{\gamma }_6,$$

(24c)

and

$$171{\delta }_8+36{\delta }_4^2={\alpha }_8+{\beta }_8+{\gamma }_8.$$

(24d)

see Equation (5) for definitions.

Remark 4.

Certainly, all equations for the sums obtained above can be differentiated with respect to  $\tau$. This does not seem very interesting due to tyhe complicated and not so explicit dependence of the involved functions on  $\tau$. For completeness, we present here the result of the differentiation of Equation (24a)—non-trivial statement if  $\mathrm{Re}\tau \ne 0$:

$$\begin{array}{l}3{\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{\begin{array}{l}m=-\infty \\ |m|+|n|\ne 0\end{array}}^{\infty }\frac{n}{{(m+n\tau )}^3}}}={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{n}{{(m+\frac{1}{2}+n\tau )}^3}}}+{\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{n+1/2}{{(m+\frac{1}{2}+(n+\frac{1}{2})\tau )}^3}}}\\ +{\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{n+1/2}{{(m+(n+\frac{1}{2})\tau )}^3}}}. \end{array}$$

The order of summation is important here.

Let us now briefly state the main results of this section. Similarly to the elliptic theta-functions, Weierstrass elliptic functions also, in a sense, can be defined via the sums over inverse powers of their poles (not zeroes now)—compare, e.g., Equations (6) and (14), and this circumstance brings certain similarities between the questions concerning the sums of inverse powers of zeroes and poles of these two groups of elliptic functions. We also would like to especially underline the results of Theorems 2–4 concerning the localization of simple zeroes of the Weierstrass zeta-function, and very transparent proof of relations (24a)–(24d) (many other relations of this type can be obtained) using the generalized Littlewood Theorem 1.

4. Sums over Powers of Zeroes of Jacobi Elliptic Functions

4.1. Jacobi Elliptic Functions as Functions of z

Jacobi elliptical functions cn(z, k), sn(z, k), dn(z, k) and other in this raw are expressible as certain ratios of the theta-functions [9,10,11,12,13,14,15]; hence, in a sense, the question of the sums of powers of the zeroes (and poles) of these functions is reduced to the already discussed question concerning zeroes of the theta-functions. Nevertheless, by historical and, first of all, application reasons, Jacobi elliptical functions usually are considered the functions of the so-called index k [9,10,11,12,13,14,15], so let us now briefly discuss this question from just the corresponding angle of view.

The location of zeroes and poles of Jacobi elliptical functions with respect to the fundamental lattice formed by the points $z=2mK+2niK\prime$, where n, m are positive or negative integers or zero, is well known [9]. First of all, we note that the simple poles for Jacobi elliptical functions sn(z, k), cn(z, k) and dn(z, k) (here we limit ourselves with these three functions; consideration for other Jacobi elliptic functions is quite similar) are located at the points $z=2mK+(2n+1)iK\prime$). Of course, this merely reflects the circumstance that all these functions are expressible as $Const\cdot \frac{{\theta }_j(\eta ,q)}{{\theta }_4(\eta ,q)}$, where j = 1, 2, 3, $\eta =\frac{\pi z}{2K(k)}$ and $q=\exp (-\frac{\pi K\prime (k)}{K(k)})$, that is $\tau =\frac{iK\prime (k)}{K(k)}$. Here

$$K(k)=\frac{\pi }{2}{{\displaystyle \sum _{n=0}^{\infty }\left[\frac{(2n-1)!!}{(2n)!!}\right]}}^2{k}^{2n}=\frac{\pi }{2}{\cdot }_2{F}_1(\frac{1}{2}{,}_{}\frac{1}{2}{;}_{}1{,}_{}{k}^2)$$

(25)

and

$$K\prime (k)=K(\sqrt{1-k^2})$$

(26)

with ${}_2{F}_1(\frac{1}{2},\frac{1}{2};1;k^2)$ being a hypergeometric function, see, e.g., [12,26,27] for the discussion of this function. The value K(k) is also named the complete elliptic integral of the first kind and/or quarter period. Thus $\tau =\frac{i{\cdot }_2{F}_1(\frac{1}{2},\frac{1}{2};1;1-k^2)}{{}_2{F}_1(\frac{1}{2},\frac{1}{2};1;k)})$. Inverse problem (so-called Jacobi inverse problem) to express k as a function of $\tau$ (or q) gives more straightforward formulae [9]: $k=\frac{{\theta }_2^2(0|\tau )}{{\theta }_3^2(0|\tau )}$, $K(k)=\frac{1}{2}\pi {\theta }_3^2(0|\tau )$, $K\prime (k)=-\frac{i\tau }{2}\pi {\theta }_3^2(0|\tau )$.

In particular, $sn(z,k)=Const\cdot \frac{{\theta }_1(\eta ,q)}{{\theta }_4(\eta ,q)}$ so that exactly the lattice points $z=2mK+2niK\prime$ are the points, where simple zeroes of the function sn(z, k) are located, and so on.

The Taylor expansions of Jacobi elliptic functions at zero are well known [9,28]. We have:

$$\frac{sn(z{,}_{}k)}{z}=1-(1+k^2)\frac{z^2}{3!}+(1+14k^2+k^4)\frac{z^4}{5!}-(1+135k^2+135k^4+k^6)\frac{z^6}{7!}+O(z^8),$$

so that

$$\ln \frac{sn(z{,}_{}k)}{z}=-(1+k^2)\frac{z^2}{3!}+(\frac{1+14k^2+k^4}{5!}-\frac{1}{2}\frac{{(1+k^2)}^2}{36})z^4+O(z^6)$$

and $\ln \frac{sn(z,k)}{z}=-(1+k^2)\frac{z^2}{6}+(\frac{-7+22k^2-7k^4}{720})z^4+O(z^6)$. Thus, we immediately, starting from ${\displaystyle \underset{C}{\overset{}{\int }}\frac{1}{z^3}\ln \frac{sn(z,k)}{z}dz}$ and using Equation (2), get

$${\displaystyle \sum _{m=-\infty }^{\infty }\prime {\displaystyle \sum _{n=-\infty }^{\infty }\left(\frac{1}{[{(2mK+(2n+1)iK\prime ]}^2}-\frac{1}{{(2mK+2niK\prime )}^2}\right)}}=-\frac{1+k^2}{3}.$$

(27)

Here and below, the prime sign after the summing sign means that the term ${(2mK+2niK\prime )}^{-2}$ corresponding to n = m = 0 should be omitted.

Starting from ${\displaystyle \underset{C}{\overset{}{\int }}\frac{1}{z^5}\ln \frac{sn(z,k)}{z}dz}$, we get ${\displaystyle \sum _{m=-\infty }^{\infty }\prime {\displaystyle \sum _{n=-\infty }^{\infty }\left(\frac{1}{{[2mK+(2n+1)iK\prime ]}^4}-\frac{1}{{(2mK+2niK\prime )}^4}\right)}}=-\frac{7+22k^2-7k^4}{180}$, and so force. For powers larger than two, here and below, the sums can be separated:

$${\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }\left(\frac{1}{{[2mK+(2n+1)iK\prime ]}^4}\right)}}-{\displaystyle \sum _{m=-\infty }^{\infty }\prime {\displaystyle \sum _{n=-\infty }^{\infty }\frac{1}{{(2mK+2niK\prime )}^4}}}=-\frac{7+22k^2-7k^4}{180},$$

(28)

and so on. For the sums involving inverse squares, such a separation requires a well-defined order of the summation, similar to the cases discussed above.

Function cn(z, k) has simple zeroes at the points $z=(2m+1)K+2niK\prime$ and Taylor expansion [9] $cn(z{,}_{}k)=1-\frac{z^2}{2!}+(1+4k^2+k^4)\frac{z^4}{4!}-(1+44k^2+16k^4)\frac{z^6}{6!}+O(z^8)$, and thus $\ln (cn(z{,}_{}k))=-\frac{z^2}{2!}+(\frac{1+4k^2+k^4}{24}-\frac{1}{2}\frac{1}{4})z^4+O(z^6)$, that is

$$\ln (cn(z{,}_{}k))=-\frac{z^2}{2!}+(\frac{-2+4k^2+k^4}{24})z^4+O(z^6).$$

We have

$${\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }\left(\frac{1}{{[2mK+(2n+1)iK\prime ]}^2}-\frac{1}{[(2m+1)K+2niK\prime ){]}^2}\right)}}=-1.$$

(29)

Note independence on k here.

Further,

$${\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }\left(\frac{1}{{[2mK+(2n+1)iK\prime ]}^4}-\frac{1}{[(2m+1)K+2niK\prime ){]}^4}\right)}}=\frac{-2+4k^2+k^4}{6},$$

(30)

and so forth.

Function dn(z, k) has simple zeroes at points $z=(2m+1)K+(2n+1)iK\prime$ and Taylor expansion [9]:

$dn(z{,}_{}k)=1-k^2\frac{z^2}{2!}+k^2(4+k^2)\frac{z^4}{4!}-k^2(16+44k^2+k^4)\frac{z^6}{6!}+O(z^8)$, thus $\ln (dn(z{,}_{}k))=-k^2\frac{z^2}{2!}+(\frac{k^2(4+k^2)}{24}-\frac{1}{2}\frac{k^4}{4})z^4+O(z^6)$, and $\ln (dn(z{,}_{}k))=-k^2\frac{z^2}{2!}+\frac{2k^2-k^4}{12}{z}^4+O(z^6)$.

We have

$${\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }\left(\frac{1}{{[2mK+(2n+1)iK\prime ]}^2}-\frac{1}{[(2m+1)K+(2n+1)iK\prime ){]}^2}\right)}}=-k^2$$

(31)

and

$${\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }\left(\frac{1}{{[2mK+(2n+1)iK\prime ]}^4}-\frac{1}{[(2m+1)K+(2n+1)iK\prime ){]}^4}\right)}}=\frac{2k^2-k^4}{3}.$$

(32)

Of course, “non-central” sums over poles and zeroes of these functions such as ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }(\frac{1}{{[2mK+(2n+1)iK\prime -a]}^2}}}-\frac{1}{{[2mK+2niK\prime -a]}^2})=\frac{d^2}{d{z}^2}\ln (sn(z{,}_{}k)){|}_{z=a}$, or even ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }(\frac{1}{2mK+(2n+1)iK\prime -a}}}-\frac{1}{2mK+2niK\prime -a})=\frac{d}{dz}\ln (sn(z{,}_{}k)){|}_{z=a}$, where a does not coincides with any pole or zero of the sn(z, k) function, can be also found. This is also evident that the sums over powers of poles and zeroes of the derivatives of the Jacobi elliptic functions can be studied in a similar way. For example, $\frac{d}{dz}sn(z{,}_{}k)=1-(1+k^2)\frac{z^2}{2!}+(1+14k^2+k^4)\frac{z^4}{4!}+O(z^6)$, hence $\ln (\frac{d}{dz}sn(z{,}_{}k))=-(1+k^2)\frac{z^2}{2!}+(1+14k^2+k^4)\frac{z^4}{24}-\frac{{(1+k^2)}^2}{8}{z}^4+O(z^6)=$$-(1+k^2)\frac{z^2}{2!}+\frac{-1+4k^2-k^4}{12}{z}^4+O(z^6)$ and, in particular, ${\displaystyle \sum _{{\rho }_l}^{}(\frac{2}{{\rho }_{l,pole}^4}-\frac{1}{{\rho }_{l,zero}^4})=\frac{-1+4k^2-k^4}{3}}$, where ${\rho }_{l,zero}$ are zeroes of the derivative $\frac{d}{dz}sn(z{,}_{}k)$ having orfer k_l and ${\rho }_{l,pole}=2mK+(2n+1)iK\prime$ are second order poles of this derivative. The order of summation is unimportant here, and the sums involving poles and zeroes can be separated.

Two circumstances finally can be noted. First, all these equalities can be differentiated with respect to k, but this does not look too interesting due to the complicated functions K(k) and K′(k). Second, they all contain the same sums over simple poles ${\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }\frac{1}{{(2mK+(2n+1)iK\prime )}^{2n}}}}$, and thus this sum can be removed by subtracting the related equalities.

4.2. Jacobi Elliptical Functions as Functions of the Index k

As a function of its index k, Jacobi elliptical functions are meromorphic on the whole complex plane [28,29] and have an infinite number of poles and zeroes (not necessarily simple). Their location again can be understood from the factorization $Const\cdot \frac{{\theta }_j(\eta ,q)}{{\theta }_4(\eta ,q)}$, see above. For example, zeroes of the sn(z, k) function coincide with the zeroes of ${\theta }_1(\frac{\pi z}{2K(k)}|\tau )$: that is, for $z\ne 0$ they are located at such points k, where $K(k)=\frac{z}{2(m+n\tau )}=\frac{z}{2(m+niK\prime (k)/K(k))}$ with m and n positive or negative integers. Thus, we have $2mK+2niK\prime =z$: this is an implicit formula not easily usable given the hypergeometric function in Equations (25) and (26).

Analysis presented in [28], see especially Theorem 4.1 there, shows that for large |k| the asymptotic of the logarithms of the theta-functions as functions of k certainly do not exceed O(|k|). (Sf., for example, valid for positive real k > 1 $sn(z{,}_{}{k}^2)=\frac{1}{k}sn(zk{,}_{}\frac{1}{k^2})$ and $sn(z{,}_{}0)=\sin z$). Thus our approach can be applied to ${\displaystyle \underset{C}{\overset{}{\int }}\frac{1}{{(k-a)}^n}\ln [sn(z,k)]dk}$ and similar integrals with $n\ge 3$. The Taylor expansions in some vicinity of zero are also known [9]:

$$sn(z{,}_{}k)=\sin z-\frac{1}{4}(z-\sin z\cos z)\cos z\cdot k^2+O(k^4),$$

(33)

thus for sin(z) not equal to zero: $sn(z,k)/\sin z=1-\frac{1}{4}(z-\sin z\cos z)\cot z\cdot k^2+O(k^4)$, and we have the following Proposition:

Proposition 6.

 Let for some fixed complex  $z\ne 0$ and such that $\sin z\ne 0$,  ${\rho }_{i,zero}$ denote zeros of the function sn(z, k) understood as a function of k, and having an order l_i; and let for the same case  ${\rho }_{i,pole}$ denote poles of the same function understood as a function of k, and having an order m_i. Then:

$${\lim }_{N\to \infty }{\displaystyle \sum _{|\rho |<N}^{}(-\frac{l_i}{{\rho }_{i,zero}{}^2}+\frac{m_i}{{\rho }_{i,pole}{}^2})}=-\frac{1}{2}(z-\sin z\cos z)\cot z.$$

(34)

This sum is equal to zero if $\cos z=0$. Simple numerical calculations show that for z = 1.854i (see Figure 1 in [28]) it is roughly equal to 5.3496 + 3.6760i, and for z = 5 (see Figure 1 in [29]) to 1.0756.

Further, $cn(z,k)=\cos z+\frac{1}{4}(z-\sin z\cos z)\sin z\cdot k^2+O(k^4)$ [9] thus we have the following proposition.

Proposition 7.

Let for some fixed complex  $z\ne 0$ and such that  $\cos z\ne 0$,  ${\rho }_{i,zero}$ denote zeros of the function cn(z, k) understood as a function of k, and having an order l_i; and let for the same case  ${\rho }_{i,pole}$ denote poles of the same function understood as a function of k, and having an order m_i. Then:

$${\lim }_{N\to +\infty }{\displaystyle \sum _{|\rho |<N}^{}(-\frac{l_i}{{\rho }_{i,zero}^2}}+\frac{m_i}{{\rho }_{i,pole}^2})=\frac{1}{2}(z-\sin z\cos z)\tan z.$$

(35)

This sum is equal to zero if $\tan z=0$.

We also know $dn(z,k)=1-\frac{1}{2}{\sin }^{2}z\cdot k^2+O(k^4)$ which gives the following formula.

Proposition 8.

Let for some fixed complex  $z\ne 0$  ${\rho }_{i,zero}$ denote zeros of the function dn(z, k) understood as a function of k, and having an order l_i; and let for the same case  ${\rho }_{i,pole}$ denote poles of the same function understood as a function of k, and having an order m_i. Then

$${\lim }_{N\to +\infty }{\displaystyle \sum _{|\rho |<N}^{}(-\frac{l_i}{{\rho }_{i,zero}^2}}+\frac{m_i}{{\rho }_{i,pole}^2})=-{\sin }^{2}z.$$

(36)

This sum is equal to zero if $\sin z=0$.

Of course, “non-central” sums over powers of zeroes of these functions also can be obtained. For example, for zeroes and poles of the sn(z, k) function and arbitrary complex number a not coinciding with any of them, we have ${\lim }_{n\to \infty }{\displaystyle \sum _{|\rho |<N}^{}(-\frac{l_i}{{({\rho }_{i,zero}-a)}^2}+\frac{m_i}{{({\rho }_{i,pole}-a)}^2})}=2\frac{d^2}{d{k}^2}\ln (sn(z{,}_{}k))dk{|}_{k=a}$. It is quite probable that here and in Equations (34)–(36), the sums over inverse squares of poles and zeroes can be separated with the proper ordering of summation similar to the functions ${\theta }_j(z|\tau ){,}_{}\zeta (z,\tau )$ and their derivatives. However, the question is delicate, and we do not consider it now.

Analogous formulae for the sums over poles and zeroes with larger powers could be established if further terms of the Taylor expansions of the type (20) are known. They can be found, for example, by substituting the expansions in powers kⁿ into the corresponding differential equations, such as $\frac{d^2}{d{z}^2}sn(z,k)=-(1+k^2)sn(z,k)+2k^{2}s{n}^3(z,k)$ [9], which, however, turns out to be quite cumbersome. The sums over powers of poles and zeroes of the derivatives of the Jacobi elliptic functions over parameter k can be studied in a similar way.

5. Conclusions

We showed how the generalized Littlewood theorem concerning contour integrals of the logarithm of analytical function can be applied to calculate different sums over poles and zeroes of elliptic functions; some more detailed conclusions are placed at the end of Section 2 and Section 3.

There is no doubt that numerous other applications of this approach will be found. Of course, at the present stage of research, this is difficult to anticipate and even simply to propose these future possible applications. However, the very broad use of elliptic functions in physics does provide a strong hope for this. Nowadays, these applications are not limited by classical mechanics, such as XIX-century physical pendulum problems or relativistic corrections to planetary motion, but include also the description of the quantum mechanical dynamics in a periodic potential, building the classical string solutions on the sphere and analyzing their stability, etc. [10,15]; see especially the Chapters 5, 6 of the book [15].

Finally, probably the following analogy will be useful or, at least, interesting. Another analytic function, which, similarly to elliptic functions, has numerous applications in physics, is Bessel function $J_{\nu }(z)$, see, e.g., [16] for a detailed discussion of this function. Zeroes $j_{\nu ,k}$ of this function (more precisely, of the function $z^{-\nu }{J}_{\nu }(z)$), as well as the sums of inverse powers of such zeroes, were studied already by Bessel (and even Euler, see [17]), and in 1874, Rayleigh introduced a special function ${\sigma }_n(\nu )={\displaystyle \sum _{k=1}^{\infty }\frac{1}{j_{\nu ,k}^{2n}}}$, $n\ge 1$ [30]. This function proved to be really important not only for the theory of Bessel functions itself (which is quite natural), but also, for example, to study heat conduction and diffusion in a periodic fluid flow. It also gives an effective method for eigenvalue estimation in certain quantum mechanical problems, and so forth; see [17] for references and discussions. In a certain sense, elliptical functions do for the elliptic geometry the same job as Bessel functions for the cylindrical one, so we dare to anticipate the certain importance of the “elliptical analogues” of the Rayleigh function.