Methods to Encrypt and Authenticate Digital Files in Distributed Networks and Zero-Trust Environments

Abstract

The methods proposed in this paper are leveraging Challenge–Response–Pair (CRP) mechanisms that are directly using each digital file as a source of randomness. Two use cases are considered: the protection and verification of authenticity of the information distributed in storage nodes and the protection of the files kept in terminal devices operating in contested zero-trust environments comprised of weak signals in the presence of obfuscating electromagnetic noise. With the use of nonces, the message digests of hashed digital files can be unique and unclonable; they can act as Physical Unclonable Functions (PUF)s in challenge–response mechanisms. During enrollment, randomly selected “challenges” result in unique output data known as the “responses” which enable the generation and distribution of cryptographic keys. During verification cycles, the CRP mechanisms are repeated for proof of authenticity and deciphering. One of the main contributions of the paper is the development of mechanisms accommodating the injection of obfuscating noises to mitigate several vectors of attacks, disturbing the side channel analysis of the terminal devices. The method can distribute error-free cryptographic keys in noisy networks with light computing elements without relying on heavy Error Correcting Codes (ECC), fuzzy extractors, or data helpers.

1. Introduction and Background Information

The objective of this work is to develop novel mechanisms that offer proof of authenticity in distributed networks and protect terminal devices operating in zero-trust areas. In our differentiated approach, we consider several complementary remedies: (i) one-time use keys for each transaction, (ii) generating keys from the message digest of each file, and (iii) in zero-trust networks; transmit the data feeding a CRP mechanism through noisy wireless channels to enable the decryption on-demand of digital files. All proposed remedies are designed to handle the erratic bits without ECC. In this section, we are summarizing some of the relevant work conducted by prior authors to secure digital files and use CRP mechanisms. Storing and distributing the cryptographic keys needed to protect sensitive information and terminal devices introduces a level of risk. Of concern are replays, man in the middle attacks, loss of information in the network, side channel analysis and physical loss to the opponent of a terminal device [1,2,3]. Storing non-encrypted files in the terminal introduces the same risk level as storing the secret keys that decrypt the cipher texts of these files. In distributed networks, the clients usually store the public–private key pairs in their terminal devices, which presents an element of risk. The opponents also inject noise to disturb the wireless communication between the ground operation and terminal device, introducing difficulty in the distribution of cryptographic keys without heavy ECC, fuzzy extractors, or data helpers, all of which are leaking information [4,5,6].

Blockchain technology with digital signatures offers protection in exposed networks, such as the non-alterability and traceability of chains of transactions [7]. Digital Signature Algorithms (DSAs) further enhance security by associating the blockchains to a set of known users and their public keys [8]. Blockchains with digital signatures are exposed to a variety of possible attacks that introduce risk in validating authenticity, specifically when operating outside a reliable network [9,10]. Concerns include possible difficulties in verifying the legitimacy of a file, the theft of private keys, and blockchains that may be forged by associating altered messages with an altered message digest. To prove the authenticity of a message in zero-trust networks, it is important to add layers of security without imposing excessive computing power consumption.

Background information in the area of file verification and distributed networks is presented in refs. [11,12,13,14,15,16,17,18,19,20,21]. In [11], a Challenge Response Authentication (CRA) of physical layers is described to avoid exposing passwords. The work presented in [12] shows the methods to provide verification of information in a ledger. The authors of [12] define a “cryptographic challenge nonce” and a protocol that enables third parties to verify information; the technology is based on digital signatures with public/private keys. In [13], document tracking schemes on a distributed ledger [13] are presented and details how to insert unique identifiers and hash values for this tracking; a processor coupled with the storage device is used in the protocols. In [14,15], the authors present a secure exchange of signed records. These records contain digital signatures of the senders and their public keys, which enhances security. Methods to authenticate data based on proof verification are shown in [16,17,18]. Some of the data may be external to the network, protected by a blockchain and DSA with public keys. Uhr et al. describe the methods to verify certificates based on blockchains. The system compares the content of a previously known certificate by a financial institution with the content of a certificate obtained at the point of use. Sheng et al. describe computationally efficient methods to audit transactions. The methods are based on blockchains, Bloom filters, and digital signatures. Information such as using a timestamp as an entry and wallet address are part of the scheme. In [19], a method to validate documents with blockchains and other information is presented. Only portions of the documents are shared; the full document is not revealed. Publication [20] describes contract agreement verifications. Electronic signatures are inserted in the contracts and the blockchains with a method to share public/private key pairs. Publication [21] presents a management system protecting enterprise data with blockchains. The computing device selects what data to incorporate in the blockchain to offer adequate protections.

The CRPs developed for PUFs provide relevant background information for our work even if they do not use a digital file [22,23,24,25,26,27,28,29,30]. Authentication based on a challenge, a response, a PUF, and machine learning are described in [22]. The development of secure digital signatures using PUF devices with reduced error rates is presented in [23,24]. Cryptographic protocols with PUF-based CRPs are shown in [25,26]. Biometry with a CRP mechanism is suggested in [27,28]. CRP mechanisms and CRA schemes are also applied to protect centralized or distributed networks [29,30,31]. An example of a scheme is the formation of a look-up table with indexes in the left column and passwords in the right column. The challenges point at an index to be paired with an associated password, which avoids the problem of having to change the passwords periodically.

Some of the contributions of this work include a novel approach based on CRP schemes to protect and authenticate each digital file individually, with the objective to mitigate several vectors of attack. The idea to inject obfuscating noise during ground-to-terminal communication is developed to limit the ability of opponents to share the same wireless network for side channel analysis. To facilitate a quick adoption of the novel methods, all encryption algorithms are standardized cryptographic algorithms recommended by the National Institute of Standards and Technologies (NIST), as well as the codes under consideration for standardization by NIST for post-quantum cryptography (PQC). The paper is organized as follows:

• [Section 2] The first layer of technology needed for our proposed schemes is described, namely the design of the CRP mechanisms directly based on digital files. The algorithms extracting the responses from randomly selected challenges are presented as well as methods to generate cryptographic keys from the CRPs.
• [Section 3] The protocols to verify the authenticity of digital files with CRP mechanisms in distributed networks are presented. The algorithms for enrolment and for verification are detailed. An example of a use case that is using these protocols with an agent, storage node, and smart contract is given. A security analysis, in which we list potential issues and remedies, is also provided.
• [Section 4] The protocols to securely distribute digital files to terminal devices exposed to zero-trust networks are suggested. A use case that distributes cryptographic keys while injecting erratic bits is presented.
• [Section 5] The potential problems created by residual erratic bits in the recovery keys are examined in detail. A model is developed and verified, and light error management schemes are suggested.

Finally, Section 6 presents the summary and future work. A table listing the acronyms used herein is presented in Attachment A, followed by the list of references.

2. CRP Mechanism Based on Digital Files

Methods to design digital file-based CRP mechanisms will now be presented. The method detailed in Section 2.1 describes a generic response generation scheme for applications in distributed networks. The implementation detailed in Section 2.2 is an example of protocol offering higher levels of security in distributed networks.

2.1. Response Generation with File-Based CRP Mechanism

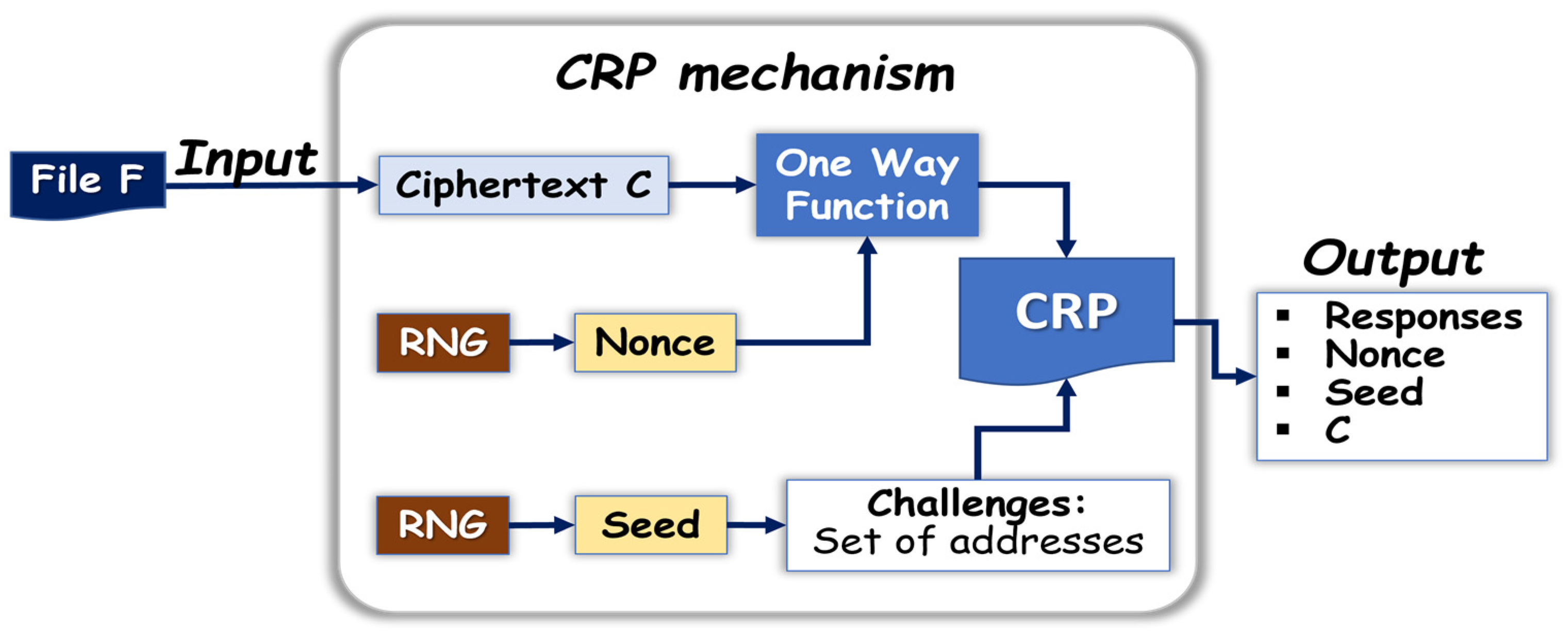
The input data of the CRP mechanism is derived from file F. Its ciphertext C is concatenated with nonce $\omega$ to generate a file C* of constant length $d{=2}^D$, where D is the number of digits (for example, if a desired $d=1$ million, then $D=20$). The resulting d bits are located at addresses varying from 1 to d. Changing a single bit in file F results in a totally different stream C*. This can be performed with a variety of methods; one possible implementation is the following:

• Encrypt F with private key Sk, and a PQC scheme (PQC and DSA) under standardization by NIST [32] such as the Cryptographic Suite for Algebraic Lattices (CRYSTALS)-Kyber [33,34], CRYSTALS-Kyber [35,36], NTRU [37,38,39], Classic McElice [40], SPHINCS [41], and Falcon [42].
• The ciphertext is hashed with Standard Hash Algorithm (SHA)-512.
• The resulting steam is XORed with 512-bit long nonce $\omega$.
• The function SHA algorithm and Keccack (SHAKE) is used to extend the 512-bit long stream to d-bits. The combination of SHA-3 and SHAKE is NIST-compliant [43,44,45].

The CRP mechanism is based on the d-bit long stream C* to generate N responses from N challenges:

• Challenges: A “challenge” is defined as the digital information needed to point at a particular position in the d-bit long stream C*. A stream of bits S* is generated by hashing and extending with eXtended output Function (XoF), creating a randomly selected seed S. The stream S* is segmented into N challenges $\left\{q_1,\dots ,q_i,\dots ,q_N\right\}$ that are D-bit long. The D bits of each challenges q_i are converted into number $x_i$, with $x_i\in \{1,d$}, which is an address in C*, resulting in N addresses $\{x_1,\dots ,x_i,\dots ,x_N\}$
• Responses: The N addresses generate the P-bit long responses $\{r_1,\dots ,r_i,\dots ,r_N\}$. From each address $x_i$, P-bit long responses are generated from C*. The iterative method to find the P positions $\{x_{i,1},\dots ,x_{i,j},\dots ,x_{i,P}\}$, and read the P-bits is the following:

The first position is: $x_{(i,j=1)}=x_i$. The other positions $x_{(i,j)}$ are given by the linear congruent random number generator, $i\in \{1,N$}, $j\in \{1,P$}, see Equation (1):

$$x_{(i,j)}=\left(\alpha x_{\left(i,j-1\right)}+\beta \right)mod\left(2^D\right); \mathrm{with} \alpha \mathrm{and} \beta \mathrm{prime} \mathrm{numbers}$$

(1)

Algorithm 1 and the block diagram shown in Figure 1 summarize the above protocol. The output after response generation is {C, $\omega$, S} and $\{r_1,\dots ,r_i,\dots ,r_N\}$. Such a CRP mechanism is highly secure as three totally independent streams are requested to uncover the responses which are C, $\omega$, and S. Protecting just one of the three provides acceptable security. The computing power, or “gas price”, required to run the CRP mechanism is low.

Algorithm 1: Generate a set of responses with C
1:	Variable input data: file {C}
2:	Nonce {$\mathsf{\omega }$}, and stream {S} $\leftarrow$ random number generator
3:	→ Module 1: Generate a set of responses with C, and {$\mathit{\omega }$,S}:
	3.1:	Static input data: positive integers d, D, N, P, $\alpha ,$ $\beta ,$ d = 2D and $\alpha$, $\beta$ are prime
	3.2:	MD $\leftarrow$Hash (C) (ex: SHA-256)
	3.3:	C* $\leftarrow$ XOV(concatenate (MD, $\mathsf{\omega }$)) (ex: SHAKE)
		[Comment: Organize C* with bits located at addresses 1 to d]
	3.4:	S*$\leftarrow$ XOV (S); with S* is a ($\mathrm{N}\times D$)-bit long stream
	3.5:	$\left\{q_1,\dots ,q_i,\dots ,q_N\right\}$ $\leftarrow$ S*; Split S* into N, D-bit long, challenges $q_i$; i$\in${1, N})
	3.6:	$\{x_1,\dots ,x_i,\dots ,x_N\}$ $\leftarrow$ $\left\{q_1,\dots ,q_i,\dots ,q_N\right\}$; for N positions $x$i in C*; $x_i\in \{1,\mathrm{d}=2^D\}$
	3.7:	$\left\{r_1,\dots ,r_i,\dots ,r_N\right\}$ $\leftarrow$ $\left\{x_1,\dots ,x_i,\dots ,x_N\right\}$; for all N, P-bit long, responses $r_i$ For each position $x_i$ generate P-bit long response $r_i$ in the following way:
		$\{x_{i,1},\dots ,x_{i,j},\dots ,x_{i,P}\}$ $\leftarrow$ $x_i$; $\mathrm{j}\in$ {1, P} [comment: find P positions ${\mathit{x}}_{\mathit{i},\mathit{j}}$ in C* with congruent linear generator]
		○ if $\mathrm{j}=1,$ then $x_{(i,j=1)}=x_i$
		○ Else, iterate: $x_{(i,j)}=\left(\alpha x_{\left(i,j-1\right)}+\beta \right)mod\left(2^D\right)$
		$r_i\leftarrow \{x_{i,1},\dots ,x_{i,j},\dots ,x_{i,P}\}$; [Comment: read the P positions ${\mathit{x}}_{\mathit{i},\mathit{j}}$ in C* to generate P-bit long response ${\mathit{r}}_{\mathit{i}}$]
4:	Output: C, {S, $\omega$,} and the N responses $\{r_1,\dots ,r_N\}$

The probability to point several times to the same position in C* is non-negligeable. This exposes the protocol to a frequency analysis and creates collisions, as several responses r_i are then identical. One solution tracks the positions with an index to generate different responses when several challenges are pointing at the same position. For example, when a position is selected a second time, the $\beta$ of Algorithm 1 step 3.7 can be replaced by $\beta +1$ which is a sufficient offset to generate a distinct response; iterating, the $\beta$ is replaced by $\beta +2$ during the third collision, et cetera.

2.2. Generation of an Orderly Subset of Responses

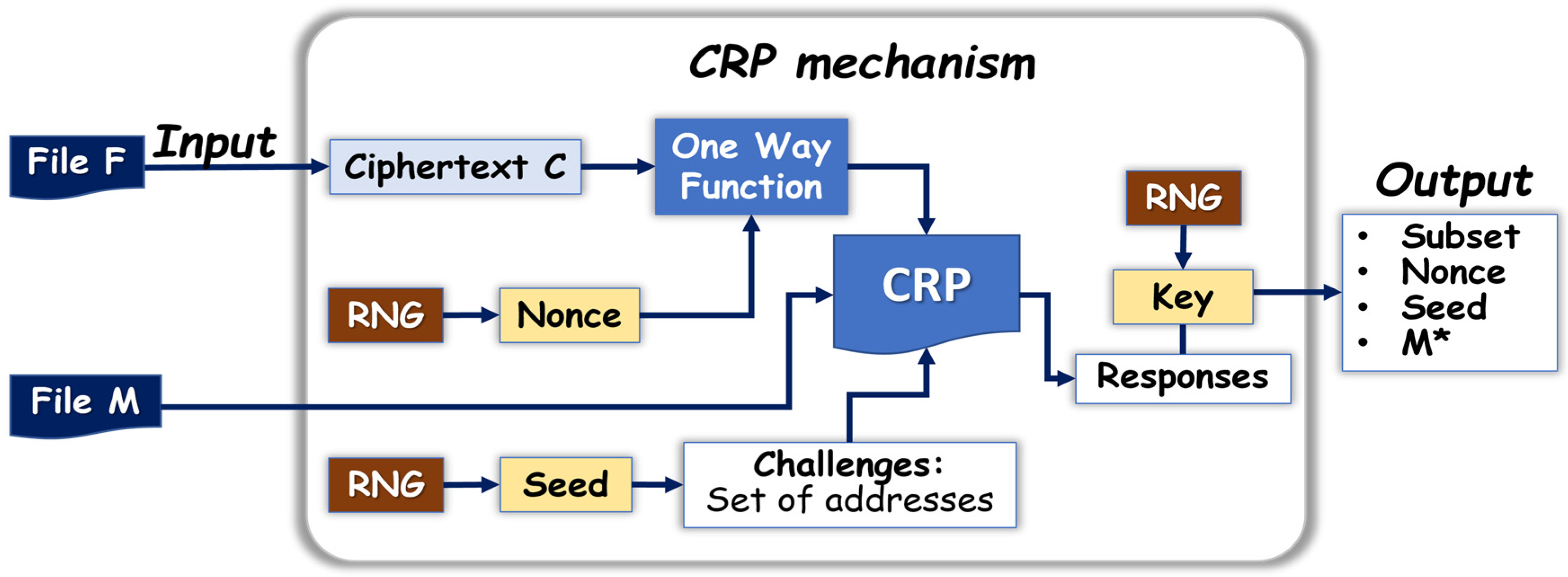
In the scheme described in Section 2.1, the responses generated from the CRP mechanism are directly converted into cryptographic keys K to encrypt a message M. To enhance security, we developed a scheme in which the ephemeral key K is picked randomly, independent from the CRP mechanism. Algorithm 2 for encryption and Algorithm 3 for decryption are summarized in Figure 2, and shown as follows:

Algorithm 2: Generate a subset of responses with C, and encrypt M
1:	Variable input data: {C}, {M}
2:	Nonce {$\mathsf{\omega }$}, and stream {S} $\leftarrow$ random number generator
3:	→ Use Module 1: Generate a set of responses with C, and {$\mathit{\omega }$,S}:
	Output data: All N, P-bit long, responses $\{r_1,\dots ,r_N\}$.
4:	→ Module 2: Encrypt M and generate a subset of responses with$\{r_1,\dots ,r_N\}$:
	4.1:	key K with f states of “1”: $\{k_1,\dots ,k_N\}$ $\leftarrow$ random number generator
	4.2:	M* $\leftarrow$ encrypt(M, K)
	4.3:	Filter subset of f responses $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_f\}$ located at positions of K with state of “1”
	4.4:	Erase M, K, and the $N-f$ responses located at positions of K with state of “0”
5:	Output: C, {S, $\omega$, M*} and the f responses $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_f\}$

Algorithm 3: Decrypt M with C and the subset of f responses
1:	Variable input data: C, {S, $\mathsf{\omega }$, M*} and the f, P-bit long, responses $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_f\}$
2:	→ Use Module 1: Generate a set of responses with C, and {$\mathsf{\omega }$,S}:
	Output data: the N, P-bit long, responses $\{r_1,\dots ,r_i,\dots ,r_N\}$, i $\in${1, N}
3:	→ Module 3: Decrypt M from M* with the f responses$\{{r^{\prime }}_1,\dots ,{r^{\prime }}_j,\dots ,{r^{\prime }}_f\}$, j $\in${1, P}:
	3.1:	Retrieve key K by comparing the N responses $r_i$ with the subset of f responses ${r^{\prime }}_j$:
		If $r_i$ matches at least one response $r_i^{\prime }$, then $k_i=1$
		Else, $k_i=0$
	3.2:	M $\leftarrow$ Decrypt(M*, K)
4:	Output: M

The key K, which is randomly picked here, has two purposes: encrypting M and generating an orderly subset of responses. Only the f positions of K with a state of “1” are pointing at positions in the sequence of N responses that are kept, while the responses at the $N-f$ positions of K with a state of “0” are skipped. The resulting orderly subset of f responses is kept for key recovery. Four totally independent streams are requested to uncover the responses, which are C, $\mathsf{\omega }$, S, and the subset of responses. 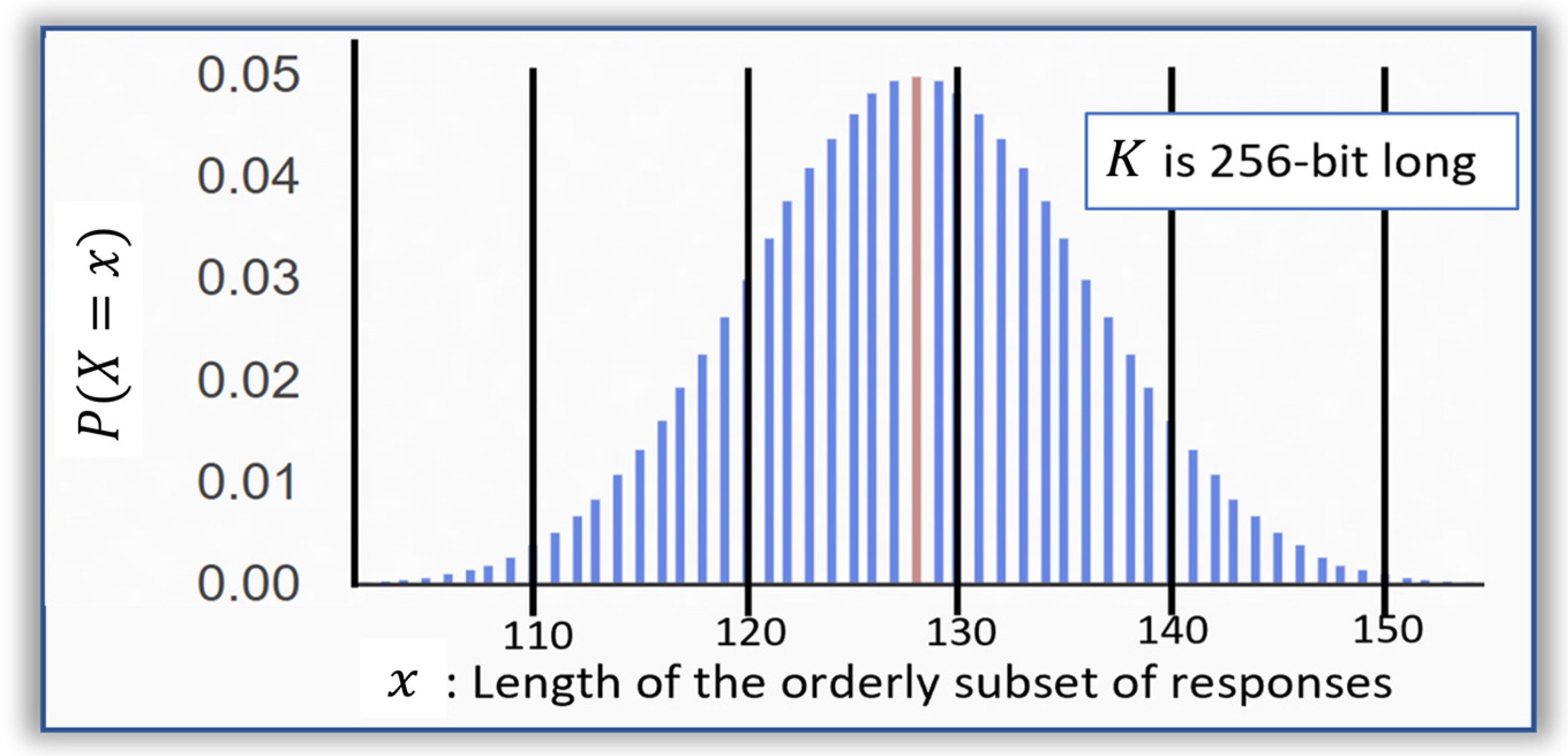The size of the responses needed to run this CRP mechanism is higher than the size as presented in Section 2.1. For example, approximately 128 responses, that are 100-bit long, are generated when K is 256-bit long. Therefore, 1.6 Kbytes are retrieved, rather than 256 bits in the simpler protocol. We notice that the orderly subset of responses does not have a fixed length. Assuming that the random number generator of the 256-bit long K has an equal probability to get a state “0” or “1”, the probability $P(X=x)$ of obtaining an x-bit long subset is shown in Figure 3. The median value of the distribution is 128 and varies approximately from 100 to 160. To obfuscate this information, we add nonces at the end of the subset to keep the length to 160 responses. The key recovery scheme as presented in Section 4 is based on a search from left to right that terminates when the sequence of 256 bits is identified; additional responses are ignored.

The injection of errors in the subset of responses is detailed in Section 4 and Section 5. Provided the BERs remain below an acceptable threshold (i.e., below 25%) the subset of orderly responses can be recognized as part of the iterative search; therefore, ephemeral key K can be recovered. In zero-trust networks, such an obfuscation can disturb opponents sharing the noisy network. Certain attacks are mitigated since the noisy responses are different than the ones generated from F and the CRP mechanism.

3. Protocols Verifying the Authenticity of Digital Files in Distributed Networks

The objective of the protocols presented in this section is to allow third parties operating openly in the distributed network to validate the authenticity of a file without the over-burdening of computational resources. The suggested protocols are based on the CRP mechanism discussed in Section 2 with the same symbols. The message of authenticity M was replaced by public key Pk computed internally to add a DSA.

3.1. Description of the Protocols with CRP Mechanisms

The overall mechanism to generate the responses is described in Section 2.1. For example, if $d=1024$, $D=10$, $N=32$, and $P=8$, the responses are 256-bit long. The entropy is about 200, as the number of possible CRPs is given by Equation (2):

$$\left(\genfrac{}{}{0pt}{}{d=1024}{N=32}\right)=4.6\times {10}^{60}\approx 2^{200}$$

(2)

3.1.1. Enrollment Cycle

The protocol has two steps: the initial set up or enrollment performed secretly by the client or designate, and the verification of the authenticity cycle performed openly in the distributed network. Algorithm 4 for enrolling file F is shown as follows:

Algorithm 4: Enrollment cycle for file F
1:	Input data: Some file F
2:	Nonce {$\mathsf{\omega }$}, stream {S}, and seed {L} $\leftarrow$ random number generator
3:	Generate ephemeral public-private key pair {Sk, Pk} from L (ex: PQC algorithm)
4:	C $\leftarrow$ Encrypt(F, Sk)
5:	M $\leftarrow$ Pk
6:	→ Use Module 1: Generate a set of N responses with C, and {$\mathsf{\omega }$,S}:
	Static input data: Positive integers d, N, P, $\alpha$, $\beta$
	Output data: All N, P-bit long, responses $\{r_1,\dots ,r_N\}$
7:	K $\leftarrow$ concatenate$\{r_1,\dots ,r_N\}$; where K is a 256-bit long key
8:	M* $\leftarrow$ Encrypt(Pk, K)
9:	Erase: {C*, Sk, Pk, K}, and $\{r_1,\dots ,r_N\}$
10:	Output: C, and steams {S, $\mathsf{\omega }$, M*}

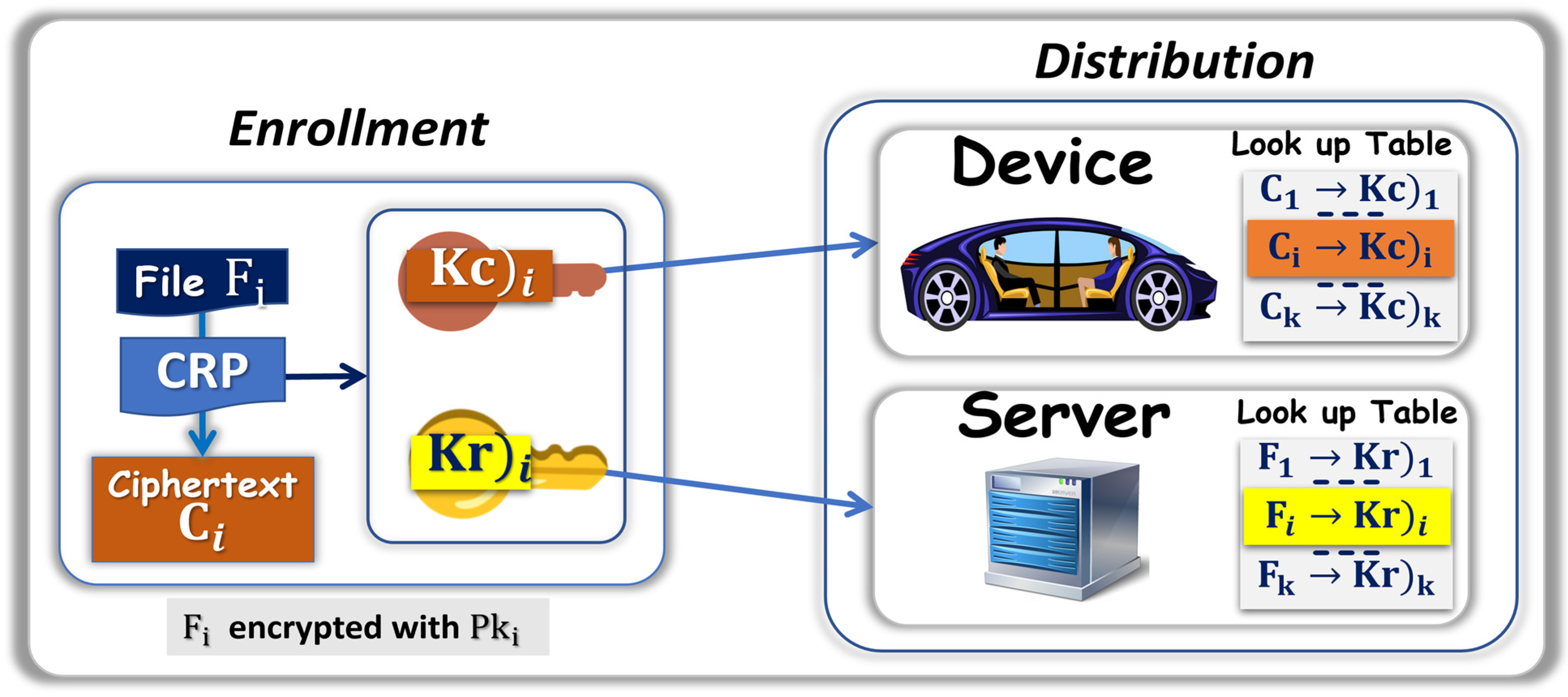
During the enrollment of File F, a randomly selected seed L generates a key pair (Sk; Pk) with an asymmetrical algorithm such as Dilithium. The file F is encrypted with Sk to generate the ciphertext C. The randomly selected nonce $\omega$ is concatenated with C to form a d-bit long file C* that is at the center of the CRP mechanism. A randomly picked seed S is converted into a set of N, D-bit long, challenges generating a set of N, P-bit long responses. The responses are concatenated to generate the ephemeral key K, which encrypts the public key Pk and forms ciphertext M*. After completion of the enrollment cycle, the responses, C*, and keys K, Sk, and Pk are erased. The output is C and stream {S, $\omega$, M*}.

3.1.2. Verification Cycle

The verification cycle follows the same steps as the enrollment cycle. The release of ω initiates the process, while {C, S, M*} are also needed. The replay of the CRP mechanism retrieves the responses from ω and {C, S}. The responses allow the recovery of K, the deciphering of Pk from M* with K, and the deciphering of C with Pk to retrieve F. Algorithm 5 is summarizing this protocol as shown below. A variation of this protocol utilizes a message of authenticity M, instead of Pk, to generate ciphertext M* with K; where, in this case, C is decrypted separately. F can remain secret; while the proof of authenticity of C can be public, informing peers that C is valid.

Algorithm 5: Decrypt file F
1:	Variable input data: {$\mathsf{\omega }$}, and {C, S, M*}
2:	→ Use Module 1: Generate a set of N responses with C, and {$\mathit{\omega }$,S}:
	Static input data: Positive integers d, N, P, $\alpha$, $\beta$
	Output data: the N, P-bit long, responses $\{r_1,\dots ,r_N\}$
3:	K $\leftarrow$ concatenate$\{r_1,\dots ,r_N\}$
4:	Pk $\leftarrow$ Decrypt(M*, K)
5:	F $\leftarrow$ Decrypt(C, Pk)
6:	Output: F, Pk

3.2. Example of Use Case in Distributed Networks

The schemes presented above in Section 3.1 benefit clients operating in a distributed network [46,47,48,49,50]. In this example, suppose a client desires to allow independent parties to verify the authenticity of a transaction contained in file F. The client keeps secret F and discloses ciphertext C. The roles of the participating parties are defined as the following:

• Client: owns file F but pays the storage agent to store C for some duration [51].
• Agent: represents the client [52].
• Storage agent: paid by the client or the agent to store information [53].
• The data is public.
• Smart contract: The client’s rent is kept in escrow in the contract until the rental expires. The smart contract is equipped to compute the proof of authenticity [54,55].

The client issues periodic challenges to check that the storage agent is faithful. If a challenge fails, the smart contract refunds the rent to the client. Since the smart contract’s state is always public, the contract cannot keep any secret data.

3.2.1. Initial Enrollment and Distribution of the Files

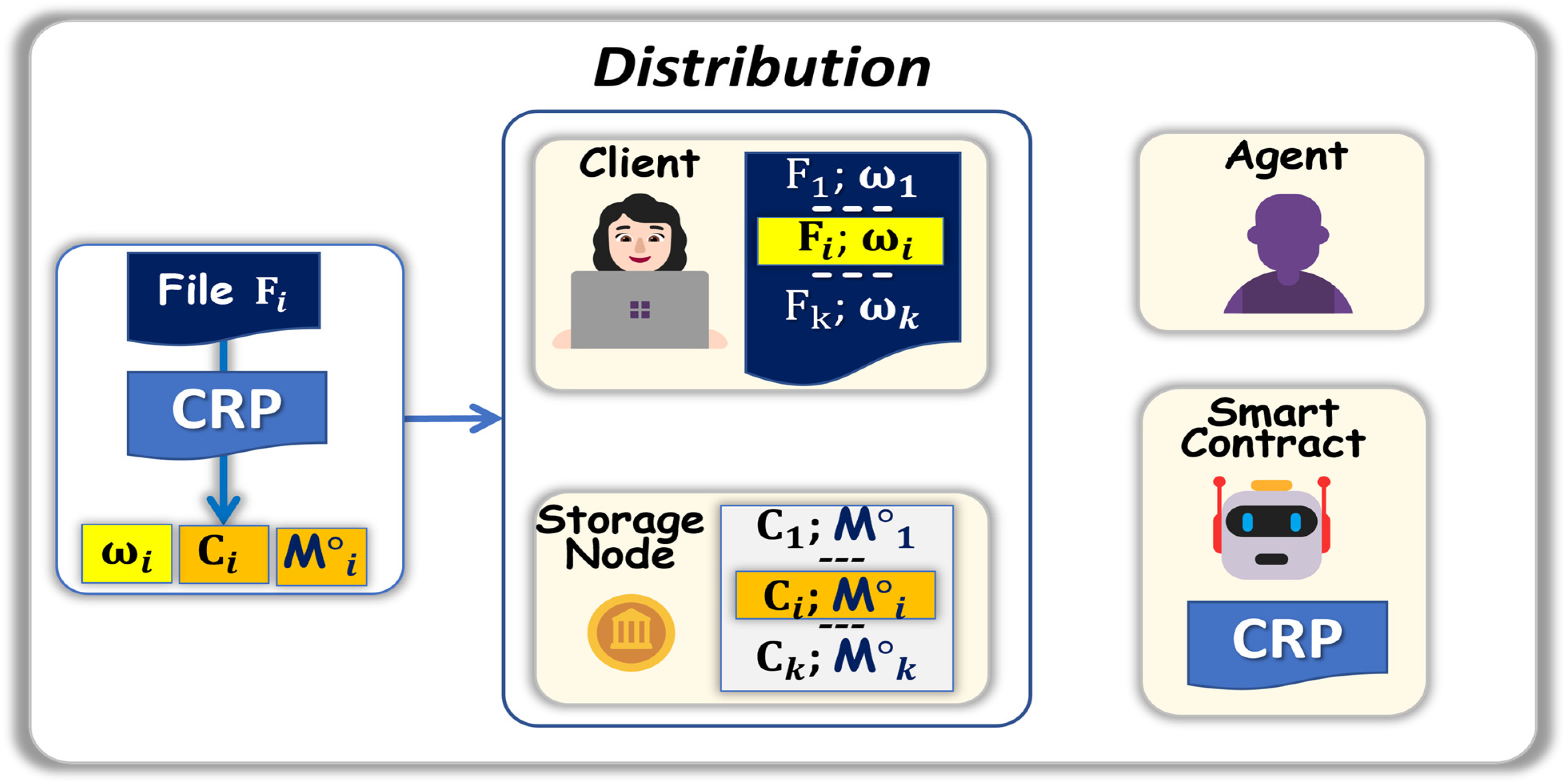
The client uses a CRP mechanism during an initial set up phase, as described in Section 3.1, then distributes the information to the network. In most implementations, a compact seed replaces the challenges, as described in Section 2. The client is either equipped with the software needed to operate a CRP mechanism or employs a contract agent to perform the confidential task. From F_i and nonce ω_i, the CRP mechanism generates the ciphertext C_i and the file M°_i: {S_i, M*_i}. The stream M*_i is the ciphertext encrypted with ephemeral key K of the message of authentication M_i, which can be the public key M_i = Pk_i needed for the DSA of F_i. An active participant such as an agent can take care of the distribution of C_i and M°_i. In Figure 4, the distribution is the following:

• The smart contract has the technical capability to perform CRP mechanisms.
• The storage node keeps C_i and M°_i.
• The client keeps F_i and ω_i.

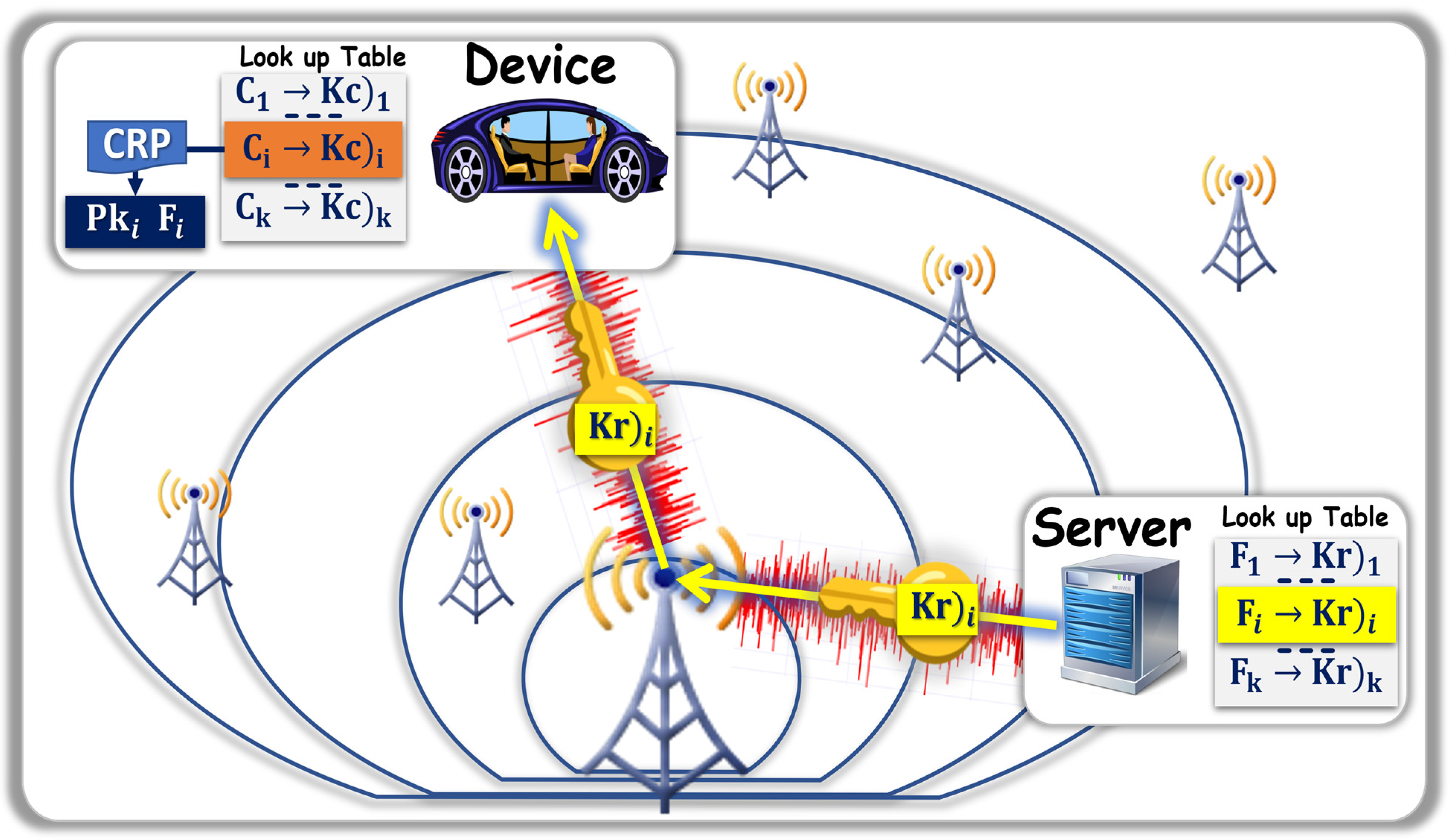
3.2.2. Verification in Distributed Networks

When the verification of the authenticity of F_i is required, the client communicates ω_i to the agent. The agent then coordinates the effort between the smart contract and the storage node, executed in the protocol shown in Figure 5, which is summarized as follows:

• The smart contract, which is equipped with the CRP mechanism collects ω_i, C_i, and M°_i = {S_i, M*_i}
• The CRP mechanism has the information needed to decrypt F_i and run the DSA verification with Pk_i.

A variation of the protocol replaces Pk_i by a message of authenticity M_i such as:

“Yes, I (client X), am confirming the authenticity of ciphertext C_i”.

This variation can be useful if the client desires to protect file F_i. The decryption of C_i can be performed separately, while outside the open network. A separate arrangement is then needed to share Pk_i; for example, through a public key infrastructure (PKI).

3.3. Security Analysis in Distributed Networks

The methods for verifying authenticity, as presented here, are based on the handling of several independent elements: File F, Ciphertext C, nonce $\omega$ and the stream M°. The client may restrict any of these streams while distributing the other three elements. The possibility matrix is shown in

Table 1. Methods to organize a collaborative network.

CASE	File F	Ciphertext C	Nonce $\mathit{\omega }$	Cipher Text M°: {S; M*}	What Is M?
1	Client	Storage	Client	Storage	M = Pk
2	Client	Storage	Client	Storage	M = message
3	Client	Client	Storage	Storage	M = Pk
4	Storage	Storage	Client	Storage	M = message
5	Storage	Storage	Storage	Client	M = message

.

The respective value of each case can be summarized as follows:

• Case 1 was discussed in Section 3.2.2 The client keeps F and ω secret after enrollment and then discloses both during verification. Such a method is valuable since the entire chain of information is obfuscated before validation. After validation, both C₁ and F₁ are public information, and the use of the DSA can further enhance the transparency of the protocol.
• Case 2 is a variation of Case 1 where M is a message of authenticity rather than a public key. The client can only disclose ω during verification, offering some homomorphic capabilities to the scheme as the open protocols verify the authenticity of ciphertext C without openly disclosing F.
• Case 3: After enrollment, the client keeps both F and C such that the level of obfuscation is also high. During validation, the client discloses both so the smart agent can verify authenticity. This method is interesting since the client cannot lie by changing F and C after the fact.
• Case 4: After enrollment, the client only keeps ω and releases both unencrypted and encrypted files. The release of the nonce enables a full verification of authenticity to include DSA. The nonce is then used as a one-time public key.
• Case 5: This is a variation of Case 4 in which only M° is kept by the client, thus utilizing M° as a one-time public key.

Discussion: The first two cases offer both high levels of security and transparency since file F is kept secret after enrollment, while ciphertext C is public information. The client could be accused of modifying the file, if it is altered; therefore, the protocol offers non-alterability and non-repudiation. In addition to the proof of authenticity of the message, by releasing the nonce, the client also provides a form of authentication. In both cases, the storage node is keeping files that can be decrypted on-demand, acting as a repository of critical information. Examples of information are medical files, financial transactions, movies, games, and/or real estate transactions.

The second case offers some homomorphic properties since the encrypted file can be authenticated without knowing the content of the file. The decryption of the files can be performed separately and secretly in a transaction between the client and a third party. The client may, for example, secretly communicate the cryptographic key needed to retrieve the file. An example of a use case could be in the handling of medical files. The doctor keeps the nonce, and the key needed to decrypt the file, while the cipher text and encrypted message of authenticity are kept by a storage node. To allow a second doctor to access the file, the doctor openly transmits the nonce, which will confirm the authenticity of the ciphertext, then secretly transmits the key deciphering the file. That way, the doctors are not required to store the files on their server to retrieve the information as needed.

The suggested protocols are relatively well protected against attack vectors such as replays, man-in-the-middle, and side channel analysis. New nonces, key pairs Sk–Pk, and seeds are generated for each file and used only once. After a proof of authenticity cycle, the entire chain of information is openly distributed: the file, the ciphertext, nonce, seeds, public key, and message of authenticity. Even the knowledge of Sk, the private key, becomes irrelevant. This is a departure from many other DSA schemes used in cryptology in which the leak of the secret key is catastrophic.

A remaining vulnerability of the protocol presented in the first two cases is the leak of nonce $\omega$. Adversaries are then enabled to decrypt the files, which defeats the purpose of the protocol. A potential remedy is to use Multi-Factor Authentication (MFA). The nonce can be XORed with a password before storage by the client. During the verification cycle, the client shall XOR it again with the password to retrieve the nonce. Another option is to use the additional layer of security presented below in Section 4.

4. Protocols Protecting Terminal Devices in Zero-Trust Networks

As discussed in Section 3 for distributed networks, the application of interest in this section is also based on CRP mechanisms; however, the constraints are different. The protocols cannot rely on third party validations and the information is restricted to a small group of participants. One of the objectives is to enable a controlling party to drive the deciphering of the files stored in a terminal device through a zero-trust network. The transfer of information from the controlling party to the device is obfuscated with heavy electromagnetic noise, either due to the fact that the signals are weak (unintentional) or to protect the device against a variety of attacks, and channel analysis (intentional).

4.1. Description of the Protocols with CRP Mechanisms

Starting with the CRP mechanism as described in Section 2.2 randomly pick ephemeral keys, and generate an orderly subset of the sequence of responses K_R in which obfuscating noise can be injected. The enrollment cycle should be completed in a secure environment (before entering the zero-trust network). During the validation cycles that are occurring in zero-trust networks, the terminal device can decrypt its files without ECC in order to reduce leaks of information while conserving computing power.

4.1.1. Enrollment Cycle

The input data in Algorithm 6 shown below are: d, N, P, and prime numbers $\mathsf{\alpha }$, $\mathsf{\beta }$. The ephemeral key K is picked randomly. K is used to select the orderly sequence of f responses K_R: $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_f\}$ from the full set of responses $\{r_1,\dots ,r_N\}$ by skipping the $N-f$ positions with a state of 0. K_R is kept secret by the controlling party. Let Kc be the stream of the nonce {$\omega$}, the seed S, and the ciphertext M*. Both C and Kc are distributed to the terminal device. All other information and cryptographic keys are erased, namely {C*, Sk, Pk, K} and the N-f responses with a state of 0.

Algorithm 6: Enrollment cycle for file F, generate subkeys Kc & Kr
1:	Input data: Some file F
2:	Nonce {$\mathsf{\omega }$}, stream {S}, seed {L} $\leftarrow$ random number generator
3:	Generate ephemeral public-private key pair {Pk, Sk} from L (ex: PQC algorithm)
4:	C $\leftarrow$ Encrypt(F, Sk)
5:	M $\leftarrow$ Pk
6:	→ Use Module 1: Generate a set of N responses with C, and {$\mathsf{\omega }$,S}:
	Static input data: Positive integers d, N, P, $\alpha$, $\beta$
	Output data: the N, P-bit long, responses $\{r_1,\dots ,r_N\}$
7:	→ Use Module 2: Generate a subset of responses from $M=Pk$ and $\{r_1,\dots ,r_N\}$:
	Key K with f states of “1” $\leftarrow$ random number generator Filter the f responses $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_f\}$
	M* $\leftarrow$ Encrypt(M, K) Erase: {Sk, Pk, K}
8:	Let subkey Kr be the f, P-bit long, responses $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_f\}$
9:	Let subkey Kc be the streams {S, $\mathsf{\omega }$, M*}

4.1.2. Verification Cycle

The terminal device can verify the authenticity of C by recovering Pk with Kr and Kc, in which Kr: $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_j,\dots ,{r^{\prime }}_f\}$ and Kc: {S, $\omega$, M*}.

• The first part of Algorithm 7 shown below is a replay of the enrollment cycle to generate the responses $\{r_1,\dots ,r_i,\dots ,r_N\}$ that each have a length equal to P-bit.
• The key K is recovered by comparing the full sequence of responses with the subset, as shown in module 4.

The injection of bad bits in the subset of the response, a process that can also be called “noise injection”, has no effect on the outcome of the protocol provided the noise level is below the threshold T that can disturb the recovery of K.

Algorithm 7: Decrypt file F with subkey Kc and noisy subkey Kr
0:	Up to T bad bits are injected in Kr
1:	Variable input data: C, Kc and the noisy Kr
2:	→ Use Module 1: Generate a set of N responses with C, and {$\mathit{\omega }$,S}:
	Static input data: Positive integers d, N, P, $\alpha$, $\beta$
	Output data: the N, P-bit long, responses $\{r_1,\dots ,r_i,\dots ,r_N\}$
3:	→ Module 4: Decrypt M from M* and the f noisy responses $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_j,\dots ,{r^{\prime }}_f\}$, j $\in${1, P}:
	3.1:	Enter both sets $\{{r^{\prime }}_1,\dots ,{r^{\prime }}_j,\dots ,{r^{\prime }}_f\}$, $\{r_1,\dots ,r_i,\dots ,r_N\}$ , and T
	3.2:	$j=1$, $i=1$
	3.3:	While $i<N+1$:
			Measure hamming distance H(${\mathrm{r}}^{\prime }$j, $\mathrm{r}$i): If $H(r_j^{\prime },r_i)\le T$: $k_i=1$; increment $i,j$ by 1 Else: $k_i=0$; increment $i$ by 1
	3.4:	(M = Pk) $\leftarrow$ Decrypt(M*, K)
4:	F $\leftarrow$ Decrypt(C, Pk)
6:	Output: F, Pk

The example shown in

Table 2. Generation of an orderly sequence of responses from K.

Responses	r1	r2	r3	r4	r5	r6	r7	r8
Key K	0	1	1	0	1	0	0	1
Subset Kr	-	${r^{\prime }}_1{=r}_2$	${r^{\prime }}_2{=r}_3$	-	${r^{\prime }}_3{=r}_5$	-	-	${r^{\prime }}_4{=r}_8$

and

Table 3. Key recovery from the orderly sequence of responses.

Subset Kr	r′1		r′2		r′3		r′4
Responses	r1	$r_2{=r^{\prime }}_1$	$r_3={r^{\prime }}_2$	r4	$r_5={r^{\prime }}_3$	r6	r7	$r_8={r^{\prime }}_4$
Key K	0	1	1	0	1	0	0	1

illustrates how the scheme operates. With the sequence $\{r_1,\dots ,r_8\}$ and key K {0,1,1,0,1,0,0,1}, Kr is $\{{r^{\prime }}_1{=r}_2,{r^{\prime }}_2{=r}_3,{r^{\prime }}_3{=r}_5,{r^{\prime }}_4{=r}_8\}$. The key K is recovered by comparing the Kr and the full sequence.

4.2. Example of Use Case in Zero-Trust Networks

The protocol presented in Section 4.1 is applied to protect autonomous vehicles operating in a zero-trust network with poor signal quality [56,57,58,59,60]. For example, the vehicle contains a set of encrypted files with the instructions and software revisions required to react to certain circumstances. The set of keys required to decrypt these files should not be stored in the vehicle for security reasons; therefore, a server transmits them through the open network as requested. The latencies of the suggested protocols must be small for near real-time operations. The use of standardized cryptographic algorithms is preferred.

4.2.1. Initial Set Up—Enrollment

The enrollment cycle performed in a secure environment is summarized in Figure 6. The CRP processing, as described in Section 4.1, enables the encryption of each file with a secret key Sk, the generation of the two sub-keys Kc and Kr required to find the public key Pk. Let M* be the encrypted Pk with ephemeral key K. Let S be the seed randomly picked to generate the challenges. Let Kc be the stream { S, $\omega$, M*}. Let Kr be the subset of responses computed from the full set and K.

After completion of the enrollment cycles, the server restricts all files Fs and associated subkeys Kr, while the autonomous vehicle restricts the ciphertexts C and subkeys Kc.

4.2.2. Verification of Authenticity—Deciphering the Files

If the vehicle encounters a problem, the engineers working remotely dictate that the vehicle should use file F_i; thus, they transmit Kr)_i through the network (see Figure 7).

Assuming that the rates of collisions between 100-bit long responses are negligeable, the vehicle can quickly determine which file to retrieve by testing a few responses. The protocol presented in Section 4.1 is able to manage poor signals and heavy-injected electromagnetic noises in the subkey Kr)_i to retrieve F_i utilizing the following process:

• Kc)_i: {S_i, $\omega$_i, M*_i} enables the generation of the full set of responses from the ciphertext C_i, and the CRP mechanism.
• Kr)_i discloses the subset of responses.
• Ephemeral key K_i is retrieved by comparing both sets of responses.
• Public key Pk_i is decrypted from M*_i with key K_i.
• File F_i is decrypted from C_i with public key Pk_i.

If required, the noise can be directly injected into Kr by the server with a random number generator. The autonomous vehicle can also be equipped with the system to emit obfuscating noise during communication with the server, which has the potential to mitigate some side channel attacks. Having noisy responses can increase the one-wayness of the CRP mechanism by obfuscating the cryptoanalysis after a verification cycle. Without such a feature, the crypto-analyst is empowered to keep track of the CRPs for future analysis.

4.3. Security Analysis in Zero-Trust Networks

The protocols using a subset of responses, as presented above, require additional protections to mitigate certain vulnerabilities. A discussion of the selected suggested mitigations is discussed next. Other strategies are part of our proposed future work.

4.3.1. Loss of Both Kr and the Information Stored in the Terminal Device

A poor environment for this protocol is when Kr is intercepted as well as the content of the terminal device; hence, the opponent would then be enabled to retrieve the files. The structure of subkey Kc)_i: {S_i, $\omega$_i, M*_i} can enable MFA:

• MFA on the seed. The terminal device XORed the S_i with a password before storing it, then XORed it again during the recovery cycle. This can obfuscate the challenges generation process.
• MFA on the nonce: Rather than applying the MFA on the seed, the XORing can be performed on the nonce. This obfuscates the file used in the CRP mechanism.
• If the terminal device is driven by an operator, then biometry can be added.
• Additional protection of the public key Pk. Rather than having M* being the ciphertext of the public key Pk; the message M decrypted from M* during recovery does not directly disclose Pk. The recovery of Pk from M could also use MFA, or a separate code transmitted by the controlling server through a separate channel.

4.3.2. Verifying the Index of the Confidential File

Opening the wrong file may not be acceptable. To mitigate errors, an index can be added to the ephemeral key. The protocol is as follows:

• During enrollment, the index of 12 bits (when 4000 files are stored) is added in the front of each ephemeral key. The number of responses is extended to 12 + N. The number of responses of the subsets also increased, accordingly, by 12.
• The terminal device stores the 12 additional responses in a look-up table.
• During recovery, the first 12 responses of the subset are used to confirm the index from the first 12 responses pointing to the right ciphertext–Kc pair to decrypt.

During the recovery cycle, such a method can quickly verify the matching index. The key and the index are then linked to each other.

4.3.3. Replays, Man-in-the-Middle, and Side Channel Analysis

Both replays and the man-in-the-middle attack disturb normal operations and should be mitigated. The opponents intercept several subkeys Kr thus preventing the terminal device from receiving them. Subsequently, the opponent sends these subkeys, but not necessarily in the right order, which could have a catastrophic impact. The mitigation of such attacks add a feedback loop to inform the controlling server that the signal was well received by the terminal device at the right time. Adding a code at the end of each file that the terminal device has to send back to the controlling server is an effective implementation. Protection against the side channel analysis should be implemented. The protocol has several advantages from that standpoint: the noise injected in the network during the transmission of Kr can disturb the side channel analysis and the subkeys are only used once.

5. Statistical Analysis of the Protocols Based on Subsets of Responses and ECC

Practical issues are expected in the implementation of the methods described above in Section 4 since the noise injection could also generate erroneous bits in the cryptographic keys. One solution is to tolerate an approximate matching between the responses of the orderly subset generated during enrollment and the responses generated during verification. However, if the threshold of acceptance is too high, the probability of having two randomly chosen responses matching can also be too high. The term commonly used to describe such unwelcome matches is “collision” [61,62]. In order to optimize the protocols, we developed a predictive modeling of these collisions. We also developed error management schemes able to process small residual erratic bits.

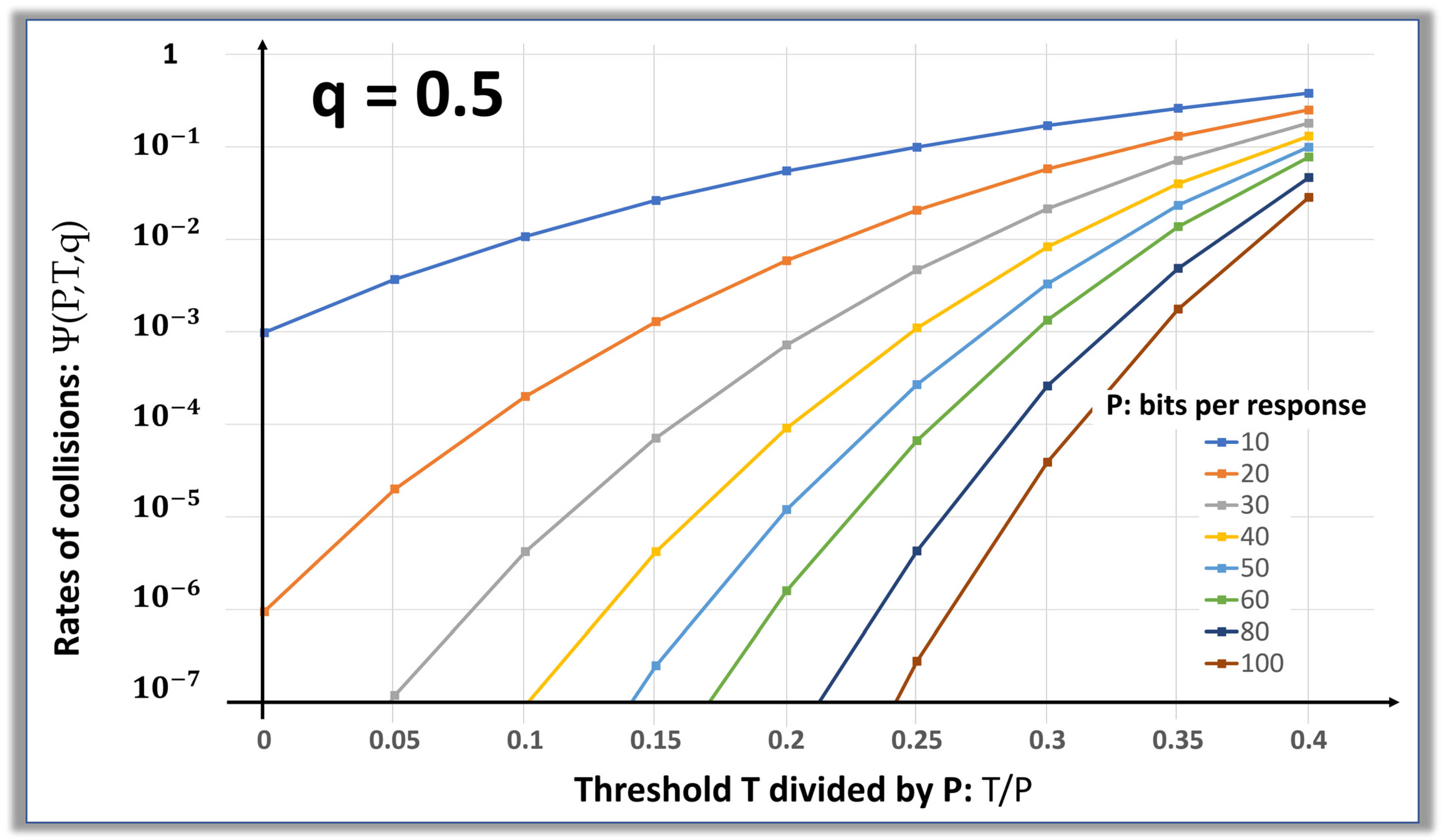
5.1. Statistical Predictive Model for Collisions

The recovery of the file, as outlined in Algorithm 6, assumes that the noise injected in the P-bit long responses creates a BER lower than 25%, an arbitrary number that can be optimized. The number of erratic bits t is bounded below the threshold T, which in this case is given by $T=0.25\times P$. If the threshold is too high, then collisions between the N responses become a source of errors during the retrieval of key K. A collision occurs when two randomly picked P-long responses r_a and r_b share at least T bits with each other. We are assuming that all responses follow a binomial distribution; one in which q, the probability to obtain a state “0”, equals the probability to obtain a state “1” ($q=0.5$). We must ensure that the probabilities of having a collision Ψ(P,T,q) between the responses of the orderly subset and a randomly picked response are acceptably low. Thus, we developed a model to optimize the protocol that focuses on three variables of Algorithm 6: the rate of bad bits injected in the subset of responses, the number of bits P of the responses, and the number of bits of threshold T. This mode is created as follows:

• Assume that we have two P-bit long streams of responses Ra and Rb:

Ra: $\{r_{a,1},\dots ,r_{a,P}\}$ ; Rb: $\{r_{b,1},\dots ,r_{b,P}\}$

• Each stream follows a binomial distribution.

The parameter q is the probability q to have a 1.

• The two streams are XORed, bit by bit:

  $$\{r_{a,1}\oplus r_{b,1}, \dots ,r_{a,P}\oplus r_{b,P}\}\leftarrow \{r_{a,1},\dots ,r_{a,P}\}\oplus \{r_{b,1},\dots ,r_{b,P}\}$$

  (3)
• The resulting stream also follows a binomial distribution with q = 0.5.
• The hamming distance H(Ra,Rb) between Ra and Rb is given by:

  $$\mathrm{H}(\mathrm{Ra},\mathrm{Rb})=(r_{a,1}\oplus r_{b,1})+\dots +(r_{a,P}\oplus r_{b,)})$$

  (4)
• There is a collision when the hamming distance between r_a and r_b is: H(ra,rb) ≤ T.
• The rate of collisions is:

  $$\mathsf{\Psi }(\mathrm{P},\mathrm{T},\mathrm{q})={\sum }_{\mathrm{t}=0}^{\mathrm{T}}[\left(\genfrac{}{}{0pt}{}{\mathrm{P}}{\mathrm{t}}\right){\mathrm{q}}^{\mathrm{t}}{(1-\mathrm{q})}^{\mathrm{P}-\mathrm{t}}]$$

  (5)

The plot shown in Figure 8 was generated using T/P in the x-axis, and Ψ(P,T,q) in the y-axis. T/P varies between 0 and 40%, and Ψ(P,T,q) varies from 10⁻⁷ and 1. In our experiment, we measured the best fit for $q=0.5$ since the distributions are almost perfectly binomial.

If we assume that there are no responses out of the f responses having the BER between enrollment and key recovery greater than the threshold T, the expected BER (E(K) in key K after recovery is expected to be given by:

$$\mathrm{E}(\mathrm{K}) \approx \frac{f}{256}\times \gamma \mathsf{\Psi }(\mathrm{P},\mathrm{T},\mathrm{q}) \approx 3 \mathsf{\Psi }(\mathrm{P},\mathrm{T},\mathrm{q})$$

(6)

where $\mathsf{\gamma }$ is the number of times each response is randomly tested in the recovery cycle. As shown in Section 5.3.3, we used $\mathsf{\gamma }=6$.

• If we assume that the BER of the noise injected in the responses are lower than $T=0.25$, then an example of predictive use of the model for a 256-bit long key is as follows:

○

$P=40$ → E(K) $\approx 1.2\times {10}^{-3}$

○

$P=60$ → E(K) $\approx 6.7\times {10}^{-5}$

○

$P=80$ → E(K) $\approx 4.3\times {10}^{-6}$

○

$P=100$ → E(K) $\approx 2.8\times {10}^{-7}$

The BERs are exponentially reduced by increasing the length P of the responses. The light error correcting schemes, as presented below, quickly increase if the BERs are creating more than one bad bit in a 256-bit long key, which corresponds to a BER of $4\times {10}^{-4}$. This model predicts that $P=80$ is acceptable and that $P=100$ is a better operating point.

5.2. Model for Heavy Noise Injections

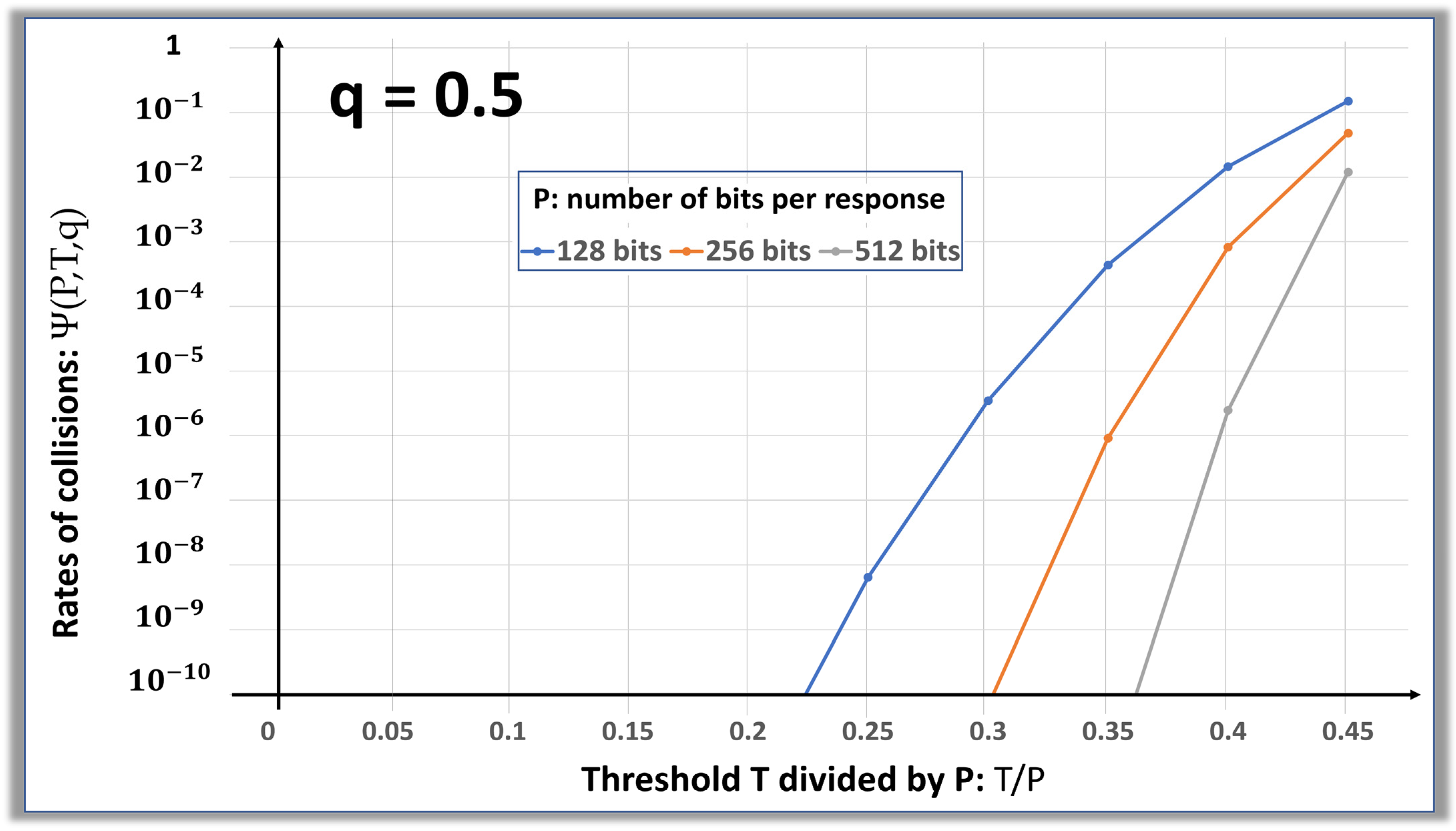
The information presented in Figure 8 shows that responses in the range of 10 to 100 bits are too small to handle a noise injection of more than 30% erratic bits. A similar analysis is shown in Figure 9 with responses in the 128- to 512-bit range, and $q=0.5$. An example of the predictive use yields the following results:

○

$P=128$ and $T=30\mathrm{\%}$ → E(K) $\approx 3.5\times {10}^{-6}$;

○

$P=256$ and $T=35\mathrm{\%}$ → E(K) $\approx 9.1\times {10}^{-7}$;

○

$P=512$ and $T=40\mathrm{\%}$ → E(K) $\approx 2.5\times {10}^{-6}$.

Such bit values of the error rates in K, which are in the part per million range (ppm), are widely acceptable for most applications. However, such an improvement introduces a negative impact on the latencies of the protocol, which are approximately proportional to the length of the responses. The bit error rates in the 35% range are large; thus, the penalty on latencies remains reasonable.

5.3. Error Management in the Cryptographic Keys

Mainstream ECC is difficult to implement in this approach since the data helpers needed to correct the key K are also affected by the noise injection. Thus, data helpers for the data helpers are called for, not an easy problem to resolve at high error rates. Therefore, we are proposing, in this section, several light error management schemes that can tolerate the residual errors created in K in the range of 1 to 3 bad bits per each 256-bit long key. With $T=0.35$ and $P=80$, 35% BERs in the responses generate $E\left(K\right){\approx 3.0\times 10}^{-4}$ BERs in the keys, which represents less than one bad bit per 256-bit long key.

5.3.1. Error Management with Response-Based Cryptography

The Response-Based Cryptographic (RBC) is a search mechanism allowing the recovery of a key when the ciphertext of the key is known [63,64]. In the protocol of Algorithms 6 and 7 with the subset of responses, the key K decrypts M* (the ciphertext of the key Pk) followed by the decryption of C and the ciphertext of the file F. This can be written as:

$$F=Decrypt\left(C,Pk\right)=Decrypt(C,Decrypt(M^{*},K\left)\right)$$

(7)

[$Decrypt\left(C,Pk\right)$: decrypt “C” with key “Pk”]

Algorithm 8 verifies authenticity and decrypts Pk and F, see as follows:

Algorithm 8: Managing erratic key K with RBC
1:	Retrieve K with CRP mechanism and from file C
2:	$x\leftarrow 0$
3:	Find all keys Kn, $n\in \{1,\left(\genfrac{}{}{0pt}{}{N}{x}\right)\}$, with hamming distance of $x$ from K
4:	Decrypt all files $Fn=Decrypt(C,Decrypt$($M^{*}$,Kn))
	If at least one of files Fn is readable; $Pk=Decrypt$($M^{*}$,Kn); $F=Fn=Decrypt\left(C,Pk\right)$ Else: ○ If $\mathrm{x}<3$: Increment $x$ by 1 and go back to step 3 ○ If $x=3$: Try again (go back to 1)

Using our computing system, we experimentally measured the throughput of the RBC at ${2.0\times 10}^8$ cycles per second for AES and at ${2.0\times 10}^6$ cycles/second for CRYSTALS-Dilithium. The code tested for Dilithium is freely available online, while AES is implemented in hardware within the computing element of our system [65]. The latencies to retrieve F through Algorithm 7 are listed in

Table 4. Latencies to verify authenticity with RBC.

Number of Errors	0	1	2	3
AES—Latencies (s)	${10}^{-8}$	${2.5\times 10}^{-6}$	${3.2\times 10}^{-4}$	${2.2\times 10}^{-3}$
Dilithium—Latencies (s)	${10}^{-5}$	${2.5\times 10}^{-3}$	0.3	27

. The latencies to retrieve F are acceptable with AES, while managing 3 bad bits with Dilithium is slow. We anticipate that the hardware implementations of Dilithium will be available in the near future.

5.3.2. Error Management of Collisions

We developed and analyzed a method to experimentally detect collisions. The approach is based on the observation that when a collision occurs between a response from the subset and a response from the full set positioned in one of the states of “0” of K, that there is also a match with a response positioned in one of the states of “1” of K; this response from the subset then contains multiple matches.

Conversely, without collision, each response from the subset has one (and only one) match in the full set of responses. After experimentally finding the ρ positions of the subset with multiple matches, we conclude that all other positions (the number of which is f-ρ) are error-free. This significantly limits how many possible keys have to be tested in a methodology similar to that described by the RBC. For example: if one response of the subset sees two matches, then the first of the two can be a state of “1”: while the second one is a state of “0” (and vice-versa). This leaves only two possible keys, which is quickly validated by computing F with Equation (7). If ρ responses from the subset create one collision each, then the number of possible keys per response is 2. This results in total $2^{\mathsf{\rho }}$ possible keys required to be checked; a lower value than the number of cases checked by the brute force RBC for the same number of errors. The latencies for 256-bit long keys K are listed in

Table 5. Latencies to find the correct key K with collision detection.

Number of Collisions ρ	0	5	10	20
AES—Latencies (s)	${1.0\times 10}^{-8}$	${3.2\times 10}^{-7}$	${1.0\times 10}^{-4}$	${1.0\times 10}^{-2}$
Dilithium—Latencies (s)	${1.0\times 10}^{-5}$	${3.2\times 10}^{-5}$	${1.0\times 10}^{-2}$	10

.

5.3.3. Failure to Detect Matching Responses

Consider the case where the errors injected in the responses of the subset are greater than threshold T. In this case, ρ responses see no matches. This type of failure creates only a limited number of possible keys K. The positions in the sequence of orderly response matching with the responses-located positions (ρ-1) and (ρ-2) are known, and only a small number of positions with state “0” are between the two. The number of possible keys is then also small, quickly validated with Equation (7). The method to handle the collisions and failures to detect matching responses is described below in Algorithm 9:

• For each of the responses of the subset, at least ${\mathsf{\gamma }}_0$ successive responses of the full set are tested for a potential match. Assume that key K has been tested to have no more than $\mathsf{\gamma }$₀ successive 0s. This property must be validated during the random pick of K. If K has more than $\mathsf{\gamma }$₀ successive 0s, then the key can be modified by inserting a few 1s to be sure that the condition is fulfilled. We picked ${\gamma }_0=6$ in our implementation.
• Detect the responses of the subset with either zero, one, or more than one matches with the responses of the full set of responses.
• List all possible keys.
• Verify the authenticity of F with all possible keys with Equation (7) of Section 5.3.1.

Algorithm 9: detecting and correcting errors during recovery of K
1:	Enter the subset of response $\{{\mathrm{r}}^{\prime }$1, …, ${\mathrm{r}}^{\prime }$j, …, ${\mathrm{r}}^{\prime }$f}, the set {$\mathrm{r}$1, …, $\mathrm{r}$i, …, $\mathrm{r}$N}, ${\mathsf{\gamma }}_0$ and T
2:	Start with $j=1$, $i=1$, and $\gamma ={\mathsf{\gamma }}_0$
3:	While $i<N+1$:
	Measure hamming distance H($\mathrm{r}$′j, $\mathrm{r}$i+k) for all responses $\mathrm{r}$i+k with $\mathrm{k}\in \{0,\mathsf{\gamma }-1$}
	If H($\mathrm{r}$′j, $\mathrm{r}$i+k) $\le$T for all $\mathsf{\gamma }$ comparisons: Increment $i,j$ by 1, $\gamma =2{\mathsf{\gamma }}_0-1$ [comment: to record that $\mathit{r}$′j has zero match] If H($\mathrm{r}$′j, $\mathrm{r}$i+k) >T for only one position: Increment $j$ by 1, $i=i+k+1,$ $\gamma =2{\mathsf{\gamma }}_0$ [comment: to record that position (i+k) is matching, and that $\mathbf{r}$′j has only one match] If H($\mathrm{r}$′j, $\mathrm{r}$i+k) >T for more than one position: ○ Find the position with the smallest number ${k=k}_{min}$, and with the largest ${k=k}_{max}$ ○ Increment $j$ by 1, $i=i+k_{min}+1$, $\mathsf{\gamma }={\mathsf{\gamma }}_0+(k_{max}-k_{min})$ [comment: to record the list of all positions (i+k) matching with $\mathbf{r}$′j]
4:	Find the correct key K
[comments: The positions $\mathit{r}$′j with only one matching response are considered correct. The positions $\mathit{r}$′j with zero match are caused by a failure to find the matching response. The positions $\mathit{r}$′j with two matching responses have at least 1 collision]
	4.1:    List all possible keys Kn from the analysis
	4.2:    Decrypt all files $Fn=Decrypt(C,Decrypt$($M^{*}$,Kn)$)$ Find readable file $F=Fn$; then Pk $=Decrypt$($M^{*}$,Kn)

Such a combined method will fail when both collision and the failure to detect occurs within the same response of the subset. When the BERs are in the 10⁻³ range, the probability of such an event is in the ${10}^{-6}$ range. In this configuration, the response in question matches with one, and only one, response of the full set of responses, as the key is unable to detect errors. One solution is to perform a brute force RBC search and in case of a failure to recover K occurs, request a new subset of response and retry.

6. Conclusions and Future Work

The suggested CRP mechanisms are directly using the digital files that must be protected and also their associated ciphertexts to generate ephemeral one-time use cryptographic keys. In these mechanisms, similarly with tracking blockchains, the digital files are hashed to be unique for non-repudiable and non-alterable operations. Two actual situations were discussed: (i) the encryption with proof of authenticity of the digital files distributed in storage nodes and (ii) the protection of the files kept in devices operating in zero-trust networks.

• In distributed networks, client devices provide the data needed for verification to agents driving smart contracts and storage nodes, the proposed protocols balance both security and transparency.
• In zero-trust networks, the sole priority is to enhance security and to protect the terminal devices. We developed a protocol allowing the injection of obfuscating noise in the keys transmitted by the controlling server to the exposed terminal device. BERS in the 25% range do not prevent the noisy key from decrypting the digital files stored in the device. To eliminate residual mismatches and generate error-free cryptographic keys, we developed and tested error management schemes to replace complex ECC, fuzzy extractors, and data helpers.

The continuation of this work will implement the algorithms for various applications to optimize security, reduce latencies, and add features specific to each application. We intend to perform an optimization with some of the following multi-factors:

• Length d of the digital file C* that is used for the CRP mechanism. Longer files are desirable to enhance randomness and minimize collisions. Excessive lengths negatively impact latencies.
• Number N of challenge–response pairs, and length P of each response. For the subset of response protocol, $N=256$ or more is needed, and P has to be sufficiently long to avoid collisions, but not so long as to increase latencies.
• The acceptable BERs shall be injected in the subset of responses and threshold T shall be set at an acceptable level for the determination of a match.

In addition to the experimental work, we are currently developing a comprehensive multi-variate predictive tool. Additional attack vectors are also being investigated with various methods to inject noise and disturb the protocol under consideration. Lastly, the quality of true random number generation (TRNG) is critical to the levels of security of the suggested protocols as well as the actual randomness of the resulting streams of responses. We are performing statistically valid experiments to enable the quantification of randomness with tools developed by NIST, DieHarder, TestU01, and others.