Chaos Controllability in Non-Identical Complex Fractional Order Chaotic Systems via Active Complex Synchronization Technique
Abstract
:1. Introduction
- The suggested HCPS methodology considers two dissimilar complex fractional order chaotic systems.
- It designs a robust HCPS strategy-based control input to achieve hybrid complex projective synchronization among considered fractional order complex systems and performs oscillation for synchronization errors with a fast rate of convergence.
- The description of HCPS scheme-based active control inputs is executed in a simplistic manner utilizing LSC and drive-response/master–salve configuration.
- Simulation outcomes depict the efficacy and superiority of the suggested HCPS strategy.
2. Preliminaries
3. Problem Formulation
4. Synchronization Phenomena
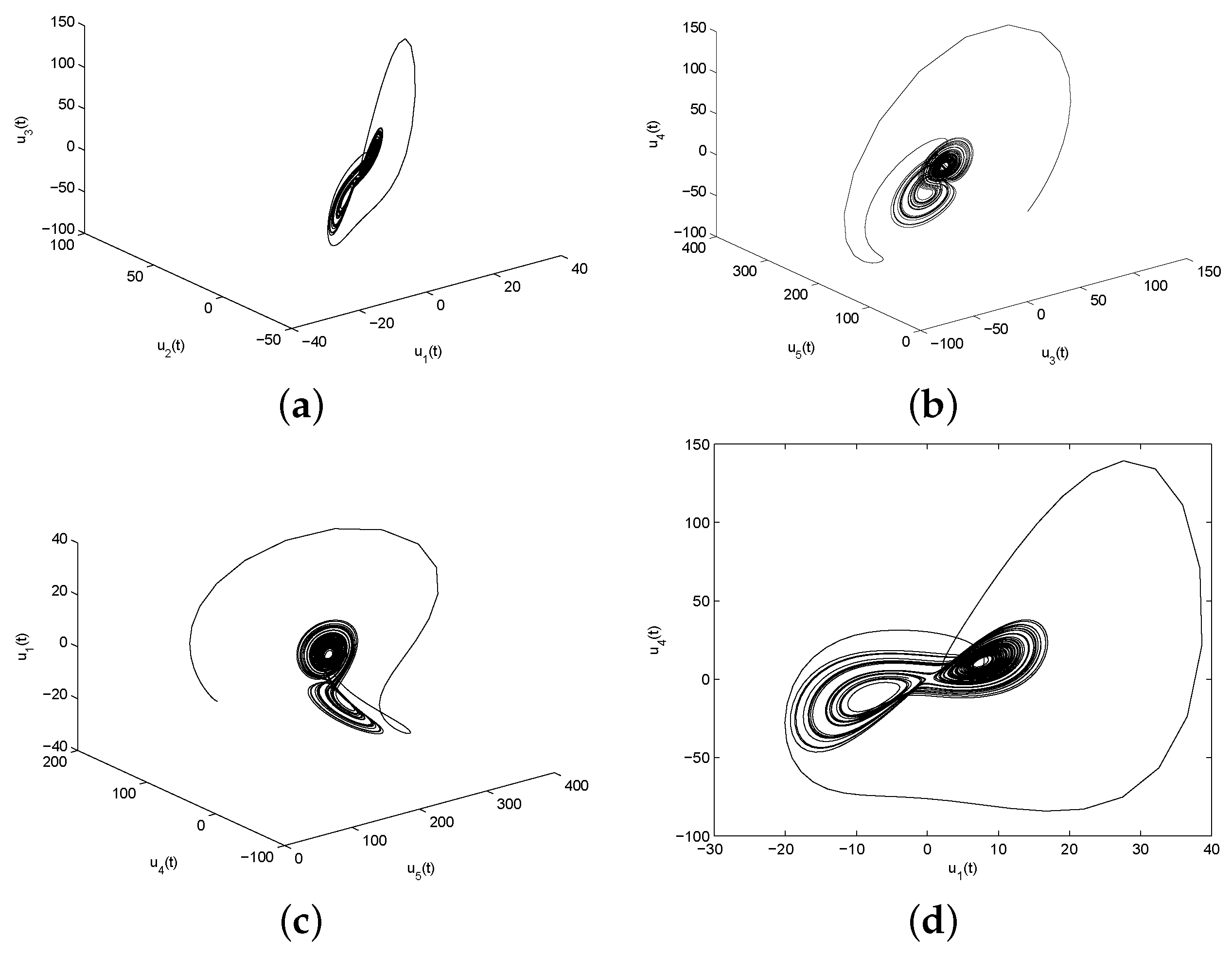
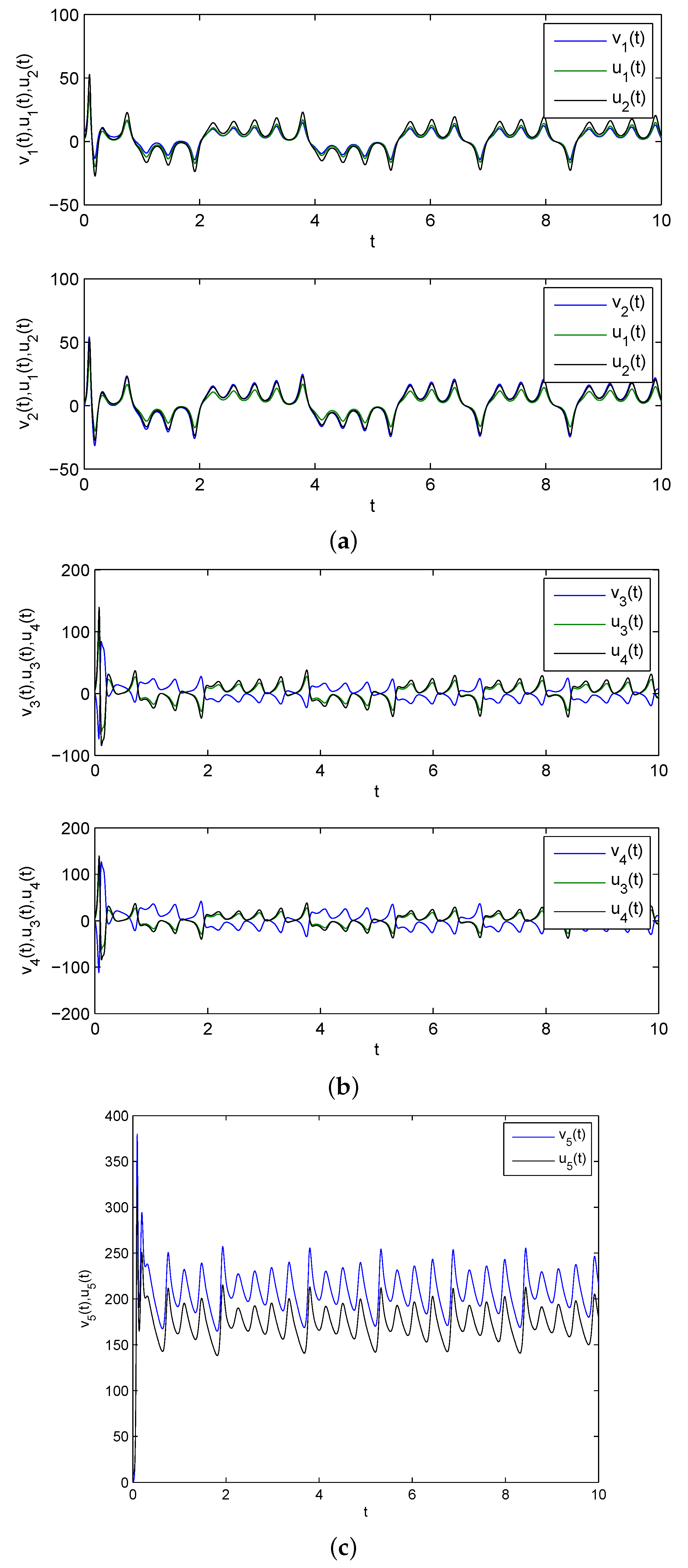
5. Numerical Simulation and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Application to Physics, Biology, Chemistry, and Engineering; Perseus Books Publishing: Reading, UK, 1994. [Google Scholar]
- Pecora, L.M.; Carroll, T.L.R. Synchronizing chaotic circuits. IEEE Trans. Circuits Syst. 1991, 38, 453–456. [Google Scholar]
- Lin, W.; He, Y. Complete synchronization of the noise-perturbed Chua’s circuits. Chaos Interdiscip. J. Nonlinear Sci. 2005, 15, 023705. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, M.; Ansari, S.P.; Agrawal, S.K.; Das, S.; Leung, A.Y.T. Anti-synchronization between identical and non-identical fractional-order chaotic systems using chaotic systems using active control method. Nonlinear Dyn. 2014, 11, 905–914. [Google Scholar] [CrossRef]
- Khan, A.; Jain, A.; Kaushik, S.; Kumar, M.; Chaudhary, H. Anti-synchronization scheme for the stability analysis of a newly designed Henon-Heiles model using adaptive control method. Appl. Appl. Math. Int. J. AAM 2021, 16, 42. [Google Scholar]
- Shshverdiev, E.M.; Sivaprakasm, S.; Shore, K.A. Lag synchronization in time-delayed systems. Phys. Lett. A 2002, 292, 320–324. [Google Scholar] [CrossRef]
- Kumar, V.; Heil, J.; Benner, P. Exponential Lag Synchronization of Cohen–Grossberg Neural Networks with Discrete and Distributed Delays on Time Scales. Neural Process. Lett. 2023, 1–23. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Phase and antiphase synchronization of two identical hyperchaotic complex nonlinear system. Nonlinear Dyn. 2010, 61, 141–152. [Google Scholar] [CrossRef]
- Khan, A. Combination Synchronization of time-delay chaotic system via robust adaptive sliding mode control. Pramana 2017, 88, 91. [Google Scholar] [CrossRef]
- Khan, A.; Bhat, M.A. Hyperchaotic analysis and adaptive multiswitching synchronization of a novel asymmetric non-linear dynamical system. Int. J. Dyn. Control 2017, 5, 1211–1221. [Google Scholar] [CrossRef]
- Sajid, M.; Chaudhary, H.; Allahem, A.; Kaushik, S. Chaos controllability in fractional-order systems via active dual combination–combination hybrid synchronization strategy. Fractal Fract. 2022, 6, 717. [Google Scholar] [CrossRef]
- Mainieri, R.; Rehacek, J. Projective synchronization in three dimensional chaotic systems. Phys. Rev. Lett. 1999, 82, 3042. [Google Scholar] [CrossRef]
- Chaudhary, H.; Khan, A.; Sajid, M. An investigation on microscopic chaos controlling of identical chemical reactor system via adaptive controlled hybrid projective synchronization. Eur. Phys. J. Spec. Top. 2022, 231, 453–463. [Google Scholar] [CrossRef]
- Chang, C.M.; Chen, H.K. Chaos and hybrid projective synchronization of commensurate and incommensurate fractional-order Chen-Lee systems. Nonlinear Dyn. 2010, 62, 851–858. [Google Scholar] [CrossRef]
- Khan, A. Hybrid function projective synchronization of chaotic systems via adaptive control. Int. J. Dyn. Control 2017, 5, 1114–1121. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, X.Y.; Hu, X.P.; Feng, M.K. Adaptive hybrid complex projective synchronization of chaotic complex system. Trans. Inst. Meas. Control 2013, 36, 1093–1097. [Google Scholar] [CrossRef]
- Delavari, H.; Mohadeszadeh, M. Hybrid complex projective synchronization of complex chaotic systems using active control technique with nonlinearity in the control input. J. Control Eng. Appl. Inform. 2018, 20, 67–74. [Google Scholar]
- Khan, T.; Chaudhary, H. Controlling and synchronizing combined effect of chaos generated in generalized Lotka-Volterra three species biological model using active control design. Appl. Appl. Math. Int. J. AAM 2020, 15, 25. [Google Scholar]
- Ali, M.K.; Fang, J.Q. Synchronization of chaos and hyperchaos using linear and nonlinear feedback functions. Phys. Rev. E 1997, 55, 5285. [Google Scholar] [CrossRef]
- Khan, A.; Khan, N.; Chaudhary, H.; Nigar, U. Analysis and control of complex variable hyper-chaotic Robinovich system with fractional derivatives. Int. J. Appl. Comput. Math. 2022, 8, 275. [Google Scholar] [CrossRef]
- Kumar, V.; Djemai, M.; Defoort, M.; Malik, M. Finite-time stability and stabilization results for switched impulsive dynamical systems on time scales. J. Frankl. Inst. 2021, 358, 674–698. [Google Scholar] [CrossRef]
- Zhang, R.X.; Yang, S.P. Adaptive Synchronization of fractional order chaotic systems via a single driving variable. Nonlinear Dyn. 2017, 66, 831–837. [Google Scholar] [CrossRef]
- Chaudhary, H.; Khan, A.; Nigar, U.; Kaushik, S.; Sajid, M. An effective synchronization approach to stability analysis for chaotic generalized Lotka-Volterra biological models using active and parameter identification methods. Entropy 2022, 24, 529. [Google Scholar] [CrossRef] [PubMed]
- Roldán-Caballero, A.; Pérez-Cruz, J.H.; Hernández-Márquez, E.; García-Sánchez, J.R.; Ponce-Silva, M.; Rubio, J.D.J.; Villarreal-Cervantes, M.G.; Martínez-Martínez, J.; García-Trinidad, E.; Mendoza-Chegue, A. Synchronization of a new chaotic system using adaptive control: Design and experimental implementation. Complexity 2023, 2023, 2881192. [Google Scholar] [CrossRef]
- Perruquetti, W.; Barbot, J.P. Sliding Mode Control in Engineering; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Tavazoei, M.S.; Haeri, M. Synchronization of chaotic fractional order systems via active sliding mode controller. Phys. A Stat. Mech. Its Appl. 2008, 387, 57–70. [Google Scholar] [CrossRef]
- Khan, A.; Tyagi, A. Fractional order disturbance observer based adaptive sliding mode synchronization of commensurate fractional order Generio-Tesi system. AEU-Int. J. Electron. Commun. 2017, 82, 346–357. [Google Scholar] [CrossRef]
- Khattar, D.; Agrawal, N.; Singh, G. Chaos synchronization of a new chaotic system having exponential term via adaptive and sliding mode control. Differ. Equ. Dyn. Syst. 2023, 1–19. [Google Scholar] [CrossRef]
- Wang, C.; Ge, S.S. Adaptive synchronization of uncertain chaotic systems via backstepping design. Chaos Solitons Fractals 2001, 12, 1199–1206. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods to Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Modanli, M.; Goktepe, E.; Akgul, A.; Alsallami Shami, A.M.; Khalil, E.M. Two approximation methods for fractional order Pseudo-Parabolic differential equations. Alex. Eng. J. 2022, 61, 10333–10339. [Google Scholar] [CrossRef]
- Kumar, V.; Malik, M.; Baleanu, D. Results on Hilfer fractional switched dynamical system with non-instantaneous impulses. Pramana 2022, 96, 172. [Google Scholar] [CrossRef]
- Koeller, R.C. Application of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1994, 51, 299–307. [Google Scholar] [CrossRef]
- Heaviside, O. Electromagnetic Theory; Chelsea: New York, NY, USA, 1971. [Google Scholar]
- Jothimani, K.; Ravich, R.C.; Kumar, V.; Djemai, M.; Nisar, K.S. Interpretation of trajectory control and optimization for the nonsense fractional calculus. Int. J. Appl. Comput. Math. 2022, 8, 273. [Google Scholar] [CrossRef]
- Balootaki, M.A.; Rahmani, H.; Moeinkhah, H.; Mohammadzadeh, A. On the synchronization and stabilization of fractional-order chaotic systems: Recent advances and future perspectives. Phys. A Stat. Mech. Its Appl. 2020, 551, 124203. [Google Scholar] [CrossRef]
- Sabatier, J.; Merveillaut, M.; Malti, R.; Oustaloup, A. How to impose physically coherent initial conditions to a fractional system. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1318–1326. [Google Scholar] [CrossRef]
- Grigorenko, I.; Grigorenko, E. Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 2003, 91, 034101. [Google Scholar] [CrossRef]
- Deng, W.H.; Li, C.P. Chaos synchronization of the fractional Lu system. Phys. A 2005, 353, 61–72. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, S.; Zhang, J. Chaos and synchronization of the fractional order Chua’s system. Chaos Solitons Fractals 2009, 39, 1595–1603. [Google Scholar] [CrossRef]
- Fowler, A.C.; Gibbon, J.D.; McGuinness, M.J. The complex Lorenz equations. Phys. D Nonlinear Phenom. 1982, 4, 139–163. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajid, M.; Chaudhary, H.; Kaushik, S. Chaos Controllability in Non-Identical Complex Fractional Order Chaotic Systems via Active Complex Synchronization Technique. Axioms 2023, 12, 530. https://doi.org/10.3390/axioms12060530
Sajid M, Chaudhary H, Kaushik S. Chaos Controllability in Non-Identical Complex Fractional Order Chaotic Systems via Active Complex Synchronization Technique. Axioms. 2023; 12(6):530. https://doi.org/10.3390/axioms12060530
Chicago/Turabian StyleSajid, Mohammad, Harindri Chaudhary, and Santosh Kaushik. 2023. "Chaos Controllability in Non-Identical Complex Fractional Order Chaotic Systems via Active Complex Synchronization Technique" Axioms 12, no. 6: 530. https://doi.org/10.3390/axioms12060530
APA StyleSajid, M., Chaudhary, H., & Kaushik, S. (2023). Chaos Controllability in Non-Identical Complex Fractional Order Chaotic Systems via Active Complex Synchronization Technique. Axioms, 12(6), 530. https://doi.org/10.3390/axioms12060530






