A New Probability Distribution: Model, Theory and Analyzing the Recovery Time Data
Abstract
1. Introduction
- Increasing, if
- Decreasing, if
- Constant, if
2. An NME-Weibull Model
3. Properties
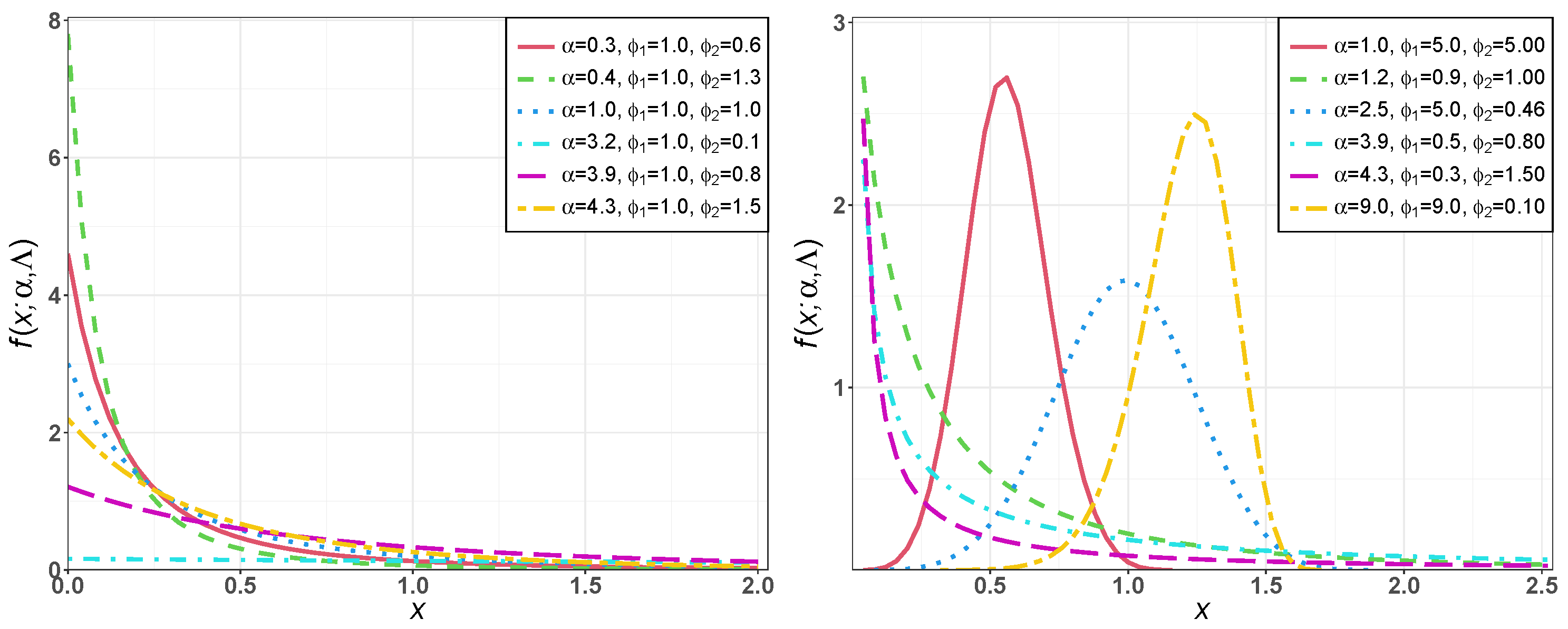
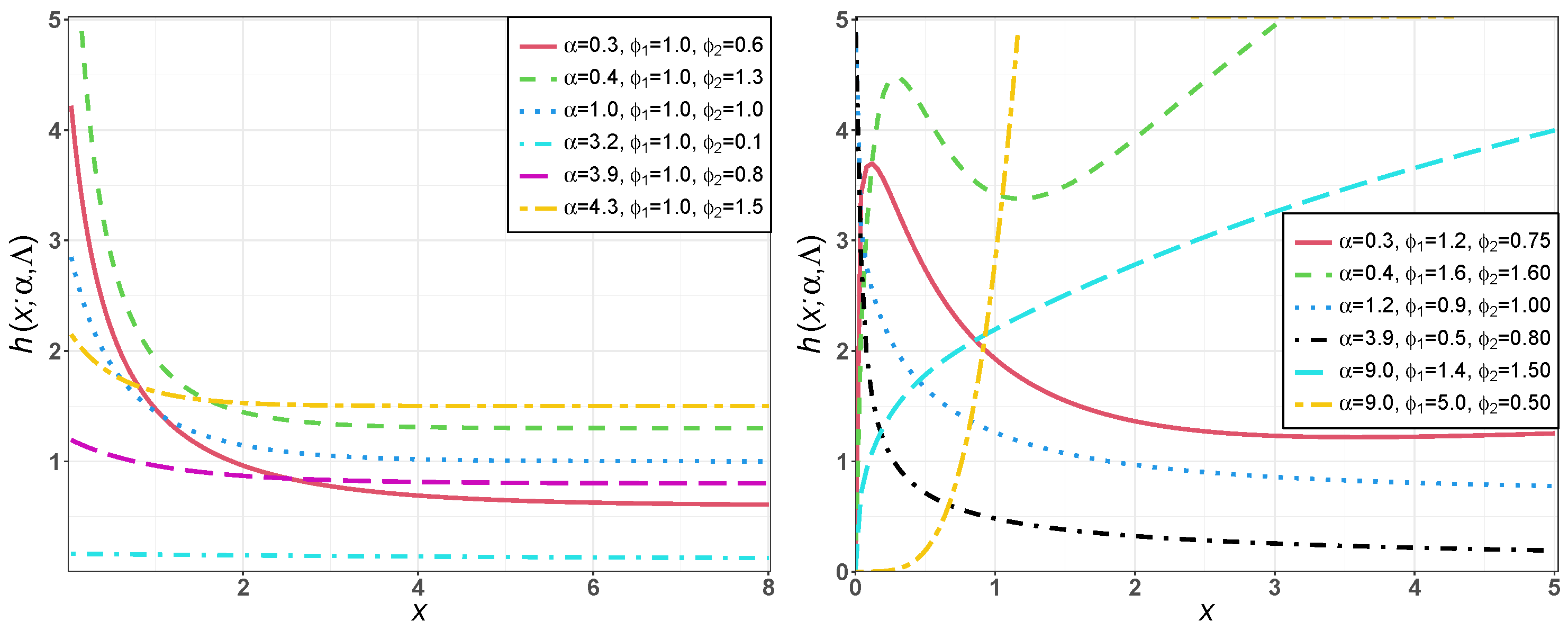
3.1. Shapes of NME-Weibull PDF and HF
3.2. The HT Characteristic
3.3. The Quantile Function
3.4. The rth Moment
3.5. The MGF
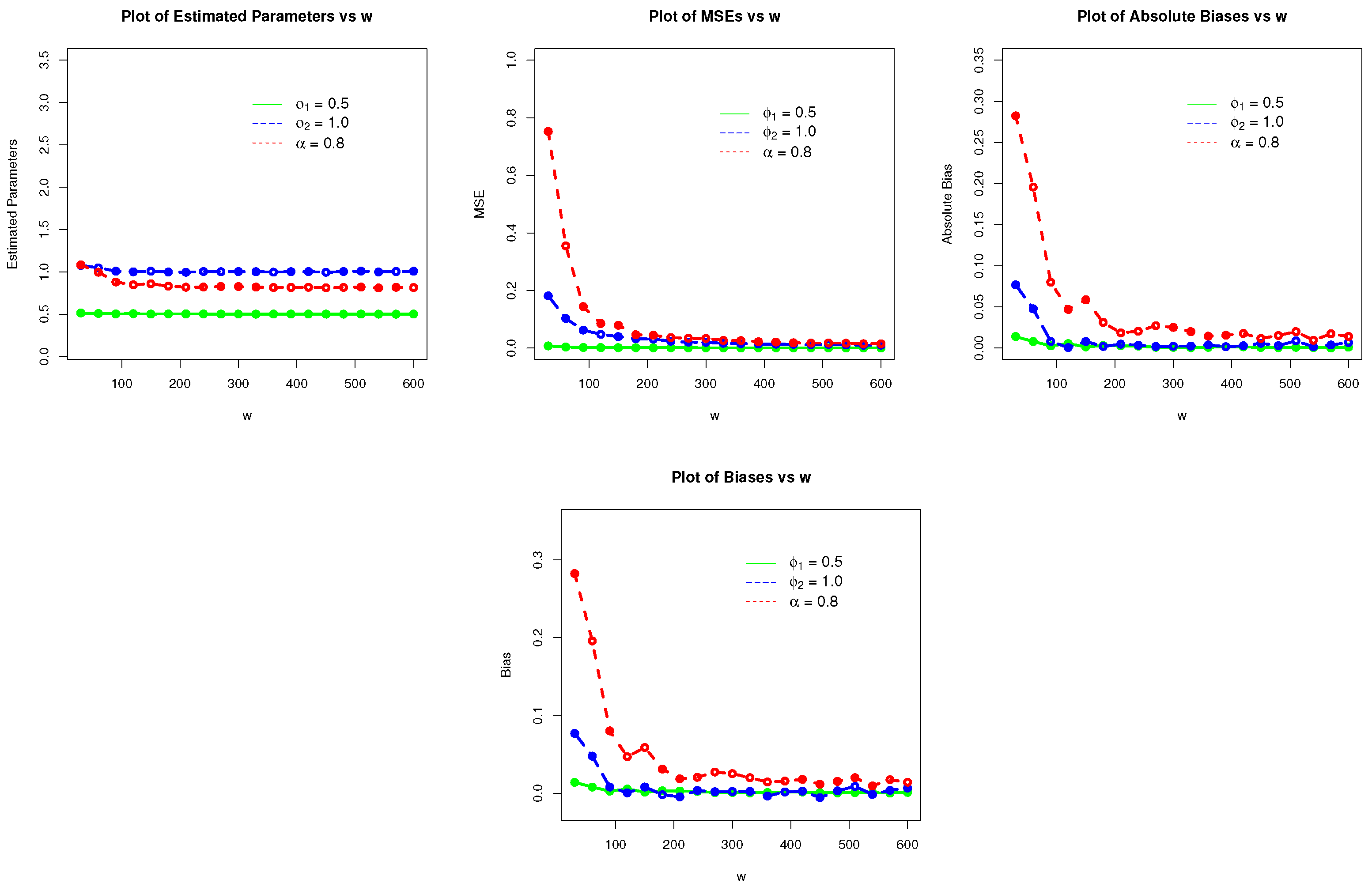
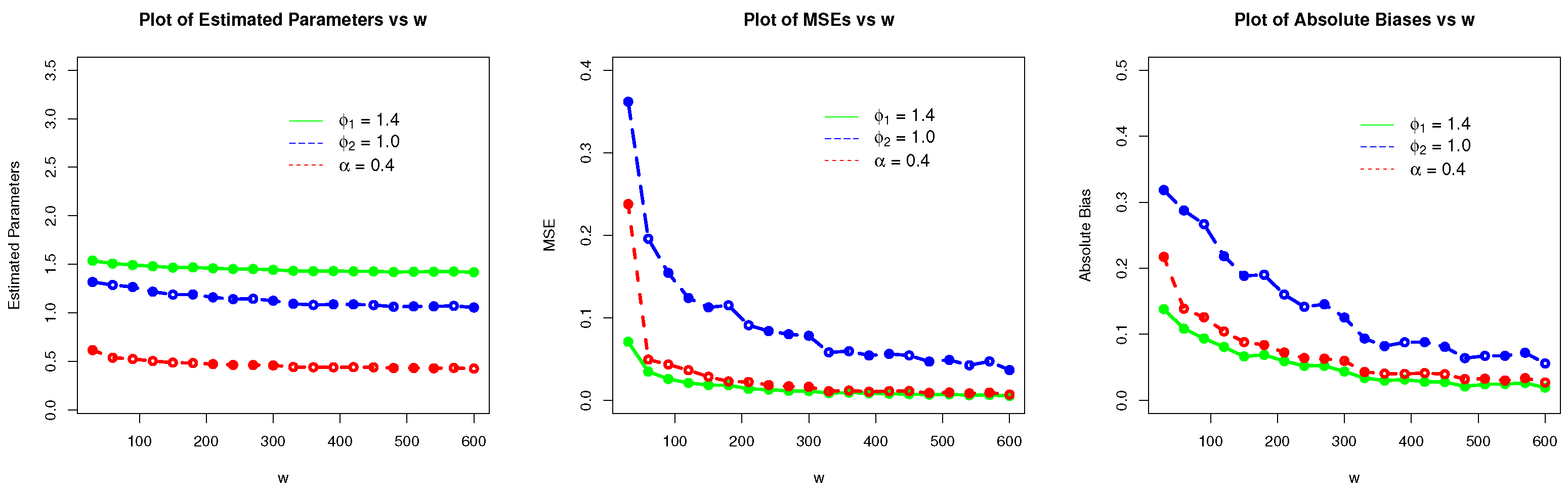
4. Estimation and Simulation
- MLEs and tend to stable.
- MSEs of and decrease.
- Biases of and tend to zero.
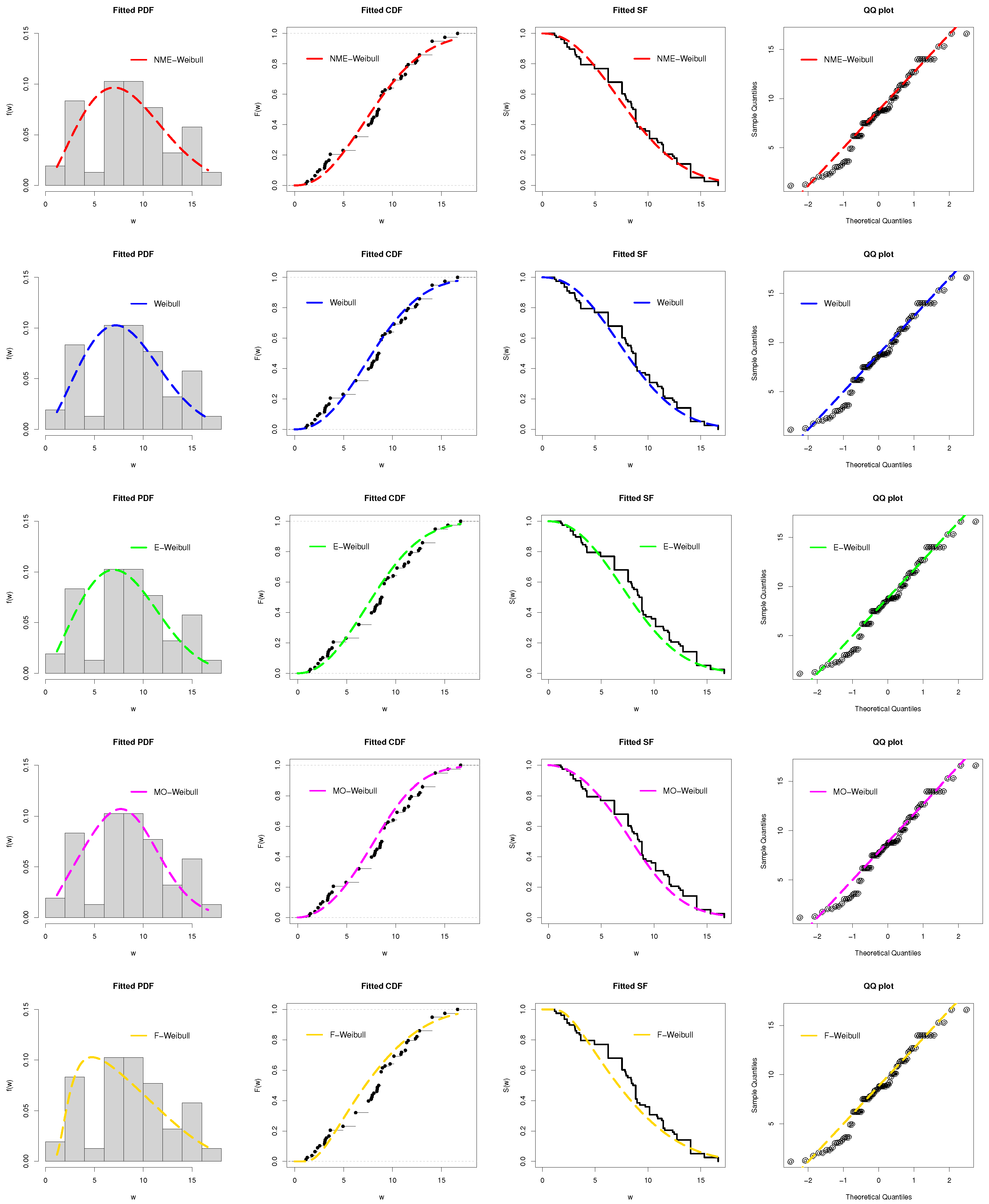
5. Practical Application
- Weibull distribution with CDF, given by
- Exponentiated Weibull (E-Weibull) distribution with CDF, expressed by
- Marshall Olkin Weibull (MO-Weibull) distribution with CDF, given below:
- Flexible Weibull (F-Weibull) distribution with CDF, provided below:
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmad, Z.; Hamedani, G.G.; Butt, N.S. Recent developments in distribution theory: A brief survey and some new generalized classes of distributions. Pak. J. Stat. Oper. Res. 2019, 15, 87–110. [Google Scholar] [CrossRef]
- Bannick, M.S.; McGaughey, M.; Flaxman, A.D. Ensemble modelling in descriptive epidemiology: Burden of disease estimation. Int. J. Epidemiol. 2020, 49, 2065–2073. [Google Scholar] [CrossRef]
- Deep, S.; Sarkar, A.; Ghawat, M.; Rajak, M.K. Estimation of the wind energy potential for coastal locations in India using the Weibull model. Renew. Energy 2020, 161, 319–339. [Google Scholar] [CrossRef]
- Mathlouthi, M.; Lebdi, F. Estimating extreme dry spell risk in Ichkeul Lake Basin (Northern Tunisia): A comparative analysis of annual maxima series with a Gumbel distribution. Proc. Int. Assoc. Hydrol. Sci. 2020, 383, 241–248. [Google Scholar] [CrossRef]
- Mori, H.; Chen, X.; Leung, Y.F.; Shimokawa, D.; Lo, M.K. Landslide hazard assessment by smoothed particle hydrodynamics with spatially variable soil properties and statistical rainfall distribution. Can. Geotech. J. 2020, 57, 1953–1969. [Google Scholar] [CrossRef]
- Alotaibi, R.; Okasha, H.; Rezk, H.; Almarashi, A.M.; Nassar, M. On a new flexible Lomax distribution: Statistical properties and estimation procedures with applications to engineering and medical data. AIMS Math. 2021, 6, 13976–13999. [Google Scholar] [CrossRef]
- Benatmane, C.; Zeghdoudi, H.; Shanker, R.; Lazri, N. Composite Rayleigh-Pareto distribution: Application to real fire insurance losses data set. J. Stat. Manag. Syst. 2021, 24, 545–557. [Google Scholar] [CrossRef]
- Shafqat, A.; Huang, Z.; Aslam, M. Design of X-bar control chart based on Inverse Rayleigh Distribution under repetitive group sampling. Ain Shams Eng. J. 2021, 12, 943–953. [Google Scholar] [CrossRef]
- Alevizakos, V.; Koukouvinos, C. Monitoring reliability for a gamma distribution with a double progressive mean control chart. Qual. Reliab. Eng. Int. 2021, 37, 199–218. [Google Scholar] [CrossRef]
- Lei, Z.; Shen, J.; Wang, J.; Qiu, Q.; Zhang, G.; Chi, S.S.; Wang, C. Composite polymer electrolytes with uniform distribution of ionic liquid-grafted ZIF-90 nanofillers for high-performance solid-state Li batteries. Chem. Eng. J. 2021, 412, 128733. [Google Scholar] [CrossRef]
- Kania, A.; Berent, K.; Mazur, T.; Sikora, M. 3D printed composites with uniform distribution of Fe3O4 nanoparticles and magnetic shape anisotropy. Addit. Manuf. 2021, 46, 102149. [Google Scholar] [CrossRef]
- Alfaer, N.M.; Gemeay, A.M.; Aljohani, H.M.; Afify, A.Z. The extended log-logistic distribution: Inference and actuarial applications. Mathematics 2021, 9, 1386. [Google Scholar] [CrossRef]
- Alshenawy, R. The Generalization Inverse Weibull Distribution Related to X-Gamma Generator Family: Simulation and Application for Breast Cancer. J. Funct. Spaces 2022, 2022, 4693490. [Google Scholar] [CrossRef]
- Almetwally, E.M. The odd Weibull inverse topp–leone distribution with applications to COVID-19 data. Ann. Data Sci. 2022, 9, 121–140. [Google Scholar] [CrossRef]
- Bo, W.; Ahmad, Z.; Alanzi, A.R.; Al-Omari, A.I.; Hafez, E.H.; Abdelwahab, S.F. The current COVID-19 pandemic in China: An overview and corona data analysis. Alex. Eng. J. 2022, 61, 1369–1381. [Google Scholar] [CrossRef]
- Rafique, M.; Ali, S.; Shah, I.; Ashraf, B. A comparison of different Bayesian models for leukemia data. Am. J. Math. Manag. Sci. 2022, 41, 244–258. [Google Scholar] [CrossRef]
- Shengjie, G.; Craig, A.; Mekiso, G.T. A New Alpha Power Weibull Model for Analyzing Time-to-Event Data: A Case Study from Football. Math. Probl. Eng. 2022, 2022, 7257264. [Google Scholar] [CrossRef]
- Penn, M.J.; Donnelly, C.A. Analysis of a double Poisson model for predicting football results in Euro 2020. PLoS ONE 2022, 17, e0268511. [Google Scholar] [CrossRef]
- Almalki, S.J.; Nadarajah, S. Modifications of the Weibull distribution: A review. Reliab. Eng. Syst. Saf. 2014, 124, 32–55. [Google Scholar] [CrossRef]
- Wilson, P.S.; Toumi, R. A fundamental probability distribution for heavy rainfall. Geophys. Res. Lett. 2005, 32, L14812. [Google Scholar] [CrossRef]
- Costa, U.M.S.; Freire, V.N.; Malacarne, L.C.; Mendes, R.S.; Picoli, S., Jr.; De Vasconcelos, E.A.; da Silva, E.F., Jr. An improved description of the dielectric breakdown in oxides based on a generalized Weibull distribution. Phys. A Stat. Mech. Appl. 2006, 361, 209–215. [Google Scholar] [CrossRef]
- Sartori, I.; de Assis, E.M.; da Silva, A.L.; de Melo, R.L.V.; Borges, E.P. Reliability modeling of a natural gas recovery plant using q-Weibull distribution. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2009; Volume 27, pp. 1797–1802. [Google Scholar]
- Zhang, F.; Ng, H.K.T.; Shi, Y. On alternative q-Weibull and q-extreme value distributions: Properties and applications. Phys. A Stat. Mech. Appl. 2018, 490, 1171–1190. [Google Scholar] [CrossRef]
- Hristopulos, D.T.; Baxevani, A. Kaniadakis Functions beyond Statistical Mechanics: Weakest-Link Scaling, Power-Law Tails, and Modified Lognormal Distribution. Entropy 2022, 24, 1362. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramirez, P.; Velazquez, S. A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands. Renew. Sustain. Energy Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Papalexiou, S.M. Rainfall Generation Revisited: Introducing CoSMoS-2s and Advancing Copula-Based Intermittent Time Series Modeling. Water Resour. Res. 2022, 58, e2021WR031641. [Google Scholar] [CrossRef]
- Zhao, Y.; Ahmad, Z.; Alrumayh, A.; Yusuf, M.; Aldallal, R.; Elshenawy, A.; Riad, F.H. A novel logarithmic approach to generate new probability distributions for data modeling in the engineering sector. Alex. Eng. J. 2022, 62, 313–325. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Ahmad, Z.; Almaspoor, Z.; Eliwa, M.S.; Iqbal, Z. A new statistical approach for modeling the bladder cancer and leukemia patients data sets: Case studies in the medical sector. Math. Biosci. Eng. 2022, 19, 10474–10492. [Google Scholar] [CrossRef]
- Ahmad, Z.; Almaspoor, Z.; Khan, F.; Alhazmi, S.E.; El-Morshedy, M.; Ababneh, O.Y.; Al-Omari, A.I. On fitting and forecasting the log-returns of cryptocurrency exchange rates using a new logistic model and machine learning algorithms. AIMS Math. 2022, 7, 18031–18049. [Google Scholar] [CrossRef]
- Ahmad, Z.; Mahmoudi, E.; Roozegar, R.; Alizadeh, M.; Afify, A.Z. A new exponential-X family: Modeling extreme value data in the finance sector. Math. Probl. Eng. 2021, 2021, 8759055. [Google Scholar] [CrossRef]
- Bhati, D.; Ravi, S. On generalized log-Moyal distribution: A new heavy tailed size distribution. Insur. Math. Econ. 2018, 79, 247–259. [Google Scholar] [CrossRef]
- Beirlant, J.; Matthys, G.; Dierckx, G. Heavy-tailed distributions and rating. ASTIN Bull. J. IAA 2001, 31, 37–58. [Google Scholar] [CrossRef]
- Seneta, E. Karamata’s characterization theorem, feller and regular variation in probability theory. Publ. L’Institut Mathématique 2002, 71, 79–89. [Google Scholar] [CrossRef]

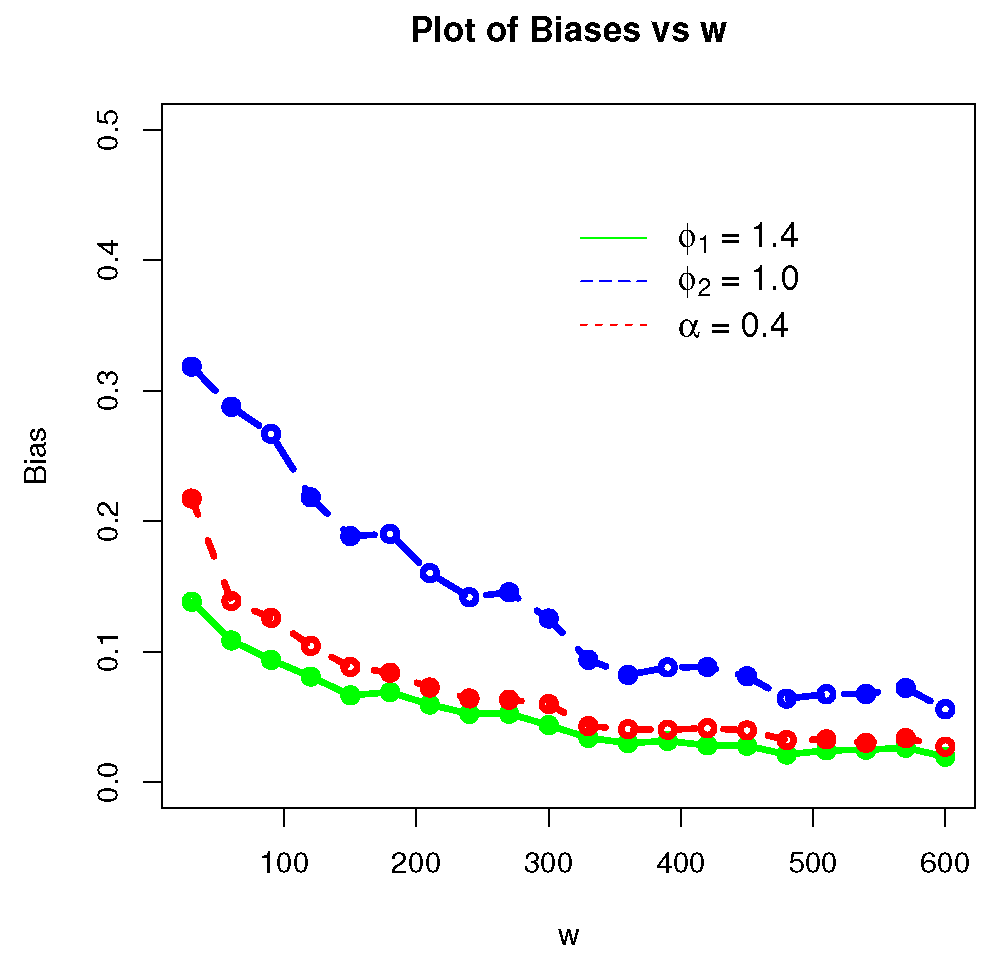
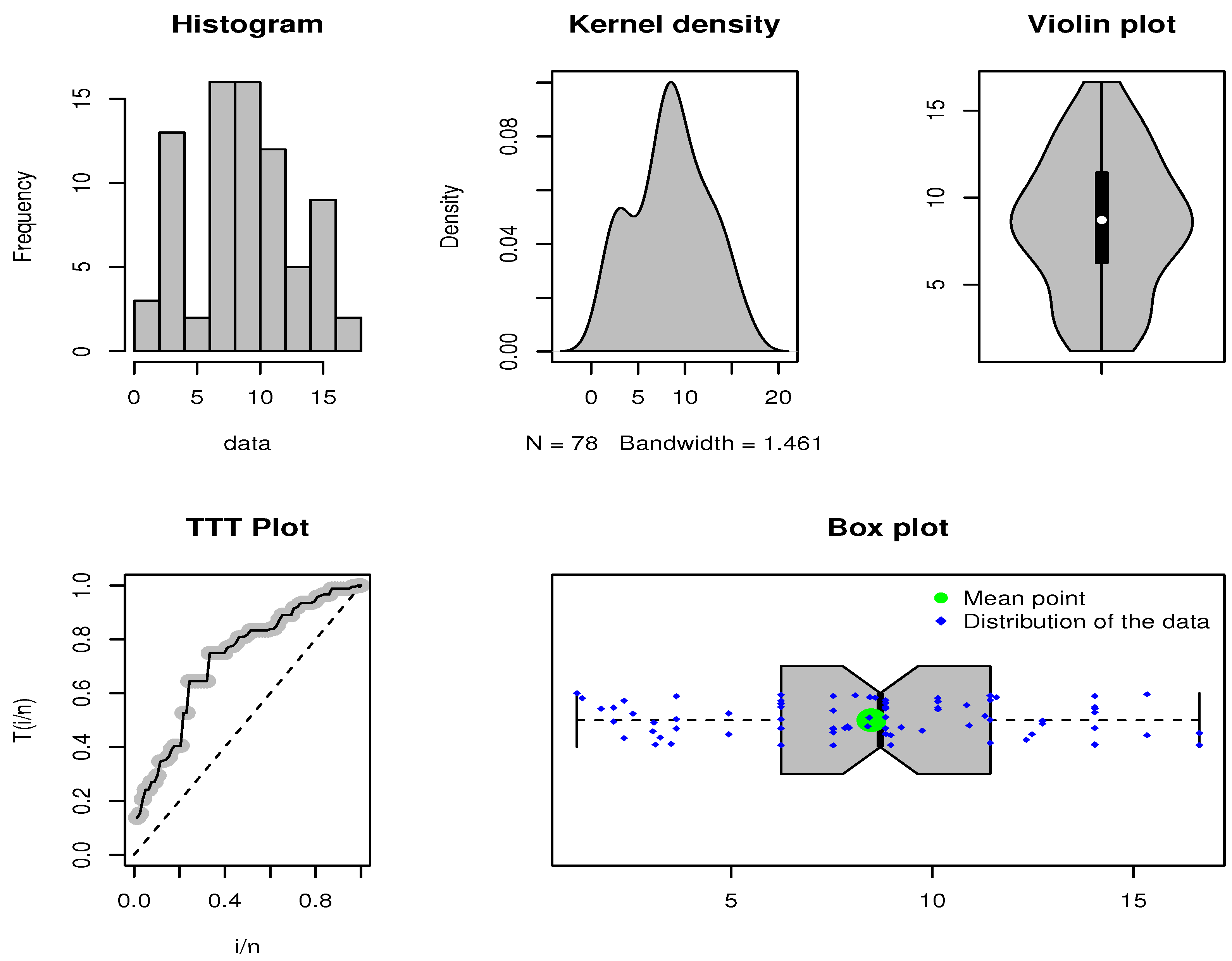
| w | Parameters | MLEs | MSEs | Biases |
|---|---|---|---|---|
| 0.5139448 | 0.0072890 | 0.01394476 | ||
| 30 | 1.0768346 | 0.1812394 | 0.07683460 | |
| 1.0823500 | 0.7523786 | 0.28234996 | ||
| 0.5079046 | 0.0036778 | 0.00790461 | ||
| 60 | 1.0476758 | 0.1027139 | 0.04767583 | |
| 0.9957742 | 0.3549299 | 0.19577419 | ||
| 0.5026137 | 0.0019558 | 0.00261367 | ||
| 90 | 1.0079573 | 0.0623915 | 0.00795731 | |
| 0.8800715 | 0.1439712 | 0.08007147 | ||
| 0.5013730 | 0.0011332 | 0.00137297 | ||
| 150 | 1.0079531 | 0.0394922 | 0.00795305 | |
| 0.8587196 | 0.0792510 | 0.05871963 | ||
| 0.5023244 | 0.0008397 | 0.00232438 | ||
| 240 | 1.0035047 | 0.0237148 | 0.00350473 | |
| 0.8204144 | 0.0362713 | 0.02041444 | ||
| 0.5003512 | 0.0005781 | 0.00035115 | ||
| 330 | 1.0023157 | 0.0164310 | 0.00231569 | |
| 0.8199299 | 0.0263909 | 0.01992986 | ||
| 0.5016130 | 0.0004197 | 0.00161304 | ||
| 420 | 1.0015546 | 0.0134669 | 0.00155455 | |
| 0.8155559 | 0.0208359 | 0.01555592 | ||
| 0.5004310 | 0.0003417 | 0.00043099 | ||
| 480 | 1.0029297 | 0.0111818 | 0.00292967 | |
| 0.8151855 | 0.0171838 | 0.01518546 | ||
| 0.5007776 | 0.0003414 | 0.00077761 | ||
| 510 | 1.0087698 | 0.0123862 | 0.00876977 | |
| 0.8199280 | 0.0177454 | 0.01992804 | ||
| 0.5001925 | 0.0002944 | 0.00019245 | ||
| 570 | 1.0036629 | 0.0096804 | 0.00366289 | |
| 0.8173364 | 0.0148489 | 0.01733639 | ||
| 0.5010761 | 0.0002891 | 0.00107609 | ||
| 600 | 1.0066832 | 0.0099113 | 0.00668317 | |
| 0.8141210 | 0.0147306 | 0.01412103 |
| w | Parameters | MLEs | MSEs | Biases |
|---|---|---|---|---|
| 0.8373597 | 0.0228400 | 3.7359 | ||
| 30 | 1.0329687 | 0.0864116 | 0.03296874 | |
| 1.6122330 | 1.6492961 | 0.41223290 | ||
| 0.8081282 | 0.0101249 | 8.1282 | ||
| 60 | 1.0124301 | 0.0579791 | 0.01243010 | |
| 1.5015600 | 1.1045864 | 0.30155973 | ||
| 0.8085094 | 0.0067330 | 8.5094 | ||
| 90 | 1.0075127 | 0.0390573 | 0.00751267 | |
| 1.3942850 | 0.5915042 | 0.19428471 | ||
| 0.8045268 | 0.0043708 | 4.5268 | ||
| 150 | 1.0174312 | 0.0221428 | 0.01743116 | |
| 1.3490600 | 0.3230241 | 0.14906040 | ||
| 0.8000402 | 0.0025746 | 4.0247 | ||
| 240 | 1.0037466 | 0.0144882 | 0.00374658 | |
| 1.2938500 | 0.1780648 | 0.09384972 | ||
| 0.8052871 | 0.0019428 | 5.2870 | ||
| 330 | 0.9942357 | 0.0099813 | −0.00576426 | |
| 1.2201170 | 0.0896011 | 0.02011655 | ||
| 0.8019934 | 0.0014204 | 1.9934 | ||
| 420 | 1.0032499 | 0.0078325 | 0.00324990 | |
| 1.2382960 | 0.0781596 | 0.03829620 | ||
| 0.7994154 | 0.0014117 | −5.8456 | ||
| 480 | 1.0062147 | 0.0074068 | 0.00621474 | |
| 1.2558040 | 0.0751255 | 0.05580425 | ||
| 0.8006431 | 0.0012915 | 6.4306 | ||
| 510 | 1.0016868 | 0.0061642 | 0.00168683 | |
| 1.2396020 | 0.0571275 | 0.03960178 | ||
| 0.8020553 | 0.0011090 | 2.0552 | ||
| 570 | 1.0010832 | 0.0055488 | 0.00108320 | |
| 1.2283470 | 0.0559610 | 0.02834659 | ||
| 0.8033656 | 0.0010878 | 3.3655 | ||
| 600 | 0.9938832 | 0.0058198 | −0.00611684 | |
| 1.2028430 | 0.0499104 | 0.00284281 |
| w | Parameters | MLEs | MSEs | Biases |
|---|---|---|---|---|
| 1.5381320 | 0.0709285 | 0.13813181 | ||
| 30 | 1.3184280 | 0.3618016 | 0.31842754 | |
| 0.6172510 | 0.2377404 | 0.21725102 | ||
| 1.5084680 | 0.0347465 | 0.10846768 | ||
| 60 | 1.2875990 | 0.1957131 | 0.28759929 | |
| 0.5387065 | 0.0493668 | 0.13870647 | ||
| 1.4935920 | 0.0258712 | 0.09359157 | ||
| 90 | 1.2668450 | 0.1543403 | 0.26684505 | |
| 0.5257774 | 0.0433562 | 0.12577736 | ||
| 1.4664260 | 0.0184980 | 0.06642592 | ||
| 150 | 1.1884770 | 0.1125613 | 0.18847743 | |
| 0.4881762 | 0.0285109 | 0.08817621 | ||
| 1.4522380 | 0.0129707 | 0.05223845 | ||
| 240 | 1.1416120 | 0.0839058 | 0.14161192 | |
| 0.4640379 | 0.0185309 | 0.06403786 | ||
| 1.4337810 | 0.0087992 | 0.03378078 | ||
| 330 | 1.0936430 | 0.0581037 | 0.09364311 | |
| 0.4428418 | 0.0110310 | 0.04284176 | ||
| 1.4280080 | 0.0080039 | 0.02800806 | ||
| 420 | 1.0881280 | 0.0561704 | 0.08812753 | |
| 0.4412527 | 0.0112033 | 0.04125268 | ||
| 1.4210270 | 0.0068960 | 0.02102729 | ||
| 480 | 1.0638800 | 0.0469817 | 0.06387966 | |
| 0.4321181 | 0.0088733 | 0.03211808 | ||
| 1.4241980 | 0.0072342 | 0.02419761 | ||
| 510 | 1.0672880 | 0.0488379 | 0.06728819 | |
| 0.4326815 | 0.0094359 | 0.03268150 | ||
| 1.4262490 | 0.0064656 | 0.02624945 | ||
| 570 | 1.0720440 | 0.0471651 | 0.07204448 | |
| 0.4335796 | 0.0092925 | 0.03357964 | ||
| 1.4193270 | 0.0052698 | 0.01932710 | ||
| 600 | 1.0558220 | 0.0365956 | 0.05582239 | |
| 0.4270003 | 0.0069440 | 0.02700025 |
| Dist. | |||||
|---|---|---|---|---|---|
| NME-Weibull | 12.36747 | 2.24515 | 0.00583 | - | - |
| Weibull | - | 2.20768 | 0.00721 | - | - |
| Exponentiated Weibull | - | 2.42247 | 0.00365 | - | 0.83154 |
| Marshall Olkin Weibull | - | 1.83785 | 0.02456 | 2.47454 | - |
| Flexible Weibull | - | 0.105291 | 8.14488 | - | - |
| Dist. | AIC | CAIC | BIC | HQIC |
|---|---|---|---|---|
| NME-Weibull | 431.3646 | 431.6889 | 438.4347 | 434.1949 |
| Weibull | 438.8245 | 438.9845 | 443.5379 | 440.7114 |
| E-Weibull | 439.5629 | 439.8872 | 446.6330 | 442.3932 |
| MO-Weibull | 438.8344 | 439.1587 | 445.9045 | 441.6647 |
| F-Weibull | 445.5514 | 445.7114 | 450.2648 | 447.4382 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshanbari, H.M.; Odhah, O.H.; Ahmad, Z.; Khan, F.; El-Bagoury, A.A.-A.H. A New Probability Distribution: Model, Theory and Analyzing the Recovery Time Data. Axioms 2023, 12, 477. https://doi.org/10.3390/axioms12050477
Alshanbari HM, Odhah OH, Ahmad Z, Khan F, El-Bagoury AA-AH. A New Probability Distribution: Model, Theory and Analyzing the Recovery Time Data. Axioms. 2023; 12(5):477. https://doi.org/10.3390/axioms12050477
Chicago/Turabian StyleAlshanbari, Huda M., Omalsad Hamood Odhah, Zubair Ahmad, Faridoon Khan, and Abd Al-Aziz Hosni El-Bagoury. 2023. "A New Probability Distribution: Model, Theory and Analyzing the Recovery Time Data" Axioms 12, no. 5: 477. https://doi.org/10.3390/axioms12050477
APA StyleAlshanbari, H. M., Odhah, O. H., Ahmad, Z., Khan, F., & El-Bagoury, A. A.-A. H. (2023). A New Probability Distribution: Model, Theory and Analyzing the Recovery Time Data. Axioms, 12(5), 477. https://doi.org/10.3390/axioms12050477





