A Statistical Dependence Framework Based on a Multivariate Normal Copula Function and Stochastic Differential Equations for Multivariate Data in Forestry

Abstract

Stochastic differential equations and Copula theories are important topics that have many advantages for applications in almost every discipline. Many studies in forestry collect longitudinal, multi-dimensional, and discrete data for which the amount of measurement of individual variables does not match. For example, during sampling experiments, the diameters of all trees, the heights of approximately 10% of the trees, and the tree crown base height and crown width for a significantly smaller number of trees are measured. In this study, for estimating five-dimensional dependencies, we used a normal copula approach, where the dynamics of individual tree variables (diameter, potentially available area, height, crown base height, and crown width) are described by a stochastic differential equation with mixed-effect parameters. The approximate maximum likelihood method was used to obtain parameter estimates of the presented stochastic differential equations, and the normal copula dependence parameters were estimated using the pseudo-maximum likelihood method. This study introduced the normalized multi-dimensional interaction information index based on differential entropy to capture dependencies between state variables. Using conditional copula-type probability density functions, the exact form equations defining the links among the diameter, potentially available area, height, crown base height, and crown width were derived. All results were implemented in the symbolic algebra system MAPLE.

1. Introduction

The modeling of the growth of the appropriate tree size variable via age is the main problem foresters have in predicting the state of the stand in the future and in choosing stand management strategies and fellings. When creating scientific models of tree growth, scientists are influenced by their perception of the “measure” of tree size. Among the many potential measures of tree size, foresters seem to focus only on a few size measurements, such as the tree diameter at breast height, height, crown base height, crown width, and potentially available area (stand density). There is no doubt that changes in each of these mentioned size measures affect the other size measure. Modeling the links among these five tree size measures enables us to predict changes in any tree size measure over time and the rest of the tree size measures and to perform a detailed tree size analysis by exploring the increments, inflection points, and more.

In order to model the rate of change of tree size measure over time, two growth models defined by ordinary differential equations (these are equations that do not take random events into account) are usually used in practice [1]. The first of these models, called exponential growth, describes populations that increase in size without ever reaching a limit. The second model, called logistic growth, is characterized by the saturation level of reproductive growth, which affects further population dynamics [2,3,4,5]. Forestry statisticians have used these general principles in their models and experiments since the first growth models of tree size measures [6]. Deterministic growth models postulate the output variable of tree size in the structure of a random variable whose deviations from the expected trend function must obey a normal distribution with constant variance. However, the actual values of the output variable of tree size are governed by the corresponding diffusion process, which possesses a probability density function typically dependent on the input variables and noise process parameters. Additionally, the solution of the stochastic differential equation describing the variable growth dynamics of a given tree size component is expressed as a function of the transition probability density. As a result, we can describe the changes in the modeled quantity not only using the mean, but it is also possible to define any moment. Unfortunately, deterministic models allow us to define only the mean growth curve. Forest science researchers often underestimate the utility of the stochastic model by stating that stochastic models are intellectually preferable to and aesthetically superior to deterministic models [7]. Stochastic differential equations are distinguished by their wide applicability in various scientific areas, such as economics, forestry, and medicine [8,9,10,11,12,13]. When it comes to data analysis, it is a multidisciplinary topic that has well survived a period of intense research where new concepts have led to exciting changes and applications for solving problems in various areas of science. Thus, for most of the previously mentioned deterministic exponential or sigmoidal growth processes described by ordinary differential equations [14], complex analyses can be performed by constructing analogies of stochastic differential equations. New synergies are expected to arise from the application of stochastic differential equations to dynamical growth processes in forestry [15]. In forestry, the stochastic differential equation analogy began to be used in the mid-twentieth century [16]. Dynamic problems of tree and stand size variables and the links among the size variables were analyzed using systems of stochastic differential equations. Traditionally, state variables used in forestry are described by two-dimensional, three-dimensional, and higher-dimensional stochastic differential equation systems, where the interaction of state variables is expressed by the corresponding covariance matrix. For example, the univariate growth processes described by a one-dimensional stochastic differential equation of tree growth are given in [17,18]; the two-dimensional growth process described by a system of stochastic differential equations of tree diameter and height is given in [19]; the three-dimensional growth processes described by a system of stochastic differential equations of tree diameter, height, and number of trees per hectare or diameter, potentially available area, and height; and the higher-dimensional growth processes described by a system of stochastic differential equations of tree diameter, height, crown base height, and crown width are given in [20,21]. It is important to note that some of the growth processes mentioned above are distinguished by the fact that the densities of the solutions of the diffusion processes used are characterized by a symmetrical one-dimensional or multi-dimensional normal distribution or by an asymmetrical one-dimensional or multi-dimensional lognormal distribution. These growth processes are formalized by the symmetrical Vasicek-type diffusion process [22,23], or the asymmetrical Gompertz-type [24], Bertalanffy-type diffusion process [25], and a hybrid mode diffusion process [26]. In order to extend the applicability of growth processes to a larger forest region, random effects are additionally included, which are expressed as random variables normally distributed with zero mean and constant variance. On the one hand, the introduction of random effects increases the number of estimated unknown parameters, and the parameter estimation procedure becomes much more complicated. The large number of computer calculations and time required to estimate the parameters of a mixed-effect parameter system of multivariate stochastic differential equations requires a methodology that divides the parameter estimation procedure for each equation separately. Since the solution of each one-dimensional stochastic equation is associated with a probability density function, it is appropriate to use the copula technique [27] to link them together. Copulas are functions that combine one-dimensional distribution functions with their joint multi-dimensional distribution function. There are several copula functions that depend on how the function generating the copula is justified. The normal copula function is defined using a multi-dimensional standard normal probability density function and a marginal probability density function to obtain the joint distribution. It can be used to model multi-dimensional joint distributions and is suitable for forest growth analysis studies [28,29,30].

In this paper, we analyze five one-dimensional random processes, each of which is described by a separate differential equation ($X_1\left(t\right)$, $X_2\left(t\right), X_3\left(t\right), X_4\left(t\right),X_5\left(t\right)$) (the tree diameter, $X_1\left(t\right)$, potentially available area, $X_2\left(t\right)$, height, $X_3\left(t\right)$, crown base height, $X_4\left(t\right)$, and crown width, $X_5\left(t\right)$), and our main interest is to determine the dependencies and functional relationships among them. The dependence structure of $(X_1\left(t\right), X_2\left(t\right), X_3\left(t\right),X_4\left(t\right), X_5\left(t\right)$) can be formalized using the normal conditional copula function.

The rest of this paper is structured as follows. The Section 2 presents models of stochastic differential equations and conditional normal copula, which are later used in the paper to formalize growth processes in forestry. In the Section 3, the parameter estimators and the joint and conditional probability density functions of the corresponding variables are defined. The Section 4 examines the goodness of fit of the newly derived functional relationships using newly defined normalized multi-dimensional interaction information indices defined by Shannon’s differential entropy [31]. The Section 5 presents the main findings and future challenges.

2. Methods

2.1. Stochastic Differential Equations

Stochastic differential equations are used to model observable variables that evolve continuously and randomly over time. Multi-dimensional stochastic differential equation models are commonly used in many scientific areas, such as biology, economics, mathematical finance, and forestry. Stochastic processes that are described by a system of stochastic differential equations include a large number of unknown parameters that must be estimated. Unfortunately, firstly, a large number of estimated parameters increases the time it takes for computer calculations, and secondly, it reduces the scope of acceptable model-fitting databases because measurements must be made for all variables at a given discrete moment in time [13,20]. As an alternative to the multi-dimensional distribution, recently, studies have adopted a “copula” approach to analyze multi-dimensional measurements. Although the copula models are promising, there are only a few studies on copula-based stochastic differential equation analysis [32] in forestry. Therefore, the main objective of this study was to comprehensively develop the methodologies and theories of a copula-based five-dimensional stochastic process, specifically for the analysis of tree diameter, potentially available area, height, crown base height, and crown width measurements in forestry. Next, we define five stochastic processes, $X_1\left(t\right),X_2\left(t\right),X_3\left(t\right),X_4\left(t\right),X_5\left(t\right)$, using a stochastic differential equation framework that formalizes the time evolution of the tree diameter, potentially available area, height, crown base height, and crown width. In this section, all theoretical derivations and applications involve one-dimensional stochastic differential equations. Let us consider the tree diameter diffusion process $\left\{X_1^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, the tree potentially available area diffusion process $\left\{X_2^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, and the tree height diffusion process $\left\{X_3^i\left(t\right)| t\in \left[t_0,T\right]\right\}$ (i = 1, …, M, where M is the number of individuals, $t_0$ is the initial time, and T is any finite number) as described by the four-parameter Gompertz-type stochastic differential equation

$$\begin{gathered} d{X}_j^i\left(t\right)=\left(\left({\alpha }_j+{\varphi }_j^i\right)-{\beta }_{j}ln\left(X_j^i\left(t\right)-{\mathsf{ɣ}}_j\right)\right)\left(X_j^i\left(t\right)-{\mathsf{ɣ}}_j\right)dt+\sqrt{{\sigma }_j}\left(X_j^i\left(t\right)-{\mathsf{ɣ}}_j\right)\cdot d{W}_j^i\left(t\right), j=1, 2, 3, \\ {X}_1^i\left(t_0\right)=x_{10},X_2^i\left(t_0\right)=x_{20}=\delta , X_3^i\left(t_0\right)=x_{30}, \end{gathered}$$

(1)

and the tree crown base height diffusion process $\left\{X_4^i\left(t\right)| t\in \left[t_0,T\right]\right\}$ and the tree crown width diffusion process $\left\{X_5^i\left(t\right)| t\in \left[t_0,T\right]\right\}$ are described by the 3-parameter Vasicek-type stochastic differential equation

$$\begin{gathered} d{X}_j^i\left(t\right)={\beta }_j\left({\alpha }_j+{\varphi }_j^i-X_j^i\left(t\right)\right)dt+\sqrt{{\sigma }_j}\cdot d{W}_j^i\left(t\right), j=4, 5, \\ {X}_4^i\left(t_0\right)=x_{40}, X_5^i\left(t_0\right)=x_{50}, \end{gathered}$$

(2)

where δ is an unknown fixed-effect parameter to be estimated, $W_j^i\left(t\right)$, j = 1, …, 5 are independent one-dimensional Brownian motions; the random effects ${\varphi }_j^i$, j = 1, …, 5 are independent and normally distributed random variables with zero mean and constant variances (${\varphi }_j^i~N\left(0;{\sigma }_{j\varphi }^2\right)$); the unknown fixed effect parameters ${\theta }_0=\left\{{\alpha }_j,{\beta }_j,{\sigma }_j,{\sigma }_{j\varphi },j=1, \dots , 5,{\gamma }_j, j=1, \dots , 3, \delta \right\}$ must be estimated.

The drift and diffusion functions for both used stochastic differential Equations (1) and (2) fulfill the regularity and smoothness conditions of the so-called global Lipschitz and growth bound [33]. Therefore, the stochastic differential Equations (1) and (2) have unique strong solutions [33]. Using state transformations $Y_j^i=e^{{\beta }_{i}t}\ln \left(X_j^i\left(t\right)-{\gamma }_j\right)$, j = 1, 2, 3, $Y_j^i=e^{{\beta }_{i}t}{X}_j^i\left(t\right)$, j = 4, 5, and Itô’s formula [33], the stochastic differential Equations (1) and (2) can be transformed into the Ornstein–Uhlenbeck process [34], which is Gaussian. Finally, by integrating and taking antilogarithms, we obtained that the conditional stochastic processes $(X_j^i\left(t\right)|X_j^i\left(t_0\right)=x_{j0})$, j = 1, 2, 3 have lognormal distributions $L{N}_1\left({\mu }_j^i\left(t\right);v_j\left(t\right)\right)$ and the conditional stochastic processes $(X_j^i\left(t\right)|X_j^i\left(t_0\right)=x_{j0})$, j = 4, 5 have normal distributions $N_1\left({\mu }_j^i\left(t\right);v_j\left(t\right)\right)$ with mean ${\mu }_j^i\left(t\right)$, variance $v_j\left(t\right),$ and probability density function $f_j^i\left(x_j,t\left|\mathsf{\Theta },{\varphi }_j^i\right.\right)$ defined as follows:

$${\mu }_j^i\left(t\right)=ln\left(x_{j0}-{\mathsf{\gamma }}_j\right)e^{-{\beta }_j\left(t-t_0\right)}+\frac{1}{{\beta }_j}\left(1-e^{-{\beta }_j\left(t-t_0\right)}\right)\left({\alpha }_j+{\varphi }_j^i-\frac{{\sigma }_j}{2}\right), j=1, 2, 3,$$

(3)

$${\mu }_j^i\left(t\right)={\alpha }_j+{\varphi }_j^i+\left(x_{j0}-\left({\alpha }_j+{\varphi }_j^i\right)\right)e^{-{\beta }_j\left(t-t_0\right)}, j=4, 5,$$

(4)

$$v_j\left(t\right)=\frac{1-e^{-2{\beta }_j\left(t-t_0\right)}}{2{\beta }_j}{\sigma }_j, j=1, \dots , 5,$$

(5)

$$f_1^i\left(x_1,t\left|{\theta }_1,{\varphi }_1^i\right.\right)=\frac{1}{\sqrt{2\pi v_1\left(t\right)}\left(x_1-{\mathsf{\gamma }}_1\right)}\mathit{exp}\left(-\frac{{\left(ln\left(x_1-{\mathsf{\gamma }}_1\right)-{\mu }_1^i\left(t\right)\right)}^2}{2v_1\left(t\right)}\right), {\theta }_1=\left({\alpha }_1,{\beta }_1,{\sigma }_1,{\gamma }_1\right),$$

(6)

$$f_2^i\left(x_2,t\left|{\theta }_2,{\varphi }_2^i\right.\right)=\frac{1}{\sqrt{2\pi v_2\left(t\right)}\left(x_2-{\mathsf{\gamma }}_2\right)}\mathit{exp}\left(-\frac{{\left(ln\left(x_2-{\mathsf{\gamma }}_2\right)-{\mu }_2^i\left(t\right)\right)}^2}{2v_2\left(t\right)}\right),{\theta }_2=\left({\alpha }_2,{\beta }_2,{\sigma }_2,{\gamma }_2,\delta \right),$$

(7)

$$f_3^i\left(x_3,t\left|{\theta }_3,{\varphi }_3^i\right.\right)=\frac{1}{\sqrt{2\pi v_3\left(t\right)}\left(x_3-{\mathsf{\gamma }}_3\right)}\mathit{exp}\left(-\frac{{\left(ln\left(x_3-{\mathsf{\gamma }}_3\right)-{\mu }_3^i\left(t\right)\right)}^2}{2v_3\left(t\right)}\right),{\theta }_3=\left({\alpha }_3,{\beta }_3,{\sigma }_3,{\gamma }_3\right),$$

(8)

$$f_4^i\left(x_4,t\left|{\theta }_4,{\varphi }_4^i\right.\right)=\frac{1}{\sqrt{2\pi v_4\left(t\right)}}\mathit{exp}\left(-\frac{{\left(x_4-{\mu }_4^i\left(t\right)\right)}^2}{2v_4\left(t\right)}\right),{\theta }_4=\left({\alpha }_4,{\beta }_4,{\sigma }_4\right),$$

(9)

$$f_5^i\left(x_5,t\left|{\theta }_5,{\varphi }_5^i\right.\right)=\frac{1}{\sqrt{2\pi v_5\left(t\right)}}\mathit{exp}\left(-\frac{{\left(x_5-{\mu }_5^i\left(t\right)\right)}^2}{2v_5\left(t\right)}\right),{\theta }_5=\left({\alpha }_5,{\beta }_5,{\sigma }_5\right).$$

(10)

In articles [21,29], we studied the problem of the estimation of the fixed-effect and mixed-effect parameters of discretely observed multi-dimensional processes by the maximum likelihood method. There are several alternative methods for obtaining the parameter estimates of stochastic differential equations using discrete measurements, such as the least squares method [35], the numerical approximation approach [36], and others [37].

The conditional density functions of the separate stochastic processes derived above significantly simplify the procedure for estimating unknown parameters because the joint multi-dimensional stochastic process is divided into five separate stochastic processes that have a number of estimated parameters five times smaller, and the parameters of each separate process are estimated using independent observed datasets.

Assume that $\left\{x_{j1}^i,x_{j2}^i,\dots ,x_{j{n}_{ij}}^i\right\}$ are the directly observed values of the jth separate stochastic process at discrete times $\left\{t_1^i,t_2^i,\dots ,t_{n_{ij}}^i\right\}$ (n_ij is the number of observed trees of the ith stand, i = 1, …, M, jth stochastic process, j = 1, …, 5).

The associated maximum likelihood function for the fixed-effect parameter separate stochastic process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M, (in this case, the random-effect parameters ${\varphi }_j^i$ are taken to be equal to the mean values Ε(${\varphi }_j^i$) = 0) has the following form:

$$L_j^1\left({\theta }_j\right)={{\displaystyle \prod }}_{i=1}^M{{\displaystyle \prod }}_{k=1}^{n_{ij}}{f}_j^i\left(x_{jk},t_k^i\left|{\theta }_j,0\right.\right),$$

(11)

and the maximum log-likelihood function is

$$L{L}_j^1\left({\theta }_j\right)={\displaystyle \sum }_{i=1}^M{\displaystyle \sum }_{k=1}^{n_{ij}}ln\left(f_j^i\left(x_{jk},t_k^i\left|{\theta }_j,0\right.\right)\right)$$

(12)

where the probability density function $f_j^i\left(x_{jk},t_k^i\left|{\theta }_j,0\right.\right)$ takes the form defined by Equations (6)–(10).

The associated maximum likelihood function for the fixed effect parameters of the separate stochastic process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M has the following form:

$$L_j^2\left({\theta }_j^{\prime },{\varphi }_j\right)={{\displaystyle \prod }}_{i=1}^M{{\displaystyle \int }}_R{{\displaystyle \prod }}_{k=1}^{n_{ij}}{f}_j^i\left(x_{jk},t_k^i\left|{\theta }_j,{\varphi }_j^i\right.\right)p\left({\varphi }_j^i\left|{\sigma }_{j\varphi }^2\right.\right)d{\varphi }_j^i, {\theta }_j^{\prime }=\left({\theta }_j,{\sigma }_{j\varphi }\right), {\varphi }_j=\left({\varphi }_j^1, \dots , {\varphi }_j^M\right)$$

(13)

where $p\left({\varphi }_j^i\left|{\sigma }_{j\varphi }^2\right.\right)$ is the normal probability density function with zero mean and constant variance, ${\sigma }_{j\varphi }^2$ and the maximum log-likelihood function is

$$L{L}_j^2\left({\theta }_j^{\prime },{\varphi }_j\right)={{\displaystyle \sum }}_{i=1}^M{{\displaystyle \int }}_R\left({{\displaystyle \sum }}_{k=1}^{n_{ij}}ln\left(f_j^i\left(x_{jk},t_k^i\left|{\theta }_j,{\varphi }_j^i\right.\right)\right)+ln\left(p\left({\varphi }_j^i\left|{\sigma }_{j\varphi }^2\right.\right)\right)\right)d{\varphi }_j^i.$$

(14)

Although the integral in (14) does not have a closed-form solution, the analytical expression of the integrand (14) is known. Therefore, the Laplace method [38] can be used. Let us define a function $g_j^i:R \to R$, j = 1, …, 5, i = 1, …, M by

$$g_j^i\left({\varphi }_j^i\left|\widehat{{\theta }_j^{\prime }}\right.\right)\equiv {{\displaystyle \sum }}_{k=1}^{n_{ij}}ln\left(f_j^i\left(x_{jk},t_k^i\left|\widehat{{\theta }_j},{\varphi }_j^i\right.\right)\right)+ln\left(p({\varphi }_j^i\left|\widehat{{\sigma }_{j\varphi }^2}\right.\right),$$

(15)

where the cap indicates the point estimate of the parameter.

Then, by a second-order Taylor series expansion [39]

$$L{L}_j^2\left({\theta }_j^{\prime },\widehat{{\varphi }_j}\right)\approx {\displaystyle \sum }_{i=1}^M\left(g_j^i\left(\widehat{{\varphi }_j^i}\left|{\theta }_j^{\prime }\right.\right)+\frac{1}{2}ln\left(2\pi \right)-\frac{1}{2}ln\left(\det {\left(\left[-\frac{{\partial }^2{g}_j^i\left({\varphi }_j^i\left|{\theta }_j,{\sigma }_{j\varphi }\right.\right)}{\partial {\left({\varphi }_j^i\right)}^2}\right]\right)}_{{\varphi }_j^i=\widehat{{\varphi }_j^i}}\right)\right),$$

(16)

where

$$\widehat{{\varphi }_j^i}=\underset{{\varphi }_j^i}{argmax}\left(g_j^i\left({\varphi }_j^i\left|\widehat{{\theta }_j^{\prime }}\right.\right)\right).$$

(17)

Maximizing $L{L}_j^2\left({\theta }_j^{\prime },{\varphi }_j\right)$ is a two-step optimization problem. The inner optimization step estimates the random effects $\widehat{{\varphi }_j^i}$ for each j = 1, …, 5, i = 1, …, M for the given values of the fixed effects $\widehat{{\theta }_j^{\prime }}$ with Equation (17). The outer optimization step maximizes $L{L}_j^2\left({\theta }_j^{\prime },\widehat{{\varphi }_j}\right)$ defined by (16) after we insert random effects $\widehat{{\varphi }_j}$ into Equation (16). In the first iteration, the values of the random effects $\widehat{{\varphi }_j}$ are set to zero, as the mean values Ε(${\varphi }_j^i$) = 0, j = 1, …, 5, i = 1, …, M. These two steps are iterated until convergence. Parameter estimates using the approximated maximum likelihood procedure are costly processes in terms of time and computational power, as many more iterations are required.

Based on estimation theory, the Cramér–Rao inequality [40] states that the covariance matrix of any unbiased estimator $\widehat{\theta }$ vector θ ∈ Θ, where Θ = $\left\{{\theta }_j,{\theta }_j^{\prime }, j=1,\dots , 5\right\}$ is the parameter space, is not less than the Fisher information matrix [31], namely, for each main diagonal element,$Cov\left(\widehat{\theta }\right)$ is greater than or equal to its corresponding element in $I^{-1}\left(\theta \right)$:

$$Cov\left(\widehat{\theta }\right)\ge I^{-1}\left(\theta \right),$$

(18)

where θ = (θ₁, …, θ_m) ∈ Θ and $\widehat{\theta }$ = ($\widehat{\theta }$₁, …, $\widehat{\theta }$_m), where m is a positive integer, and both the covariance matrix $Cov\left(\widehat{\theta }\right)$ and the inverse Fisher information matrix $I^{-1}\left(\theta \right)$ are m × m matrices. In order to calculate the observed Fisher information matrix $I\left(\theta \right)$, the maximum log-likelihood function for θ is needed. The approximate asymptotic standard errors $SE\left(\widehat{\theta }\right)$ of the fixed-effect parameters estimates $\widehat{\theta }$ for both the fixed- and mixed-effect scenarios (if $\widehat{\theta }=\widehat{{\theta }_j}$, then $L{L}_j\left(\widehat{\theta }\right)=L{L}_j^1\left(\widehat{{\theta }_j}\right)$, and it $\widehat{\theta }=\widehat{{\theta }_j^{\prime }}$, then $L{L}_j\left(\widehat{\theta }\right)=L{L}_j^2\left({\theta }_j^{\prime },{\varphi }_j\right)$, j = 1, …, 5) are defined by the diagonal elements of the inverse observed Fisher information matrix $F{I}^{-1}\left(\widehat{\theta }\right)$. By defining the matrix $\left[\frac{{\partial }^{2}L{L}_j\left(\theta \right)}{\partial {\theta }_k\partial {\theta }_l}\right], j=1,\mathrm{..5}$, the observed Fisher information matrix takes the following form

$$FI\left(\widehat{\theta }\right)={\left[-\frac{{\partial }^{2}L{L}_j\left(\theta \right)}{\partial {\theta }_k\partial {\theta }_l}\right]}^T{|}_{\theta =\widehat{\theta }}.$$

(19)

The approximate asymptotic standard errors of the fixed effects parameters are defined by

$$SE\left(\widehat{\theta }\right)=\sqrt{F{I}^{-1}\left(\widehat{\theta }\right)}.$$

(20)

The random effects for the newly derived probability density functions (6)–(10) can be calibrated for a new individual (for example, a plot of trees) if we have appropriate measurements for this new individual. The random effect ${\varphi }_j$, j = 1, …, 5 can be calibrated using the newly observed dataset $\left\{x_{j1},x_{j2},\dots ,x_{jm}\right\}$ at discrete times $\left\{t_1,t_2,\dots ,t_m\right\}$ (where m is the number of observed objects of the new individual) as

$$\widehat{{\varphi }_j}=\underset{{\varphi }_j}{argmax}\left({{\displaystyle \sum }}_{k=1}^{m}ln\left(f_j^i\left(x_{jk},t_k^i\left|\widehat{{\theta }_j},{\varphi }_j^i\right.\right)\right)+ln\left(p({\varphi }_j^i\left|\widehat{{\sigma }_{j\varphi }^2}\right.\right)\right).$$

(21)

2.2. Copulas and Dependence

The interest in copulas comes from several perspectives. First, studies often have more information about the separate distributions of the variables involved and richer databases for estimating one-dimensional distributions than for their multi-dimensional distributions. Second, multi-dimensional copulas can be used for determining the dependence of pairs of random variables. In summary, copulas are functions that connect multi-dimensional distributions to their one-dimensional marginals. According to Sklar’s theorem [27], a copula is a multi-dimensional distribution function connecting two or more marginal distributions to accurately form the joint distribution.

Thus [27], if F is an m-dimensional distribution function with margins F₁, …, F_m, then there exists an m-dimensional copula $C_{1,\dots ,m},$ such that for all x_k ∊ R, k = 1, …, m,

$$F\left(x_1, \dots , x_m\right)=C_{1,\dots ,m}\left(F_1\left(x_1\right), \dots , F_m(x_m)\right)$$

(22)

Additionally, if F₁, …, F_m are continuous, then $C_{1,\dots ,m}$ is unique, and conversely, if $C_{1,\dots ,m}$ is an m-dimensional copula and F₁, …, F_m are distribution functions, then the function F in (22) is an m-dimensional distribution function with marginals F₁, …, F_m.

Let f, c, and f_k, k = 1, …, m be the densities of the distribution functions F, $C_{1,\dots ,m},$ and F_m, respectively; then,

$$\begin{gathered} f\left(x_1, \dots , x_m\right)=\frac{{\partial }^{m}F\left(x_1, \dots , x_m\right)}{\partial x_1\dots \partial x_m}=\frac{{\partial }^m{C}_{1,\dots ,m}\left(F_1\left(x_1\right), \dots , F_m(x_m)\right)}{\partial x_1\dots \partial x_m} \\ ={\left.\frac{{\partial }^m{C}_{1,\dots ,m}\left(u_1, \dots , u_m\right)}{\partial u_1\dots \partial u_m}\right|}_{u_k=F\left(x_k\right)}{\displaystyle \prod }_{k=1}^{m}f\left(x_k\right) \\ =c_{1,\dots ,m}\left(F_1\left(x_1\right), \dots , F_m(x_m|P\right){{\displaystyle \prod }}_{k=1}^{m}f\left(x_k\right). \end{gathered}$$

(23)

Recently, many different copula-type functions have been analyzed. In this article, we limit ourselves to the multi-dimensional normal copula function up to five dimensions, since five different distributions were derived, which are defined by Equations (6)–(10). A normal copula is elliptical and symmetric, which gives it excellent analytical properties that are entirely determined by its correlation matrix [41]. For the specified correlation matrix P, the m-dimensional (m = 1, …, 5) normal copula $C_{1,\dots ,m}: {\left[0,1\right]}^m\to R$ can be written as

$$C_{1,\dots ,m}\left(u_1, \dots ,u_m|P \right)={\Phi }_m\left({\Phi }^{-1}\left(u_1\right), \dots ,{\Phi }^{-1}\left(u_m\right) \right),$$

(24)

where ${\Phi }^{-1}$ is the inverse cumulative distribution function of the standard normal distribution, and ${\Phi }_m$ is the m-dimensional normal cumulative distribution function with a mean vector μ and covariance matrix Σ. According to the basic principles of invariance properties (see [42]), the N_m (μ, Σ) copula is the same as N_m (0, P), where P is the correlation matrix corresponding to the covariance matrix Σ. So, the normal copula is determined using only the correlation matrix P. Although there is no simple analytical formula for the copula function, it can only be defined using integration, but the density can be written as

$$c_{1,\dots ,m}\left(u_1, \dots , u_m|P\right)=\frac{1}{\sqrt{\left|P\right|}}exp\left(-\frac{1}{2}{\left(\begin{array}{c}{\Phi }^{-1}\left(u_1\right)\\ ⋮\\ {\Phi }^{-1}\left(u_m\right)\end{array}\right)}^T·\left(P^{-1}-I\right)·\left(\begin{array}{c}{\Phi }^{-1}\left(u_1\right)\\ ⋮\\ {\Phi }^{-1}\left(u_m\right)\end{array}\right)\right),$$

(25)

where I is the identity matrix and P takes the form

$$P=\left(\begin{array}{cccc}1& {\rho }_{12}& \dots & {\rho }_{1m}\\ {\rho }_{12}& 1& \dots & {\rho }_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ {\rho }_{1m}& {\rho }_{2m}& \dots & 1\end{array}\right).$$

(26)

The classical maximum likelihood method can be successfully used to estimate the parameters of the joint density function (23). This procedure involves estimating all parameters simultaneously and can be computationally complex, as numerical optimization with a large number of parameters is time-consuming in practice. Alternatively, there is a two-step estimation of the copula model parameters that obtains estimates, in the first step, for the parameters of the marginal densities and, in the second step, assumes that the variables are independent, retrieving the copula density parameter estimates by maximizing

$$l\left(P\right)={{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{j=1}^{n_{ij}}ln\left(c_{1,\dots ,m}\left({\Phi }^{-1}\left(F_1\left(x_{1j}^i,t_j^i\right)\right),\dots ,{\Phi }^{-1}\left(F_m\left(x_{mj}^i,t_j^i\right)\right)\left|P\right.\right)\right),$$

(27)

where $F_m\left(x_m,t\right)={{\displaystyle \int }}_z^{x_m}{f}_m\left(y,t\right)dy$, $f_k\left(y,t\right)$, k = 1, …, 5 are defined by Equations (6)–(10); z = $\widehat{{\gamma }_k}$ if k = 1, 2, 3; z = −∞ if k = 4, 5.

This estimate still remains asymptotically normal [43]. The asymptotic standard errors of the normal copula density parameters are defined by the diagonal elements of the observed Fisher information matrix ${\left[FI\left(\widehat{P}\right)\right]}^{-1}$. By defining the matrix $\left[\frac{{\partial }^{2}l\left(P\right)}{\partial {\rho }_i\partial {\rho }_j}\right]$, the observed Fisher information matrix takes the following form

$$FI\left(\widehat{P}\right)={\left[-\frac{{\partial }^{2}l\left(P\right)}{\partial {\rho }_i\partial {\rho }_j}\right]}^T{|}_{P=\widehat{P}}$$

(28)

The asymptotic standard errors of the normal copula density parameters are defined

$$SE\left(\widehat{P}\right)=\sqrt{{\left[FI\left(\widehat{P}\right)\right]}^{-1}}$$

(29)

3. Results

3.1. Parameter Estimates

We used the MAPLE symbolic algebra system [44] to implement maximum likelihood procedures as well as assessments of the derived probability density functions, the normalized conditional entropies, and stand attributes models. It should be noted that standard statistical packages cannot be used to implement our proposed SDE models. The joint copula-type representation of the probability density function (23) implies the two-step maximum log-likelihood decomposition, namely, separately estimating the parameters of the marginal distributions defined by Equations (1) and (2) and the parameters of the copula defined by Equation (25). The first step estimates the approximated maximum log-likelihood contribution defined by Equations (16) and (17) from each margin (under the assumption of independence) using a random sample of discrete measurements of tree diameter (x₁), potentially available area (x₂), height (x₃), crown base height (x₄), and crown width $\left\{x_{j1}^i,x_{j2}^i,\dots ,x_{j{n}_{ij}}^i\right\}$, at discrete times $\left\{t_1^i,t_2^i,\dots ,t_{n_{ij}}^i\right\}$, i = 1, …, M, j = 1, …, 5. The second step estimates the contribution of the maximum log-likelihood defined by Equation (27) from the copula using a random sample of discrete measurements $\left\{\left(x_{11}^i,x_{21}^i,x_{31}^i,x_{41}^i,x_{51}^i\right),\left(x_{12}^i,x_{22}^i,x_{32}^i,x_{42}^i,x_{52}^i\right),\dots ,\left(x_{1n_{i1}}^i,x_{2n_{i2}}^i,x_{3n_{i3}}^i,x_{4n_{i4}}^i,x_{5n_{i5}}^i\right)\right\}$ at discrete times $\left\{t_1^i,t_2^i,\dots ,t_{n_{ij}}^i\right\}$, i = 1, …, M, j = 1, …, 5. The measurements of all observed trees were used to estimate the parameters of the stochastic differential Equation (1) that determine the growth of the tree diameter and potentially available area. Another smaller set of measurements was used to estimate the parameters of the tree height growth Equation (1). Finally, the smallest set of measurements was used to estimate the parameters of the tree crown base height and crown width growth Equation (2) and to estimate the dependence parameters matrix P. The parameter estimates of the stochastic differential Equations (1) and (2), and the parameters matrix P of the dependencies defined by Equation (26) for the copula-type probability density function using observed datasets from mixed-species, uneven stands in Lithuania (see

Table A1. Tree age, diameter, potentially available area, height, crown base height, and crown width summary statistics for model estimation.

Data Level	Data	Number of Trees	Min	Max	Mean	St. Dev.
First (48 plots)	t * (year)	39,437	12.0	211.0	59.25	26.36
	d (cm)	39,437	0.1	72.2	16.95	10.22
	p (m2)	39,437	0.09	173.82	10.37	8.95
Second (48 plots)	t (year)	8804	12.0	211.0	52.88	29.93
	h (cm)	8604	1.30	38.00	15.62	9.16
Third (31 plots)	t (year)	1378	46.0	211.0	83.98	24.39
	d (cm)	1378	3.20	62.40	24.12	10.38
	p (m2)	1378	1.37	161.51	15.27	11.57
	h (m)	1378	1.30	37.80	22.73	6.84
	hc (m)	1378	0.90	29.70	14.85	6.39
	wc (m)	1378	0.58	115.84	12.00	9.94

* t—tree age, d—tree diameter, p—tree potentially available area (the area of the polygon formed by the Voronoi diagram [26]), h—tree height, hc—tree crown base height, wc—tree crown width.

) are presented in

Table 1. Parameter estimates (standard errors) for mixed-effect mode of the stochastic differential Equations (1) and (2).

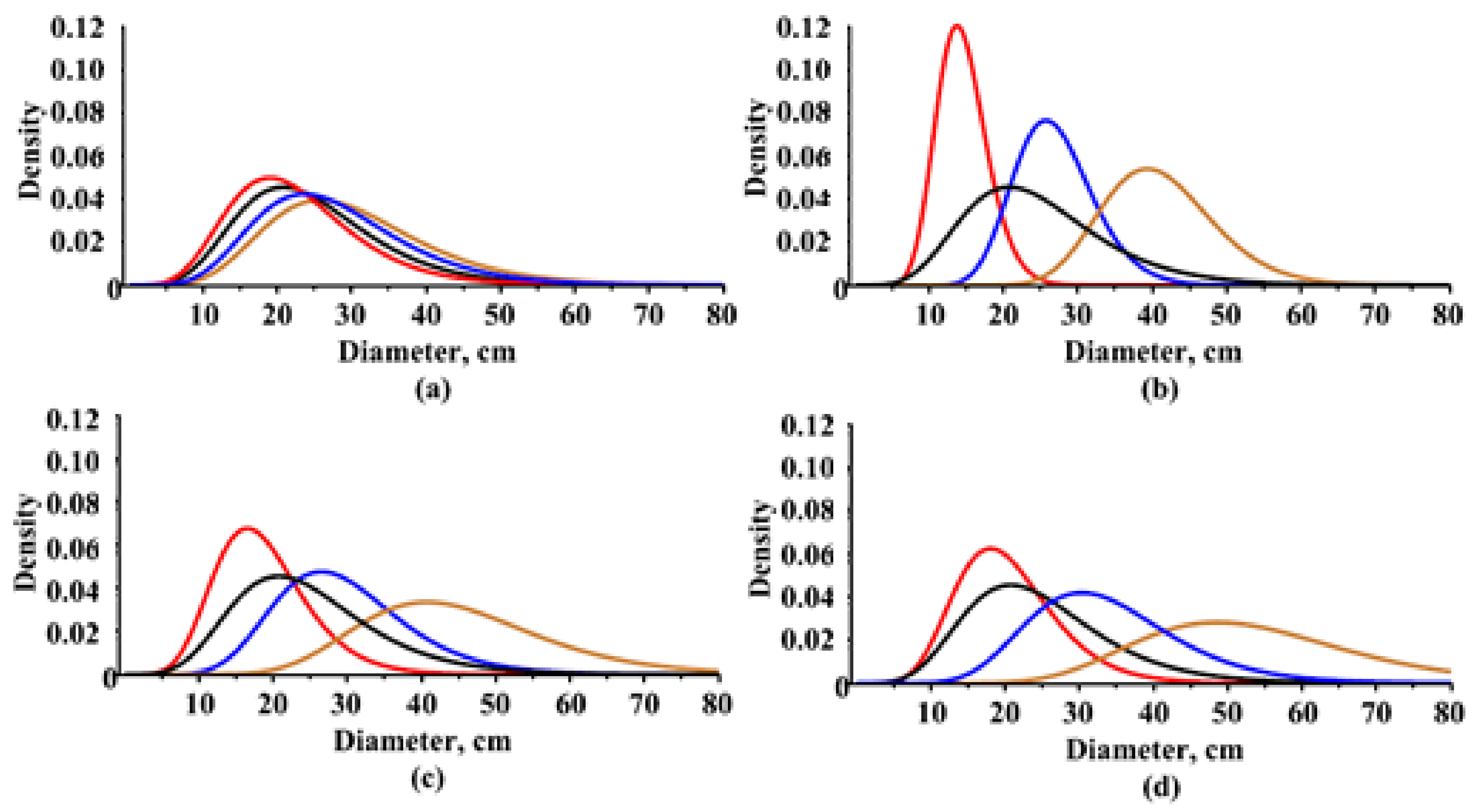
Equations	α	β	ɣ	σ	δ	σϕ
Diameter	0.0850 (0.0007)	0.0226 (0.0002)	−7.1108 (0.0954)	0.0042 (6.8 × 10−5)	-	0.0069 (0.0010)
Potentially available area	0.0617 (0.0006)	0.0182 (0.0002)	−1.3259 (0.0358)	0.0102 (0.0001)	1.6151 (0.0237)	0.0094 (0.0014)
Height	0.0827 (0.0011)	0.0213 (0.0003)	−13.1583 (0.3489)	0.0013 (4.8 × 10−5)	-	0.0044 (0.0006)
Crown base height	18.1688 (0.4625)	0.0226 (0.0020)	-	1.3386 (0.1148)	-	4.4846 (0.5687)
Crown width	156.869 (15.8329)	0.0010 (0.0001)	-	1.0703 (0.0413)	-	33.9665 (3.6940)

and

Table 2. Parameter estimates (standard errors), ρ_ij, for copula probability density function.

	ρi1	ρi2	ρi3	ρi4	ρi5
1	1	0.2913 (0.0270)	0.8916 (0.0041)	0.6272 (0.0132)	0.6268 (0.0143)
2	0.2913 (0.0270)	1	0.2336 (0.0276)	0.0635 (0.0279)	0.3105 (0.0266)
3	0.8916 (0.0041)	0.2336 (0.0276)	1	0.7359 (0.0101)	0.4612 (0.0187)
4	0.6272 (0.0132	0.0635 (0.0279)	0.7359 (0.0101)	1	0.1618 (0.0237)
5	0.6268 (0.0143)	0.3105 (0.0266)	0.4612 (0.0187)	0.1618 (0.0237)	1

, respectively. All parameter estimates are significant (p < 0.05).

3.2. Joint and Conditional Densities

First, in this section, we review some of the most useful conditional probability density functions defined using five-, four-, three-, and two-dimensional copulas and the probability density functions defined by Equations (6)–(10) that can be successfully applied to relate the response variable to several remaining explanatory variables. We formalize the conditional density functions using the well-known Bayes’ rule. Second, we visually compare several two-dimensional probability density functions and assess which dependence is stronger.

The joint copula-type probability density function for two diffusion processes $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$ and $\left\{X_k^i\left(t\right)| t\in \left[t_0,T\right]\right\}$ for list $B_2=\left\{\left.j,k\right|j,k\in \left\{1,2,3,4,5\right\},j\ne k\right\}$, i = 1, …, M is defined as

$$f_{j,k}^i\left(x_j^i,x_k^i,t|\widehat{{\rho }_{jk}}\right)=c_{j,k}^i\left(G_j^i\left(x_j^i,t\right),G_k^i\left(x_k^i,t\right)|\widehat{{\rho }_{jk}}\right){{\displaystyle \prod }}_{l\in B_2}\widehat{f_l^i}\left(x_l^i,t\right).$$

(30)

where $\widehat{f_j^i}\left(x_j^i,t\right)=f_j^i\left(x_j^i,t\left|\widehat{{\theta }_j},\widehat{{\varphi }_j^i}\right.\right)$, $F_j^i\left(x_j^i,t\right)={{\displaystyle \int }}_z^{x_j^i}\widehat{f_j^i}\left(y,t\right)dy$, $z=\widehat{{ɣ}_j}$, if j = 1, 2, 3, z = −∞, if j = 4, 5 and $G_j^i\left(x_j^i,t\right)={\Phi }^{-1}\left(F_j^i\left(x_j^i,t\right)\right)$.

The joint copula-type probability density function for three diffusion processes $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, $\left\{X_k^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, and $\left\{X_m^i\left(t\right)| t\in \left[t_0,T\right]\right\}$ for list $B_3=\left\{\left.j,k,m\right|j,k,m\in \left\{1,2,3,4,5\right\},j\ne k\ne m\right\}$, i = 1, …, M is defined as

$$f_{j,k,m}^i\left(x_j^i,x_k^i,x_m^i,t|\widehat{P}\right)=c_{j,k,m}^i\left(G_j^i\left(x_j^i,t\right),G_k^i\left(x_k^i,t\right),G_m^i\left(x_m^i,t\right)|\widehat{P}\right){{\displaystyle \prod }}_{l\in B_3}\widehat{f_l^i}\left(x_l^i,t\right).$$

(31)

The joint copula-type probability density function for four diffusion processes $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, $\left\{X_k^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, $\left\{X_m^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, and $\left\{X_n^i\left(t\right)| t\in \left[t_0,T\right]\right\}$ for list for list $B_4=\left\{\left.j,k,m,n\right|j,k,m,n\in \left\{1,2,3,4,5\right\},j\ne k\ne m\ne n\right\}$, i = 1, …, M is defined as

$$f_{j,k,m,n}^i\left(x_j^i,x_k^i,x_m^i,x_n^i,t|\widehat{P}\right)=c_{j,k,m,n}^i\left(G_j^i\left(x_j^i,t\right),G_k^i\left(x_k^i,t\right),G_m^i\left(x_m^i,t\right),G_n^i\left(x_n^i,t\right)|\widehat{P}\right){\displaystyle \prod }_{l\in B_4}\widehat{f_l^i}\left(x_l^i,t\right)$$

(32)

The joint copula-type probability density function for all five diffusion processes is defined as

$$f_{1,2,3,4,5}^i\left(x_1^i,x_2^i,x_3^i,x_4^i,x_5^i,t|\widehat{P}\right)=c_{1,2,3,4,5}^i\left(G_1^i\left(x_1^i,t\right),G_2^i\left(x_2^i,t\right),G_3^i\left(x_3^i,t\right),G_4^i\left(x_4^i,t\right),G_5^i\left(x_5^i,t\right)|\widehat{P}\right){\displaystyle \prod }_{j=1}^5\widehat{f_j^i}\left(x_j^i,t\right).$$

(33)

The conditional probability density function for diffusion process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M given $\left\{X_k^i\left(t\right)=x_k^i| t\in \left[t_0,T\right]\right\}$, $k\in \left\{1,2,3,4,5\right\}\backslash j$ is defined as

$$f_{j|k}^i\left(x_j^i,t|\widehat{{\rho }_{jk}},x_k^i\right)=c_{j,k}^i\left(G_j^i\left(x_j^i,t\right),G_k^i\left(x_k^i,t\right)|\widehat{{\rho }_{jk}}\right)\widehat{f_j^i}\left(x_j^i,t\right).$$

(34)

The conditional probability density function for diffusion process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M, given $\left\{X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i| t\in \left[t_0,T\right]\right\}$, $k,m\in \left\{1,2,3,4,5\right\}\backslash j$ is defined as

$$f_{j|k,m}^i\left(x_j^i,t|\widehat{P},x_k^i,x_m^i\right)=\frac{c_{j,k,m}^i\left(G_j^i\left(x_j^i,t\right),G_k^i\left(x_k^i,t\right),G_m^i\left(x_m^i,t\right)|\widehat{P}\right)\widehat{f_j^i}\left(x_j^i,t\right)}{c_{k,m}^i\left(G_k^i\left(x_k^i,t\right),G_m^i\left(x_m^i,t\right)|\widehat{{\rho }_{km}}\right)}.$$

(35)

The conditional probability density function for diffusion process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M, given $\left\{X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i,X_n^i\left(t\right)=x_n^i| t\in \left[t_0,T\right]\right\}$, $k,m,n\in \left\{1,2,3,4,5\right\}\backslash j$ is defined as

$$\begin{gathered} f_{j|k,m,n}^i\left(x_j^i,t|\widehat{P},x_k^i,x_m^i,x_n^i\right) \\ =\frac{c_{j,k,m,n}^i\left(G_j^i\left(x_j^i,t\right),G_k^i\left(x_k^i,t\right),G_m^i\left(x_m^i,t\right),G_n^i\left(x_n^i,t\right)|\widehat{P}\right)\widehat{f_j^i}\left(x_j^i,t\right)}{c_{k,m,n}^i\left(G_k^i\left(x_k^i,t\right),G_m^i\left(x_m^i,t\right),G_n^i\left(x_n^i,t\right)|\widehat{P}\right)} \end{gathered}$$

(36)

The conditional probability density function for diffusion process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M, given $\left\{X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i,X_n^i\left(t\right)=x_n^i,X_s^i\left(t\right)=x_s^i| t\in \left[t_0,T\right]\right\}$, $k,m,n,s\in \left\{1,2,3,4,5\right\}\backslash j$ is defined as

$$\begin{gathered} f_{j|k,m,n,s}^i\left(x_j^i,t|\widehat{P},x_k^i,x_m^i,x_n^i,x_s^i\right) \\ =\frac{c_{j,k,m,n,s}^i\left(G_j^i\left(x_j^i,t\right),G_k^i\left(x_k^i,t\right),G_m^i\left(x_m^i,t\right),G_n^i\left(x_n^i,t\right),G_s^i\left(x_s^i,t\right)|\widehat{P}\right)\widehat{f_j^i}\left(x_j^i,t\right)}{c_{k,m,n,s}^i\left(G_k^i\left(x_k^i,t\right),G_m^i\left(x_m^i,t\right),G_n^i\left(x_n^i,t\right),G_s^i\left(x_s^i,t\right)|\widehat{P}\right)}. \end{gathered}$$

(37)

The statistical dependence of the observed multivariate dataset is the relationship between any two or more measured random variables. The dependency structure is important to determine the adequacy of a particular mathematical model to represent the observed dataset. The simplest visual way to assess the independence of two random variables is to visually check whether a change in the values of one variable affects the distribution of the values of the other variable. To see the independence of the variables in a graph, we used a graph of conditional distributions for different values of the explanatory variable. Figure 1a–d shows the conditional probability density functions of the tree diameter defined by Equation (34) as functions of the tree potentially available area, height, crown base height, and crown width, respectively.

The dependence of the tree diameter on the potentially available area, height, crown base height, and crown area is shown in Figure 1a–d by plotting the marginal diameter probability density function and conditional density functions at three different values of an exploratory variable (potentially available area, height, crown base height, and crown area). Obviously, those three conditional densities are different, which confirms that the tree diameter behaves differently when conditioned on different values of an explanatory variable. This is another way to make sure that the tree diameter and other explanatory variables under analysis are dependent. As can be seen in Figure 1, the smallest influence on the development of the tree diameter is provided by its potentially available area (see Figure 1a), while the height has the greatest influence on the tree diameter, because not only the bias of the distribution is changed but also the shape changes significantly. Moreover, the probability density function of the tree diameter becomes flatter as the values of any explanatory variable increase, indicating an increase in variance.

Similar conclusions can be drawn from the values of the Pearson linear correlation presented in the first row of Table 2. We can see that the strongest linear relationship is between the tree diameter and height, and the weakest relationship is between the tree diameter and the area it occupies.

4. Discussion

The comparisons among the conditional probability density functions for the tree diameter shown in Figure 1 indicate that all explanatory variables significantly change the conditional probability density functions of the tree diameter. Visually, the maximum differences between the conditional probability density functions of the diameter and the marginal probability density function of the diameter revealed that height is an explanatory variable. The reason for the biggest difference is due to the greatest influence of height on the evolution of tree diameter.

The best fitting of the conditional probability density functions defined by Equations (34)–(37) could include integrated plotting functions, such as a histogram, along with the estimated probability density functions and Q–Q plots. Since conditional probability density functions defined by Equations (34)–(37) functionally depend on random effects for different population individuals (plots), they are difficult to use to compare distribution models, even in the case of normal random effects. The output of this comparative analysis of densities was determining which list of explanatory variables best improves the fit of the response variable to the set of observational data obtained during the measurements.

Entropy is the most appropriate concept for comparing the uncertainty of multi-dimensional probability density functions [45]. In addition, the conditional probability densities of the response variable may face the redundancy of the explanatory variables. The Shannon differential entropy [46] of the probability density function $f\left(x,y\right)$ for two random variables X and Y, whose support is a set $X\times Y$ and is written as

$$\begin{gathered} H\left(X,Y\right)=-{{\displaystyle \int }}_{XxY}f\left(x,y\right)lo{g}_{2}f\left(x,y\right)dxdy \\ =H\left(X/Y\right)+H\left(Y\right) \end{gathered}$$

(38)

For two random variables X and Y, $H\left(X/Y\right)\le H\left(X\right)$ with equality if and only if X and Y are independent. In this study, the parameters of the marginals and copula densities were estimated by a two-stage approximated maximum likelihood procedure (see Table 1 and

Table 3. Normalized information indices $R_{1/·}$ (Equations (48)–(51)) and ${\overline{R}}_{1/·}$ (Equations (52)–(55)).

k	2	3	4	5
$R_{1/k}$	0.48694	0.52886	0.47929	0.52043
${\overline{R}}_{1/k}$	0.66816	0.73356	0.68590	0.68535
k, m	2, 3	2, 4	2, 5	3, 4	3, 5	4, 5
$R_{1/k,m}$	0.69803	0.66093	0.67514	0.67547	0.71624	0.68761
${\overline{R}}_{1/k,m}$	0.81637	0.78519	0.78232	0.81561	0.82636	0.80151
k, m, n	2, 3, 4	2, 3, 5	2, 4, 5	3, 4, 5
$R_{1/k,m,n}$	0.76585	0.79030	0.76747	0.77910
${\overline{R}}_{1/k,m,n}$	0.81653	0.82653	0.80227	0.82658
k, m, n, s	2, 3, 4, 5
$R_{1/k,m,n,s}$	0.79949
${\overline{R}}_{1/k,m,n,s}$	0.79949

). The conditional and multi-dimensional differential entropies were computed for the estimated probability density functions defined by Equations (34)–(37) and (30)–(33), respectively. Here, the entropies were estimated using

$$H\left(X,Y\right)=-E\left(lo{g}_{2}f\left(x,y\right)\right)$$

(39)

which takes the following forms for the two-, three-, four-, and five-dimensional probability density functions (30)–(33):

$$H\left(X_j,X_k\right)=-{{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{v=1}^{n_i}{log}_2\left(f_{j,k}^i\left(x_{jv}^i,x_{kv}^i,t_v^i|\widehat{{\rho }_{jk}}\right)\right), j,k\in \left\{1,2,3,4,5\right\}$$

(40)

$$H\left(X_j,X_k,X_m\right)=-{{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{v=1}^{n_i}{log}_2\left(f_{j,k,m}^i\left(x_{jv}^i,x_{kv}^i,x_{mv}^i,t_v^i|\widehat{P}\right)\right), j,k,m\in \left\{1,2,3,4,5\right\}$$

(41)

$$H\left(X_j,X_k,X_m,X_n\right)=-{{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{v=1}^{n_i}{log}_2\left(f_{j,k,m,n}^i\left(x_{jv}^i,x_{kv}^i,x_{mv}^i,x_{nv}^i,t_v^i|\widehat{P}\right)\right), j,k, m, n\in \left\{1,2,3,4,5\right\}$$

(42)

$$H\left(X_1,X_2,X_3,X_4,X_5\right)=-{\displaystyle \sum }_{i=1}^M{\displaystyle \sum }_{v=1}^{n_i}{log}_2\left(f_{1,2,3,4,5}^i\left(x_{1v}^i,x_{2v}^i,x_{3v}^i,x_{4v}^i,x_{5v}^i,t_v^i|\widehat{P}\right)\right)$$

(43)

For conditional probability density functions (34)–(37), j = 1, ….5, we have conditional entropies

$$H\left(X_j/X_k\right)=-{{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{v=1}^{n_i}{log}_2\left(f_{j|k}^i\left(x_{jv}^i,t|\widehat{{\rho }_{jk}},x_{kv}^i\right)\right), k\in \left\{1,2,3,4,5\right\}\backslash j$$

(44)

$$H\left(X_j/X_k,X_m\right)=-{{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{v=1}^{n_i}{log}_2\left(f_{j|k,m}^i\left(x_{jv}^i,t_v^i|\widehat{P},x_{kv}^i,x_{mv}^i\right)\right), k,m\in \left\{1,2,3,4,5\right\}\backslash j$$

(45)

$$H\left(X_j/X_k,X_m,X_n\right)=-{{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{v=1}^{n_i}{log}_2\left(f_{j|k,m,n}^i\left(x_{jv}^i,t_v^i|\widehat{P},x_{kv}^i,x_{mv}^i,x_{nv}^i\right)\right), j,k,m\in \left\{1,2,3,4,5\right\}\backslash j$$

(46)

$$H\left(X_j/X_k,X_m,X_n,X_s\right)=-{{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{v=1}^{n_i}{log}_2\left(f_{j|k,m,n,s}^i\left(x_{jv}^i,t_v^i|\widehat{P},x_{2v}^i,x_{3v}^i,x_{4v}^i,x_{5v}^i\right)\right), k,m,n,s\in \left\{1,2,3,4,5\right\}\backslash j$$

(47)

The purpose of selecting explanatory variables is to correctly select variables from a set of candidate variables containing all processes as input variables. Since we can combine the four remaining random processes for modeling the j-th stochastic process, it is possible to formalize mathematically a total of 2⁴ − 1 = 15 different nonlinear relationships. The relationships among the two-dimensional, marginal, and conditional entropies are shown in Figure 2.

From a theoretical interaction information measurement perspective, the theoretical values of entropy can take normalized forms [45]. In this paper, we introduce a new conditional entropy normalization method that uses multi-dimensional entropy as the denominator to adjust the conditional entropy value within [0, 1] (see Figure 2). Unlike the correlation metric, the conditional entropies defined by Equations (44)–(47) can be normalized, for each stochastic process j = 1, …, 5, as

$$R_{j/k}=1-\frac{H\left(X_j/X_k\right)}{H\left(X_j,X_k\right)}, k\in \left\{1,2,3,4,5\right\}\backslash j$$

(48)

$$R_{j/k,m}=1-\frac{H\left(X_j/X_k,X_m\right)}{H\left(X_j,X_k,X_m\right)}, k,m\in \left\{1,2,3,4,5\right\}\backslash j$$

(49)

$$R_{j/k,m,n}=1-\frac{H\left(X_j/X_k,X_m,X_n\right)}{H\left(X_j,X_k,X_m,X_n\right)}, j,k,m\in \left\{1,2,3,4,5\right\}\backslash j$$

(50)

$$R_{j/k,m,n,s}=1-\frac{H\left(X_j/X_k,X_m,X_n,X_s\right)}{H\left(X_j,X_k,X_m,X_n,X_s\right)}, j,k,m,n,s\in \left\{1,2,3,4,5\right\}\backslash j$$

(51)

It is noteworthy that the normalized interaction information indices defined by Equations (48)–(51) may be the definition of the informational measure of the dependency between the response variable and one explanatory variable, two explanatory variables, and three explanatory variables, respectively, but they are not sensitive to the entropy of the entire multi-dimensional process or the relations among them. From the application point of view, it is reasonable to change all normalizing denominators in Equations (48)–(51) to the entropy of all five random processes $X_1\left(t\right),X_2\left(t\right),X_3\left(t\right),X_4\left(t\right),X_5\left(t\right)$ in the following forms:

$${\overline{R}}_{j/k}=1-\frac{H\left(X_j/X_k\right)}{H\left(X_1,X_2,X_3,X_4,X_5\right)}, k\in \left\{1,2,3,4,5\right\}\backslash j$$

(52)

$${\overline{R}}_{j/k,m}=1-\frac{H\left(X_j/X_k,X_m\right)}{H\left(X_1,X_2,X_3,X_4,X_5\right)}, k,m\in \left\{1,2,3,4,5\right\}\backslash j$$

(53)

$${\overline{R}}_{j/k,m,n}=1-\frac{H\left(X_j/X_k,X_m,X_n\right)}{H\left(X_1,X_2,X_3,X_4,X_5\right)}, k,m, n\in \left\{1,2,3,4,5\right\}\backslash j$$

(54)

$${\overline{R}}_{j/k,m,n,s}=1-\frac{H\left(X_j/X_k,X_m,X_n,X_s\right)}{H\left(X_1,X_2,X_3,X_4,X_5\right)}, k,m,n,s\in \left\{1,2,3,4,5\right\}\backslash j$$

(55)

In forestry sciences, the ability to detect highly linked stochastic growth processes and their interactions might be very beneficial in understanding how trees in a stand interact and affect each other [47,48]. The normalized information indices calculated by Equations (52)–(55) for the stochastic growth process of tree diameter are presented in Table 3. The comparison of the normalized information index values $R_{1/k}$, $R_{1/k,m}$, and $R_{1/k,m,n}$ (see Table 3) supports the conclusion that the stochastic tree height growth process is the best fit among all models with one explanatory variable; the stochastic tree height and crown width growth processes are the best fit among all models with two explanatory variables; and the stochastic tree potentially available area, height, and crown width growth processes are the best fit among all models with three explanatory variables. Similarly, comparing the values of the normalized information index ${\overline{R}}_{1/k}$, ${\overline{R}}_{1/k,m}$, and ${\overline{R}}_{1/k,m,n}$ showed that the stochastic growth processes of the tree potentially available area, height, and crown width are best suited for analyzing all possible combinations of explanatory variables.

The relationships among the growth processes of individual tree size components (for example, diameter) and other tree size components (for example, potentially available area, height, etc.) are very important tools for modeling stand productivity and increments because these models are very useful in formulating forest management plans [49,50]. The newly developed methodology of linking stochastic differential equations and the normal copula function makes it possible to formalize the evolution of individual components of tree size with respect to other components of tree size by using nonlinear relationships. Using the probability density functions (6)–(10), we define the dynamics of the mean, $m_j^{i }\left(t\right)$ i = 1, …, M, of the stochastic process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$ as follows:

$$\begin{array}{c}{m}_j^{i }\left(t\right)=E\left(X_j^i\left(t\right)\right)=exp\left({\mu }_j^i\left(t\right)+\frac{1}{2}{v}_j\left(t\right)\right),j=1,2,3\\ m_j^{i }\left(t\right)=E\left(X_j^i\left(t\right)\right)={\mu }_j^i\left(t\right),j=4,5\end{array}$$

(56)

Using the conditional probability density function (34) and the integration operation, we define the dynamics of the mean of the stochastic process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M, given $\left\{X_k^i\left(t\right)=x_k^i| t\in \left[t_0,T\right]\right\}$, $k\in \left\{1,2,3,4,5\right\}\backslash j,$ as follows:

$$m_j^{i }\left(x_k^i,t\right)=E\left(X_j^i\left(t\right)|X_k^i\left(t\right)=x_k^i\right)={{\displaystyle \int }}_{{{\rm Y}}_j}{x}_j^i·f_{j/k}^i\left(x_j^i,t|\widehat{{\rho }_{jk}},x_k^i\right)d{x}_j^i$$

(57)

where ${{\rm Y}}_{\mathrm{j}}$ is a support of the density function, ${{\rm Y}}_j=\left[{\widehat{\gamma }}_j,+\infty \right)$, j = 1, 2, 3, and ${{\rm Y}}_j=\left(-\infty ,+\infty \right)$, j = 4, 5.

Using the conditional probability density function (35) and the integration operation, we define the dynamics of the mean of the stochastic process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M, given $\left\{X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i| t\in \left[t_0,T\right]\right\}$, $k,m\in \left\{1,2,3,4,5\right\}\backslash j,$ as follows:

$$m_j^{i }\left(x_k^i,x_m^i,t\right)=E\left(X_j^i\left(t\right)|X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i\right)={{\displaystyle \int }}_{{{\rm Y}}_j}{x}_j^i·f_{j/k}^i\left(x_j^i,t|\widehat{P},x_k^i,x_m^i\right)d{x}_j^i$$

(58)

Using the conditional probability density function (36) and the integration operation, we define the dynamics of the mean of the stochastic process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M, given $\left\{X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i,X_n^i\left(t\right)=x_n^i| t\in \left[t_0,T\right]\right\}$, $k,m,n\in \left\{1,2,3,4,5\right\}\backslash j,$ as follows:

$$\begin{gathered} m_j^{i }\left(x_k^i,x_m^i,x_n^i,t\right)=E\left(X_j^i\left(t\right)|X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i,X_n^i\left(t\right)=x_n^i\right) \\ ={{\displaystyle \int }}_{{{\rm Y}}_j}{x}_j^i·f_{j/k}^i\left(x_j^i,t|\widehat{P},x_k^i,x_m^i,x_n^i\right)d{x}_j^i \end{gathered}$$

(59)

Using the conditional probability density function (37) and the integration operation, we define the dynamics of the mean of the stochastic process $\left\{X_j^i\left(t\right)| t\in \left[t_0,T\right]\right\}$, j = 1, …, 5, i = 1, …, M, given $\left\{X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i,X_n^i\left(t\right)=x_n^i,X_s^i\left(t\right)=x_s^i| t\in \left[t_0,T\right]\right\}$, $k,m,n,s\in \left\{1,2,3,4,5\right\}\backslash j,$ as follows:

$$\begin{array}{cc}{m}_j^{i }\left(x_k^i,x_m^i,x_n^i,x_s^i,t\right)& =E\left(X_j^i\left(t\right)|X_k^i\left(t\right)=x_k^i,X_m^i\left(t\right)=x_m^i,X_n^i\left(t\right)=x_n^i,X_s^i\left(t\right)=x_s^i\right)\\ & ={{\displaystyle \int }}_{{{\rm Y}}_j}{x}_j^i·f_{j/k}^i\left(x_j^i,t|\widehat{P},x_k^i,x_m^i,x_n^i,x_s^i\right)d{x}_j^i \end{array}$$

(60)

The calculated statistical indices, defined as the coefficient of determination and root mean square error for all tree diameter (j = 1) 15 models, defined by Equations (49)–(53), are summarized in

Table 4. Two statistical indices for fifteen different nonlinear models of the tree diameter (j = 1), defined by Equations (56)–(60), coefficient of determination, R², and root mean square error, RMSE.

Equation	Statistical Indices
(56)	R2	0.3678
	RMSE	8.2050
	k	2	3	4	5
(57)	R2	0.3931	0.8260	0.5367	0.5280
	RMSE	8.0855	4.3294	7.0631	7.1321
	k, m	2, 3	2, 4	2, 5	3, 4	3, 5	4, 5
(58)	R2	0.8312	0.5752	0.5309	0.8283	0.8360	0.6703
	RMSE	4.2645	6.7633	7.1102	4.3002	4.1997	5.9608
	k, m, n	2, 3, 4	2, 3, 5	2, 4, 5	3, 4, 5
(59)	R2	0.8323	0.8738 *	0.6687	0.8687
	RMSE	4.2497	3.6863 *	5.9758	3.7624
	k, m, n, s	2, 3, 4, 5
(60)	R2	0.8666
	RMSE	3.7898

* The best value of the statistical index in bold.

. The ranking of all 15 formulated nonlinear models defined by Equations (56)–(60) according to model fitness using statistical indices defined by the coefficient of determination and the root mean square error shows that this ranking corresponds to the above-discussed comparison of model adequateness by using the newly defined normalized interaction information index ${\overline{R}}_{j/·}$ j = 1, …, 5. Finally, we can conclude that to define the evolution of the mean tree diameter with three explanatory variables, it is appropriate to use the potentially available area, height, and crown width of the tree; with two explanatory variables, it is appropriate to use tree height and crown width; and with one explanatory variable, it is appropriate to use tree height.

Using Equations (39)–(60), analogous conclusions can be drawn for other components of tree size, such as potentially available area, height, crown base height, and crown area.

5. Conclusions

We emphasize that previously used multi-dimensional stochastic differential equation models are not a complete description of the dependence structure, and their practical realization faces a rather large number of calculations. The current work describes an alternative copula-based methodology for prediction models in growth-process research. Newly derived copula-type multi-dimensional and conditional probability density functions, defined by Equations (30)–(37), make it possible to predict not only the mean dynamics of individual stochastic processes X_j j = 1,…, 5 but also the corresponding means of other attributes, for example, in forestry, tree or stand basal area, tree or stand volume, tree slenderness, number of trees per hectare, and others. This study introduced the normalized multi-dimensional interaction information index based on differential entropy to capture dependencies between state variables. Using conditional copula-type probability density functions, the exact form equations defining the links among the diameter, potentially available area, height, crown base height, and crown width were derived. The main statistical advantage of copulas is the ability to model different datasets with any modified type of marginal distribution.

Future research could be related to the use of an asymmetric multivariate log-normal copula and covering a wider range of diffusion processes.