A Statistical Dependence Framework Based on a Multivariate Normal Copula Function and Stochastic Differential Equations for Multivariate Data in Forestry
Abstract
1. Introduction
2. Methods
2.1. Stochastic Differential Equations
2.2. Copulas and Dependence
3. Results
3.1. Parameter Estimates
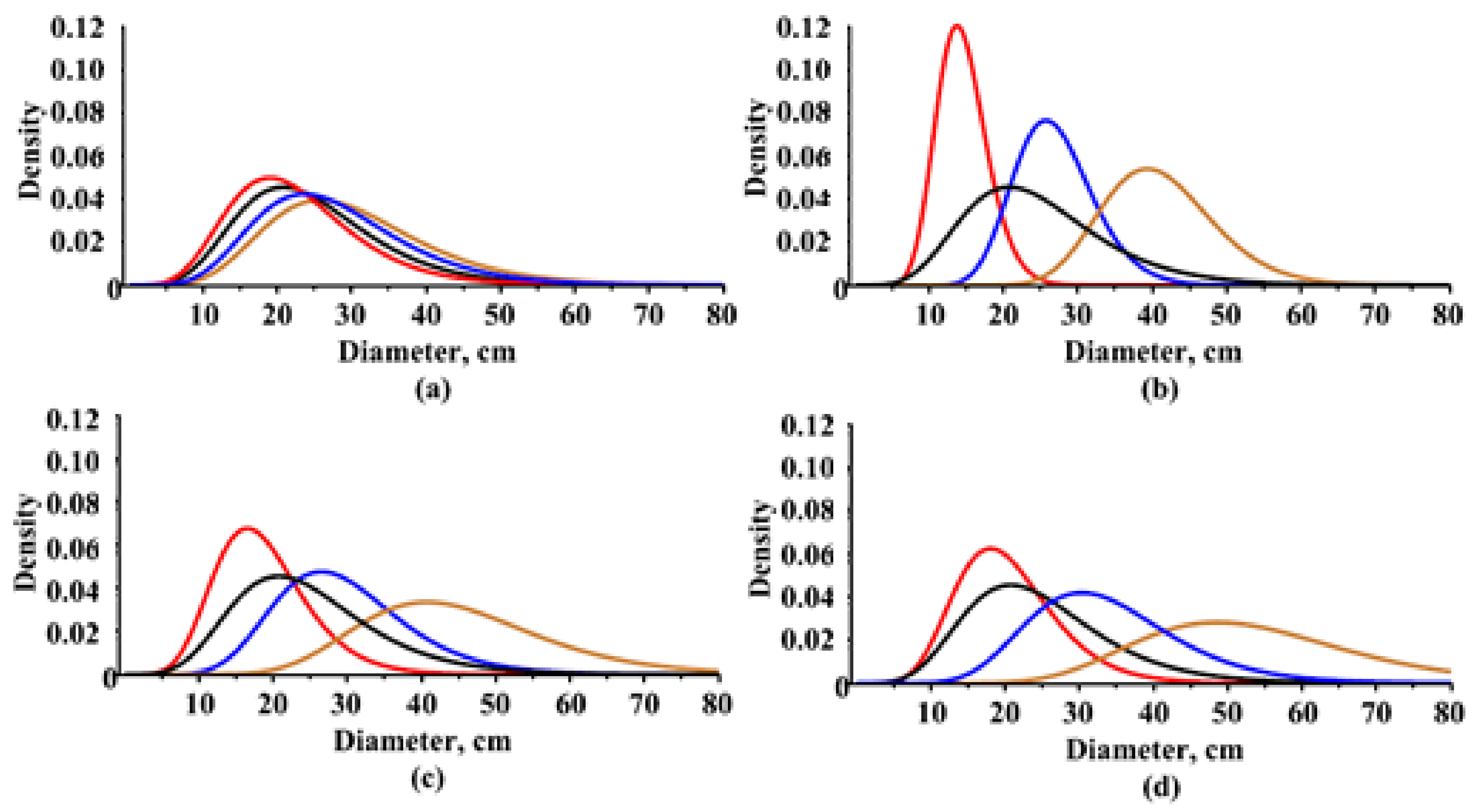
3.2. Joint and Conditional Densities
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Data
| Data Level | Data | Number of Trees | Min | Max | Mean | St. Dev. |
|---|---|---|---|---|---|---|
| First (48 plots) | t * (year) | 39,437 | 12.0 | 211.0 | 59.25 | 26.36 |
| d (cm) | 39,437 | 0.1 | 72.2 | 16.95 | 10.22 | |
| p (m2) | 39,437 | 0.09 | 173.82 | 10.37 | 8.95 | |
| Second (48 plots) | t (year) | 8804 | 12.0 | 211.0 | 52.88 | 29.93 |
| h (cm) | 8604 | 1.30 | 38.00 | 15.62 | 9.16 | |
| Third (31 plots) | t (year) | 1378 | 46.0 | 211.0 | 83.98 | 24.39 |
| d (cm) | 1378 | 3.20 | 62.40 | 24.12 | 10.38 | |
| p (m2) | 1378 | 1.37 | 161.51 | 15.27 | 11.57 | |
| h (m) | 1378 | 1.30 | 37.80 | 22.73 | 6.84 | |
| hc (m) | 1378 | 0.90 | 29.70 | 14.85 | 6.39 | |
| wc (m) | 1378 | 0.58 | 115.84 | 12.00 | 9.94 |
References
- Ginzburg, L.R. The theory of population dynamics: I. Back to first principles. J. Theor. Biol. 1986, 122, 385–399. [Google Scholar] [CrossRef]
- Turchin, P. Does population ecology have general laws? Oikos 2001, 94, 17–26. [Google Scholar] [CrossRef]
- Hara, T. A stochastic model and the moment dynamics of the growth and size distribution in plant populations. J. Theor. Biol. 1984, 109, 173–190. [Google Scholar] [CrossRef]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. A 1825, 115, 513–585. [Google Scholar]
- Verhulst, P.F. Deuxième mémoire sur la loi d’accroissement de la population. Mém. Acad. R. Sci. Lett. B Arts Belg. 1847, 20, 142–173. [Google Scholar]
- Zeide, B. Analysis of Growth Equations. For. Sci. 1993, 39, 594–616. [Google Scholar] [CrossRef]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994; 312p. [Google Scholar]
- Yanishevskyi, V.S.; Baranovska, S.P. Path integral method for stochastic equations of financial engineering. Math. Model. Comput. 2022, 9, 166–177. [Google Scholar] [CrossRef]
- Shao, Y. Dynamics of an Impulsive Stochastic Predator–Prey System with the Beddington–DeAngelis Functional Response. Axioms 2021, 10, 323. [Google Scholar] [CrossRef]
- Petrauskas, E.; Bartkevičius, E.; Rupšys, P.; Memgaudas, R. The use of stochastic differential equations to describe stem taper and volume. Baltic For. 2013, 19, 43–151. [Google Scholar]
- Madheswaran, M.; Lingaraja, K.; Duraisamy, P. Econometric and stochastic analysis of stock price before and during COVID-19 in India. Environ. Dev. Sustain. 2023, 1–16. [Google Scholar] [CrossRef]
- Ali, I.; Khan, S.U. A Dynamic Competition Analysis of Stochastic Fractional Differential Equation Arising in Finance via Pseudospectral Method. Mathematics 2023, 11, 1328. [Google Scholar] [CrossRef]
- Bonaccorsi, S.; Ottaviano, S. A stochastic differential equation SIS model on network under Markovian switching. Stoch. Anal. Appl. 2022, 1–29. [Google Scholar] [CrossRef]
- García, O. New class of growth models for even-aged stands: Pinus radiata in Golden Downs Forest. N. Z. J. For. Sci. 1984, 14, 65–88. [Google Scholar]
- Sloboda, B. Kolmogorow–Suzuki und die stochastische Differentialgleichung als Beschreibungsmittel der Bestandesevolution. Mitt. Forstl. Bundes Vers. Wien 1977, 120, 71–82. [Google Scholar]
- Suzuki, T. Forest transition as a stochastic process (I). J. Jpn. For. Sci. 1966, 48, 436–439. [Google Scholar]
- Narmontas, M.; Rupšys, P.; Petrauskas, E. Models for Tree Taper Form: The Gompertz and Vasicek Diffusion Processes Framework. Symmetry 2020, 12, 80. [Google Scholar] [CrossRef]
- Garcia, O. A parsimonious dynamic stand model for interior spruce in British Columbia. For. Sci. 2011, 57, 265–280. [Google Scholar]
- Rupšys, P. Generalized fixed-effects and mixed-effects parameters height–diameter models with diffusion processes. Int. J. Biomath. 2015, 8(5), 1550060. [Google Scholar] [CrossRef]
- Rupšys, P. Modeling Dynamics of Structural Components of Forest Stands Based on Trivariate Stochastic Differential Equation. Forests 2019, 10, 506. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Analysis of Longitudinal Forest Data on Individual-Tree and Whole-Stand Attributes Using a Stochastic Differential Equation Model. Forests 2022, 13, 425. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A.; Pascual, A. Detection, modelling and estimation of non-linear trends by using a non-homogeneous Vasicek stochastic diffusion. Application to CO2 emissions in Morocco. Stoch. Environ. Res. Risk Assess. 2011, 26, 533–543. [Google Scholar] [CrossRef]
- Vasicek, O.A. The distribution of loan portfolio value. Risk 2002, 15, 160–162. [Google Scholar]
- Román-Román, P.; Serrano-Pérez, J.J.; Torres-Ruiz, F. A Note on Estimation of Multi-Sigmoidal Gompertz Functions with Random Noise. Mathematics 2019, 7, 541. [Google Scholar] [CrossRef]
- Barrera, A.; Román-Román, P.; Torres-Ruiz, F. Hyperbolastic Models from a Stochastic Differential Equation Point of View. Mathematics 2021, 9, 1835. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Symmetric and Asymmetric Diffusions through Age-Varying Mixed-Species Stand Parameters. Symmetry 2021, 13, 1457. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Bhatti, M.I.; Do, H.Q. Development in Copula Applications in Forestry and Environmental Sciences. In Statistical Methods and Applications in Forestry and Environmental Sciences; Springer Nature: Singapore, 2020; Volume 13386, pp. 213–231. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. On the Construction of Growth Models via Symmetric Copulas and Stochastic Differential Equations. Symmetry 2022, 14, 2127. [Google Scholar] [CrossRef]
- Liu, J.; Wan, Y.; Qu, S.; Qing, R.; Sriboonchitta, S. Dynamic Correlation between the Chinese and the US Financial Markets: From Global Financial Crisis to COVID-19 Pandemic. Axioms 2023, 12, 14. [Google Scholar] [CrossRef]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. A 1922, 222, 309–368. [Google Scholar]
- Rupšys, P.; Petrauskas, E. Modeling Number of Trees per Hectare Dynamics for Uneven-Aged, Mixed-Species Stands Using the Copula Approach. Forests 2023, 14, 12. [Google Scholar] [CrossRef]
- Mackevičius, V. Introduction to Stochastic Analysis: Integrals and Differential Equations; ISTE: Washington, DC, USA; Wiley: London, UK, 2011. [Google Scholar] [CrossRef]
- Uhlenbeck, G.E.; Ornstein, L.S. On the Theory of Brownian Motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- García, O. Estimating reducible stochastic differential equations by conversion to a least-squares problem. Comput. Stat. 2019, 34, 23–46. [Google Scholar] [CrossRef]
- Shoji, I.; Ozaki, T. A statistical method of estimation and simulation for systems of stochastic differential equations. Biometrika 1998, 85, 240–243. [Google Scholar] [CrossRef]
- Han, Y.; Yin, Z.; Zhang, D. Parameter Estimation of Linear Stochastic Differential Equations with Sparse Observations. Symmetry 2022, 14, 2500. [Google Scholar] [CrossRef]
- Picchini, U.; Ditlevsen, S. Practical estimation of high dimensional stochastic differential mixed-effectsmodels. Comput. Stat. Data Anal. 2011, 55, 1426–1444. [Google Scholar] [CrossRef]
- Joe, H. Accuracy of Laplace approximation for discrete response mixed models. Comput. Stat. Data Anal. 2008, 52, 5066–5074. [Google Scholar] [CrossRef]
- Rao, C.R. Linear Statistical Inference and Its Applications; Wiley: New York, NY, USA, 1965. [Google Scholar]
- Ashrafi, M.; Soltanian-Zadeh, H. Multivariate Gaussian Copula Mutual Information to Estimate Functional Connectivity with Less Random Architecture. Entropy 2022, 24, 631. [Google Scholar] [CrossRef] [PubMed]
- McNeil, J.; Frey, R.; Embrechts, P. Quantitative Risk Management; Princeton Series in Finance; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Joe, H. Asymptotic efficiency of the two-stage estimation method for copula based models. J. Multivar. Anal. 2005, 94, 401–419. [Google Scholar] [CrossRef]
- Monagan, M.B.; Geddes, K.O.; Heal, K.M.; Labahn, G.; Vorkoetter, S.M.; Mccarron, J. Maple Advanced Programming Guide; Maplesoft: Waterloo, ON, Canada, 2007. [Google Scholar]
- Rupšys, P. Understanding the Evolution of Tree Size Diversity within the Multivariate nonsymmetrical Diffusion Process and Information Measures. Mathematics 2019, 7, 761. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- DSouza, A.M.; Abidin, A.Z.; Leistritz, L.; Wismüller, A. Exploring connectivity with large-scale Granger causality on resting-state functional MRI. J. Neurosci. Methods 2017, 287, 68–79. [Google Scholar] [CrossRef]
- Islam, M.R.; Ahmed, B.; Hossain, M.A.; Uddin, M.P. Mutual Information-Driven Feature Reduction for Hyperspectral Image Classification. Sensors 2023, 23, 657. [Google Scholar] [CrossRef] [PubMed]
- Gavrikov, V.L.; Fertikov, A.I.; Vidus, V.E.; Sharafutdinov, R.A.; Vaganov, E.A. Elemental Variability in Stems of Pinus sylvestris L.: Whether a Single Core Can Represent All the Stem. Diversity 2023, 15, 281. [Google Scholar] [CrossRef]
- Seo, Y.; Lee, D.; Choi, J. Developing and Comparing Individual Tree Growth Models of Major Coniferous Species in South Korea Based on Stem Analysis Data. Forests 2023, 14, 115. [Google Scholar] [CrossRef]
| Equations | α | β | ɣ | σ | δ | σϕ |
|---|---|---|---|---|---|---|
| Diameter | 0.0850 (0.0007) | 0.0226 (0.0002) | −7.1108 (0.0954) | 0.0042 (6.8 × 10−5) | - | 0.0069 (0.0010) |
| Potentially available area | 0.0617 (0.0006) | 0.0182 (0.0002) | −1.3259 (0.0358) | 0.0102 (0.0001) | 1.6151 (0.0237) | 0.0094 (0.0014) |
| Height | 0.0827 (0.0011) | 0.0213 (0.0003) | −13.1583 (0.3489) | 0.0013 (4.8 × 10−5) | - | 0.0044 (0.0006) |
| Crown base height | 18.1688 (0.4625) | 0.0226 (0.0020) | - | 1.3386 (0.1148) | - | 4.4846 (0.5687) |
| Crown width | 156.869 (15.8329) | 0.0010 (0.0001) | - | 1.0703 (0.0413) | - | 33.9665 (3.6940) |
| ρi1 | ρi2 | ρi3 | ρi4 | ρi5 | |
|---|---|---|---|---|---|
| 1 | 1 | 0.2913 (0.0270) | 0.8916 (0.0041) | 0.6272 (0.0132) | 0.6268 (0.0143) |
| 2 | 0.2913 (0.0270) | 1 | 0.2336 (0.0276) | 0.0635 (0.0279) | 0.3105 (0.0266) |
| 3 | 0.8916 (0.0041) | 0.2336 (0.0276) | 1 | 0.7359 (0.0101) | 0.4612 (0.0187) |
| 4 | 0.6272 (0.0132 | 0.0635 (0.0279) | 0.7359 (0.0101) | 1 | 0.1618 (0.0237) |
| 5 | 0.6268 (0.0143) | 0.3105 (0.0266) | 0.4612 (0.0187) | 0.1618 (0.0237) | 1 |
| k | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|
| 0.48694 | 0.52886 | 0.47929 | 0.52043 | |||
| 0.66816 | 0.73356 | 0.68590 | 0.68535 | |||
| k, m | 2, 3 | 2, 4 | 2, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.69803 | 0.66093 | 0.67514 | 0.67547 | 0.71624 | 0.68761 | |
| 0.81637 | 0.78519 | 0.78232 | 0.81561 | 0.82636 | 0.80151 | |
| k, m, n | 2, 3, 4 | 2, 3, 5 | 2, 4, 5 | 3, 4, 5 | ||
| 0.76585 | 0.79030 | 0.76747 | 0.77910 | |||
| 0.81653 | 0.82653 | 0.80227 | 0.82658 | |||
| k, m, n, s | 2, 3, 4, 5 | |||||
| 0.79949 | ||||||
| 0.79949 |
| Equation | Statistical Indices | ||||||
|---|---|---|---|---|---|---|---|
| (56) | R2 | 0.3678 | |||||
| RMSE | 8.2050 | ||||||
| k | 2 | 3 | 4 | 5 | |||
| (57) | R2 | 0.3931 | 0.8260 | 0.5367 | 0.5280 | ||
| RMSE | 8.0855 | 4.3294 | 7.0631 | 7.1321 | |||
| k, m | 2, 3 | 2, 4 | 2, 5 | 3, 4 | 3, 5 | 4, 5 | |
| (58) | R2 | 0.8312 | 0.5752 | 0.5309 | 0.8283 | 0.8360 | 0.6703 |
| RMSE | 4.2645 | 6.7633 | 7.1102 | 4.3002 | 4.1997 | 5.9608 | |
| k, m, n | 2, 3, 4 | 2, 3, 5 | 2, 4, 5 | 3, 4, 5 | |||
| (59) | R2 | 0.8323 | 0.8738 * | 0.6687 | 0.8687 | ||
| RMSE | 4.2497 | 3.6863 * | 5.9758 | 3.7624 | |||
| k, m, n, s | 2, 3, 4, 5 | ||||||
| (60) | R2 | 0.8666 | |||||
| RMSE | 3.7898 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krikštolaitis, R.; Mozgeris, G.; Petrauskas, E.; Rupšys, P. A Statistical Dependence Framework Based on a Multivariate Normal Copula Function and Stochastic Differential Equations for Multivariate Data in Forestry. Axioms 2023, 12, 457. https://doi.org/10.3390/axioms12050457
Krikštolaitis R, Mozgeris G, Petrauskas E, Rupšys P. A Statistical Dependence Framework Based on a Multivariate Normal Copula Function and Stochastic Differential Equations for Multivariate Data in Forestry. Axioms. 2023; 12(5):457. https://doi.org/10.3390/axioms12050457
Chicago/Turabian StyleKrikštolaitis, Ričardas, Gintautas Mozgeris, Edmundas Petrauskas, and Petras Rupšys. 2023. "A Statistical Dependence Framework Based on a Multivariate Normal Copula Function and Stochastic Differential Equations for Multivariate Data in Forestry" Axioms 12, no. 5: 457. https://doi.org/10.3390/axioms12050457
APA StyleKrikštolaitis, R., Mozgeris, G., Petrauskas, E., & Rupšys, P. (2023). A Statistical Dependence Framework Based on a Multivariate Normal Copula Function and Stochastic Differential Equations for Multivariate Data in Forestry. Axioms, 12(5), 457. https://doi.org/10.3390/axioms12050457









