A Relational Semantics for Ockham’s Modalities
Abstract
1. Introduction
2. Ockham’s Account: De dicto/De re Distinction
In the sense of composition it is always asserted that such a mode is truly predicated of the proposition corresponding to the dictum in question. For example, by means of “That every man is an animal is necessary” it is asserted that the mode “necessary” is truly predicated of the proposition “Every man is an animal”, the dictum of which is “That every man is an animal” ([5] II, 9, 13–17, transl. p. 109).
However, the sense of division of such a proposition is always equipollent to a proposition taken with a mode and without such a dictum. For example, “That every man is an animal is necessary”; in the sense of division is equipollent to “Every man is of necessity (or necessarily) an animal”. ([5] II, 9, 19–23, transl. p. 109)
“It is necessary that every man is white” is true in the divided senseif and only if“This man (hoc) is white” and “That man is white”, etc., are all true and necessary(See [5] II, 10, 11–24).
An example: “both parts of a contradiction can be true” is false in the sense of composition and true in the sense of division, since each singular is true ([6], II, q. 5, 131 67–69, transl. p. 112).
- (a)
- A dictum is true and cannot be false: (), e.g., “every man is an animal”.
- (b)
- A dictum is false and cannot be true: (), e.g., “every white thing is a black thing”.
- (c)
- A dictum can be either true or false: (), e.g., “every man is white”.
3. Extension of Ockham’s Modal Squares
- A is ∀x (Sx Px);
- E is ∀x (Sx Px);
- I is ∃x (Sx Px);
- O is ∃x (Sx Px);
- A is ∀x (Sx Px);
- E is ∀x (Sx Px);
- I is ∃x (Sx Px);
- O is ∃x (Sx Px);
- .
- )
- It is contingent that every man is an animal = it is possible that every man is an animal, and it is possible that every man is not an animal.
- It is not contingent that every man is an animal = it is necessary that some man is an animal or it is necessary that some man is not an animal. (Note that the dicta “every man is an animal” and “some man is an animal” are of the form () and hence they are de dicto.)
- It is contingent that some man is white = some man can be white and some man can not be white.
- It is not contingent that some man is white = every man is necessarily white or every man is necessarily not white.
- De dicto
- De re
- De dicto
- De re
- A is
- E is
- I is
- O is
- Y is
- U is
- A is
- E is
- I is
- O is
- Z is
- K is
- Internal: e.g., “every S is possibly not P”.
- External: e.g., “not every S is possibly P” = “some S is possibly not P”.
4. Logical Analysis
4.1. Syntax
- : “It is necessary that … S is … P”(i) □A: “It is necessary that every S is P”(ii) □E: “It is necessary that every S is not P”(iii) □I: “It is necessary that some S is P”(iv) □O: “It is necessary that some S is not P”
- : “It is possible that … S is … P”(v) ⋄A: “It is possible that every S is P”(vi) ⋄E: “It is possible that every S is not P”(vii) ⋄I: “It is possible that some S is P”(viii) ⋄O: “It is possible that some S is not P”
- : “It is determinate that … S is … P”(ix) A: “It is determinate that every S is P”(x) E: “It is determinate that every S is not P”(xi) I: “It is determinate that some S is P”(xii) O: “It is determinate that some S is not P”
- : “It is contingent that … S is … P”(xiii) ∇A: “It is contingent that every S is P”(xiv) ∇E: “It is contingent that every S is not P”(xv) ∇I: “It is contingent that some S is P”(xvi) ∇O: “It is contingent that some S is not P”
- (i)
- □A:
- (ii)
- □E:
- (iii)
- □I:
- (iv)
- □O:
- (v)
- ⋄A:
- (vi)
- ⋄E:
- (vii)
- ⋄I:
- (viii)
- ⋄O:
- (ix)
- A:
- (x)
- E:
- (xi)
- I:
- (xii)
- O:
- (xiii)
- ∇A:
- (xiv)
- ∇E:
- (xv)
- ∇I:
- (xvi)
- ∇O:
- (xvii)
- A□:
- (xviii)
- A⋄:
- (xix)
- A:
- (xx)
- A∇:
- (xxi)
- E□:
- (xxii)
- E⋄:
- (xxiii)
- E:
- (xxiv)
- E∇:
- (xxv)
- I□:
- (xxvi)
- I⋄:
- (xxvii)
- I:
- (xxviii)
- I∇:
- (xxix)
- O□:
- (xxx)
- O⋄:
- (xxxi)
- O:
- (xxxii)
- O∇:
4.2. Semantics
4.2.1. Relational Statements
4.2.2. Relational Semantics
- 1 =
- 2 =
- 3 =
- 4 =
- 5 =
- 6 =
- 7 =
- 8 =
- 9 =
- 10 =
- 11 =
- 12 =
- 13 =
- 14 =
- 15 =
- 16 =
4.2.3. Numbering Semantics
- (1)
- (□A) = (A□) =
- (2)
- (□E) = (E□) =
- (3)
- (□I) = {1, 2, 3, 4, 5, 6, 8, 9, 11}
- (4)
- (□O) = {6, 8, 9, 11, 12, 13, 14, 15, 16}
- (5)
- (⋄A) = {1, 2, 3, 4, 5, 7, 10}
- (6)
- (⋄E) = {7, 10, 12, 13, 14, 15, 16}
- (7)
- (⋄I) = (I⋄) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
- (8)
- (⋄O) = (O⋄) = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}
- (9)
- (A) = (O) = {1, 6, 8, 9, 11, 12, 13, 14, 15, 16}
- (10)
- (E) = (I) = {1, 2, 3, 4, 5, 6, 8, 9, 11, 16}
- (11)
- (∇A) = (∇O) = {2, 3, 4, 5, 7, 10}
- (12)
- (∇E) = (∇I) = {7, 10, 12, 13, 14, 15}
- (13)
- (A⋄) = {1, 2, 3, 4, 5, 7, 8, 9, 10}
- (14)
- (A) = (E) = {1, 6, 11, 16}
- (15)
- (A∇) = (E∇) = {7, 8, 9, 10}
- (16)
- (E⋄) = {7, 8, 9, 10, 12, 13, 14, 15, 16}
- (17)
- (I□) = {1, 2, 3, 4, 5, 6, 11}
- (18)
- (I) = (O) = {1, 2, 3, 4, 5, 6, 11, 12, 13, 14, 15, 16}
- (19)
- (I∇) = (O∇) = {2, 3, 4, 5, 7, 8, 9, 10, 12, 13, 14, 15}
- (20)
- (O□) = {6, 11, 12, 13, 14, 15, 16}
4.2.4. Logical Relations
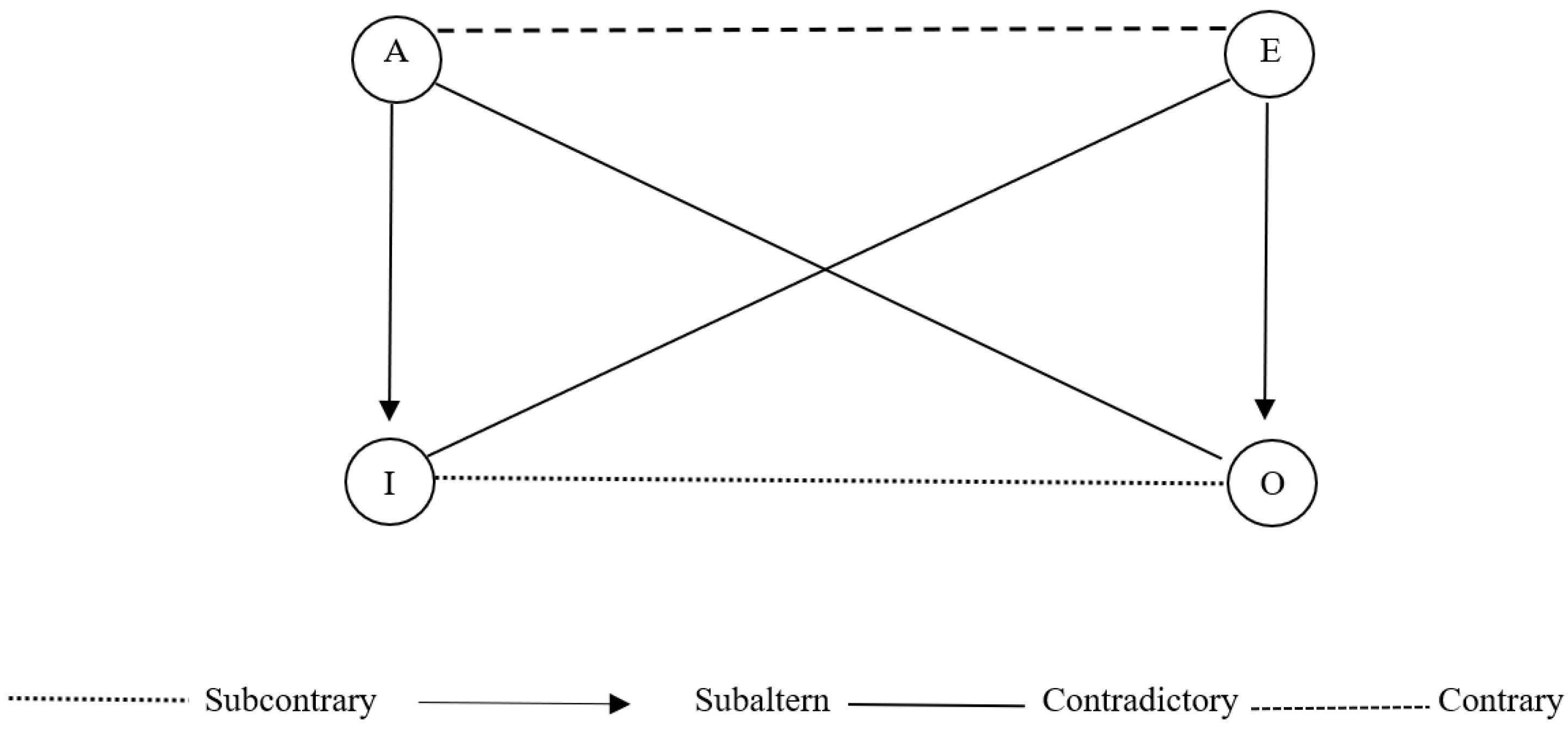
- X and Y are contraries (symbol: ) every model of X is a counter-model of Y, but not every counter-model of X is a model of Y.
- X and Y are contradictories (symbol: ) every model of X is a counter-model of Y, and every counter-model of X is a model of Y.
- X and Y are subcontraries (symbol: ) every counter-model of X is a model of Y, but not every model of X is a counter-model of Y.
- Y is subaltern to X (symbol: ) every model of X is a model of Y, and every counter-model of Y is a counter-model of X.
- Finally, X and Y are independent from each other (symbols: ind) whenever they do not satisfy any of the above conditions.
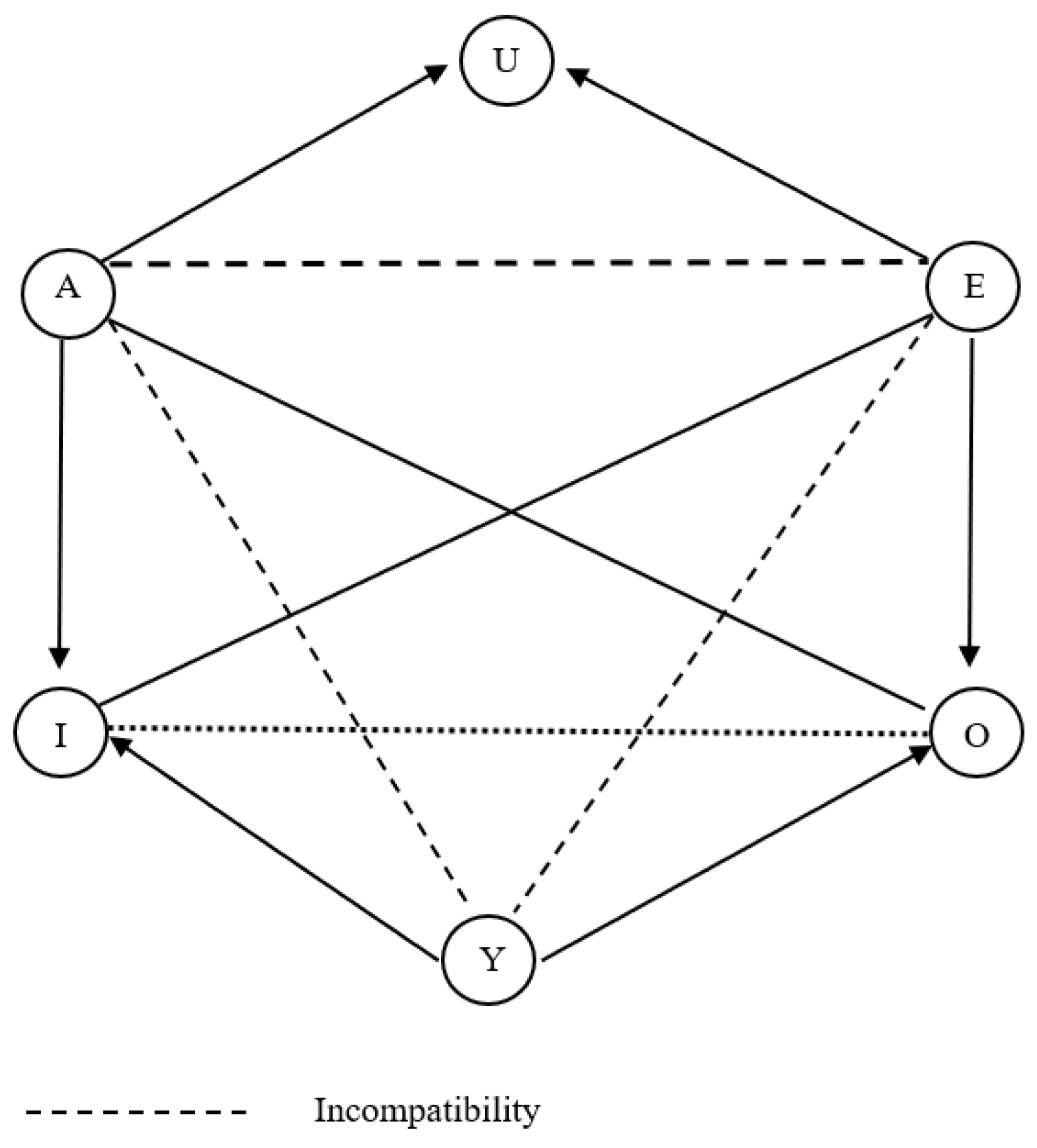
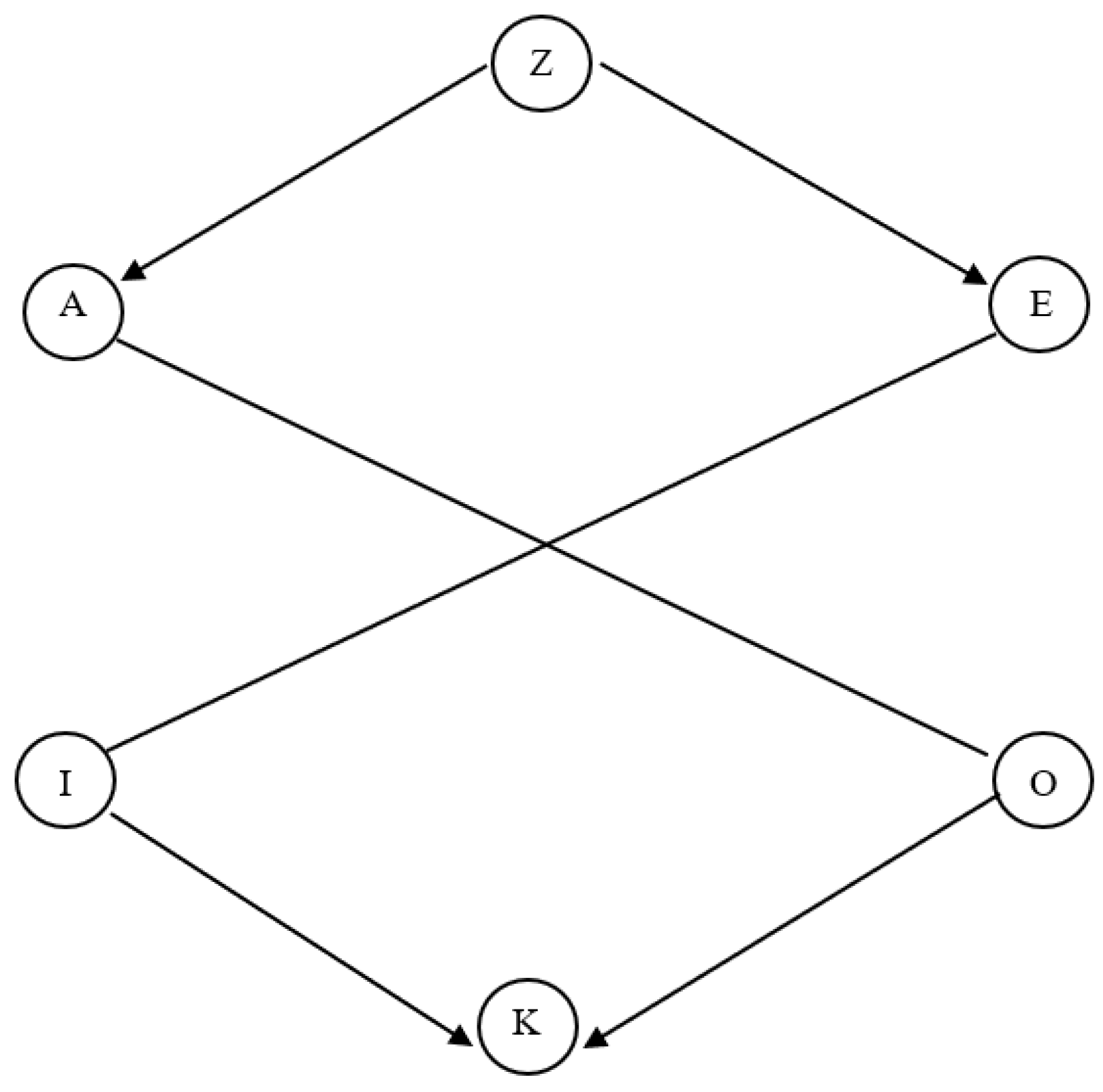
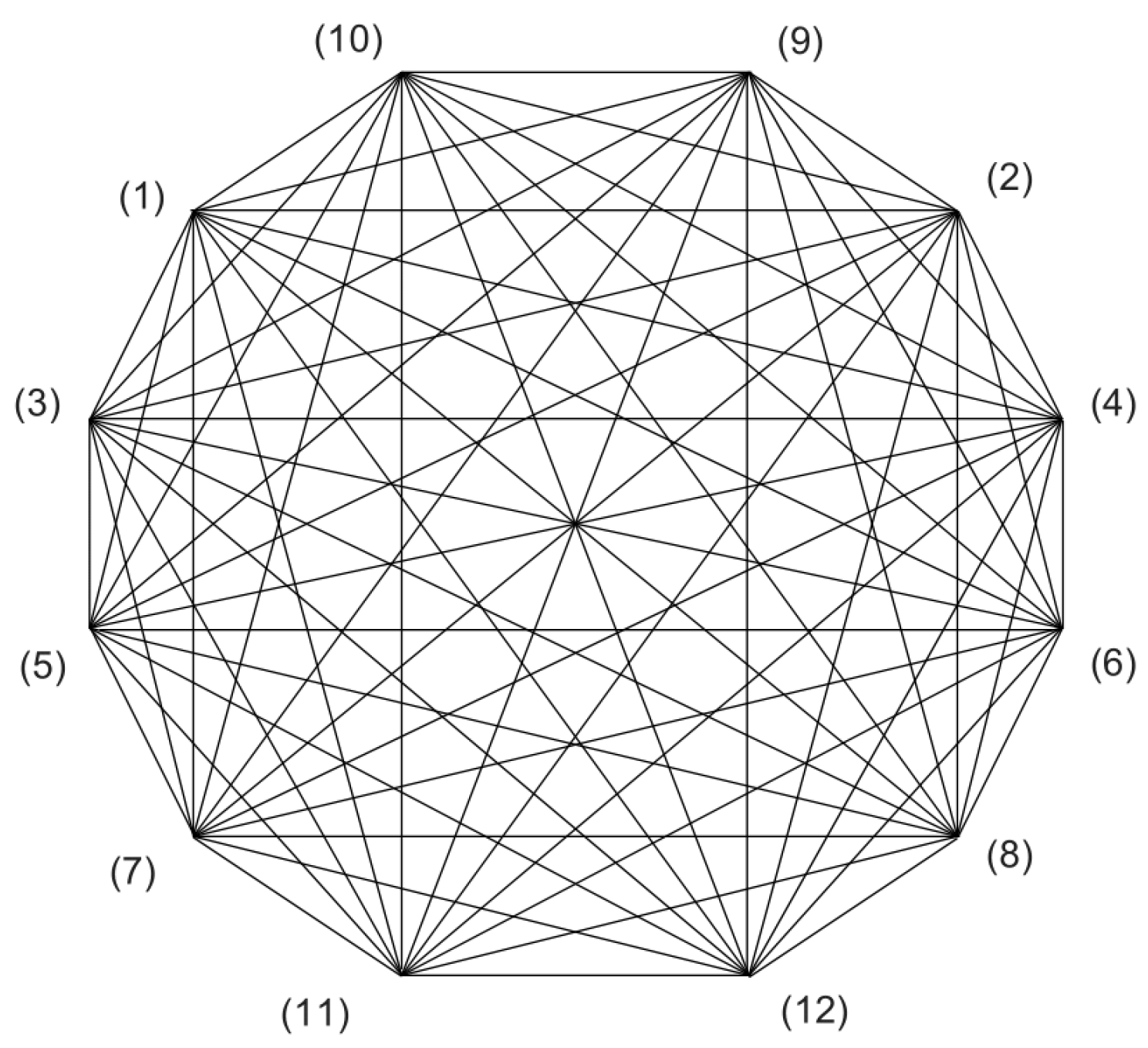
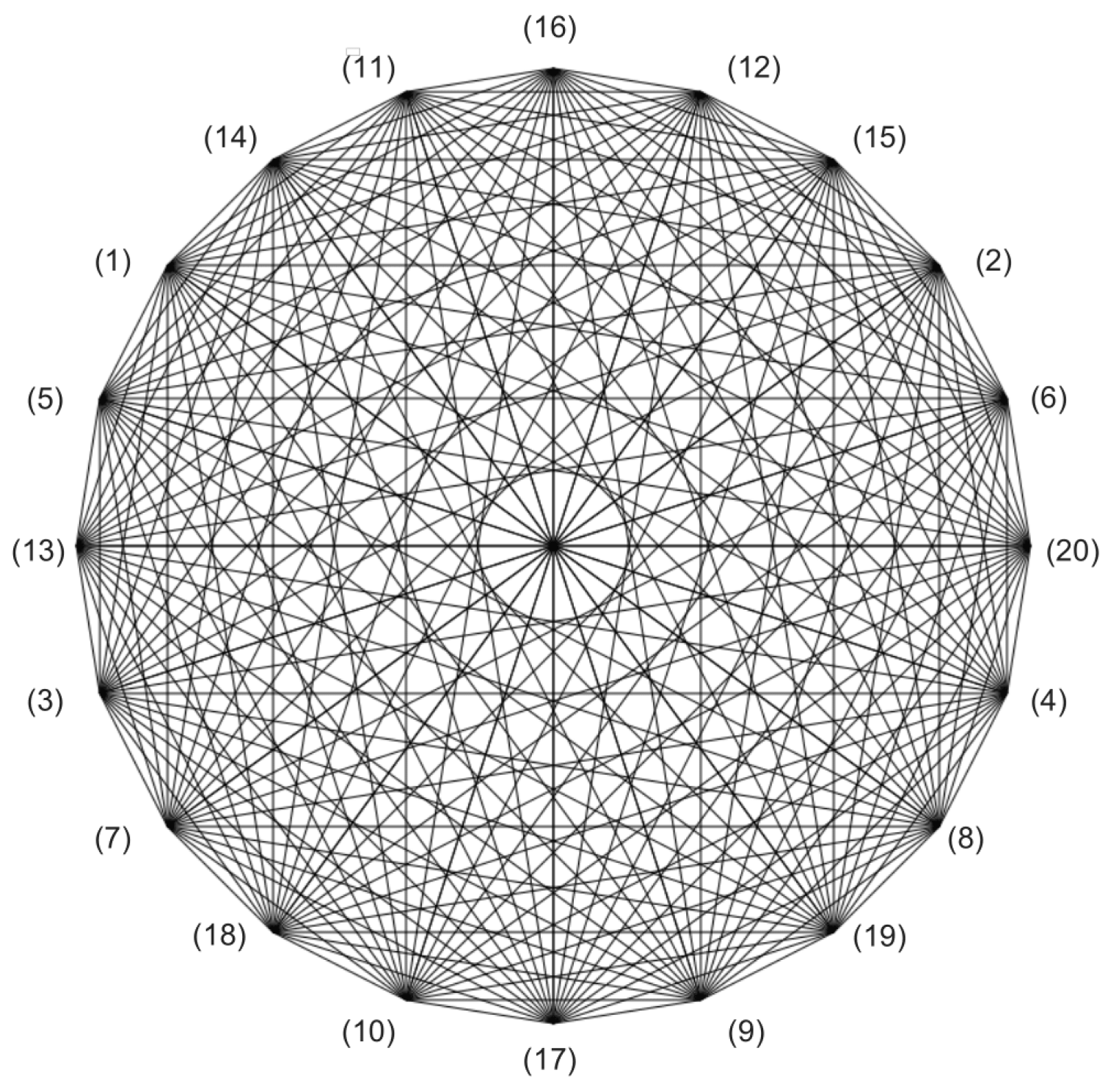
4.2.5. Increasing Diagrams
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Numbering Semantics for De dicto and De re Modal Statements
Appendix B. Logical Relations between De dicto and De re Modal Statements
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |
| (1) | ct | sp | ct | sp | ct | sp | cd | sp | sp | |
| (2) | ct | ct | sp | ct | sp | cd | sp | sp | sp | |
| (3) | sb | ct | ind | ind | cd | sp | sct | ind | sp | |
| (4) | ct | sb | ind | cd | ind | sct | sp | sp | ind | |
| (5) | sb | ct | ind | cd | ind | sp | sct | sct | ind | |
| (6) | ct | sb | cd | ind | ind | sct | sp | ind | sct | |
| (7) | sb | cd | sb | sct | sb | sct | sct | sct | sct | |
| (8) | cd | sb | sct | sb | sct | sct | sct | sct | sct | |
| (9) | sb | sb | ind | sb | sct | ind | sct | sct | ind | |
| (10) | sb | sb | sb | ind | ind | sct | sct | sct | ind |
| (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | |
| (11) | ind | sp | ct | ind | ind | ind | ind | sp | ct | |
| (12) | ind | ind | ct | ind | sp | ct | ind | sp | ind | |
| (13) | sb | ind | ind | sb | ind | ind | sct | ind | cd | |
| (14) | ct | ct | ind | ct | ind | ind | sp | cd | ind | |
| (15) | ind | ind | sp | ct | sp | ct | cd | sp | ct | |
| (16) | ind | sb | ind | ind | sb | cd | sct | ind | ind | |
| (17) | ind | ct | ind | ind | ct | cd | sp | ind | ind | |
| (18) | ind | ind | sct | sb | cd | sct | sb | sct | sb | |
| (19) | sb | sb | ind | ind | sb | ind | ind | sct | ind | |
| (20) | ct | ind | cd | ind | ct | ind | ind | sp | ind |
| (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | |
| (1) | ct | ct | sp | sp | ct | ct | sp | sp | ct | ct |
| (2) | ct | ct | ct | sp | ct | sp | ct | sp | ct | sp |
| (3) | ind | ct | ind | ind | ind | sct | sb | ind | ind | ind |
| (4) | ct | ind | sct | ind | ind | ind | ind | ind | ind | sb |
| (5) | sb | ind | sp | ind | ind | ind | ind | ind | ind | ct |
| (6) | ind | sb | ind | ind | ind | sp | ind | ind | ind | ind |
| (7) | sb | sb | sb | sct | sb | sct | sb | sct | sb | sct |
| (8) | sb | sb | sct | sct | sb | sb | sct | sct | sb | sb |
| (9) | cd | ind | sct | sb | ind | ind | ind | ind | sct | sb |
| (10) | ind | cd | ind | sb | ind | sct | sb | ind | sct | ind |
- SQ1: (1)-(2)-(7)-(8); SQ2: (1)-(4)-(5)-(8); SQ3: (1)-(6)-(3)-(8); SQ4: (1)-(11)-(9)-(8);
- SQ5: (1)-(12)-(10)-(8); SQ6: (1)-(15)-(18)-(8); SQ7: (1)-(16)-(17)-(8); SQ8: (1)-(19)-(14)-(8)
- SQ9: (1)-(20)-(13)-(8); SQ10: (2)-(3)-(6)-(7); SQ11: (2)-(5)-(4)-(7); SQ12: (2)-(11)-(9)-(7)
- SQ13: (2)-(12)-(10)-(7); SQ14: (2)-(13)-(20)-(7); SQ15: (2)-(15)-(18)-(7); SQ16: (2)-(17)-(16)-(7)
- SQ17: (2)-(19)-(14)-(7); SQ18: (3)-(12)-(10)-(8); SQ19: (4)-(11)-(9)-(5); SQ20: (5)-(20)-(13)-(4)
- SQ21: (11)-(14)-(19)-(9); SQ22: (11)-(20)-(13)-(9); SQ23: (12)-(14)-(19)-(10); SQ24: (12)-(17)-(16)-(10)
- SQ25: (14)-(15)-(13)-(19); SQ26: (15)-(17)-(16)-(13); SQ27: (15)-(20)-(13)-(18).
References
- Knuuttila, S. Modalities in Medieval Philosophy, 2nd ed.; Routledge: London, UK; New York, NY, USA, 1993. [Google Scholar]
- Read, S. Modality in Medieval Philosophy. In The Routledge Handbook of Modality; Bueno, O., Shalkowski, S., Eds.; Routledge: New York, NY, USA; London, UK, 2021; pp. 344–354. [Google Scholar]
- Karger, E. A Study of William of Ockham’s Modal Logic. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 1976. [Google Scholar]
- Normore, C.G. The Logic of Time and Modality in the Later Middle Ages: The Contribution of William of Ockham. Ph.D. Thesis, University of Toronto, Toronto, ON, USA, 1975. [Google Scholar]
- Ockham, W. Summa Logicae (Opera Philosophica et Theologica); Boehner, P., Gal, G., Brown, S., Eds.; St Bonaventure Institute: New York, NY, USA, 1974; Volume I, The Translation of Part II of the Summa logicae is provided by: Freddoso, A.J.; Schuurman, H. Ockham’s Theory of Propositions. Part II of the Summa Logicae; St. Augustine’s Press: South Bend, IN, USA, 1980. [Google Scholar]
- Ockham, W. Quodlibeta Septem (Opera Philosophica et Theologica); Wey, J.C., Ed.; St Bonaventure Institute: New York, NY, USA, 1980; Volume IX, The Translation of Quodlibeta septem is provided by: Freddoso, A.J.; Kelley, F.E. Quodlibetal Questions: Quolibets 1–7; Yale University Press: London, UK, 1998. [Google Scholar]
- Hintikka, J. Time and Necessity: Studies in Aristotle’s Theory of Modality; Oxford University Press: Oxford, UK, 1973. [Google Scholar]
- Ockham, W. Expositio in Librum Perihermeneias (Opera Philosophica); Gambatese, A., Brown, S., Eds.; St Bonaventure Institute: New York, NY, USA, 1978; Volume 2. [Google Scholar]
- Pizzi, C.E. Possibility and Dyadic Contingency. J. Log. Lang. Inf. 2022, 31, 451–463. [Google Scholar] [CrossRef]
- Blanché, R.; Davy, G. Structures intellectuelles. Les Études Philos. 1966, 21, 541–542. [Google Scholar]
- Quine, W.V.O. Methods of Logic, 4th ed.; Harvard Univ. Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Demey, L. Boolean considerations on John Buridan’s octagons of opposition. Hist. Philos. Log. 2019, 40, 116–134. [Google Scholar] [CrossRef]
- Demey, L.; Smessaert, H. Combinatorial Bitstring Semantics for Arbitrary Logical Fragments. J. Philos. Log. 2018, 47, 325–363. [Google Scholar] [CrossRef]
- Schang, F. End of the Square? S. Am. J. Log. 2018, 4, 485–505. [Google Scholar]
- Hayaki, R. Contingent Objects and the Barcan Formula. Erkenntnis 2006, 64, 87–95. [Google Scholar] [CrossRef]
- Campos-Benítez, J.M. The medieval octagon of opposition for sentences with quantified predicates. Hist. Philos. Log. 2014, 35, 354–368. [Google Scholar] [CrossRef]
- Demey, L.; Steinkrüger, P. The logical geometry of John Buridan’s modal octagon. Tijdschr. Voor Filos. 2017, 79, 217–239. [Google Scholar]
- Chatti, S. Les carrés d’Avicenne”. In Le Carré et ses Extensions: Approches Théoriques, Pratiques et Historiques; Ben Aziza, H., Chatti, S., Eds.; Publications de la Faculté des Sciences Humaines et Sociales de Tunis: Tunis, Tunisia, 2015. [Google Scholar]
- Yi, B. Categorical Propositions and Existential Import: A Post-modern Perspective. Hist. Philos. Log. 2021, 42, 307–373. [Google Scholar] [CrossRef]
- Keynes, J.N. Studies and Exercises in Formal Logic, 1st ed.; Macmillan: London, UK, 1884. [Google Scholar]
- Moktefi, A.; Schang, F. Another Side of Categorical Propositions: The Keynes–Johnson Octagon of Oppositions. Hist. Philos. Log. 2023, 43, 309–326. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falessi, D.; Schang, F. A Relational Semantics for Ockham’s Modalities. Axioms 2023, 12, 445. https://doi.org/10.3390/axioms12050445
Falessi D, Schang F. A Relational Semantics for Ockham’s Modalities. Axioms. 2023; 12(5):445. https://doi.org/10.3390/axioms12050445
Chicago/Turabian StyleFalessi, Davide, and Fabien Schang. 2023. "A Relational Semantics for Ockham’s Modalities" Axioms 12, no. 5: 445. https://doi.org/10.3390/axioms12050445
APA StyleFalessi, D., & Schang, F. (2023). A Relational Semantics for Ockham’s Modalities. Axioms, 12(5), 445. https://doi.org/10.3390/axioms12050445




