Granular Computing Approach to Evaluate Spatio-Temporal Events in Intuitionistic Fuzzy Sets Data through Formal Concept Analysis

Abstract

Knowledge discovery through spatial and temporal aspects of data related to occurrences of events has many applications in digital forensics. Specifically, in electronic surveillance, it is helpful to construct a timeline to analyze information. The existing techniques only analyze the occurrence and co-occurrence of events; however, in general, there are three aspects of events: occurrences (and co-occurrences), nonoccurrences, and uncertainty of occurrences/non-occurrences with respect to spatial and temporal aspects of data. These three aspects of events have to be considered to better analyze periodicity and predict future events. This study focuses on the spatial and temporal aspects given in intuitionistic fuzzy (IF) datasets using the granular computing (GrC) paradigm; formal concept analysis (FCA) was used to understand the granularity of data. The originality of the proposed approach is to discover the periodicity of events data given in IF sets through FCA and the GrC paradigm that helps to predict future events. An experimental evaluation was also performed to understand the applicability of the proposed methodology.

1. Introduction

An event is the occurrence of something at some place and time which involves some actors as objects and spatio-temporal features as attributes. In theliterature, the idea of spatial, temporal, and spatio-temporal co-occurrences can be found. In general, spatial co-occurrence is defined as when two or more events occur at the same place, temporal co-occurrence as when a number of events occur at the same time or in the same time-interval, and spatio-temporal co-occurrence as when events occur at the same place and time. Periodical events are those that occur at the same time intervals, for example, an event that occurs every day, weekend, month, or year. In the application domain, it is important to analyze these aspects of events. In the context of smart video surveillance, it is possible to discover the periodical and same-place movements of pedestrians to predict a crime before it happens. Moreover, in the context of intuitionistic fuzzy (IF) sets, there are some membership and nonmembership values that can be indicated for events occurring at some place and time. Existing approaches only work on occurrences and co-occurrences of events; however, in real life, there can be three aspects: occurrences (and co-occurrences), nonoccurrences, and the uncertainty of occurrences/nonoccurrences. The limitation of focusing only on the occurrences and co-occurrences of events is that it indicates the data related to event occurrences that may be missing the elicitation of complete and important knowledge related to event nonoccurrences, as well as the uncertainty of occurrences/non-occurrences. Motivated by these limitations, this research provides a novel approach based on granular computing (GrC) to discover these three aspects of events at the same places and in the periodical form in the IF sets, where $\mu$ (membership), $\gamma$ (non-membership), and $\pi$ (uncertainty) values indicate the occurrences (and co-occurrences), nonoccurrences, and the uncertainty of occurrences/nonoccurrences of events, respectively. GrC was used to discover the periodicity in data at various abstraction levels. Moreover, formal concept analysis (FCA) was used to discover the granulation levels and process the granulation measures to understand the IF concepts, where the events indicated as objects and spatio-temporal occurrences showed the attributes of lattices formed by formal concepts. The originality of the proposed approach is to discover the periodicity of spatial–temporal occurrences data of events given in IF sets through GrC and FCA. Moreover, this approach helps predict the occurrence (co-occurrence), nonoccurrence, and uncertainty of occurrence/nonoccurrence of events for spatial and temporal aspects of data through IF sets. The motivation for the use of IF sets instead of fuzzy sets in this proposed approach is the three-tuple nature of the IF sets, which contain the $\mu$ (membership), $\gamma$ (nonmembership), and $\pi$ (IF set index or indeterminacy, which expresses the degree of uncertainty) values of the elements. Here, $\pi$ is used in the computation of GrC measures i.e., IG and COV that help in the process of decision making. This paper is organized as follows: Section 2 discusses the related works; Section 3 provides the definitions of IF sets and FCA specifically used in the context of the IF sets data; Section 4 explains the GrC; Section 5 explains the proposed methodology; Section 6 demonstrates the experimental evaluation; Section 7 gives the results and discussion; Section 8 explains the comparison of the proposed approach with existing SOTA (state of the art) approaches; and Section 9 contains the conclusion and future work, followed by the references.

2. Related Works

In the literature, research work related to spatio-temporal and periodical occurrences and co-occurrences can be found. The most important task regarding periodical occurrences is to determine the data blocks in the whole dataset from which suitable views can be analyzed. For example, in a dataset of hundred events, discovering seventy events that always occur on a Sunday may be more interesting than ninety events occurring on the weekends. For this type of task, views are determined by selecting the temporal attributes and adjusting the temporal units in a way that helps to create a temporal zoom operation on data and discover the more interesting data blocks in the form of periodical occurrences. Depending on the data and objective, some data analysis techniques are required to evaluate the data blocks aiming to discover the periodical co-occurrences of events. Based on the GrC paradigm and FCA, different computational approaches are proposed to discover the spatio-temporal co-occurrences for different purposes. As in [1], FCA as a central tool for the proposed method is used to combine time-based granulation and three-way decisions to understand the learned granular structures conceptualizing spatio-temporal events. Moreover, the GrC is integrated with FCA as concept learning via GrC [2], granular rule acquisition in decision formal contexts [3], GrC approach based on FCA in fuzzy datasets [4], granular transformations, and irreducible element judgement [5]. There are two types of granules in FCA, one is the granule made by the set of objects in formal concept and the other is the one formed by the individual objects. Some research studies show that the granule formed by the individual objects play a vital role, with a strong correlation with object granules, object concepts [5], and granular concepts [6]. Additionally, there exist many other types of granules in FCA; however, the classification and the criteria for the classification of information granules in FCA are still an open research direction.

Yang et al. in [7] explained the sequential approach of three-way GrC by a framework of spatio-temporal multilevel granular structure, described with temporality of data and spatiality of parameters. Moreover, in the context of three-way decision approaches in [8], an IF three-way decision model based on IF sets is proposed to improve the ability to process complex fuzzy incomplete information systems. Zhao et al., in [9], proposed a novel spatial–temporal fuzzy information granule (STFIG) model to achieve the multistep forecasting of time series. In [10], the method puts forward research on the optimal route planning of traffic multisource routes based on GrC. GrC is used with set theory, shadowed sets, rough sets, fuzzy sets, etc. In each of these sets’ environments, the granules or the granulation processing is defined in different ways, as well as a tentative one to find similarity and bridge the gap between these settings, as described in [11]. Additionally, the IF sets using an FCA algorithm have already been discussed in the literature [12]; for example, in [13], the structure of formal concept forming operators is given in the form of fuzzy dilation and fuzzy erosion operators of bipolar fuzzy mathematical morphology, and in [14], attribute reduction in IF concept lattices is discussed.

This methodology uses the GrC paradigm and FCA with IF datasets as spatio-temporal attributes to realize the granulation or abstraction of data related to the periodical timeslots in temporal attributes of formal contexts, which were formed from the IF datasets; the granules involving spatio-temporal attributes were used to determine the co-occurrences of events with respect to space and time. In addition, the granulation measures of lattices made from the formal contexts of IF sets were discussed, such as information granulation (IG), coverage (COV), specificity (SP), and unique index (Q) value, to evaluate the granule according to its information related to spatio-temporal and periodical co-occurrences.

3. Preliminaries

3.1. Intuitionistic Fuzzy (IF) Sets

In [15], the notion of fuzzy sets is given as

$$C^{{}^{\prime }}=\left\{\langle x,{\mu }_{C^{{}^{\prime }}}\left(x\right)\rangle \mid x\in X\right\}$$

where ${\mu }_{C^{{}^{\prime }}}\left(x\right)\in [0,1]$ is the membership function of the fuzzy set $C^{{}^{\prime }}$. The notion of IF set [16,17,18] is given as

$$C=\left\{\langle x,{\mu }_C\left(x\right),{\gamma }_C\left(x\right)\rangle \mid x\in X\right\},$$

where ${\mu }_C:X\to [0,1]$ and ${\gamma }_C:X\to [0,1]$, such that

$$0\le {\mu }_C\left(x\right)+{\gamma }_C\left(x\right)\le 1.$$

Here, ${\mu }_C\left(x\right),{\gamma }_C\left(x\right)\in [0,1]$ indicate the degree of membership and the degree of nonmembership of $x\in C$, respectively. Each fuzzy set in terms of IF sets can be represented as

$$C=\left\{\langle x,{\mu }_{C^{{}^{\prime }}}\left(x\right),1-{\mu }_{C^{{}^{\prime }}}\left(x\right)\rangle \mid x\in X\right\}.$$

In addition to this, the important concept of each IF set C in X is given as

$${\pi }_C\left(x\right)=1-{\mu }_C\left(x\right)-{\gamma }_C\left(x\right).$$

Here, ${\pi }_C\left(x\right)$ is called the “hesitation degree” of $x\in C$, which indicates the uncertainty or the lack of the knowledge of whether $x\in C$ or $x\notin C$. Moreover, it is clear that $0\le {\pi }_C\left(x\right)\le 1,\forall x\in X$. This hesitation degree plays an important role in distance [19,20], similarity [20], and entropy [21,22], which are key measures that are used specially in the information processing tasks. Additionally, hesitation degree also plays a significant role in image processing [23], multicriteria group decision making [24], IF decision trees [25], genetic algorithms [26], and many other situations. In addition to this, let $C_1,C_2\in IF\left(U\right),C_1\subseteq C_2\iff {\mu }_{C_1}\left(x\right)\le {\mu }_{C_2}\left(x\right)$ and ${\gamma }_{C_1}\left(x\right)\ge {\gamma }_{C_2}\left(x\right),\forall x\in U$. If both $C_1\subseteq C_2$ and $C_2\subseteq C_1$ then, $C_1=C_2$ and $C_2=C_1$. The universe set U and null set ∅ are the special type of IF sets, where $U=\left\{\langle x,1,0\rangle \mid x\in U\right\}$ and $\varnothing =\left\{\langle x,0,1\rangle \mid x\in U\right\}$.

3.2. Formal Concept Analysis (FCA)

The FCA method was proposed in early 1980 by R. Wille for when a set of objects share a set of attributes. The foundation of FCA is built on the notions of lattice and set theory. This method outputs two sets of data. The first one provides the hierarchical relationship of constructed concepts in the form of a diagram called “Concept Lattice”. The second set of data provides the list of the interdependencies among all the attributes in a formal context.

Definition 1.

In FCA, the relation $K=(G,M,I)$ is called a formal context, where G and M denote the set of objects and set of attributes, respectively. In addition to this, $I\subseteq G\times M$ shows the relationship between G objects (extents) and M attributes (intents). Moreover, the relation $(g,m)\in I$ shows that the object g has attribute m, which can also be written as $gIm$.

Definition 2.

For a subset $A\subseteq G$ of objects then, the subset of the attributes common to all the objects in A is given as

$$A\uparrow =\left\{m\in M\mid \forall g\in A,gIm\right\}.$$

Likewise, given a subset $B\subseteq M$ of attributes, the subset of objects having all the attributes in set B is given as

$$B\downarrow =\left\{g\in G\mid \forall m\in B,gIm\right\}.$$

Definition 3

([26]). A formal context $K=(G,M,I)$ is defined as a pair $(A,B)$, where $A\subseteq G$, $B\subseteq M$ and $A\uparrow =B,B\downarrow =A$, where A denotes the objects (extents) and B indicates the attributes (intents) of the pair $(A,B)$. Let $(A_1,B_1)$ and $(A_2,B_2)$ be the two formal concepts of a formal context $K=(G,M,I)$; $(A_1,B_1)$ is called a superconcept of $(A_2,B_2)$, and $(A_2,B_2)$ is called a subconcept of $(A_1,B_1)$ if it satisfies the equivalent condition given as

$$(A_1,B_1)\le (A_2,B_2)\iff A_1\subseteq A_2\iff B_2\subseteq B_1$$

The set of all the superconcept and subconcept interrelations construct a design structure known as a lattice. The lattice is an abstract structure with join (denoted by “∨”) and meet (denoted by “∧”) operations. The above expression in this definition, in the form of join and meet, is

$$(A_1,B_1)\vee (A_2,B_2)=((A_1\cup A_2)\downarrow \uparrow ,B_1\cap B_2),$$

$$(A_1,B_1)\wedge (A_2,B_2)=(A_1\cap A_2,(B_1\cup B_2)\downarrow \uparrow )$$

where “∨” and “∧” indicate the supermum and infimum operations, respectively.

For any $\forall g\in G$, the pair $(g\uparrow \downarrow ,g\uparrow )$ is called the object concept, and $\forall m\in M$, the pair $(m\uparrow \downarrow ,m\uparrow )$ is called the attribute concept. In a lattice diagram, when two branches join below, it is called a join operation “∨”, and the point where two branches meet above is known as a meet operation “∧”. This interprets the relationship among the concepts, objects, and attributes. The nodes in this diagram express the concepts. However, this diagram is a type of directed acyclic graph. In IF sets, FCA is used for decision making, data analysis, knowledge discovery, and especially for forecasting purposes.

Definition 4.

Let $C_1,C_2\in IF\left(U\right)$ be the two IF sets, given as

$$\begin{array}{c}\hfill C_1=\left\{\left(x,{\mu }_{C_1}\left(x\right),{\gamma }_{C_1}\left(x\right)\right)\mid x\in U\right\},\\ \hfill C_2=\left\{\left(x,{\mu }_{C_2}\left(x\right),{\gamma }_{C_2}\left(x\right)\right)\mid x\in U\right\}.\end{array}$$

where ${\mu }_{C_1}\left(x\right),{\gamma }_{C_1}\left(x\right):U\to [0,1]$ and ${\mu }_{C_2}\left(x\right),{\gamma }_{C_2}\left(x\right):U\to [0,1]$ such that

$$0\le {\mu }_{C_1}\left(x\right)+{\gamma }_{C_1}\left(x\right)\le 1,$$

$$0\le {\mu }_{C_2}\left(x\right)+{\gamma }_{C_2}\left(x\right)\le 1.$$

Here, ${\mu }_{C_1}\left(x\right),{\gamma }_{C_1}\left(x\right)\in [0,1]$ indicate the degree of membership and nonmembership of $x\in C_1$, and ${\mu }_{C_2}\left(x\right),{\gamma }_{C_2}\left(x\right)\in [0,1]$ indicate the degree of membership and nonmembership of $x\in C_2$ IF sets, such that $\forall x\in U$.

Definition 5.

Let $C_1,C_2\in IF\left(U\right)$ be the two IF sets given in Definition 4, then these two sets through FCA algorithm are evaluated as

$$C_{1,2}=\left\{\left(x,min\left(\begin{array}{c}{\mu }_{C_1}\left(x\right),{\mu }_{C_2}\left(x\right)\end{array}\right),max\left(\begin{array}{c}{\gamma }_{C_1}\left(x\right),{\gamma }_{C_2}\left(x\right)\end{array}\right)\right)\mid x\in U\right\}.$$

These are the basic mathematical definitions which define the FCA and its operations with respect to IF sets. Moreover, later sections explain it more in detail by means of the GrC approach.

4. Granular Computing (GrC)

GrC is an emerging field for information processing [27,28] through the basic building blocks of information, named granules. In the data science literature, the granule is defined as the cluster or set of objects extracted or grouped together by similarity, uniformity, proximity, predictability, resemblance, physical adjacency, or functionality. These granules can be represented in interval values, rough sets, neutrosophic sets [29], fuzzy sets [30], IF sets, etc. Moreover, these granules can be partitioned into finer or smaller granules called subgranules. In order to compose and decompose the granules, specific measures called granulation measures are employed.

In this study, the GrC approach is used with FCA by considering the IF datasets containing various events as objects having spatio-temporal attributes. Moreover, different GrC measures are used, including IG, COV, SP, and Q value for the IF datasets. Here, for the first decomposition, IF datasets are decomposed in different granules, while each granule consists of the set of events as objects having spatio-temporal attributes. In the first decomposition, the IG of each granule is determined, and the granule (having more IG) is selected for further granulation measures i.e., COV and SP. For the second decomposition, the granule determined in the first decomposition (for the further granulation measures) is further decomposed into subgranules, the IG of each subgranule is found, the subgranule (with higher IG) for further granulation measures is determined, and so on. This process is performed until the granules/subgranules are obtained, with interesting granulation measures having more COV, less SP, and higher Q value.

5. Proposed Methodology

5.1. Periodic Occurrences (Co-Occurrences), Nonoccurrences, and Uncertainty of Occurrences/Nonoccurrences of Events in the Form of IF Datasets

In real life, an event can be represented by spatio-temporal occurrences and co-occurrences. Based on the specific time unit, different timelines can be assumed for the temporal information related to the occurrences and co-occurrences of events [31]. For example, the time unit is a day or a month, considering the timeline based on the day or the month, respectively. A timeslot is the sequence of time units (days or months); if the timeline is considered based on the days, then each day corresponds to a timeslot. Hence, different timelines can provide temporal granularity.

In the literature, spatial and temporal events data are evaluated through FCA and the GrC paradigm using classical single-attribute value in FCA data [31]. This proposed methodology uses the IF datasets, in which events occur at a certain place (spatial aspect) and time (temporal aspect) with certain membership and nonmembership values.

Definition 6.

Let $G_i$ be the set of objects having $M_j$ set of attributes, where $i=1,2,3,\dots$ and $j=1,2,3,\dots$ denote the number of objects and attributes, respectively, such that each $M_j$ attribute has IF set values ${\mu }_{i,j}$ and ${\gamma }_{i,j}$ as membership and nonmembership of the $G_i$ object in the $M_j$ attribute, respectively.

$$\begin{array}{c}\hfill M_j=\left\{\left(x,{\mu }_{i,j}\left(x\right),{\gamma }_{i,j}\left(x\right)\right)\mid \forall x\in M_j\right\}\end{array}$$

Definition 7.

Formally, consider an IF formal context $K_{i,j}=(G_i,M_j,I)$ such that $G_i,M_j$, and I indicate the objects, attributes (given in Definition 6), and relation between the objects and the attributes, respectively, as shown in

Table 1. Objects having attributes in the form of IF sets.

	${\mathrm{𝐌}}_1$	${\mathrm{𝐌}}_2$	${\mathrm{𝐌}}_3$	⋯	${\mathit{M}}_{\mathit{j}}$
${\mathtt{G}}_{\mathtt{1}}$	${\mu }_{1,1},{\gamma }_{1,1}$	${\mu }_{1,2},{\gamma }_{1,2}$	${\mu }_{1,3},{\gamma }_{1,3}$	⋯	${\mu }_{1,j},{\gamma }_{1,j}$
${\mathtt{G}}_{\mathtt{2}}$	${\mu }_{2,1},{\gamma }_{2,1}$	${\mu }_{2,2},{\gamma }_{2,2}$	${\mu }_{2,3},{\gamma }_{2,3}$	⋯	${\mu }_{2,j},{\gamma }_{2,j}$
${\mathtt{G}}_{\mathtt{3}}$	${\mu }_{3,1},{\gamma }_{3,1}$	${\mu }_{3,2},{\gamma }_{3,2}$	${\mu }_{3,3},{\gamma }_{3,3}$	⋯	${\mu }_{3,j},{\gamma }_{3,j}$
⋮	⋮	⋮	⋮	⋮	⋮
$G_i$	${\mu }_{i,1},{\gamma }_{i,1}$	${\mu }_{i,2},{\gamma }_{i,2}$	${\mu }_{i,3},{\gamma }_{i,3}$	⋯	${\mu }_{i,j},{\gamma }_{i,j}$

, where

$$\begin{array}{c}\hfill G_i=\left\{{\mathtt{G}}_{\mathtt{1}},{\mathtt{G}}_{\mathtt{2}},{\mathtt{G}}_{\mathtt{3}},\dots \right\},\\ \hfill M_j=\left\{{\mathtt{M}}_{\mathtt{1}},{\mathtt{M}}_{\mathtt{2}},{\mathtt{M}}_{\mathtt{3}},\dots \right\}.\end{array}$$

Definition 8.

Let a subset $G_i\subseteq G$ of the objects, then the subset of the attributes to all the objects in $G_i$ is given as

$$G_i\uparrow =\left\{m\in M\mid \forall g\in G_i,gIm\right\}$$

Likewise, given a subset $M_j\subseteq M$ of attributes, the subset of objects having all the attributes in set $M_j$ is given as

$$M_j\downarrow =\left\{g\in G\mid \forall m\in M_j,gIm\right\}$$

Definition 9.

According to FCA, for an IF formal concept of a formal context $K_{i,j}=(G_i,M_j,I)$, let there be a pair $(G_i,M_j)$, where $G_i\subseteq G,M_j\subseteq M$ and $G_i\uparrow =M_j,M_j\downarrow =G_i$, where $G_i$ denotes the objects (extents) and $M_j$ indicates the attributes (intents) of the pair $(G_i,M_j)$.

Definition 10.

Let the IF concept lattice $L_{i,j}=(G_i,M_j,I)$, constructed with all the concepts of IF formal concepts of $K_{i,j}=(G_i,M_j,I)$, such that $({\mathtt{G}}_{\mathtt{1}},{\mathtt{M}}_{\mathtt{1}})$ and $({\mathtt{G}}_{\mathtt{2}},{\mathtt{M}}_{\mathtt{2}})$ are the two IF formal concepts of the IF formal context $K_{i,j}=(G_i,M_j,I)$, where $({\mathtt{G}}_{\mathtt{1}},{\mathtt{M}}_{\mathtt{1}})$ is called a superconcept of $({\mathtt{G}}_{\mathtt{2}},{\mathtt{M}}_{\mathtt{2}})$, and $({\mathtt{G}}_{\mathtt{2}},{\mathtt{M}}_{\mathtt{2}})$ is called a subconcept of $({\mathtt{G}}_{\mathtt{1}},{\mathtt{M}}_{\mathtt{1}})$ if it satisfies the equivalent condition given as

$$({\mathtt{G}}_{\mathtt{1}},{\mathtt{M}}_{\mathtt{1}})\le ({\mathtt{G}}_{\mathtt{2}},{\mathtt{M}}_{\mathtt{2}})\iff {\mathtt{G}}_{\mathtt{1}}\subseteq {\mathtt{G}}_{\mathtt{2}}\iff {\mathtt{M}}_{\mathtt{2}}\subseteq {\mathtt{M}}_{\mathtt{1}}$$

Definition 11.

The set of all the IF superconcept and the subconcept interrelations construct a lattice. The lattice is an abstract structure with join (denoted by “∨”) and meet (denoted by “∧”) operations. Hence, the above expression of the IF superconcept and subconcept in this definition, in the form of join and meet, is

$$({\mathtt{G}}_{\mathtt{1}},{\mathtt{M}}_{\mathtt{1}})\vee ({\mathtt{G}}_{\mathtt{2}},{\mathtt{M}}_{\mathtt{2}})=(({\mathtt{G}}_{\mathtt{1}}\cup {\mathtt{G}}_{\mathtt{2}})\downarrow \uparrow ,{\mathtt{M}}_{\mathtt{1}}\cap {\mathtt{M}}_{\mathtt{2}}),$$

$$({\mathtt{G}}_{\mathtt{1}},{\mathtt{M}}_{\mathtt{1}})\wedge ({\mathtt{G}}_{\mathtt{2}},{\mathtt{M}}_{\mathtt{2}})=({\mathtt{G}}_{\mathtt{1}}\cap {\mathtt{G}}_{\mathtt{2}},({\mathtt{M}}_{\mathtt{1}}\cup {\mathtt{M}}_{\mathtt{2}})\downarrow \uparrow )$$

In this mathematical form, “∨” and “∧” indicate the supermum and infimum operations of IF formal concepts, respectively.

Definition 12.

The IF formal concept of the given set of $G_i$ objects with $M_j$ attributes having the IF values $({\mu }_{i,j},{\gamma }_{i,j})\to [0,1]$ in $K_{i,j}=(G_i,M_j,I)$ formal context is evaluated as

$$\left(min\left({\mu }_{i,j}\right),max\left({\gamma }_{i,j}\right)\right)$$

where $i\in G,j\in M$.

Example 1.

Let the IF formal concept for ${\mathtt{G}}_{\mathtt{1}}$ and ${\mathtt{G}}_{\mathtt{2}}$ objects having $M_j$$(j=1,2,3,\dots )$ attributes (given in Table 1) be computed as

$$\begin{array}{c}\hfill {\mathtt{G}}_{\mathtt{12}}=[\left(min({\mu }_{1,1},{\mu }_{2,1}),max({\gamma }_{1,1},{\gamma }_{2,1})\right),\left(min({\mu }_{1,2},{\mu }_{2,2}),max({\gamma }_{1,2},{\gamma }_{2,2})\right),\\ \hfill \left(min({\mu }_{1,3},{\mu }_{2,3}),max({\gamma }_{1,3},{\gamma }_{2,3})\right),\dots ,\left(min({\mu }_{1,j},{\mu }_{2,j}),max({\gamma }_{1,j},{\gamma }_{2,j})\right)]\end{array}$$

In this prposed methodology, the objects $G_i$ indicate the events, and the attributes $M_j$ indicate the occurrence of those events at a certain place and time, with certain membership $\mu$ (occurrence/co-occurrence), nonmembership $\gamma$ (nonoccurrence), and uncertainty $\pi$ (uncertainty of occurrence/nonoccurrence) values provided in the IF datasets. For example, in Table 1, let ${\mathtt{G}}_{\mathtt{1}}$ be one of the events, ${\mathtt{M}}_{\mathtt{1}}$ and ${\mathtt{M}}_{\mathtt{2}}$ be two places, and ${\mathtt{M}}_{\mathtt{3}},\dots ,M_j$ be the number of times an event has occurred with some $\mu$ membership of occurrence and $\gamma$ nonmembership of nonoccurrence values; then, it can be said that the event ${\mathtt{G}}_{\mathtt{1}}$ has occurred at ${\mathtt{M}}_{\mathtt{1}}$ and ${\mathtt{M}}_{\mathtt{2}}$ places at ${\mathtt{M}}_{\mathtt{3}},\dots ,M_j$ different times with $\mu$ happening and $\gamma$ not happening values of events.

Example 2.

Let ${\mathtt{M}}_{\mathtt{3}}$ be the one-year temporal attribute showing the events occurring in the ${\mathtt{M}}_{\mathtt{3}}$ year. For the temporal granulation of the ${\mathtt{M}}_{\mathtt{3}}$ year attribute, let $Q_1,Q_2,Q_3,$ and $Q_4$ be the four quarters, indicating data for January, February, and March; April, May, and June; July, August, and September; and October, November, and December, given that each month’s data are a basic granule. Hence, for the first decomposition, there will be four granules containing data for events occurring in the four quarters of the year. For example, $E_1$ event’s data in the $Q_1$ quarter of the ${\mathtt{M}}_{\mathtt{3}}$ year in the form of IF sets is given as $(0.3,0.6)$, where $\mu =0.3$, (membership) indicates the $E_1$ event’s occurrence (co-occurrence) and $\gamma =0.6$ (nonmembership) indicates the $E_1$ event’s nonoccurrence. Moreover, $\pi =0.1$ (IF set index or indeterminacy) indicates the $E_1$ event’s uncertainty of occurrence/nonoccurrence, which is used to compute the IG later in this section.

Existing approaches only work on the periodical occurrences and co-occurrences of events using the GrC paradigm and FCA by considering single-value attributes for formal concepts. However, in the proposed approach, three aspects of the phenomenon of events are considered: event occurrence (co-occurrence), nonoccurrence, and the uncertainty of occurrence/nonoccurrence using GrC and the FCA algorithm by considering the IF datasets. Furthermore, the events data are represented in the form of three-tuple IF datasets as $\mu$ (membership), $\gamma$ (nonmembership), and $\pi$ (IF set index or indeterminacy), indicating the event occurrence (co-occurrence), nonoccurrence, and the uncertainty of occurrence/nonoccurrence, respectively. This timed granulation of occurring event data is further explained and analyzed for the knowledge discovery in Section 6.

Here, the IF datasets (containing the objects and attributes relationship) are divided into multiple parts, and each part is considered as the IF granule. Moreover, the lattice of each IF granule is designed for the data analysis using FCA and IF granulation measures.

5.2. Computation of an IF Granule

In [32], fuzzy information granules and the hierarchical structures of IF rough sets from the viewpoint of GrC are presented. In addition to this, FCA is also widely used in IF sets, such as the research study in [33], which mainly focuses on the FCA in an IF formal context. Moreover, in [33], the primitive notions in concept lattice theory are also extended to the IF environment. In this research, the idea of IF granule evaluation is performed by calculating $IG$, $COV$, $SP$, and the Q value of the IF concept lattice, where each concept lattice is treated as an individual granule.

5.3. Information Granulation (IG)

IG $\left(IG\right):IG=|1-IE|$ provides the information on the granule within the lattice by taking into account the extensional parts (objects) included in the granule [31]. Information entropy (IE) is an important measure to evaluate the uncertainty in data [34,35], which is why the term $|1-IE|$ gives the total IG obtained from the data granule or the concept lattice. According to Shannon’s theory, IE is the key information measure in data analysis. Based on the IF sets, different types of IE measures may be needed, depending upon the evaluation. In [36], the authors introduce IE into the field of FCA to quantify the weight of the concepts’ intent. A type of nonprobabilistic entropy measure for IF is proposed in [37]. Here, in [37], the entropy measure is the result of the IF sets’ geometric interpretation, and it uses the ratio of distances between them, defined in terms of the ratio of the IF sets’ cardinalities of $F\cap F^c$ and $F\cup F^c$, where $F^c$ is the complement of the F IF set. Two methods to determine the attribute weights are proposed in [38]. The first is when the information regarding the attributes is completely unknown, and the second is when partial information about attribute weights is known. Moreover, in [38], the attribute weights’ identification based on the IF entropy is offered in the context of IF sets. In the literature, every type of uncertainty measure, such as information Shannon entropy, information granularity, rough entropy, and IE, is called by a common name: information granularity. The distance-based information granularity for IF and multigranulation IF granular spaces is presented in [39]; moreover, the author used this distance-based information granularity to construct a novel hierarchical structure on such spaces. In [40], the authors compute the information granularity by taking into account the number of objects (extensional parts) included in the granule; hence, in this study, IG and IE provide the framework to evaluate the set of granulation. Let $K=(G,M,I)$ be the IF formal context of IF granule and $L=(G,M,I)$ be its corresponding lattice. The first granulation measure for the designed lattice of IF formal context is given as

$$IG\left(L\right)=\frac{1}{G}\sum \left[\frac{1}{n}\sum _{j=1}^{n}1-\left({\gamma }_j+\frac{{\pi }_j}{2}\right)\right],$$

(1)

where “G” is the number of objects involved in the IF granule, “n” is the number of attributes of each object, $j=1,2,3,\dots$ shows the number of attributes, and “${\gamma }_j$” and “${\pi }_j$” are the nonmembership and hesitancy degree of the “jth” attribute. For the different IF formal contexts from the IF datasets, $K_x=(G_x,M,I_x)$ and $L_x=(G_x,M,I_x)$, where $K_x$ indicates the formal contexts, $L_x$ indicates their corresponding lattices, and $x=1,2,3,\dots$ denotes the number of formal contexts and their lattices. If the $IG$ of lattice $L_1=({\mathtt{G}}_{\mathtt{1}},\mathtt{M},{\mathtt{I}}_{\mathtt{1}})$ is greater than that of $L_2=({\mathtt{G}}_{\mathtt{2}},\mathtt{M},{\mathtt{I}}_{\mathtt{2}})$, then the $K_1$ formal context contains more IG and is more interesting with respect to providing spatio-temporal information in the IF GrC perspective.

Let $E_1,E_2,E_3$, and $E_4$ be the four events as objects; $Plac{e}_1,Plac{e}_2,Plac{e}_3$, and $Plac{e}_4$ be the four spatial attributes; and $Q_1$ and $Q_2$ be the two parts of one-year data, such that $Q_1$ consists of Jan, Feb, Mar, Apr, May, and June and $Q_2$ consists of July, Aug, Sep, Oct, Nov, and Dec temporal attributes data in the form of IF sets, as given in the

Table 2. Four Events as Objects with Four Spatial and Two Temporal Attributes Data.

	${\mathit{Place}}_1$	${\mathit{Place}}_2$	${\mathit{Place}}_3$	${\mathit{Place}}_4$	${\mathit{Q}}_1$	${\mathit{Q}}_2$
$E_1$	(0.9, 0.1)	(0.6, 0.2)	(0.3, 0.7)	(0.8, 0.1)	(0.3, 0.6)	(0.9, 0.0)
$E_2$	(0.3, 0.5)	(0.5, 0.5)	(0.8, 0.2)	(0.2, 0.5)	(0.7, 0.2)	(0.8, 0.1)
$E_3$	(0.8, 0.2)	(0.6, 0.2)	(0.7, 0.1)	(0.2, 0.7)	(0.4, 0.6)	(0.1, 0.8)
$E_4$	(0.2, 0.6)	(0.3, 0.6)	(0.6, 0.3)	(0.1, 0.6)	(0.2, 0.8)	(0.7, 0.2)

. Furthermore, let the events $E_1,E_2,E_3,$ and $E_4$ occur at the given spatiality, with $Q_1$ temporality in the $K_1$ formal context and with $Q_2$ temporality in the $K_2$ formal context.

Hence, the $IG$ of $K_1$ and $K_2$ formal contexts is given as

$$\begin{array}{ll}IG\left(K_1\right)=& \\ & \frac{1}{4}\sum \left\{\frac{1}{5}\left(1-\left(0.1+\frac{0}{2}\right)\right)+\left(1-\left(0.2+\frac{0.2}{2}\right)\right)+\left(1-\left(0.7+\frac{0}{2}\right)\right)+\left(1-\left(0.1+\frac{0.1}{2}\right)\right)+\left(1-\left(0.6+\frac{0.1}{2}\right)\right)\right\}+\\ & \left\{\frac{1}{5}\left(1-\left(0.5+\frac{0.2}{2}\right)\right)+\left(1-\left(0.5+\frac{0}{2}\right)\right)+\left(1-\left(0.2+\frac{0}{2}\right)\right)+\left(1-\left(0.5+\frac{0.3}{2}\right)\right)+\left(1-\left(0.2+\frac{0.1}{2}\right)\right)\right\}+\\ & \left\{\frac{1}{5}\left(1-\left(0.2+\frac{0}{2}\right)\right)+\left(1-\left(0.2+\frac{0.2}{2}\right)\right)+\left(1-\left(0.1+\frac{0.2}{2}\right)\right)+\left(1-\left(0.7+\frac{0.1}{2}\right)\right)+\left(1-\left(0.6+\frac{0}{2}\right)\right)\right\}+\\ & \left\{\frac{1}{5}\left(1-\left(0.6+\frac{0.2}{2}\right)\right)+\left(1-\left(0.6+\frac{0.1}{2}\right)\right)+\left(1-\left(0.3+\frac{0.1}{2}\right)\right)+\left(1-\left(0.6+\frac{0.3}{2}\right)\right)+\left(1-\left(0.8+\frac{0}{2}\right)\right)\right\},\\ IG\left(K_1\right)=& 0.53\\ IG\left(K_2\right)=& \\ & \frac{1}{4}\sum \left\{\frac{1}{5}\left(1-\left(0.1+\frac{0}{2}\right)\right)+\left(1-\left(0.2+\frac{0.2}{2}\right)\right)+\left(1-\left(0.7+\frac{0}{2}\right)\right)+\left(1-\left(0.1+\frac{0.1}{2}\right)\right)+\left(1-\left(0+\frac{0.1}{2}\right)\right)\right\}+\\ & \left\{\frac{1}{5}\left(1-\left(0.5+\frac{0.2}{2}\right)\right)+\left(1-\left(0.5+\frac{0}{2}\right)\right)+\left(1-\left(0.2+\frac{0}{2}\right)\right)+\left(1-\left(0.5+\frac{0.3}{2}\right)\right)+\left(1-\left(0.1+\frac{0.1}{2}\right)\right)\right\}+\\ & \left\{\frac{1}{5}\left(1-\left(0.2+\frac{0}{2}\right)\right)+\left(1-\left(0.2+\frac{0.2}{2}\right)\right)+\left(1-\left(0.1+\frac{0.2}{2}\right)\right)+\left(1-\left(0.7+\frac{0.1}{2}\right)\right)+\left(1-\left(0.8+\frac{0.1}{2}\right)\right)\right\}+\\ & \left\{\frac{1}{5}\left(1-\left(0.6+\frac{0.2}{2}\right)\right)+\left(1-\left(0.6+\frac{0.1}{2}\right)\right)+\left(1-\left(0.3+\frac{0.1}{2}\right)\right)+\left(1-\left(0.6+\frac{0.3}{2}\right)\right)+\left(1-\left(0.2+\frac{0.1}{2}\right)\right)\right\},\\ IG\left(K_2\right)=& 0.58\end{array}$$

Hence, the $IG$ of the $K_2$ IF formal context is greater than the $IG$ of the $K_1$ IF formal context, implying that the events with given spatial and $Q_2$ temporal attributes are more interesting with respect to providing more spatio-temporal information in the periodical IF GrC perspective. Moreover, for the further process, the $K_2$ IF formal context will be decided for the computation of granulation measures, which is discussed in Section 6.

5.4. Granular Computing Measures for the Interestingness Level of IF Lattice

In the literature, there are various proposed granular measures based on FCA which identify the interestingness level of the granule. The GrC and FCA measures defined in [41] and [42], respectively, include COV, SP, stability, robustness, probability, separation, etc. The most important granular measures are COV and SP, which are used in the GrC approach based on FCA. In this study, COV, SP, and Q value are used to analyze the interestingness level of the IF lattice.

5.5. Coverage (COV)

COV is the most important granulation measure to evaluate the granule within the spatial, temporal, or spatio-temporal granulation perspective [31]. COV indicates the data granule to represent or cover the given data. The main objective of calculating the COV in this study is to find the IF lattice granule data objects’ COV which contains the interesting information. Generally, the larger the data objects being covered the higher the COV of the interesting information granule. In [43], the concept of COV with invariability and its interconnections are analyzed from the viewpoint of algebraic properties of a fuzzy system, including membership function, inclusion, union and intersection, and support and fuzzy relation. Depending on the nature of granule, the definition of COV can be properly expressed, as in [44], where the concept of COV is defined with the fuzzy perspective of GrC. Here, the COV for the IF concept lattice objects using membership values in the perspective of GrC approach is computed as

$$COV\left(C\right)=\left[\left(\frac{D}{G}\times \frac{1}{N}\sum _{i=1}^{N}C\left(x_{{\mu }_j}\right)\right)+\frac{{\pi }_j}{2}\right],$$

(2)

where “N” is the number of elements in the IF concept lattice C granule, ${\mu }_j$, where $j=1,2,3,\dots$, is the number of membership values, and ${\pi }_j$ is the hesitation degree of each attribute involved in the granule. Here, D shows the involved objects, and G indicates the total number of objects in the granule. In the above Equation (2), $\left(\frac{{\pi }_j}{2}\right)$ is used because the uncertainty can be membership or nonmembership of the IF set value.

The motivation behind the use of Equation (2) is the computation of COV for the formal concept granule containing the event’s spatio-temporal information in the form of IF sets. The COV for the IF formal concept as a granule C for the involved objects (events) $\frac{D}{G}$ [31] is the sum of membership grades [44] $\frac{1}{N}{\sum }_{i=1}^{N}C\left(x_{{\mu }_j}\right)$ in the IF formal concept. Additionally, the term $\frac{{\pi }_j}{2}$ indicates the membership value in the $\pi$ degree of indeterminacy. The illustration to compute the COV is given in Example 3.

Example 3.

Let $X=\left\{x_1,x_2,x_3,x_4,x_5\right\}$ and $\tilde{C}\left(x\right)$ be the IF formal concept of IF formal context, consisting of $E_1$ event as an involved object with $Q_1$ temporal data given in Table 2, such that

$$\begin{array}{c}\hfill \tilde{C}\left(x\right)=\left\{(0.9,0.1,x_1),(0.6,0.2,x_2),(0.3,0.7,x_3),(0.8,0.1,x_4),(0.3,0.6,x_5)\right\}.\end{array}$$

Let $D=1$ and $G=4$, because the object involved in the $\tilde{C}$ IF formal concept is one, i.e., $E_1$, and the total number of objects is four, i.e., $E_1,E_2,E_3,$ and $E_4$, respectively. Moreover, $N=5$ is the number of IF attributes in the data, and ${\pi }_j$ is the total degree of indeterminacy in all the attributes of the $\tilde{C}$ IF formal concept.

$$\begin{array}{c}\hfill COV\left(C\right)=\left[\left(\frac{1}{4}\times \frac{1}{5}\sum _{i=1}^{5}0.9+0.6+0.3+0.8+0.3\right)+\frac{0.4}{2}\right]=0.34.\end{array}$$

5.6. Specificity (SP)

The SP measure is the fundamental granulation measure used to find the abstract, precise, or specific level of the granule in GrC. SP’s role in IF sets is similar to the role of entropy in probability theory, as entropy estimates the probability of the specific event under consideration, which encapsulates the information about the fundamental probability distribution. The author of [45] states that in expert- and knowledge-based systems, SP plays a fundamental role in determining the usefulness of the information provided by these systems. Moreover, an increase in the abstract level of the SP of the information provided increases the information’s usefulness. For example, a system shows the prediction of tornado storm occurrences in different states at different times. Additionally, this system, in most cases, will correctly predict the situation of the tornado’s occurrence in both spatial and temporal perspectives. This system will not be of much use if it does not determine which type of precautionary measures should be taken at particular states at a particular time. This scenario points out a very important uncertainty principle of information theory, which is called the specificity–correctness trade-off.

An important idea to note is that the higher the SP, the lower the granule level of abstraction. In this study, the concept of SP is used for the spatio-temporality (two perspectives) of the IF concept lattice granule measure by using the $len\left(d\right)$ and $range$ concepts. As explained in [31], $len\left(d\right)$ and $range$ indicate the length of the involved temporal slot and the sum of the lengths of all temporal slots, respectively. According to refs. [31,45], SP is measured as follows:

$$SP\left(C\right)=\left[1-\frac{len\left(d\right)}{range}\right]\times \left[\alpha -\frac{1}{n-1}\sum _{x\in X\ne X^{*}}^{}G\left(x\right)\right].$$

(3)

Here, the IF set’s concept lattice is considered. Let $X=\left\{x_1,x_2,x_3,\dots ,x_n\right\}$ be the set of attributes in set X and C be the IF set with $(C^{+}\left(x\right),C^{-}\left(x\right))$ membership and nonmembership of the IF ordered pair. In Equation (3) $\alpha =Ma{x}_x\left[C^{+}\left(x\right)\right]$, assuming that it occurs at $x_m$ such that $\alpha =C^{+}\left(x_n\right),\forall x_n\ne x_m$, calculate $G\left(x\right)=\alpha \wedge \left(1-C^{-}\left(x\right)\right)$ to compute the SP of IF set C [45]. The illustration of calculating SP is given in Example 4.

Example 4.

Let $X=\left\{x_1,x_2,x_3,x_4,x_5\right\}$ and $\tilde{C}\left(x\right)$ be the IF formal concept, such that

$$\begin{array}{c}\hfill \tilde{C}\left(x\right)=\left\{(0.9,0.1,x_1),(0.6,0.2,x_2),(0.3,0.7,x_3),(0.8,0.1,x_4),(0.3,0.6,x_5)\right\}.\end{array}$$

Here, the value of $\alpha =0.9$ occurs in $x_1$, then $G\left(x\right)=\alpha \wedge \left(1-C^{-}\left(x\right)\right)$ is computed for the $x\ne x_1$ as

$$\begin{array}{c}\hfill G\left(x_2\right)=0.9\wedge \left(1-0.2\right)=0.8,\\ \hfill G\left(x_3\right)=0.9\wedge \left(1-0.7\right)=0.3,\\ \hfill G\left(x_4\right)=0.9\wedge \left(1-0.1\right)=0.9,\\ \hfill G\left(x_5\right)=0.9\wedge \left(1-0.6\right)=0.4.\end{array}$$

For example, $\tilde{C}\left(x\right)$ is one of the IF formal concepts of the IF formal context, with $Q_1$ temporal data given in Table 2; then, $len\left(d\right)=6$ and $range=12$.

$$\begin{array}{c}\hfill SP\left(\tilde{C}\left(x\right)\right)=\left[1-\frac{6}{12}\right]\times \left[0.9-\frac{1}{5-1}\sum (0.8+0.3+0.9+0.4)\right]=0.15.\end{array}$$

The SP of individual IF concept lattice granules is calculated in Section 6.

5.7. Unique Index (Q) Value

In ref. [31], the authors define the aggregation of COV and SP as the Q value. In the Q value, the COV(C) determines the objects representing the IF concept lattice granule COV; on the other hand, SP(C) indicates the SP for the IF concept lattice granule in the perspectives of spatial and temporal attributes using the GrC approach. The mathematical measure to compute the Q value is given as

$$Q\left(C\right)=COV\left(C\right)\times {\left(SP\left(C\right)\right)}^{\zeta }$$

(4)

Here, the exponent on SP, “$\zeta$”, is the aspect of the SP. It shows the change in the partition level of the data. Moreover, the higher the value of “$\zeta$”, the more important the aspect of the SP. The idea of “$\zeta$” is more understandable later in the experimental analysis. In ref. [31], the authors also propose the average Q value of data granules; here, the IF concept lattice granule average Q value can be computed as follows:

$$\overline{Q}\left(L\right)=\sum _{(A,B)\in L}^{}\frac{Q\left(C\right)}{n}$$

(5)

In this expression, the IF concept lattice granule C shows the object or the set of objects A, which contains the attributes in the form of membership and nonmembership B of the IF set.

To assess different hierarchical levels of data, granulation measures can be compared by checking which granulation level provides more interesting results. To assess the hierarchical levels, a particular attribute is decomposed to check whether the data granulation provides improved results over the previous ones. Here, the focus was spatial and temporal attributes. Suppose that temporal attributes are decomposed, such that T denotes the temporal attribute, and after decomposing T in n attributes $\left\{T_1,T_2,T_3,\dots ,T_n\right\}$, it can be determined through the granulation measures which temporal decomposition provides more interesting results. Additionally, the formal context related to the T temporal attribute is shown as $K=(G,M,I)$, while that related to the decomposed temporal attributes, i.e., $T_1,T_2,T_3,\dots ,T_n$, is given by $K^{{}^{\prime }}=(G^{{}^{\prime }},M^{{}^{\prime }},I^{{}^{\prime }})$. Moreover, the granulation measures are expressed for different hierarchical levels accordingly. With this, the COV for different granularity levels can be shown as

$$COV\left(C\right)\ge COV\left(C^{{}^{\prime }}\right)$$

(6)

In addition to this, the SP for the different granular levels can also hold the following statement:

$$SP\left(C\right)\le SP\left(C^{{}^{\prime }}\right)$$

(7)

To check the granularity level of interestingness for a particular timeslot, [31] can be computed as

$$\overline{Q}\left(T\right)=\sum _{}^{}\frac{Q\left(C\right)}{n_T}$$

(8)

where $n_T$ is the cardinality of the set of IF formal concepts having T temporal attributes. It is obvious that the granulation through the decomposition of temporal attribute may lead to better results, such as

$$Q\left(C\right)\ge Q\left(C^{{}^{\prime }}\right)$$

(9)

In this way, the level of interestingness is assessed in different hierarchical granule levels by checking that the greater $Q\left(C\right)$ value is the more suitable granule in terms of interestingness.

6. Experimental Evaluation

In this section, experimental analysis for the proposed IF concept lattice granule through GrC methodology is discussed. The objective of this study is to analyze the spatio-temporal perspectives of the IF granule. The results may be used to predict the spatiality and periodicity of the information granule, particularly when the data are provided in the IF sets. The datasets used in this experiment consist of the four activity records of providing information related to spatiality and temporality of the activities executed by a specific actor or user. Here, the activities are indicated as four events, $E_1,E_2,E_3,$ and $E_4$; four places, $Plac{e}_1,Plac{e}_2,Plac{e}_3,$ and $Plac{e}_4$, denoting spatiality; and four quarters, $Q_1,Q_2,Q_3,$ and $Q_4$, of the year, denoting temporality, where events indicate objects, and places and quarters of the year indicate the attributes. The main focus of this experiment is the periodical granulation of the IF concept lattice granules. There may be hundreds of events indicating object occurrences at different spatio-temporal attributes, but here, four events as objects and four spatial and four temporal attributes for the experimental analysis are considered, as presented in

Table 3. Four Events as Objects with Four Spatial and Four Temporal Attributes Data.

	${\mathit{Place}}_1$	${\mathit{Place}}_2$	${\mathit{Place}}_3$	${\mathit{Place}}_4$	${\mathit{Q}}_1$	${\mathit{Q}}_2$	${\mathit{Q}}_3$	${\mathit{Q}}_4$
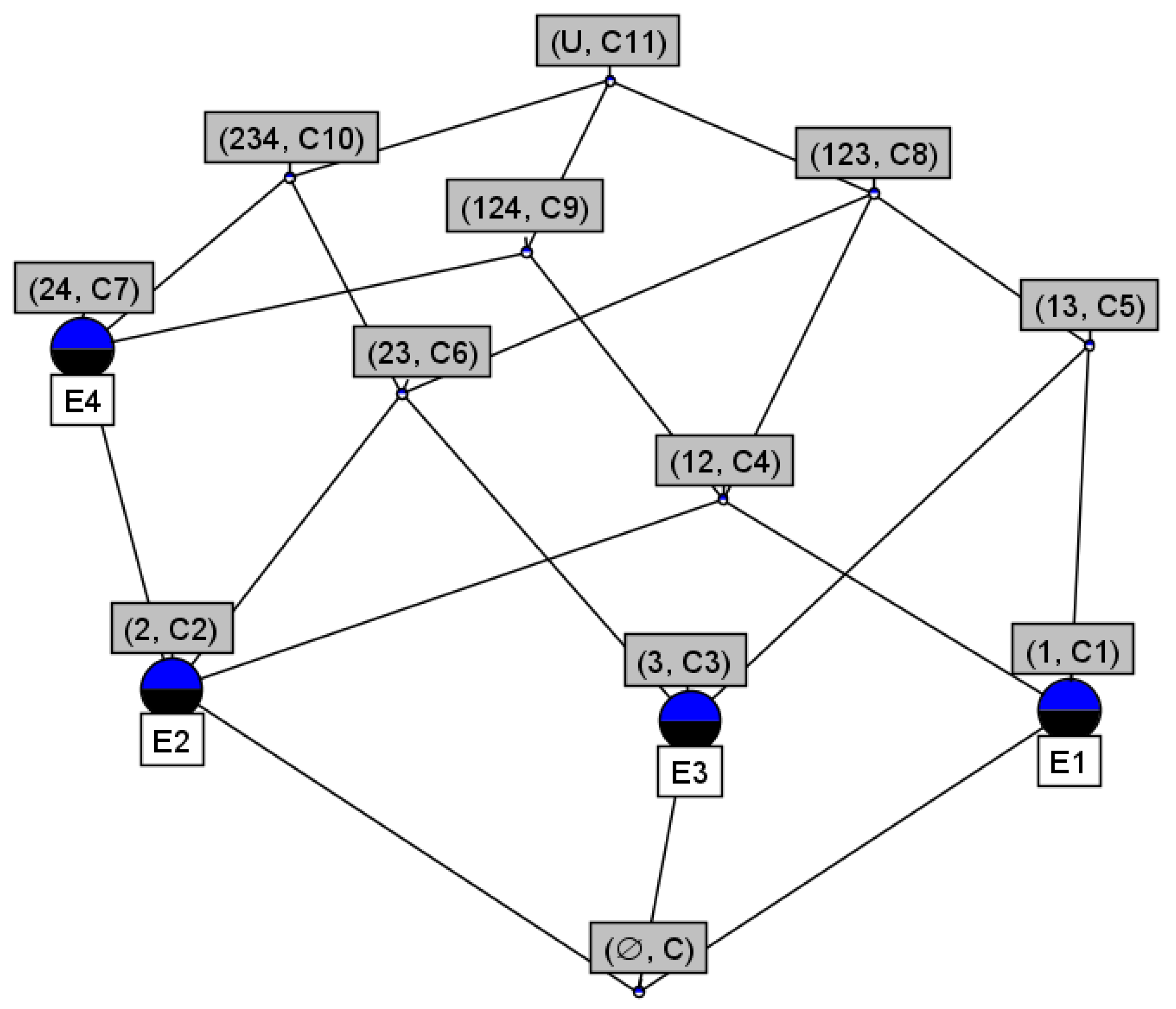
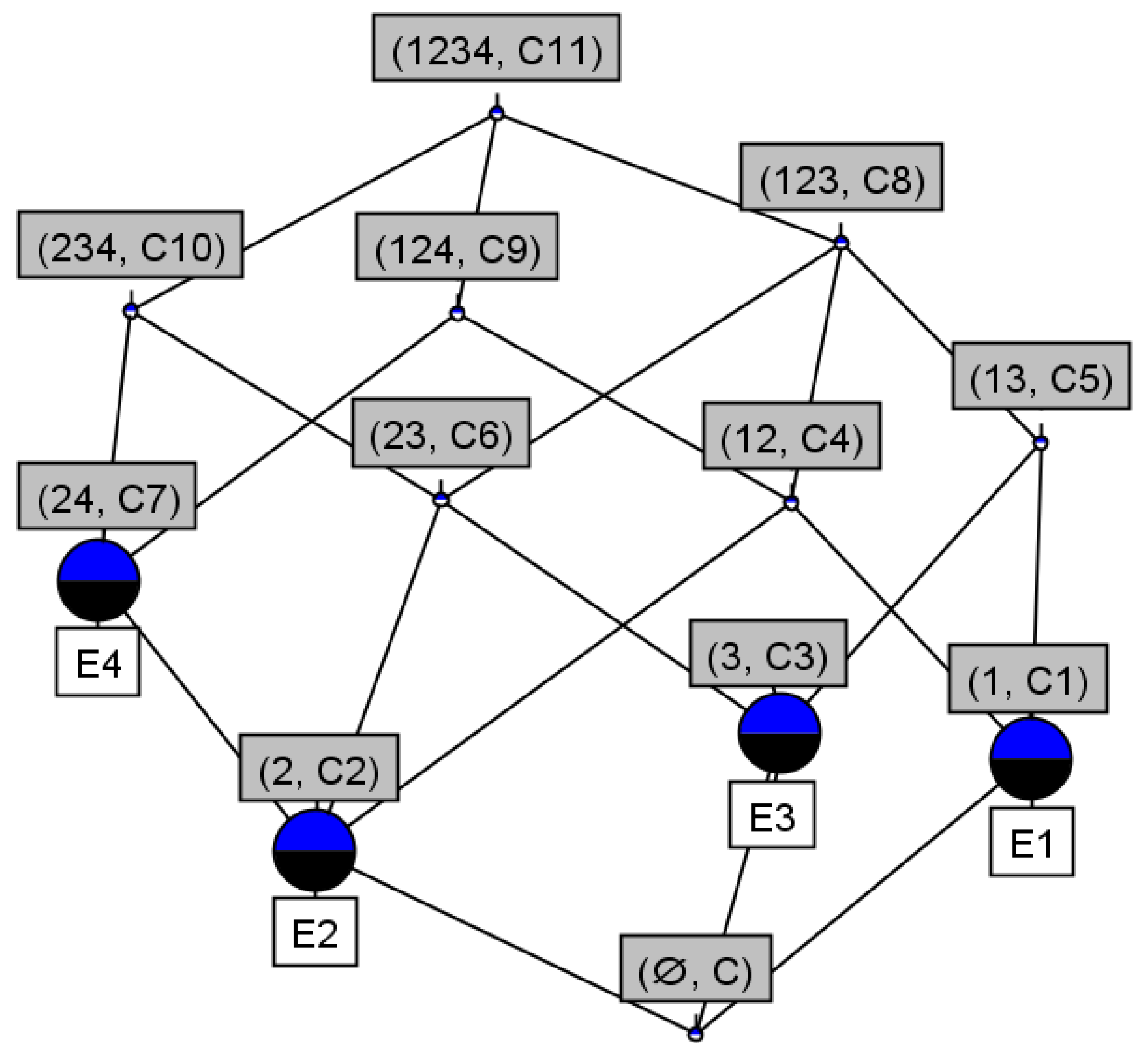
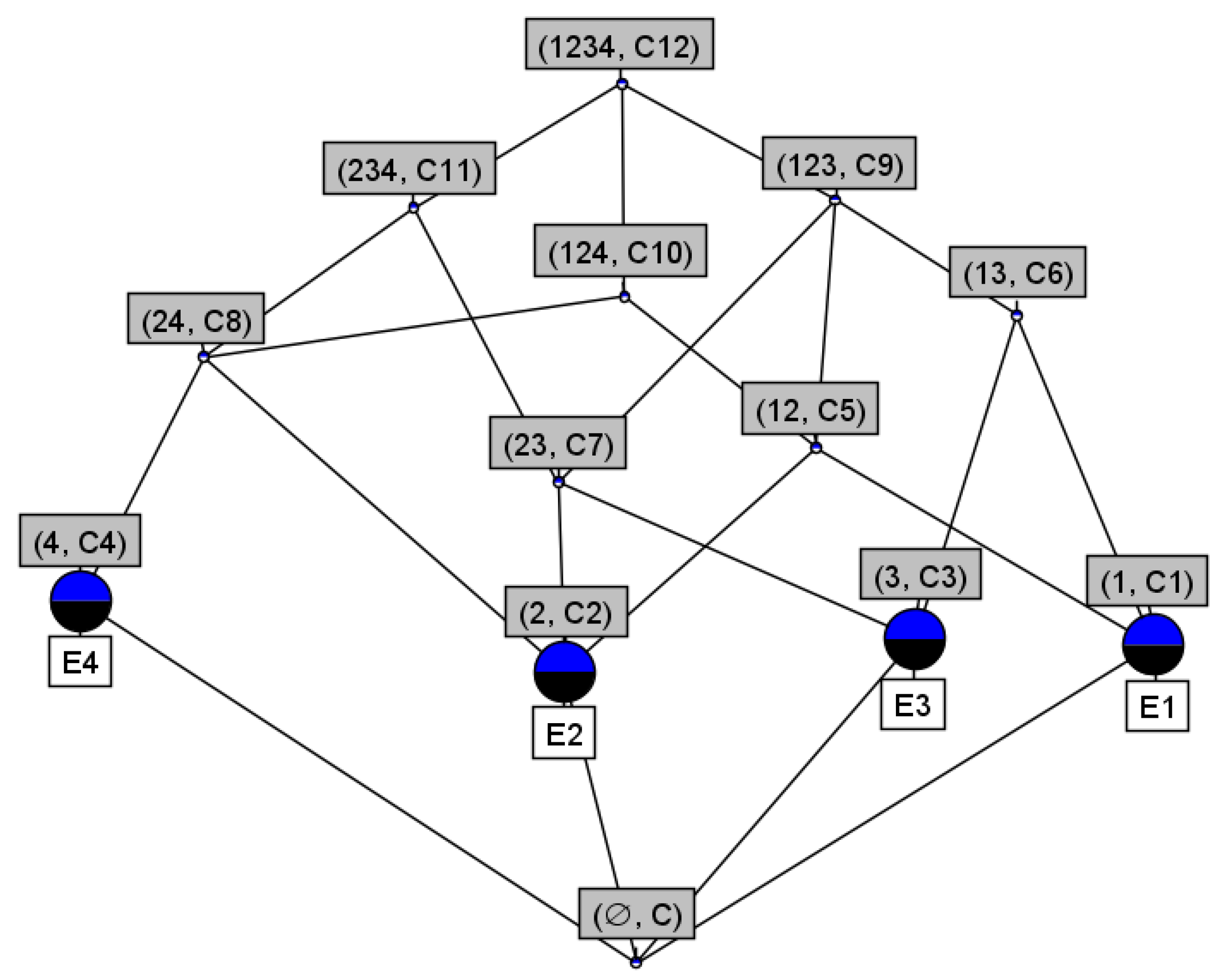
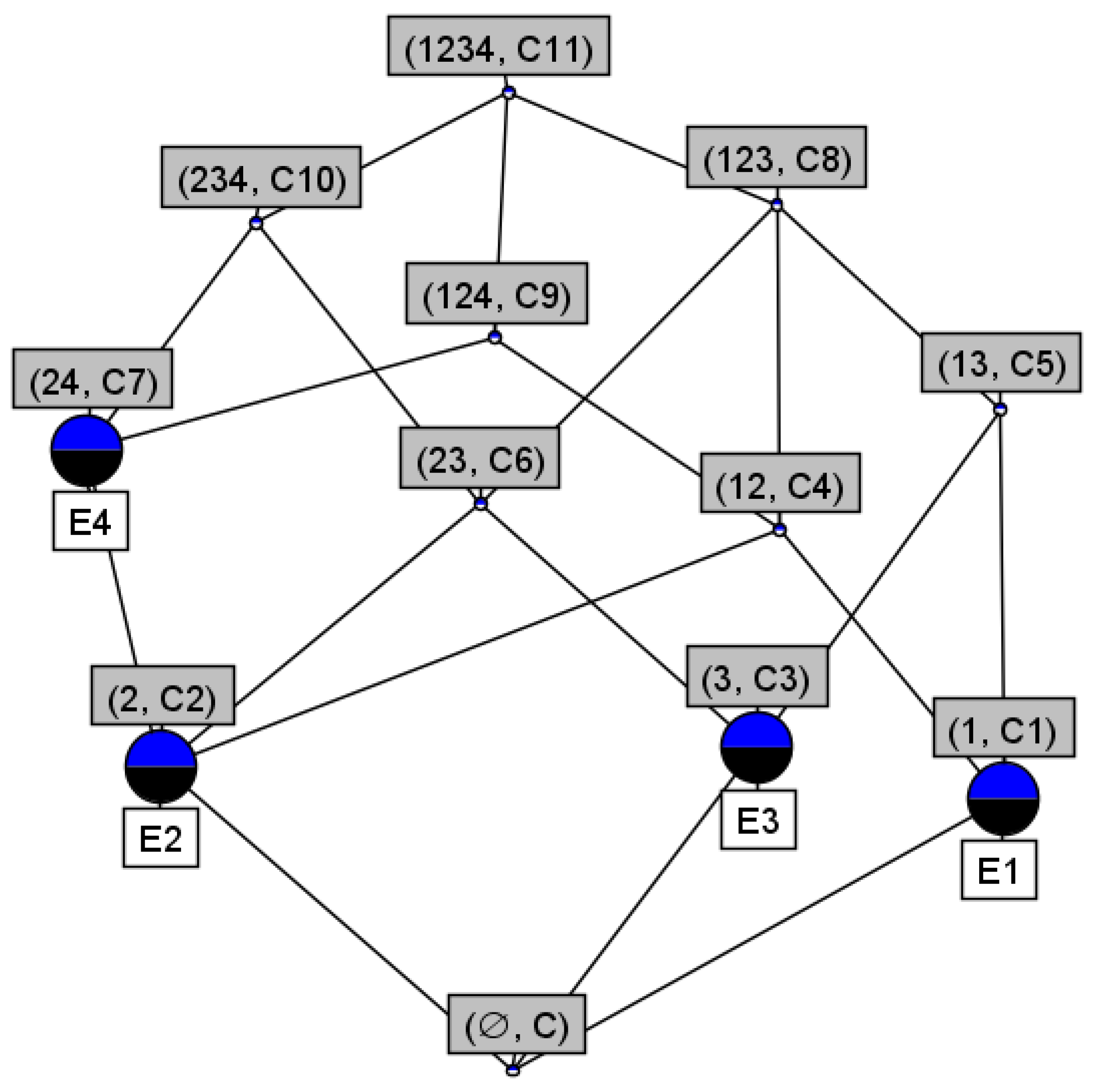
$E_1$	(0.9, 0.1)	(0.6, 0.2)	(0.3, 0.7)	(0.8, 0.1)	(0.3, 0.6)	(0.9, 0.0)	(0.7, 0.2)	(0.4, 0.3)
$E_2$	(0.3, 0.5)	(0.5, 0.5)	(0.8, 0.2)	(0.2, 0.5)	(0.7, 0.2)	(0.8, 0.1)	(0.8, 0.2)	(0.5, 0.4)
$E_3$	(0.8, 0.2)	(0.6, 0.2)	(0.7, 0.1)	(0.2, 0.7)	(0.4, 0.6)	(0.1, 0.8)	(0.7, 0.3)	(0.2, 0.7)
$E_4$	(0.2, 0.6)	(0.3, 0.6)	(0.6, 0.3)	(0.1, 0.6)	(0.2, 0.8)	(0.7, 0.2)	(0.8, 0.1)	(0.1, 0.6)

. In the temporal perspective of attributes, annual periodicity of time granulation is decomposed into four quarters, $Q_1,Q_2,Q_3,$ and $Q_4$, where these timed granulation quarters consists of Jan, Feb, and Mar; Apr, May, and June; July, Aug, and Sep; and Oct, Nov, and Dec, respectively. Additionally, the GrC approach is performed by considering the periodicity of the temporal attribute, in which the first decomposition of periodicity is set to months.

The IF concepts of the given four objects with spatial attributes in the $Q_1$ quarter of time granule are $(1,{\tilde{C}}_1^1)),(2,{\tilde{C}}_2^1),(3,{\tilde{C}}_3^1),(12,{\tilde{C}}_4^1),(13,{\tilde{C}}_5^1),(23,{\tilde{C}}_6^1),(24,{\tilde{C}}_7^1),(123,{\tilde{C}}_8^1),(124,{\tilde{C}}_9^1),(234,{\tilde{C}}_{10}^1),(U,{\tilde{C}}_{11}^1)and(\varnothing ,{\tilde{C}}_{\varnothing }^1)$ where:

$$\begin{gathered} {\tilde{C}}_1^1=\left\{(0.9,0.1),(0.6,0.2),(0.3,0.7),(0.8,0.1),(0.3,0.6)\right\},{\tilde{C}}_2^1=\left\{(0.3,0.5),(0.5,0.5),(0.8,0.2),(0.2,0.5),(0.7,0.2)\right\} \\ {\tilde{C}}_3^1=\left\{(0.8,0.2),(0.6,0.2),(0.7,0.1),(0.2,0.7),(0.4,0.6)\right\},{\tilde{C}}_4^1=\left\{(0.3,0.5),(0.5,0.5),(0.3,0.7),(0.2,0.5),(0.3,0.6)\right\} \\ {\tilde{C}}_5^1=\left\{(0.8,0.2),(0.6,0.2),(0.3,0.7),(0.2,0.7),(0.3,o.6)\right\},{\tilde{C}}_6^1=\left\{(0.3,0.5),(0.5,0.5),(0.7,0.2),(0.2,0.7),(0.4,0.6)\right\} \\ {\tilde{C}}_7^1=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.6),(0.2,0.8)\right\},{\tilde{C}}_8^1=\left\{(0.3,0.5),(0.5,0.5),(0.3,0.7),(0.2,0.7),(0.3,0.6)\right\} \\ {\tilde{C}}_9^1=\left\{(0.2,0.6),(0.3,0.6),(0.3,0.7),(0.1,0.6),(0.2,0.8)\right\},{\tilde{C}}_{10}^1=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.7),(0.2,0.8)\right\} \\ {\tilde{C}}_{11}^1=\left\{(0.2,0.6),(0.3,0.6),(0.3,0.7),(0.1,0.7),(0.2,0.8)\right\},{\tilde{C}}_{\varnothing }^1=\left\{(1,0),(1,0),(1,0),(1,0),(1,0)\right\} \end{gathered}$$

The IF values of the IF formal concepts are evaluated according to the expression $\left(min\left({\mu }_{i,j}\right),max\left({\gamma }_{i,j}\right)\right)$, given in Definition 12. The IF concept’s lattice design of the given four objects with spatio-temporal attributes with the $Q_1$ quarter of time granule is given in Figure 1.

Similarly, the IF concepts of the given four objects with spatial attributes in the $Q_2$ quarter of time granule are $(1,{\tilde{C}}_1^2),(2,{\tilde{C}}_2^2),(3,{\tilde{C}}_3^2),(12,{\tilde{C}}_4^2),(13,{\tilde{C}}_5^2),(23,{\tilde{C}}_6^2),(24,{\tilde{C}}_7^2),(123,{\tilde{C}}_8^2),(124,{\tilde{C}}_9^2),(234,{\tilde{C}}_{10}^2),(1234,{\tilde{C}}_{11}^2),(\varnothing ,{\tilde{C}}_{\varnothing }^2)$ where:

$$\begin{gathered} {\tilde{C}}_1^2=\left\{(0.9,0.1),(0.6,0.2),(0.3,0.7),(0.8,0.1),(0.9,0.0)\right\},{\tilde{C}}_2^2=\left\{(0.3,0.5),(0.5,0.5),(0.8,0.2),(0.2,0.5),(0.8,0.1)\right\} \\ {\tilde{C}}_3^2=\left\{(0.8,0.2),(0.6,0.2),(0.7,0.1),(0.2,0.7),(0.1,0.8)\right\},{\tilde{C}}_4^2=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.6),(0.7,0.2)\right\} \\ {\tilde{C}}_5^2=\left\{(0.8,0.2),(0.6,0.2),(0.3,0.7),(0.2,0.7),(0.1,0.8)\right\},{\tilde{C}}_6^2=\left\{(0.3,0.5),(0.5,0.5),(0.7,0.2),(0.2,0.7),(0.1,0.8)\right\} \\ {\tilde{C}}_7^2=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.6),(0.7,0.2)\right\},{\tilde{C}}_8^2=\left\{(0.3,0.5),(0.5,0.5),(0.3,0.7),(0.2,0.7),(0.1,0.8)\right\} \\ {\tilde{C}}_9^2=\left\{(0.2,0.6),(0.3,0.6),(0.3,0.7),(0.1,0.6),(0.7,0.2)\right\},{\tilde{C}}_{10}^2=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.7),(0.1,0.8)\right\} \\ {\tilde{C}}_{11}^2=\left\{(0.2,0.6),(0.3,0.6),(0.3,0.7),(0.1,0.7),(0.1,0.8)\right\},{\tilde{C}}_{\varnothing }^2=\left\{(1,0),(1,0),(1,0),(1,0),(1,0)\right\} \end{gathered}$$

The IF concept’s lattice design of the given four objects with spatio-temporal attributes with the $Q_2$ quarter of time granule is given in Figure 2.

Moreover, the IF concepts of the given four objects with spatial attributes in the $Q_3$ quarter of time granule are $(1,{\tilde{C}}_1^3),(2,{\tilde{C}}_2^3),(3,{\tilde{C}}_3^3),(4,{\tilde{C}}_4^3),(12,{\tilde{C}}_5^3),(13,{\tilde{C}}_6^3),(23,{\tilde{C}}_7^3),(24,{\tilde{C}}_8^3),(123,{\tilde{C}}_9^3),(124,{\tilde{C}}_{10}^3),(234,{\tilde{C}}_{11}^3),(1234,{\tilde{C}}_{12}^3),(\varnothing ,{\tilde{C}}_{\varnothing }^3)$ where:

$$\begin{gathered} {\tilde{C}}_1^3=\left\{(0.9,0.1),(0.6,0.2),(0.3,0.7),(0.8,0.1),(0.7,0.2)\right\},{\tilde{C}}_2^3=\left\{(0.3,0.5),(0.5,0.5),(0.8,0.2),(0.2,0.5),(0.8,0.2)\right\} \\ {\tilde{C}}_3^3=\left\{(0.8,0.2),(0.6,0.2),(0.7,0.1),(0.2,0.7),(0.7,0.3)\right\},{\tilde{C}}_4^3=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.6),(0.8,0.1)\right\} \\ {\tilde{C}}_5^3=\left\{(0.3,0.5),(0.5,0.5),(0.3,0.7),(0.2,0.5),(0.7,0.2)\right\},{\tilde{C}}_6^3=\left\{(0.8,0.2),(0.6,0.2),(0.3,0.7),(0.2,0.7),(0.7,0.3)\right\} \\ {\tilde{C}}_7^3=\left\{(0.3,0.5),(0.5,0.5),(0.7,0.2),(0.2,0.7),(0.7,0.3)\right\},{\tilde{C}}_8^3=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.6),(0.8,0.2)\right\} \\ {\tilde{C}}_9^3=\left\{(0.3,0.5),(0.5,0.5),(0.3,0.7),(0.2,0.7),(0.7,0.3)\right\},{\tilde{C}}_{10}^3=\left\{(0.2,0.6),(0.3,0.6),(0.3,0.7),(0.1,0.6),(0.7,0.2)\right\} \\ {\tilde{C}}_{11}^3=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.7),(0.7,0.3)\right\},{\tilde{C}}_{12}^3=\left\{(0.2,0.6),(0.3,0.6),(0.3,0.7),(0.1,0.7),(0.7,0.3)\right\} \\ {\tilde{C}}_{\varnothing }^3=\left\{(1,0),(1,0),(1,0),(1,0),(1,0)\right\} \end{gathered}$$

The IF concept’s lattice design of the given four objects with spatio-temporal attributes with the $Q_3$ quarter of time granule is given in Figure 3.

Similarly, the IF concepts of the given four objects with spatial attributes in the $Q_4$ quarter of time granule are $(1,{\tilde{C}}_1^4),(2,{\tilde{C}}_2^4),(3,{\tilde{C}}_3^4),(12,{\tilde{C}}_4^4),(13,{\tilde{C}}_5^4),(23,{\tilde{C}}_6^4),(24,{\tilde{C}}_7^4),(123,{\tilde{C}}_8^4),(124,{\tilde{C}}_9^4),(234,{\tilde{C}}_{10}^4),(1234,{\tilde{C}}_{11}^4),(\varnothing ,{\tilde{C}}_{\varnothing }^4)$ where:

$$\begin{gathered} {\tilde{C}}_1^4=\left\{(0.9,0.1),(0.6,0.2),(0.3,0.7),(0.8,0.1),(0.4,0.3)\right\},{\tilde{C}}_2^4=\left\{(0.3,0.5),(0.5,0.5),(0.8,0.2),(0.2,0.5),(0.5,0.4)\right\} \\ {\tilde{C}}_3^4=\left\{(0.8,0.2),(0.6,0.2),(0.7,0.1),(0.2,0.7),(0.2,0.7)\right\},{\tilde{C}}_4^4=\left\{(0.3,0.5),(0.5,0.5),(0.3,0.7),(0.2,0.5),(0.4,0.4)\right\} \\ {\tilde{C}}_5^4=\left\{(0.8,0.2),(0.6,0.2),(0.3,0.7),(0.2,0.7),(0.2,0.7)\right\},{\tilde{C}}_6^4=\left\{(0.3,0.5),(0.5,0.5),(0.7,0.2),(0.2,0.7),(0.2,0.7)\right\} \\ {\tilde{C}}_7^4=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.6),(0.1,0.6)\right\},{\tilde{C}}_8^4=\left\{(0.3,0.5),(0.5,0.5),(0.3,0.7),(0.2,0.7),(0.2,0.7)\right\} \\ {\tilde{C}}_9^4=\left\{(0.2,0.6),(0.3,0.6),(0.3,0.7),(0.1,0.6),(0.1,0.6)\right\},{\tilde{C}}_{10}^4=\left\{(0.2,0.6),(0.3,0.6),(0.6,0.3),(0.1,0.7),(0.1,0.7)\right\} \\ {\tilde{C}}_{11}^4=\left\{(0.2,0.6),(0.3,0.6),(0.3,0.7),(0.1,0.7),(0.1,0.7)\right\},{\tilde{C}}_{\varnothing }^4=\left\{(1,0),(1,0),(1,0),(1,0),(1,0),(1,0)\right\} \end{gathered}$$

Here, the IF concept’s lattice design of the given four objects with spatio-temporal attributes with the $Q_4$ quarter of time granule is given in Figure 4.

Now, according to Equation (1), the IG of each lattice designed with the four events showing the objects along with each quarter of the time granulation is given below:

$Lattic{e}_1$(designed with $Q_1$ quarter of time granulation) $IG:$ 0.53

$Lattic{e}_2$(designed with $Q_2$ quarter of time granulation) $IG:$ 0.58

$Lattic{e}_3$(designed with $Q_3$ quarter of time granulation) $IG:$ 0.60

$Lattic{e}_4$(designed with $Q_4$ quarter of time granulation) $IG:$ 0.52

Here, $Lattic{e}_3$, designed with the $Q_3$ quarter of time granulation, gives more IG than the other three lattices designed with the other three quarters of time granulation, respectively. A higher IG leads to more interesting results with a less focused view of the data. Now, the granulation measures COV and SP of $Lattic{e}_3$ IF concepts can be measured through Equation (2) and Equation (3), respectively. According to Equations (2)–(4), the COV, SP, and Q value of each IF concept of $Lattic{e}_3$ is given in

Table 4. Granulation measures of each IF concept of $Lattic{e}_3$.

	$\mathit{COV}\left(\mathit{C}\right)=$$\left[\left(\frac{\mathit{D}}{\mathit{G}}\times \frac{1}{\mathit{N}}{\sum }_{\mathit{i}=1}^{\mathit{N}}\mathit{C}\left({\mathit{x}}_{{\mathit{\mu }}_{\mathit{j}}}\right)\right)+\frac{{\mathit{\pi }}_{\mathit{j}}}{2}\right]$	$\mathit{SP}\left(\mathit{C}\right)=$$\left[1-\frac{\mathit{len}\left(\mathit{d}\right)}{\mathit{range}}\right]\times$$\left[\mathit{\alpha }-\frac{1}{\mathit{n}-1}{\sum }_{\mathit{X}\ne {\mathit{X}}^{*}}^{}\mathit{G}\left(\mathit{x}\right)\right]$	$\mathit{Q}\left(\mathit{C}\right)=$$\mathit{COV}\left(\mathit{C}\right)\times {\left(\mathit{SP}\left(\mathit{C}\right)\right)}^{\mathit{\zeta }}$
$C_1$	0.365	0.95	0.34675
$C_2$	0.38	0.89	0.3382
$C_3$	0.4	0.96	0.384
$C_4$	0.5	0.92	0.46
$C_5$	0.5	0.93	0.465
$C_6$	0.41	0.93	0.3813
$C_7$	0.44	0.92	0.4048
$C_8$	0.55	0.92	0.506
$C_9$	0.45	0.92	0.414
$C_{10}$	0.59	0.92	0.5428
$C_{11}$	0.585	0.94	0.5499
$C_{12}$	0.57	0.91	0.5187
$C_{13}$	0	0	0

.

Now, if the $Q_3$ quarter of time granulation is decomposed into more parts, then this decomposition of the $Q_3$ quarter may provide more interesting results. For this purpose, let $Q_{3,1},Q_{3,2}$, and $Q_{3,3}$ contain the July, August, and September IF data, respectively. This is the second decomposition of the IF concept lattice designed through the $Q_3$ quarter of time granulation. Thus, the four events’ IF data with spatio-temporal attributes of the $Q_3$ quarter’s second decomposition are given in

Table 5. Events with Four Spatial and Three (decomposed) $Q_{3,1},Q_{3,2}$, and $Q_{3,3}$ Temporal Attributes Data.

	${\mathit{Place}}_1$	${\mathit{Place}}_2$	${\mathit{Place}}_3$	${\mathit{Place}}_4$	${\mathit{Q}}_{3,1}$	${\mathit{Q}}_{3,2}$	${\mathit{Q}}_{3,3}$
$E_1$	(0.9, 0.1)	(0.6, 0.2)	(0.3, 0.7)	(0.8, 0.1)	(0.9, 0.0)	(0.0, 0.9)	(0, 0)
$E_2$	(0.3, 0.5)	(0.5, 0.5)	(0.8, 0.2)	(0.2, 0.5)	(1, 0)	(0, 1)	(0, 0)
$E_3$	(0.8, 0.2)	(0.6, 0.2)	(0.7, 0.1)	(0.2, 0.7)	(0.8, 0.1)	(0.1, 0.9)	(0, 0)
$E_4$	(0.2, 0.6)	(0.3, 0.6)	(0.6, 0.3)	(0.1, 0.6)	(0.9, 0.1)	(0.1, 0.8)	(0, 0)

.

The IG of each lattice, $Lattic{e}_{3,1},Lattic{e}_{3,2}$, and $Lattic{e}_{3,3}$, with second decomposition of $Q_{3,1},Q_{3,2}$, and $Q_{3,3}$ quarters of time granulation, respectively, is given below:

$Lattic{e}_{3,1}$ (designed with $Q_{3,1}$ quarter of time granulation) $IG:$ 0.63

$Lattic{e}_{3,2}$ (designed with $Q_{3,2}$ quarter of time granulation) $IG:$ 0.46

$Lattic{e}_{3,3}$ (designed with $Q_{3,3}$ quarter of time granulation) $IG:$ 0.44

It shows that $Lattic{e}_{3,1}$, made with the $Q_{3,1}$ quarter of time granulation, gives more IG than the other lattices of timed granulations. Moreover, the granulation measures of the each concept lattice (as made with $Lattic{e}_3$), i.e., made with the $Q_{3,1}$ quarter of time granulation, are given as in

Table 6. Granulation measures of each IF concept of $Lattic{e}_{3,1}$.

	$\mathit{COV}\left(\mathit{C}\right)=$$\left[\left(\frac{\mathit{D}}{\mathit{G}}\times \frac{1}{\mathit{N}}{\sum }_{\mathit{i}=1}^{\mathit{N}}\mathit{C}\left({\mathit{x}}_{{\mathit{\mu }}_{\mathit{j}}}\right)\right)+\frac{{\mathit{\pi }}_{\mathit{j}}}{2}\right]$	$\mathit{SP}\left(\mathit{C}\right)=$$\left[1-\frac{\mathit{len}\left(\mathit{d}\right)}{\mathit{range}}\right]\times$$\left[\mathit{\alpha }-\frac{1}{\mathit{n}-1}{\sum }_{\mathit{X}\ne {\mathit{X}}^{*}}^{}\mathit{G}\left(\mathit{x}\right)\right]$	$\mathit{Q}\left(\mathit{C}\right)=$$\mathit{COV}\left(\mathit{C}\right)\times {\left(\mathit{SP}\left(\mathit{C}\right)\right)}^{\mathit{\zeta }}$
$C_1$	0.365	0.9	0.3285
$C_2$	0.39	0.89375	0.3485625
$C_3$	0.455	0.91875	0.4180313
$C_4$	0.52	0.8875	0.4615
$C_5$	0.47	0.8875	0.417125
$C_6$	0.5	0.93125	0.465625
$C_7$	0.56	0.89375	0.5005
$C_8$	0.515	0.9	0.4635
$C_9$	0.57	0.86875	0.4951875
$C_{10}$	0.65	0.9125	0.593125
$C_{11}$	0.64	0.8875	0.568
$C_{12}$	0	0	0

.

Likewise, it can be observed that the granule $Lattic{e}_2$, designed with the $Q_2$ quarter of time granulation with an IG of 0.58, is the second highest IG. So, the granulation measures COV, SP, and the Q value of the lattice, i.e., made with the $Q_2$ quarter of time granulation, are given as in

Table 7. Granulation measures of each IF concept of $Lattic{e}_2$.

	$\mathit{COV}\left(\mathit{C}\right)=$$\left[\left(\frac{\mathit{D}}{\mathit{G}}\times \frac{1}{\mathit{N}}{\sum }_{\mathit{i}=1}^{\mathit{N}}\mathit{C}\left({\mathit{x}}_{{\mathit{\mu }}_{\mathit{j}}}\right)\right)+\frac{{\mathit{\pi }}_{\mathit{j}}}{2}\right]$	$\mathit{SP}\left(\mathit{C}\right)=$$\left[1-\frac{\mathit{len}\left(\mathit{d}\right)}{\mathit{range}}\right]\times$$\left[\mathit{\alpha }-\frac{1}{\mathit{n}-1}{\sum }_{\mathit{X}\ne {\mathit{X}}^{*}}^{}\mathit{G}\left(\mathit{x}\right)\right]$	$\mathit{Q}\left(\mathit{C}\right)=$$\mathit{COV}\left(\mathit{C}\right)\times {\left(\mathit{SP}\left(\mathit{C}\right)\right)}^{\mathit{\zeta }}$
$C_1$	0.175	0.9	0.1575
$C_2$	0.13	0.89375	0.116188
$C_3$	0.12	0.93125	0.11175
$C_4$	0.21	0.9125	0.191625
$C_5$	0.2	0.9	0.18
$C_6$	0.18	0.91875	0.165375
$C_7$	0.19	0.94375	0.179313
$C_8$	0.21	0.95625	0.200813
$C_9$	0.24	0.91875	0.2205
$C_{10}$	0.195	0.93125	0.181594
$C_{11}$	0.2	0.975	0.195
$C_{12}$	0	0	0

.

Note, the value of “$\zeta =1$” is used because of the primary decomposition of the granules. Here, primary decomposition means partitioning the data into months, because the first decided decomposition is set to one month. Moreover, partitioning one month into two timeslots would be the secondary decomposition; in that case, the value of “$\zeta$” is 0.5. The applicability of the proposed approach is the knowledge discovery of periodical events’ occurrences (co-occurrences), nonoccurrences, and uncertainty of occurrences/nonoccurrences in spatial and temporal aspects through IF datasets by applying FCA and GrC.

7. Results and Discussion

The experiments were performed on a 64-bit system (Intel Core i3-4010U, 1.70 GHz, 4 GB RAM). Python (version 3.7) was used to construct the IF concepts’ lattice structures in the experimental evaluation section. In the experimental evaluation of this research article, IF data are taken to process the proposed methodology. Additionally, this IF data contain four events, happening at four places in a year. For the first decomposition, one-year timeslot data are partitioned into four quarters of the time granulation of events happening at the given four places, where events show the objects and places, with time granulation data indicating the attributes. The purpose of this methodology is to analyze the spatio-temporal perspectives of the IF granule. More specifically, the idea is to find out whether the granulation of IF data provides more interesting results. In the experimental evaluation, the IG of the four lattices designed with the four events (objects) is analyzed first, which happens at four places in four different quarters of the year, showing the spatio-temporal attributes given as

$Lattic{e}_1$(designed with $Q_1$ quarter of time granulation) $IG:$ 0.53

$Lattic{e}_2$(designed with $Q_2$ quarter of time granulation) $IG:$ 0.58

$Lattic{e}_3$(designed with $Q_3$ quarter of time granulation) $IG:$ 0.60

$Lattic{e}_4$(designed with $Q_4$ quarter of time granulation) $IG:$ 0.52

Hence, the IG of $Lattic{e}_3$ made with the $Q_3$ quarter of time granulation is higher than the IG of all three lattices, so $Lattic{e}_3$ is chosen for further granulation measures. The COV, SP, and Q value of each of $Lattic{e}_3$’s IF concept are calculated and given in Table 4. For the second decomposition, the $Q_3$ quarter is partitioned into three more timeslots, $Q_{3,1},Q_{3,2}$, and $Q_{3,3}$, and the IG of lattices is made with the second partitioned timeslots, given as

$Lattic{e}_{3,1}$ (designed with $Q_{3,1}$ quarter of time granulation) $IG:$ 0.63

$Lattic{e}_{3,2}$ (designed with $Q_{3,2}$ quarter of time granulation) $IG:$ 0.46

$Lattic{e}_{3,3}$ (designed with $Q_{3,3}$ quarter of time granulation) $IG:$ 0.44

It can be observed that the IG of the lattice with the $Q_{3,1}$ quarter of time granulation is greater than all the other IGs of the second decomposition lattices; therefore, if the granulation measures of $Lattic{e}_{3,1}$ with the $Q_{3,1}$ quarter of time granulation are checked in Table 6, it can be seen that most of the IF concepts of the second decomposed lattice have more COV and Q values than those of $Lattic{e}_3$ with the $Q_3$ quarter of time granulation. Hence, the granularity of data in IF sets gives more interesting results.

8. Comparison with Previous SOTA (State of the Art) Approaches

8.1. Comparison with Previous Spatial and Temporal Approaches Using FCA and GrC

This approach and its results are compared with other SOTA methodologies based on the research methodology, the GrC perspective of spatial and temporal aspects and the data viewpoint with the FCA algorithm. In [1], the authors present and evaluate a method which uses an existing approach to discover periodic events in the data to combine time-based granulation and three-way decisions to support decision makers in understanding and reasoning on the learned granular structures conceptualizing spatial–temporal events. In [7], the methodology interprets, represents, and implements sequential three-way GrC with a framework of temporal–spatial multigranularity learning, which is described with the temporality of data and the spatiality of parameters. The method in [31], based on the GrC and FCA technique, proposes an approach which focuses on the temporal aspect of data to extracte knowledge concerning the periodic occurrences of events. In the context of three-way GrC, the authors in [46] introduce three extensional ideas, temporal, spatial, spatial–temporal-based trisecting–acting–outcome (TAO) frameworks for the construction of a multilevel composite granular structure.

In the literature, knowledge discovery through spatial and temporal aspects of data uses the classical FCA algorithm (using single-value attributes) and the GrC paradigm for the occurrences and co-occurrences of events. However, there can be three aspects of events: occurrences (and co-occurrences), nonoccurrences, and uncertainty of occurrences/nonoccurrences with respect to spatial and temporal aspects of data. In this proposed approach, IF datasets were used for events, such that event occurrences (and co-occurrences), nonoccurrences, and uncertainty of occurrences/nonoccurrences in spatial and temporal views can be indicated through the $\mu ,$$\gamma$, and $\pi$ values, respectively. GrC was used to discover the periodicity in the data at various abstraction levels, while FCA was used to discover the granulation levels and process the granulation measures to understand IF concepts. References [1,31] use an FCA-based single-value attribute for the single aspect of event occurrences (and co-occurrences) with respect to the spatial and temporal aspects, while [7,46] use granular structures for the spatial and temporal aspects of data. The main advantages of the proposed approach over the existing approaches are discovering the periodicity of spatial–temporal events data given in IF sets through GrC and the FCA algorithm and predicting event occurrences, (and co-occurrences), nonoccurrences, and uncertainty of occurrences/nonoccurrences in spatial and temporal views of data through IF sets. The comparison of the proposed approach with other SOTA approaches is presented in

Table 8. Comparison with other SOTA approaches.

Research Article	Research Methodology	GrC (Spatial or Temporal) Perspective	Data Viewpoint with FCA/IF Sets
[1]	A method to combine time-based granulation and three-way decisions to understand and reason on learned granular structures and discover periodic events.	Spatial and temporal aspects of data granularity	FCA-based single-value attribute
[7]	The method implements sequential three-way GrC by a spatial–temporal multigranularity learning framework, described with the temporality of data and spatiality of parameters.	Spatial and temporal aspects of data granularity	-
[31]	A method based on GrC and FCA to focus the temporal aspect and extract the knowledge concerning periodic occurrences of events in data.	Temporal aspect of data granularity.	FCA-based single-value attribute.
[46]	Temporal, spatial, and spatial–temporal-based trisecting–acting–outcome (TAO) frameworks for the construction of multilevel composite granular structures are introduced.	Spatial, temporal, and spatial–temporal aspects of data granularity	-
Proposed Approach	This approach analyzes and predict event occurrences, nonoccurrences, and uncertainty of occurrences/nonoccurrences through spatial and temporal aspects given in IF sets’ data using GrC and FCA.	Temporal aspect of data granularity in IF datasets	IF set values using granular computing and the FCA algorithm

.

8.2. Comparison with Finding IE/IG

IG is computed through IE (uncertainty) in data. In GrC, the approaches [31,35] calculate IE and IG using single-value attributes for the FCA while considering the one aspect of event occurrences (co-occurrences). However, the proposed approach based on the GrC paradigm uses IF datasets for the attributes of FCA that improves the results of IG. Additionally, unlike the existing approaches, the proposed approach provides three aspects of event occurrences (co-occurrences), nonoccurrence, and uncertainty of occurrence/nonoccurrence in the spatial and temporal views of data. The comparison of (improved results computed through) the proposed approach with other SOTA approaches [31,35] is presented in

Table 9. Comparison with other research methodologies to find IG. Higher values are bolded.

Lattice No.	Results Obtained with Approaches Used [31,35]	Results Obtained with the Proposed Approach
$Lattic{e}_1$	0.25	0.53
$Lattic{e}_2$	0.25	0.58
$Lattic{e}_3$	0.25	0.60
$Lattic{e}_4$	0.25	0.52
$Lattic{e}_{3,1}$	0.25	0.63
$Lattic{e}_{3,2}$	0.25	0.46
$Lattic{e}_{3,3}$	0.25	0.44

.

Here, the IG results obtained with the approaches of [31,35] are unchanged due to the different IF $\mu$ and $\gamma$ values in all the attributes shared by the objects in each lattice.

8.3. Comparison with Finding COV, SP, and Q Value

COV, SP, and Q value are important granulation measures to analyze the granule. In [31], granules are represented in the form of formal concepts and GrC and evaluated through these granulation measures; moreover, in [44,45], these granulation measures are proposed for the granules represented in fuzzy and IF sets. In existing approaches, granulation measures are used only in the perspectives of GrC with the FCA algorithm [31], or on fuzzy and IF sets [44,45]. However, the granulation measures in the proposed approach are used in the perspective of GrC, FCA, and IF sets. In the proposed approach, IF concepts are made and represented as granules, where the granulation measures are used to evaluate those granules. The comparison given in

Table 10. Comparison with other Research Methodologies to find the granulation measures (COV, SP, and Q value) of $Lattic{e}_3$. Higher values are bolded.

	COV, SP and Q Value Obtained with Approaches Used in [44,45]			COV, SP and Q Value Obtained with Proposed Approach
${\mathit{Lattice}}_{\mathbf{3}}$ IF Concepts	COV	SP	Q Value	COV	SP	Q Value
$C_1$	0.66	0.175	0.1155	0.365	0.95	0.34675
$C_2$	0.52	0.425	0.221	0.38	0.89	0.3382
$C_3$	0.6	0.15	0.09	0.4	0.96	0.384
$C_4$	0.4	0.325	0.13	0.5	0.92	0.46
$C_5$	0.4	0.25	0.1	0.5	0.93	0.465
$C_6$	0.52	0.275	0.143	0.41	0.93	0.3813
$C_7$	0.48	0.325	0.156	0.44	0.92	0.4048
$C_8$	0.4	0.325	0.13	0.55	0.92	0.506
$C_9$	0.4	0.3	0.12	0.45	0.92	0.414
$C_{10}$	0.32	0.325	0.104	0.59	0.92	0.5428
$C_{11}$	0.38	0.25	0.095	0.585	0.94	0.5499
$C_{12}$	0.32	0.35	0.112	0.57	0.91	0.5187
$C_{13}$	1	0	0	0	0	0

and

Table 11. Comparison with other Research Methodologies to find the granulation measures (COV, SP, and Q value) of $Lattic{e}_{3,1}$. Higher values are bolded.

	COV, SP and Q Value Obtained with Approaches Used in [44,45]			COV, SP and Q Value Obtained with Proposed Approach
${\mathit{Lattice}}_{\mathbf{3},\mathbf{1}}$ IF Concepts	COV	SP	Q Value	COV	SP	Q Value
$C_1$	0.66	0.4	0.264	0.365	0.9	0.328
$C_2$	0.56	0.425	0.238	0.39	0.89375	0.348
$C_3$	0.62	0.325	0.2015	0.455	0.91875	0.418
$C_4$	0.44	0.45	0.198	0.52	0.8875	0.462
$C_5$	0.54	0.45	0.243	0.47	0.8875	0.417
$C_6$	0.5	0.275	0.1375	0.5	0.931	0.466
$C_7$	0.42	0.425	0.179	0.56	0.894	0.5005
$C_8$	0.42	0.4	0.168	0.515	0.9	0.464
$C_9$	0.36	0.525	0.189	0.57	0.86875	0.495
$C_{10}$	0.4	0.35	0.14	0.65	0.9125	0.593
$C_{11}$	0.34	0.45	0.153	0.64	0.8875	0.568
$C_{12}$	1	0	0	0	0	0

shows that the granulation measures used in the proposed approach give improved results.

The proposed approach is compared with other SOTA approaches by applying granulation measures on the IF datasets given in Section 6 (experimental evaluation). These IF datasets contain events as objects and spatial and temporal attributes, in which the temporal attribute is decomposed into four quarters, $Q_1,Q_2,Q_3,$ and $Q_4$ of the annual periodicity of time granulation, and four granules are created in the first decomposition. Afterwards, the IG of each granule is computed to determine the granule with more IG. FCA is then used to construct lattices from each granule, and granulation measures are performed on the decided granule (with more IG). As shown in Table 9, the IG obtained with the proposed approach is greater than that obtained with other approaches [31,35]. In Table 9, the IG obtained with the other approaches is the same for all the lattices, because none of the objects have identical IF values. Furthermore, in Table 10 and Table 11, most of the granulation measures (COV, SP, and Q value) of $Lattic{e}_3$ and $Lattic{e}_{3,1}$ obtained with the proposed approach are greater than the existing approaches [44,45]. Hence, it can be observed that the proposed approach provides improved results for IG, COV, and Q value obtained from the IF datasets and processed through GrC and the FCA algorithm.

9. Conclusions and Future Work

This research suggests a novel approach to determine occurrences (and co-occurrences), nonoccurrences, and uncertainty of occurrences/nonoccurrences of events based on GrC and IF datasets with spatio-temporal attributes. The FCA algorithm was used to analyze the granulation level and granulation measures. Furthermore, different measures are proposed to analyze granulation levels formed with the IF datasets. The originality of this proposed methodology is to discover the periodical occurrences (and co-occurrences), nonoccurrences, and uncertainty of occurrences/nonoccurrences in IF datasets with spatio-temporal attributes using FCA and granulation measures. Here, the limited IF datasets indicating the spatial and temporal aspects of data are considered for the experimentation and work of the proposed methodology. This can be implemented on a large number of IF datasets in the context of big data for the scalability of the proposed methodology. In the real world, this approach can be used to discover the significance in periodicities of data related to storm occurrences, digital forensics, and electronic and smart video surveillance by constructing a timeline to analyze and predict information. Moreover, the proposed approach does not provide an automatic or semiautomatic process to predict an event’s occurrence in granular structures. The authors aim to address these additions in future works.