Disturbance Attenuation Trajectory Tracking Control of Unmanned Surface Vessel Subject to Measurement Biases
Abstract
1. Introduction
- The proposed controller was recursively synthesized under the backstepping control framework. Particularly, two disturbance observers were incorporated to estimate the mismatched and matched lumped disturbances. In this way, the proposed controller is robust against model uncertainties and external disturbances and insensitive to measurement biases.
- Meanwhile, the proposed controller is structurally simple and user friendly. Only four parameters need to be adjusted to achieve satisfactory tracking performance.
- The uniform ultimate boundedness of the closed-loop system is strictly proven. The stability argument shows that all error signals under the proposed controller can regulate to the small neighborhoods about the origin.
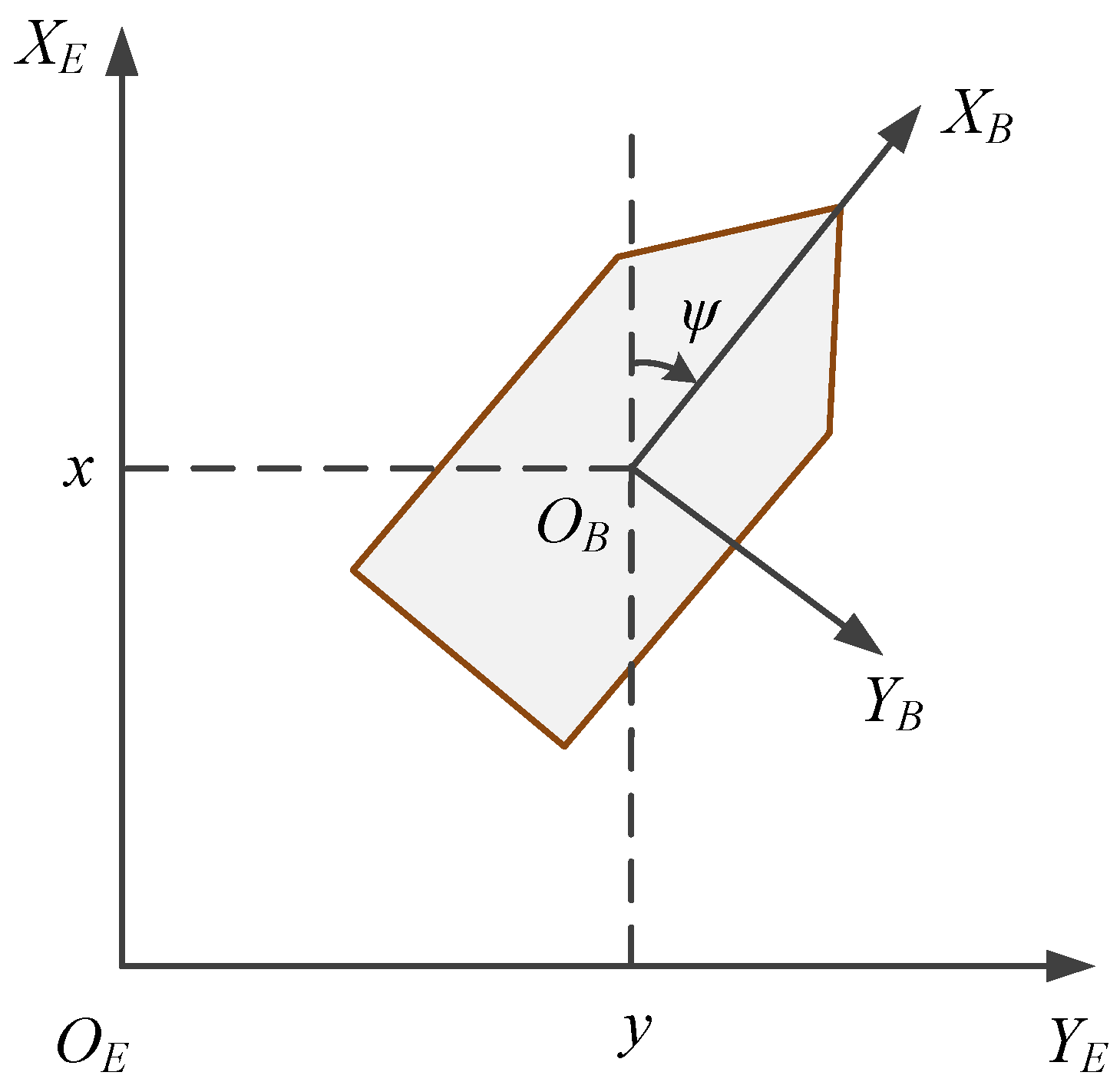
2. Problem Description
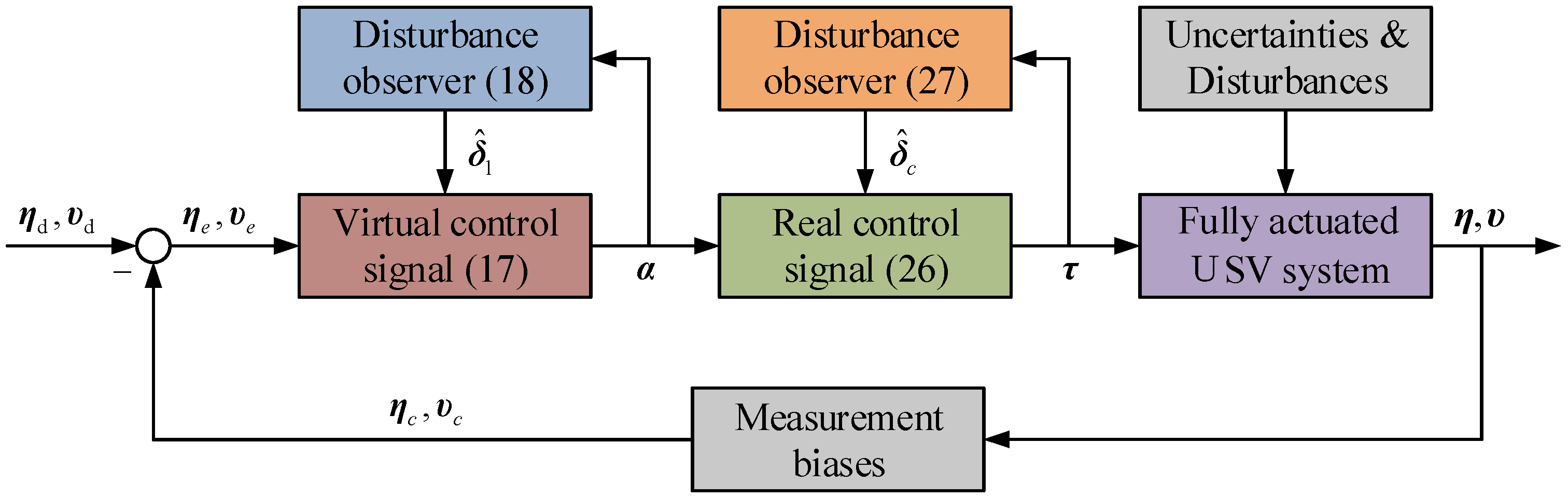
3. Control Design and Stability Argument
3.1. Control Design
3.2. Stability Argument
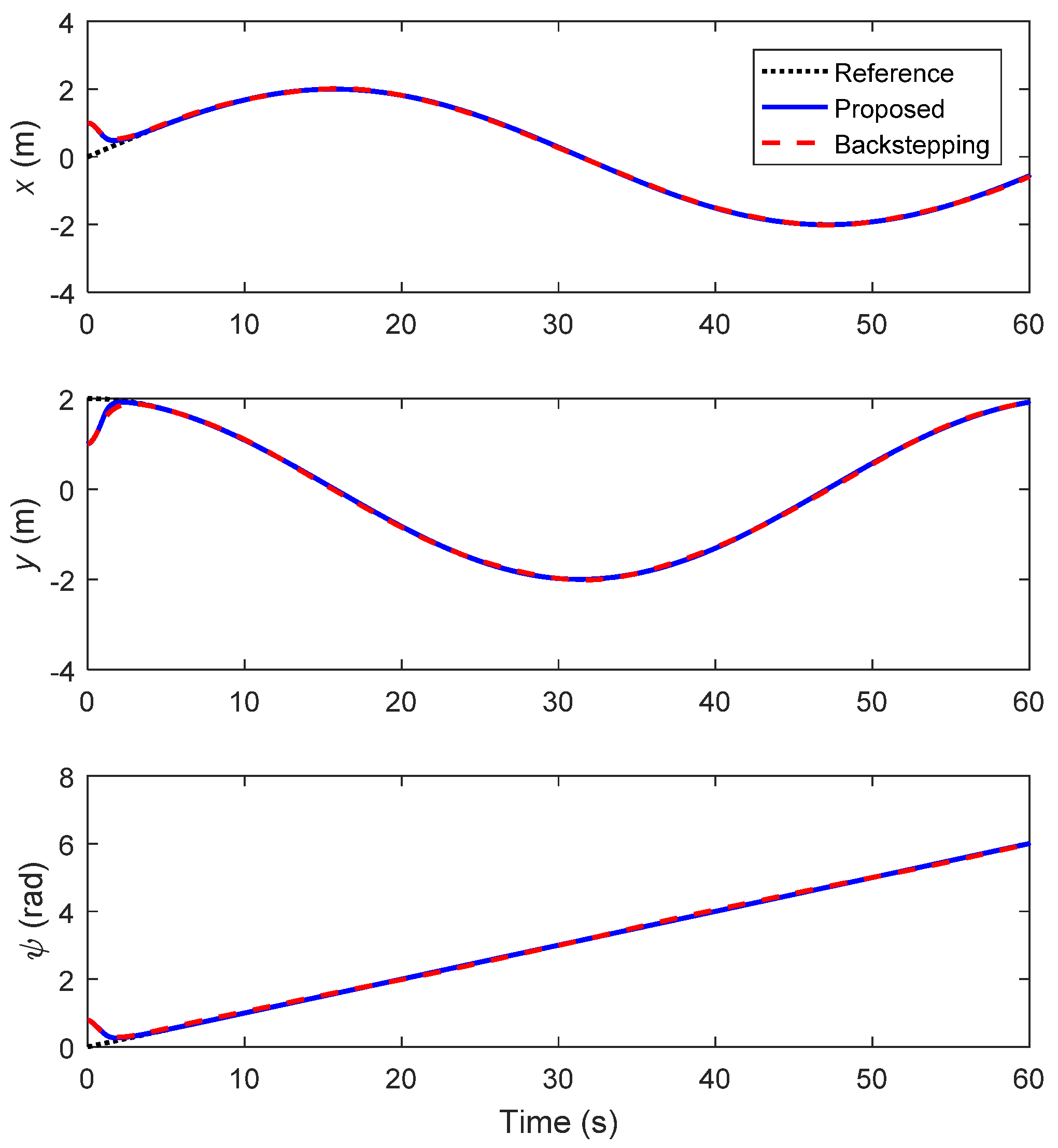
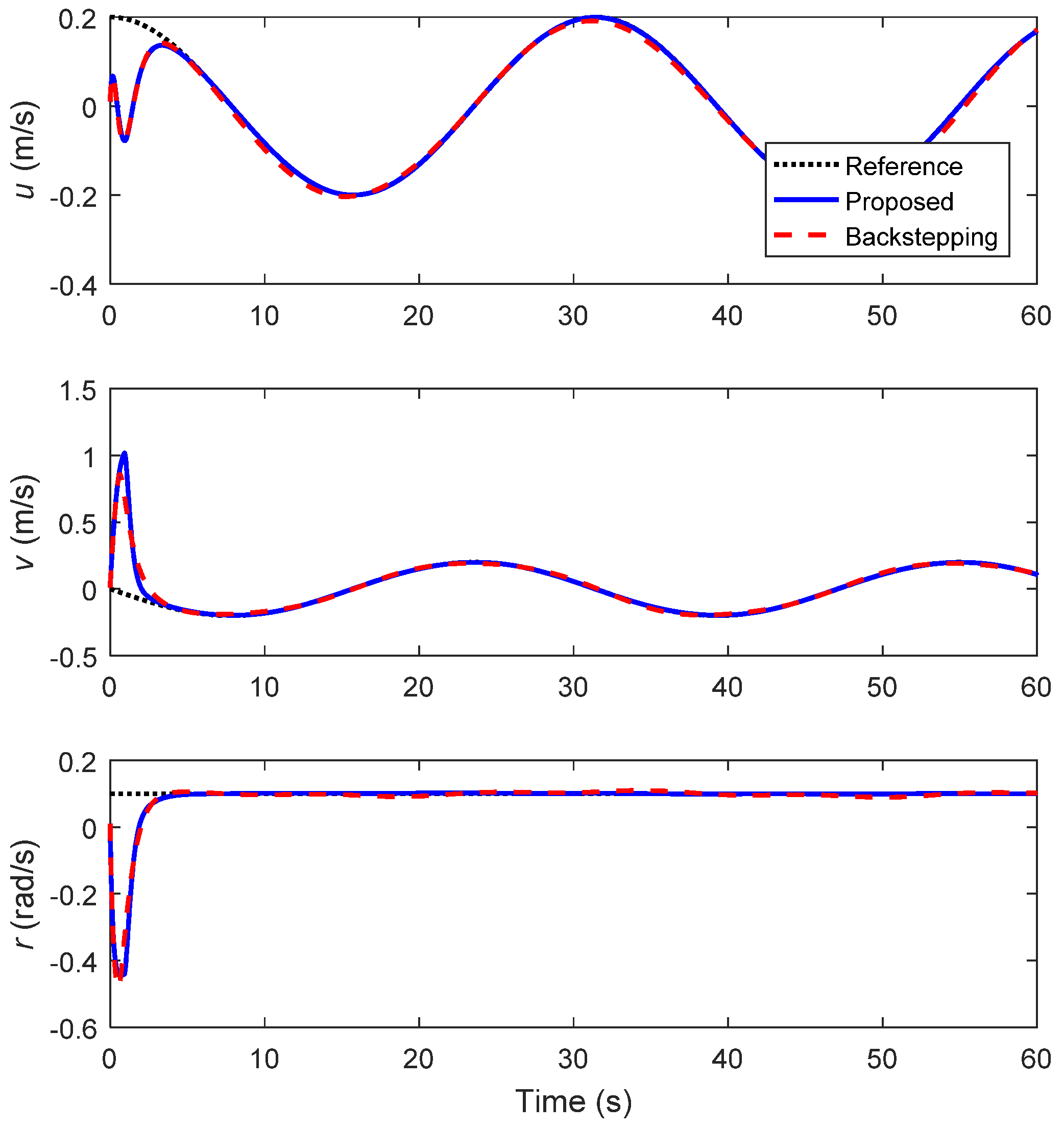
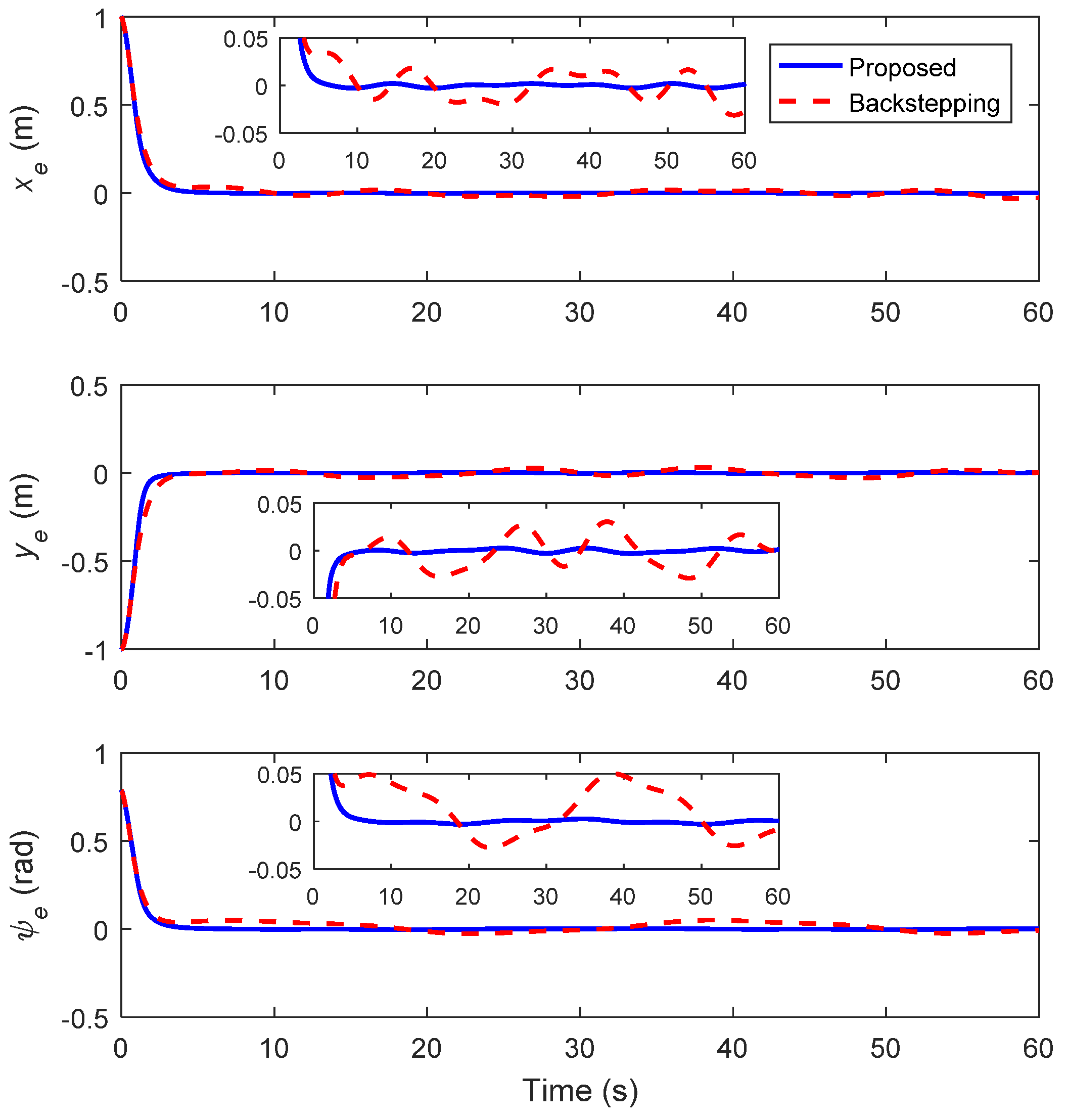
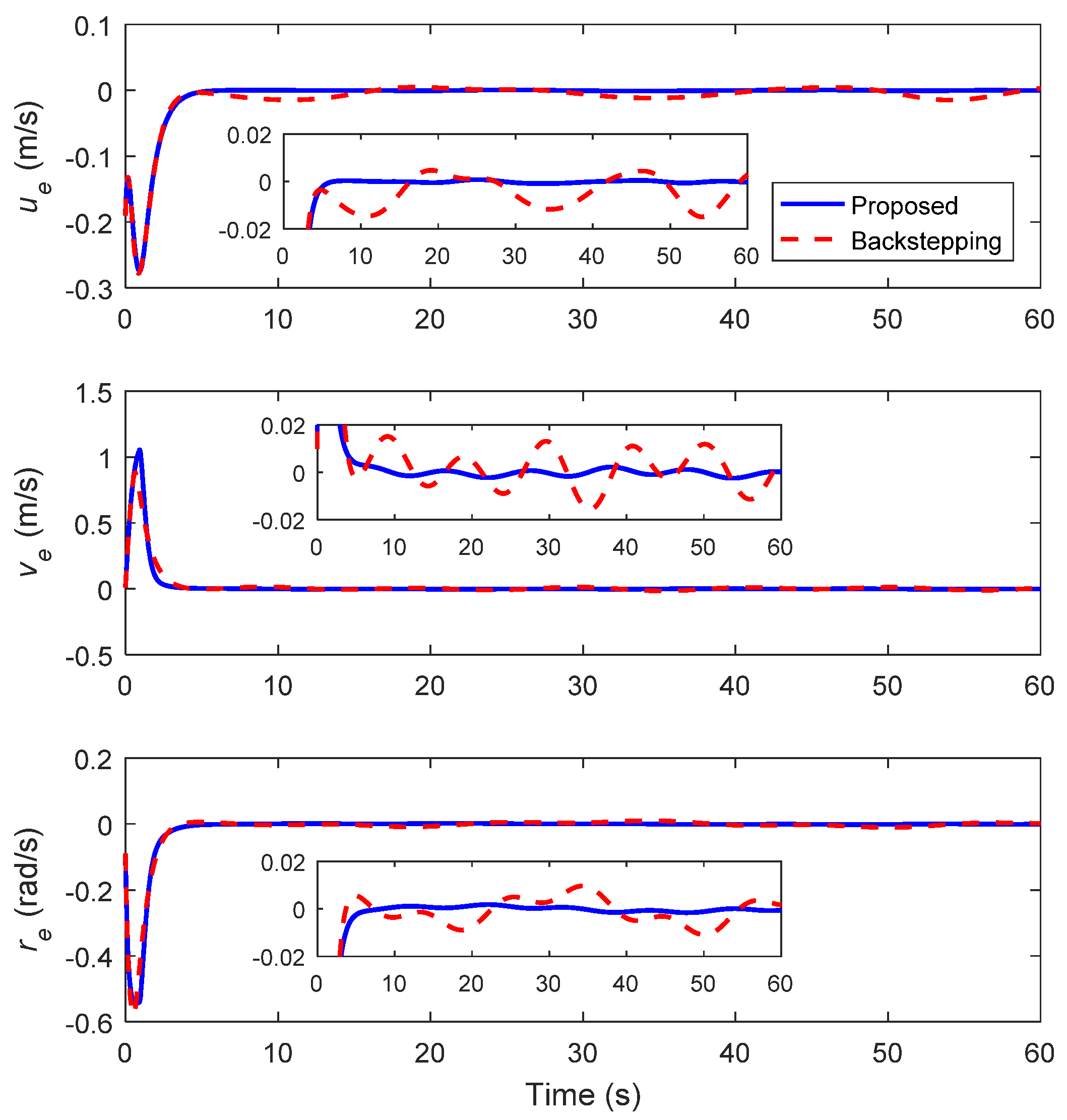
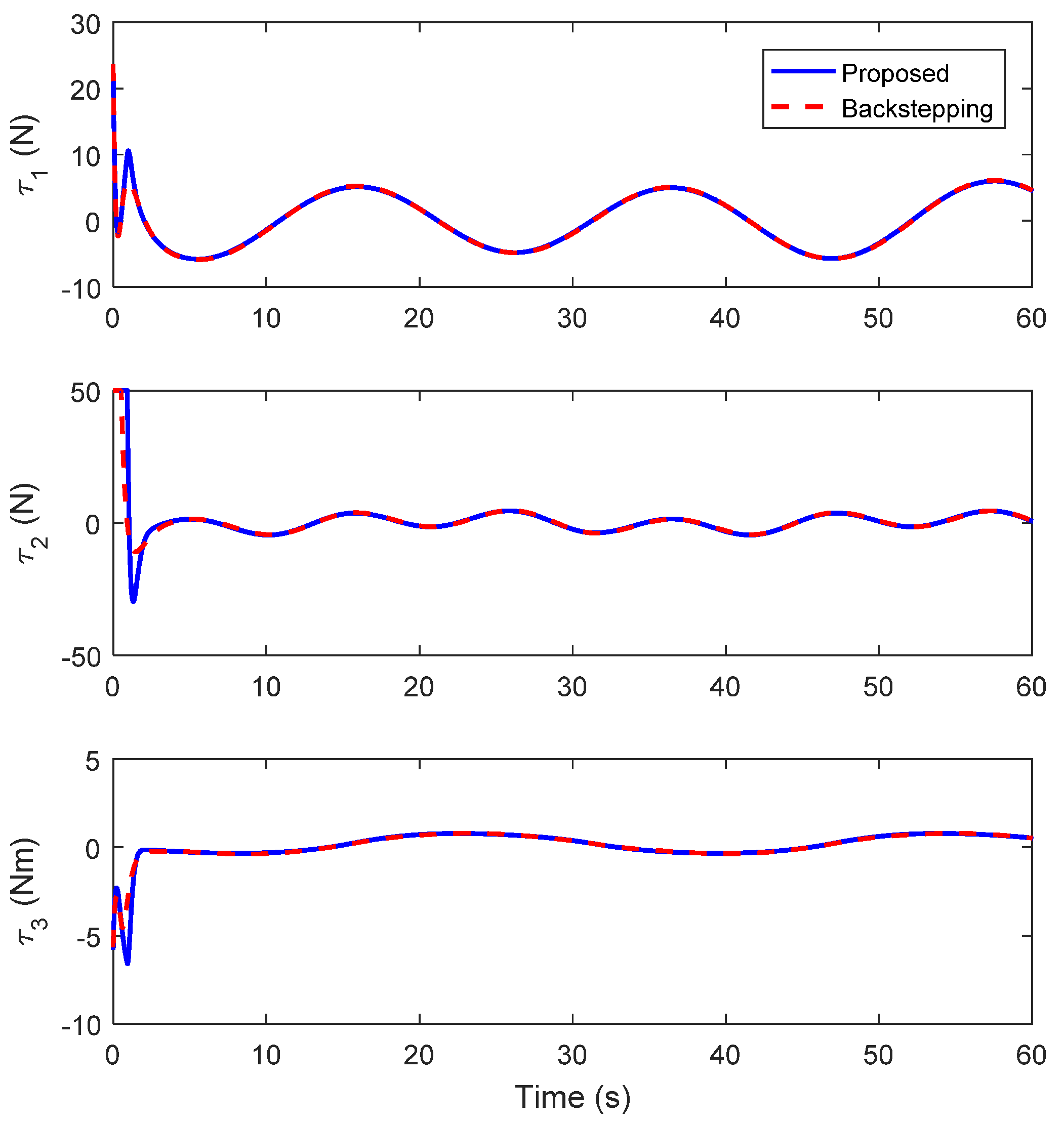
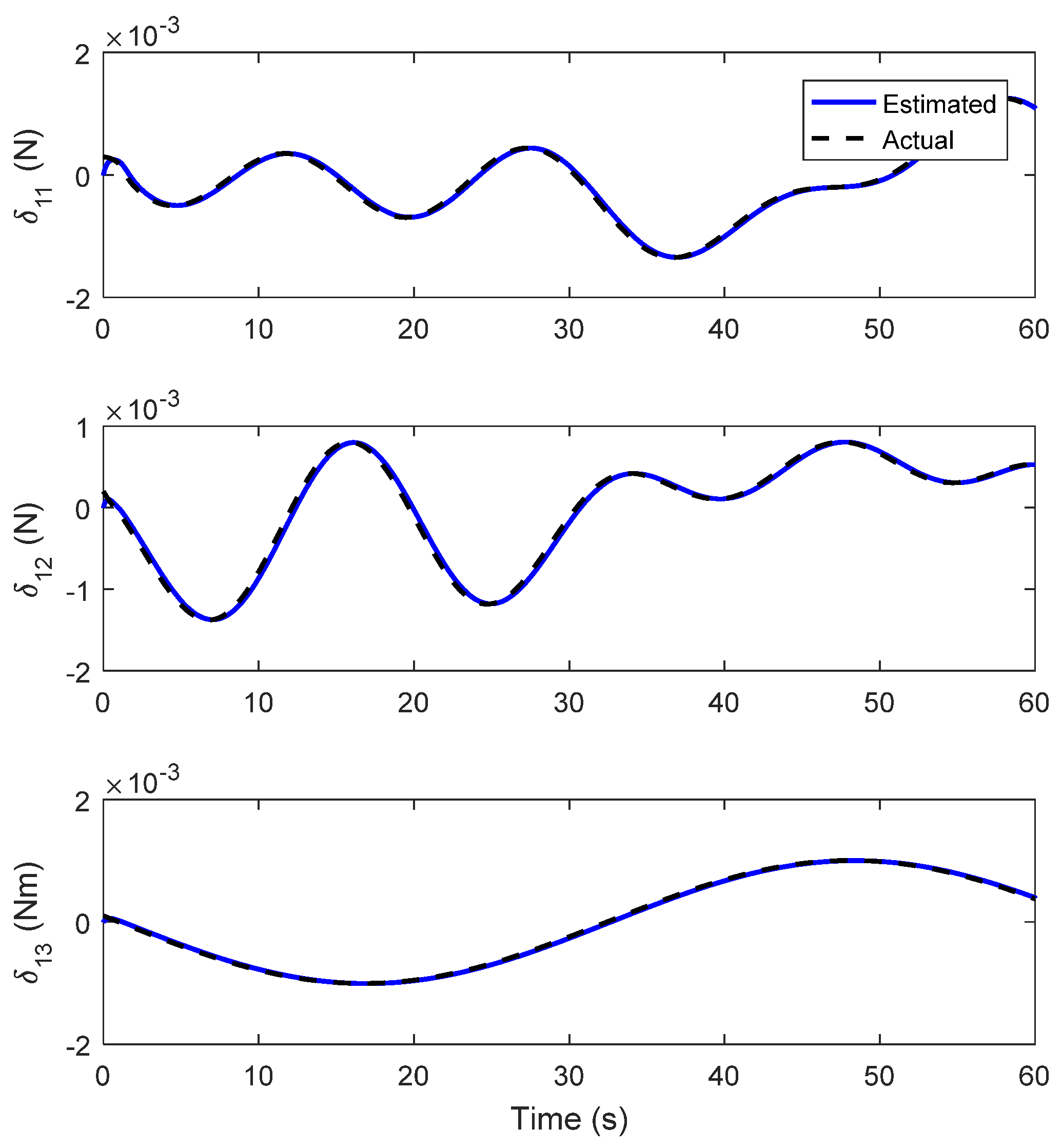
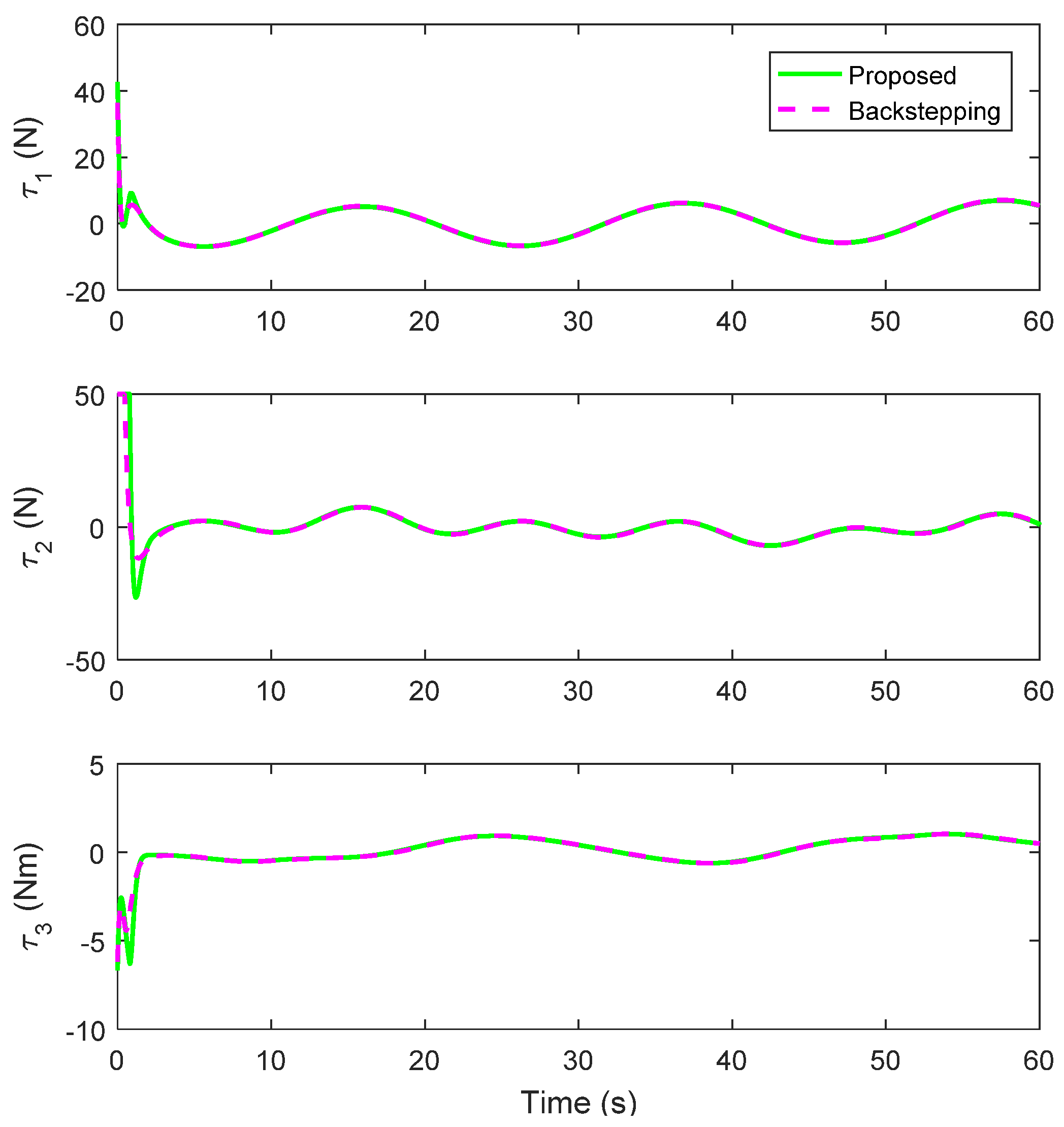
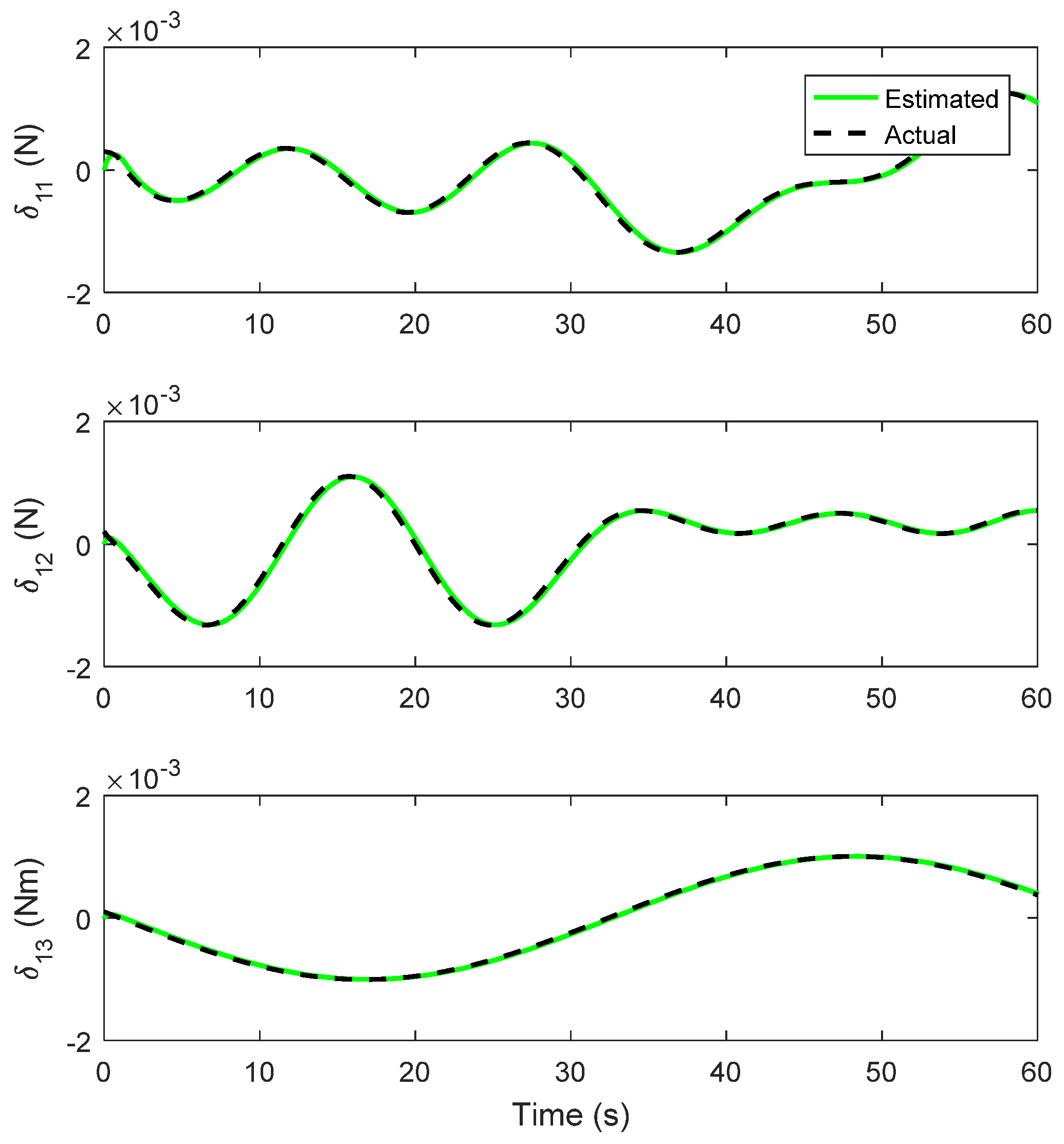
4. Simulation Results
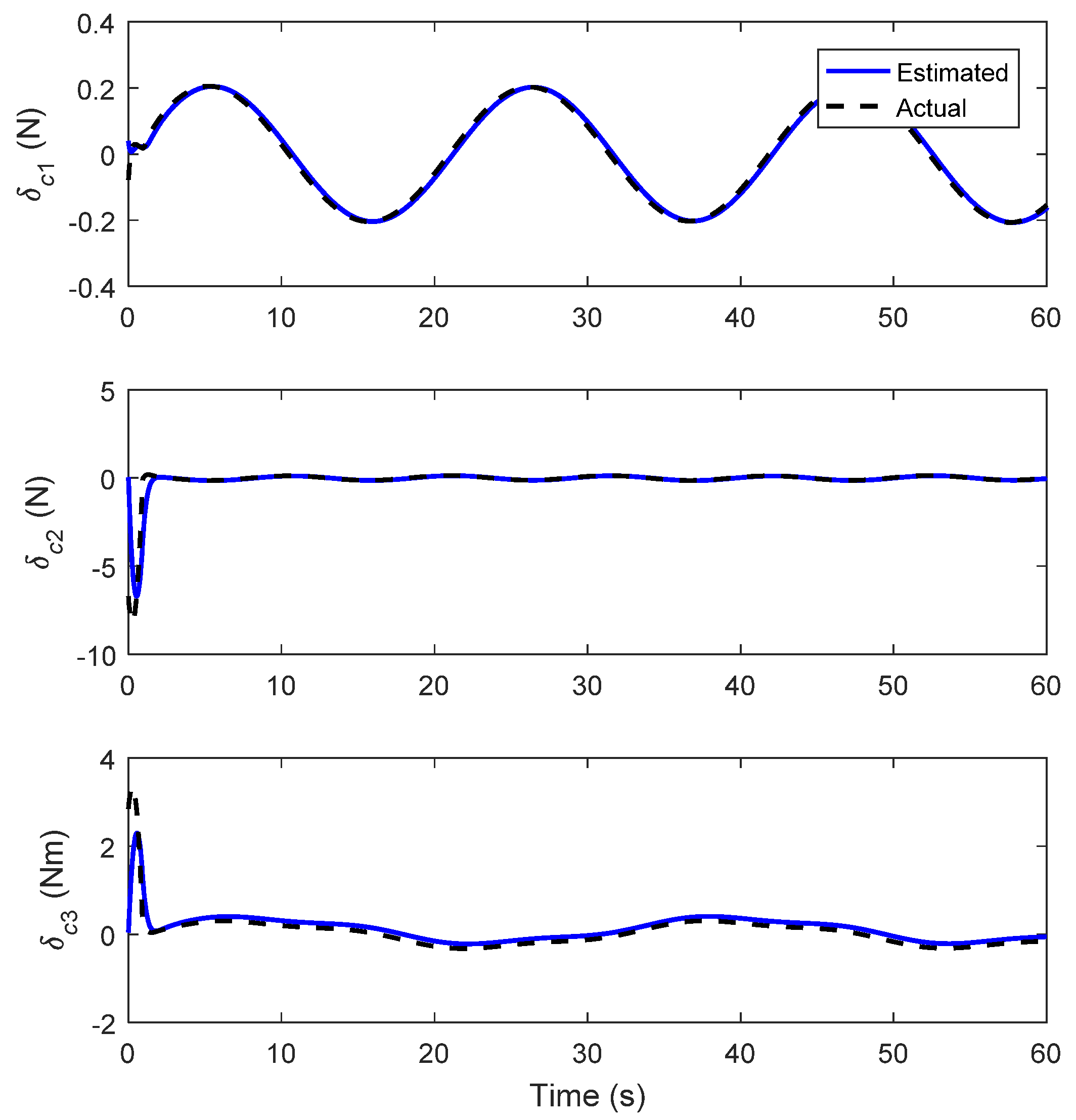
4.1. Circular Trajectory Tracking
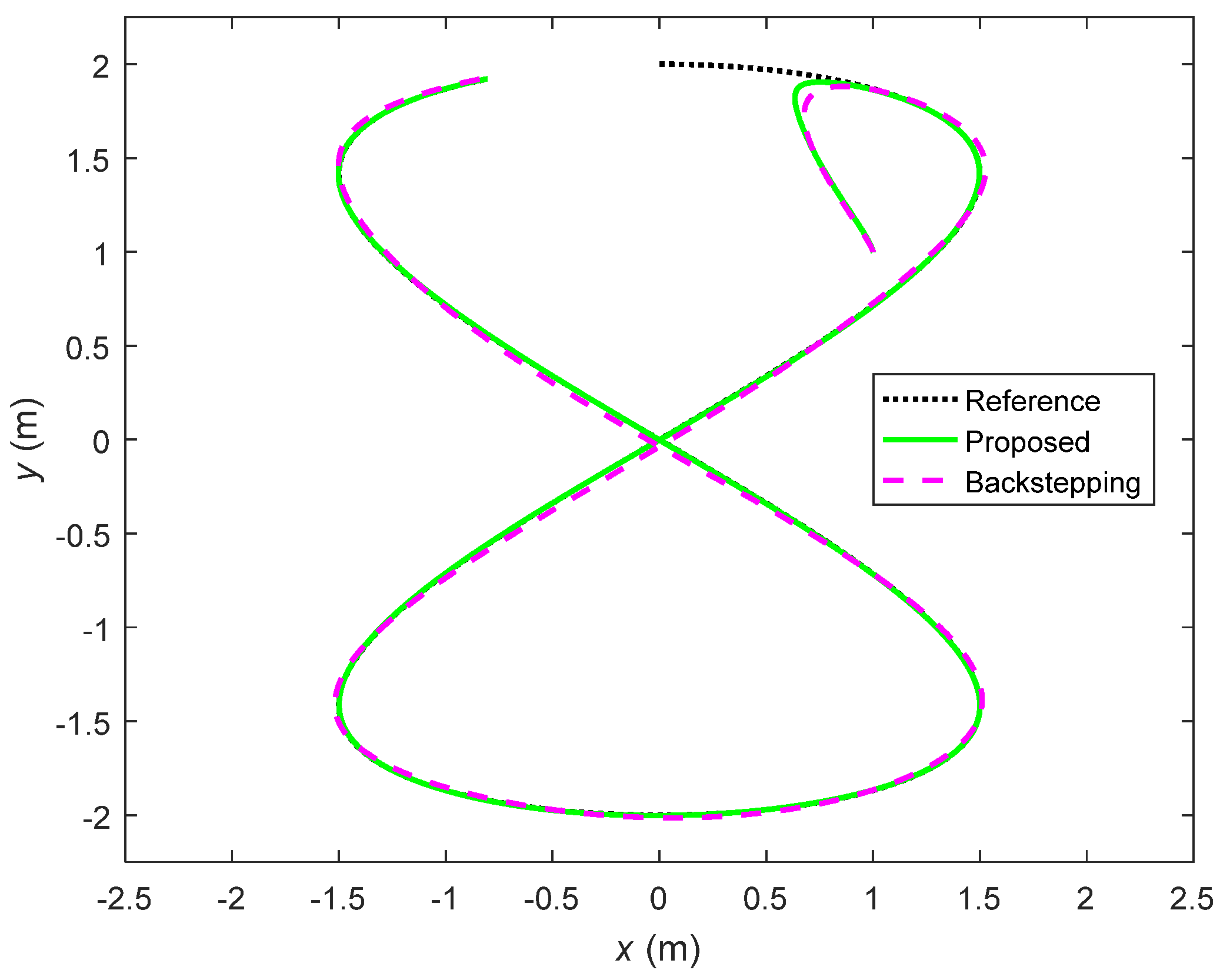
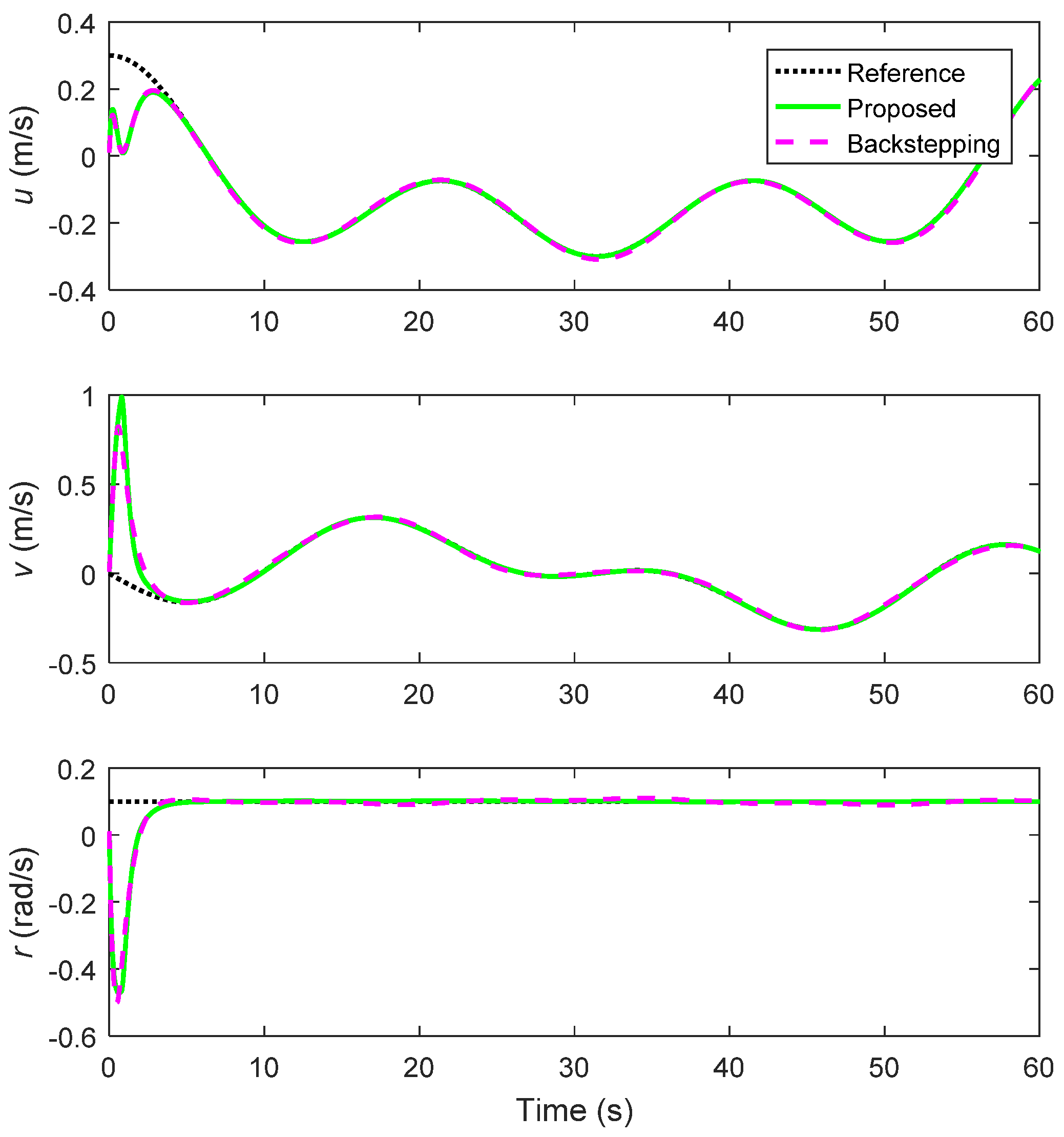
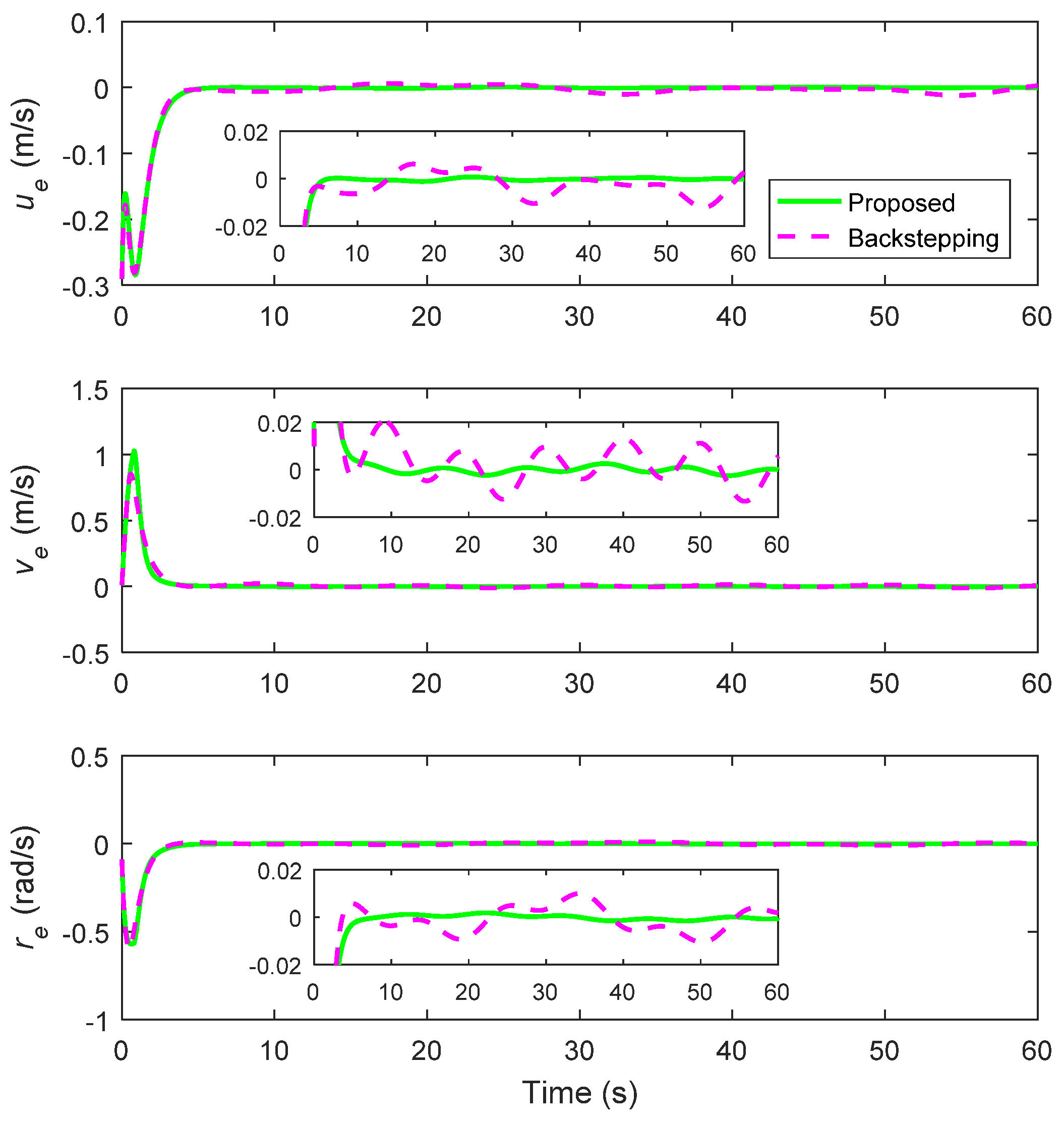
4.2. Lemniscate Trajectory Tracking
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Zhang, Y.; Yu, X.; Yuan, C. Unmanned surface vehicles: An overview of developments and challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Shi, Y.; Shen, C.; Fang, H.; Li, H. Advanced control in marine mechatronic systems: A survey. IEEE/ASME Trans. Mechatron. 2017, 22, 1121–1131. [Google Scholar] [CrossRef]
- Karimi, H.R.; Liu, Y. Guidance and control methodologies for marine vehicles: A survey. Control Eng. Pract. 2021, 111, 104785. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C.; Mercorelli, P. Nonlinear PD fault-tolerant control for dynamic positioning of ships with actuator constraints. IEEE/ASME Trans. Mechatron. 2017, 22, 1132–1142. [Google Scholar] [CrossRef]
- Mazenc, F.; Pettersen, K.; Nijmeijer, H. Global uniform asymptotic stabilization of an underactuated surface vessel. IEEE Trans. Autom. Control 2002, 47, 1759–1762. [Google Scholar] [CrossRef]
- Pettersen, K.Y.; Mazenc, F.; Nijmeijer, H. Global uniform asymptotic stabilization of an underactuated surface vessel: Experimental results. IEEE Trans. Control Syst. Technol. 2004, 12, 891–903. [Google Scholar] [CrossRef]
- Skjetne, R.; Fossen, T.I.; Kokotović, P.V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 2005, 41, 289–298. [Google Scholar] [CrossRef]
- Ghommam, J.; Mnif, F.; Benali, A.; Derbel, N. Asymptotic backstepping stabilization of an underactuated surface vessel. IEEE Trans. Control Syst. Technol. 2006, 14, 1150–1157. [Google Scholar] [CrossRef]
- Yang, Y.; Du, J.; Liu, H.; Guo, C.; Abraham, A. A trajectory tracking robust controller of surface vessels with disturbance uncertainties. IEEE Trans. Control Syst. Technol. 2014, 22, 1511–1518. [Google Scholar] [CrossRef]
- Yin, S.; Xiao, B. Tracking control of surface ships with disturbance and uncertainties rejection capability. IEEE/ASME Trans. Mechatron. 2017, 22, 1154–1162. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.P.; McNinch, L.C.; Soltan, R.A. Sliding-mode tracking control of surface vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Wang, N.; Lv, S.; Zhang, W.; Liu, Z.; Er, M.J. Finite-time observer based accurate tracking control of a marine vehicle with complex unknowns. Ocean Eng. 2017, 145, 406–415. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G.; Yang, J.; Zhang, W. Research on the sliding mode control for underactuated surface vessels via parameter estimation. Nonlinear Dyn. 2018, 91, 1163–1175. [Google Scholar] [CrossRef]
- Wang, N.; Karimi, H.R.; Li, H.; Su, S.-F. Accurate trajectory tracking of disturbed surface vehicles: A finite-time control approach. IEEE/ASME Trans. Mechatron. 2019, 24, 1064–1074. [Google Scholar] [CrossRef]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Adaptive sliding mode trajectory tracking control for unmanned surface vehicle with modeling uncertainties and input saturation. Appl. Sci. 2019, 9, 1240. [Google Scholar] [CrossRef]
- Yao, Q. Adaptive finite-time sliding mode control design for finite-time fault-tolerant trajectory tracking of marine vehicles with input saturation. J. Franklin Inst. 2020, 357, 13593–13619. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Y.; Yu, H.; Guo, C. Finite-time adaptive tracking control of marine vehicles with complex unknowns and input saturation. Ocean Eng. 2020, 198, 106980. [Google Scholar] [CrossRef]
- Yao, Q. Fixed-time trajectory tracking control for unmanned surface vessels in the presence of model uncertainties and external disturbances. Int. J. Control 2022, 95, 1133–1143. [Google Scholar] [CrossRef]
- Weng, Y.; Wang, N. Finite-time observer-based model-free time-varying sliding-mode control of disturbed surface vessels. ISA Trans. 2022, 251, 110866. [Google Scholar] [CrossRef]
- Rodriguez, J.; Castañeda, H.; Gonzalez-Garcia, A.; Gordillo, J.L. Finite-time control for an unmanned surface vehicle based on adaptive sliding mode strategy. Ocean Eng. 2022, 254, 111255. [Google Scholar] [CrossRef]
- Pan, C.-Z.; Lai, X.-Z.; Yang, S.X.; Wu, M. An efficient neural network approach to tracking control of an autonomous surface vehicle with unknown dynamics. Expert Syst. Appl. 2013, 40, 1629–1635. [Google Scholar] [CrossRef]
- Wang, N.; Er, M.J. Self-constructing adaptive robust fuzzy neural tracking control of surface vehicles with uncertainties and unknown disturbances. IEEE Trans. Control Syst. Technol. 2015, 23, 991–1002. [Google Scholar] [CrossRef]
- Shojaei, K. Neural adaptive robust control for underactuated marine surface vehicles with input saturation. Appl. Ocean Res. 2015, 53, 267–278. [Google Scholar] [CrossRef]
- Wang, N.; Er, M.J. Direct adaptive fuzzy tracking control of marine vehicles with fully unknown parametric dynamics and uncertainties. IEEE Trans. Control Syst. Technol. 2016, 24, 1845–1852. [Google Scholar] [CrossRef]
- Wang, R.; Li, D.; Miao, K. Optimized radial basis function neural network based intelligent control algorithm of unmanned surface vehicles. J. Mar. Sci. Eng. 2020, 8, 210. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, X.; Im, N.; Zhang, G.; Zhang, Q. Adaptive fuzzy tracking control for underactuated surface vessels with unmodeled dynamics and input saturation. ISA Trans. 2020, 103, 52–62. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Zhao, H.; Ahn, C.K. Reinforcement learning-based optimal tracking control of an unknown unmanned surface vehicle. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3034–3045. [Google Scholar] [CrossRef] [PubMed]
- Taghieh, A.; Zhang, C.; Alattas, K.A.; Bouteraa, Y.; Rathinasamy, S.; Mohammadzadeh, A. A predictive type-3 fuzzy control for underactuated surface vehicles. Ocean Eng. 2022, 266, 113014. [Google Scholar] [CrossRef]
- Fossen, T.I.; Grovlen, A. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping. IEEE Trans. Control Syst. Technol. 1998, 6, 121–128. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S. Control of fully actuated ocean surface vessels using a class of feedforward approximators. IEEE Trans. Control Syst. Technol. 2006, 14, 750–756. [Google Scholar] [CrossRef]
- Wondergem, M.; Lefeber, E.; Pettersen, K.Y.; Nijmeijer, H. Output feedback tracking of ships. IEEE Trans. Control Syst. Technol. 2011, 19, 442–448. [Google Scholar] [CrossRef]
- Dai, S.-L.; Wang, M.; Wang, C.; Li, L. Learning from adaptive neural network output feedback control of uncertain ocean surface ship dynamics. Int. J. Adapt. Control Signal Process. 2014, 28, 341–365. [Google Scholar] [CrossRef]
- Park, B.S.; Kwon, J.-W.; Kim, H. Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica 2017, 77, 353–359. [Google Scholar] [CrossRef]
- Hao, L.-Y.; Yu, Y.; Li, H. Fault tolerant control of UMV based on sliding mode output feedback. Appl. Math. Comput. 2019, 359, 433–455. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, C.; Wang, J.; Li, C. Neuro-adaptive trajectory tracking control of underactuated autonomous surface vehicles with high-gain observer. Appl. Ocean Res. 2020, 97, 102051. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, C.; Wei, Y.; Wang, J. Observer-based adaptive tracking control of underactuated autonomous marine vehicle with uncertainty dynamic. Appl. Ocean Res. 2020, 104, 102364. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.-H.; Chen, X. Generalized extended state observer based control for systems with mismatched uncertainties. IEEE Trans. Ind. Electron. 2012, 59, 4792–4802. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Yu, X. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer. IEEE Trans. Ind. Electron. 2013, 60, 160–169. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Su, J.; Yu, X. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances. Automatica 2013, 49, 2287–2291. [Google Scholar] [CrossRef]
- Li, S.; Sun, H.; Yang, J.; Yu, X. Continuous finite-time output regulation for disturbed systems under mismatching condition. IEEE Trans. Autom. Control 2015, 60, 277–282. [Google Scholar] [CrossRef]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods–an overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Xia, Y.; Zuo, Z.; Wang, Y. Disturbance observer-based integral sliding-mode control for systems with mismatched disturbances. IEEE Trans. Ind. Electron. 2016, 63, 7040–7048. [Google Scholar] [CrossRef]
- Yao, Q. Dual-disturbance-observer-based robust finite-time trajectory tracking control for robotic surface vehicle under measurement uncertainties. Ocean Eng. 2021, 242, 110183. [Google Scholar] [CrossRef]
- Fossen, T.I. Marine Control Systems: Guidance, Navigation, and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernetics AS: Trondheim, Norway, 2002. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Q.; Jahanshahi, H.; Liu, C.; Alotaibi, A.; Alsubaie, H. Disturbance Attenuation Trajectory Tracking Control of Unmanned Surface Vessel Subject to Measurement Biases. Axioms 2023, 12, 361. https://doi.org/10.3390/axioms12040361
Yao Q, Jahanshahi H, Liu C, Alotaibi A, Alsubaie H. Disturbance Attenuation Trajectory Tracking Control of Unmanned Surface Vessel Subject to Measurement Biases. Axioms. 2023; 12(4):361. https://doi.org/10.3390/axioms12040361
Chicago/Turabian StyleYao, Qijia, Hadi Jahanshahi, Chengliang Liu, Ahmed Alotaibi, and Hajid Alsubaie. 2023. "Disturbance Attenuation Trajectory Tracking Control of Unmanned Surface Vessel Subject to Measurement Biases" Axioms 12, no. 4: 361. https://doi.org/10.3390/axioms12040361
APA StyleYao, Q., Jahanshahi, H., Liu, C., Alotaibi, A., & Alsubaie, H. (2023). Disturbance Attenuation Trajectory Tracking Control of Unmanned Surface Vessel Subject to Measurement Biases. Axioms, 12(4), 361. https://doi.org/10.3390/axioms12040361





