Efficient Technique for Solving (3+1)-D Fourth-Order Parabolic PDEs with Time-Fractional Derivatives

Abstract

In this presented research, a hybrid technique is proposed for solving fourth-order (3+1)-D parabolic PDEs with time-fractional derivatives. For this purpose, we utilized the Elzaki integral transform with the coupling of the homotopy perturbation method (HPM). From performing various numerical experiments, we observed that the presented scheme is simple and accurate with very small computational errors.

1. Introduction

The topic of the numerical study of fractional differential equations has attracted the attention of many researchers. Three-dimensional partial differential equations are frequently employed in applied research and engineering. Due to the vast number of applications, fractional calculus has emerged as a key mathematical tool in many fields of engineering and sciences. Fractional-order problems have numerous applications in scientific disciplines including chemistry, biology, diffusion, control theory, rheology, and viscoelasticity and have attracted a lot of interest, as discussed in [1,2]. In order to give more accurate representations of real-world phenomena, various definitions of fractional derivatives have been proposed in the literature. Riemann–Liouville, modified Riemann–Liouville, Caputo, Hadmard, Erdelyi–Kober, Riesz, Grunwald–Letnikov, Marchaud, and other fractional derivatives are examples of well-known fractional derivatives (see [3]). A lie symmetry analysis of conformable differential equation has been discussed in [4]. As the methodology for finding the approximate and accurate solutions to the fourth-order partial differential equations is a crucial task, it constitutes a vigorous research area for scientists and researchers. The partial differential equations are frequently challenging to solve, and their fractional-order varieties are particularly challenging, as discussed in [5,6,7,8,9]. Several techniques have been developed to find the solutions to some nonlinear fractional differential equations such as the homotopy perturbation method [10,11,12,13,14], sub-ODE method [15,16], generalized tanh method [17], and residual power series method [17,18]. Different integral transform (such as Elzaki, Laplace, and Sumudu)-based efficient techniques have been presented in [19,20,21,22,23,24]. Various wavelet-based techniques for solving differential and integral equations have been discussed in [25,26,27]. Other classical and efficient techniques have been explained in [28,29,30,31,32]. Some physical phenomena modeled by fourth-order partial differential equations include ice formation (see [33,34]), fluids on lungs (see [35]), brain warping (see [36,37]), and designing special curves on surfaces (see [36,38]). Some other problems related to waves have been discussed in [39,40].

In this research, let us consider the general form of (3+1)-D fourth-order parabolic PDEs with time-fractional derivatives:

$$\frac{{\partial }^{2k}w}{\partial t^{2k}}+f_1\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\alpha }^4}+f_2\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\beta }^4}+f_3\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\gamma }^4}=F\left(\alpha ,\beta ,\gamma \right),$$

(1)

in the domain bounded by $c<\left\{\alpha ,\beta ,\gamma \right\}〈d, t〉0,$ subject to the initial conditions

$$w\left(\alpha ,\beta ,\gamma ,0\right)=F_0\left(\alpha ,\beta ,\gamma \right), \frac{\partial w}{\partial t}\left(\alpha ,\beta ,\gamma ,0\right)=F_1\left(\alpha ,\beta ,\gamma \right).$$

Here, $0<k<1$ and $f_1,f_2,f_3$ are functions of $\alpha ,\beta ,\gamma$.

This research paper is organized as: Section 2 and Section 3 contain some basic definitions related to fractional calculus and the Elzaki transform, respectively. The classical homotopy perturbation method is discussed in Section 4. The proposed technique, which is the coupling of the Elzaki transform and the homotopy perturbation method, is discussed in Section 5. A convergence analysis of the proposed scheme is explained through some statements of theorems in Section 6. Numerical examples are solved to illustrate the accuracy and simplicity of the proposed scheme.

2. Some Basic Definitions

Definition 1.

The general form of the Caputo fractional derivative of the function $h\left(\tau \right)$is:

$$\frac{{\partial }^k}{\partial {\tau }^k}h\left(\tau \right)=J^{\left(n-k\right)}\frac{{\partial }^n}{\partial {\tau }^n}h\left(\tau \right)=\frac{1}{\mathrm{\Gamma }\left(n-k\right)}\underset{0}{\overset{\tau }{{\displaystyle \int }}}{\left(\tau -\mathrm{\Omega }\right)}^{n-k-1}{h}^n\left(\mathrm{\Omega }\right)d\mathrm{\Omega },$$

where $h\in S_{-1}^n, n-1〈k\le n, n\in \mathbb{N}, \tau 〉0$. Here,$\frac{{\partial }^k}{\partial {\tau }^k}$ represents the Caputo derivative operator and $\mathrm{\Gamma }$ represents the gamma function.

Definition 2.

The real function $g\left(t\right)\in S_{\mu }, t>0, \mu \in \mathcal{R}$ if $\exists q\in \mathcal{R};\left(q>\mu \right),$ s.t $g\left(t\right)=t^q{m}_1\left(t\right),$where $m_1\left(t\right)\in C\left[0,\infty \right)$ and $g\left(t\right)\in S_{\mu }^n$ if $g^{\left(n\right)}\in S_{\mu }, n\in N$.

Definition 3.

The basic definition of the Elzaki integral transform of any function of the form $g_1\left(t\right)$ is:

$$E_L\left\{g_1\left(t\right)\right\}=v\underset{0}{\overset{\infty }{{\displaystyle \int }}}{g}_1\left(t\right)·dt,t>0$$

Definition 4.

For the two parameters $a$ and $b$, the Mittag–Leffler function is written as:

$$E_{a, b}\left(\tau \right)={\displaystyle \sum }_{n=0}^{\infty }\frac{{\tau }^n}{\mathrm{\Gamma }\left(an+b\right)},a,b>0$$

3. Basic Properties

• The implementation of the Elzaki integral transform to the Caputo fractional derivative of the function $h\left(\tau \right)$ is as follows:

  $$E_L\left\{\frac{{\partial }^{\alpha }}{\partial {\tau }^{\alpha }}h\left(\tau \right)\right\}=\frac{E_L\left\{h\left(\tau \right)\right\}}{v^{\alpha }}-{\displaystyle \sum }_{k=0}^{n-1}{v}^{k-\alpha +2}{h}^k\left(0\right),n-1<k\le n$$

  (2)
• The Elzaki integral transform of some of the partial derivatives is given below:

  (a)

  $E_L\left[\frac{\partial }{\partial t}G\left(x,y,z,t\right)\right]=\frac{E_L\left[G\left(x,y,z,t\right)\right]}{v}-v·G\left(x,y,z,0\right),$

  (b)

  $E_L\left[\frac{{\partial }^2}{\partial t^2}G\left(x,y,z,t\right)\right]=\frac{1}{v^2}{E}_L\left[G\left(x,y,z,t\right)\right]-G\left(x,y,z,0\right)-v·\frac{\partial G}{\partial t}\left(x,y,z,0\right),$

  (c)

  $E_L\left[\frac{\partial }{\partial x}G\left(x,y,z,t\right)\right]=\frac{d}{dx}{E}_L\left[G\left(x,y,z,t\right)\right],$

  (d)

  $E_L\left[\frac{{\partial }^2}{\partial x^2}G\left(x,y,z,t\right)\right]=\frac{d^2}{d{x}^2}{E}_L\left[G\left(x,y,z,t\right)\right]$.

• The Elzaki transforms of some functions are listed here:

  $$E_L\left(1\right)=v^2, E_L\left(t\right)=v^3, E_L\left(t^n\right)=n!v^{n+2}, E_L\left(e^{at}\right)=\frac{v^2}{1-av}, E_L(\sin at)=\frac{a{v}^3}{1+a^2{v}^2}$$

  (3)

4. Classical Homotopy Perturbation Method (HPM)

Consider a nonlinear differential equation

$$\mathrm{\Gamma }\left(w\right)=B\left(r\right),r\in \mathrm{\Omega }$$

(4)

Let the boundary condition be

$$\mathrm{{\rm Y}}\left(w, \frac{\partial w}{\partial x}\right)=0,r\in \mathrm{\Lambda }$$

where $\mathrm{\Gamma }$ represents the general differential operator, $\mathrm{{\rm Y}}$ represents the boundary operator, $B\left(r\right)$ represents any function in the R.H.S, and $\mathrm{\Lambda }$ represents the boundary. Split the operator $\mathrm{\Gamma }$ into two portions $P$ and $Q$. The part $P$ denotes the linear operator, whereas the part $Q$ denotes the nonlinear one. Now write Equation (4) as follows:

$$P\left(w\right)+Q\left(w\right)-B\left(r\right)=0$$

Now according to the homotopy technique, we need to establish a homotopy by considering the following function $w\left(r,e\right):\mathrm{\Omega }\times \left[0, 1\right]\to \mathcal{R}$ which satisfies

$$H\left(w,e\right)=\left(1-e\right)\left[P\left(w\right)-P\left(w_0\right)\right]+e\left[\mathrm{\Gamma }\left(w\right)-B\left(r\right)\right]=0, e\in \left[0,1\right], r\in \mathrm{\Omega }$$

Or

$$P\left(w\right)-P\left(w_0\right)-eP\left(w\right)+eP\left(w_0\right)+e\left[P\left(w\right)+Q\left(w\right)-B\left(r\right)\right]=0$$

This implies

$$H\left(w,e\right)=P\left(w\right)-P\left(w_0\right)+eP\left(w_0\right)+e\left[Q\left(w\right)-B\left(r\right)\right]=0$$

(5)

where $e$ is the embedding parameter in $\left[0, 1\right]$ and the initial guess of (4) is $w_0$, which will satisfy the conditions at the boundary points. From (5), we obtain

$$H\left(w,0\right)=P\left(w\right)-P\left(w_0\right)=0$$

and

$$H\left(w, 1\right)=\mathrm{\Gamma }\left(w\right)-B\left(r\right)=0$$

There is no topology as $e$ changes from zero to one; similarly, $w\left(r, e\right)$ will change from $w_0\left(r\right)$ to $w\left(r\right),$ and this process is called deformation. The quantities $P\left(w\right)-P\left(w_0\right)$ and $\mathrm{\Gamma }\left(w\right)-B\left(r\right)$ are known as homotopy. Suppose the solution of (4) can be presented as a power series in terms of $h$:

$$w=w_0+e{w}_1+e^2{w}_2+\dots$$

Letting $e=1$, the solution of (4) is:

$$w=\underset{e\to 1}{\lim }w=w_0+w_1+w_2+\dots$$

5. Elzaki Transform Homotopy Perturbation Method (ETHPM)

Let us suppose the general form of (3+1)-dimensional fourth-order parabolic PDEs with time-fractional derivatives as given in Equation (1). Using the Elzaki integral transform in Equation (1), we obtain

$$E_L\left\{\frac{{\partial }^{2k}w}{\partial t^{2k}}+f_1\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\alpha }^4}+f_2\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\beta }^4}+f_3\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\gamma }^4}-F\left(\alpha ,\beta ,\gamma \right)\right\}=0$$

(6)

Using Equation (2), we obtain

$$\begin{array}{ll}{E}_L\left\{w\right\}& ={\displaystyle {\displaystyle \sum }_{i=0}^{n-1}}{v}^{i+2}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)\\ & -v^{2k}{E}_L\left\{f_1\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\alpha }^4}+f_2\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\beta }^4}+f_3\left(\alpha ,\beta ,\gamma \right)\frac{{\partial }^{4}w}{\partial {\gamma }^4}-F\left(\alpha ,\beta ,\gamma \right)\right\}\end{array}$$

Using the inverse Elzaki transform, we obtain

$$w\left(\alpha ,\beta ,\gamma ,t\right)={\displaystyle \sum }_{i=0}^{n-1}\frac{t^i}{i!}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)-E_L{}^{-1}\left\{v^{2k}{E}_L\left\{f_1\frac{{\partial }^{4}w}{\partial {\alpha }^4}+f_2\frac{{\partial }^{4}w}{\partial {\beta }^4}+f_3\frac{{\partial }^{4}w}{\partial {\gamma }^4}-F\left(\alpha ,\beta ,\gamma \right)\right\}\right\}$$

(7)

Applying the HPM, we obtain

$$w\left(\alpha ,\beta ,\gamma ,t\right)={\displaystyle \sum }_{n=0}^{\infty }{e}^n{w}_n\left(\alpha ,\beta ,\gamma ,t\right)$$

(8)

The decomposition of the nonlinear term can be as follows:

$$N\left[w\left(\alpha ,\beta ,\gamma ,t\right)\right]={\displaystyle \sum }_{n=0}^{\infty }{e}^n{H}_n\left(w\right)$$

(9)

where $H_n(w$) is He’s polynomial and is given as:

$$H_n\left(w_0,w_1,w_2,\dots ,w_n\right)=\frac{1}{n!}\frac{{\partial }^n}{\partial e^n}{\left[\left({\displaystyle \sum }_{j=0}^{\infty }{e}^j{w}_j\right)\right]}_{e=0}, n=0, 1, 2, 3, \dots$$

(10)

From Equation (7),

$${\displaystyle \sum }_{n=0}^{\infty }{e}^n{w}_n =w\left(\alpha ,\beta ,\gamma ,0\right)+e\left({\displaystyle \sum }_{i=1}^{n-1}\frac{t^i}{i!}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)-E_L{}^{-1}\left\{v^{2k}{E}_L\left\{{\displaystyle \sum }_{n=0}^{\infty }{e}^n{H}_n\left(w\right) \right\}\right\}\right)$$

(11)

Comparing the like powers of $e$, we obtain

$$e^0 : w_0=w\left(\alpha ,\beta ,\gamma ,0\right),$$

$$e^1 : w_1={\displaystyle \sum }_{i=1}^{n-1}\frac{t^i}{i!}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)-E_L{}^{-1}\left\{v^{2k}{E}_L\left(H_0\left(w\right)\right) \right\},$$

$$e^2 : w_2=-E_L{}^{-1}\left\{v^{2k}{E}_L\left(H_1\left(w\right)\right) \right\},$$

$$e^3 : w_3=-E_L{}^{-1}\left\{v^{2k}{E}_L\left(H_2\left(w\right)\right) \right\},$$

$$⋮$$

Therefore, the series solution is given by

$$w\left(\alpha ,\beta ,\gamma ,t\right)=\underset{e\to 1}{\lim }{w}_n\left(\alpha ,\beta ,\gamma ,t\right)$$

$$w\left(\alpha ,\beta ,\gamma ,t\right)=w_0+w_1+w_2+w_3+···$$

(12)

6. Convergence Analysis

This section contains some statements of theorems to demonstrate the convergence of the proposed scheme:

Theorem 1.

In a Banach space, we defined two functions $w\left(\alpha ,\beta ,\gamma , t\right)$ and $w_j\left(\alpha ,\beta ,\gamma ,t\right)$. The solution given in terms of an infinite series

$$w\left(\alpha ,\beta ,\gamma ,t\right)={\displaystyle \sum }_{j=0}^{\infty }{e}^j{w}_j\left(\alpha ,\beta ,\gamma ,t\right),$$

(13)

will converge to the solution of Equation (1) if there exists $\rho \in \left(0, 1\right)$, such that

$$\parallel w_{j+1}\parallel \le \rho \parallel w_j\parallel$$

This condition was presented in [24,26].

Theorem 2.

The truncation error of the series solution as given in Equation (13) is written as:

$$\left|w\left(\alpha ,\beta ,\gamma ,t\right)-{\displaystyle \sum }_{j=0}^n{w}_j\left(\alpha ,\beta ,\gamma ,t\right)\right|\le \frac{{\rho }^{j+1}}{1-\rho }\parallel w_0\parallel .$$

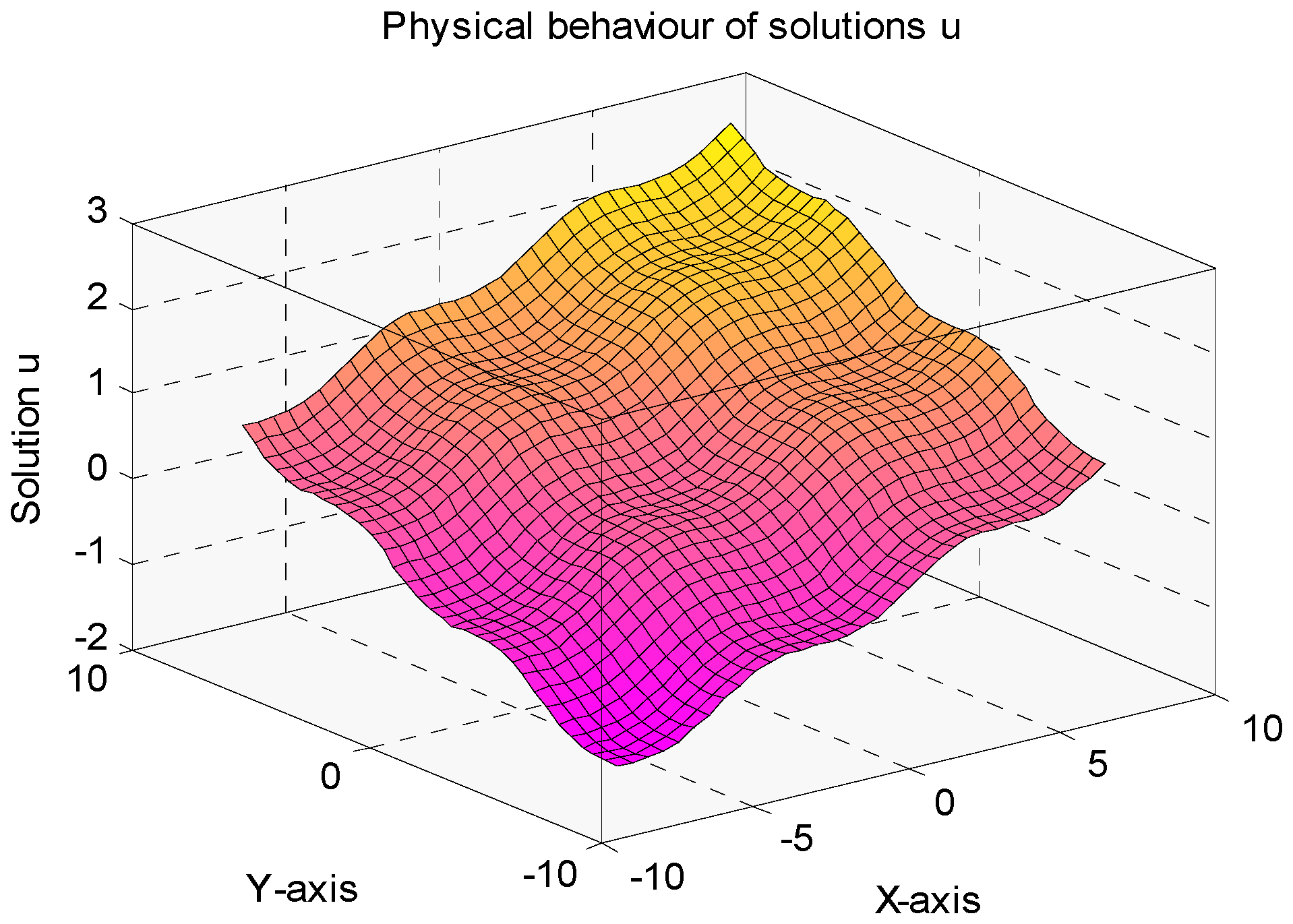
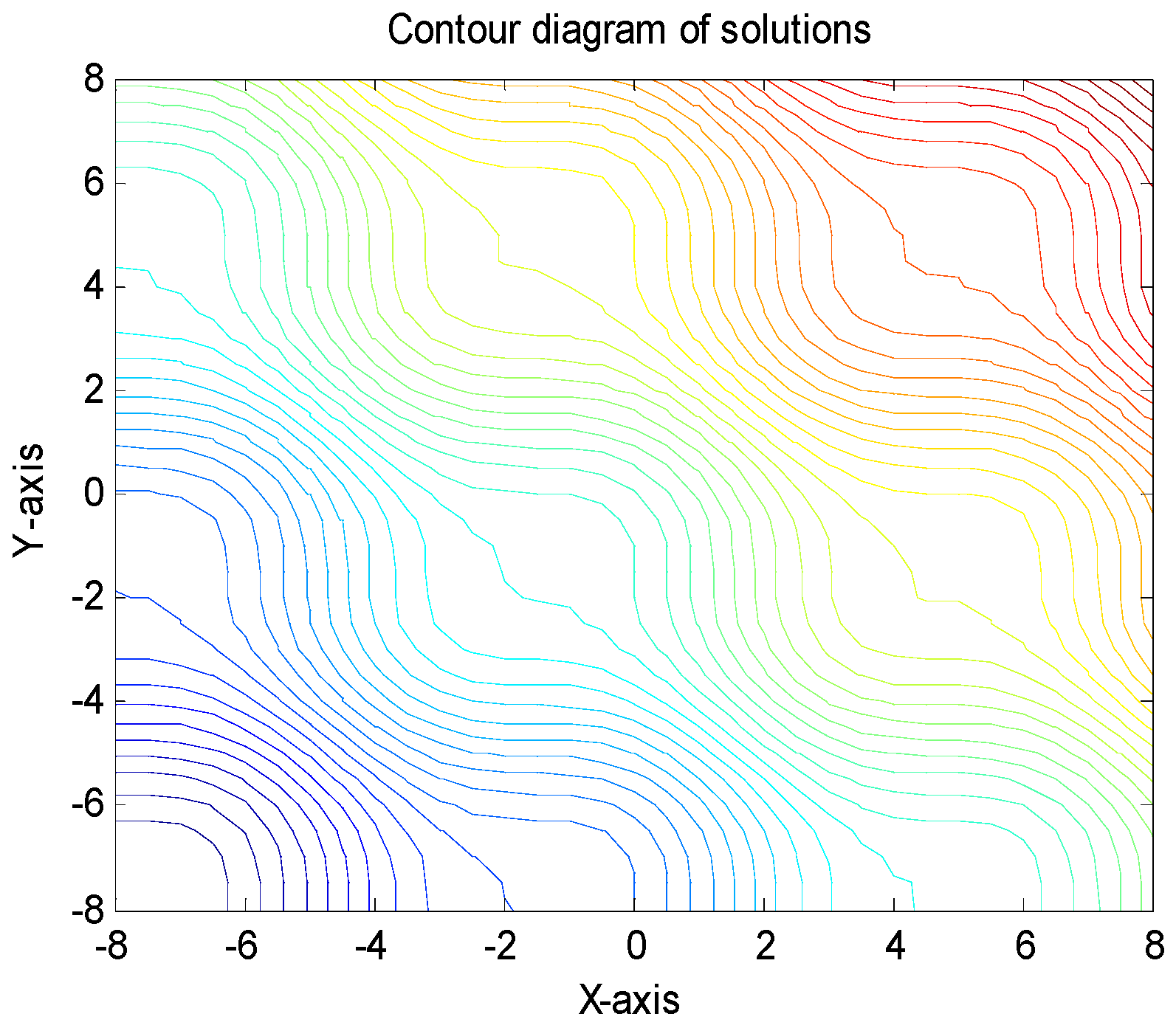
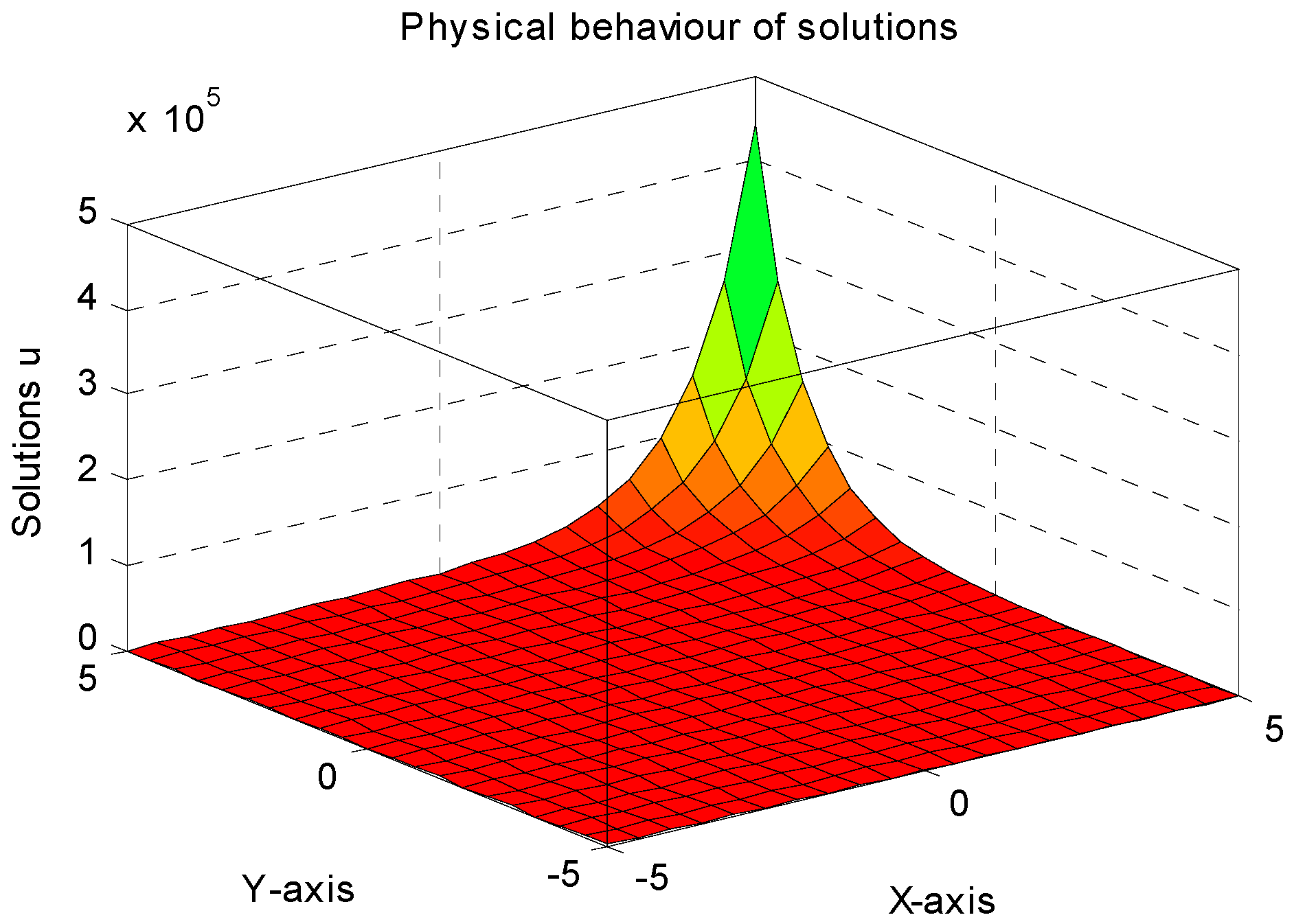
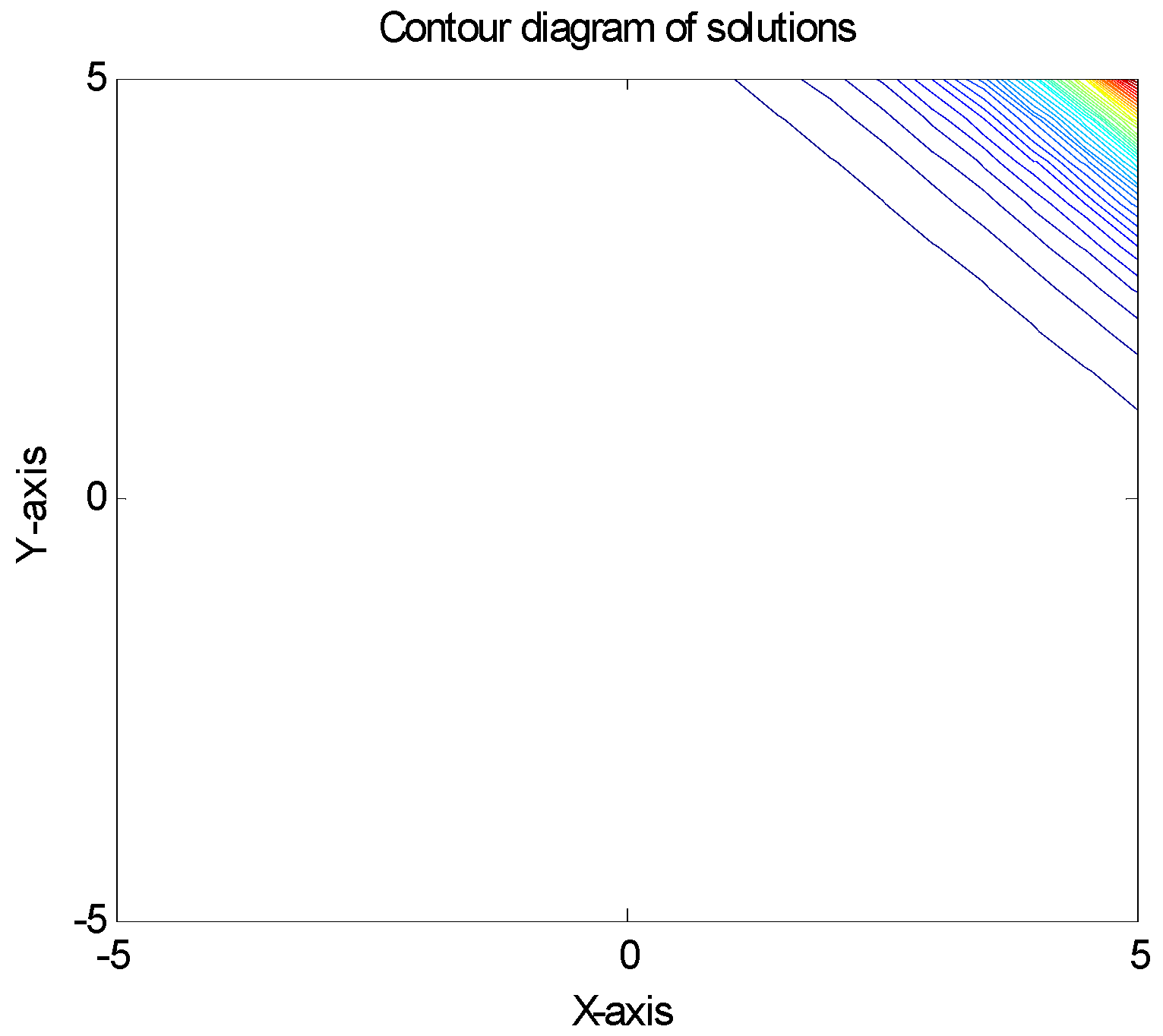
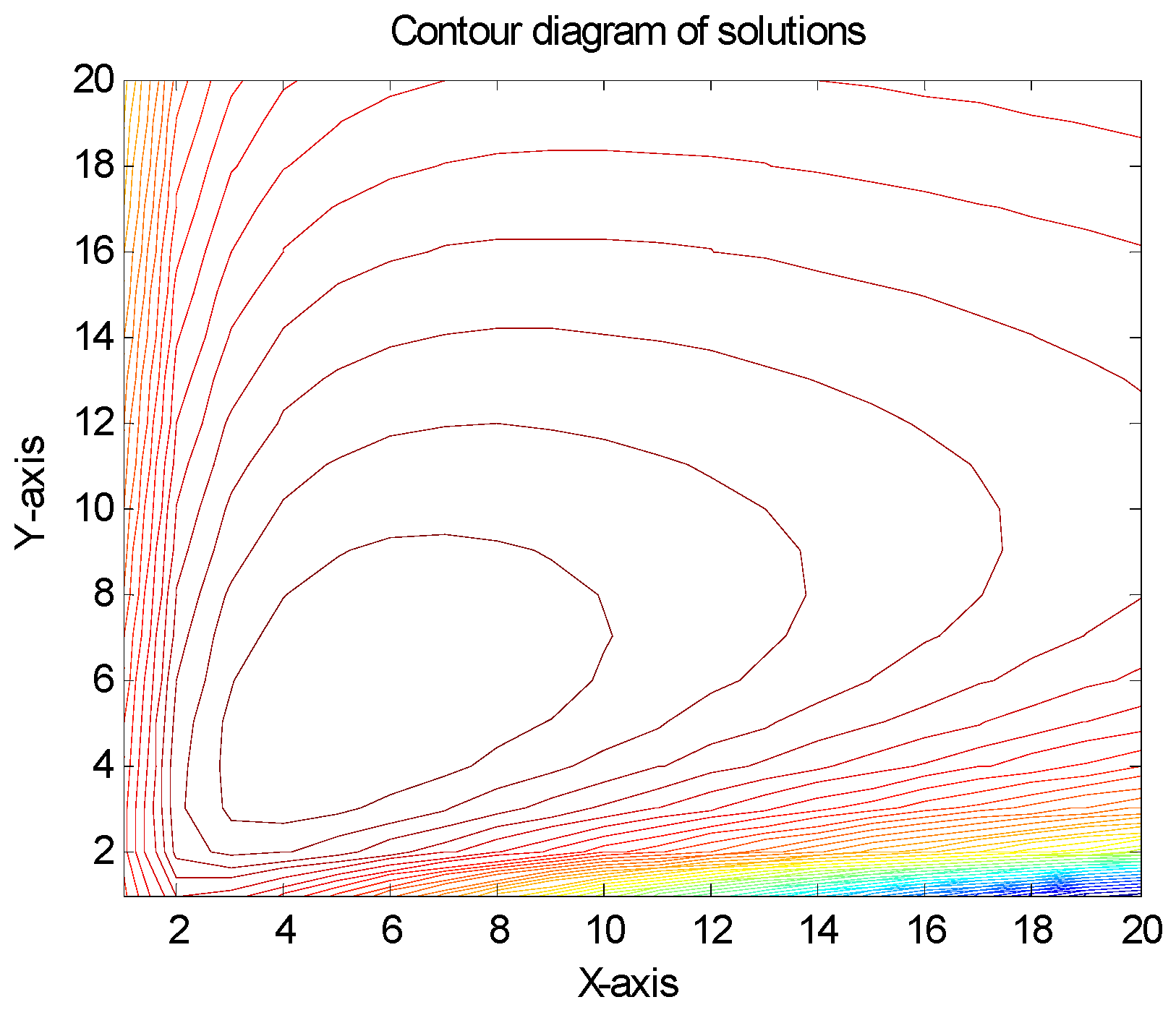
7. Numerical Experiments

The numerical observations in this section serve to demonstrate the accuracy and simplicity of the proposed method for solving (3+1)-D fourth-order parabolic PDEs with time-dependent fractional derivatives. In all the diagrams, we let $\alpha =x, \beta =y$ and $\gamma =z.$

Example 1.

Consider the following fourth-order (3+1)-D PDEs with time-fractional derivatives [32]

$$\frac{{\partial }^{2k}w}{\partial t^{2k}}+\left(\frac{\beta +\gamma }{2\cos \alpha }-1\right)\frac{{\partial }^{4}w}{\partial {\alpha }^4}+\left(\frac{\gamma +\alpha }{2\cos \beta }-1\right)\frac{{\partial }^{4}w}{\partial {\beta }^4}+\left(\frac{\alpha +\beta }{2\cos \gamma }-1\right)\frac{{\partial }^{4}w}{\partial {\gamma }^4}=0,$$

(14)

where $0<\alpha ,\beta ,\gamma <\frac{\pi }{3}, t>0, 0<k<1,$ subject to the initial conditions

$$w\left(\alpha ,\beta ,\gamma ,0\right)=\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)$$

and

$$\frac{\partial w}{\partial t}\left(\alpha ,\beta ,\gamma ,0\right)=\left(\cos \alpha +\cos \beta +\cos \gamma \right)-\left(\alpha +\beta +\gamma \right).$$

Equation (14) can be written as:

$$\frac{{\partial }^{2k}w}{\partial t^{2k}}=-\left(\frac{\beta +\gamma }{2\cos \alpha }-1\right)\frac{{\partial }^{4}w}{\partial {\alpha }^4}-\left(\frac{\gamma +\alpha }{2\cos \beta }-1\right)\frac{{\partial }^{4}w}{\partial {\beta }^4}-\left(\frac{\alpha +\beta }{2\cos \gamma }-1\right)\frac{{\partial }^{4}w}{\partial {\gamma }^4},$$

Using the Elzaki transform in the above equation, we obtain

$$E_L\left(\frac{{\partial }^{2k}w}{\partial t^{2k}}\right)=-E_L\left\{\left(\frac{\beta +\gamma }{2\cos \alpha }-1\right)\frac{{\partial }^{4}w}{\partial {\alpha }^4}+\left(\frac{\gamma +\alpha }{2\cos \beta }-1\right)\frac{{\partial }^{4}w}{\partial {\beta }^4}+\left(\frac{\alpha +\beta }{2\cos \gamma }-1\right)\frac{{\partial }^{4}w}{\partial {\gamma }^4}\right\}$$

This implies

$$E_L\left(w\right)={\displaystyle \sum }_{i=0}^{n-1}{v}^{i+2}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)+v^{2k}·E_L\left\{N\left(w\right)\right\},$$

After using the Elzaki inverse transform in the above equation, we obtain

$$w={\displaystyle \sum }_{i=0}^{n-1}\frac{t^i}{i!}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)+E_L^{-1}\left(v^{2k}·E_L\left\{N\left(w\right)\right\}\right)$$

Using the homotopy perturbation method, we have

$${\displaystyle \sum }_{n=1}^{\infty }{e}^n{w}_n=w\left(\alpha ,\beta ,\gamma ,0\right)+e·\left({\displaystyle \sum }_{i=1}^{n-1}\frac{t^i}{i!}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)+E_L^{-1}\left(v^{2k}·E_L\left\{{\displaystyle \sum }_{n=0}^{\infty }{e}^n·H_n\left(w\right)\right\}\right)\right),$$

(15)

where

$$\left\{\begin{array}{c}{H}_0\left(w\right)=\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right),\hfill \\ H_1\left(w\right)=\left\{\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)\right\}·\left(-t+\frac{t^2}{2!}\right), \hfill \\ H_2\left(w\right)=\left\{\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)\right\}·\left(-\frac{t^3}{3!}+\frac{t^4}{4!}\right),\hfill \\ \hfill ⋮\hfill \end{array}\right.$$

(16)

From (15), we obtain

$$\left\{\begin{array}{c}{w}_0=\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right),\hfill \\ w_1=\left\{\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)\right\}·\left(-t+\frac{t^{2k}}{\left(2k\right)!}\right),\hfill \\ w_2=\left\{\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)\right\}·\left(-\frac{t^{2k+1}}{\left(2k+1\right)!}+\frac{t^{4k}}{\left(4k\right)!}\right) \hfill \\ \hfill ⋮\hfill \end{array}\right.$$

(17)

The solution is

$$w=w_0+w_1+w_2+···$$

It implies

$$w=\left(\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)\right)·\left(1-t+\frac{t^{2k}}{\left(2k\right)!}-\frac{t^{2k+1}}{\left(2k+1\right)!}+\frac{t^{4k}}{\left(4k\right)!}-···\right)$$

For $k=1,$

$$\left\{\begin{array}{c}{w}_0=\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right),\hfill \\ w_1=\left(\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)\right)·\left(-t+\frac{t^2}{2!}\right),\hfill \\ w_2=\left(\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)\right)·\left(-\frac{t^3}{3!}+\frac{t^4}{4!}\right),\hfill \\ \hfill ⋮\hfill \end{array}\right.$$

(18)

The solution approaches

$$w=\left(\left(\alpha +\beta +\gamma \right)-\left(\cos \alpha +\cos \beta +\cos \gamma \right)\right)·e^{-t}$$

(19)

as $n\to \infty$.

Figure 1 and Figure 2 describe the physical interpretation of the solutions and the contour diagram of the solutions of Example 1, respectively, for $-8\le \alpha ,\beta \le 8$, and $\gamma =5$ at $t=2$.

Example 2.

Consider the following fourth-order (3+1)-D parabolic PDEs with time-fractional derivatives

$$3\frac{{\partial }^{2k}w}{\partial t^{2k}}-\frac{{\partial }^{4}w}{\partial {\alpha }^4}-\frac{{\partial }^{4}w}{\partial {\beta }^4}-\frac{{\partial }^{4}w}{\partial {\gamma }^4}=0, t>0$$

(20)

with the following initial conditions

$$w\left(\alpha ,\beta ,\gamma ,0\right)=e^{\alpha +\beta +\gamma },$$

and

$$\frac{\partial w}{\partial t}\left(\alpha ,\beta ,\gamma ,0\right)=e^{\alpha +\beta +\gamma }.$$

Equation (20) can be written as:

$$3·\frac{{\partial }^{2k}w}{\partial t^{2k}}=\frac{{\partial }^{4}w}{\partial {\alpha }^4}+\frac{{\partial }^{4}w}{\partial {\beta }^4}+\frac{{\partial }^{4}w}{\partial {\gamma }^4},$$

Using the Elzaki integral transform, we obtain

$$E_L\left(\frac{{\partial }^{2k}w}{\partial t^{2k}}\right)=\frac{1}{3}·E_L\left\{\frac{{\partial }^{4}w}{\partial {\alpha }^4}+\frac{{\partial }^{4}w}{\partial {\beta }^4}+\frac{{\partial }^{4}w}{\partial {\gamma }^4}\right\}$$

This implies

$$E_L\left(w\right)={\displaystyle \sum }_{i=0}^{n-1}{v}^{i+2}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)+\frac{1}{3}·v^{2k}·E_L\left\{N\left(w\right)\right\},$$

Applying the Elzaki inverse integral transform, we obtain

$$w={\displaystyle \sum }_{i=0}^{n-1}\frac{t^i}{i!}{w}^{\left(i\right)}\left(\alpha ,\beta ,\gamma ,0\right)+\frac{1}{3}·E_L^{-1}\left(v^{2k}·E_L\left\{N\left(w\right)\right\}\right)$$

Using the homotopy perturbation method, we have

$${\displaystyle \sum }_{n=1}^{\infty }{e}^n{w}_n=w\left(\alpha ,\beta ,\gamma ,0\right)+e·\left(t·\frac{\partial w}{\partial t}\left(\alpha ,\beta ,\gamma ,0\right)+\frac{1}{3}·E_L^{-1}\left(v^{2k}·E_L\left\{{\displaystyle \sum }_{n=0}^{\infty }{e}^n·H_n\left(w\right)\right\}\right)\right),$$

(21)

where

$$\left\{\begin{array}{c}{H}_0\left(w\right)=3·e^{\alpha +\beta +\gamma },\hfill \\ H_1\left(w\right)=3·e^{\alpha +\beta +\gamma }·\left(-t+\frac{t^2}{2!}\right),\hfill \\ H_2\left(w\right)=3·e^{\alpha +\beta +\gamma }·\left(-\frac{t^3}{3!}+\frac{t^4}{4!}\right),\hfill \\ \hfill ⋮\hfill \end{array}\right.$$

(22)

From (21), we obtain

$$\left\{\begin{array}{c}{w}_0=e^{\alpha +\beta +\gamma },\hfill \\ w_1=e^{\alpha +\beta +\gamma }·\left(-t+\frac{t^{2k}}{\left(2k\right)!}\right),\hfill \\ w_2=e^{\alpha +\beta +\gamma }·\left(-\frac{t^{2k+1}}{\left(2k+1\right)!}+\frac{t^{4k}}{\left(4k\right)!}\right),\hfill \\ \hfill ⋮\hfill \end{array}\right.$$

(23)

The solution is

$$w=w_0+w_1+w_2+···$$

It implies

$$w=e^{\alpha +\beta +\gamma }·\left(1-t+\frac{t^{2k}}{\left(2k\right)!}-\frac{t^{2k+1}}{\left(2k+1\right)!}+\frac{t^{4k}}{\left(4k\right)!}-···\right)$$

For $k=1,$ as $n\to \infty$, the solution approaches

$$w=e^{\alpha +\beta +\gamma }·e^{-t}$$

(24)

Figure 3 and Figure 4 describe the physical interpretation of the solutions and the contour diagram of the solutions of Example 2, respectively, for $-5\le \alpha ,\beta \le 5$, and $\gamma =5$ at $t=2$.

Example 3.

Consider the following three-dimensional fourth-order fractional partial differential equation [32]

$$\frac{{\partial }^{2k}w}{\partial t^{2k}}+\frac{1}{4!}·\left(\frac{1}{\gamma }\frac{{\partial }^{4}w}{\partial {\alpha }^4}+\frac{1}{\alpha }\frac{{\partial }^{4}w}{\partial {\beta }^4}+\frac{1}{\beta }\frac{{\partial }^{4}w}{\partial {\gamma }^4}\right)=\left(-\frac{\alpha }{\beta }-\frac{\beta }{\gamma }-\frac{\gamma }{\alpha }+\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right)\cos t,$$

(25)

with initial conditions

$$w\left(\alpha ,\beta ,\gamma ,0\right)=\frac{\alpha }{\beta }+\frac{\beta }{\gamma }+\frac{\gamma }{\alpha }$$

and

$$\frac{\partial w}{\partial t}\left(\alpha ,\beta ,\gamma ,0\right)=0.$$

Particularly for $k=1$, from Equation (25), we have

$$\frac{{\partial }^{2}w}{\partial t^2}=\left(-\frac{\alpha }{\beta }-\frac{\beta }{\gamma }-\frac{\gamma }{\alpha }+\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right)\cos t-\frac{1}{4!·\gamma }\frac{{\partial }^{4}w}{\partial {\alpha }^4}-\frac{1}{4!·\alpha }\frac{{\partial }^{4}w}{\partial {\beta }^4}-\frac{1}{4!·\beta }\frac{{\partial }^{4}w}{\partial {\gamma }^4},$$

After applying the Elzaki transform in the above equation, we obtain

$$E_L\left(\frac{{\partial }^{2}w}{\partial t^2}\right)=E_L\left\{\left(-\frac{\alpha }{\beta }-\frac{\beta }{\gamma }-\frac{\gamma }{\alpha }+\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right)\cos t-\frac{1}{4!·\gamma }\frac{{\partial }^{4}w}{\partial {\alpha }^4}-\frac{1}{4!·\alpha }\frac{{\partial }^{4}w}{\partial {\beta }^4}-\frac{1}{4!·\beta }\frac{{\partial }^{4}w}{\partial {\gamma }^4}\right\}$$

This implies

$$E_L\left(w\right)=v^2·w\left(\alpha ,\beta ,\gamma ,0\right)+v^3·\frac{\partial w}{\partial t}\left(\alpha ,\beta ,\gamma ,0\right)+v^2·E_L\left\{N\left(w\right)\right\},$$

Using the Elzaki inverse transform in the above equation, we obtain

$$w=w\left(\alpha ,\beta ,\gamma ,0\right)+t·\frac{\partial w}{\partial t}\left(\alpha ,\beta ,\gamma ,0\right)+E_L^{-1}\left(v^2·E_L\left\{N\left(w\right)\right\}\right)$$

Using the homotopy perturbation method, we have

$${\displaystyle \sum }_{n=1}^{\infty }{e}^n{w}_n=w\left(\alpha ,\beta ,\gamma ,0\right)+e·\left(t·\frac{\partial w}{\partial t}\left(\alpha ,\beta ,\gamma ,0\right)+E_L^{-1}\left(v^2·E_L\left\{{\displaystyle \sum }_{n=0}^{\infty }{e}^n·H_n\left(w\right)\right\}\right)\right),$$

(26)

where,

$$\begin{array}{c}{H}_0\left(w\right)=\left(-\frac{\alpha }{\beta }-\frac{\beta }{\gamma }-\frac{\gamma }{\alpha }+\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right)\cos t-\left(\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right),\hfill \\ H_1\left(w\right)=\left(\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}-\frac{70}{\alpha ·{\beta }^9}-\frac{70}{\beta ·{\gamma }^9}-\frac{70}{\gamma ·{\alpha }^9}\right)\left(1-\cos t\right)+70\left(\frac{1}{\alpha ·{\beta }^9}+\frac{1}{\beta ·{\gamma }^9}+\frac{1}{\gamma ·{\alpha }^9}\right)\frac{t^2}{2!},\hfill \\ H_2\left(w\right)=-70\left(\frac{1}{\alpha ·{\beta }^9}+\frac{1}{\beta ·{\gamma }^9}+\frac{1}{\gamma ·{\alpha }^9}\right)\left(\cos t-1+\frac{t^2}{2!}\right)\hfill \\ +34650\left(\frac{1}{{\alpha }^2·{\beta }^{13}}+\frac{1}{{\beta }^2·{\gamma }^{13}}+\frac{1}{{\gamma }^2·{\alpha }^{13}}\right)\left(-\cos t+1-\frac{t^2}{2!}+\frac{t^4}{4!}\right)\\ +70\left(\frac{1}{\alpha ·{\beta }^5·{\gamma }^9}+\frac{1}{\beta ·{\gamma }^5·{\alpha }^9}+\frac{1}{\gamma ·{\beta }^5·{\alpha }^9}\right)\left(-\cos t+1-\frac{t^2}{2!}+\frac{t^4}{4!}\right)\end{array}$$

and so on. From (26), we obtain

$$\begin{array}{c}{w}_0=\left(\frac{\alpha }{\beta }+\frac{\beta }{\gamma }+\frac{\gamma }{\alpha }\right),\hfill \\ w_1=\left(\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right)\left(-\cos t+1-\frac{t^2}{2!}\right)+\left(\frac{\alpha }{\beta }+\frac{\beta }{\gamma }+\frac{\gamma }{\alpha }\right)\left(\cos t-1\right),\hfill \\ w_2=\left(\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right)\left(\cos t-1+\frac{t^2}{2!}\right)+70\left(\frac{1}{\alpha ·{\beta }^9}+\frac{1}{\beta ·{\gamma }^9}+\frac{1}{\gamma ·{\alpha }^9}\right)\left(-\cos t+1-\frac{t^2}{2!}+\frac{t^4}{4!}\right),\hfill \\ w_3=70\left(\frac{1}{\alpha ·{\beta }^9}+\frac{1}{\beta ·{\gamma }^9}+\frac{1}{\gamma ·{\alpha }^9}\right)\left(\cos t-1+\frac{t^2}{2!}-\frac{t^4}{4!}\right)\hfill \\ +34650\left(\frac{1}{{\alpha }^2·{\beta }^{13}}+\frac{1}{{\beta }^2·{\gamma }^{13}}+\frac{1}{{\gamma }^2·{\alpha }^{13}}\right)\left(-\cos t+1-\frac{t^2}{2!}+\frac{t^4}{4!}-\frac{t^6}{6!}\right)\\ +70\left(\frac{1}{\alpha ·{\beta }^5·{\gamma }^9}+\frac{1}{\beta ·{\gamma }^5·{\alpha }^9}+\frac{1}{\gamma ·{\beta }^5·{\alpha }^9}\right)\left(-\cos t+1-\frac{t^2}{2!}+\frac{t^4}{4!}-\frac{t^6}{6!}\right),\end{array}$$

and so on. The solution is

$$w=w_0+w_1+w_2+\dots$$

This implies

$$\begin{array}{c}w=\left(\frac{\alpha }{\beta }+\frac{\beta }{\gamma }+\frac{\gamma }{\alpha }\right)+\left(\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right)\left(-\cos t+1-\frac{t^2}{2!}\right)\hfill \\ +\left(\frac{\alpha }{\beta }+\frac{\beta }{\gamma }+\frac{\gamma }{\alpha }\right)\left(\cos t-1\right)+\left(\left(\frac{1}{{\alpha }^5}+\frac{1}{{\beta }^5}+\frac{1}{{\gamma }^5}\right)\right)\left(\cos t-1+\frac{t^2}{2!}\right)\hfill \\ +70\left(\frac{1}{\alpha ·{\beta }^9}+\frac{1}{\beta ·{\gamma }^9}+\frac{1}{\gamma ·{\alpha }^9}\right)\left(-\cos t+1-\frac{t^2}{2!}+\frac{t^4}{4!}\right)+\dots \hfill \end{array}$$

As $n\to \infty$, the solution approaches

$$w=\left(\frac{\alpha }{\beta }+\frac{\beta }{\gamma }+\frac{\gamma }{\alpha }\right)\cos t$$

(27)

Figure 5 and Figure 6 describe the physical interpretation of the solutions and the contour diagram of the solutions of Example 3, respectively, for $0\le \alpha ,\beta \le 20$ and $\gamma =5$ at $t=2$.

8. Conclusions

When k = 1, the EHPM solutions of the mentioned examples are in excellent agreement with the exact solutions of their corresponding classical (nonfractional) form. The exact solution of a linear, fourth-order, three-dimensional, time-fractional, partial differential equation was successfully determined in this study using the coupling of the Elzaki integral transform and the homotopy perturbation method. All of the examples demonstrate how well the results of the proposed method match those of the exact solution. It is evident that the Elzaki-integral-transform-based homotopy perturbation method is a very effective, simple, and powerful technique for evaluating analytical solutions for a variety of time-fractional linear problems.