Abstract
Understanding the soil mass and how it behaves is determinant to the quality and reliability of a foundation design. Normally, such behavior is predicted based on laboratory and in situ tests. In the big data era, instead of executing more tests, engineers should understand how to take advantage of ordinary execution procedures to obtain the parameters of interest. Sensors are key components in engineering big data frameworks, as they provide a large number of valuable measured data. In particular, the building process (excavation and concreting) of continuous flight auger piles (CFAPs) can be fully monitored by collecting data from sensors in the drilling machine. This makes this type of pile an ideal candidate to utilize a big data methodology to indirectly obtain some constitutive parameters of the soil being drilled. Thus, in the present paper, the drilling process of CFAPs is modeled by a new physical model which predicts the energy spending during the execution of this type of pile. This new model relies on other fundamental properties of the soils drilled, such as unit weight, cohesion and internal friction angle. In order to show the applicability of the big data methodological framework hereby developed, a case study was conducted. A work site in Brasília-DF, Brazil, was studied and the execution of three CFAPs was monitored. Soil surveys were carried out to identify the soil strata in the site and, therefore, to validate the estimates of Young’s moduli provided by the new formulas. The 95% confidence intervals of Young’s moduli obtained for silty clay, clayey silt and silt were, in MPa, , and , respectively. These intervals are consistent with literature reports for the following materials: stiff to very stiff clays with low-medium plasticity, medium silts with slight plasticity, and stiff to very stiff silts with low plasticity, respectively. These were the types of materials observed during the site surveys; therefore, the results obtained are consistent with literature reports as well as with field surveys. This new framework may be useful to provide real-time estimates of the drilled soil’s parameters, as well as updating CFAPs designs during their execution. This way, sustainable designs can be achieved, where substrata materials are better characterized, avoiding over-designed structures.
MSC:
86-10; 62R07; 00A69
1. Introduction
Every foundation designer must have access to subsurface medium characterization experiments. This is because constitutive models are dependent on specific parameters that are only assessed during such testing. In general, foundation design must account for strength and deformability parameters, which are often achieved through laboratory or in situ measurements [1].
Controlling environmental variables, such as confining pressure and temperature, may result in more trustworthy results, which is an advantage of laboratory tests. However, these tests may not be appropriate, particularly when undisturbed samples are required [1].
When cost is an issue, in situ tests are an excellent option because they are normally less expensive than laboratory procedures. However, this price decrease is accompanied by reduced control over environmental variables and experimental techniques, which may result in poorly executed or poorly situated tests [1].
In the big data era, every expert should try to use the available data to discover new knowledge indirectly. As a result, engineers must learn how to use standard executive processes to estimate the parameters required to predict soil behavior.
The transformation of raw data into information is one of the primary concerns of modern data scientists and should also figure as the main concern for engineers trying to estimate soil’s constitutive parameters from indirect measurements. A classic analytics workflow for big data typically includes the following phases: data mining from data sources, data management, data modeling, and result analysis and visualization [2].
According to Assunção et al. [2], data from various sources are used to build models. Pre-processing procedures for integrating, cleaning, and filtering the data may be necessary in a big data context due to the huge amount and variety of the dataset. The prepared data are subsequently used to train a model and estimate its parameters, according to those authors. Prior to using the model, after the parameters have been computed, validation must be carried out.
After the model is validated, Assunção et al. [2] indicate that it can be applied to data as it arrives. Predictions, prescriptions, and recommendations are produced using this process, known as model scoring. The findings are analyzed and interpreted, they are combined with pre-processed data, or they are utilized to create new models or calibrate current ones [2].
Directly considering the big data analytics (BDA) workflow as presented in [2] is not straightforward for geotechnical engineering applications. The very first step (data mining from data sources) is a big obstacle since the data standard is not unified between geological models and engineering models [3]. The second step (data management) also is problematic, as there are no universally adopted data management procedures in this field, even though the literature brings several attempts in this regard [3,4]. Issues are also present in the third step (data modeling), as correlations between raw data (laboratory index test or a field tests) were generally developed by curve-fitting procedures based on laboratory or field data; therefore, they tend to be case specific and may not generalize to other or new soils/sites. In using these correlations, the caveat is to apply engineering judgment, which is not deterministic nor broadly reproducible [5].
This way, in the present paper, a big data analytics workflow shall be explored to obtain the Young’s modulus of soils drilled during the execution of continuous flight auger piles (CFAPs). In short, two important issues are addressed: how to incorporate big data analytics principles in the execution process of CFAPs (especially enhancing data pre-processing procedures) and how a physically consistent (and not merely based on curve fitting) model can be built to relate the execution energy to the Young’s modulus of soils. Then, in order to show the applicability of the methodological framework hereby developed, a case study is conducted. A work site in Brasília-DF, Brazil, was studied, and the execution of three CFAPs was monitored. Soil surveys were carried out to identify the soil strata in the site and, therefore, to validate the estimates of Young’s moduli provided by the new formulas.
2. CFAPs and Their Execution
Continuous flight auger piles are a type of deep foundation, whose use emerged in the United States in the 1950s, being later disseminated throughout Europe and Japan in the 1980s. In several countries, such as Brazil, this type of pile is the preferred technique for builders when it comes to deep foundations, not only due to its productivity and good cost–benefit relation but also due to the absence of noise and vibrations in relation to neighboring buildings and the progress of the installation itself [6]. This execution technique has been enhanced over the years, as well as combined with other techniques, such as using competent caliche layers bonded to the top and bottom of CFAPs [7].
The execution of CFAPs is possible in both cohesive and sandy soils, in the presence or absence of the water table, and crosses layers of resistant soils with NSPT indexes greater than 50 depending on the type of equipment [8].
The drilling process of the CFAPs should be a continuous operation starting with the introduction of the auger or drilling helix (consisting of a continuous helical auger with its helices around a hollow central tube) into the ground. By applying a sufficient torque, the drilling helix will be introduced into the ground, surpassing the drilling resistance of the soil. Literature indicates that there is a relationship between the overall energy expenditure in the drilling process and the resistance of the soil [6,9,10].
The equipment for electronic monitoring the drilling process of CFAPs can be schematically seen in Figure 1. In short, by analyzing Figure 1 and the numbers thereby indicated, such equipment allows obtaining data on depth (1), tower inclination (2), rotation speed (3), torque (4) as well as by-products of such measurements, such as execution time and auger penetration speed. For this research, the field monitoring was performed using SACI-type data acquisition equipment, from Geodigitus, one of several options available in the market [11]. In this case, data are transmitted automatically to a cloud server and can be retrieved with SoftSaci software for analysis, storage and printing of reports and graphical results.
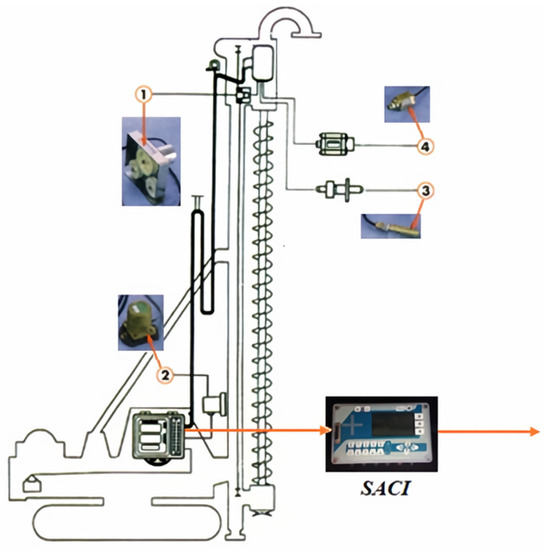
Figure 1.
General setup for the monitoring of CFAPs modified from [6].
According to the SACI operation manual [11], the depth recording starts by resting the auger on the ground surface, with a 1 cm measurement precision performed by a proximity sensor and a set of pulleys installed on the drilling table. To control the tilt and verticality of the pile, the sensor located in the machine’s tower is used, with an accuracy of 0.1 degrees. The rotation speed is obtained by the sensor installed inside the torque motor or near the drilling head, which detects the passage of metal pins that are installed in the auger’s axis. Its function is to count the number of times the pins pass the sensor due to the rotation of the auger, and to calculate the speed, both in terms of rotation and auger penetration. Finally, torque is measured by a pressure transducer that is installed in the oil pipe of the rotary table motor’s hydraulic system.
The recorded data can be stored in Microsoft Access files (i.e., .mdb files), which are not standard for big data analytics. On the other hand, this is a limitation of the data acquisition systems available in the market.
Torque is physically understood as a parameter related to the rotational movement of a body after the application of a given force on it. In the case of the execution of CFAPs, torque is applied by means of the rotary table located at the top of the auger, mentioned and illustrated in Figure 1, resulting in a certain speed of penetration and rotation of the auger. Of the parameters obtained during the executive process, the torque presents correlations with the shear force and the load capacity of the soil [9,10].
During the drilling process, not only torque is applied to the auger but also external forces, such as pull-down and gravitational forces. The work done by these forces enables one to calculate the energy needed to excavate the CFAP, and the literature reveals that such energy is a variable capable of representing the state of the terrain around the pile; therefore, it is of interest to use this quantity to estimate the deformability and strength parameters of the soil being drilled.
Obtaining Strength and Deformability Parameters of Soils from Drilling Performance Indicators
According to Li and Itakura [12], a promising in situ technique that has been studied by numerous researchers is using the drilling data of geomaterials to determine strength characteristics. According to Behboud et al. [13], geomaterials, such as rock and soil, which are understood as the formation to be drilled, are extremely important in determining drilling speed, machine depreciation, and overall drilling expenses. To choose the machines and forecast the execution schedules, it is crucial to understand the drilling environment and the properties of the in situ rock mass [13].
Strength parameters can be estimated from drilling data by both theoretical and experimental approaches [10]. These approaches, on the other hand, are common in engineering practice but uncommon in BDA, as they are connected to the physical modeling of the phenomena themselves. There are some works on using machine learning and artificial intelligence to predict the behavior of structural elements in engineering [14], which would be standard practice in BDA, but using these types of models is not within the scope of the present paper.
This way, Warren [15] presented the development of a penetration rate () model for soft-formation bits under conditions where cuttings removal does not impede this rate. This model relates to weight on bit, rotary speed, rock strength, and bit size. The same author further developed this model and then presented a model that includes the effect of both the initial chip formation and cuttings-removal processes [16].
Li and Itakura [12] proposed an analytical model to describe rock drilling processes using drag bits and rotary drills, and to deduce the relations among rock properties, bit shapes, and drilling parameters (rotary speed, thrust, torque and stroke). These authors then could estimate the unconfined compressive strength (UCS) of rocks from drilling data [1].
On the other hand, Kahraman et al. [17] studied percussive blast hole drills and experimentally connected the drills’ net penetration rates to strength characteristics. These authors gathered rock samples from some drilling sites, and both in the field and in the lab, they measured the physical and mechanical characteristics of the rocks. They investigated the relationships between penetration rates and the following properties: uniaxial compressive strength, Brazilian tensile strength, point load strength, Schmidt hammer value, impact strength, Young’s modulus (E), natural density, and P-wave velocity.
Besides the penetration rate, the literature reveals that the energy required for drilling a given volume of material can also be correlated to strength and deformability parameters of the drilled materials [1]. Ozelim et al. [18], for example, used literature data to build simple regression models to estimate the unconfined compressive strength of the excavated soil layers based on the execution energy of CFAPs. Ozelim et al. [10], on the other hand, estimated shear strength properties of the drilled based on such execution energy.
By noticing that CFAPs can have their execution fully monitored and that literature indicates that there exists a relationship between deformability parameters and the execution energy of CFAPs, a BDA workflow is proposed. In the next section, it is indicated why a big data methodology is needed.
3. Big Data Analytics: Challenges and Perspectives for Geotechnical Engineering Applications
Although Moore’s law has guided the development of computing hardware for several decades, managing enormous amounts of data remains a challenge as the era of big data approaches [19]. Because of this, Fisher et al. [20] noted that big data means the data cannot be handled and processed by the majority of current information systems or methods. This is because not only will data in the big data era grow too large to be loaded into a single machine but it is also suggested that the majority of traditional data mining methods or data analytics developed for a centralized data analysis process may not be able to be applied directly to big data.
Together with the problems with data size, Laney [21] offered the 3Vs concept of “large” data, which stands for volume, velocity, and variety. According to the definition of 3Vs, there will be a lot of data, they will be produced quickly, they will exist in many forms, and they will be obtained from various sources. Subsequent investigations indicated that the 3Vs concept may be insufficient to understand the enormous data that we are currently dealing with [19], but for the purpose of the present paper, only these aspects suffice and will be discussed.
3.1. Volume
The overwhelming amount of incoming data is the first issue we must address from a volume standpoint since it might render data analytics useless. Different from traditional data analytics, for sensor network data analysis, Baraniuk [22] pointed out that the bottleneck of big data analytics would be relocated from sensor to processing, transmission, storage of sensing data. This is due to the fact that although sensors are capable of collecting a lot more data, uploading such vast amounts of data to systems at higher layers may result in bottlenecks everywhere. This is the case of the sensors in the drilling machines of CFAPs, which acquire data in real time. Such data must be pre-processed prior to its storage or transmission.
Pre-processing is necessary to prepare the input data so that the computer, platform, and analytic program can handle it [19]. The classic data preparation approaches [23] are believed to be able to work well in the big data age. Literature, however, suggests that future research will concentrate on ways to simplify input complexity. Sampling and compression are two examples of data reduction techniques for big data analytics because smaller data sets are easier to process computationally, leading to quicker data analytics, especially for data that enter the system quickly.
By proposing a pre-processing step which transforms drilling data into the energy needed to drill a certain amount of soil, such a step is a powerful pre-processing stage which compresses information: from several input values (for example, the parameters of the hydraulic system responsible for applying the pull-down force and the toque, the weight of the drilling auger, its rotation speed, the area of the hole or excavation—which represents the geometry of the pile—and the penetration rate), a single meaningful output value (excavation energy per volume) can be obtained.
Let one assume that n data points are collected every 1 drilled meter; thus, a dimensional array can be converted to array, where m is the number of features collected every measuring step. In the particular case of the present paper, the SACI data acquisition system collects four intermediate features, which are used to calculate the final values of torque, rotations per second and penetration rate. Other parameters, which are characteristics of the drilling machine, are recorded only once for every machine (i.e., not stored at every measuring step). Additionally, if the drilling energy is summarized in a by meter basis, this reduction becomes even greater, from to a single element. In the case of the present paper, CFAP execution data are acquired every 8 cm of depth. Thus, 1/50 ( to ) in reduction can be achieved when a meter-by-meter energy approach is considered.
3.2. Velocity
Additionally, real-time or streaming data present the issue of a significant volume of data entering data analytics within a short period of time, yet the device and system may not be able to manage these input data. This is known as the velocity problem. This circumstance is comparable to network flow analysis, where we normally are unable to mirror and analyze all of the data [19].
To avoid the application-level slow down caused by the compression process, in [24], Jun et al. attempted to use the FPGA to accelerate the compression process. Therefore, the sampling and compression algorithms should be as simple as possible, allowing their implementation in FPGAs or even single-board computers (such as RaspberryPis) because the data need to be converted and processed on the fly. In the case of the monitoring of CFAPs, the formulas considered in the BDA need to match such simplicity criteria. In particular, a new model needs to be developed to relate the excavation energy to the Young’s moduli of the drilled soils since no other physically consistent alternative has been introduced so far.
By using easy-to-implement and lightweight models, parallel processing is enabled at the very tip of the system: as soon as data are acquired, the processing is performed by a simple single-board computer attached to the drilling machine and its sensors. This avoids the need to upload data to the cloud for further processing, for example, and provides a faster BDA scheme overall.
3.3. Variety
Currently, the data that need to be examined are massive, high dimensional, diverse, complicated, unstructured, incomplete, noisy, and erroneous [25]. Although it seems like big data makes it easier for us to collect more data to uncover more relevant information, the fact is that more data does not necessarily guarantee more usable information. It can include more anomalous or unclear data.
How to manage them also raises another challenge for the input operators of data analytics from the variety perspective since the entering data may employ various forms or have missing data. Not many researchers considered techniques for pulling data from related and external knowledge sources to support BDA further [19].
In this regard, the workflow hereby proposed is easily combined with information fusion approaches, which will enhance the outcomes of BDA for CFAPs monitoring. Normally, field engineers can only rely on site surveys to understand how the soil strata behave. On the other hand, by considering the BDA hereby proposed, execution energy becomes available and can be combined with such surveys to provide better information to the designers. They should be able to fuse these two groups of information in a clear and direct way.
In the BDA workflow hereby presented, since changes in nature are normally smooth (i.e., not abrupt), the particular choice of considering energy values and Young’s moduli is of the utmost importance to the assessment of noise, outliers, incomplete, and inconsistent data. Data fusion (drilling sensors with soil surveys, for example) together with the usual natural smoothness allow engineers to clearly identify outliers on the fly. These outliers can be related to measurement problems or to actual changes in the geological formation, which would be promptly highlighted and reported to the operator and the engineers.
From all the information discussed, it is clear that a BDA is appropriate to provide a real-time assessment of the soil’s deformability (Young’s modulus, in particular) based on monitoring the execution of CFAPs.
4. Proposition of a Big Data Workflow for CFAPs Real-Time Assessment
As previously indicated, the common phases of a traditional analytics workflow for big data are: data mining from data sources, data management, data modeling and result analysis and visualization [2]. Therefore, each of the next subsection will explore these phases. The following general workflow is similar to the one explored by Ozelim et al. [10].
4.1. Data Mining
Engineering data mining typically relies on data collection from laboratory or in-situ experiments. On the other hand, since the construction of CFAPs may be completely monitored, the main data-mining procedure taken into consideration in the present article is gathering the data that were recorded by sensors in the drilling machine.
4.2. Data Management
The act of turning raw input data into pre-processed information can be thought of as the data management step in the big data pipeline. This procedure includes both data manipulation and storage.
The raw monitoring data from CFAPs data acquisition systems is typically saved on Microsoft Access files (i.e., .mdb database files) before being aggregated and processed. Even though this format is not standard in BDA, it is used because this is the only possible output from the sensors. The following variables are generally included in the dataset gathered: depth, rotation speed, torque, vertical tilt of the drilling auger, and pressure of the injected concrete.
One can determine how much energy is needed to carry out the drilling operation by using the raw data previously given. The pre-processed data can then be simulated to accurately forecast several key parameters.
4.3. Data Modelling
Besides the models presented in the Introduction, the literature presents some formulations which account for the energy spent during the drilling process. Teale [26] indicated that the specific energy (), defined as the work done per unit volume excavated, is a useful parameter which can be defined and studied during drilling processes. Teale [26] also indicated that can be taken as an index of the mechanical efficiency of a rock-working process. The author stated that the minimum value of the specific energy seems to be very roughly correlated with the crushing strength of the medium drilled in for rotary, percussive-rotary and roller-bit drilling. Thus, understanding the drilling problem from an energetic point of view is a valid and promising approach.
For CFAPs, rotary non-percussive drilling is present. In this case, let M, L and T denote units of mass, length and time, respectively. Then, work is performed both by the thrust, F [MLT], and the torque, T [MLT]. If the rotation speed is N [T], the area of the hole or excavation A [L] and the penetration rate [LT], the total work done is . The volume of rock excavated is . Ref. [26] mathematically described the specific energy [MLT] as
Energetic measurements of drilling performance for soils are also presented in the literature. Perko [27] proposed a theoretical model to relate the energy exerted during installation of helical piles to the energy required to displace the foundation or anchor once in place. Through the equivalence of energy, the model relates bearing and pullout capacity directly to the installation torque. Perko [27] considered the influence of downward force during installation, helical blade geometry, multiple helices, blade pitch per revolution, and hub radius to build his formula.
A clear relationship between the drilling torque and the specific energy is shown by Equation (1). As a result, energy-based models and torque-based models both belong to the same category. The physical model developed by Tsuha and Aoki [28] offers a theoretical relationship between the uplift capability and installation torque of deep helical piles in sand.
On the other hand, Silva et al. [9] addressed the use of the SCCAP methodology, which was created to control the execution of CFAPs foundations. By comparing the energy required to excavate a specific pile to the statistical characteristics of the energetic population of similar piles, the SCCAP methodology suggests formulations, routines, and criteria for pile acceptance. According to Silva et al. [9], this method improves the accuracy and reduces the associated risks of geotechnical operations. They also suggest that it is possible to correlate a pile’s excavation energy to its bearing capacity using the SCCAP methodology.
Recently, Ozelim et al. [1] considered the datasets of Reddish and Yasar [29] and Moronkeji et al. [30] and proposed preliminary models to relate the penetration rate of drills to the energy spent during the drilling process and, ultimately, to the Young’s moduli of the drilled material. Their methodology, on the other hand, needs a more robust physical model, as the datasets used were collect from drilling tests on rocks, not soils.
This way, to overcome the limitation of the work of Ozelim et al. [1], in Section 5, we obtain a new physical model, which shall be used to estimate the Young’s modulus of the stratum being drilled. This new model is chosen to be part of the big data workflow considered in the present paper.
4.4. Result Analysis and Visualization
The analysis and visualization of the results is the last step in the big data pipeline that is taken into consideration here. Spreadsheets are a basic resource that can be used to accomplish this. The results will be displayed in the current paper as a table with color codes.
Similar to [10], a site in Brasilia-DF, Brazil, was chosen to perform a case study on the new model’s correctness. The project is of a residential building and contemplates more than three hundred CFAPs that are 50 cm in diameter. The length of the piles varied from around 8 m to 15 m [10].
The work site’s soil profile was determined by four surveys, which showed the presence of strata of silty clay, clayey silt, and silt. Additionally, NSPT tests were carried out. We chose the pile that was nearest to each of the surveys in order to accurately depict the soil profiles at the piles that were drilled. The chosen piles were P9CF, PR6, P9AF, and P6AD.
The final step to assess the correctness of the model is to compare the Young’s moduli estimations obtained by the new formulas to the values reported in the literature for the drilled materials. Obrzud and Truty [31] compiled data from Kezdi [32] and Prat et al. [33], obtaining the usual Young’s moduli presented in Table 1.

Table 1.
Usual values for Young’s moduli of soils [31].
Thus, direct comparison of the predicted values and those in Table 1 enables one to check the consistency of the estimates hereby presented.
In order to compare the results obtained in the present paper and the ones reported in Table 1, the confidence intervals of the former are compared to the latter. Since the statistical distribution of the Young’s moduli is not known beforehand, a nonparametrical approach is better suited to estimate the boundaries of the interval. A potential small sample problem is shown, as the number of samples obtained during the case study is not big. Therefore, the bootstrap method is considered.
Bootstrap
There are a variety of methodologies for determining the confidence interval of a statistic in large samples. In the case of small samples, it is important to assess how reliable the obtained asymptotic interference is. Usually, the methodologies use considerations related to the central limit theorem and consider normality for the random variables involved.
When it comes to obtaining the distribution of the statistic that determines the hypothesis test that generates the confidence interval, in many cases, such prediction becomes analytically unfeasible due to its complexity. Therefore, resampling methods show up as interesting alternatives since they do not impose normality as an essential prerequisite and do not require their samples to be considerably large. In addition, the methods have greater practical accuracy and are mostly similar for a large number of statistics, requiring no new formulas for each one. Finally, they make it possible to calculate the confidence interval of any statistic.
In the present paper, the bootstrap method [34] is considered. The method, based on available data, allows the quantification of uncertainties through calculations of standard errors and confidence intervals, as well as the performance of significance tests of interest. According to Moore [35], resampling methods require fewer assumptions and typically provide more accurate answers than traditional methods, reducing biases and providing more reliable standard deviations. As such, they are able to estimate the sampling distribution of a given statistic by taking a representative sample from the population, in which observations are independent and identically distributed. Efron and Tibshirani [34] compared the bootstrap method with conventional methods.
Among the possible bootstrap alternatives to calculate the confidence interval, the bias-corrected and accelerated (BCa) approach is considered, which is able to correct for bias and skewness in the distribution of bootstrap estimates [34]. This method has been used in numerous engineering applications, such as [36], and is widely implemented in computational packages. In the present paper, the implementation available in the Python package scikit-learn [37] is used.
5. Young’s Modulus Behavior and Estimation
Like most of the engineering parameters, Young’s modulus is stress dependent. Such dependency can be formulated based on a power-hyperbolic model of the type [38]
where E is the Young’s modulus with respect to confining stress , is the Young’s modulus with respect to confining stress , c is the cohesion of the soil, and its internal friction angle. Equation (2) reveals that stress dependency must be accounted for when estimating E along a soil profile with increasing confining pressures.
In general, besides triaxial tests, field engineers tend to estimate the Young’s modulus based on other information readily available. This parameter may be estimated in kPa based on data as [39]
in which and K are coefficients which depend on the type of soil considered. Table 2 and Table 3 present the corresponding values of such coefficients.

Table 2.
Coefficient [39].

Table 3.
Coefficient K [39].
Regarding other strength parameter, the literature also indicates that the unconfined compressive strength, , may be estimated in kPa for low plasticity clays and for clayey silts based on NSPT data as [40]
In order to estimate strength characteristics, field engineers and designers typically rely on available data. Based on field test data, such as NSPT and CPT values, this estimation is carried out. The purpose of the current research is to extend this logical process to take into account a big data approach to the issue: use current data that are continuously gathered on the field to estimate strength characteristics.
As previously said, CFAPs’ execution can be meticulously monitored. The energy utilized to drill the pile shaft is the most significant pre-processed data that might be derived from the raw data gathered. Thus, to use the data available (big data as a huge number of piles are drilled everyday), either a good experimental relation or a consistent physical model are needed. In the next subsection, the derivation of a simple, yet powerful, physical model for the drilling phenomena is presented.
Novel Simplified Model for Young’s Moduli Prediction
As previously discussed, the concepts introduced by Teale [26] and further developed by other authors, such as Hughes [41], indicate that the specific energy, , can be correlated to the unconfined compressive strain, , of a given rock by means of the following equation:
in which represents the efficiency of the drilling process. Greater values of imply less efficient drilling processes.
By combining Equations (3) and (4), it is possible to correlate the UCS with Young’s modulus as
where is a material-dependent coefficient. For example, the literature shows that, in general, for rocks, [42].
Finally, by the direct combination of Equations (5) and (6), the specific energy can be correlated to the Young’s modulus of the material being drilled (rocks) or excavated (soils). Mathematically, in a similar fashion as presented by Hughes [41], one can write
One shall notice, on the other hand, that the Young’s modulus calculated by means of Equation (7) incorporates some in situ characteristics, namely, depth dependence, degree of saturation, stress memory and so on. Therefore, direct comparison of the values obtained from Equation (7) to values obtained in general compression tests is not possible.
As indicated, the stress dependency of Young’s modulus can be formulated based on a hyperbolic model of the type presented in Equation (2). The confining pressure can be taken as equal to the horizontal stress, , and, based on the linear relation assumed between vertical and horizontal stresses, at rest, horizontal stresses may be estimated as
where is the coefficient of earth pressure at rest.
Assuming that simple compression tests have a null confining pressure, the Young’s modulus obtained for these tests, , can be compared to the ones obtained by means of Equation (7) by using Equation (2) to account for confinement:
By adopting a linearly increasing stress profile, , and combining Equations (7) and (9), the specific energy can be directly correlated to the Young’s modulus of the soil excavated as
where is the bulk specific weight of the soil stratum and represents the coefficient of earth pressure at rest based on Jaky’s formula [43]. Using Jaky’s formula is not a major drawback whenever the soil analyzed is considered to be normally consolidated.
For a general n-layered profile, where each layer has a 1 m depth, Equation (9) can be rewritten by noticing that the vertical stress can be calculated as and
where [] indicates the value of property [] at depth i.
Finally, Equation (10) can be modified to calculate the Young’s modulus at depth n by means of the specific energy at depth n as
6. Results and Discussions
In the current section, the results and discussions shall be presented. In particular, it will be shown how to estimate the Young’s moduli of the drilled materials and compare those to the literature values. It is important to highlight that some parameters will be estimated either from the soil surveys carried out at the specific site or from the literature results. Future works may consider Bayesian approaches, such as the ones discussed in [44], to better understand how each parameter’s estimation uncertainty affects the final Young’s moduli estimation.
Young’s Moduli Estimation
In order to use Equation (12), we need to estimate the parameters , , c, , and m for each of the soils considered.
- Estimating :
Based on Equation (6), Table 2 and Table 3, for the silty clay, = 7 and K = 0.2 MPa, and thus = 176.14. On the other hand, for the clayey silt, = 5 and K = 0.25 MPa; therefore, = 157.27. Finally, for the silt, = 5 and K = 0.35 MPa, which leads to = 220.18.
- Estimating m:
The literature reveals that m ranges from 0.5 to 1 [45]. For clays, in general, m is close to 1. Thus, for the silty clay, m is taken as 0.9. On the other hand, as coarser grains are present in the soil, m is closer to 0.5. Based on the authors knowledge on the local soil, in the cases considered, for the clayey silt, m = 0.8, and for the silt, m = 0.7.
- Estimating :
The bulk specific weights of the soils studied are vastly reported in the literature. To the best of the author’s knowledge, a mean value of 15 kN/m is consistent and shall be considered for all the soils.
- Estimating c and :
As in the case of bulk specific weight, strength parameters c and are readily available for the soils considered. Again, based on the authors knowledge on the local soil, for the silty clay, c = 15 kPa and = 20 degrees. For the clayey silt c = 9 kPa and = 25 degrees, and for the silt c = 7 kPa and = 33 degrees.
- Estimating :
The energetic balance while drilling is related to the efficiency parameter . According to Teale [26], it is axiomatic that a specific theoretically feasible minimum amount of energy will be needed to drill/crush a particular volume of rock. The type of material being drilled determines how much energy is required. According to that author, actual mechanical processes may or may not come close to this theoretical minimum. The difference between actual and theoretical energetic requirements can be explained by factors such as the work expended breaking the excavated material into smaller fragments than necessary, friction between tools and material (which may be equivalent on a microscopic scale), or mechanical losses outside the rock/soil system.
He also emphasizes that reducing the debris to “smaller particles than necessary” could significantly increase the amount of energy required to excavate a given volume. In addition to unnecessarily breaking more particles, reducing the particle size results in a significant rise in the specific energy [26]. Because of this, it is assumed that drilling soils is much less efficient than drilling rocks, which suggests that the measured specific energies are much higher than the bare minimum needed for drilling into soil [1].
This specific real-world project has been also considered by Ozelim et al. [10], where the values of were calculated. Those authors fitted a line to the relation between and , where this last parameter was estimated from NSPT data by using Equation (4). Thus, based on the linear regressions indicated, for the silty clay, clayey silt and silt, the values of are 48.06, 41.04 and 33.86, respectively [10]. Overall, different soils have different values of . Greater values of this parameter indicate less energy-efficient drilling because more energy is required to complete the drilling (assuming there is an optimal value). Obviously, drilling is generally more efficient in soils with reduced plasticity.
With all the parameters obtained, one may proceed to use Equation (12) to estimate the Young’s moduli of the soils. Table 4 presents the results. Table 1 can be used to calculate the 95% confidence intervals (BCa bootstrap with 9999 re-samplings) for the Young’s moduli obtained for silty clay, clayey silt and silt, which were, in MPa, , and , respectively. As indicated before, the confidence intervals were calculated by using the nonparametric methodology of bootstrap [34], specifically the BCa variant. This is of interest since the number of samples is not big (only 10 for silts), and the distribution of the values is unknown.

Table 4.
Estimated Young’s moduli using new formula. Color code: silty clay (light gray); clayey silt (medium gray); silt (dark gray).
The confidence intervals obtained are consistent with Table 4 and correspond to the following materials: stiff to very stiff clays with low-medium plasticity, medium silts with slight plasticity, and stiff to very stiff silts with low plasticity, respectively. These were the types of materials observed during the site surveys; therefore, the results obtained are consistent with literature reports as well as with field surveys.
It is important to note that the method provided is only a first approximation of the process of developing physically sound models to predict soil deformability characteristics from drilling data. The linearity assumptions of Equations (5) and (7) between energy data and strength and deformability parameters need to be further investigated.
7. Conclusions
Engineers should create models that can utilize common executive approaches to estimate the parameters required to describe soil behavior, especially by taking into account the large amount of data available in the literature.
The relationship between the continuous flight auger piles’ execution energy and the soil mass’s Young’s modulus is examined in the current paper. The data were examined, and the Young’s moduli of the excavated soil strata were able to be calculated using a new physical model. The model created, in short, is based on estimating the precise energy used during the drilling process.
The 95% confidence intervals for the Young’s moduli obtained for silty clay, clayey silt and silt were, in MPa, , and , respectively. These intervals are consistent with literature reports for the following materials: stiff to very stiff clays with low-medium plasticity, medium silts with slight plasticity, and stiff to very stiff silts with low plasticity, respectively. These were the types of materials observed during the site surveys; therefore, the results obtained are consistent with literature reports as well as with field surveys.
The methodology hereby suggested allows for immediate update of designs. Additionally, standard engineering parameter estimation procedures involve collecting a few samples and then spatially interpolating the properties of interest. This new approach, which allows the obtention of the Young’s modulus during the execution of the pile itself, makes such interpolation unnecessary, as the property of interest is estimated exactly at the pile location. The predictions were reasonably accurate, although the model that is being suggested here may use more data to enhance its capabilities.
Author Contributions
Conceptualization, D.J.F.d.C. and L.C.d.S.M.O.; methodology, L.C.d.S.M.O.; software, L.C.d.S.M.O.; validation, L.C.d.S.M.O. and D.J.F.d.C.; formal analysis, D.J.F.d.C., L.C.d.S.M.O. and A.L.B.C.; investigation, D.J.F.d.C. and L.C.d.S.M.O.; writing—original draft preparation, L.C.d.S.M.O.; writing—review and editing, A.L.B.C. and J.C.d.C.; supervision, J.C.d.C. and A.L.B.C.; funding acquisition, A.L.B.C. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed in part by the Coordination for the Improvement of Higher Education Personnel (CAPES)—Finance Code 001. The authors also acknowledge the support of the National Council for Scientific and Technological Development (CNPq Grant 305484/2020-6) and of Research Support Foundation of the Federal District (FAP-DF 00193.00000920/2021-12). The APC was partially waived by the Editorial Office of Axioms, and the remaining value was fully funded by University of Brasilia (EDITAL DPI/DPG/BCE N.01/2023).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used are available upon request to the corresponding author.
Acknowledgments
The authors acknowledge the support provided by the University of Brasilia (UnB).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ozelim, L.C.S.M.; de Campos, D.J.F.; de Carvalho, J.C.; Cavalcante, A.L.B. Indirect In-situ Tests During the Execution of Deep Foundations: Relating the Excavation Energies to the Young’s Moduli of the Surrounding Soils. In Sustainability Issues for the Deep Foundations. GeoMEast 2018. Sustainable Civil Infrastructures; El-Naggar, H., Abdel-Rahman, K., Fellenius, B., Shehata, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 191–205. [Google Scholar]
- Assunção, M.; Calheiros, R.N.; Bianchi, S.; Netto, M.; Buyya, R. Big Data computing and clouds: Trends and future directions. J. Parallel Distrib. Comput. 2014, 79, 3–15. [Google Scholar] [CrossRef]
- Wu, J.; Chen, J.; Chen, G.; Wu, Z.; Zhong, Y.; Chen, B.; Ke, W.; Huang, J. Development of Data Integration and Sharing for Geotechnical Engineering Information Modeling Based on IFC. Adv. Civ. Eng. 2021, 2021, 8884864. [Google Scholar] [CrossRef]
- Lee, F.; Tan, T.; Karunaratne, G.P.; Lee, S. Geotechnical Data Management System. J. Comput. Civ. Eng. 1990, 4, 239–254. [Google Scholar] [CrossRef]
- Phoon, K.K.; Cao, Z.J.; Ji, J.; Leung, Y.F.; Najjar, S.; Shuku, T.; Tang, C.; Yin, Z.Y.; Ikumasa, Y.; Ching, J. Geotechnical uncertainty, modeling, and decision making. Soils Found. 2022, 62, 101189. [Google Scholar] [CrossRef]
- Ferrari de Campos, D.J. Big Data and Artificial Intelligence Applied to Foundations. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of Brasília, Brasilia, Brazil, 2022. (In Portuguese). [Google Scholar]
- Stone, R.C.; Farhangi, V.; Fatahi, B.; Karakouzian, M. A novel short pile foundation system bonded to highly cemented layers for settlement control. Can. Geotech. J. 2023. [Google Scholar] [CrossRef]
- Hachich, W.; Falconi, F.F.; Saes, J.L.; Frota, R.G.; Carvalho, C.S.; Niyama, S. Fundações: Teoria e Prática, 2nd ed.; PINI Ltda.: São Paulo, Brazil, 1998. [Google Scholar]
- Silva, C.M.; Camapum de Carvalho, J.; Cavalcante, A.L.B. Energy and Reliability Applied to Continuous Flight Auger Pilings—The SCCAP Methodology. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–7 September 2013; pp. 2807–2810. [Google Scholar]
- Ozelim, L.C.d.S.M.; Ferrari de Campos, D.J.; Cavalcante, A.L.B.; Camapum de Carvalho, J.; Silva, C.M. Estimating Shear Strength Properties of the Surrounding Soils Based on the Execution Energies of Piles. Geotechnics 2022, 2, 457–466. [Google Scholar] [CrossRef]
- Geodigitus. Manual de Instruções SACI2 e SoftSACI2—Operação SACI; Franmar Eletrônica do Brasil Ltda: Belo Horizonte, Brazil, 2010. [Google Scholar]
- Li, Z.; Itakura, K. An analytical drilling model of drag bits for evaluation of rock strength. Soils Found. 2012, 52, 216–227. [Google Scholar] [CrossRef]
- Behboud, M.M.; Ramezanzadeh, A.; Tokhmechi, B. Studying empirical correlation between drilling specific energy and geo-mechanical parameters in an oil field in SW Iran. J. Min. Environ. 2017, 8, 393–401. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Farhangi, V. Determination of piers shear capacity using numerical analysis and machine learning for generalization to masonry large scale walls. Structures 2023, 49, 443–466. [Google Scholar] [CrossRef]
- Warren, T.M. Drilling Model for Soft-Formation Bits. Soc. Pet. Eng. 1981, 33, 963–970. [Google Scholar] [CrossRef]
- Warren, T.M. Penetration Rate Performance of Roller Cone Bits. Soc. Pet. Eng. 1987, 2, 9–18. [Google Scholar] [CrossRef]
- Kahraman, S.; Bilgin, N.; Feridunoglu, C. Dominant rock properties affecting the penetration rate of percussive drills. Int. J. Rock Mech. Min. Sci. 2003, 40, 711–723. [Google Scholar] [CrossRef]
- Ozelim, L.C.S.M.; Ferrari de Campos, D.J.; Camapum de Carvalho, J.; Cavalcante, A.L.B. On the Relation between the Excavation Energies of Continuous Flight Auger Piles and the Unconfined Compressive Strength of the Surrounding Soils. In Geotechnical Engineering in the XXI Century: Lessons Learned and Future Challenges; López-Acosta, N.P., Martínez-Hernández, E., Espinosa-Santiago, A.L., Mendoza-Promotor, J.A., López, A.O., Eds.; IOS Press: Amsterdan, The Netherlands, 2019; pp. 1117–1124. [Google Scholar]
- Tsai, C.W.; Lai, C.F.; Chao, H.C.; Vasilakos, A.V. Big data analytics: A survey. J. Big Data 2015, 2, 21. [Google Scholar] [CrossRef]
- Fisher, D.; DeLine, R.; Czerwinski, M.; Drucker, S. Interactions with Big Data Analytics. Interactions 2012, 19, 50–59. [Google Scholar] [CrossRef]
- Laney, D. 3D Data Management: Controlling Data Volume, Velocity, and Variety; Technical Report; META Group: Stamford, CT, USA, 2001. [Google Scholar]
- Baraniuk, R.G. More Is Less: Signal Processing and the Data Deluge. Science 2011, 331, 717–719. [Google Scholar] [CrossRef]
- Famili, A.; Shen, W.M.; Weber, R.; Simoudis, E. Data preprocessing and intelligent data analysis. Intell. Data Anal. 1997, 1, 3–23. [Google Scholar] [CrossRef]
- Jun, S.W.; Fleming, K.E.; Adler, M.; Emer, J. ZIP-IO: Architecture for application-specific compression of Big Data. In Proceedings of the 2012 International Conference on Field-Programmable Technology, Seoul, Republic of Korea, 10–12 December 2012; pp. 343–351. [Google Scholar] [CrossRef]
- Ma, C.; Zhang, H.H.; Wang, X. Machine learning for Big Data analytics in plants. Trends Plant Sci. 2014, 19, 798–808. [Google Scholar] [CrossRef]
- Teale, R. The concept of specific energy in rock drilling. Int. J. Rock Mech. Min. Sci. 1965, 2, 57–71. [Google Scholar] [CrossRef]
- Perko, H.A. Energy Method for Predicting the Installation Torque of Helical Foundations and Anchors. In New Technological and Design Developments in Deep Foundations; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 342–352. [Google Scholar]
- Tsuha, C.d.H.C.; Aoki, N. Relationship between installation torque and uplift capacity of deep helical piles in sand. Can. Geotech. J. 2010, 47, 635–647. [Google Scholar] [CrossRef]
- Reddish, D.; Yasar, E. A new portable rock strength index test based on specific energy of drilling. Int. J. Rock Mech. Min. Sci. 1996, 33, 543–548. [Google Scholar] [CrossRef]
- Moronkeji, D.; Villegas, R.; Shouse, R.; Prasad, U. Rock strength prediction during coring operation. In Proceedings of the International Symposium of the Society of Core Analysts: SCA2017-048, Vienna, Austria, 28–31 August 2017; pp. 9p. [Google Scholar]
- Obrzud, R.; Truty, A. The Hardening Soil Model—A Practical Guidebook Z Soil; PC 100701 Report; Zace Services Ltd., Software Engineering: Préverenges, Switzerland, 2012. [Google Scholar]
- Kezdi, A. Handbook of Soil Mechanics; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Prat, M.; Bisch, E.; Millard, A.; Mestat, P.; Cabot, G. La Modelisation des Ouvrages; Hermes: Paris, France, 1995. [Google Scholar]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Champman & Hall: London, UK, 1993. [Google Scholar]
- Moore, D. The Practice of Business Statistics: Using Data for Decisions; W.H. Freeman and Company: New York, NY, USA, 2009. [Google Scholar]
- Ozelim, L.C.S.M.; Cavalcante, A.L.B. Representative Elementary Volume Determination for Permeability and Porosity Using Numerical Three-Dimensional Experiments in Microtomography Data. Int. J. Geomech. 2018, 18, 04017154. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Schanz, T.; Vermeer, P.A.; Bonnier, P.G. The Hardening soil model: Formulation and verification. In Beyond 2000 in Computational Geotechnics—10 Years of PLAXIS; Balkema: Rotterdam, The Netherlands, 1999. [Google Scholar]
- Teixeira, A.H.; Godoy, N.S. Análise, projeto e execução de fundações rasas. In Fundações: Teoria e Prática; PINI: Sao Paulo, Brazil, 1996; Chapter 7; pp. 227–264. [Google Scholar]
- NAVFAC-DM7; Design Manual: Soil Mechanics, Foundations and Earth Structures. U.S. Department of the Navy: Washington, DC, USA, 1971.
- Hughes, H.M. Some Aspects of Rock Machining. Int. J. Rock Mech. Min. Sci. 1972, 9, 205–211. [Google Scholar] [CrossRef]
- Farmer, J.W. Engineering Properties of Rocks; E. & F. N. Spon: London, UK, 1968. [Google Scholar]
- Jaky, J. The coefficient of earth pressure at-rest. J. Soc. Hung. Archit. Eng. 1993, 30, 647–666. [Google Scholar]
- Corani, G.; Benavoli, A.; Demšar, J.; Mangili, F.; Zaffalon, M. Statistical comparison of classifiers through Bayesian hierarchical modelling. Mach. Learn. 2017, 106, 1817–1837. [Google Scholar] [CrossRef]
- Surarak, C.; Likitlersuang, S.; Wanatowski, D.; Balasubramaniam, A.; Oh, E.; Guan, H. Stiffness and strength parameters for hardening soil model of soft and stiff Bangkok clays. Soils Found. 2012, 52, 682–697. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).